Atomistic and experimental study on thermal conductivity of bulk and porous cerium dioxide

Abstract

Cerium dioxide (CeO₂) is a surrogate material for traditional nuclear fuels and an essential material for a wide variety of industrial applications both in its bulk and nanometer length scale. Despite this fact, the underlying physics of thermal conductivity (k_L), a crucial design parameter in industrial applications, has not received enough attention. In this article, a systematic investigation of the phonon transport properties was performed using ab initio calculations unified with the Boltzmann transport equation. An extensive examination of the phonon mode contribution, available three-phonon scattering phase space, mode Grüneisen parameter and mean free path (MFP) distributions were also conducted. To further augment theoretical predictions of the k_L, measurements were made on specimens prepared by spark plasma sintering using the laser flash technique. Since the sample porosity plays a vital role in the value of measured k_L, the effect of porosity on k_L by molecular dynamics (MD) simulations were investigated. Finally, we also determined the nanostructuring effect on the thermal properties of CeO₂. Since CeO₂ films find application in various industries, the dependence of thickness on the in-plane and cross-plane k_L for an infinite CeO₂ thin film was also reported.

Introduction

The lattice thermal conductivity (k_L) depends on the mean free path (MFP), i.e. the distance travelled by the phonons before the occurrence of any scattering events. A detailed quantitative understanding of the mode dependent phonon properties and the bulk MFPs in each material is imperative to exercise control over its thermal management. Furthermore, the thermal transport properties of the bulk and the nanostructured (wires, films, porous, and nanocrystalline material) counterparts of a given material differ significantly due to increased boundary scattering in the latter. Understanding this phenomenon becomes necessary when studying thermal conductivity of materials such as Cerium dioxide (CeO₂), which finds applications in both bulk and nanostructured form. Bulk CeO₂ is frequently used as a surrogate material in the nuclear industry, as an oxygen storage material in automobile exhaust systems¹, and as an electrolyte in solid oxide fuel cells². Also, nanostructured CeO₂ is used for diverse applications in various industries. For instance, in electronics, the thin films of CeO₂ are among the most prospective buffer layers for high-temperature semiconductor and ferroelectric films deposited on silicon^3,4. In the nuclear industry, CeO₂ thin film deposits have been proposed for controlling the oxidation of nickel alloys⁵, and microspheres of CeO₂ have been synthesized for space nuclear applications⁶. Unfortunately, to date, accurate atomic-scale investigation on the details of mode-wise thermal transport properties and MFP of CeO₂ have not been reported.

Although several studies have reported the k_L of CeO₂, the value remains ambiguous. Experimentally, k_L of CeO₂ has been determined using laser flash technique. Nelson et al.⁷ and Khafizov et al.⁸ measured the k_L of 95% dense CeO₂ pellet and reported respective values of 6.6 W/mK and 17.5 W/mK (correcting for porosity using a modified Loeb expression), at room temperature. The ab initio theoretical calculations for the k_L of CeO₂ performed by Xiao et al.⁹ and the molecular dynamics (MD) study by Khafizov et al.⁸ predict the k_L as 12 W/mK and 19 W/mK respectively. However, Xiao et al.⁹ used the analytical Slack model¹⁰, which heavily relied on the fitting parameters that may obscure the underlying physics of heat transfer. Whereas, the MD simulations performed by Khafizov et al.⁸ could have over-predicted the k_L at lower temperatures as MD simulations do not account for intrinsic scattering at these temperatures. Right through the literature, the value of k_L of CeO₂ at room temperature has varied between (6.6 W/mK and 19 W/mK) and thus exists a disparity. To resolve this aberration, we perform an ab initio calculation using density functional theory (DFT)¹¹, density functional perturbation theory (DFPT)¹² and lattice dynamics in concord with the Boltzmann transport equation (BTE) using ShengBTE¹³. This theoretical approach does not require any assumption on the phonon lifetime to predict the k_L. BTE has been successfully utilized in the investigations of phonon transport properties for many materials^{14,15,16,17,18,19} with high accuracy. In addition to the ab initio calculations, MD simulations were carried out to understand the effect of porosity on the k_L of CeO₂. Moreover, using the laser flash experiment technique, the thermal conductivity of porous CeO₂ pellets prepared by spark plasma sintering (SPS) method has also been reported be a restrictive factor for the heat transfer.

In nanostructured materials, where the phonon MFP is comparable to the grain size, grain boundaries can modulated thermoreflectance technique and an analytical solution of BTE to understand the thermal transport properties of ceria thin films grown by unbalanced magnetron sputtering. The significantly reduced conductivity of these thin films compared to the bulk CeO₂ was attributed to the combined effect of the point defects, grain boundaries, and dislocations. However, their study was not able to shed light on the influence of nanostructuring. For nanoscale applications, the characteristic lengths of the nanostructures can be a limiting factor in the thermal transport. To have a comprehensive understanding of this limiting factor, it is critical to know MFP of CeO₂. It is also important to know what specific length of the nanostructure is going to be significant for CeO₂. Therefore, in this work, the ab initio prediction of the MFP, the relaxation time of the phonons, their mode-wise contribution to thermal conductivity, and the effect of nanostructuring on the reduction of thermal conductivity were investigated. These findings will aid the selection of the size and thickness of the nanostructures in tuning the thermal properties. Furthermore, the effect of nanostructuring by studying the cross plane and in-plane thermal conductivity of CeO₂ thin films and the impact of the thickness of the thin films and temperature on the thermal conductivity was also performed. These predicted results not only enable the accurate explanation of the experimental results but also guide further designs and applications.

Results and Discussion

Crystal Structure and elastic constants

CeO₂ has a fluorite structure with three independent atoms per unit cell and belongs to the space group of Fm-3m (225), as shown in Fig. 1. The equilibrium lattice constants were obtained by minimizing the total energy with respect to the lattice parameter and atomic positions. The detailed description of the optimized parameter and the pseudopotential used for the simulation were provided in section 4.1. Table 1. presents the calculated lattice constant (a), bulk modulus (B) and stiffness constants (C_ij) of CeO₂ in comparison with the values from the previous DFT calculations^20,21,22,23 and the experiment²⁴. The PBEsol functional predicted the lattice constant within an error less than 0.01% compared with the experimental data reported by Nakajima et al.²⁴ As expected, the new PBEsol functional was able to quantify the ground state structural properties more accurately than previous DFT calculations performed using linear density approximation (LDA)²⁰, GGA²¹, Hartwigsen- Goedecker-Hutter (HGH)²² and PAW²³ pseudopotentials.

Figure 1

Crystal structure of CeO₂ in the conventional cubic unit cell (blue and red represent Ce and O atoms respectively.

Table 1 Structural and mechanical properties of CeO₂ compared with previous DFT calculations and the experiment.

The elastic constants are important parameters that provide information on the properties of a material such as stiffness, strength, mechanical stability, hardness, and ductility or brittleness²⁵. We evaluated the single crystal stiffness constants of CeO₂ by using a stress-strain method^26,27 with the help of our in-house interface qe-nipy-advanced²⁸. The stiffness constants for a mechanically stable cubic structure should satisfy the following Born’s mechanical stability criteria²⁹ ${C}_{11}-{C}_{12} > 0,\,{C}_{11}+2{C}_{12} > 0,\,{C}_{44} > 0$. The listed stiffness constants have satisfied these criteria indicating that the system is mechanically stable.

From the calculated stiffness constants, the polycrystalline bulk modulus, shear modulus, Young’s modulus and Poisson’s ratio (listed in Table 1) were determined using the Voigt-Reuss-Hill approach^30,31,32. From Table 1. the bulk modulus values (192 GPa) at zero temperature obtained from PBEsol method is only about 6% lower than the experimental value of 204 GPa²⁴ at room temperature. Since the calculated structural and mechanical properties are in excellent agreement with the experimental data, the same PBEsol functional pseudopotentials were used for the study of phonon properties and the k_L of CeO₂.

Lattice dynamics

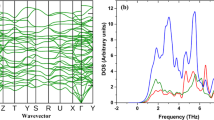
Lattice dynamics is critical for understanding the thermal properties of crystalline solids at finite temperatures. For instance, the phonon densities of states are required to evaluate thermodynamic properties such as thermal expansion coefficient (α), C_V, entropy (S) and k_L. Moreover, the fundamental reasons for unique thermal characteristics of a material can be ascertained by analyzing the phonon scattering mechanism through phonon group velocities, and phonon mean free path, relaxation time and phonon scattering phase space³³. At present, two approaches the linear-response approach³⁴ and the direct approach^35,36 are widely used to evaluate the phonon dispersion. In Fig. 2a the calculated phonon dispersion spectra using these two approaches the linear-response approach (QE) and the direct approach (Phonopy) are presented along the Γ-X-Γ-L high symmetry points in the Brillouin zone and compared with the known experimental data.

Figure 2

(a) Phonon spectra of CeO₂ predicted by the linear response approach using q-point of 6 × 6 × 6 (red line) and the finite displacement (FD) methods (dotted green line) compared with the experiment done by Clausen K. et al.³⁷ (blue dots). (b) Partial (dotted lines) and total phonon density of states (solid black line).

The predicted phonon spectra using both the linear-response approach and the finite displacement (FD) methods are in good agreement with the experimental data generated by Clausen K et al.³⁷, for the entire Brillouin zone using inelastic neutron scattering at 293 K. CeO₂ has three (n) atoms per primitive unit cell and thus there are in three dimensions (d = 3) three acoustic mode phonons and d (n − 1) = 6 optical phonons. The group theory analysis gives the decomposition of the zone centre modes as doubly degenerate transverse optical (TO) mode, the triply degenerate Raman active mode and the non-degenerate longitudinal optical (LO) mode. The three-zone center frequencies are 8.42 (8.15), 13.03 (13.94), and 15.93(17.84) THz respectively (shown in brackets are the experimental value from the ref.³⁸). The partial lifting of degeneracy between the LO and TO phonons at the Brillouin zone centre is due to the polarization effect, which indicates that the CeO₂ is a polar material as shown in Fig. 2a The Born effective charge for an insulator is a measure of the change in electronic polarization due to ionic displacements. These charges are essential for elucidating the physical understanding of piezoelectric and ferroelectric properties since they describe the coupling between lattice displacements and the electric field. The Born effective charges, ${Z}_{Ce}^{\ast }$ = 5.793 (5.746) ${Z}_{O}^{\ast }$ = 2.896 (2.873), agrees well with the values reported (shown in brackets) by Xiao et al.⁹ The calculated dielectric constant value 7.87 (6.0) is in reasonable agreement the work done by Santha et al.³⁸.

The partial and total phonon density of states is shown in Fig. 2b. The partial density of the state shows that the frequency vibrations lower than 6.0 THz are dominated by the Ce ions and the higher frequency vibrations are mainly contributed by the dynamics of O ions. The phonon dispersion of CeO₂ along Γ-X-Γ-L, high symmetry points in the Brillouin zone does not display frequency gap between optical and acoustic phonons. The absence of frequency gap in case of CeO₂ indicates that three-phonon scattering is dominant resulting in relatively lower phonon relaxation time thereby leading to lower k_L. The accurate prediction of phonon dispersion curve of CeO₂ using both the linear-response approach and direct approach enables reasonable precision in the projection of phonon-assisted properties.

Three-phonon scattering phase space and Grüneisen parameter

Three-phonon scattering phase space (P₃) quantitatively describes the number of scattering channels available for a phonon being scattered³⁹. The available P₃ gives an insight into the k_L of a material i.e. larger available P₃, will have more channels for scattering and subsequently lower k_L. The P₃ is solely determined from a material’s phonon spectra and is defined as³³,

$${P}_{3}(q,j)=\frac{1}{3{\rm{\Omega }}}(2{P}_{3}^{(+)}(qj)+{P}_{3}^{(-)}(qj))$$

(1)

where q is the momenta of phonons, j is the phonon branches, ${\rm{\Omega }}={n}_{j}^{3}{V}_{BZ}^{2}$ is the normalized factor equal to unrestricted phase space for each type of process. ${P}_{3}^{+}$ and ${P}_{3}^{-}$ are the absorption and emission processes respectively, defined by,

$${P}_{3}^{\pm }(q,j)=\frac{1}{{N}_{q}}\sum _{{q}_{1},{q}_{2},{j}_{1},{j}_{2}}\,\delta ({\omega }_{qj}\pm {\omega }_{{q}_{1}{j}_{1}}-{\omega }_{{q}_{2}{J}_{2}}){\delta }_{q\pm {q}_{1},q+G}$$

(2)

where N_q is the total number of q points in the first Brillouin zone. Figure 3a shows the P₃ of CeO₂ for the acoustic and optical modes. To gain a quantitative understanding of available P₃ on k_L, the total volume in phase space for three phonon processes (P₃_total) for CeO₂ is compared with our previously reported results of a relatively higher k_L material such as silicon carbide (420 W/mK at 300 K)¹⁷. The P₃_total (in units of 1/rad/ps) predicted along the same Brillioun path is higher for CeO₂ (4.18 × 10⁻³) than SiC (1.66 × 10⁻³); clearly indicating that CeO₂ has a larger three phonons scattering phase space, more channels for scattering and hence lower thermal conductivity than SiC. Lindsay and Broido³³ have already established the phase space available for the three-phonon scattering for semiconductors. In this work, the possible P₃ for a lanthanide oxide was illustrated, and these findings would aid in qualitatively determining the thermal conductivities of new materials with known phonon dispersion.

Figure 3

(a) Three-phonon scattering phase space. (b) Mode Grüneisen parameter (γ_qj).

Grüneisen parameter (y) illustrates the anharmonicity in a crystal and is defined as the shift in phonon frequency with change in volume. It is an established fact that anharmonicity in an ordered crystal structure determines the strength of each scattering channel and the efficiency of each phonon mode in heat conduction is inversely proportional to square of Grüneisen parameter. To quantitatively examine the anharmonicity of CeO₂, we plot the mode Grüneisen parameters at zero temperature (as shown in Fig. 3b) derived from the third-order anharmonic force constants (shown in Eq. (3)) as implemented in the ShengBTE¹³ and is defined as:

$${\gamma }_{p}(q){|}_{anh}=-\,\frac{1}{6{\omega }_{p}{(q)}^{2}}\sum _{nl^{\prime} }\sum _{n^{\prime\prime} l^{\prime\prime} }\sum _{\alpha \beta \gamma }{\Phi }_{{n}^{o},n^{\prime} l^{\prime} ,n^{\prime\prime} {\rm{l}}^{\prime\prime} }^{\alpha \beta \gamma }\times (\frac{\,{e}_{{\alpha }_{\eta }}^{p}({q}^{\ast }){e}_{\beta \eta ^{\prime} }^{p}(q)}{\sqrt{{M}_{\eta }{M^{\prime} }_{\eta }}}){e}^{-iq{R^{\prime} }_{i}{r}_{\eta ^{\prime\prime} l^{\prime\prime} \gamma ^{\prime} }}$$

(3)

where ${{\rm{\Phi }}}_{{n}^{o},n^{\prime} l^{\prime} ,nl}^{\alpha \beta \gamma }$ are the third-order force constants, e is the phonon eigenvectors, n denotes the n^th primitive cell in the supercell, α is the Cartesian components of x, y, or, z, M_n refers to the mass of the atomic type n in the primitive cell and r_ηl is the position vector of the η^th atom in the l^th primitive cell. According to Fig. 3b, the sum of all mode Grüneisen parameters are positive indicating volume expansion. At zero temperature, the average Grüneisen coefficient over the whole frequency range was 2.07. The mode Grüneisen parameter near 7 THz (near the TO mode) is higher, indicating that the scattering of acoustic phonons by the optical mode caused hindrance to heat conduction. Changes in mode Grüneisen parameter with different q-points in the second order force constant and the neighboring atoms in the third order force constant is given as Supplementary Information (S.I) in S.I.1 (Fig. S1).

Theoretical prediction of thermal conductivity and mode contribution

The full iterative solution of BTE for CeO₂ is shown in Fig. 4a. As expected, the k_L of CeO₂ decreases with increasing temperature because the phonon-phonon scattering dominates the k_L at high temperatures. The k_L at 300 K is 16.71 W/mK. Our predictions were made assuming a defect-free crystal and thus could potentially represent the upper limit of k_L. The previous experimental value of thermal conductivity for CeO₂ appears to be scattered. For example, for ~95% dense pellets at 373 K, Jakub et al.⁴⁰ and Nelson et al.⁷ reported a value of 9.58 W/mK and 6.2 W/mK, respectively. These scattered values of k_L reported in the literature are generally justified by pointing to microstructures. This may not be true under all circumstances. In these situations, an accurate theoretical prediction without the usage of fitting parameters can significantly help in arriving at a meaningful physical explanation. The highest reported experimental value for CeO₂ for a ~95% dense pellet at room temperature is by Jakub et al.⁴⁰ (14.1 W/mK) and our theoretical predictions at 300 K is 16.71 W/mK (red dots) for 100% dense single crystal, are in excellent agreement. Furthermore, the difference in k_L values obtained through our theoretical prediction and the previously reported simulated value of 12 W/mK at 300 K by Xiao et al.⁹ (using fitting parameters) clearly indicate the apparent disadvantages of using fitting parameters. We also noted that Xiao et al. obtained the second order force constant required for their calculation using the finite difference (FD) method. Our k_L predictions using the second order force constant from the FD method (green dot) has also underpredicted the value of k_L by 19% in comparison with the k_L predicted using the second order force constant obtained from DFPT method. Moreover, accurate theoretical predictions enable us to arrive at a rational expression for the porosity correction, as there is a multitude of expressions to choose from, depending on the material and temperature range.

Figure 4

(a) The temperature dependence of the phonon k_L in CeO₂ using BTE and experiment compared to previous theoretical⁹ and experimental⁷ values of k_L. (b) The mode-wise k_L of CeO₂ in comparison with the simulated results for UO₂ by Pang et al.⁴².

Furthermore, we probe the relative contribution of the acoustic and optical phonon modes to the total k_L of CeO₂. Typically, for ceramic materials, there is a tendency to neglect the optical contribution owing to their consistently low group velocities and shorter lifetimes⁴¹. However, the Uranium dioxide (UO₂) with a reported critical optical mode is an exception⁴². In the wake of this, it would be interesting to know the mode-wise thermal conductivity of the popular nuclear fuel surrogate CeO₂. To best of author’s knowledge, the mode-dependent k_L of CeO₂ has not received enough attention. Figure 4b shows the simulated contribution of mode-wise k_L of CeO₂ compared with UO₂ at room temperature previously calculated by Pang et al.⁴². In CeO₂ the optical phonons contribute to about 27% of the total k_L compared to the acoustic modes. The optical contributions at 300 K can be precisely broken down to 13.1%, 13.7%, and ~1% from the doubly degenerate transverse optical mode, the triply degenerate Raman active mode and the non-degenerate longitudinal optical mode, respectively. The theory predicts that like UO₂, its surrogate CeO₂ will also have strong optical mode contribution to k_L. However, in the case of UO₂, Pang et al.⁴² have experimentally proved that the contribution of the TO branch to thermal conductivity is, in fact, higher than the theoretical prediction. Our theoretical predictions suggest an even more significant contribution of the TO branch towards thermal conductivity of CeO₂, and could, therefore, make an experimental validation worthwhile.

Effect of porosity on the thermal conductivity using MD simulations and experiments

So far in this manuscript, the primary focus was in understanding the underlying physics of thermal transport and determining the k_L of a defect-free single crystal CeO₂ using first principles approach. However, manufacturing a defect-free specimen of CeO₂ with 100% theoretical density (TD) is impracticable, and most importantly k_L of a sample with porosity and defects are expected to be lower than 100% dense CeO₂. Therefore, it is essential to determine the effect of porosity on k_L of CeO₂ quantitatively. Hence, the effect of porosity on the k_L of CeO₂ has been determined using both simulation (MD approach) and experiment. It has to be noted that evaluation of the effect of porosity using first principles is still in genesis, and for that reason, MD simulations were used. Moreover, the theoretical prediction of k_L using both BTE and MD approach complement each other well. The BTE calculates the quantum mechanical scattering rates directly by considering only the lowest order of phonon-phonon interactions and hence become less accurate at very high temperatures where higher order interactions become significant. In contrast, the MD simulations based on classical potential are less reliable at a lower temperature. However, at high temperatures, the phonon-phonon interactions of all orders are duly considered.

In this work, the k_L of CeO₂ by MD simulations were calculated on systems of 8 × 8 × 8 (6144 atoms), 10 × 10 × 10 (12000 atoms), 12 × 12 × 12 (20736 atoms) and 20 × 20 × 20 (96000 atoms), using the Embedded Atom Many-body (EAM) potentials developed by Cooper et al.⁴³. Table 2 shows that there is no noticeable difference in the k_L of CeO₂ at 300 K with different supercell sizes, suggesting that 8 × 8 × 8 system is sufficient enough to represent all the phonon modes available to reproduce the phonon-phonon scattering present in the bulk CeO₂⁴⁴. For investigating the porosity influence on the k_L of CeO_2, two cases with the cell sizes of 10 × 10 × 10 and 20 × 20 × 20 were considered. In each of the supercells, only one pore was introduced by manually removing 5% of atoms, in such a way that for every cerium atom two oxygen atoms are considered, to maintain the charge neutrality of the system. The supercell with vacancies are then made to relax keeping the cell volume same, and then MD calculations were carried out to evaluate the thermal conductivity of porous CeO₂ (as explained in section 4.1).

Table 2 The size dependence of k_L of bulk CeO₂ at a temperature of 300 K presented using EMD simulation and the Green-Kubo method.

Figure 5a compares the experimental data to the predicted k_L values of CeO₂ using MD for a pure crystalline CeO₂ (black dots) and porous CeO₂ (red dots) modelled on a 20 × 20 × 20 supercell. The k_L values predicted for pure crystalline CeO₂ are in reasonable agreement with the experimental data (orange square dots) provided by Khafizov et al.⁸. As expected, the k_L of the porous CeO₂ is lower than the pure crystalline CeO₂. The measurements made by Nelson et al.⁷ (navy blue dots) for a specimen of 95% TD was 6.22 W/mK at 100 °C, which is a reduction of almost 55% in the k_L value when compared to the pure crystalline CeO₂. Suzuki et al.⁴⁵ (dark green square dot) investigated the reason for this unusual degradation in the k_L value of a 5% porous CeO₂ and found that the purity of CeO₂ is an essential factor (in work done by Nelson et al. cerium constituted only 98% of the metallic content of the feedstock). Furthermore, our EMD simulations performed for a 5% porous CeO₂ (red dots) are in reasonable agreement with the work done by Suzuki et al.⁴⁵. Besides, we also noted that k_L values predicted for porous CeO₂ is significantly dependent on the size of supercell considered. Even though the porosity was modelled the same way in both the supercells, the k_L for the case of 10 × 10 × 10 is considerably lower than the case of 20 × 20 × 20. The Fig. 5b clearly shows that compared to the pure crystalline CeO₂ at 300 K the k_L predicted for a porous CeO₂ on a 10 × 10 × 10 supercell has reduced by 52%, whereas the same amount of porosity created on a 20 × 20 × 20 supercell decreased the k_L by 12%. The fact that the k_L is significantly lower for the 10x10x10 case and can be explained by the increased phonon scattering on the surface of the pores due to the decreased average distance between the pores, which directly can be compared to the mean free path of the phonons, as shown previously by Nichenko et al.⁴⁶

Figure 5

(a) Simulated and experimental k_L of porous CeO₂ as a function of temperature. (b) Influence of porosity on the k_L of CeO₂, by considering the same porosity on a cell size of 10 × 10 × 10 (blue line) and 20 × 20 × 20 (red line) unit cells.

To validate the theoretical predictions and further expand the quantitative understanding of the effect of porosity on thermal conductivity, the experiments were carried out on the specimens prepared by SPS technique. The pellets of CeO₂ with varying densities were made by controlling the sintering parameters such as the sintering temperature, pressure, hold time, and the sintering atmosphere. The more detailed description of the sintering conditions and its effect on density and the microstructure of CeO₂ are given in our previous work⁴⁷. Therefore for brevity, discussions would be limited to the samples on which the thermal conductivity measurements were made. In this work, the experiments were performed on CeO₂ pellets prepared at a sintering temperature of 1000 °C and 1100 °C by maintaining the pressure and hold time at 50 MPa and 10 min respectively. However, for the benefit of the readers, it is important to note that as the sintering temperature increased (>1500 °C), the CeO₂ reduced to Ce₂O₃. Moreover, in our previous work⁴⁷, it was observed that at a high sintering temperature (>1100 °C) and reductive atmosphere CeO₂ exhibited a range of stoichiometry and such non-stoichiometric oxide had been susceptible to chemical expansion⁴⁸ leading to the disintegration of the sintered pellets. It was for this reason that the experimental determination of thermal conductivity was limited to two samples sintered at 1000 °C and 1100 °C.

These sintered pellets were characterized using XRD for the determination of the phase, and the XRD patterns revealed that the pellet sintered at 1000 °C (green line) and 1100 °C (pink line) have a face-centred cubic crystal structure (as illustrated in S.I.2 (Fig. S2)). The density of CeO₂ was measured using the Archimedes principle, and the density of these pellets sintered at 1000 °C and 1100 °C were 70% and 75% respectively. As stated earlier in section 4.2, the thermal diffusivity can be determined using the Laser flash apparatus and Fig. 6 shows the variations of thermal diffusivity of these pellets as a function of temperature. Figures 5a and 6 respectively demonstrate that higher the density of the pellet, higher the thermal diffusivity and thermal conductivity. Moreover, we found that the density of the specimens played a vital role in the measured k_L values (as shown in Fig. 6) at lower temperatures (<1000 °C), however, at a higher temperature, the difference is less significant.

Figure 6

The thermal diffusivity of CeO₂ as a function of temperature for specimens sintered at 1000 °C and 1100 °C. The uncertainty in the data point from the laser flash apparatus is ±4.5%.

Nanoscale size effect, cross-plane, and in-plane thermal conductivity

CeO₂ nanostructures like wires, films, porous and nanocrystalline materials find applications in energy conversion, sensors, and microelectronics where tailoring of thermal transport property is essential. Moreover, a recent work evinces the capabilities of the ultra-thin CeO₂ for oxygen storage⁴⁹. It is established that the nanostructure surfaces significantly reduce the k_L compared to its bulk counterpart, due to the scattering of the energy carriers. The interplay between the characteristic length and the bulk MFP of the energy carriers is the fundamental physics that determines the dominance of the boundary scattering. The size of the crystalline domain, therefore, acts as limiting length for phonons MFP. Pertaining to this context, a detailed quantitative understanding of the MFP of CeO₂ is certainly advantageous.

In Fig. 7 the dependence of normalized cumulative k_L on phonon MFP at 300 K are presented. The normalized k_L increases with the increase in MFP, with significant contributions to the k_L of CeO₂ coming from the phonons with MFP between 1 nm to 100 nm. The contribution of phonons mode to k_L is uneven, and the phonons of MFP below 50 nm constitute 80% of k_L, indicating that curtailing the size below 50 nm can effectively reduce the k_L of CeO₂. Therefore, this grasp of the MFP of CeO₂ will aid the selection of sample size (thickness for thin film, diameter for nanowires and nanoparticles) for diverse technological applications that require a notable deviation from bulk thermal properties.

Figure 7

Thermal conductivity accumulation as a function of phonon MFP at room temperature.

To investigate the influence of nanostructuring on k_L of CeO₂, we demonstrate the thickness dependence in the cross-plane and in-plane k_L of CeO₂ along the (001) and (100) planes respectively at 300 K, as shown in Fig. 8a. For these predictions, we utilized almaBTE⁵⁰ a solver of the space-time dependent BTE for phonons in the structured material. The effective in-plane (‖) and cross-plane (⊥) thermal conductivity (k_eff) in relaxation time approximation for a film of thickness L are evaluated as:

$${k}_{eff}(L)=\sum _{q}\,{S}_{q}(L){C}_{q}\parallel {v}_{q}\parallel {\wedge }_{q}\,{\cos }^{2}{\vartheta }_{q}$$

(4)

where S is, the suppression function that considers the additional phonon scattering instigated by the film boundaries, C_q is the mode contribution to the volumetric heat capacity, v_q the group velocity, ∧_q is the mean free path and ϑ is the angle between the group velocity and transport axis. The sum over q must be interpreted as the combination of a sum of branches and an average over the Brillouin zone. As anticipated, due to the boundary scattering the in-plane and cross-plane k_L of thin films reduced with the reduction in the thickness. If the thickness of CeO₂ is slashed to 10 nm, its cross-plane (in-plane) k_L is only 4.96 (8.50) W/mK at 300 K. To verify the theoretical findings, we compared the results with experiment. It should be noted that theory predicts the k_L for the infinite two-dimensional CeO₂ and therefore, the presence of defects would further scatter the phonons and reduce the k_L of CeO₂ films. Khafizov et al.⁸ reported k_L of 7.2 W/mK, for a film of long columnar grain size structure with an average column radius of ~450 nm and the film thickness of 12 μm.

Figure 8

(a) In-plane and cross-plane thermal conductivity of CeO₂. (b) Cross-plane conductivity as a function of temperature.

Here, the thickness of 12 μm exceeds the condition that the characteristic size of CeO₂ must be 50 nm to have a significant reduction in k_L. However, our simulation predicts a k_L of 13.0 W/mK for a thickness of 12 μm. The difference between theory and experiment can be primarily associated with the presence of defects and not to the effect of nanostructuring. Therefore, we can surmise that CeO₂ thin films below ~50 nm with defects can reduce the k_L drastically. Metal oxides generally have large Seebeck coefficient at high temperatures and hence can be considered as candidate materials for advanced thermoelectric.

The coating of CeO₂ on several alloys has improved the oxidation resistance and can be used in high-temperature applications in industries such as automobiles, aerospace and nuclear, where the knowledge of CeO₂ cross-plane thermal conductivity as a function of coating thickness and temperature becomes vital. Therefore, in Fig. 8b we have presented the effect of temperature on the k_L of thin film and have observed that the k_L for thin films reduces considerably with an increase in temperature. The presented theoretical work can equip material scientists with vital information required for designing CeO₂ thin films of optimal thickness that will aid in the design of experiments.

Summary

We have presented an extensive analysis of the k_L of CeO₂ both in its bulk and nanoforms. The theoretical predictions of k_L using first principles unified with BTE not only provides an insight into the underlying physics of k_L of CeO₂ but also helps explain the large discrepancy in the k_L value of CeO₂ reported previously. The structural and mechanical properties of CeO₂ could be predicted with better precision by the recently developed pseudopotential with PBEsol functional than any other previously reported DFT calculations. The phonon dispersions spectra of CeO₂ is evaluated by both direct approach and linear response approach and could describe its polar nature while aptly showing good agreement with the experiment. An investigation of the available three-phonon scattering phase space and mode Grüneisen parameter of CeO₂, reveals that the lower k_L of CeO₂ is primarily due to increased scattering and strong anharmonicity respectively. Along with the theoretical investigation of k_L and its dependence on temperature, we also predict the mode wise contribution to the total k_L of CeO₂. The analysis of mode wise k_L of CeO₂ indicated the notable contribution to the overall thermal conductivity from the optical modes (~30%), akin to UO₂. Additionally, we prepared CeO₂ pellets of varying density by SPS technique and measured the thermal conductivity of these pellets using laser flash technique. The experimental analysis of the samples reveals the dependence of sintering parameters on the density of the CeO₂ sample and its effect on its measured thermal conductivity. Moreover, we also conducted a theoretical study using the classical MD approach to corroborate the effect of porosity on thermal conductivity. Besides the detailed investigation of the thermal conductivity of CeO₂ in its bulk form, this article also sheds light on the thermal transport property of nanostructured CeO₂. We demonstrate the phonon MFP distribution of CeO₂ is critical in the study of nanostructured materials and devices. The contribution of phonons modes to k_L is uneven, and the phonons of MFP below 65 nm constitute 80% of k_L, indicating that limiting the size below 65 nm can efficiently reduce the k_L of CeO₂. The in-plane and cross-plane thermal conductivity of CeO₂ thin film as a function of film thickness are also reported. These findings have an impact on heat dissipation in nanoelectronics and photonics, as well as the design of nanostructured thermoelectric materials with reduced thermal conductivity. To conclude, this work serves to moderate the existing ambiguity in the thermal conductivity value of CeO₂ and provides practical information on CeO₂ nanostructuring that will potentially meet the demands of numerous industrial applications.

Methods

Computational details

All the first principles calculations were performed using the DFT as implemented in the open source Quantum ESPRESSO⁵¹ code. The pseudopotential used were norm conserved, and the electronic exchange-correlation is based on the generalized gradient approximation (GGA) with the Perdew, Burke, and Ernzerhof functional for solids (PBEsol)⁵². Geometry optimization evaluates the structural properties at zero Kelvin temperature by minimizing the total energy by varying both cell parameter and atom positions. We obtained the total energy convergence of CeO₂, using an electron wave vector grid and the plane wave energy cutoff of 950 eV and 8 × 8 × 8 respectively. The criteria for the electronic energy convergence and the force convergence was respectively set a value of 10⁻¹² eV and 10⁻⁷ eV/Å. The ground state structural properties were also assessed using the Birch-Murnaghan equation of state⁵³. The elastic constants were calculated using the stress-strain method^26,27. From the elastic constants, the mechanical properties such as the bulk modulus (B), shear modulus (G), Young’s modulus (Y), and Poisson’s ratio (η) were determined using the Voigt-Reuss-Hill averaging scheme^30,31,32. Because we are analyzing a cubic, polycrystalline structure, therefore the elastic moduli can be evaluated assuming an isotropic aggregate of grains with non-isotropic elastic properties. For a cubic symmetry, there are three independent elastic constants: C₁₁, C₁₂, and C₄₄. The bulk modulus for a cubic structure is the same for the Voigt, Reuss, and Hill averages, as shown in Eq. (5).

$$B=\frac{1}{3}({C}_{11}+2{C}_{12})$$

(5)

Eq. (6) gives the shear modulus in the Voigt average:

$${G}_{V}=\frac{{C}_{11}-{C}_{12}+3{C}_{44}}{5}$$

(6)

while Eq. (7) gives the Reuss average:

$${G}_{R}=\frac{(5({C}_{11}-{C}_{12}){C}_{44})}{4{C}_{44}+3({C}_{11}-{C}_{12})}$$

(7)

The arithmetic mean (Hill) G = (G_V + G_R)/2 is taken as shear modulus.

The Young’s modulus is calculated as:

$$Y=\frac{9BG}{3B+G}$$

(8)

The Poisson’s ratio is calculated as:

$$\eta =\frac{3B-2G}{2(3B+G)}$$

(9)

The k_L of CeO₂ is predicted by solving the phonon BTE iteratively using the open source ShengBTE¹³ code. The inputs required to solve the BTE are the second order force constants (harmonic force constant) and third order force constants (anharmonic force constants), which are defined as the second and third derivative of the potential energy (V) with respect to the atomic displacements respectively. The potential energy of the crystal with a unit cell characterized by a vector ‘l’ and the atomic positions in each unit cell described by the vector ‘b’, can be expanded in a Taylor series in power of the atomic displacement u (l, b). The first three terms of such a Taylor series expansion is given in Eq. (10) as stated in the ref.⁵⁴.

$$\begin{array}{rcl}V & = & {V}_{o}+\,\sum _{lb\alpha }\,\frac{\partial V}{\partial {u}_{\alpha }(l,b)}|\,{}_{0}\,{u}_{\alpha }(lb)+\frac{1}{2}\sum _{lb,l^{\prime} b^{\prime} }\,\sum _{\alpha \beta }\,\frac{{\partial }^{2}V}{\partial {u}_{\alpha }(lb)\partial {u}_{\beta }(l^{\prime} b^{\prime} )}|\,{}_{0}\,{u}_{\alpha }(lb){u}_{\beta }(l^{\prime} b^{\prime} )\\ & & +\,\frac{1}{3!}\sum _{{\rm{lb}},{\rm{l}}^{\prime} {\rm{b}}^{\prime} ,{\rm{l}}^{\prime\prime} {\rm{b}}^{\prime\prime} }\,\sum _{{\rm{\alpha }}{\rm{\beta }}{\rm{\gamma }}}\,\frac{{\partial }^{3}{\rm{V}}}{\partial {{\rm{u}}}_{{\rm{\alpha }}}({\rm{lb}})\partial {{\rm{u}}}_{{\rm{\beta }}}(l^{\prime} b^{\prime} )\,\partial {{\rm{u}}}_{{\rm{\gamma }}}1^{\prime\prime} {\rm{b}}^{\prime\prime} )}|\,{}_{0}\,{{\rm{u}}}_{{\rm{\alpha }}}({\rm{lb}}){{\rm{u}}}_{{\rm{\beta }}}(l^{\prime} b^{\prime} ){{\rm{u}}}_{{\rm{\gamma }}}({\rm{l}}^{\prime\prime} {\rm{b}}^{\prime\prime} )\end{array}$$

(10)

The second order force constant (${{\rm{\Phi }}}_{{\rm{\alpha }}{\rm{\beta }}}(lb,l^{\prime} b^{\prime} )$) and the third order force constant (${{\rm{\Phi }}}_{{\rm{\alpha }}{\rm{\beta }}{\rm{\gamma }}}({\rm{lb}},{\rm{l}}^{\prime} {\rm{b}}^{\prime} ,{\rm{l}}^{\prime\prime} {\rm{b}}^{\prime\prime} )$ are defined as shown in Eqs (11) and (12) respectively.

$${\Phi }_{\alpha \beta }(lb,l^{\prime} b^{\prime} )={\frac{{\partial }^{2}V}{\partial {u}_{\alpha }(lb)\partial {u}_{\beta }(l^{\prime} b^{\prime} )}|}_{0}$$

(11)

$${\Phi }_{\alpha \beta \gamma }(lb,l^{\prime} b^{\prime} ,l^{\prime\prime} b^{\prime\prime} )={\frac{{\partial }^{3}V}{\partial {u}_{\alpha }(lb)\partial {u}_{\beta }(l^{\prime} b^{\prime} )\partial {u}_{\gamma }(l^{\prime\prime} b^{\prime\prime} )}|}_{0}$$

(12)

The dynamical matrices for evaluating the phonon density of states is obtained from the second order force constant as follows,

$${D}_{\alpha \beta }(bb^{\prime} {|}_{q})=\frac{1}{\sqrt{{m}_{b}{m}_{b^{\prime} }\,}}\,\sum _{{l}^{\text{'}}}\,{{\rm{\Phi }}}_{\alpha \beta }(0b,l^{\prime} b^{\prime} )exp(iq.l^{\prime} )$$

(13)

where q is the wave vector and m denote the mass of an atom at a site in the crystal. Further, diagonalizing the dynamical matrix yields the phonon frequencies (ω), which in turn provides the phonon group velocities and heat capacity at a fixed volume (C_v). In this work, the harmonic force constant is calculated using both linear approach (DFPT)¹² and direct approach (Parlinski-Li-Kawazoe method)³⁵, based on the supercell approach with finite displacement method as implemented in the Phonopy package⁵⁵. To obtain the converged phonon properties, the calculations of the harmonic force constant were done using a q-point mesh of 8 × 8 × 8 (phonon dispersion for different q-points are shown as S.I.3, (Fig. S3)) and a 5 × 5 × 5 supercell of the primitive cell containing 375 atoms. The calculation of the third order force constants was performed on a 4 × 4 × 4 supercell, and the force cutoff distance was set to the ninth nearest neighboring atoms. The convergence of the k_L with respect to the number of q points used in the second order force constant, the number of neighboring atoms considered in third order force constant and the number of grid planes along each axis in the reciprocal space for solving the BTE is detailed in Fig. 9. From the cubic force constants, the phonon scattering processes are evaluated using Fermi’s golden rule, and finally, the k_L is calculated using the iterative solutions of the BTE as implemented in ShengBTE. In the approach implemented in ShengBTE, Eq. (14) gives the expression to compute the lattice thermal conductivity tensor,

$${k}_{L}^{\alpha \beta }=\frac{1}{N{K}_{B}{T}^{2}{\rm{\Omega }}}\,\sum _{{\rm{\lambda }}}^{\infty }\,{f}_{0}({\omega }_{{\rm{\lambda }}}){f}_{0}({\omega }_{{\rm{\lambda }}}+1){({\rm{\hbar }}{\omega }_{{\rm{\lambda }}})}^{2}{v}_{{\rm{\lambda }}}^{\alpha }{v}_{{\rm{\lambda }}}^{\beta }{\tau }_{{\rm{\lambda }}}$$

(14)

where Ω is the volume of the primitive cell, α and β are the Cartesian components of x, y, or z, k_B is the Boltzmann constant, ω_λ and υ_λ are the angular frequency and group velocity respectively, τ_λ is the relaxation time of mode λ and f₀(ω_λ) is the Bose-Einstein distribution function. The k_L presented in this work are the fully iterative solution of the Peierls-equation, and the convergence of k_L with the number of iterations starting from the zeroth-order approximation (which is equivalent to operating under RTA) and the k_L at low temperature (<300 K) are shown in S.I.4 (Fig. S4) and S.I.5 (Fig. S5) respectively.

Figure 9

Convergence of the k_L with respect to (a) the q-points considered for the second order force constants (by maintaining n = 9 and N = 18 × 18 × 18 for all the cases); (b) the number of neighboring atoms considered for calculating the third order force constant (by keeping q = 8 × 8 × 8 and N = 18 × 18 × 18 for all the cases); (c) the number of grid planes along each axis in reciprocal space for solving the BTE (by considering q = 8 × 8 × 8 and n = 9 for all the cases).

For a polar material, the interatomic forces are divided into two additive contributions; the analytic and non-analytic contributions (nac). The analytic contribution accounts for all the forces under the restricted periodic boundary conditions under which the averaged electric field is assumed to be zero. The nonanalytic contribution accounts the additional forces owing to non-zero averaged electric field⁵⁶. The classical Newton’s second law of motion for describing the atomic vibrations for a polar solid is as shown in Eq. (15),

$$mj({\partial }^{2}\frac{{u}_{\alpha }(t,j;P)}{\partial {t}^{2}})=-\,(\frac{\partial E(U)}{\partial {u}_{\alpha }(t,j;P)})+e{Z}_{\alpha }(j).E.$$

(15)

where m_j denotes the atomic mass of the j^th atom in the primitive unit cell, α (α = x, y, z) is the component of the atomic displacement from its equilibrium position of the j^th atom in the P^th reference primitive unit cell within a supercell, as detailed in ref.⁵⁶. The first term on the right-hand side of the Eq. (15) corresponds to the analytical force arising due to the short-range interatomic interactions. The U and E (U) in the first term represent the whole set of atomic displacements and the total energy respectively. In the second term, the dot product between the Born effective charge (Z) and the average of the electric field (E) induced by the atomic vibrations accounts for the non-analytic force due to the long-range coulombic interaction. In this work, CeO₂ being a polar material, the non-analytical contribution was considered, and the Born charges and the dielectric constant required to evaluate the non-analytical contribution were calculated using the DFPT. Therefore, the nac contribution needs to be included in the k_L calculation of CeO₂.

For MD simulations, we used the equilibrium classical MD techniques together with the Green-Kubo linear response formalism⁵⁷ as implemented in LAMMPS (Large-scale Atomic/Molecular Massively Parallel Simulator) MD simulation code⁵⁸. The Green-Kubo formalism uses the heat current autocorrelation function (HCACF) (shown in Fig. 10) which decay along a direction as described in ref.⁵⁷. To predict the k_L of CeO₂, the Verlet leapfrog algorithm was implemented⁵⁹. Further, the system was first simulated in a constant number of atoms, pressure, and temperature (NPT) ensemble for 4 ns to ensure it reached equilibrium at the desired temperatures, then the ensemble was switched into a constant number of atoms, volume, and temperature (NVT) ensemble and ran for 4 ns. The heat current autocorrelation function (HCACF) were estimated along with an NVE ensemble calculation which generates an 8 ns raw heat current data at every calculation. Finally, the k_L value was computed by averaging the k_L over the time range were the fluctuations were minimal as shown in the inset of Fig. 10b.

Figure 10

(a) The HFACF for CeO₂ at a temperature of 300 K with a system size of 10 × 10 × 10 and 20 × 20 × 20 unit cells. (b) The HFACF for CeO₂ at a temperature of 300 K and 1500 K with a system size of 10 × 10 × 10 unit cells; inset shows the k_L fluctuations with time and the shaded region indicates the time range over which the HCACF integral is averaged to predict the k_L.

Finally, to study the effect of the nanostructuring and calculate the in-plane and cross-plane thermal conductivity of thin films of CeO₂ we used the open source almaBTE code⁵⁰. Recently, an exact solution to evaluate the BTE in the cross-plane geometries has been obtained. The film conductivity at thickness L as an integral of phonon frequency is given as,

$$k(L)=\int S(\omega ,L)k(\omega )d\omega $$

(16)

where S is a suppression function that contains the thin film physics and k(ω) denotes the bulk spectral conductivity. More detailed description of the procedure can be found in the following refs^50,60. It has to be noted that the almaBTE code uses the second order force constant predicted by the FD method. Hence the k_L values for the nanostructured cases are underpredicted by ~19% as shown for the bulk CeO₂.

Materials and experimental details

The 99.9% pure CeO₂ powder was obtained from ACROS Organics. The as-received powder was observed under the scanning electron microscope, the micrograph as shown in Fig. 11a revealed that the particles were needle-shaped with dimensions around 20 μm long and 5 μm wide. The as-received powder was sintered using SPS (Thermal Technology LLC 10-3 system) in a graphite die-punch setup as shown in Fig. 11b. The powder die contacts were separated by graphite foils to protect the die from contamination and to reduce friction between the powders and die. A 6 mm hole was drilled from the inner surface of the die, and a pyrometer was focused on this hole to record the temperature of the die. The temperature was controlled by regulating the current passing through the die-punch system, and a Data Acquisition System was used to record displacement, temperature and pressure data.

Figure 11

(a) Scanning electron micrograph of as-received CeO₂ powders from ACROS Organic. (b) Schematic diagram of SPS sintering of CeO₂.

The pellets were sintered by varying the sintering parameters such as temperature, pressure and hold time. The sintered pellets were then subjected to X-Ray Diffraction (XRD) using BRUKER D8 with Chromium K-alpha radiation to determine the phase and the presence of any residual carbon during the SPS sintering. The Archimedes’ method was used to determine the density of each pellet. Finally, the thermal conductivity was calculated using the laser flash apparatus; Laser flash technique records the thermal diffusivity (α) of the specimens using the Parkers relations⁶¹ given as shown in Eq. (17):

$$\alpha =0.1388\times \frac{{L}^{2}}{{t}_{\frac{1}{2}}}$$

(17)

where L is the thickness of the specimen and t_1/2 is the half of the maximum time taken for the signal to reach the detector. From the measured α, the thermal conductivity as a function of temperature (k (T)) can be measured using the relation (18):

$$\alpha (T)=\frac{k(T)}{\rho (T)\times {C}_{p}(T)}$$

(18)

where ρ(T) and Cp(T) is the density and heat capacity at constant pressure as a function of temperature respectively. In this work the Cp changes as a function of temperature was determined by comparing the maximum value of the temperature rise with that of a reference pellet, using the relation Cp = Q/(dT.m), where Q represent the energy of the pulsed laser beam, m mass of the specimen, and dT is the maximum value of the temperature rise. The reference pellet used was a certified stainless steel. However, the density changes as a function of temperature has been kept constant. The thermal conductivity measurements were made on cylindrical pellets of diameter 12.7 mm and thickness 2–3 mm.