Abstract
The role of electron-phonon interactions in iron-based superconductor is currently under debate with conflicting experimental reports on the isotope effect. To address this important issue, we employ the renormalization-group method to investigate the competition between electron-electron and electron-phonon interactions in these materials. The renormalization-group analysis shows that the ground state is a phonon-dressed unconventional superconductor: the dominant electronic interactions account for pairing mechanism while electron-phonon interactions are subdominant. Because of the phonon dressing, the isotope effect of the critical temperature can be normal or reversed, depending on whether the retarded intra- or inter-band interactions are altered upon isotope substitutions. The connection between the anomalous isotope effect and the unconventional pairing symmetry is discussed at the end.
Similar content being viewed by others
Introduction
Superconductivity1,2,3,4,5 is a novel phenomenon of zero electric resistance in some materials when cooled below the characteristic critical temperature Tc. The magic arises from electron pairing in superconductors such that the low-energy excitations are described by an exotic quantum condensate without any dissipation. In conventional superconductors, such as aluminium, the interactions between electrons and the lattice vibrations generate effective attraction and lead to electron pair formation. In quantum language, these vibrations can be treated as particle-like excitations named phonons. It is generally believed that the electron-phonon interactions explain the pairing mechanism for conventional superconductors.
On the contrary, the pairing mechanism of the unconventional superconductors, such as cuprates, seems to stem from the strong electron-electron interactions. Despite of intensive experimental and theoretical studies1,2 in the past decades, there are still plenty of unsettled controversies about these unconventional superconductors. One of the most important issues is the interplay between the electron-electron and the electron-phonon interactions6,7,8,9,10,11,12,13,14,15,16,17,18. The recently discovered iron-based superconductors3,4,5,19,20,21,22,23 provide a unique testing ground to address this issue24,25,26,27. Gathered from theoretical and experimental investigations, the interaction strength in the iron-based superconductors is only weak to medium, rendering controlled theoretical understanding possible.
One of the checking points is the critical temperature of superconductivity upon isotope substitutions28,29,30,31. According to the Bardeen-Cooper-Schrieffer theory for the conventional superconductors, the critical temperature Tc is related to the mass of the isotope element M,
where α is the exponent for the isotope effect. If the dominant interaction is electron-phonon in nature, theoretical calculations give \(\alpha =1/2\). In the extreme opposite, if the pairing is completely driven by electron-electron interactions, the critical temperature should not change with isotope substitutions and the corresponding exponent is \(\alpha \approx 0\). In realistic superconductors, we expect the isotope exponent to be in-between. Note that, in unconventional superconductors, the phonon-mediated interactions are insufficient to explain the pairing mechanism and it is of crucial importance to study the interplay between electron-electron and electron-phonon interactions24,25,26,27. For instance, even when the pairing mechanism is electronic origin, dispersions observed in angle-resolved photoemission spectroscopy manifest distortions upon isotope substitutions13,14,15,16,17,18,27.
The isotope effect observed in iron-based superconductor28,29,30,31,32,33,34 seems to tell a more complicated story. For instance, a strong isotope effect by iron substitution28 is found in SmFeAs(O, F) and (Ba, K)Fe2As2, almost as large as that in conventional superconductors. On the contrary, inverse isotope effect29 is spotted in (Ba, K)Fe2As2 with different isotope substitutions. Later, it was proposed that the isotope substitutions may give rise to structural change35 and further complicate the story. On the theoretical side, Yanagisawa et al.36 proposed a multi-band and multi-channel model to explain the possibility of observing the inverse isotope effect. However, Bussmann-Holder and Keller37 commented that an inversion of the exponent cannot occur upon iron isotope substitutions. The controversies about the isotope effect of the iron-based superconductor are still on. And, it is of crucial importance to clarify the subtle role of the electron-phonon interactions in iron-based superconductors.
Results
Instantaneous and retarded interactions
Motivated by the controversy, we investigate the competition between electron-electron and electron-phonon interactions by the unbiased renormalization-group (RG) method. Due to the retarded nature of the phonon-mediated interactions, the energy dependence must be included. The minimal approach to include both simultaneous and retarded interactions can be accomplished by the step-shape approximation38,39,40,41 as shown in Fig. 1(a),
where gi and \({\tilde{g}}_{i}\) represent (instantaneous) electronic interactions and (retarded) phonon-mediated ones. The energy scale for the retarded interactions is set by the Debye frequency \({\omega }_{D}\). Our RG analysis reveals that the pairing mechanism is dominated by the electronic interactions gi. But, the retarded interactions \({\tilde{g}}_{i}\) also grow under RG transformation and become relevant in low-energy limit. Inclusion of these subdominant interactions leads to anomalous isotope effect. The isotope exponent α can be extracted numerically from RG flows in weak coupling. It is quite remarkable that the sign of the exponent α sensitively depends on whether the inter- and/or intra-band interactions are altered by isotope substitutions.
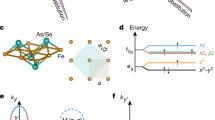
(a) Step-like interaction profile for simultaneous and retarded interactions. A sharp step is assumed at the Debye frequency \({\omega }_{D}\). (b) Fermiology of the five-band model \(x=0.1\). These Fermi surfaces are well sampled by five pairs of Fermi points, equivalent to the four-leg geometry with quantized momenta (dashed lines).
Multi-band model
To illustrate how the RG scheme works, we start with a five-orbital tight-binding model for iron-based superconductors with generalized on-site interactions,
where \(a,b=1,2,\ldots ,5\) label the five d-orbitals of Fe, \(1:{d}_{3{Z}^{2}-{R}^{2}}\), \(2:{d}_{XZ}\), \(3:{d}_{YZ}\), \(4:{d}_{{X}^{2}-{Y}^{2}}\), \(5:{d}_{XY}\), and α = ↑,↓ is the spin index. The kinetic matrix Kab in the momentum space has been constructed in previous studies42. The generalized on-site interactions consist of three parts: intra-orbital U1, inter-orbital U2 and Hund’s coupling JH. Adopted from previous studies, we choose the values, \({U}_{1}=4\,{\rm{eV}}\), \({U}_{2}=2\,{\rm{eV}}\) and \({J}_{H}=0.7\,{\rm{eV}}\) for numerical studies here.
Fermiology is important in the multi-band superconductors. The electron doping x is related to the band filling \(n=6+x\) (\(n=10\) for completely filled bands) here and the Fermi surface at \(x=0.1\) is illustrated in Fig. 1(b). There are five active bands: two hole pockets centered at (0, 0) and another hole pocket centered at (π, π) while two electron pockets located at (π, 0)and (0, π) points43. To simplify the RG analysis, we sample each pocket with one pair of Fermi points (required by time-reversal symmetry). This is equivalent to a four-leg ladder geometry with quantized momenta as shown in Fig. 1(b). In the low-energy limit, the effective Hamiltonian44,45,46 is captured by five pairs of chiral fermions with different velocities. The RG equations for all couplings can be found in Methods.
Pairing mechanism
By integrating the two sets of RG equations numerically, we found all couplings are well described the scaling ansatz47,
where Gi, \({\tilde{G}}_{i}\) are non-universal constants and \({\gamma }_{{g}_{i}}\), \({\gamma }_{{\tilde{g}}_{i}}\) are RG exponents for simultaneous and retarded couplings. The divergent length scale ld, associated with the pairing gap, is solely determined by electronic origin. The dominant pairing occur within band 1 and band 2 and the Cooper scatterings c11, c22 c12 have maximum exponent \({\gamma }_{i}=1\). Other Cooper scatterings are subdominant with exponents close to 0.9, as shown in Fig. 2(a). Meanwhile, by Abelian bosonization45,46, the signs of cij from numerics lead to sign-revised (between electron and hole pockets) s±-wave pairing, agreeing with the previous functional RG study48. Note that these exponents are rather robust within the doping range where the same Fermiology maintains. What about the phonon-mediated interactions? As clearly indicated in Fig. 2(b), the RG exponents for \({\tilde{c}}_{11}\), \({\tilde{c}}_{22}\) are roughly 0.6, much smaller than the dominant electronic interactions, showing the pairing mechanism is electronic origin. However, since the RG exponents are positive, the retarded interactions also grow under RG transformation. These subdominant phonon-mediated interactions can lead to anomalous isotope effect as explained in the following.
Two-step RG scheme
To achieve quantitative understanding in weak coupling, the rescaled Debye frequency must be taken into account carefully. Under RG transformations, \({\omega }_{D}\to {\omega }_{D}{e}^{l}\) as shown in Fig. 3. At the (logarithmic) length scale \({l}_{D}\equiv \,\mathrm{log}({{\rm{\Lambda }}}_{0}/{\omega }_{D})\), the difference between gi and \({\tilde{g}}_{i}\) disappears. The Debye frequency \({\omega }_{D}\sim 30\,{\rm{meV}}\) in iron-based materials24 and the band width (thus Λ0) is 3–4 eV, giving rise to lD ~ 5. Note that the RG is truncated at the cutoff length scale lc where the maximal coupling reaches order one. In weak coupling, it is clear that \({l}_{c} > {l}_{D}\) and thus the RG scheme must be divided into two steps. For \(l < {l}_{D}\), both sets of RG equations are employed. At \(l={l}_{D}\), the functional form for the retarded interactions is the same as the instantaneous one. Thus, one should add up both types of couplings \({g}_{i}({l}_{D})+{\tilde{g}}_{i}({l}_{D})\) and keep running RG by just the first set of equations. In physics terms, this means that the difference between simultaneous and retarded interactions vanishes before the pairing gaps open.
(a) Interaction profile of the dominant intra-band C and inter-band C⊥ Cooper scatterings before RG transformation. (b) As RG progresses, the step evolves since the Debye energy is rescaled, \({\omega }_{D}(l)={\omega }_{D}{e}^{l}\). (c) For \(l > {l}_{D}\), the distinction between simultaneous and retarded interactions disappears. (d) Schematic picture for phonon-dressed unconventional superconductor.
Extracting isotope exponent
Numerical results for the two-step RG indicate the same superconducting phase as described in previous paragraphs but the isotope exponent α can be extracted numerically. Under RG transformation, the critical temperature satisfies the scaling form, \({k}_{B}{T}_{c}\sim {\rm{\Delta }}\,[g(0)]={{\rm{\Delta }}}_{c}{e}^{-{l}_{c}}\), where Δc is the pairing gap at the cutoff length scale. By varying the length scale lD, the critical temperature changes, i.e.
Furthermore, from the definition of the isotope exponent, the standard scaling argument under RG transformation gives rise to the isotope exponent.
where \(d(\mathrm{log}\,M)=-\,2d(\mathrm{log}\,{\omega }_{D})=2d{l}_{D}\), because \({\omega }_{D}\sim {M}^{-1/2}\). The above formula for the isotope exponent α is the central result in this paper. For conventional superconductor, \({{\rm{\Delta }}}_{c}\sim {\omega }_{D}\) and the cutoff length scale is not sensitive to the Debye frequency (the second term vanishes). Thus, \(\alpha \approx 1/2\). On the other hand, for unconventional superconductors without relevant electron-phonon interactions, \({{\rm{\Delta }}}_{c}\sim {{\rm{\Lambda }}}_{0}\) and the cutoff length scale is also not sensitive to the Debye frequency. It is clear that α = 0 in this case. But, what happens if the electron-phonon interactions, though not dominant, are actually relevant under RG transformation? We shall elaborate the details in Discussion.
Discussion
To extract the isotope exponent, we study how the cutoff length scale lc varies with different Debye frequencies due to isotope substitutions. In weak coupling, we found that gi are much larger than \({\tilde{g}}_{i}\). Thus, Δc has very weak dependence on \({\omega }_{D}\) and the first term can be ignored. The contribution from the second term is shown in Fig. 4. We tried two different profiles for the retarded interactions. Include only intra-band interactions, \({\tilde{c}}_{ii}(0)=-\,0.3\,U\) first, where U is the strength of electron-electron interactions. The isotope exponent is positive (reading from the slope), \(\alpha \approx 0.1\), with very smooth variation. On the other hand, with only inter-band interactions, \({\tilde{c}}_{ij}(0)=-\,0.14\,U\), the isotope exponent is negative and changes gradually from zero to \(\alpha \approx -\,0.03\).
The cutoff length scale lc versus lD for inclusion of intraband interactions \({\tilde{c}}_{ii}(0)=-\,0.3\,U\) (blue circles) and interband ones \({\tilde{c}}_{ij}(0)=-\,0.14\,U\) (red square), where U is the strength of electron-electron interactions. For convenience, the axes are rescaled in the unit of le, the cutoff length scale with electronic interactions only. The inset shows the isotope exponent by taking numerical derivative.
These anomalous isotope effects are closely related to the unconventional pairing symmetry. For the s±-wave pairing, \({c}_{ii} < 0\) but \({c}_{ij} > 0\) at the cutoff length scale. The phonon-mediated intra-band interactions \({\tilde{c}}_{ii} < 0\) help to develop the pairing instability and thus lead to a positive isotope exponent. On the other hand, the inter-band ones \({\tilde{c}}_{ij} < 0\) have opposite sign with their simultaneous counterparts cij. In consequence, the pairing instability is suppressed and an inverses isotope effect is in order. The RG analysis presented here provides clear and natural connection between the anomalous isotope effect and the unconventional pairing symmetry.
Although the isotope exponent α can be extracted numerically in weak coupling, extending the quantitative description to intermediate coupling may not be easy. If the pairing gaps open before hitting the Debye energy scale, i.e. \({l}_{c} < {l}_{D}\), our numerical results show that lc solely depend on electronic interactions and thus \(d{l}_{c}/d{l}_{D}=0\). The isotope exponent in this regime mainly arises from the first term. The pairing gap \({{\rm{\Delta }}}_{c}={{\rm{\Delta }}}_{c}({{\rm{\Lambda }}}_{0},{\omega }_{D}{e}^{l})\), depending on both the bandwidth and the rescaled Debye frequency, is now quite complicated. The RG analysis alone is not sufficient to obtain α in a quantitative fashion. However, we recently found that the effective Hamiltonian at the cutoff length scale is well captured by mean-field theory (not yet published). In principle, one can combine RG and mean-field approaches together to compute the isotope exponent in intermediate coupling more accurately.
In the end, we discuss the recent discovery of superconductivity in FeSe/STO systems49,50. We emphasize that our current approach includes fermiology, electron-electron interactions, and electron-phonon interactions within only the superconducting(SC) layers. One crucial assumption is the profile of the mediated electron-phonon interactions can be captured by the step function. The RG scheme built upon this approximation works as explained in the manuscript. However, according to the recent literatures in FeSe/STO systems49,50,51,52,53,54,55,56, to include the non-SC (SrTiO3) layers we need to devise a new theoretical approach which is beyond our model at this point. The profile of the electron-phonon interactions arisen from non-SC layers is probably not captured by the simple step function anymore. One needs to find out the interaction profile generated by the non-SC layers first so that one can devise the RG scheme accordingly. This is going to be an interesting and challenging topic to explore in the future.
Methods
RG equations
The interactions between these chiral fermions fall into two categories39: Cooper scattering \({c}_{ij}^{l}\), \({c}_{ij}^{s}\) and forward scattering \({f}_{ij}^{l}\), \({f}_{ij}^{s}\). The retarded ones share the same classification, denoted with an extra tilde symbol. The RG equations for the simultaneous interactions are,
where \(\dot{g}=dg/dl\), where \(l=\,\mathrm{ln}({{\rm{\Lambda }}}_{0}/{\rm{\Lambda }})\) is the logarithm of the ratio between bare energy cutoff \({{\rm{\Lambda }}}_{0}\) and the running cutoff \({\rm{\Lambda }}\). The tensor \({\alpha }_{ij,k}=({v}_{i}+{v}_{k})\,({v}_{j}+{v}_{k})/[2{v}_{k}({v}_{i}+{v}_{j})]\) with vi representing the Fermi velocities.
The second set of equations describes how the retarded interactions are renormalized,
Note that we separate the intra-band and inter-band couplings for clarity, i.e. \(i\ne j\) in the above RG equations. In fact, the separation is necessary because we shall see later that inter-band and intra-band couplings play different roles in the low-energy limit. In addition, \({f}_{ii}=0\) and \({\tilde{f}}_{ii}=0\) to avoid double counting.
References
Kresin, V., Morawitz, H. & Wolf, S. A. Mechanism of Conventional and High Tc Superconductivity. (Oxford Press, Oxford, 1993).
Anderson, P. W. Theory of Superconductivity in the High-Tc Cuprates. (Princeton University Press, Princeton, 1997).
Paglione, J. & Greene, R. L. High-temperature superconductivity in iron-based materials. Nature Phys. 6, 645–658 (2010).
Norman, M. R. The Challenge of Unconventional Superconductivity. Science 332, 196–200 (2011).
Stewart, G. R. Superconductivity in iron compounds. Rev. Mod. Phys. 83, 1589–1652 (2011).
Kresin, V. Z. & Wolf, S. A. Electron-lattice interaction and its impact on high Tc superconductivity. Rev. Mod. Phys. 81, 481–501 (2009).
Bud’ko, S. L. et al. Boron Isotope Effect in Superconducting MgB2. Phys. Rev. Lett. 86, 1877–1880 (2001).
Iliev, M. N. et al. Raman phonons and ageing-related surface disorder in NaxCoO2. Physica C 402, 239–242 (2004).
Lupi, S., Ortolani, M. & Calvani, P. Optical conductivity of single crystals of Na0.57CoO2. Phys. Rev. B 69, 180506(R) (2004).
Uchiyama, H. et al. Softening of Cu-O Bond Stretching Phonons in Tetragonal HgBa2CuO4+δ. Phys. Rev. Lett. 92, 197005 (2004).
Lee, J. et al. Interplay of electron-lattice interactions and superconductivity in Bi2Sr2CaCu2O8+δ. Nature 442, 546–550 (2006).
Yokoi, M., Kobayashi, Y., Sato, M. & Sugai, S. Isotope Effect on Superconducting Transition Temperature of NaxCoO2·yH2O. J. Phys. Soc. Jpn. 77, 094713 (2008).
Lanzara, A. et al. Evidence for ubiquitous strong electron? Phonon coupling in high-temperature superconductors. Nature 412, 510–514 (2001).
Hasan, M. Z. et al. Fermi Surface and Quasiparticle Dynamics of Na0.7CoO2 Investigated by Angle-Resolved Photoemission Spectroscopy. Phys. Rev. Lett. 92, 246402 (2004).
Yang, H.-B. et al. ARPES on Na0.6CoO2: Fermi Surface and Unusual Band Dispersion. Phys. Rev. Lett. 92, 246403 (2004).
Gweon, G.-H. et al. An unusual isotope effect in a high-transition-temperature superconductor. Nature 430, 187–190 (2004).
Iwasawa, H. et al. Isotopic Fingerprint of Electron-Phonon Coupling in High-T c Cuprates. Phys. Rev. Lett. 101, 157005 (2008).
Giustino, F., Cohen, M. L. & Louie, S. G. Small phonon contribution to the photoemission kink in the copper oxide superconductors. Nature 452, 975–978 (2008).
Aswathy, P. M., Anooja, J. B., Sarun, P. M. & Syamaprasad, U. An overview on iron based superconductors. Superconductor Science and Technology 23, 7 (2010).
Chubukov, A. V. Pairing Mechanism in Fe-Based Superconductors. Annu. Rev. Condens. Matter Phys. 3, 57 (2012).
Chen, X., Dai, P., Feng, D., Xiang, T. & Zhang, F.-C. Iron-based high transition temperature superconductors. National Science Review 1, 371 (2014).
Chubukov, A. & Hirschfeld, P. J. Iron-based superconductors, seven years later. Physics Today 68(6), 46 (2015).
Hosono, H. & Kuroki, K. Iron-based superconductors: Current status of materials and pairing mechanism. Physica C 514, 399 (2015).
Boeri, L., Dolgov, O. V. & Golubov, A. A. Is LaFeAsO1−xFx an Electron-Phonon Superconductor? Phys. Rev. Lett. 101, 026403 (2008).
Granath, M., Bielecki, J., Holmlund, J. & Börjesson, L. Anharmonic softening of Raman active phonons in iron-pnictides: Estimating the Fe isotope effect due to anharmonic expansion. Phys. Rev. B 79, 235103 (2009).
Le Tacon, M. et al. Inelastic x-ray scattering study of superconducting SmFeAsO1−xFy single crystals: Evidence for strong momentum-dependent doping-induced renormalizations of optical phonons. Phys. Rev. B 80, 220504(R) (2009).
Richard, P. et al. Angle-Resolved Photoemission Spectroscopy of the Fe-Based Ba0.6K0.4Fe2As2 High Temperature Superconductor: Evidence for an Orbital Selective Electron-Mode Coupling. Phys. Rev. Lett. 102, 047003 (2009).
Liu, R. H. et al. A large iron isotope effect in SmFeAsO1−xFx and Ba1−xKxFe2As2. Nature 459, 64–67 (2009).
Shirage, P. M. et al. Inverse Iron Isotope Effect on the Transition Temperature of the (Ba,K)Fe2As2 Superconductor. Phys. Rev. Lett. 103, 257003 (2009).
Shirage, P. M. et al. Absence of an Appreciable Iron Isotope Effect on the Transition Temperature of the Optimally Doped SmFeAsO1−y Superconductor. Phys. Rev. Lett. 105, 037004 (2010).
Khasanov, R. et al. Iron isotope effect on the superconducting transition temperature and the crystal structure of FeSe1−x. New J. Phys. 12, 073024 (2010).
Chu, W. et al. Iron Isotope Effect and Local Lattice Dynamics in the (Ba, K)Fe2As2 Superconductor Studied by Temperature-Dependent EXAFS. Scientific Reports 3, 1750 (2013).
Singh, B., Shirage, P. M., Iyo, A. & Kumar, P. Iron isotope effect in SmFeAsO0.65 and SmFeAsO0.77H0.12 superconductors: A Raman study. AIP Advances 6, 105310 (2016).
Khasanov, R. Isotope Effect on the Transition Temperature Tc in Fe-Based Superconductors: The Current Status. High-Tc Copper Oxide Superconductors and Related Novel Materials 255 (Springer, Cham, 2017).
Khasanov, R., Bendele, M., Bussmann-Holder, A. & Keller, H. Intrinsic and structural isotope effects in iron-based superconductors. Phys. Rev. B 82, 212505 (2010).
Yanagisawa, T. et al. Isotope Effect in Multi-Band and Multi-Channel Attractive Systems and Inverse Isotope Effect in Iron-Based Superconductors. J. Phys. Soc. Jpn. 78, 094718 (2009).
Bussmann-Holder, A. & Keller, H. Comment on “Isotope Effect in Multi-Band and Multi-Channel Attractive Systems and Inverse Isotope Effect in Iron-Based Superconductors”. J. Phys. Soc. Jpn. 79, 126001 (2010).
Zimanyi, G. T., Kivelson, S. A. & Luther, A. Superconductivity from Predominantly Repulsive Interactions in Quasi One-Dimensional Systems. Phys. Rev. Lett. 60, 2089–2092 (1988).
Seidel, A., Lin, H.-H. & Lee, D.-H. Phonons in Hubbard ladders studied within the framework of the one-loop renormalization group. Phys. Rev. B 71, 220501(R) (2005).
Cai, Y., Huang, W.-M. & Lin, H.-H. Renormalization-group exponents for superconducting phases in two-leg ladders. Phys. Rev. B 85, 134502 (2012).
Okamoto, J., Mathey, L. & Huang, W.-M. Influence of electron-phonon coupling on the low-temperature phases of metallic single-wall carbon nanotubes. Phys. Rev. B 98, 205122 (2018).
Kuroki, K. et al. Unconventional Pairing Originating from the Disconnected Fermi Surfaces of Superconducting LaFeAsO1−xFx. Phys. Rev. Lett. 101, 087004 (2008).
Ding, H. et al. Observation of Fermi-surface? Dependent nodeless superconducting gaps in Ba0.6K0.4Fe2As2. Europhys. Lett. 83, 47001 (2008).
Balents, L. & Fisher, M. P. A. Weak-coupling phase diagram of the two-chain Hubbard model. Phys. Rev. B 53, 12133–12141 (1996).
Lin, H.-H., Balents, L. & Fisher, M. P. A. N-chain Hubbard model in weak coupling. Phys. Rev. B 56, 6569–6593 (1997).
Lin, H.-H., Balents, L. & Fisher, M. P. A. Exact SO(8) symmetry in the weakly-interacting two-leg ladder. Phys. Rev. B 58, 1794–1825 (1998).
Shih, H.-Y., Huang, W.-M., Hsu, S.-B. & Lin, H.-H. Hierarchy of relevant couplings in perturbative renormalization group transformations. Phys. Rev. B 81, 121107(R) (2010).
Wang, F., Zhai, H., Ran, Y., Vishwanath, A. & Lee, D.-H. Functional Renormalization-Group Study of the Pairing Symmetry and Pairing Mechanism of the FeAs-Based High-Temperature Superconductor. Phys. Rev. Lett. 102, 047005 (2009).
He, S. et al. Phase diagram and electronic indication of high-temperature superconductivity at 65 K in single-layer FeSe films. Nature Materials 12, 605 (2013).
Tan, S. et al. Interface-induced superconductivity and strain-dependent spin density waves in FeSe/SrTiO3 thin films. Nature Materials 12, 634 (2013).
Lee, J. J. et al. Interfacial mode coupling as the origin of the enhancement of T c in FeSe films on SrTiO3. Nature 515, 245 (2014).
Fan, Q. et al. Plain s-wave superconductivity in single-layer FeSe on SrTiO3 probed by scanning tunnelling microscopy. Nature Physics 11, 946 (2015).
Lee, D.-H. What makes the Tc of FeSe/SrTiO3 so high? Chin. Phys. B 24, 117405 (2015).
Tian, Y. C. et al. Ultrafast Dynamics Evidence of High Temperature Superconductivity in Single Unit Cell FeSe on SrTiO3. Phys. Rev. Lett. 116, 107001 (2016).
Tang, C. et al. Interface-enhanced electron-phonon coupling and high-temperature superconductivity in potassium-coated ultrathin FeSe films on SrTiO3. Phys. Rev. B 93, 020507(R) (2016).
Wang, Q.-Y. et al. Interface-Induced High-Temperature Superconductivity in Single Unit-Cell FeSe Films on SrTiO3, Chin. Phys. Lett. 29, 037402 (2012).
Acknowledgements
We acknowledge supports from the National Science Council in Taiwan through grant MOST 107-2112-M-005-008-MY3 and MOST 106-2112-M-007-011-MY3. Financial supports and friendly environment provided by the National Center for Theoretical Sciences in Taiwan are also greatly appreciated.
Author information
Authors and Affiliations
Contributions
Both W.M.H. and H.H.L. contribute extensively to the work in all aspects. W.M.H. and H.H.L. prepare the manuscript together.
Corresponding authors
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Huang, WM., Lin, HH. Anomalous isotope effect in iron-based superconductors. Sci Rep 9, 5547 (2019). https://doi.org/10.1038/s41598-019-42041-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-019-42041-z
This article is cited by
-
Pairing mechanism in multiband superconductors
Scientific Reports (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.