Abstract
Benign and malignant tumors differ in the viscoelastic properties of their cellular microenvironments and in their spatiotemporal response to very low frequency stimuli. These differences can introduce a unique viscoelastic biomarker in differentiation of benign and malignant tumors. This biomarker may reduce the number of unnecessary biopsies in breast patients. Although different methods have been developed so far for this purpose, none of them have focused on in vivo and in situ assessment of local viscoelastic properties in the ultra-low (sub-Hertz) frequency range. Here we introduce a new, noninvasive model-free method called Loss Angle Mapping (LAM). We assessed the performance results on 156 breast patients. The method was further improved by detection of out-of-plane motion using motion compensation cross correlation method (MCCC). 45 patients met this MCCC criterion and were considered for data analysis. Among this population, we found 77.8% sensitivity and 96.3% specificity (p < 0.0001) in discriminating between benign and malignant tumors using logistic regression method regarding the pre known information about the BIRADS number and size. The accuracy and area under the ROC curve, AUC, was 88.9% and 0.94, respectively. This method opens new avenues to investigate the mechanobiology behavior of different tissues in a frequency range that has not yet been explored in any in vivo patient studies.
Similar content being viewed by others
Introduction
Almost one century ago D’Arcy Thomson proposed that the spatiotemporal alterations in tissue mechanics inevitably alter its mechanoenvironemtal properties. These local biphasic mechanical properties, such as stiffness and fluidity, determine the system response to generated forces. This theory has been accepted widely1,2,3,4,5,6,7.
Rheological techniques are rarely used for medical diagnosis of living tissue due to the invasive nature of rheological tests such as indentation experiments, torsional resonators and oscillatory shear testing devices8,9,10. These methods do allow for exploration of the viscoelastic properties of the medium in a wide range of frequencies, including the ultra-low frequency range (less than 1 Hz). Although a rheometer can assess the viscoelastic behavior of a medium in ultra-low frequency ranges, it is a time consuming and cumbersome process to use it in such a low frequency range11,12,13.
Over a decade ago, non-invasive elastography methods were developed with the capability of remotely inducing shear waves in tissue and measuring its elasticity by recording the deflection response by MRI14 and ultrasound15. Later the in vivo application of elastography in measuring the stiffness of different tissues and organs like liver16,17,18, breast19,20, brain21,22, heart23,24 and muscle25,26 were reported. Although elasticity measurements were the focus of these efforts, a few studies considered the estimation of both elasticity and viscosity of in vivo tissues20,22,27,28.
While it is possible to use shear wave elastography methods for in vivo cases, the frequency range to explore the viscoelasticity of tissue is much narrower than with rheology methods20,22,27. With shear wave elastography methods, reaching the ultra-low frequency range is almost impossible because there is always a tradeoff between the resolution of the resulting map and the frequency of vibration and shear waves29.
In this paper, we introduce the noninvasive, Loss Angle Mapping (LAM) method, which is based on measuring the local displacement and strain behaviors under constant stress as a function of frequency. Technical details were explained in our previous work30. The LAM method can monitor the viscoelastic properties of the tissue with high resolution due to its high accuracy in displacement measurement at the micrometer level. High frame rate ultrasound strain imaging, which is the essential part of the LAM method, allows capturing the local viscoelastic parameters in vivo like breast tissue. The main components of the LAM test are a compression mechanism that is used to exert an approximately step-force on the tissue and a high-frame rate ultrasound system for monitoring the internal local strain responses. In other words, a step-force is used as a stimulus for a certain amount of time, and the transient strain response, which is governed by viscoelastic properties of the medium, is monitored by analyzing a sequence of radiofrequency (RF) data during the excitation31,32. In the LAM method the local tissue behavior in the sub-Hertz frequency range is used because at this frequency range the local biphasic behavior of tissue is more evident compared to other frequency ranges33,34,35,36,37.
Results
Viscoelastic gel phantom
Gel phantom can be used as a simplified mechanical model for breast tissue. Gel consists of collagen type I matrix that is saturated in water38, similar to breast tissue. The matrix peptide chain in this type of collagen is responsible for the dense electric charge associated with the hydrophilic properties of collagen fibers and culminates in the viscoelastic properties of the medium39. The same mechanism can happen in breast tissue in which the glycoproteins are responsible for viscoelastic properties due to their hydrophilic nature39. The viscosity of the fluid for these two media, however, is different. The solid matrix in both gel and tissue makes a porous structure which helps move the fluid when the medium is compressed or under load40. Fluid viscosity is responsible for the viscoelastic response of the media or tissue. In addition the hydrogen crosslinks between the fibers in a solid matrix can trigger the viscoelastic response40.
To verify the performance of the proposed model-free method, a viscoelastic inclusion phantom was made. The inclusion part of the phantom was made with 25.14 grams of gelatin (Sigma-Aldrich, St. Louis, MO), 60 ml propylene glycol (Sigma-Aldrich, St. Louis, MO), and 4 grams cellulose (ultrasound scattering; Sigma-Aldrich) in distilled water for a total volume of 300 ml. The background part of the phantom was made with 32.3 grams gelatin, 30 ml Vanicream Lite (Pharmaceutical Specialties, Inc., Rochester, MN), 6 grams cellulose (ultrasound scatterer; Sigma-Aldrich) and potassium sorbate (preservative; Sigma-Aldrich) in distilled water with a total volume of 600 ml30. The inclusion phantom dimensions were 7.5 cm × 5.5 cm × 5.5 cm (L × W × H), with the cylindrical inclusion having a diameter of 1.5 cm.
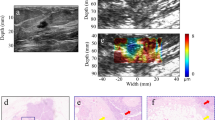
An ultrasound B-mode image of the gel phantom can be seen in Fig. 1. For demonstration purposes, two points were selected: point 1 in the background and point 2 in the inclusion. The results of the temporal strain profile for these points can be seen in Fig. 2a. Loss angle profiles for these 2 points were obtained in the frequency range less than 10 Hz (Fig. 2b) and less than 0.35 Hz (c). Similar to the above mentioned 2 points the viscoelastic map created by processing all the spatial points at a frequency of 0.033 Hz using the LAM method as shown in Fig. 2(d).
Profiles obtained on the inclusion gel phantom. (a) Temporal strain profile of point 1 (background, red) and point 2 (inclusion, blue) in the phantom imaged in Fig. 1. (b) Loss angle profile of point 1 (background, red) and point 2 (inclusion, blue) in a frequency range less than 10 Hz. (c) Loss angle profile of point 1 (background, red) and point 2 (inclusion, blue) in a frequency range less than 0.35 Hz. (d) Viscoelastic map produced at 0.033 Hz based on the LAM method.
In vivo patient study
Patient study
The phantom study results encouraged us to apply the LAM method on breast patients. The patient study was approved by the Institutional Review Board of the Mayo Clinic, Rochester MN, and informed consent was signed by each enrolled patient. This study was also compliant with the Health Insurance Portability and Accountability Act (HIPPA) in the Mayo Clinic.
A total of 156 female patients with visible breast lesions in US images were recruited at Mayo Clinic from November 2014 to September 2016. The data from the first five patients were used to test the device and algorithm and were eliminated from the final study. Thus, a total of 151 breast patients were included in the study. Amongst them after applying the motion compensated cross-correlation metric (MCCC), 45 patients were selected for analysis. The rest of the patients were rejected. The mean patient age was 56 ± 15 years within the age range of 25–85 years.
Breast lesions were categorized using the Breast Imaging Reporting and Data System (BI-RADS). Figure 3 illustrates the distribution of lesion type in this patient population and Table 1 shows the BI-RADS distribution among them.
BI-RADS determination of lesions. The BI-RADS value was determined for each lesion according to the sonographic features found in clinical US images obtained during a clinical procedure at Mayo Clinic. The patient’s eligibility for biopsy was decided based on this value. For BI-RADS 5 and 6, a biopsy is always prescribed; as such, cases are highly suggestive of malignancy. A BI-RADS value of 3 or 4 is challenging as this covers a wide range of suspicion, including low, intermediate, and moderate. In our study, all the BI-RADS 3 and BI-RADS 4 were biopsied.
The LAM technique was performed after determination of the lesion BI-RADS and location, and prior to the biopsy procedure.
Histology. Surgical excision biopsy or US-guided core needle biopsy was performed as a part of clinical care and the histology results for all patients in this study were available. In the latter cases, five core biopsy samples of each lesion were acquired by one of our certified radiologists. An experienced Mayo Clinic pathologist with more than 15 years of experience provided the histopathological diagnosis. Surgical histopathology was considered conclusive over core needle biopsy.
LAM results. As mentioned before, 156 patients were recruited for the study. The statistical results related to the whole patient population are depicted in supplementary part of this paper. Amongst those patients, 45 patients passed, the criterion set by MCCC metric. Only these female patients with a suspicious breast lesion (15.93 ± 8 mm) visible in ultrasound images were considered in this study. The mean and median age for this group was 56 and 55 years, respectively. The youngest participant was 25 and the oldest was 85 years old. All the patients underwent a biopsy procedure after the LAM test.
Figures 4–7 illustrate examples of the loss angle maps of various malignant and benign lesion types. In all of these images, the LAM map is created at the frequency of 0.033 Hz. for each patient. we examined the clinical image, the corresponding B-mode image as seen using the I-Q data from the programmable ultrasound machine (Verasonics), an overlay of the estimated loss angle, a loss angle map with unreliable areas excluded (white areas in Figs 4(d),5(d),6(d) and 7(d)), a graph of the normalized applied stress, and representative temporal normalized strain curves from the lesion and normal tissue areas and corresponding estimated loss angle as a function of frequency.
Imaging of a benign tumor. (a) Ultrasound clinical B-mode image of a benign tumor. (b) Ultrasound Verasonics B-mode image of the same tumor. (c) 2D color map of the loss angle overlay on the B-mode image produced at 0.033 Hz based on the LAM method. (d) 2D color map of the loss angle produced at 0.033 Hz. (e) Normalized strain temporal behavior of the two specified points in (d) accompanied with a normalized stress profile. (f) Spectral behavior of the two specified points in (d) in a frequency range less than 1 Hz.
Imaging of a malignant tumor. (a) Ultrasound clinical B-mode image of a malignant tumor. (b) Ultrasound Verasonics B-mode image of the same tumor. (c) 2D color map of the loss angle overlay on the B-mode image produced at 0.18 rad/s (~0.03 Hz) based on the LAM method. (d) 2D color map of the loss angle produced at 0.03 Hz. (e) Normalized strain temporal behavior of two specified points in (d) accompanied with the normalized stress profile. (f) Spectral behavior of two specified points in (d) in a frequency range less than 1 Hz.
Imaging of a malignant tumor. (a) Ultrasound clinical B-mode image of a malignant tumor. (b) Ultrasound Verasonics B-mode image of same tumor. (c) 2D color map of the loss angle overlay on B-mode image produced at 0.033 Hz based on the LAM method. (d) 2D color map of the loss angle produced at 0.033 Hz. (e) Normalized strain temporal behavior of two specified points in (d) accompanied with the normalized stress profile. (f) Spectral behavior of two specified points in (d) in a frequency range less than 1 Hz.
Imaging of benign tumor. (a) Ultrasound clinical B-mode image of benign tumor. (b) Ultrasound Verasonics B-mode image of the same tumor. (c) 2D color map of the loss angle overlay on the B-mode image produced at 0.033 Hz based on the LAM method. (d) 2D color map of the loss angle produced a0.033 Hz. (e) Normalized strain temporal behavior of two specified points in (d) accompanied with the normalized stress profile. (f) Spectral behavior of two specified points in (d) in a frequency range less than 1 Hz.
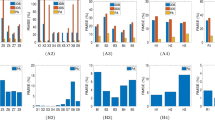
Among 45 patients, 27 cases were diagnosed as benign and 18 as malignant. LAM method, Eqs (1 and 2), is used to estimate the complex modulus parameters (storage, loss) as was illustrated in Figs 4–7 for delta, δ. The overall results are depicted in following figures. Figure 8 shows the result based on the contrast, average and standard deviation measured in tumor part.
In the next step, the Logistic regression is applied on all of these aforementioned parameters shown in Fig. 8. The relevant ROC (Receiver Operating Characteristic) curve for each analysis is illustrated in Fig. 9.
The measured sensitivity is 77.8%, and the estimated specificity is 96.3%. The accuracy comes to 88.9%. The Area under Curve, AUC, is 0.94. The standard error is 0.04. 95% Confidence interval is 0.82 to 0.99. Detailed information is shown in Table 2 in the supplementary part. It should be noted that, the BI-RDAS results were considered in the aforementioned statistical results.
Discussion
Due to biphasic properties of soft tissue, there is always some phase lag between applied stress and the resulting strain. In addition to storage and loss modulus magnitude, the LAM method can leverage the phase lag between these two parameters to study the local viscoelastic properties of living tissue in more details31,41. The resulting contrast based on the storage and loss modulus or their ratio can be even more conspicuous in a lower frequency range. Mizuno et al.11 reported that nonequiliburium fluctuations were observable in cytoskeletal networks in a frequency range less than 10 Hz using an active rheometer. Implementing micro rheology on cardiac thin filaments also demonstrated that, in a frequency range less than 10 Hz, both the storage and loss modulus had been elevated by increasing the Ca2+12. In addition, it has been shown that in living cells, more complex behavior at low frequency ranges can occur42. Rheometry techniques also have been used on variety of tissue samples to validate the newly developed elastography techniques43,44,45. In the most recent study, the rheometer results confirmed the higher contrast in viscosity in the frequency range less than 1 Hz45.
Benign breast tumors are generally more viscous with higher phase lag, Fig. 8(g), than the malignant ones, particularly with fibroadenoma cases31,32. The extra cellular matrix (ECM) is mainly made of a collagen fiber network to which proteoglycan molecules are attached46,47,48,49. The primary part of these molecules is the dense and hydrophilic sulfate groups50. Increasing the concentration of proteoglycan, and consequently the surrounding water molecules in ECM, can cause an increase in viscosity31. The collagen fibers in ECM are interconnected toward their ends but sparsely connected in the middle, with strong covalent cross-links, which are responsible for the elastic response of the tissue to stress31.
According to electron microscopy observation of malignant breast lesions such as infiltrating ductal carcinoma, the number of sulfated proteoglycan molecules, which are mainly responsible for viscosity, declines at least five times per unit in connective tissues. Thus, while viscosity decreases in malignant lesions, they can be stiffer than surrounding tissue due to increased collagen fibers and covalent cross-links46,49,50. There is, however, no sign of elevation in viscosity in the formation course of this kind of lesions46,49. The common feature in benign solid lesions, such a fibroadenomas, is higher collagen density compared to surrounding tissues. An increase in the number of fibers leads to a greater number of proteoglycan molecules and decreased inter-fiber distance. The lower distance between collagen fibers will cause a greater H-bonded cross-link density. Generally, H-bonds help in stabilizing the ECM matrix by keeping the helical shapes within fibers. This functionality of H-bonded cross-links has an important role in creating an elastic restoring force immediately after being stressed. However, these fragile bonds break and reform during the stress application and some of the strain energy is dissipated. This causes the strain response delay in returning to the initial steady state, (usually in less than 5 seconds31). In other words, this is the reason for viscoelastic response of the external compression, which occurs at a very low frequency range based on its retardation time. Thus, collagen density determines the strength and density of inter-fiber H-bonded links. Some fibrous tumors are not necessarily stiffer than surrounding regions, but due to higher cross-link density, can create a longer delay for a full strain response32,46,47,48,49,50. This phenomenon is the basis of viscoelastic methods like LAM method. Thus, in the case of fibroadenomas and other collagenous benign lesions, the lesion can be stiffer than the surrounding tissues but they are more viscous in contrast to malignant lesions31,32,49 Fig. 8(g) also showed that phenomena. To observe such differences, it is necessary to evaluate tissue’s viscoelastic response in a period of 1–10 s, which corresponds to a frequency range less than 1 Hz32,34.
This work on breast patients showed that considering the viscoelastic behavior of tissue by estimating the complex elasticity parameters like storage, loss and delta in an ultra-low frequency range could provide reliable biomarkers for differentiation of benign and malignant tumors in breast patients. The distinctive characteristic of the LAM method is its sensitivity to viscoelastic properties of breast tissue in this range of frequency. This characteristic correlates well with the biochemical construction of benign and malignant breast lesions. The sensitivity and specificity of this method in differentiation of benign and malignant lesions were 77.8% and 96.3% respectively.
A possible contributing factor in misclassifications is measurement error. Lesion mobility can adversely affect the quality of recorded data. Patient motion during a test can also negatively affect data quality. Some patients were not able to hold their breath for the entire duration of data collection, which resulted in tissue motion. Cardiac motion was not considered as a major source of error as the frequency of such motion is around 1 Hz, which is somewhat outside the frequency band of these ultra-low frequency range calculation, less than 0.05 Hz.
Due to all aforementioned reasons, we tried to apply more restrictions on our motion measurement algorithm. The initial patient population that was considered for this study was 156 patients. The statistical outcomes of these patients are shown in Figs S1 and S2, Tables S1 and S2 in supplementary part. However, applying MCCC algorithm in order to detect the out-of-plane and non-axial motion while doing compression was a great assistance to identify cases with mostly axial compression with minimal out-of-plane motions. While this is done retrospectively, if implemented to operate in real-time, such metric can be utilized to ensure proper lesion compression and data collection. Reconsidering these data and using MCCC algorithm resulted in 45 cases out of 156 cases as they have been discussed already. In addition, a multi-parameters analysis using the features obtained from the all creep data (i.e. storage, loss modulus and delta) in conjunction with contrast, average and standard deviation measurement, provided and enhanced classification of the breast tumors in this study, Figs 8 and 9. Future studies would include expanding the cohort and studying the sources of error in our measurement. This multi factorial analysis is another advantage of the LAM method.
LAM can be utilized in conjunction of other ultrasound-derived lesion characteristics such as BI-RADS and size. Comparing Tables 2 and 3, with and without considering BI-RADS respectively shows that both the specificity and sensitivity have been elevated from 89.29% to 96.3% and 68.42% to 77.78% respectively. The combined value of LAM and ultrasound imaging features promise better diagnosis without requiring more expensive and contrast-based imaging modalities such as contrast-enhanced magnetic resonance imaging.
Another important aspect of this study is the automated ROI (Region of Interest) selection to remove the subjectivity associated with manual selection of data processing. In other words, all of the patient data was processed in a consistent manner without human input for selecting the region of interest or changing other parameters involved in data processing. First, the eligibility of data was tested for out-of-plane motions and then the processing began automatically either in selecting the lesion from normal part or in setting the creep legitimate time duration in which the monotonous increasing of compliance curve was counted. This procedure went through all the collected patient data.
It should be noted that as the results show, the LAM method could be a very effective method in the context of non-invasive diagnostic/prognostic mechanical testing especially for soft tissue; however, it may not be a solid candidate for mechanical property estimation in general.
In addition, the LAM method was observed to present a solid contrast between benign and malignant lesions at frequency range less than 0.033 Hz, however it needs more comprehensive studies to find the optimum frequency with highest contrast in this ultra-low frequency range. This would be explored in future work.
Methods
LAM technique
In this patient study, an automated compression device was used to apply a ramp-and-hold force excitation for a duration of time automatically set based on monotonically elevation of creep response. The ultrasound probe is part of this device for recording the viscoelastic response of the underlying tissue. This device is portable, light-weight and easy to use for patient studies to explore the tissue dynamics under external stress30.
For the gel study, 8 N force with the speed of 16 N/s ramp was used. For the patient study, 2–4 N force with 8–12 N/s ramp were applied. To monitor the local viscoelastic response, an ultrasound system (Verasonics, Inc., Kirkland, WA, USA) with a linear array transducer (L11-4v, Verasonics, Inc., Kirkland, WA, USA) was used. In these experiments, the ultrasound center frequency was 6.43 MHz and the frame rate was 200 Hz during the acquisition time of 12 seconds.
To track the fast tissue deformation under compression, a two-dimensional autocorrelation method was employed for a particle velocity calculation from adjacent frames. The integration of the particle velocity in time resulted in a displacement estimation51. After performing the displacement estimation for all consecutive IQ data, the gradient of the resulting displacement was computed to measure the corresponding local strain30.
For patient studies, an experienced sonographer with more than 28 years of experience in breast ultrasound assisted with manual delineation of the lesion in B-mode US images obtained from the Verasonics system at the beginning of each patient data acquisition. Using the radiofrequency data, the loss angle maps were reconstructed offline at a frequency range less than one Hertz. Supplementary video is available online.
Dynamic complex measurement
It was shown that the dynamic complex modulus in the frequency domain, E*(ω), can be directly derived using the strain time data (local creep response) in a model-free fashion with some assumption about the experimental creep response13,52,53, Eq. 1.
where J(n) represents the strain data sampled at time point with index n. The parameter \(\eta \) represents the steady state viscosity which is estimated by extrapolation of strain data to t → ∞.
Hence, the loss angle can be directly derived as
where \({E}_{l}^{\ast }(\omega )\) and \({E}_{s}^{\ast }(\omega )\) are the imaginary and the real parts of the complex shear modulus, corresponding to the loss and storage modulus, respectively, and δ is the loss angle which represents the phase difference between the storage and loss modulus of the medium due to its viscoelastic properties13,52.
Measurement
Strain Quality Assessment, SQA. Our main assumption in this study is the linear viscoelastic behavior of the material being tested (phantoms or tissue). Applying an approximate step force results in a temporal strain response, or creep response, which increases monotonically. This behavior is called a normal strain response. Applying this method for in vivo studies, however, requires introduction of additional constraints to avoid estimation of unrealistic values. Here, we define a new parameter as Strain Quality Assessment (SQA). SQA verifies two parameters: the total strain and the slope of the final part of the creep response. For each point in the viscoelasticity map reconstruction domain, SQA assigns a value of one for points that have both a positive total strain value and positive final slope, and zero if either of these criteria is violated. All the white areas in Figs 4(d), 5(d), 6(d) and 7(d) are excluded due to SQA.
Contrast: Contrast refers to a comparison between features of a lesion to those of the surrounding, or background, tissues. For in vivo studies, measuring contrast parameters is important for diagnostic purposes. In some cases, measuring the contrast is even more important than measuring the parameter values32. In order to measure contrast we use the Eq. (3).
In this equation Slesion is the mean value in the lesion area and Sbackground represents the mean value of the normal background tissue surrounding the lesion. To measure contrast, the mean value of S for the lesion and background parts should be determined. This is performed by first determining the lesion boundaries from a registered B-mode image within the region of interest (ROI). The automatic ROI was applied to remove the subjectivity about lesion and normal tissue values. In addition, the creep duration was selected automatically based on monotonic increasing compliance curve. As it has been emphasized before all data in this manuscript was analyzed at 0.033 Hz.
Rejection of data based on MCCC metric: The displacement field obtained from the phase sensitive speckle tracking was utilized to stretch each frame back to its original location, as explained in54. Briefly, the normalized cross correlation was performed between the pre-compressed and motion-compensated post-compressed echoes in the lesion area. This value served as a quality metric to assess the uniaxiality of the induced motions. Given substantial decorrelation that may occur during compression, a minimum normalized cross correlation value of 10% was chosen to declare a successful uniaxial deformation. Using this criterion, cases/acquisitions that did not meet a required threshold value of MCCC metric were excluded from the analysis.
Statistical Analysis
MedCalc Statistical Software version 15.8 (MedCalc Software bvba, Ostend, Belgium; https://www.medcalc.org; 2015) was employed for statistical analysis. The receiver operator curve (ROC) was used to find the best diagnostic discrimination threshold for the estimated loss angle contrast in comparison with the pathology outcomes. The confidence intervals for sensitivity and specificity were found using bias-corrected and accelerated bootstrapping of 1000 trials. Resulting sensitivity, specificity and area under the curve were reported.
The Wilcoxon analysis was performed with 95% confidence interval to represent a statistically significant difference for all analysis. All multi-parameter analyses were performed using a logistic regression method in MedCalc.
References
Thompson, D. W. On Growth and Form. (Dover, 1942).
Gonzalez‐Rodriguez, D., Guevorkian, K., Douezan, S. & Brochard‐Wyart, F. Soft matter models of developing tissues and tumors. Science. 338, 910–917 (2012).
Heisenberg, C. & Bellaïche, Y. Forces in tissue morphogenesis and patterning. Cell. 153, 948–962 (2013).
Guillot, C. & Lecuit, T. Mechanics of epithelial tissue homeostasis and morphogenesis. Science. 340, 1185–1189 (2013).
Miller, C. J. & Davidson, L. A. The interplay between cell signaling and mechanics in developmental processes. Nat. Rev. Genet. 14, 733–744 (2013).
Polacheck, W. J. & Chen, C. S. Measuring cell‐generated forces: a guide to the available tools. Nat. Methods. 13, 415–423 (2016).
Serwane, F. et al. In Vivo quantification of spatially varying mechanical properties in developing tissues. Nat. Methods. 14, 181–186 (2016).
Valtorta, D. & Mazza, E. Measurement of rheological properties of soft biological tissue with a novel torsional resonator device. Rheol. Acta. 45, 677 (2006).
Liu, Z. & Bilston, L. On the viscoelastic character of liver tissue: experiments and modelling of the linear behavior. Biorheology. 37, 191–201 (2000).
Nicolle, S., Lounis, M., Willinger, R. & Palierne, J. F. Shear linear behavior of brain tissue over a large frequency range. Biorheology. 42, 209–223 (2005).
Mizuno, D. et al. Nonequilibrium mechanics of active cytoskeletal networks. Science. 315, 370–373 (2007).
Tassieri, M. et al. The self-assembly, elasticity, and dynamics of cardiac thin filaments. Biophysical journal. 94, 2170-2178 (2008).
Tassieri, M. et al. I-Rheo: Measuring the materials’ linear viscoelastic properties “in a step”! J. Rheol. 60, 649–660 (2016).
Muthupillai, R. et al. Magnetic resonance elastography by direct visualization of propagating acoustic strain waves. Science. 269, 1854–1857 (1995).
Sarvazyan, A. et al. An overview of elastography-an emerging branch of Medical imaging. Current Medical Imaging Reviews. 7, 255–282 (2011).
Ziol, M. et al. Noninvasive assessment of liver fibrosis by measurement of stiffness in patients with chronic hepatitis C. Hepatology. 41, 48–54 (2005).
Rouviere, O. et al. MR elastography of the liver: preliminary results. Radiology. 240, 440–448 (2006).
Klatt, D. et al. In vivo determination of hepatic stiffness using steady-state free precession Magnetic Resonance elastography. Invest. Radiol. 41, 841–848 (2006).
Bercoff, J. et al. In vivo breast tumor detection using transient elastography. Ultrasound Med. Biol. 29, 1387–1396 (2003).
Sinkus, R. et al. Viscoelastic shear properties of in vivo breast lesions measured by MR Elastography. Magn. Reson. Imaging. 23, 159–165 (2005).
McCracken, P. J., Manduca, A., Felmlee, J. & Ehman, R. L. Mechanical transient-based magnetic resonance elastography. Magn. Reson. Med. 53, 628–639 (2005).
Sack, I., Beierbach, B., Hamhaber, U., Klatt, D. & Braun, J. Rapid noninvasive measurement of brain viscoelasticity using magnetic resonance elastography. NMR Biomed. 21, 265–271 (2007).
Arani, A. et al. In vivo, high‐frequency three‐dimensional cardiac MR elastography: Feasibility in normal volunteers. Magn. Reson. Med. 77, 351–360 (2017).
Song, P. et al. Quantitative Assessment of Left Ventricular Diastolic Stiffness Using Cardiac Shear Wave Elastography. J. Ultrasound Med. 35, 1419–1427 (2016).
Uffmann, K. et al. In Vivo elasticity measurements of extremity skeletal muscle with MR elastography. NMR Biomed. 17, 181–190 (2004).
Gennisson, J. L., Cornu, C., Catheline, S., Fink, M. & Portero, P. Human muscle hardness. Assessment during incremental isometric contraction using transient elastography. J. Biomech. 38, 1543–1550 (2005).
Chen, S. et al. Shearwave dispersion ultrasound vibrometry (SDUV) for measuring tissue elasticity and viscosity. IEEE Transaction on Ultrasonics, Ferroelectrics, and FrequencControl. 56, 55–62 (2009).
Kumar, V. et al. Viscoelastic parameters as discriminators of breast masses: Initial human study results. PloS one 13(10), e0205717 (2018).
Klatt, D., Hamhaber, U., Asbach, P., Braun, J. & Sack, I. Noninvasive assessment of the rheological behavior of human organs using multifrequency MR elastography: a study of brain and liver viscoelasticity. Phys. Med. Biol. 52, 7281–7294 (2007).
Nabavizadeh, A. et al. Automated Compression Device for Viscoelasticity Imaging. IEEE Transactions on Biomedical Engineering. 64, 1535–1546 (2017).
Sridhar, M. & Insana, M. F. Ultrasonic measurements of breast viscoelasticity. Med. Phys. 34, 4757–4767 (2007).
Qiu, Y., Sridhar, M., Tsou, J. K., Lindfors, K. K. & Insana, M. F. Ultrasonic Viscoelasticity imaging of nonpalpable breast tumors: preliminary results. Acad. Radiol. 15, 1526–1533 (2008).
Kiss, M. Z., Varghese, T. & Hall, T. J. Viscoelastic characterization of in vitro canine tissue. Phys. Med. Biol. 49, 4207–4218 (2004).
Palacio‐Torralba, J. et al. Quantitative diagnostics of soft tissue through viscoelastic characterization using time‐based instrumented palpation. Journal of the mechanical behavior of biomedical materials. 41, 149–160 (2015).
Deffieux, T., Montaldo, G., Tanter, M. & Fink, M. Shear wave spectroscopy for in vivo quantification of human soft tissues visco-elasticity. IEEE Transactions on Medical Imaging. 28, 313–322 (2009).
Vappou, J., Maleke, C. & Konofagou, E. E. Quantitative viscoelastic parameter measured by Harmonic motion imaging. Phys. Med. Biol. 54, 3579–3594 (2009).
Klatt, D. et al. Viscoelastic properties of liver measured by oscillatory rheometry and multifrequency magnetic resonance elastography. Biorheology. 47, 133–141 (2010).
Fung, Y. C. Biomechanics: Mechanical Properties of Living Tissues. (Berlin:Springer, 1993).
Sridhar, M., Liu, J. & Insana, M. F. Viscoelasticity imaging using ultrasound: parameters and error analysis. Phys. Med. Biol. 52, 2425–2443 (2007).
Muir, H. Proteoglycans as organizers of the intercellular matrix. Biochemical Society Transaction. 11, 613–622 (1983).
Insana, M. F., Liu, J., Sridhar, M. & Pellot‐Barakat, C. Ultrasonic mechanical relaxation imaging and the material science of breast cancer. Ultrasonics Symposium, 2005 IEEE. 739–742 (2005).
Tassieri, M. Microrheology with Optical Tweezers of gel-like materials’ is not an option’!. Optics in the Life Sciences 2015© OSA 2015 (2015).
Chatelin, S. et al. In vivo liver tissue mechanical properties by transient elastography: Comparison with dynamic mechanical analysis. Biorheology. 48, 75–88 (2011).
Vappou, J. et al. Magnetic resonance elastography compared with rotational rheometry for in vitro brain tissue viscoelasticity measurement. Magn. Reson. Mater. Phy. 20, 273–278 (2007).
Shahmirzadi, D. et al. Ex Vivo characterization of canine liver tissue Viscoelasticity after high-intensity focused ultrasound ablation. Ultrasound Med. Biol. 40, 341–350 (2014).
Wang, Y. & Insana, M. F. Viscoelastic properties of rodent mammary tumors using ultrasonic shear‐wave imaging. Ultrasonic Imaging. 35, 126–145 (2013).
Lodish, H. et al. Molecular Cell Biology. (ed. 5th, W.H. Freeman and Co. New York, 2004).
Losa, G. A. & Alini, M. Sulfated proteoglycans in the extracellular matrix of human breast Tissues with infiltrating carcinoma. Int. J. Cancer. 54, 552‐557 (1993).
Drost‐Hansen, W. Temperature effects on cell-functioning - a critical role for vicinal water. Cell. Mol.Biol. 47, 865–883 (2001).
Samani, A., Zubovits, J. & Plewes, D. Elastic moduli of normal and pathological human breast tissues: An inversion technique‐based investigation of 169 samples. Phys. Med. Biol. 52, 1565–1576 (2007).
Loupas, T. et al. An axial velocity estimator for ultrasound blood flow imaging, based on a full evaluation of the Doppler equation by means of a two-dimensional autocorrelation approach. IEEE transactions on ultrasonics, ferroelectrics, and frequency control. 42, 672–688 (1995).
Evans, R., Tassieri, M., Auhl, D. & Waigh, T. A. Direct conversion of rheological compliance measurements into storage and loss moduli. Physical Review E. 80, 12501–12504 (2009).
Amador, C., Urban, M. W., Chen, S. & Greenleaf, J. F. Loss tangent and complex Modulus estimated by acoustic radiation force creep and shear wave dispersion. Phys. Med. Biol. 57, 1263–1282 (2012).
Bayat, M. et al. Multi-Parameter Sub-Hertz Analysis of Viscoelasticity with a Quality Metric for Differentiation of Breast Masses, (need to be submitted).
Acknowledgements
The authors would like to express their appreciation to Mr. Duane Meixner for ultrasound scanning of the breast patients, and Mr. Randall Kinnick for his technical support. This work was supported by grant R01CA168575 from the National Cancer Institute (NCI) and the National Institutes of Health (NIH).
Author information
Authors and Affiliations
Contributions
A.N. phantom experiment, patient data collection, writing computer code, analyzing LAM data, statistical analysis, writing the manuscript. M.B. patient data collection, statistical analysis, writing comuter code and analyzing LAM data. V.K. patient data collection. A.G. patient data collection and statistical analysis. J.W. patient data collection. A.A. funding acquisition, leading human study, study design, team supervision, and manuscript editing. M.F. funding acquisition, leading the project, study design, and editing manuscript.
Corresponding author
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Nabavizadeh, A., Bayat, M., Kumar, V. et al. Viscoelastic biomarker for differentiation of benign and malignant breast lesion in ultra- low frequency range. Sci Rep 9, 5737 (2019). https://doi.org/10.1038/s41598-019-41885-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-019-41885-9
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.