Abstract
A simple Discrete-Time Quantum Walk (DTQW) on the line is revisited and given an hydrodynamic interpretation through a novel relativistic generalization of the Madelung transform. Numerical results show that suitable initial conditions indeed produce hydrodynamical shocks and that the coherence achieved in current experiments is robust enough to simulate quantum hydrodynamical phenomena through DTQWs. An analytical computation of the asymptotic quantum shock structure is presented. The non-relativistic limit is explored in the Supplementary Material (SM).
Similar content being viewed by others
Introduction
Quantum walks (DTQWs) are unitary quantum automata that can be viewed as formal generalizations of classical random walks. Following the seminal work of Feynman1 and Aharonov2 they were considered in a systematic way by Meyer3. DTQWs have been realized experimentally with a wide range of physical objects and setups4,5,6,7,8,9,10, and are studied in a large variety of contexts, ranging from quantum optics10 to quantum algorithmics11,12, solid-state physics13,14,15,16 and biophysics17,18. The aim of this Letter is to show on a simple example, through both literal and numerical computations, that QW dynamics can be mapped unto quantum fluid dynamics (QFD) and that QWs can thus be used to model and experimentally simulate quantum fluids. In particular, DTQWs are thus natural candidates for future laboratory simulation of matter wave interferences in quantum fluids, dispersive hydrodynamics19 and extreme astrophysical plasmas (see e.g. §3.2.3 and §3.2.4 in20).
We focus on a simple spatially homogeneous and time independent DTQW on the line whose continuous limit is identical to the free Dirac equation in flat 2D space-time. We then introduce a new relativistic generalization of the Madelung transform which maps this Dirac equation into a 2D dispersive hydrodynamics for relativistic quantum fluids. In the non relativistic limit, the two component spinor which obeys the Dirac equations degenerates into a single wave-function which obeys the Schrödinger equation, which can also be viewed as the continuous space limit of a continuous time quantum walk. The relativistic Madelung transform then becomes the usual Galilean Madelung transform. To prove that the hydrodynamical vision goes beyond a mere rewriting of the equations, we demonstrate through direct numerical simulations that the DTQW can actually model QFD shocks. We also present an analytical computation of the asymptotic Galilean shock structure through Pearcey integral commonly used in Optics.
Methods
The DTQW
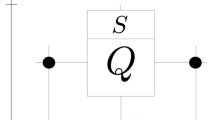
The Hilbert space of the DTQW is the tensor product \({ {\mathcal H} }_{p}\otimes { {\mathcal H} }_{s}\), where \({ {\mathcal H} }_{p}\) is the discrete line with basis n, \(n\in {\mathbb{Z}}\) and \({ {\mathcal H} }_{s}\) is the ‘spin’-space with basis vectors \(|L\rangle ={(1,0)}^{T}\) and \(|R\rangle ={(0,1)}^{T}\). The evolution is controlled by the unitary operator \(U=TC\), where \(T={\sum }_{n}\,[|n-1,L\rangle \,\langle n,L|+|n+1,R\rangle \,\langle n,R|]\) is the translation operator and \(C={e}^{-i\theta {\sigma }_{1}}\) is the quantum coin operator defined from the first Pauli matrix σ1 and an arbitrary constant angle θ. The explicit evolution equation of the walk reads:
where the index l represents the iteration or discrete time.
Continuous Limit
Introduce now two positive real numbers m and \(\varepsilon \), choose \(\theta (\varepsilon ,m)=\varepsilon m\), consider that \({{\rm{\Psi }}}_{L/R}(l,n)\) are the values taken by some differentiable functions \({{\rm{\Psi }}}_{L/R}(t,x)\) at point \({t}_{l}=l\varepsilon \) and \({x}_{n}=n\varepsilon \). Equation (1) then admits a continuous limit which coincides with the Dirac equation21
where \(\psi ={({{\rm{\Psi }}}_{L},{{\rm{\Psi }}}_{R})}^{T}\), \({\gamma }^{0}={\sigma }_{1}\), \({\gamma }^{1}=i{\sigma }_{2}\) (σ2 is the second Pauli matrix) and \(\hslash =c=1\). The mass m is thus homogeneous to the inverse of a length.
Dirac Eq. (2) can be obtained from the Lagrangian density \( {\mathcal L} =\frac{i}{2}(\overline{\psi }{\gamma }^{\mu }{\partial }_{\mu }\psi -{\partial }_{\mu }\overline{\psi }{\gamma }^{\mu }\psi )-m\overline{\psi }\psi \) where \(\overline{\psi }={\psi }^{\dagger }{\gamma }^{0}\). The associated particle current is \({j}^{\mu }=\overline{\psi }{\gamma }^{\mu }\psi \) and the stress energy tensor reads \({T}^{\mu \nu }=\frac{i}{4}[\overline{\psi }{\gamma }^{\mu }{\partial }^{\nu }\psi -\)\({\partial }^{\nu }\overline{\psi }{\gamma }^{\mu }\psi +(\mu \leftrightarrow \nu )]\). Both j and T are conserved i.e. \({\partial }_{\mu }{T}^{\mu \nu }=0\) and \({\partial }_{\mu }{j}^{\mu }=0\). Note that the above Lagrangian density leads to a symmetric canonical stress-energy tensor.
Results
New variables
The definition of j leads to \({j}^{0}=|{\psi }_{R}{|}^{2}+|{\psi }_{L}{|}^{2}\) and \({j}^{1}=|{\psi }_{R}{|}^{2}-|{\psi }_{L}{|}^{2}\). Note that \({({j}^{0})}^{2}-{({j}^{1})}^{2}=\)\(4|{\psi }_{L}{|}^{2}|{\psi }_{R}{|}^{2}\ge 0\) so that the current j is necessarily timelike or null. We then introduce \({\phi }_{\pm }={\phi }_{L}\pm {\phi }_{R}\) where \({\phi }_{L/R}\) is the phase of \({{\rm{\Psi }}}_{L/R}\) and replace the variables \((|{\psi }_{L}{|}^{2},|{\psi }_{R}{|}^{2},{\varphi }_{L},{\varphi }_{R})\) by \(({j}^{0},{j}^{1},{\phi }_{+},{\phi }_{-})\). In particular, the spinor \(\psi \) now reads
and \({\phi }_{+}/2\) can be viewed as the global phase of \(\psi \).
In terms if these new variables, the Lagrangian density and the stress energy tensor read \( {\mathcal L} =-\,m{({j}_{\mu }{j}^{\mu })}^{1/2}\)\(\cos \,{\phi }_{-}-\frac{1}{2}({j}^{\mu }{\partial }_{\mu }{\phi }_{+}-{\varepsilon }^{\mu \nu }{j}_{\nu }{\partial }_{\mu }{\phi }_{-})\) and \({T}^{\mu \nu }=-\,\frac{1}{4}({j}^{\mu }{\partial }^{\nu }{\phi }_{+}-{\varepsilon }^{\mu \alpha }{j}_{\alpha }{\partial }^{\nu }{\phi }_{-}+(\mu \leftrightarrow \nu ))\), where \({\varepsilon }^{\mu \nu }\) denotes the completely antisymmetric symbol of rank two, with the convention \({\varepsilon }^{01}=-\,{\varepsilon }^{10}=1\).
The dynamical equations derived from \( {\mathcal L} ({j}^{0},{j}^{1},{\phi }_{+},{\phi }_{-})\) are
Dirac quantum hydrodynamics
Since j is time-like or null, one can define the density n of the (1 + 1)D Dirac fluid by \(n={({j}_{\mu }{j}^{\mu })}^{1/2}\). We now suppose that j is not null and define the vector \(u=j/n\) as the 2-velocity of the fluid, normed to unity. The two variables j0 and j1 can then be replaced by n and u1 i.e. the density and the spatial part of the fluid 2-velocity. Equation (5) can then be re-written as \(m\,\cos \,{\phi }_{-}\,{u}^{\mu }=-\,\frac{1}{2}\,({\partial }^{\mu }{\phi }_{+}+{\varepsilon }^{\mu \nu }{\partial }_{\nu }{\phi }_{-})\) and, in this form, brings to mind the standard relation \(\frac{w}{n}{u}^{\mu }=-\,{\partial }^{\mu }\phi \) which links the velocity u of a relativistic potential flow to its potential \(\phi \), the enthalpy per unit volume w and the particle density n. We thus retain \(w=mn\,\cos \,{\phi }_{-}\) as the enthalpy per unit volume of the (1 + 1)D Dirac fluid. The velocity field u then derives from two potentials. One is \({\phi }_{+}/2\) i.e. the global phase of the spinor \(\psi \) and contributes to u in the standard way. The other potential is the phase differential \({\phi }_{-}/2\) and contributes to u in a non-standard way, by contraction of its gradient with the (1 + 1)D completely antisymmetric symbol.
Using ((5)), one then finds that
to be compared with the stress-energy tensor \({T}^{\mu \nu }=w{u}^{\mu }{u}^{\nu }-p{\eta }^{\mu \nu }\) of a relativistic perfect fluid of pressure p. The pressure of the Dirac fluid thus vanishes. This is not surprising because classical pressure in spin-0 superfluids is generated by non-linearities22,23,24 in the wave equation and the free Dirac Eq. (2) is linear.
The last two terms on the right-hand side of (7) depend on the gradient of \({\phi }_{-}\) and, thus, on the gradient of w/n. Indeed, the definition of w leads to \({\sin }^{2}\,{\phi }_{-}=1-{(\frac{w}{mn})}^{2}\) and \(\sin \,{\phi }_{-}d{\phi }_{-}=-\,d(\frac{w}{mn})\), so that, if \(w\ne nm\),
where σ is the sign of \(\sin \,{\varphi }_{-}\). As for relativistic spin 0 superfluids25, the two extra-terms in the above expression of the stress-energy tensor thus depend on the gradient of a thermodynamic function (the enthalpy per particle w/n) and are therefore best viewed as generalized ‘quantum pressure’ terms. As shown in the SM the two component spinor which obeys Dirac equation degenerates, in the Galilean limit, into a single wave-function which obeys the Schrödinger equation and the relativistic hydrodynamics degenerates into the standard26,27,28 Madelung hydrodynamics.
Numerical shock simulation
The above generalization of the Madelung transform strongly suggests that the original DTQW can be used to simulate quantum flows. First note that a general positive energy plane wave solution of (2) can be written as (see (3–6)) \({j}^{0}=n\sqrt{1+{q}^{2}}\), \({j}^{1}=nq\), \({\phi }_{+}/2=-\,m(\sqrt{1+{q}^{2}}t-qx)\), \({\phi }_{-}=0\), where q denotes both wave-number and momentum in unit of m (remember \(\hslash =c=1\)). The spinor
thus describes, at \(t=0\), a unit density fluid (\(n=1\)) in motion with constant velocity u1 given by \({u}^{1}=q=\partial \varphi /\partial x\).
In order to simulate quantum flows, we now select the initial conditions of the form (9) but with
with \({q}_{{\rm{\max }}}=m{u}_{{\rm{\max }}}\) this choice corresponds to the velocity field \({u}^{1}={u}_{{\rm{\max }}}(\sin (x)-\,\sin (3x)-\,\sin (2x+0.9))\). These initial conditions are inspired by the similar (but somewhat simpler) choice \(\varphi ={q}_{{\rm{\max }}}\,\cos (x)/m\) which has already been used in the cosmological context to simulate the dynamics of (i) a non-quantum cosmological fluid?, (ii) a Bose-Einstein condensates of axions? Figure 1 shows the evolution of the initial condition (10) through the DTQW for various values of m and constant qmax (the larger the mass, the less relativistic the propagation) and displays multiple shocks. The evolution of (11) is shown in Fig. 2 (compare Fig. 2a,b), which displays a single symmetric shock. Thus, both figures reveal that the DTQW can indeed be used to simulate hydrodynamical shocks in a quantum fluid29,30.
Unitary evolution of density \({j}^{0}=|{{\rm{\Psi }}}_{L}{|}^{2}+|{{\rm{\Psi }}}_{R}{|}^{2}\) for the DTQW defined in Eq. (1) with initial conditions: \(\varphi ={q}_{{\rm{\max }}}[\cos (x)+\frac{1}{3}\,\cos (3x)+\frac{1}{2}\,\cos (2x+0.9)]/m\) where \(m\,:\,=25.6\), 64, 128 and 512, \({q}_{{\rm{\max }}}=51.2\) and \({u}_{{\rm{\max }}}=2\), 0.8, 0.4 and 0.1 (see Eqs (9) and (10)). The grid has \(N={2}^{12}\) points, \(\varepsilon =2\pi /N\).
Let us stress that the shock is present, not only at high resolutions, but also for resolutions as low as \(n=64\) (see Fig. 2), which is well within current experimental limits31,32.
Analytical shock computation in the Galilean regime
We now present an analytical computation which reproduces the shock solution in the Galilean limit where the DTQW becomes a continuous time quantum walk and the Dirac equation goes, as shown in the Supplemental Material, into the (\(\hslash =0\)) Schrödinger equation \(i{\partial }_{t}\psi =-\,\frac{1}{2m}{\partial }_{xx}\psi \).
The Green function for the Schrödinger equation reads
The single-shock solution (\({t}_{0}=0\) and \({u}_{{\rm{\max }}}=1\)) thus reads
In the large-m limit, this integral can be computed by making use of methods that are standard in optics33 and involve Pearcey’s integral34 defined by
To wit, we set in the large-m limit, \(\psi ({\bf{x}},t)\approx A({\bf{x}},t){I}_{{\mathscr{P}}}(\,-\,T(t),X({\bf{x}},t))\) with \(T(t)={a}^{-\frac{1}{2}}(\frac{t-1}{2\varepsilon t})\), \(X({\bf{x}},t)=\)\(-\,{a}^{-\frac{1}{4}}(\frac{x}{\varepsilon t})\) and \(A({\bf{x}},t)={e}^{i(1+\frac{{x}^{2}}{2t})/\varepsilon }{(2i\pi t\varepsilon \sqrt{a})}^{-1/2}\) where \(a=m/4!\) and \(\varepsilon =1/m\). In this way, Pearcey’s integral Eq. (13) alone can correctly reproduces the structure of the shock (see Fig. 2c).
Useful asymptotic expansions of \({I}_{{\mathscr{P}}}\) are given in35,36 and §36.2 of 37. In particular, the steepest descent method can be directly used in zone I (see Fig. 2d) where \(m\gg t/{x}^{2}\). It yields the the following asymptotic form:
where \({\rm{\Phi }}(u)={u}^{4}-T{u}^{2}+Xu\) and the single saddle-point uc obeys \({\rm{\Phi }}^{\prime} ({u}_{c})=0\). Near the caustic, in zone II of Fig. 2d, 2 new saddle-points appear and the wavefunction can be written in terms of the Airy function \(Ai(x)=\frac{1}{\pi }\,{\int }_{-\infty }^{\infty }\,{\rm{dt}}\,\cos (\frac{{t}^{3}}{3}+xt)\). Well inside the caustic in zone III, the function can be written as the sum of 3 interfering contributions (see Fig. 2c,d).
Details of the evolution of the density \(n=|\psi {|}^{2}\) and velocity \(v={\partial }_{x}\varphi /m\) of the Schrödinger shock are presented in Fig. 3.
Evolution of velocity \(v={m}^{-1}{\partial }_{x}\phi \) (left) and density n (right) for 3 values of time and \({m}^{-1}=0.01\) obtained from a numerical solution of Schrödinger equation \(i{\partial }_{t}\psi =-\,\frac{1}{2m}{\partial }_{xx}\psi \), with \(\psi ={n}^{1/2}\,\exp \,i\phi \) and initial conditions \(\phi =m\,\cos \,x\) and \(n=1\).
Conclusion
We have shown through a novel generalization of the Madelung transform that one of the simplest DTQWs on the line can be considered as a minimalist model of quantum fluids. This conclusion has been supported by numerical simulations which show that, even within the coherence limit of current experiments, the DTQW evolves an initial condition already considered in the literature into a quantum hydrodynamic shock29,30. Thus, under current experimental conditions, DTQW can exhibit hydrodynamical behaviour and, therefore, be used to simulate quantum fluid dynamics. We have also computed the asymptotic shock structure analytically in the non-relativistic limit and proposed an extensive discussion of this limit in the SM.
Quantum walks have already been linked to with hydrodynamics in38,39, but these earlier results address the quantum Boltzmann equation and transport phenomena, and are thus quite different from those presented in this Letter.
Note that the quantum fluid described in this article exhibits a non-vanishing quantum pressure but its traditional pressure vanishes identically because the underlying QW is linear. The results presented in this article can be generalised to quantum fluids with non vanishing traditional pressure by working with non-linear QWs such as those already considered in40,41,42. The non-linearity of these walks can be reconciled with the linearity of Quantum Physics by viewing the non-linear terms as an effective description of (self-)interaction, generated for example by the coupling of QWs through gauge fields21,43,44,45. Let us note that non-linear QWs can in principle be realized experimentally, at least through non-linear optics experiments46,47.
The present work should be extended to higher dimensions and higher spins. Also, classical pressure terms should be added by considering non-linear DTQWs41, or DTQWs with site to site interactions. One should finally incorporate in the Madelung transform the natural coupling of DTQWs to gauge fields21,44,45,48, thus obtaining novel models of superconducting quantum fluids or of quantum fluids in relativistic gravitational fields.
References
Feynman, R. & Hibbs, A. Quantum mechanics and path integrals. International Series in Pure and Applied Physics (McGraw-Hill Book Company, 1965).
Aharonov, Y., Davidovich, L. & Zagury, N. Quantum random walks. Phys. Rev. A 48, 1687–1690, https://doi.org/10.1103/PhysRevA.48.1687 (1993).
Meyer, D. A. From quantum cellular automata to quantum lattice gases. Journal of Statistical Physics 85, 551–574, https://doi.org/10.1007/BF02199356 (1996).
Schmitz, H. et al. Quantum walk of a trapped ion in phase space. Phys. Rev. Lett. 103, 090504, https://doi.org/10.1103/PhysRevLett.103.090504 (2009).
Zähringer, F. et al. Realization of a quantum walk with one and two trapped ions. Phys. Rev. Lett. 104, 100503 (2010).
Schreiber, A. et al. Photons walking the line: A quantum walk with adjustable coin operations. Phys. Rev. Lett. 104, 050502, https://doi.org/10.1103/PhysRevLett.104.050502 (2010).
Karski, M. et al. Quantum walk in position space with single optically trapped atoms. Science 325, 174–177, https://doi.org/10.1126/science.1174436 (2009).
Sansoni, L. et al. Two-particle bosonic-fermionic quantum walk via integrated photonics. Phys. Rev. Lett. 108, 010502, https://doi.org/10.1103/PhysRevLett.108.010502 (2012).
Sanders, B., Bartlett, S., Tregenna, B. & Knight, P. Two-particle bosonic-fermionic quantum walk via 3d integrated photonics. Phys. Rev. A 67, 042305 (2003).
Perets, B. et al. Realization of quantum walks with negligible decoherence in waveguide lattices. Phys. Rev. Lett. 100, 170506 (2008).
Ambainis, A. Quantum walk algorithm for element distinctness. SIAM Journal on Computing 37, 210–239 (2007).
Magniez, F., A. Nayak, J. R. & Santha, M. Search via quantum walk. SIAM Journal on Computing - Proceedings of the thirty-ninth annual ACM symposium on Theory of computing (New York, ACM, 2007).
Aslangul, C. Quantum dynamics of a particle with a spin-dependent velocity. Journal of Physics A: Mathematical and Theoretical 38, 1–16 (2005).
Bose, S. Quantum communication through an unmodulated spin chain. Phys. Rev. Lett. 91, 207901 (2003).
Burgarth, D. Quantum state transfer with spin chains. University College London PhD thesis (2006).
Bose, S. Quantum communication through spin chain dynamics: an introductory overview. Contemporary Physics 48, 13–30, https://doi.org/10.1080/00107510701342313 (2007).
Collini, E. et al. Coherently wired light-harvesting in photosynthetic marine algae at ambient temperature. Nature 644 (2010).
Engel, G. S. et al. Evidence for wavelike energy transfer through quantum coherence in photosynthetic systems. Nature 446, 782–786 (2007).
Hoefer, M., Engels, P. & Chang, J. Matter–wave interference in bose–einstein condensates: A dispersive hydrodynamic perspective. Physica D: Nonlinear Phenomena 238, 1311–1320, https://doi.org/10.1016/j.physd.2008.08.021, Nonlinear Phenomena in Degenerate Quantum Gases (2009).
Uzdensky, D. A. & Rightley, S. Plasma physics of extreme astrophysical environments. Reports on Progress in Physics 77, 036902 (2014).
Molfetta, G. D., Brachet, M. & Debbasch, F. Quantum walks in artificial electric and gravitational fields. Physica A: Statistical Mechanics and its Applications 397, 157–168, https://doi.org/10.1016/j.physa.2013.11.036 (2014).
Nore, C., Brachet, M. & Fauve, S. Numerical study of hydrodynamics using the nonlinear schrödinger equation. Physica D: Nonlinear Phenomena 65, 154–162, https://doi.org/10.1016/0167-2789(93)90011-O (1993).
Nore, C., Abid, M. & Brachet, M.-E. Decaying Kolmogorov turbulence in a model of superflow. Phys. Fluids 9, 2644–2669 (1997).
Dalfovo, F., Giorgini, S., Pitaevskii, L. P. & Stringari, S. Theory of Bose-Einstein condensation in trapped gases. Rev. Mod. Phys. 71 (1999).
Debbasch, F. & Brachet, M. Relativistic hydrodynamics of semiclassical fluids. Physica D 82, 255 (1995).
Madelung, E. Eine anschauliche deutung der gleichung von schrödinger. Naturwissenschaften 14, 1004–1004, https://doi.org/10.1007/BF01504657 (1926).
Madelung, E. Quantentheorie in hydrodynamischer form. Zeitschrift für Physik 40, 322–326, https://doi.org/10.1007/BF01400372 (1927).
Donnelly, R. J. Quantized Vortices in Helium II (Cambridge University Press, 1991).
Hoefer, M. A. et al. Dispersive and classical shock waves in bose-einstein condensates and gas dynamics. Phys. Rev. A 74, 023623, https://doi.org/10.1103/PhysRevA.74.023623 (2006).
Wan, W., Jia, S. & Fleischer, J. W. Dispersive superfluid-like shock waves in nonlinear optics. Nat Phys 3, 46–51 (2007).
Boutari, J. et al. Large scale quantum walks by means of optical fiber cavities. Journal of Optics 18, 094007 (2016).
Regensburger, A. et al. Photon propagation in a discrete fiber network: An interplay of coherence and losses. Physical review letters 107, 233902 (2011).
Berry, M. V. & Klein, S. Colored diffraction catastrophes. Proceedings of the National Academy of Sciences 93, 2614–2619 (1996).
Pearcey, T. Xxxi. the structure of an electromagnetic field in the neighbourhood of a cusp of a caustic. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science 37, 311–317, https://doi.org/10.1080/14786444608561335 (1946).
Kaminski, D. Asymptotic expansion of the pearcey integral near the caustic. SIAM Journal on Mathematical Analysis 20, 987–1005, https://doi.org/10.1137/0520066 (1989).
López, J. L. & Pagola, P. J. The pearcey integral in the highly oscillatory region. Applied Mathematics and Computation 275, 404–410, https://doi.org/10.1016/j.amc.2015.11.080 (2016).
NIST Digital Library of Mathematical Functions. http://dlmf.nist.gov/, Release 1.0.17 of, Olver, F. W. J. et al. eds (12-22-2017).
Succi, S., Fillion-Gourdeau, F. & Palpacelli, S. Quantum lattice boltzmann is a quantum walk. EPJ Quantum Technology 2, 1–17, https://doi.org/10.1140/epjqt/s40507-015-0025-1 (2015).
Mezzacapo, A. et al. Quantum simulator for transport phenomena in fluid flows. Scientific Reports 5, 13153, https://doi.org/10.1038/srep13153 (2015).
Shikano, Y., Wada, T. & Horikawa, J. Discrete-time quantum walk with feed-forward quantum coin. Scientific reports 4, 4427 (2014).
Di Molfetta, G., Debbasch, F. & Brachet, M. Nonlinear optical galton board: Thermalization and continuous limit. Phys. Rev. E 92, 042923, https://doi.org/10.1103/PhysRevE.92.042923 (2015).
Vakulchyk, I., Fistul, M., Qin, P. & Flach, S. Nonlinear disordered discrete time quantum walks. Bulletin of the American Physical Society (2018).
Márquez-Martn, I., Arnault, P., Di Molfetta, G. & Pérez, A. Electromagnetic lattice gauge invariance in two-dimensional discrete-time quantum walks. Physical Review A 98, 032333 (2018).
Arnault, P., Di Molfetta, G., Brachet, M. & Debbasch, F. Quantum walks and non-abelian discrete gauge theory. Phys. Rev. A 94, 012335, https://doi.org/10.1103/PhysRevA.94.012335 (2016).
Arnault, P. & Debbasch, F. Quantum walks and discrete gauge theories. Phys. Rev. A 93, 052301, https://doi.org/10.1103/PhysRevA.93.052301 (2016).
Lee, C.-W., Kurzyński, P. & Nha, H. Quantum walk as a simulator of nonlinear dynamics: Nonlinear dirac equation and solitons. Physical Review A 92, 052336 (2015).
Javadi, A. et al. Single-photon non-linear optics with a quantum dot in a waveguide. Nature communications 6, 8655 (2015).
Arnault, P. & Debbasch, F. Quantum walks and gravitational waves. Annals of Physics 383, 645–661, https://doi.org/10.1016/j.aop.2017.04.003 (2017).
Author information
Authors and Affiliations
Contributions
Author’s individual contribution: M.H., G.D.M., M.B. and F.D. wrote the main manuscript text and G.D.M. prepared Figures 1–3.
Corresponding author
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hatifi, M., Di Molfetta, G., Debbasch, F. et al. Quantum walk hydrodynamics. Sci Rep 9, 2989 (2019). https://doi.org/10.1038/s41598-019-40059-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-019-40059-x
This article is cited by
-
Long time dynamics of a single-particle extended quantum walk on a one-dimensional lattice with complex hoppings: a generalized hydrodynamic description
Quantum Information Processing (2023)
-
Quantum control using quantum memory
Scientific Reports (2020)
-
A systematic method to building Dirac quantum walks coupled to electromagnetic fields
Quantum Information Processing (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.