Abstract
Fundamental control of magnetic coupling through heterostructure morphology is a prerequisite for rational engineering of magnetic ground states. We report the tuning of magnetic interactions in superlattices composed of single and bilayers of SrIrO3 inter-spaced with SrTiO3 in analogy to the Ruddlesden-Popper series iridates. Magnetic scattering shows predominately c-axis antiferromagnetic orientation of the magnetic moments for the bilayer, as in Sr3Ir2O7. However, the magnetic excitation gap, measured by resonant inelastic x-ray scattering, is quite different between the two structures, evidencing a significant change in the stability of the competing magnetic phases. In contrast, the single layer iridate hosts a more bulk-like gap. We find these changes are driven by bending of the c-axis Ir-O-Ir bond, which is much weaker in the single layer, and subsequent local environment changes, evidenced through x-ray diffraction and magnetic excitation modeling. Our findings demonstrate how large changes in the magnetic interactions can be tailored and probed in spin-orbit coupled heterostructures by engineering subtle structural modulations.
Similar content being viewed by others
Introduction
Atomic scale layering of disparate materials to form an artificial heterostructure is a promising method for the intelligent design of emergent properties1,2,3. Systems incorporating strong spin-orbit coupling are particularly intriguing as candidates for designer magnetic phases due to the coupling of the magnetic moments to structural distortions. Towards this goal, iridates, compounds composed of active Ir 5d orbitals in oxygen octahedra, have emerged as an important new class of correlated material4,5,6,7,8,9,10,11,12,13. The combination of crystal field interactions and strong spin-orbit coupling, λ~0.5 eV, generates narrow bands often leading to Mott insulating antiferromagnetic ground states despite the modest values of the Coulomb repulsion U~1 eV5,14,15. The resulting \({J}_{{\rm{eff}}}=\frac{1}{2}\) pseudospin states are then intimately coupled with the Ir orbitals and thus are much more sensitive to structural changes than pure spin \(S=\frac{1}{2}\) moments. This is exemplified by the different magnetic ground states appearing in iridates composed of similar Ir-O octahedra when they are subtly distorted or interspaced with different atoms. For instance, Sr2IrO4, hosting isolated IrO2 layers, forms an ab-plane canted antiferromagnetic state6,16, while Sr3Ir2O7, hosting isolated IrO2 bi-layers, has robust c-axis collinear antiferromagnetic ordering stabilized by a 90 meV magnon gap17,18. These competing magnetic ground states establish the iridates as ideal candidates for utilizing controlled structural perturbation to rationally engineer the magnetic behavior.
Towards this goal, layered iridate heterostructures, or superlattices (SL), were recently realized via alternating layers of nSrIrO3 and SrTiO3 (nSIO/1STO) opening up routes to tailor magnetic phenomena within artificial Ruddlesden-Popper analogues14,19. How magnetic couplings change within such heterostructures as compared to their bulk analogues is, however, unknown, with conflicting reports of c-axis versus canted ab-plane magnetic ground states for n = 219,20,21. The issue is rooted in the challenge of pinpointing and quantifying the various magnetic interactions in ultrathin heterostructures. In this paper, we directly probe the magnetic behavior of nSIO/1STO and extend the sensitivity of Ir L3 resonant inelastic x-ray scattering (RIXS) to quantify the interactions that stabilize this state. While the bulk-like spin-flop transition is preserved, the relative stability of the magnetic ground state is severely perturbed in the bilayer moving this system towards a quantum phase transition. We find structural leveraging through direct interfacial octahedra manipulation destabilizes the magnetic order via the spin-orbit coupling, revealing a promising new route to engineer the magnetic structure and an experimental scheme to determine the outcome.
Results
Crystal and magnetic structure
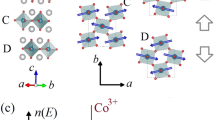
Figure 1(a) shows the structure of SLs studied here. SLs of nSIO/1STO with n = 1, 2, 3 all displayed a net ferromagnetic moment, which was taken as evidence for the stabilization of canted ab-plane magnetic moments as in Sr2IrO4 19. Although there is a strong consensus that this is valid for 1SIO/1STO, the result for 2SIO/1STO is more controversial as it breaks the analogy between n = 2 and Sr3Ir2O7, which has c-axis nearly-collinear antiferromagnetism implying only a very small spontaneous net moment18,19. The moment seen in 2SIO/1STO was nearly an order of magnitude larger than seen in bulk22. This result is quite striking as the magnetic ground state for Sr3Ir2O7 was shown to be very stable for bilayer iridates in general18,23. Theory also predicted c-axis moments for n = 2 and posited that the observed net ferromagnetic moment instead comes from oxygen vacancies20,24. Establishing the true magnetic ground state is of high importance towards extracting the magnetic exchange parameters that ultimately dictate the overall magnetic behavior of these heterostructures.
(a) Structure of the two SLs. Red arrows show in-plane magnetic exchange pathways and the pink arrow shows the out-of-plane exchange in the bilayer. (b) Left panel: Integrated intensity as a function of the azimuthal angle for the (0.5, 0.5, 9.5) magnetic reflection of the 2SIO/1STO sample is shown as red circles, along with the expected response for c-axis (solid grey line) and in-plane moment orientations (blue dashed lines). Right panel: Normalized magnetic Bragg peaks at maximum azimuth (90°) and where no intensity is expected for in-plane moments (7°).
In view of this controversy, we directly measured the spin ordering direction using azimuthal resonant elastic x-ray scattering (REXS) scans, as was done in Sr3Ir2O7 23,25. This dependence is shown for 2SIO/1STO in Fig. 1(b,c). For the magnetic reflection, the SL structure is used for the reciprocal lattice units (r. l. u.), with a ≈ b ≈ c/3. The calculated azimuthal dependence for c-axis oriented antiferromagnetic moments, shown as the grey line, matches the data well and establishes predominately c-axis moments. Furthermore, the key difference between the two orderings is the 2π (c-axis oriented) vs. π (ab-plane canted) angular period of the peaks, with our data clearly only being consistent with the prior. To further emphasize this distinction, we also show the magnetic Bragg peaks where the maximum intensity for both cases is expected (−90°), and also where no intensity for in-plane moments is expected (7°), Fig. 1(b), right panel. Clearly, a magnetic peak persists with integrated intensity that matches that expected for c-axis oriented moments (~30%). These results then agree with theoretical predictions, showing the 2SIO/1STO SL maintains the same magnetic ground state as Sr3Ir2O7, strengthening the analogy to Ruddlesden-Popper series iridates20. Armed with the correct ground state, the magnetic excitation spectrum can be correctly interpreted, allowing the quantification of the magnetic exchange couplings to unravel the true impact of heterostructuring.
Quantifying magnetic interactions
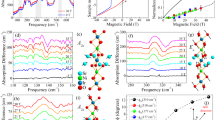
To directly probe the magnetic interactions, we utilize RIXS to map the dispersion of magnetic excitations above the established ground state. Here the Jeff = 1/2 spin-wave spectra, which incorporate the SOC effects, occur below ~0.2 eV followed by features at ~0.6 eV corresponding to dd-excitations, as seen previously13,23,26,27,28,29,30,31,32,33. Although Ir L3-edge RIXS has been applied extensively to bulk iridate crystals, a full 2D magnetic dispersion curve has never been characterized on SLs due to the relatively large (5 μm) x-ray penetration depth at the Ir L3 edge, with only one report observing a magnetic excitation32. This challenge was overcome by growing relatively thick SLs (60 IrO2 planes) and working near grazing incidence (1°). Raw RIXS spectra for the SLs are displayed in Fig. 2. Each spectra displays a high energy feature around 0.6 eV energy loss, corresponding to both an intra-t2g orbital excitation and the e−h continuum34. A sharp peak arises at zero energy due to elastic scattering, along with a very weak phonon feature at around 0.04 eV. The elastic feature is more intense in comparison to single crystal studies due to the large x-ray penetration depth leading to significant diffuse scattering from the STO substrate. Finally, a dispersive feature from 50 to 140 meV is seen in all spectra, and is identified as the magnon excitation, with the higher energy tail including multimagnon excitations13,23,26,27,31,33. Only one magnetic excitation was observed for both samples, despite the presence of both optical and acoustic modes for the bilayer. This is due to the intensity dependence of each mode as discussed in the supplemental. The spectra were fit using a combination of peaks in a similar approach to that used previously (see supplemental materials)23,27,29,34. Examples of fits along the nodal direction for each sample are displayed in Fig. 3(a). We note that using an alternative magnon line shape returned very similar fitting results. We furthermore measured a second 2SIO/1STO sample which also returned very similar results, see supplemental materials. From these fits one can extract the energy, width, and integrated intensity of the magnetic excitation, Fig. 3(b). The intensity peaks at the magnetic ordering wave vector (0.5, 0.5) and the energy loss is within the bandwidth seen for Sr2IrO4 and Sr3Ir2O7, corroborating our assignment of the feature as a magnetic excitation23,26.
(a) RIXS spectra for 1SIO/1STO (top) and 2SIO/1STO (bottom). Spectra colors follow from Fig. 2. The magnon feature is displayed in red, the excitonic features in green, and the elastic line in blue, while the total of these fitting contributions is a dark grey line. (b) Extracted energy loss (left), width (middle), and integrated intensity (right) of the magnon feature across reciprocal space. The dashed red (cyan) line is the magnon dispersion fit for 2SIO/1STO (Sr3Ir2O7)23. The errors are statistical from the fitting, with the errors carried through the area integration calculation.
From the extracted magnon dispersion, some important observations are immediately clear: (i) both SLs have nearly identical dispersion around the (0.25, 0.25) and (0.5, 0) points with maxima of ~120 and 150 meV, respectively, (ii) both samples show magnon gaps. The zone boundary dispersion at (0.5, 0) is intriguingly similar for both samples, being much smaller than Sr2IrO4 and slightly lower than Sr3Ir2O7. This behavior is likely due to the more uniform octahedra present in the heterostructures4,35,36. For 1SIO/1STO, a small gap of 31.8 ± 6 meV is found. Spin gaps of a similar size have been discussed for doped/undoped Sr2IrO4 29. For 2SIO/1STO, a larger gap is defined as 57 ± 5 meV at (0.5, 0.5) where the combination of maximum magnon intensity with only one dominant mode gives a high degree of certainty to the fit, as discussed in the supplemental. The massive difference in the magnon gap of 33 meV at (0.5, 0.5), in comparison to Sr3Ir2O7, evidences a very significant modulation of the magnetic interactions. Confidence intervals up to 99.73% for the (0.5, 0.5) points were obtained for both samples, detailed in the supplemental.
We analyzed the origin of this anomalous behavior using linear spin wave theory (LSWT), which is the leading order term in the expansion of the magnetic excitation spectra where the excitation is taken as a flipped spin distributed throughout the lattice. This was projected to the \({J}_{{\rm{eff}}}=\frac{1}{2}\) states to account for the spin-orbit coupling, as discussed in the supplemental15,23. This method was applied to the Hamiltonian described in ref.23, with ab-plane canted and c-axis collinear ground states for the single and bilayer SLs, respectively23. Importantly, the canted nature of the moments in 1SIO/1STO gives a dispersion relation that fundamentally differs from the out-of-plane Néel state23. As was the case for Sr3Ir2O7, the nine magnetic couplings can be parameterized in terms of: (i) the tetragonal distortion θ, defined by \(\tan \,2\theta =\frac{2\sqrt{2}\lambda }{\lambda -2{\rm{\Delta }}}\), with spin-orbit coupling λ and tetragonal crystal field splitting Δ, (ii) the magnetic bandwidth, \(W=\frac{4{t}^{2}}{U}\), (iii) \(\eta =\frac{{J}_{H}}{U}\), with Hund’s coupling JH and Coulomb repulsion U, and (iv) the octahedral rotation angle α. The form of the exchange couplings in terms of these parameters is described in the supplemental (\({J}_{ab}^{^{\prime} }\), \({J}_{ab}^{\text{'}\text{'}}\), and \({J}_{c}^{\text{'}}\) are treated as free fit parameters)18,23. Concerning (ii), as shown in Fig. 4(b), the magnetic phase transition is not sensitive to η in the relevant regime, nor is the dispersion fit. η = 0.24 was established for Sr3Ir2O7 and is unlikely to change significantly, leaving the tetragonal distortion, bandwidth, and rotation angles to explain the observed dispersion and magnon gaps.
(a) Rotation and tilt peaks, left and right panels, for n = 1, 2 SLs. Sharp features at Q c = 1.5 are substrate reflections, while broad features are SL reflections. (b) Classical phase diagram as a function of η and θ. Phase boundaries between the canted in-plane |xy〉 and collinear out-of-plane |z〉 orderings are displayed for single layer (blue) and bilayer iridates (red). The position for Sr3Ir2O7 (green triangle) was taken from23. The two SLs occupy very similar positions (similar to Sr2IrO4)15, but on different sides of their respective phase transition boundaries, in agreement with the different observed magnetic ground states. Solid lines are the phase boundaries for monolayer (blue) and bilayer (red) iridates. Error bars are propagated from the uncertainty in the magnon energy.
Regarding α, Sr2IrO4 and Sr3Ir2O7 both feature large in-plane rotations (α = 12° and 11° respectively), but no tilts (Sr2IrO4) or very small tilts (Sr3Ir2O7 ~1°), with tilts defined as rotations about a/b axes that bend the c-axis bond4,17,35. Bulk-like SIO films, on the other hand, show substantial tilts and rotations implying that similar effects may be present in SLs36. We consequently tested for the presence of octahedral tilts and rotations by scanning the half order Bragg peak’s locations. While an exact structural solution of the SLs is unfeasible due to the complex orthorhombic structure of SIO36, published methods allow us to associate different half order reflections with different antiphase distortions37,38,39. We measured several reflections for the n = 1 and 2 samples and illustrate the important behavior in Fig. 4(a). The \((\frac{1}{2},\,\frac{3}{2},\,\frac{3}{2})\) reflection (left panel) arises from a combination of rotations and tilts; whereas the \((\frac{1}{2},\,\frac{1}{2},\,\frac{3}{2})\) reflection (right panel) comes from only tilts. Both peaks are of similar magnitude for n = 2, but the tilt-peak is suppressed by an order of magnitude in n = 1. This data suggests that both SLs have similar rotations of ~8° as found by Matsuno et al.19. Interestingly, theory results predicted larger rotations of ~14°, but the different values return very similar results in the LSWT analysis and we thus chose to use the experimental values20. In contrast with the nearly straight (~1°) c-axis bonds seen in Sr3Ir2O7 4,17, n = 2 likely hosts tilting of a similar size (of order 8°), while n = 1 has small, but finite tilts. Most importantly, the presence of tilting generates the ab-plane ferromagnetic moment in 2SIO/1STO, observed experimentally19,40, through canting the c-axis antiferromagnetic moments, resolving the conflict between previous experimental interpretations and theory for 2SIO/1STO20,21. In-plane moments can also be theoretically argued to originate from oxygen vacancies, but such random tilting would give a smaller total moment and a change in Ir valence, not observed here21.
Tuning magnetic ground states
Having established the approximate rotation angles of both samples as α = 8°, we can fit the dispersion of the SLs, as discussed above, displayed for 2SIO/1STO in Fig. 3(b) left panel. This allows extraction of the parameterized tetragonal distortion, θ, which controls the magnetic phase stability15,18,23. In the case of 1SIO/1STO, we find θ = (0.226 ± 0.012)π29. For 2SIO/1STO, we find θ = (0.231 ± 0.008)π. For bilayer iridates, optical and acoustic modes are present, but only one mode is observed due to the Q-dependence of their intensities, discussed in the supplemental. Both of these θ values are near to that observed for Sr2IrO4 (~0.235 π), but well below that found for Sr3Ir2O7 (θ = (0.26 ± 0.01)π), Fig. 4(b) 17,23,35,36,41. These results point to the substrate imposed epitaxial structure as the dominant determinant of θ, likely due to the identical compressive strain applied to the SIO layers leading to similar local tetragonal distortions, despite the different layering schemes.
Extracted values of the exchange couplings for each of the SLs are shown in Table 1, these are obtained from equations depending only on θ, bandwidth W, η, and α. For 1SIO/1STO, the values are similar to those found in both doped and undoped Sr2IrO4, owing to the relatively small change in θ between the 1SIO/1STO and Sr2IrO4 (~0.01π)29. This indicates the 1SIO/1STO provides another magnetic analogue to cuprates, similar to that found in Sr2IrO4, but with the higher tunability afforded by heterostructuring7,12,42,43. Comparing 2SIO/1STO with Sr3Ir2O7, on the other hand, the changes are quite substantial, owing to the significant shift of θ (0.029π) between these two materials23. Importantly, a 34% decrease in the pseudodipolar anisotropic coupling Γc is observed, which is chiefly responsible for stabilizing the c-axis magnetic ground state. This decrease derives almost exclusively from the smaller magnon gap at (0.5, 0.5), indicative of the destabilization of this c-axis anisotropy and consistent with the addition of octahedral tilting in the artificial heterostructure. This is also consistent with the observation of more bulk-like behavior for 1SIO/1STO, where the octahedral tilting is much weaker.
To investigate the stability of the observed magnetic phases, we map the SLs on the classical (θ, η) magnetic phase diagram in Fig. 4(b) alongside Sr2IrO4 and Sr3Ir2O7 18. Intriguingly, both SLs lie close to their respective phase transitions. This is especially significant for 2SIO/1STO which lies much closer to the phase transition than Sr3Ir2O7, within 0.02π, corresponding to a ~10 meV tetragonal splitting change15. The fact that such a shift happens despite the similar structures of 2SIO/1STO and Sr3Ir2O7 demonstrates how relatively small distortions can strongly modify the magnetic interactions. Further bending of the c-axis bond can thus be expected to drive the system closer to, and eventually through, a quantum critical point between the ab-plane canted and c-axis antiferromagnetic states. This could be accomplished through applying epitaxial tensile strain by changing the substrate or by substituting Sr with Ca, with the outcome now being observable with RIXS as we demonstrate here. Based on the calculated change in the crystal field of strained films of Sr2IrO4, applied strain of only a few percent could be enough to drive 2SIO/1SIO to the quantum critical point20,30. Importantly, the distortions observed here are ubiquitous for epitaxially strained SLs, which naturally accommodate the imposed lattice parameters through these means. Thus this methodology should be applicable in a wide range of systems. In this way, heterostructuring of systems hosting strong spin-orbit coupling provides a means to exploit small structural distortions to stabilize large changes in the magnetic ground state.
To summarize, utilizing REXS and RIXS we investigated the magnetic structure and interactions in iridate heterostructures and pinpoint their position on the magnetic phase diagram, pushing RIXS to include thin film iridate SLs. We find that the magnetic structures replicate the expected spin-flop transition, but the relative stability of the magnetic phase is strongly perturbed by tilting of the octahedra as evidenced by the reduced magnon gap observed for 2SIO/1STO but not for 1SIO/1STO, which hosts much weaker tilting. Heterostructuring iridates and probing their magnetic interactions with RIXS thus reveals that spin orbit coupling can leverage small structural distortions to potentially dictate the magnetic structure with the additional possibility to engineer quantum critical points.
Methods
Sample preparation
SLs of form [nSIO/1STO]×m with n = 1, 2 and m = 60, 30, respectively, were grown with pulsed laser deposition using methods described in ref.40, as depicted in Fig. 1(a). High sample quality was verified by x-ray diffraction, x-ray magnetic circular dichroism, transport and magnetometry measurements (Figs S1–S3 of the supplemental material), consistent with previous studies19,40. Reflectively measurements and SL peaks confirm the B-site ordering and lack of stacking faults. Previous measurements of the heterostructures studied here have shown no appreciable deviation of the Ti valance from its 4 + state in bulk STO40,44,45. The STO layers in nSIO/1STO are consequently expected to have a negligible contribution to the magnetism studied here, although such effects have been discussed in other heterostructures46,47,48.
X-ray measurements
REXS, RIXS, and non-resonant diffraction data were taken at the 6-ID-B, 27-ID-B, and 33-BM-C beamlines of the Advanced Photon Source at Argonne National Laboratory at base temperature (~14 K). The RIXS energy resolution was 35 meV, full width half maximum. All Q-points were taken in grazing incidence with nearly 90° scattering to suppress non spin-flip processes. The resolution in reciprocal space was ± 0.072 r.l.u. A mask was used to improve the resolution to 0.12 Å−1 (0.018 r.l.u.) for the (0.5, 0.5) and (0, 0) Q-points for both samples. All REXS data were taken with a graphite polarization analyzer to minimize non-magnetic scattering. Furthermore, both on and off-resonance scans were taken for every azimuth to remove any charge signal leakage and normalize out any extrinsic effects. Further details including analysis and fitting procedures are available in the Supplemental Material.
Linear spin-wave theory
Linear spin-wave theory was applied to the anisotropic Hamiltonian for the IrO2 single and bi-layers as done in previous works18,23.
Data Availability
The data that support the findings of this study are available from the corresponding authors upon reasonable request.
References
Chakhalian, J., Freeland, J. W., Millis, A. J., Panagopoulos, C. & Rondinelli, J. M. Colloquium: emergent properties in plane view: Strong correlations at oxide interfaces. Rev. Mod. Phys. 86, 1189–1202 (2014).
Hwang, H. Y. et al. Emergent phenomena at oxide interfaces. Nat. Mater. 11, 103–113 (2012).
Mannhart, J. & Schlom, D. Oxide interfacesan opportunity for electronics. Science 327, 1607–1611 (2010).
Crawford, M. K. et al. Structural and magnetic studies of Sr2IrO4. Phys. Rev. B 49, 9198–9201 (1994).
Kim, B. J. et al. Novel J eff = 1/2 Mott State Induced by Relativistic Spin-Orbit Coupling in Sr2IrO4. Phys. Rev. Lett. 101, 076402 (2008).
Kim, B. J. et al. Phase-sensitive observation of a spin-orbital Mott state in Sr2IrO4. Science 323, 1329–1332 (2009).
Mitchell, J. F. Sr2IrO4: Gateway to cuprate superconductivity? APL Materials 3, 062404 (2015).
Witczak-Krempa, W., Chen, G., Kim, Y. B. & Balents, L. Correlated quantum phenomena in the strong spin-orbit regime. Annu. Rev. Condens. Matter Phys. 5, 57–82 (2014).
Wang, F. & Senthil, T. Twisted Hubbard Model for Sr2IrO4: Magnetism and Possible High Temperature Superconductivity. Phys. Rev. Lett. 106, 136402 (2011).
Kim, Y. K. et al. Fermi arcs in a doped pseudospin-1/2 Heisenberg antiferromagnet. Science 345, 187–190 (2014).
Cao, Y. et al. Hallmarks of the Mott-Metal Crossover in the Hole Doped Pseudospin-1/2 Mott insulator Sr2IrO4. Nat. Commun. 7, 11367 (2016).
Kim, Y. K., Sung, N. H., Denlinger, J. D. & Kim, B. J. Observation of a d-wave gap in electron-doped Sr2IrO4. Nat. Phys. 12, 37–41 (2016).
Liu, X. et al. Anisotropic softening of magnetic excitations in lightly electron-doped Sr2IrO4. Phys. Rev. B 93, 241102 (2016).
Kim, S. Y. et al. Manipulation of electronic structure via alteration of local orbital environment in [(SrIrO3)m, (SrTiO3)] (m = 1, 2 and ∞) superlattices. Phys. Rev. B 94, 245113 (2016).
Jackeli, G. & Khaliullin, G. Mott Insulators in the Strong Spin-Orbit Coupling Limit: From Heisenberg to a Quantum Compass and Kitaev Models. Phys. Rev. Lett. 102, 017205 (2009).
Cao, G., Bolivar, J., McCall, S., Crow, J. E. & Guertin, R. P. Weak ferromagnetism, metal-to-nonmetal transition, and negative differential resistivity in single-crystal Sr2IrO4. Phys. Rev. B 57, R11039–R11042 (1998).
Cao, G. et al. Anomalous magnetic and transport behavior in the magnetic insulator Sr3Ir2O7. Phys. Rev. B 66, 214412 (2002).
Kim, J. W. et al. Dimensionality Driven Spin-Flop Transition in Layered Iridates. Phys. Rev. Lett. 109, 037204 (2012).
Matsuno, J. et al. Engineering a Spin-Orbital Magnetic Insulator by Tailoring Superlattices. Phys. Rev. Lett. 114, 247209 (2015).
Kim, B., Liu, P. & Franchini, C. Dimensionality-strain phase diagram of strontium iridates. Phys. Rev. B 95, 115111 (2017).
Kim, B., Liu, P. & Franchini, C. Magnetic properties of bilayer Sr3Ir2O7: Role of epitaxial strain and oxygen vacancies. Phys. Rev. B 95, 024406 (2017).
Dhital, C. et al. Spin ordering and electronic texture in the bilayer iridate Sr3Ir2O7. Phys. Rev. B 86, 100401 (2012).
Kim, J. et al. Large Spin-Wave Energy Gap in the Bilayer Iridate Sr3Ir2O7: Evidence for Enhanced Dipolar Interactions Near the Mott Metal-Insulator Transition. Phys. Rev. Lett. 109, 157402 (2012).
Nagai, I. et al. Canted antiferromagnetic ground state in Sr3Ir2O7. J. Phys. Cond. Matter 19, 136214 (2007).
Boseggia, S. et al. On the magnetic structure of Sr3Ir2O7: an x-ray resonant scattering study. J. Phys. Cond. Matter 24, 312202 (2012).
Kim, J. et al. Magnetic Excitation Spectra of Sr2IrO4 Probed by Resonant Inelastic X-Ray Scattering: Establishing Links to Cuprate Superconductors. Phys. Rev. Lett. 108, 177003 (2012).
Cao, Y. et al. Giant spin gap and magnon localization in the disordered Heisenberg antiferromagnet Sr2Ir1-xRuxO4. Phys. Rev. B 95, 121103 (2017).
Moretti Sala, M. et al. Evidence of quantum dimer excitations in Sr3Ir2O7. Phys. Rev. B 92, 024405 (2015).
Pincini, D. et al. Anisotropic exchange and spin-wave damping in pure and electron-doped sr 2 iro 4. Physical Review B 96, 075162 (2017).
Lupascu, A. et al. Tuning Magnetic Coupling in Sr2IrO4 Thin Films with Epitaxial Strain. Phys. Rev. Lett. 112, 147201 (2014).
Gretarsson, H. et al. Persistent Paramagnons Deep in the Metallic Phase of Sr2−xLaxIrO4. Phys. Rev. Lett. 117, 107001 (2016).
Gruenewald, J. H. et al. Engineering 1D Quantum Stripes from Superlattices of 2D Layered Materials. Advanced Materials 29, 1603798 (2017).
Lu, X. et al. Doping Evolution of Magnetic Order and Magnetic Excitations in (Sr1−xLax)3Ir2O7. Phys. Rev. Lett. 118, 027202 (2017).
Kim, J. et al. Excitonic quasiparticles in a spin–orbit Mott insulator. Nat. Commun. 5, 4453 (2014).
Hogan, T. et al. Structural investigation of the bilayer iridate Sr3Ir2O7. Phys. Rev. B 93, 134110 (2016).
Liu, J. et al. Strain-induced nonsymmorphic symmetry breaking and removal of Dirac semimetallic nodal line in an orthoperovskite iridate. Phys. Rev. B 93, 085118 (2016).
May, S. J. et al. Quantifying octahedral rotations in strained perovskite oxide films. Phys. Rev. B 82, 014110 (2010).
Brahlek, M., Choquette, A. K., Smith, C. R., Engel-Herbert, R. & May, S. J. Structural refinement of Pbnm-type perovskite films from analysis of half-order diffraction peaks. J. Appl. Phys. 121, 045303 (2017).
Glazer, A. M. Simple ways of determining perovskite structures. Acta Cryst. A 31, 756–762 (1975).
Hao, L. et al. Giant magnetic response of a two-dimensional antiferromagnet. Nature Physics. 1804, 08780 (2018).
Bogdanov, N. A. et al. Orbital reconstruction in nonpolar tetravalent transition-metal oxide layers. Nat. Commun. 6, 7306 (2015).
Gao, Y., Zhou, T., Huang, H. & Wang, Q.-H. Possible superconductivity in Sr2IrO4 probed by quasiparticle interference. Scientific Reports 5, 9251 (2015).
Yan, Y. J. et al. Electron-Doped Sr2IrO4: An Analogue of Hole-Doped Cuprate Superconductors Demonstrated by Scanning Tunneling Microscopy. Phys. Rev. X 5, 041018 (2015).
Meyers, D. et al. Decoupling carrier concentration and electron-phonon coupling in oxide heterostructures observed with resonant inelastic x-ray scattering. Physical Review Letters 121, 236802 (2018).
Hao, L. et al. Two-dimensional j eff = 1/2 antiferromagnetic insulator unraveled from interlayer exchange coupling in artificial perovskite iridate superlattices. Physical Review Letters 119, 027204 (2017).
Banerjee, H., Banerjee, S., Randeria, M. & Saha-Dasgupta, T. Electronic structure of oxide interfaces: A comparative analysis of GdTiO3/SrTiO3 and LaAlO3/SrTiO3 interfaces. Scientific Reports 5, 18647 (2015).
Zhang, J. Y. et al. Correlation between metal-insulator transitions and structural distortions in high-electron-density SrTiO3 quantum wells. Physical Review B 89, 075140 (2014).
Bjaalie, L., Janotti, A., Himmetoglu, B. & Van de Walle, C. G. Metal versus insulator behavior in ultrathin SrTiO3-based heterostructures. Physical Review B 94, 035115 (2016).
Acknowledgements
We would like to acknowledge helpful discussions with G. Jackeli, G. Khaliullin, Wei-Guo Yin, and Yilin Wang and experimental assistance from C. Rouleau, Z. Gai and J. K. Keum. This material is based upon work supported by the U.S. Department of Energy, Office of Basic Energy Sciences, Early Career Award Program under Award No. 1047478. Work at Brookhaven National Laboratory was supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, under Contract No. DE-SC0012704. J.L. acknowledges the support by the Science Alliance Joint Directed Research & Development Program and the Transdisciplinary Academy Program at the University of Tennessee. J. L. also acknowledges support by the DOD-DARPA under Grant No. HR0011-16-1-0005. A portion of the fabrication and characterization was conducted at the Center for Nanophase Materials Sciences, which is a DOE Office of Science User Facility. Use of the Advanced Photon Source, an Office of Science User Facility operated for the U.S. DOE, OS by Argonne National Laboratory, was supported by the U.S. DOE under Contract No. DE-AC02-06CH11357. X. Liu acknowledges support by MOST (Grant No. 2015CB921302) and CAS (Grant No. XDB07020200).
Author information
Authors and Affiliations
Contributions
D.M. and M.P.M.D. wrote the manuscript. D.M., Y. Cao, G.F., L. Hao, J. Lin, D.C., J.-W.K., Y. Choi, P.J.R., L. Horak, X.L., J. Liu and M.P.M.D. took the experimental data. D.M., L. Hao, C.F., N.T., J.Y. and J. Liu grew the samples. N.J.R. computed the linear spin wave theory. M.H.U., D.C., J.-W.K., T.G., E.K., Y. Choi, D.H. and P.J.R. assisted in the synchrotron experiments setup.
Corresponding authors
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Meyers, D., Cao, Y., Fabbris, G. et al. Magnetism in iridate heterostructures leveraged by structural distortions. Sci Rep 9, 4263 (2019). https://doi.org/10.1038/s41598-019-39422-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-019-39422-9
This article is cited by
-
Evolution of electronic and magnetic properties of Sr2IrO4 under strain
npj Quantum Materials (2022)
-
Anomalous magnetoresistance due to longitudinal spin fluctuations in a Jeff = 1/2 Mott semiconductor
Nature Communications (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.