Abstract
The La Niña and El Niño phases of the El Niño-Southern Oscillation (ENSO) have major impacts on regional rainfall patterns around the globe, with substantial environmental, societal and economic implications. Long-term perspectives on ENSO behaviour, under changing background conditions, are essential to anticipating how ENSO phases may respond under future climate scenarios. Here, we derive a 7700-year, quantitative precipitation record using carbon isotope ratios from a single species of leaf preserved in lake sediments from subtropical eastern Australia. We find a generally wet (more La Niña-like) mid-Holocene that shifted towards drier and more variable climates after 3200 cal. yr BP, primarily driven by increasing frequency and strength of the El Niño phase. Climate model simulations implicate a progressive orbitally-driven weakening of the Pacific Walker Circulation as contributing to this change. At centennial scales, high rainfall characterised the Little Ice Age (~1450–1850 CE) in subtropical eastern Australia, contrasting with oceanic proxies that suggest El Niño-like conditions prevail during this period. Our data provide a new western Pacific perspective on Holocene ENSO variability and highlight the need to address ENSO reconstruction with a geographically diverse network of sites to characterise how both ENSO, and its impacts, vary in a changing climate.
Similar content being viewed by others
Introduction
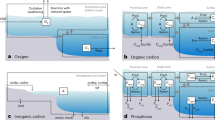
The El Niño-Southern Oscillation (ENSO) describes variation in tropical Pacific Ocean temperatures and the resulting changes in atmospheric pressure gradients. The atmospheric changes widely propagate the effects of ENSO variability, making ENSO a major component of regional climate across much of the world1. The impacts of changes in regional temperature and precipitation patterns associated with El Niño and La Niña phases of ENSO have wide-ranging environmental, societal and economic consequences. The El Niño phase manifests as a warming of central and/or eastern Pacific sea surface temperature (SST) with resulting increased precipitation in northern South America and western North America (Fig. 1). Conversely, the associated cooling in the western Pacific during El Niño events is associated with drought, forest fires and reduced agricultural yield in the western tropical Pacific, including the eastern half of Australia2. The opposing La Niña phase is equally important as a driver of drought in the eastern Pacific and positive precipitation anomalies in the west Pacific2. This was most recently evident during the 2010/11 La Niña, when the volume of precipitation over land was sufficient to reduce global sea levels by 5 mm, with much of this falling on Australia3. This resulted in catastrophic flooding in the sub-tropics and massive carbon uptake via greening of the vast arid and semi-arid regions of the continent4,5.
ENSO influence on surface precipitation. Spatial correlation between mean precipitation (Nov–Oct: the local hydrological year17) across the greater ENSO region and mean sea surface temperature for the Nino3.4 region (box) for the period 1980–2016 CE. Location of the study site and other locations mentioned in the text are illustrated.
Given these wide-ranging effects, it is essential to understand how both phases of ENSO will respond to future climate change. Reducing predictive model uncertainties requires proxy data of ENSO behaviour under different background states, as well as in response to local and extra-regional influences from all ENSO-sensitive areas6,7. The Holocene provides fruitful opportunities for this, with millennial-scale changes in orbital radiation forcing and centennial-scale global temperature changes, such as the Little Ice Age (~1450–1850)8. However, the evolution of ENSO through the Holocene remains unclear, with discrepancies between central Pacific SST proxies9 and eastern Pacific proxies of both precipitation10 and SST11, particularly during the mid-Holocene. Additionally, there are very few proxy ENSO records that can resolve centennial-scale trends in changing ENSO mean state. This is important as changes in the dominant phase of ENSO have been linked to solar irradiance12, orbital forcing13, average global temperatures14 and fresh water fluxes in the North Atlantic7.
We present a new ~7700-year quantitative precipitation record from subtropical eastern Australia, where La Niña and El Niño conditions are associated with positive and negative rainfall anomalies, respectively2 (Fig. 1). The precipitation reconstruction is derived from the carbon isotope ratio (δ13C) of leaves from the evergreen tree Melaleuca quinquenervia ((Cav.) S.T. Blake) preserved in the Holocene sediments of Swallow Lagoon on Minjerribah (North Stradbroke Island), the world’s second largest sand island. Swallow Lagoon (27°29′55″S: 153°27′17″E) is a small (0.27 ha), perched, freshwater lake that is isolated from the regional water table15. With no inflow or outflow streams, the balance of precipitation over evaporation determines lake level (Fig. S1) and moisture availability for the isolated stand of M. quinquenervia that fringes the lake (Supplementary Information). Sediments from a 370 cm core were sieved at contiguous one-centimetre resolution for M. quinquenervia leaf fragments, yielding 284 samples. Each datum represents the δ13C of all leaf fragments at that depth and is an average for the period encapsulated by that centimetre of sediment, which ranges from two to 77 years (avg. 24.4 yrs; s.d. 15.6 yrs). As such, these data do not represent El Niño or La Niña events, but represent mean conditions of individual time-slices. Age control is provided by 18 accelerator mass spectrometry 14C dates on short-lived terrestrial macrofossils, including M. quinquenervia leaves (Table S1).
Our new rainfall reconstruction builds on a well-established relationship between carbon isotope fractionation in C3 plant leaves and moisture availability (e.g., ref.16). In a novel approach, we utilise a relationship established specifically for M. quinquenervia using a 12-year collection of monthly litterfall samples from a nearby south-east Queensland wetland, which demonstrated a linear relationship (r2 = 0.67, p = 0.002) between the carbon isotope discrimination of M. quinquenervia leaves, relative to atmosphere, and mean annual rainfall17. We apply this calibration to sub-fossil M. quinquenervia leaf fragments from Swallow Lagoon to derive a quantitative estimate of mean annual rainfall. The linear nature of the model may skew precipitation estimates to the lower end and affect apparent variability; however, our calibration has advantages over other potential datasets as it uses location-specific climate data and is species-specific, as opposed to using modelled rainfall estimates16 or averaged data from all C3 plants at a location18. Comparing our results against various reconstructions from global datasets demonstrate that they consistently reconstruct higher precipitation estimates, however the patterns of change and variance, although accentuated, do not differ and our findings based on the species-specific calibration remain robust (Fig. S4).
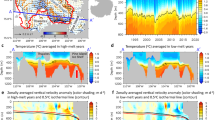
The inferred rainfall record from Swallow Lagoon covers the last 7700 years (Fig. 2) and displays a transition from predominantly high precipitation with low frequency variability during the mid-Holocene, to a drier climate with enhanced centennial-scale variability after ca. 3200 cal yr before present (3.2 cal kyr BP, where ‘present’ is 1950 CE). However, both non-constant sampling through time and varying numbers of years per sample could affect the variability in our record. To assess the fidelity of this shift in variability, we use a generalized additive location scale model (GAM-LS) to simultaneously estimate trends in both the mean (μ) and the standard deviation (σ) of the rainfall record. We find a statistically significant trend in σ. To test if this trend was influenced by sampling resolution, the estimated model was tested against a null model using 1000 simulated time series that follow the nonlinear trend estimated by our GAM-LS model but importantly with constant variance. This process demonstrates the range of trends in σ we might expect if there were no systematic change in variance. Simulation results demonstrate the estimated trend in σ is not an artefact arising from varying sampling resolution in time (Fig. S5). The combination of the fidelity of the variability in the record, the similarities between this and the general pattern of Holocene ENSO variability seen in other proxy records11,19,20,21, and the ENSO-sensitive location of the study region, provide confidence that rainfall variability in the record reflects ENSO variability through the Holocene. We therefore interpret the record in terms of mean ENSO conditions of individual time slices, as discussed above. Alternative explanations involving changes in ENSO ‘flavour’22 or shifting teleconnection patterns23,24 are not as firmly grounded in the palaeoclimate literature, although we cannot rule these out.
The Swallow Lagoon precipitation record. (a) The number of individual samples per non-overlapping century. (b) The Swallow Lagoon rainfall reconstruction with standard error (±88 mm; grey shading) and generalised additive location-scale model (GAM-LS: orange line with 95% confidence level shaded) illustrating significant trends in the data. Horizontal black dashed lines indicate ±2σ of the record, dotted line is the mean (1742 mm). (c) Standard deviation (σ) in mean annual rainfall with 95% confidence level shaded (see methods).
The nature of Holocene ENSO variance remains a subject of debate; central Pacific coral records suggesting no change in variance9 contrast with eastern Pacific ENSO proxies indicating enhanced variance in the late Holocene11,19,25. A recent analysis of coral and mollusc δ18O records from across the Pacific concluded marked changes in variance are in fact evident between the middle and late Holocene, and that tropical Pacific climate was susceptible to millennial-scale quiescent periods unrelated to orbital forcing20. In contrast, model simulations suggest the discrepancies between variability in eastern and central Pacific palaeoclimate data may be due to a differential response to insolation changes driven by orbital forcing22. Our record provides a new perspective from the southwestern Pacific and clearly demonstrate marked changes in rainfall variability over the last ~7700 years (Fig. 2). Prior to 5 cal kyr BP, variability is low, before a gradual increase ~5–2.5 cal kyr BP, and a further increase from ~1.2 cal kyr BP to present. The similarities between the timing of onset and trends in the variance between the eastern and western Pacific SSTs and teleconnected precipitation (Fig. 3) imply a common forcing mechanism.
(a) Swallow Lagoon precipitation record (as per Fig. 2); (b) West Pacific warm pool SST32; (c) lake sediment sand content from El Junco Lake, Galápagos Islands19, and (d) sediment deposition at Laguna Pallcacocha, Ecuador25, as proxies for El Niño event frequency; (e) simulated amplitude of ENSO variability as reflected by Nino3.4 SST variability with 95% confidence interval shaded and, (f) simulated strength of the Pacific Walker circulation in the Nino4 region with 95% confidence interval shaded, according to the CSIRO Mk3L climate system model (see methods); (g) Standard deviation in mean annual rainfall record from Swallow Lagoon (as per Fig. 2c); eastern tropical Pacific measures of ENSO variability derived from (h) variance of individual foraminifera11 (grey bars; original sample at 7 cal kyr BP not shown as it is considered spurious by the authors), (i) bivalves63 (blue boxes), and (j) Laguna Pallcacocha variance, in 100-year non-overlapping windows, derived from normal-transformed data64 (black solid line). Inverted triangles represent the location of radiocarbon ages in the Swallow Lagoon record. LIA: Little Ice Age.
Model simulations at 6 kyr and 0 kyr identify a strengthened Pacific Walker Circulation (PWC), driven by high boreal summer insolation and a stronger monsoon system, as the primary driver of reduced ENSO variability evident in proxy records during the mid-Holocene7,26,27. In this setting, strengthened trade winds foster more La Niña-like conditions and restrict the formation of El Niño events. To investigate the evolution of this scenario over time, we expand on these simulations using nine equilibrium climate model simulations spanning 8 kyr to 0 kyr, and derive metrics for the amplitude of ENSO variability and strength of the PWC (methods). Each simulation consists of a 1200-year model simulation (with the last 1000 years being used for analysis) and differs only via changes in the Earth’s orbital parameters. The model reproduces the long-term trends in ENSO variability over the last 8000 years seen in proxy records, with lower variability during the mid-Holocene (8–5 kyr) and gradually increasing late Holocene variability (Fig. 3). Modelled PWC strength suggests it reached a peak at 5 kyr, before decreasing towards 0 kyr. However, there is little difference between simulations either side of this peak, with the largest changes evident after 3 kyr, mirroring the pattern of rainfall variability at Swallow Lagoon (Fig. 3). Though it is likely that other factors beyond orbital forcing also influence ENSO, and the PWC, during the Holocene28, the simulations provide a mechanistic explanation for the coeval changes noted in proxy-ENSO records and rainfall in the Australian subtropics.
As our record tracks both wet and dry anomalies, we can characterise the shift at 3.2 cal kyr BP in terms of changes in the distribution as well as the amplitude of extremes. Prior to 3.2 cal kyr BP, no events exceeded ±2σ of the record mean; after 3.2 cal kyr BP, there are 12 dry excursions greater than 2σ, but only one wet excursion of this magnitude. While an increase in resolution towards the top of the record will naturally lead to the preservation of more short-lived events, we note that dry anomalies dominate and the transition towards an overall drier mean state, as illustrated by the GAM-LS (Fig. 2b), remains evident when the data are interpolated to a common centennial scale (Fig. S6). This trend suggests that the enhanced amplitude of late Holocene variability evident at Swallow Lagoon, and in other equatorial Pacific palaeoclimate records19,20,21,25, is driven by increasing strength of the El Niño phase alone, rather than simply a more variable system. While this has previously been implied from a marked shift in vegetation across eastern Australia towards more drought tolerant species around 3 cal kyr BP29, the Swallow Lagoon record confirms the one-sided nature of late-Holocene ENSO intensification.
The mid-Holocene (~7.7–3.5 cal kyr BP) at Swallow Lagoon is dominated by precipitation estimates above the mean (analogous to La Niña conditions in the instrumental record) though some dry periods are evident. The most extensive of these are apparent around 6.9, 6.8 and 5.8 cal kyr BP, suggesting El Niño was still active at this time. During the period 5.5–3.5 cal kyr BP, rainfall at Swallow Lagoon was generally stable, around a wet La Niña-like mean state. This period closely corresponds with a time of low variance in eastern Pacific SSTs11 from ~6–4 cal kyr and when Galápagos lake sediments suggest both phases of ENSO were less frequent21. Though some temporal smoothing is expected in the Galápagos record, as well as at Swallow Lagoon, the timing is also in general agreement with a “quiescent period” evident in high-resolution carbonate δ18O records from discrete periods between 5–3 cal kyr BP20. The GAM-LS model illustrates a period of very high rainfall at Swallow Lagoon around 3.5–3.0 cal kyr BP, which corresponds with a marked cool and dry period reflected in Galápagos lake sediments, also at 3.5–3.0 cal kyr BP21. Taken together, these findings suggest a centennial-scale period of enhanced zonal SST gradient, a persistently strong PWC and a more La Niña-like mean state.
The shift towards drier climates at Swallow Lagoon aligns with increasing SST variability in the eastern equatorial Pacific11 and the onset of more frequent El Niño events evident in sediment records from the Galápagos19 and Ecuador25 (Fig. 3; although we note the veracity of the Ecuadorean record in documenting El Niño events has recently been challenged30). Enhanced El Niño conditions in the west Pacific warm pool are evident in discreet coral records from Papua New Guinea around this time31, with notable prolonged and extreme events at ~2.5 and 2.04 ka corresponding with dry periods that exceed 2σ of the Swallow Lagoon record around 2.47 and 2.04 cal kyr BP. These events at Swallow Lagoon occur in a cluster of dry events during the ~2.6–2.0 cal kyr BP period, suggesting prolonged or extreme El Niño events, such as those evident in the coral records, may have occurred more regularly during this time. An absence of long coral records from the west Pacific precludes precise correlation with subsequent late-Holocene dry extremes in the Swallow Lagoon record, though a general agreement between rainfall trends (as illustrated by the GAM-LS) and west Pacific warm pool SSTs32 is evident through this period (Fig. 3).
A notable exception to the drier and more variable climate in the late Holocene at Swallow Lagoon is the stable high rainfall phase during the Little Ice Age (LIA: ~1450–1850)8, a period of globally cool temperatures14,33. ENSO variability during the LIA has been debated in recent research8,14,34,35,36. Problems in interpretation arise because of the heterogeneous relationship among terrestrial hydroclimate proxies, oceanic SST proxies and theoretical and physical models of predicted responses to globally cool periods36,37,38. A strengthened zonal gradient is indicated by hydrological records of a generally dry eastern Pacific19,21,25 contrasting with a wet western Pacific34,36, whereas a weakened zonal gradient is indicated by proxy records of relatively cool eastern and western Pacific SSTs8,39. The Swallow Lagoon record indicates persistently high rainfall during the LIA (Fig. 3). This is consistent with lake40 and tree-ring41 records from southern Australia that also find wet and low-variability LIA climate, which is inconsistent with El Niño-like conditions14. However, dry climate in northern Australia during the LIA37 is inconsistent with La Niña-like conditions. Thompson et al. (ref.21) suggest the pattern of reduced SST gradient described above is reminiscent of El Niño Modoki conditions; these can drive large-scale decreases in precipitation over northern Australia42, although they are unable to explain a wet southeastern40 or subtropical Australia (Swallow Lagoon). Given the critical impacts ENSO has on water resources in teleconnected regions, understanding this apparent disparity between SST and hydroclimate proxies highlights the need for further research into the response of ENSO to changes in global climate.
Conclusions
Understanding ENSO variability is critically important because of its effects on precipitation regimes in teleconnected regions. The Swallow Lagoon precipitation record provides a new, quantitative, southwestern Pacific perspective of the influence of both ENSO phases over the mid- to late Holocene. The record has enabled, for the first time, an assessment of centennial- to millennial-scale variability in Australian subtropical rainfall. The pattern of low variability during the mid-Holocene, increasing after ca. 3 kyr cal BP, mirrors the variance evident in ENSO records from across the Pacific. The ~7.7–3.5 kyr cal BP period of low variability is characterised by predominantly wet climates at Swallow Lagoon, which implies a dominance of the La Niña phase during this time. After ~3 kyr cal BP, increasing variability is driven by the occurrence of extreme dry events, highlighting a strengthened El Niño phase as the primary driver of this change. Our climate model simulations implicate a progressive orbitally-driven weakening of Pacific Walker Circulation, particularly after 3 ka, as a contributing factor. At centennial scales, the record presents the first insights into subtropical Australian hydroclimates during the LIA, and we find that persistently high rainfall marks this period as anomalous in the context of the late Holocene. This contributes to a complex picture in which there is an apparent decoupling of SST and terrestrial hydroclimates during this interval. This requires further investigation as understanding ENSO response to radiative forcing is key to understanding the sensitivity of the system to anthropogenic climate changes35.
Methods
Chronology
An age model was developed based on 18 accelerator mass spectrometry (AMS) radiocarbon dates on short-lived terrestrial macrofossils (Table S1, Fig. S2). The samples were treated using the standard acid-alkali-acid pre-treatment to remove all carbon contamination. A radiocarbon chronology (Fig. S2) was constructed using the (Bayesian) OxCal P_Sequence deposition model with a low k parameter of 0.5 cm−1. The agreement index of the model Amodel of 76% was good as it is higher than the accepted level of 60%43. Radiocarbon calibration data used for calendar age conversion are the post-bomb 14C data for Southern Hemisphere zone 1–244 extended back in time by the SHCal13 calibration curve45. All calibrated ages are reported in cal. yr BP, with 0 yr BP being 1950 CE.
Isotope analysis
All leaf samples were freeze dried for 24 hours and ground to a homogenous fine powder. Carbon isotope analyses were performed at the Natural Environment Research Council’s Isotope Geosciences Laboratory at the British Geological Survey in Nottingham, United Kingdom, by combustion in a Costech Elemental Analyser on-line to a VG TripleTrap and Optima dual-inlet mass spectrometer. δ13C values were calculated relative to the Vienna Pee-Dee Belemnite (VPDB) scale using within-run laboratory standards calibrated against NBS-18, NBS-19 and NBS-22. Replicate analysis of well-mixed samples indicated a precision of < 0.1‰ (1 SD).
Precipitation reconstruction
There is a significant relationship (r2 = 0.64) between annual mean M. quinquenervia Δleaf sensu Farquhar et al. (ref.46) and mean annual rainfall17 which is improved slightly by taking into account the effect of atmospheric CO2 changes on Δleaf. Δleaf in the Swallow Lagoon record was calculated using the atmospheric δ13Catm from Elsig et al. (ref.47) between 7520 cal yr BP and 550CE and δ13Catm for the remaining period calculated using Ferrio et al. (ref.48). We inferred rainfall using the relationship between rainfall and a discrimination anomaly17, that is, the difference between Δleaf predicted using Farquhar et al. (ref.46) and that predicted from CO2 using Schubert and Jahran (ref.49). We utilised CO2 data from Monin et al. (ref.50) for the period to 245 cal yr BP, from Law Dome51 from 245 to −20 cal yr BP (1970 CE) and from Cape Grim (www.csiro.au) from 1971 CE to present.
Assessing variability
To simultaneously estimate trends in the mean and variance of the reconstructed rainfall time series requires a modelling approach that allows for linear predictors for each parameter of the conditional distribution of the response. Therefore, we chose to analyse the time series using a location scale generalized additive model (GAM-LS). Models of this type are also contained in the generalised additive model of location, scale, shape (GAMLSS) class52 and are more generally known as distributional models (e.g., ref.53). Our GAM-LS model includes smooth functions of time to simultaneously estimate trends in mean and variance of the observed time series. Because the models use smooth functions to estimate trends they do not require the response variable to be regularly spaced in time54,55. Furthermore, they do not suffer from edge effects in the same way as moving window methods, thus allowing continuous estimates of changes in variance over the entire time series. Edge effects do lead to increased uncertainty in trend estimates from GAM-LS models, but this additional uncertainty is accounted for in the standard errors of estimates from the model which are used to produce credible intervals for the estimated trends.
Rainfall values per year are typically observations of continuous random variables, bounded at 0. However, given the large rainfall values observed here, the Gaussian distribution is a close approximation for their conditional distribution. The Gaussian distribution is defined by two parameters; the mean (μ) and the standard deviation (σ). The GAM-LS approach allows both parameters to be modelled via separate linear predictors to capture variation in both the mean and the variance of the time series. The specific GAM-LS fitted here has the following form:
which states that the ith δ13C observation (yi) is distributed Gaussian with mean µi and variance \({\sigma }_{i}^{2}\). We model µi as a smooth function (f1) of time (calibrated radiocarbon years BP) plus a constant term α (the model intercept). The linear predictor for σi is also modelled as a constant term, γ, plus a smooth function of time (f2), plus a linear parametric effect of the amount of time represented by each sample (tii). σi is modelled on the log scale with a small lower bound b (0.01) to ensure parameter estimates remain positive and avoid issues with singularities in the likelihood of the model56. Any deviation from the assumed Gaussian distribution was assessed using standard model diagnostic plots for GAMs.
Thin plate spline bases were used for both smooth functions f1 and f2 with 200 and 75 basis functions respectively, to allow for potentially complex fitted trends in mean and variance. A penalty on the second derivative of the fitted smooths was used to control the amount of wiggliness in the estimated functions. Smoothness parameters, used to balance the fit and complexity of the model, were estimated via penalized maximum likelihood57. This has the effect of slightly biasing downwards the estimated variance trend. Dropping f2 from the model allows a test to be performed for a trend in variance over and above that which we might expect to observe due to varying sedimentation rates and time averaging present in each sample. Additionally, AIC was used to select between these two models.
Periods of significant change in the estimated trend in σi were identified using the first derivatives of f2, calculated using the method of finite differences. Periods of significant change exist where the 95% confidence interval on the first derivative of the smooth does not include a value of zero slope.
To investigate whether the estimated trend in σi was the result of variation in sedimentation rates, time averaging, and the uneven spacing of samples in time (not already accounted for by the tii term in the model), we compared our estimated variance trend with those estimated from 1000 null models fitted to simulated time series. Simulated time series \(({\tilde{y}}_{i})\) were generated at an annual time step according to \({\tilde{y}}_{i}=N({\hat{\mu }}_{i},{\sigma }^{2})\), where \({\hat{\mu }}_{i}\) is the predicted trend from the full GAM-LS model described above but with constant standard deviation σ, determined from the standard error of the residuals of the GAM-LS fitted without f2 (hence we account for the heterogeneity implied by the varying amounts of time averaging in each sample when selecting the value of σ). Each annual value was assigned to a cm sediment slice following the age-depth relationship of the observed sediment record, and averaged to provide a mean value of the response for each slice. This process approximates the time averaging of individual years in the observed record. We then fitted the same GAM-LS model to each simulated series, including the smooth f2; any trend in σi estimated by f2 would be spurious, the result of either stochastic variation or the time averaging process, because the data were initially simulated with constant variance. We then compared the observed trend in σi with those estimated from the simulated time series (Fig. S4), and reject the null hypothesis that the observed trend in σi is a data artefact if it is extreme relative to the trends in the simulated series which were generated with no trend in variance. The GAM-LS models were estimated using the mgcv package57 for R58.
Climate modelling
Snapshot simulations of the state of the global climate at 8, 7, 6, 5, 4, 3, 2 and 1 kyr BP, conducted using the CSIRO Mk3L climate system model v1.159,60, were used. A pre-industrial control simulation provides the state of the global climate at 0 kyr BP. The snapshot simulations took into account the effects of orbital forcing, with the model being driven with the appropriate values of the Earth’s orbital parameters61 for each epoch. Otherwise, each snapshot simulation was identical to the pre-industrial control, with an atmospheric CO2 concentration of 280 ppm and a solar constant of 1365 Wm−2. The snapshot simulations were initialised from the state of the pre-industrial control simulation at the end of model year 100. Each snapshot simulation was then integrated for 1,100 years. The first 100 years were regarded as a spin-up period, with the final 1,000 years being used to derive statistics. The simulations are described in further detail by Phipps and Brown (ref.62).
For this study, two metrics were derived: (i) the amplitude of variability in El Niño-Southern Oscillation (ENSO), and (ii) the strength of the Pacific Walker Circulation. The amplitude of ENSO variability was diagnosed by calculating the monthly-mean sea surface temperature (SST) for the Niño 3.4 region (170–120°W, 5°S–5°N). A 2–7 year bandpass filter was then applied to extract ENSO variability. The ENSO amplitude was derived by calculating the standard deviation of the bandpass-filtered SST. The strength of the Pacific Walker circulation was diagnosed by calculating the monthly-mean strength of the zonal wind at 850 hPa for the Niño 4 region (160°E–150°W, 5°S–5°N). For both metrics, a block bootstrap was used to derive the 95% confidence interval.
Data Availability
Data relating to this study can be found at https://figshare.com/s/b4b5431fd9577afd95ef.
Change history
01 April 2021
A Correction to this paper has been published: https://doi.org/10.1038/s41598-021-86998-2
References
McPhaden, M. J., Zebiak, S. E. & Glantz, M. H. ENSO as an integrating concept in Earth science. Science 314, 1740–1745, https://doi.org/10.1126/science.1132588 (2006).
Dai, A. & Wigley, T. M. L. Global patterns of ENSO-induced precipitation. Geophysical Research Letters 27, 1283–1286 (2000).
Boening, C., Willis, J. K., Landerer, F. W., Nerem, R. S. & Fasullo, J. The 2011 La Niña: So strong, the oceans fell. Geophysical Research Letters 39, https://doi.org/10.1029/2012gl053055 (2012).
Cleverly, J. et al. The importance of interacting climate modes on Australia’s contribution to global carbon cycle extremes. Scientific Reports 6, 1–10, https://doi.org/10.1038/srep23113 (2016).
Poulter, B. et al. Contribution of semi-arid ecosystems to interannual variability of the global carbon cycle. Nature 509, 600–603, https://doi.org/10.1038/nature13376 (2014).
Brown, J., Collins, M., Tudhope, A. W. & Toniazzo, T. Modelling mid-Holocene tropical climate and ENSO variability: towards constraining predictions of future change with palaeo-data. Climate Dynamics 30, 19–36, https://doi.org/10.1007/s00382-007-0270-9 (2008).
Braconnot, P., Luan, Y., Brewer, S. & Zheng, W. Impact of Earth’s orbit and freshwater fluxes on Holocene climate mean seasonal cycle and ENSO characteristics. Climate dynamics 38, 1081–1092 (2012).
Rustic, G. T., Koutavas, A., Marchitto, T. M. & Linsley, B. K. Dynamical excitation of the tropical Pacific Ocean and ENSO variability by Little Ice Age cooling. Science 350, 1537–1541 (2015).
Cobb, K. M. et al. Highly Variable El Niño–Southern Oscillation Throughout the Holocene. Science 339, 67–70, https://doi.org/10.1126/science.1228246 (2013).
Rein, B., Luckge, A. & Sirocko, F. A major Holocene ENSO anomaly during the Medieval period. Geophysical Research Letters 31, L17211 (2004).
Koutavas, A. & Joanides, S. El Niño-Southern Oscillation extrema in the Holocene and Last Glacial Maximum. Paleoceanography 27, PA4208, https://doi.org/10.1029/2012PA002378 (2012).
Emile-Geay, J., Cane, M., Seager, R., Kaplan, A. & Almasi, P. El Niño as a mediator of the solar influence on climate. Paleoceanography 22, PA3210, https://doi.org/10.1029/2006PA001304 (2007).
Clement, A. C., Seager, R. & Cane, M. A. Suppression of El Niño during the mid-Holocene by changes in the Earth’s orbit. Paleoceanography 15, 731–737 (2000).
Mann, M. E. et al. Global Signatures and Dynamical Origins of the Little Ice Age and Medieval Climate Anomaly. Science 326, 1256–1260, https://doi.org/10.1126/science.1177303 (2009).
Leach, L. M. Hydrological and physical setting of North Stradbroke Island. Proceedings of the Royal Society of Queensland 117, 21–46 (2011).
Diefendorf, A. F., Mueller, K. E., Wing, S. L., Koch, P. L. & Freeman, K. H. Global patterns in leaf 13C discrimination and implications for studies of past and future climate. Proceedings of the National Academy of Sciences 107, 5738–5743, https://doi.org/10.1073/pnas.0910513107 (2010).
Tibby, J. et al. Carbon isotope discrimination in leaves of the broad-leaved paperbark tree, Melaleuca quinquenervia, as a tool for quantifying past tropical and subtropical rainfall. Global Change Biology 22, 3474–3486 (2016).
Kohn, M. J. Carbon isotope compositions of terrestrial C3 plants as indicators of (paleo)ecology and (paleo)climate. Proceedings of the National Academy of Sciences of the United States of America 107, 19691–19695 (2010).
Conroy, J. L., Overpeck, J. T., Cole, J. E., Shanahan, T. M. & Steinitz-Kannan, M. Holocene changes in eastern tropical Pacific climate inferred from a Galápagos lake sediment record. Quaternary Science Reviews 27, 1166–1180 (2008).
Emile-Geay, J. et al. Links between tropical Pacific seasonal, interannual and orbital variability during the Holocene. Nature Geoscience 9, 168–173, https://doi.org/10.1038/NGEO2608 (2016).
Thompson, D. M. et al. Tropical Pacific climate variability over the last 6000 years as recorded in Bainbridge Crater Lake, Galápagos. Paleoceanography (2017).
Karamperidou, C., Di Nezio, P. N., Timmermann, A., Jin, F. F. & Cobb, K. M. The response of ENSO flavors to mid‐Holocene climate: implications for proxy interpretation. Paleoceanography 30, 527–547 (2015).
Cai, W., Van Rensch, P., Cowan, T. & Sullivan, A. Asymmetry in ENSO Teleconnection with Regional Rainfall, Its Multidecadal Variability, and Impact. Journal of Climate 23, 4944–4955 (2010).
Westra, S., Renard, B. & Thyer, M. The ENSO–precipitation teleconnection and its modulation by the interdecadal Pacific oscillation. Journal of Climate 28, 4753–4773 (2015).
Moy, C. M., Seltzer, G. O., Rodbell, D. T. & Anderson, D. M. Variability of El Nino/Southern Oscillation activity at millennial timescales during the Holocene epoch. Nature 420, 162–165 (2002).
Liu, Z., Kutzbach, J. & Wu, L. Modeling climate shift of El Nino variability in the Holocene. Geophysical Research Letters 27, 2265–2268 (2000).
Zheng, W., Braconnot, P., Guilyardi, E., Merkel, U. & Yu, Y. ENSO at 6ka and 21ka from ocean–atmosphere coupled model simulations. Climate Dynamics 30, 745–762 (2008).
Pausata, F. S. et al. Greening of the Sahara suppressed ENSO activity during the mid-Holocene. Nature Communications 8 (2017).
Donders, T. H., Haberle, S. G., Hope, G., Wagner, F. & Visscher, H. Pollen evidence for the transition of the Eastern Australian climate system from the post-glacial to the present-day ENSO mode. Quaternary Science Reviews 26, 1621–1637 (2007).
Schneider, T., Hampel, H., Mosquera, P. V., Tylmann, W. & Grosjean, M. Paleo-ENSO revisited: Ecuadorian Lake Pallcacocha does not reveal a conclusive El Niño signal. Global and Planetary Change, https://doi.org/10.1016/j.gloplacha.2018.06.004 (2018).
McGregor, H. & Gagan, M. Western Pacific coral δ18O records of anomalous Holocene variability in the El Niño–Southern Oscillation. Geophysical Research Letters 31 (2004).
Stott, L., Cannariato, K., Thunell, R., Huag, G. H., Koutavas, A. & Lund, S. Decline of surface temperature and salinity in the western tropical Pacific Ocean in the Holocene epoch. Nature 431, 56–59 (2004).
Marcott, S. A., Shakun, J. D., Clark, P. U. & Mix, A. C. A Reconstruction of Regional and Global Temperature for the Past 11,300 Years. Science 339, 1198–1201, https://doi.org/10.1126/science.1228026 (2013).
Yan, H. et al. A record of the Southern Oscillation Index for the past 2,000 years from precipitation proxies. Nature Geoscience 4, 611–614, https://doi.org/10.1038/ngeo1231 (2011).
Emile-Geay, J., Cobb, K. M., Mann, M. E. & Wittenberg, A. T. Estimating Central Equatorial Pacific SST Variability over the Past Millennium. Part II: Reconstructions and Implications. Journal of Climate 26, 2329–2352, https://doi.org/10.1175/Jcli-D-11-00511.1 (2013).
Griffiths, M. L. et al. Western Pacific hydroclimate linked to global climate variability over the past two millennia. Nature communications 7 (2016).
Yan, H. et al. Dynamics of the intertropical convergence zone over the western Pacific during the Little Ice Age. Nature Geoscience 8, 315 (2015).
Clement, A. C., Seager, R., Cane, M. A. & Zebiak, S. E. An Ocean Dynamical Thermostat. Journal of Climate 9, 2190–2196 (1996).
Conroy, J. L., Overpeck, J. & Cole, J. E. El Niño/Southern Oscillation and changes in the zonal gradient of tropical Pacific sea surface temperature over the last 1.2 ka. PAGES news 18, 32–34 (2010).
Barr, C. et al. Climate variability in south-eastern Australia over the last 1500 years inferred from the high-resolution diatom records of two crater lakes. Quaternary Science Reviews 95, 115–131 (2014).
Cook, E. R., Buckley, B. M., D’Arrigo, R. D. & Peterson, M. J. Warm-season temperatures since 1600 BC reconstructed from Tasmanian tree rings and their relationship to large-scale sea surface temperature anomalies. Climate Dynamics 16, 79–91 (2000).
Taschetto, A. S. & England, M. H. El Niño Modoki impacts on Australian rainfall. Journal of Climate 22, 3167–3174 (2009).
Bronk Ramsey, C. Deposition models for chronological records. Quaternary Science Reviews 27, 42–60 (2008).
Hua, Q., Barbetti, M. & Rakowski, A. Z. Atmospheric Radiocarbon for the Period 1950–2010. Radiocarbon 55, 2059–2072 (2013).
Hogg, A. G. et al. SHCal13 Southern Hemisphere Calibration, 0–50,000 Years cal BP. Radiocarbon 55, 1889–1903 (2013).
Farquhar, G. D., Ehleringer, J. R. & Hubick, K. T. Carbon isotope discrimination and photosynthesis. Annual Review of Plant Physiology and Plant Molecular Biology 40, 503–537 (1989).
Elsig, J. et al. Stable isotope constraints on Holocene carbon cycle changes from an Antarctic ice core. Nature 461, 507–510, https://doi.org/10.1038/nature08393 (2009).
Ferrio, J. P., Araus, J. L., Buxó, R., Voltas, J. & Bort, J. Water management practices and climate in ancient agriculture: inference from the stable isotope composition of archaeobotanical remains. Vegetation History and Archaeobotany 14, 510–517 (2005).
Schubert, B. A. & Jahren, A. H. The effect of atmospheric CO2 concentration on carbon isotope fractionation in C3 land plants. Geochimica et Cosmochimica Acta 96, 29–43, https://doi.org/10.1016/j.gca.2012.08.003 (2012).
Monnin, E. et al. Evidence for substantial accumulation rate variability in Antarctica during the Holocene, through synchronization of CO2 in the Taylor Dome, Dome C and DML ice cores. Earth and Planetary Science Letters 224, 45–54 (2004).
Etheridge, D. M. et al. Natural and anthropogenic changes in atmospheric CO2 over the last 1000 years from air in Antarctic ice and firn. Journal of Geophysical Research: Atmospheres 101, 4115–4128, https://doi.org/10.1029/95jd03410 (1996).
Rigby, R. A. & Stasinopoulos, D. M. Generalized additive models for location, scale and shape. Journal of the Royal Statistical Society: Series C (Applied Statistics) 54, 507–554 (2005).
Klein, N., Kneib, T., Lang, S. & Sohn, A. Bayesian structured additive distributional regression with an application to regional income inequality in Germany. The Annals of Applied Statistics 9, 1024–1052 (2015).
Bunting, L. et al. Increased variability and sudden ecosystem state change in Lake Winnipeg, Canada, caused by 20th century agriculture. Limnology and Oceanography 61, 2090–2107 (2016).
Simpson, G. L. & Anderson, N. Deciphering the effect of climate change and separating the influence of confounding factors in sediment core records using additive models. Limnology and Oceanography 54, 2529–2541 (2009).
Wood, S. N. Generalized additive models: an introduction with R. (CRC press, 2017).
Wood, S. N., Pya, N. & Säfken, B. Smoothing parameter and model selection for general smooth models. Journal of the American Statistical Association 111, 1548–1563 (2016).
R: A language and environment for statistical computing. v. 3. 4.1 (R Foundation for Statistical Computing, Vienna, Austria, https://www.r-project.org/, 2017).
Phipps, S. J. et al. The CSIRO Mk3L climate system model version 1.0 - Part 1: Description and evaluation. Geoscientific Model Development 4, 483–509, https://doi.org/10.5194/gmd-4-483-2011 (2011).
Phipps, S. J. et al. The CSIRO Mk3L climate system model version 1.0 - Part 2: Response to external forcings. Geoscientific Model Development 5, 649–682, https://doi.org/10.5194/gmd-5-649-2012 (2012).
Berger, A. Long-term variations of daily insolation and Quaternary climatic changes. Journal of the atmospheric sciences 35, 2362–2367 (1978).
Phipps, S. J. & Brown, J. N. In IOP Conference Series: Earth and Environmental Science. 012010 (IOP Publishing).
Carré, M. et al. Holocene history of ENSO variance and asymmetry in the eastern tropical Pacific. Science 345, 1045–1048 (2014).
Emile-Geay, J. & Tingley, M. Inferring climate variability from nonlinear proxies: application to palaeo-ENSO studies. Climate of the Past 12, 31–50 (2016).
Acknowledgements
We acknowledge Minjerribah (North Stradbroke Island) and the surrounding waters as Quandamooka Country and would like to thank Aunty Marg, Minjerribah Moorgumpin elders, for support to undertake research on Country. The project was supported by the Australian Research Council (grants LP0990124 and DP150103875) and the Australian Institute of Nuclear Science Engineering (grants ALNGRA11005P and ALNGRA15524). JTO and JEC were supported by U.S. National Science Foundation EaSM2 Grant (AGS1243125). S.J.P. was supported under the Australian Research Council’s Special Research Initiative for the Antarctic Gateway Partnership (Project ID SR140300001).
Author information
Authors and Affiliations
Contributions
C.B., J.T., J.C.M. and G.B.M. conceived of the original project and undertook all fieldwork. C.B. managed the project, undertook laboratory analyses and led the manuscript development. M.J.L. oversaw all isotope analyses and interpretation of results. J.T. led the initial modern calibration component. C.B., J.T., J.J.T., A.C.G.H., J.T.O., J.E.C. and J.C.M. contributed equally to the palaeoclimate aspect of the study. J.J.T. and F.H.M. contributed early statistical analyses; G.L.S. undertook all final statistical analyses. S.J.P. undertook all analysis of the climate modelling experiments; Q.H. supervised radiocarbon analyses and undertook all age modelling. All authors contributed to editing and revision of the manuscript.
Corresponding author
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The original online version of this Article was revised: The original version of this Article contained an error in Reference 32, which was incorrectly given as: Stott, L., Poulsen, C., Lund, S. & Thunell, R. Super ENSO and Global Climate Oscillations at Millennial Time Scales. Science 297, 222–226 (2002). The correct reference is: Stott, L., Cannariato, K., Thunell, R., Huag, G.H., Koutavas, A. & Lund, S. Decline of surface temperature and salinity in the western tropical Pacific Ocean in the Holocene epoch. Nature 431, 56–59 (2004).
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Barr, C., Tibby, J., Leng, M.J. et al. Holocene El Niño–Southern Oscillation variability reflected in subtropical Australian precipitation. Sci Rep 9, 1627 (2019). https://doi.org/10.1038/s41598-019-38626-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-019-38626-3
This article is cited by
-
The Plata plume water penetration into the southwestern Atlantic shelf during the Holocene
Geo-Marine Letters (2024)
-
Soaring migrants flexibly respond to sea-breeze in a migratory bottleneck: using first derivatives to identify behavioural adjustments over time
Movement Ecology (2023)
-
Long-term stability of temperate Australian wet forest-moorland mosaics despite recurrent fires associated with late Holocene climate change
Landscape Ecology (2023)
-
A synoptic bridge linking sea salt aerosol concentrations in East Antarctic snowfall to Australian rainfall
Communications Earth & Environment (2022)
-
Pacific decadal variability over the last 2000 years and implications for climatic risk
Communications Earth & Environment (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.