Abstract
In this research, vibration frequency analysis of three layered functionally graded material (FGM) cylinder-shaped shell is studied with FGM central layer and the internal and external layers are of homogenous material. Strain and curvature-displacement relations are taken from Sander’s shell theory. The shell frequency equation is obtained by employing the Rayleigh Ritz method. Influence on natural frequencies (NFs) is observed for various thickness of the middle layer. The characteristics beam functions are used to estimate the dependence of axial modal. Results are obtained for thickness to radius ratios and length to radius ratios for different edge conditions. The validity of this method is checked for numerous results in the open literature.
Similar content being viewed by others
Introduction
Vibration of FGM cylindrical shell is a widely studied area of research in theoretical and applied mechanics. Among a large number of studies on vibrations of cylindrical shells (CS) we cite a few. Arnold and War-burton1,2 is executed some influential work on shell frequency analysis. Shell vibration analysis carried out by employing different numerical techniques like Galerkin method, Rayleigh Ritz method, different quadrature method and finite difference method. These shells are fabricated by isotropic, laminated and multi-layered materials. Functionally graded materials have been developed by applying powder technology. Functionally graded materials are utilized for various objectives because of their proper material distribution in their fabrication. They are mostly used for high pressure and heat dominant surroundings. Sharma et al.3 scrutinized behaviour of vibrations for cylinder-shaped shells by employing the Rayleigh Ritz technique for clamped-free boundary conditions. Loy et al.4 analysed the fundamental frequencies of circular shaped shells by a generalized differential quadrature method (DQM). Further Loy et al.5 investigated the vibrations of functionally graded (FG) cylindrical shells fabricated by stainless steel and nickel. They showed the effects of formations of essential constituents on the frequencies. Moreover, Pardhan et al.6 explored vibration behaviour of FG cylindrical shells fabricated by stainless steel and zirconia for different edge conditions. Zhang et al.7 scrutinized free vibrations of cylindrical shells for different edge conditions by employing a local adaptive DQM. Naeem et al.8 employed a generalized DQM for the functionally graded material cylindrical shells to investigate vibration behaviour. Pellicano9 showed the response of an isotropic cylindrical shell for linear and non-linear vibrations by employing analytical experiment method. Vibration study of FG cylindrical shells has been done by Iqbal et al.10 and the shell governing motion equations were solved by using wave propagation technique. This technique was exceptionally helpful for vibration analysis. Axial modal dependence was estimated with help of beam functions in exponential form. Li et al.11 determined free vibration analysis of three layered cylindrical shells with FG material central layer. Flugge’s shell theory was used by them. Vel12 observed free and forced vibration of cylinder-shaped shell by using the elasticity solution technique for simply - supported conditions at both ends. Lam et al.13 showed the frequency vibration behaviour of multi layered FGM cylindrical shells for different edge conditions. Arshad et al.14,15 studied the FGM cylindrical shell for vibration frequency analysis with simply - supported end point conditions under different volume fraction laws. They used Love’s shell theory. Rayleigh Ritz technique was employed by them to solve the problem. Further he investigated vibration characteristics of FGM cylindrical shell with the effect of different edge conditions for exponential volume fraction law. Shah et al.16 analysed vibrations of NFs for fluid filled and empty CS constructed by elastic foundation. Naeem et al.17 explored the vibration behaviour of three layered functionally graded material cylindrical shell for different edge conditions. The internal and external layers were fabricated by FG materials whereas the central layer was of isotropic material. They used the Love’s thin shell theory. Arshad et al.18 examined the vibrations of natural frequencies of bi-layered cylinder-shaped shell. One layer was fabricated by isotropic material and the other was of functionally graded material. Rayleigh Ritz technique was utilized. Shah et al.19 scrutinized the vibration behaviour of three layered FGM CS constructed by Winkler and Pasternak basis. They used wave propagation approach for the solution of the model.
Ahmad and Naeem20 investigated vibrations of rotating cylindrical shells composed of FG materials. Natural frequencies of cylindrical shell were studied with effects of volume fraction law and different ratios.
Theoretical Consideration
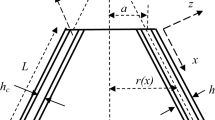
Consider a cylinder-shaped shell of radius R, thickness h and length L as shown in Fig. 1. An orthogonal coordinate system (x, θ, z) is fixed at the middle surface of the cylindrical shell, where x, θ and z lie in the axial, circumferential and radial directions of the shell, and (u, v, w) are the displacements of the shell in x, θ and z directions respectively.
The strain energy for a CS is represented by \(\Im \) and is written as
where
where ε1, ε2, γ and K1, K2, τ represent the strains and curvatures reference surface relations respectively. Prime (′) denotes the transpose of a matrix. These relations are taken from Sanders’ shell theory and written as:
and [S] is defined as
where aij denote the extensional stiffness, bij the coupling stiffness and dij the bending stiffness. (i, j = 1, 2 and 6). They are defined as:
For isotropic materials \({{,}\kern-0.4em \rm{O}}_{ij}\) is the reduced stiffness stated as Loy et al.5
Here Young’s modulus represented by E and \({{\rm{{-}\kern-0.5em \lambda}}}\) denotes the Poisson ratio. The bij coupling stiffness turn to zero for homogenous CS and ≠0 for FGM cylindrical shells and values of bij depend on the material distribution. Also bij become negative and positive due to irregularity of material properties at the mid plan. \({{,}\kern-0.4em \rm{O}}_{ij}\) depend on physical properties of FG materials.
With the help of expression (2) and (5), \(\Im \) is written as:
By putting these expressions (3) and (4) in the expression (8) then \(\Im \) attains the following form:
Shell kinetic energy is symbolized by Ì and is stated as:
Here variable t designates the time. Mass density is represented by ρ and ρt denotes the mass density for each unit length and it is expressed as:
The Lagrange energy functional denoted by \( {\mathcal L} \) for a cylinder-shaped shell is formulated by the difference of kinetic and strain energies as:
Numerical Procedure
The Rayleigh-Ritz procedure is used to achieve the natural frequencies of cylindrical shell. Now the displacement fields are presummed by the following relations:
where xm, ym and zm represent the amplitudes of vibration in the x, θ and z direction respectively, the axial and circumferential wave numbers of mode shapes are denoted by m and n respectively, ω signifies the angular vibration frequency of the shell wave. U(x), V(x), and W(x), denotes the axial model dependence in the longitudinal, circumferential and transverse directions respectively. Here we take \(U(x)=\frac{d\phi (x)}{dx},\,V(x)=\phi (x),\,W(x)=\phi (x)\), where φ(x) represents the axial function which satisfies the geometric edge conditions.
The axial function φ(x is taken as the beam function in the following form,
Here values of βi are changed with respect to the edge conditions. (i = 1, 2, 3, 4) μm signify the roots of some transcendental equations and σm are parameters which depend on the values of μm.
For generalization of this problem following non-dimensional parameters are used.
Now expression (13) is altered into the following form
After substituting expression (3.4) into the expressions for \(\Im \) and Ì, we get \(\Im \)max, Ìmax and \({ {\mathcal L} }_{max}.\) Then Lagrangian functional \({ {\mathcal L} }_{max}\) transformed into the following form by applying the principle of maximum energy.
Rayleigh-Ritz procedure is employed to get the eigenvalue form problem of the shell frequency equation. The Lagrangian energy functional \({ {\mathcal L} }_{{\max }}\) is minimized with regarding the vibration amplitudes xm, ym and zm as follows,
The obtained equations by arrangements of terms are written in matrix form as
where
where [C] and [\({,}\kern-.5em \rm{M}\)] are the stiffness and mass matrices of the cylindrical shell respectively and its values are given supplementary file, and [C] contains the terms related material moduli nd the mass matrix [\({,}\kern -.5em \rm{M}\)] contains terms associated with shell mass,
the shell vibrations are determined after solving the eigenvalue equation (19) with the help of MATLAB software.
Classifications of Materials
In present study a cylindrical shell is considered constructed from three layers, the internal and external layers are fabricated by isotropic material while the central layer is constructed from FG materials nickel and stainless steel. The volume fractions14 of the shell middle layer constructed from two constituents using trigonometric volume fraction law (VFL) are given by the following relations:
These relations satisfy the VFL i.e.Vf1+Vf2 = 1, where h is the shell thickness and υ denotes the power law exponent. It is presumed that each layer is of thickness h/3. Following are the material parameters: \({E}_{1},{{{\rm{{-}\kern-0.5em \lambda}}}}_{1},{\rho }_{1}\,and\,{E}_{2},{\rho }_{2},{{{\rm{{-}\kern-0.5em \lambda}}}}_{2}\) for nickel and stainless steel respectively. Then the effective material quantities: \({E}_{fgm},{{{\rm{{-}\kern-0.5em \lambda}}}}_{1fgm}\,and\,{\rho }_{fgm}\) for one type of the configuration are given as:
From expression (23) at z = −h/6, Efgm = E2, \({{{\rm{{-}\kern-0.5em \lambda}}}}_{fgm}={{{\rm{{-}\kern-0.5em \lambda}}}}_{2}\), ρfgm = ρ2 and the material properties at z = h/6 becomes:
Thus the shell is consisted of purely stainless steel at z = −h/6 and the properties of material are combination of stainless steel and nickel at z = +h/6. The stiffness moduli are modified as:
where i = 1, 2, 6 and (iso) represents the internal and external isotropic layers and FGM represents the central functionally graded material layer.
Results and Discussion
Results for an isotropic cylindrical shell with following edge conditions, simply supported-simply supported (\({{,} \kern -.3em \rm{s}}\)-\({{,} \kern -.3em \rm{s}}\)), clamped-clamped (ς- ς) and clamped-free (ς-\({{,} \kern -.27em \rm{f}}\)), are compared with the results available in open literature to ensure the validity, authenticity and robustness of the current technique. Tables 1 and 2 show the comparisons of frequency parameters with those in the Zhang et al.7 for \({{,} \kern -.3em \rm{s}}\)-\({{,} \kern -.3em \rm{s}}\) and ς- ς isotropic cylindrical shells. Comparison of natural frequencies (Hz) with those available in Loy & Lam4 for ς-\({{,} \kern -.27em \rm{f}}\) isotropic cylindrical shell is presented in the Table 3. It can be noticed clearly that the current results are in agreement with the results in open literature.
Table 4 represents the types of three layered FGM cylinder shaped shell by interchanging the FG constituent materials. where Z1, Z2 and Z3 represent Aluminium, Stainless Steel and Nickel respectively. Material properties for the above materials are presented in refs5,19. Different arrangements of thickness for shell layers are presented in Table 5.
Here q1 = h/3, q2 = h/4, q3 = h/2, q4 = h/5, q5 = 3h/5.
Tables 6 and 7 represent natural frequencies (Hz) functionally graded material cylindrical shell versus against n for case-II, type-I & II with different power exponent law γ respectively. In these tables influence of υ is examined which is different for both types. The natural frequencies (Hz) are decreased for type-I and increased for type-II less than 1% when power exponent law increased from υ = 1–20 for n = 1–5. Hence natural frequencies are affected by the configuration of the essential materials in the three layered CS.
Figures 2–7 represent the natural frequencies (NFs) (Hz) of FGM cylinder-shaped shell against n for different thickness of the central layer under six edge conditions; \({{,} \kern -.3em \rm{s}}\)-\({{,} \kern -.3em \rm{s}}\), ς-ς, \({{,} \kern -.27em \rm{f}}\)-\({{,} \kern -.27em \rm{f}}\), ς-\({{,} \kern -.3em \rm{s}}\) (clamped-simply supported), ς-\({{,} \kern -.27em \rm{f}}\) (clamped-free), \({{,} \kern -.27em \rm{f}}\)-\({{,} \kern -.3em \rm{s}}\) (free-simply supported). In Figs 2–4 Natural frequencies are presented for cylindrical shells of type I. Natural frequencies decrease for n = 2 and starts increase at n = 3 in each case. It is seen that the natural frequencies are minimum for clamped-free edge condition as compare to other five edge conditions and its maximum for free-free end point condition. The behavior of natural frequencies (Hz) remains same for all cases. Natural frequencies decreased <1% when thickness of the shell middle layer increased 66% or 100%. Figures 5–7 demonstrate the results for cylindrical shells of type-II. It is clearly seen that the natural frequencies are little high for cylindrical shells of type-II as compare to type-I shells.
Figures 8–13 show the behavior of natural frequencies (Hz) versus n for various L/R ratios and for various edge conditions. It is seen that the natural frequencies (Hz) are decreased when the L/R ratios are increased. When L/R ratios are increased from 10 to 20, 30, and 50 then natural frequencies are decreased 72%, 87% and 95% respectively for n = 1. Natural frequencies (Hz) for different h/R ratios against n are presented in Figs 14–19 under six edge conditions. Natural frequencies (Hz) are increased with the increasing h/R ratios. In these figures, frequencies first decreased from n = 1 to 2 then increased from 2 to onwards. Natural frequencies are increased with the increasing h/R ratios from 0.001 to 0.005, 0.005 to 0.01 and 0.01 to 0.02 at n = 2 for different boundary conditions such as for simply supported - simply supported boundary condition 298%, 98% and 100% for ς-ς and f-f boundary conditions 105%, 84% and 95% for ς-\({{,} \kern -.3em \rm{s}}\) and \({{,} \kern -.27em \rm{f}}\)-\({{,} \kern -.3em \rm{s}}\) boundary condition 165%, 92% and 98% for ς-\({{,} \kern -.27em \rm{f}}\) boundary condition 365%, 100% and 100% for respective ratios. Thus Natural frequencies affected significantly by h/R ratios.
Conclusions
In present study, frequency analysis of three layered FGM cylinder shaped shell is done for different thickness of the shell middle layer. Strain and curvature displacement relationships are adopted from Sander’s theory. To solve the current problem Rayleigh Ritz method is employed. Natural frequencies are examined for six edge conditions. It is noticed that Natural frequencies becomes minimum with the increase in thickness of the shell FGM middle layer. These also decreased with the increased of L/R ratios. When L/R ratios increased 100%, 200% and 500% then natural frequencies decreased 72%, 87% and 95% respectively for n = 1. Frequencies increased with the increased of h/R ratios. Thickness to radius ratios has significant effect on natural frequencies (Hz).
References
Arnold, R. N. & Warburton, G. B. Flexural vibrations of the walls of thin cylindrical shells having freely supported ends. Proceedings of the Royal Society of London A 197, 238–256 (1948).
Arnold, R. N. & Warburton, G. B. The flexural vibrations of thin cylinders. Proc. Inst. Mech. Engrs. London 167, 62–80 (1953).
Sharma, C. B. & Johns, D. J. Vibrations characteristics of clamped-free and clamped-ring-stiffened circular cylindrical shells. Journal of Sound and Vibration 14, 459–474 (1971).
Loy, C. T., Lam, K. Y. & Shu, C. Analysis of cylindrical shells using generalized differential quadrature method. Shock and Vibrations 4, 193–198 (1997).
Loy, C. T., Lam, K. Y. & Reddy, J. N. Vibration of functionally graded cylindrical shells. International Journal of Mechanical Sciences 41, 309–324 (1999).
Pradhan, S. C., Loy, C. T., Lam, K. Y. & Reddy, J. N. Vibration characteristics of functionally graded cylindrical shells under various boundary conditions. Applied Acoustics 61, 111–129 (2000).
Zhang, L., Xiang, Y. & Wei, G. W. Local adaptive differential quadrature for free vibration analysis of cylindrical shells with various boundary conditions. International Journal of Mechanical Sciences 48, 1126–1138 (2006).
Naeem, M. N., Ahmad, M., Shah, A. G., Iqbal, N. & Arshad, S. H. Applicability of generalized differential quadrature method for vibration study of FGM cylindrical shells. European Journal of Scientific Research 47, 82–99 (2010).
Pellicano, F. Vibration of circular cylindrical shells: theory and experiments. Journal of sound and vibration 303, 154–170 (2007).
Iqbal, Z., Naeem, M. N. & Sultana, N. Vibration characteristics of FGM circular cylindrical shells using wave propagation approach. Acta Mechanica 30, 37–47 (2009).
Li, S. R., Fu, X. H. & Batra, R. C. Free vibration of three-layer circular cylindrical shells with functionally graded middle layer. Mechanics Research Communications 3, 577–580 (2010).
Vel, S. S. Exact elasticity solution for the vibration of functionally graded an isotropic cylindrical shell. Composite Structures 92, 2712–2727 (2010).
Lam, K. Y. & Loy, C. T. Effects of boundary conditions on frequencies of a multilayered cylindrical shell. Journal of Sound and Vibration 188, 363–384 (1995).
Arshad, S. H., Naeem, M. N. & Sultana, N. Frequency analysis of functionally graded cylindrical shells with various volume fraction laws. Journal of Mechanical Engineering Science 221(C), 1483–1495 (2007).
Arshad, S. H., Naeem, M. N., Sultana, N., Iqbal, Z. & Shah, A. G. Effects of exponential volume fraction law on the natural frequencies of FGM cylindrical shells under various boundary conditions. Archive of Applied Mechanics 81, 999–1016 (2011).
Shah, A. G., Mahmood, T., Naeem, M. N. & Arshad, S. H. Vibration characteristics of fluid-filled cylindrical shells based on elastic foundations. Acta Mechanica 216, 17–28 (2011).
Naeem, M. N., Khan, A. G., Arshad, S. H., Shah, A. G. & Gamkhar, M. vibration of three-layered FGM cylindrical shells with middle layer of isotropic material for various boundary conditions. World Journal of Mechanics 4, 315–331 (2014).
Arshad, S. H., Naeem, M. N., Sultana, N., Iqbal, Z. & Shah, A. G. Vibration of bi-layered cylindrical shells with layers of different materials. Journal of Mechanical Science and Technology 24, 805–810 (2010).
Shah, A. G., Ali, A., Naeem, M. N. & Arshad, S. H. Vibrations of three-layered cylindrical shells with fgm middle layer resting on winkler and pasternak foundations, Advances in Acoustics and Vibration (2012).
Ahmad, M. & Naeem, M. N. Vibration characteristics of rotating FGM circular cylindrical shell using wave propagation method. European Journal of Scientific Research 36, 184–235 (2009).
Acknowledgements
This work was supported by the Government College University, Faisalabad, Pakistan and Higher Education Commission Pakistan.
Author information
Authors and Affiliations
Contributions
M.G. and M.N.N. designed the problem, S.C. M.G. and M.K. proved the results. M.G. and M.I. verified the results and wrote this paper.
Corresponding author
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ghamkhar, M., Naeem, M.N., Imran, M. et al. Vibration frequency analysis of three-layered cylinder shaped shell with effect of FGM central layer thickness. Sci Rep 9, 1566 (2019). https://doi.org/10.1038/s41598-018-38122-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-018-38122-0
This article is cited by
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.