Abstract
While bismuth ferrite BiFeO3 (BFO) is a well studied multiferroic material, its electronic and magnetic properties in the presence of A-site dopants have not been explored widely. Here we report the results of a systematic study of the local electronic structure, spontaneous polarization, and magnetic properties of lanthanum (La) and strontium (Sr) doped rhombohedral bismuth ferrite within density functional theory. An enhanced ferroelectric polarization of 122.43 μC/cm2 is predicted in the uniformly doped BiLaFe2O6. We find that substitution of Sr in the A-site drives the system into a metallic state. The nature of magnetism arises mainly from the B-site Fe exhibiting a G-type antiferromagnetic ordering. Our study finds that upon dopant substitution, the local magnetic moment is decreased and its magnitude is dependent on the distance between the Fe and the dopant atom. The correlation between the local moment and the distance between the Fe and the dopant atom is discussed.
Similar content being viewed by others
Introduction
The correlation between magnetic, electronic, and ferroelectric properties of transition-metal oxides has been studied for several technological applications ranging from tunable multifunctional spintronics to magnetoelectric random access memory devices and various kinds of optoelectronic devices. The most well-studied single-phase multiferroic1,2,3,4,5,6,7,8,9,10,11,12,13 material is the perovskite BiFeO3 (BFO)3, which shows a strong coupling between the spontaneous electric polarization and magnetic ground state. BFO undergoes two phase transitions upon cooling; one at its Curie temperature of 830 °C, from a paraelectric to ferroelectric and one where it becomes magnetically ordered at its Néel temperature of 370 °C. Hence, the low temperature phase with rhombohedrally distorted perovskite structure, which is both ferroelectric and anti-ferromagnetic, is of interest to our research. This phase has been reported both theoretically and experimentally, to show high spontaneous polarization and weak ferromagnetic ordering. The large orbital radius of the Bi 6s2 lone pairs is responsible for the spontaneous electric polarization whereas the magnetism originates from Fe 3d electrons. One of the challenges is that BFO thin films exhibit low electrical resistivity14, which limits its application in designing novel multifunctional non-volatile random-access memory devices.
Recent research to enhance electronic and magnetic properties of BFO has shown that the presence of common A-site dopants such as La and Sr can have a significant effect on decreasing leakage current in BFO thin films15,16,17,18,19,20,21,22,23. Furthermore, such additions may also control the volatile nature of Bi atoms, whereas B-site dopants are also studied in order to enhance the magnetic ordering in BiFeO3 which may help with loss and leakage24,25,26,27,28,29,30,31,32,33,34,35,36. Formation of oxygen vacancies may also be suppressed in the presence of these dopants due to charge compensation. Oxygen vacancies have also been shown to affect significantly the electronic and magnetic properties of related double perovskites37. Therefore, improving the antiferromagnetic ordering along with retaining high spontaneous polarization of BFO through judicious doping to make it technologically more feasible has captured much interest in the condensed matter and materials physics communities. We note that both La and Sr are commonly used dopants in prototypical ferroelectrics such as PLZT ((Pb1−xLax)(Zr1−yTiy)O3), SBT (SrBi2(Ta2O9)), SBN (SrBi2(Nb2O9)), BST (BaxSr1−xTiO3) and BIT (Bi4Ti3O12) to improve characteristic functional/physical properties. In lead zirconate titanate (PZT) thin films, La3+ dopants help to increase dielectric constant and reduce the coercive field to make it more useful for ferroelectric memory and sensing/actuating applications38,39. For BIT thin films, La3+ helps to improve fatigue characteristics while maintaining high remanent polarization40,41. Sr2+ in BST thin films shifts its paraelectric-ferroelectric transformation temperature to near room temperature for applications in telecommunications which require highly electrically tunable dielectric responses42. The presence of Bi3+ improves dielectric properties in SBT and SBN thin films by increasing its Curie temperature43. Previous reports44,45 also indicate suppression of local magnetic moments and enhancement of overall magnetic ordering in the presence of Sr doping while electronic properties and size of ferroelectric polarization for La-doped BFO is comparable46,47,48 to that of pristine BFO in thin films.
The purpose of the present work is to investigate dopant effects, specifically that of La and Sr on the electronic, magnetic and ferroelectric properties of BFO within density functional theory. The paper is organized as follows: Sec. II briefly reviews the computational details of formulating structural optimization, calculations of magnetic moment and spontaneous polarization using the Berry phase method of various supercells within first-principles theory. In Secs. III and IV, we discuss the results of our calculations, progressing from smallest unit cells to bigger supercells. Finally, Sec. V presents concluding remarks.
Computational Details
We perform first-principles calculations using the projector-augmented plane-wave (PAW) method as implemented in the Vienna ab initio Simulation Package49,50. The generalized gradient approximation (GGA) is adopted for the exchange-correlation functional. The GGA + U method is introduced to capture the strong correlation in d localized orbitals.
We use a Hubbard parameter Ueff = 2 eV, which is shown to be reasonable in previous calculations51,52. We note that other values of Ueff around 4 eV have also been used in the literature. We have systematically studied the band gap for Ueff = 0, 2, 4 and 6 eV with the GGA exchange-correlation functional for the pristine BFO in primitive unit cell and obtained values of 1.0 eV, 2.2 eV, 2.5 eV and 3.2 eV respectively. Throughout the work, we report the results for Ueff = 2 eV. Although the corresponding band gap value is slightly lower than the experimental band gap53,54,55,56,57, this difference should not significantly affect the trend in electronic and magnetic properties for doped BFO systems.
For all calculations, we consider G-type antiferromagnetic ordering on Fe cations with spins aligned oppositely in two sublattices.
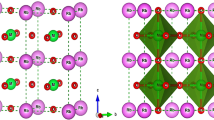
We first perform the structure optimization of the rhombohedral 2 formula units of (10 atoms) BiFeO3 by relaxing the atoms steadily toward the equilibrium until the Hellman-Feynman forces are less than 10−3 eV/Å. We refer to this 2 formula unit crystal cell as the primitive unit cell hereafter. We use these lattice parameters to construct the supercells for the exploration of the dopant effects with varying concentrations. In this primitive unit cell, substitution of one La or Sr for one Bi gives rise to compound BiLaFe2O6 and BiSrFe2O6 as shown in Fig. 1. These two specific structures also provide us an opportunity to compare the results for 50% doped BFO as calculated in the supercell technique. We note that for the rare-earth-based ferrites the crystal structure can be orthorhombic58,59, which could originate from the 4f-electron physics. Therefore, we also check the possible structure change for 50% La-doped BFO when we do the ferroelectric polarization calculations and find the R3-rhombohedral structure still sustained. The reason lies in the fact that the La has no active 4f-electron physics involved.
In the 2 × 2 × 2 supercell with 16 formula units of BFO (80 atoms), we vary the concentration of dopant atoms by 6%, 25% and 50% to study the response of electronic and magnetic properties. For 50% doping, it is also interesting to explore the connection of the results in primitive unit cells and supercells. All calculations for the primitive unit cells and supercells are performed with a 5 × 5 × 5 Monkhorst-Pack60 k-point mesh51 centered at Γ and a 500 eV plane-wave cut off energy, for which the results are converged. For both 25% and 50% concentrations, we build three supercells. For each of them, the distances between the dopant atoms are varied as shown in Fig. 1. For both 25% and 50% dopant concentrations, Configuration III represents the structural model where the dopants are placed at the most elongated position along [111] direction in the supercell. Configuration I has the dopants most packed with respect to each other, i.e. has the minimum average distance between dopants. Configuration II is such designed where the dopant atoms are placed in between these two extremums. We also provide an example of how this average distance between dopants are calculated as well as atomic coordinates of A-site and B-site atoms for all of these configurations in Supplementary Material (See SM-1 and SM-2, respectively). The structural relaxations were performed only for the pristine BFO, 6% doped, 25% and 50% doped in Configuration III, for which the spontaneous polarization exists. We choose Configuration III only because we anticipate that this quantity is insensitive to the distribution of the dopants. These relaxations followed the same convergence criterion as explained previously in the section. The choices of supercells are based on experimental evidence reported elsewhere15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36. These particular cases are chosen to explore the location (with respect to Fe atoms) dependence of dopant effects in these supercells.
The macroscopic polarization in an infinite periodic solid can be written as the sum of ionic and electronic terms:
where V is the volume of the unit cell, Zτ and bτ are the charge and position of the τ-th atom in the cell, and ρ(r) is the cell-periodic density of electron charge. The electron-charge density can be expanded into the sum of occupied Bloch states ψikσ(r) or Wannier functions Wiσ(r) as represented below within modern theory of polarization61,62:
Utilizing the Bloch-state representation for ρ(r) one can calculate the total electronic contribution of polarization as the solutions to the delocalized Bloch functions along a density-sampled string of neighboring points in k-space for a given crystalline geometry. For a specific choice of basis vectors, the ionic contribution is calculated by summing the product of the position of each ion in the unit cell with the nominal charge of its rigid core. Therefore, the total spontaneous polarization is obtained by summing the electronic and ionic part of the polarizations using Berry phase method. Using the Berry phase approach, the total polarization can only be reported up to integer multiples of the indeterminate polarization quanta with the latter computed by eR/Ω. Structurally, displacements of ions along [111] and counter-rotations about the oxygen octahedra about [111] of cubic perovskite (undistorted structure) yields rhombohedral R3c (fully distorted) structures for pristine BFO and R3 for La-doped BFO. To avoid any discrepancy in choosing one specific path that connects the smallest polarization of the undistorted phase to that of the fully distorted phase, we only look at the residual polarizations by following the procedure proposed in ref.51. In other words, we first calculate the total polarizations of both phases for each system. We then compare those to the polarization quanta and take the difference of their residues for the true polarization.
Results
In this section, we report comparative results of the electronic, magnetic properties of BiLaFe2O6 and BiSrFe2O6 and other doped BFO treated in the supercells.
BiLaFe2O6 and BiSrFe2O6
We observe the change in the electronic and magnetic properties for BiLaFe2O6 and BiSrFe2O6 as compared to pristine BFO. The relaxed structure parameters of the 10-atom unit cell of BFO belonging to R3c 161 space group are a = b = c = 5.69Å and αrh = 58.54°. The relaxed cell volume is 125.72 Å3. This is in good agreement with previous experimental and theoretical predictions51,63. We have used these same lattice parameters for the doped unit cells, noting that the minimal changes in atomic positions during additional structural optimization do not affect the metallic or insulating states obtained for these configurations. The band structure calculations for primitive unit cells are performed along high-symmetry-k-points for a rhombohedral crystal system (F-Γ-Z-L-F) as shown in Fig. 2. The system remains insulating for pristine BFO and BiLaFe2O6. The indirect band gap is smaller in BiLaFe2O6 as compared to BFO. The valence band maxima (VBM) is located in between F and Γ points for BFO while the conduction band minimum (CBM) is located at Z. For BiLaFe2O6 and BiSrFe2O6, the VBM and CBM are both located at point Z. The locations of the energy levels as shown in Fig. 2 are referenced with respect to the low-lying O 2s states, whose energy is considered to be the same in all the compounds considered in this study. This is done specifically to emphasize the upward/downward shifts of the bands in energy in the doped BiFeO3 compounds. A few electronic bands in the valence band (Γ-Z-L) region are shifted above the Fermi level for BiSrFe2O6 leading to a metallic state. This is due to the hole doping effect when Sr atoms are substituted for Bi atoms with Sr giving up nominally two electrons in its divalent state. It leads to the shift of the chemical potential with the minor change of bonding nature. As shown in Fig. 3, this corresponds to the crossing of the Fe-3d band with the Fermi energy, driving the system to be metallic. Our finding for Sr-doped BFO is consistent with the observation from the electronic structure calculations for SrFeO3 in AFM state64,65.
Band structures of (a,d) pristine BFO, (b,e) BiLaFe2O6 and (c,f) BiSrFe2O6 in [−4, 4] eV energy range as calculated along high-symmetry-k-points for a rhombohedral crystal system along (F-Γ-Z-L-F). Blue represents spin-up and red represents spin-down bands. Energy is measured with respect to the Fermi energy.
The nature of magnetism is assumed to be G-type66,67,68 arising from Fe atoms. In addition, with the A-site substitution, the results from our first-principles calculations follow the Goodenough-Kanamori rules that the partially filled d orbitals of two Fe ions can have a strong antiferromagnetic superexchange coupling when they form a 180 degree Fe3+-O2−-Fe3+ bonds. A table listing total energies for all doped and undoped systems in the primitive unit cell and the supercell with G-type AFM and FM ordering is given in Supplementary Material (See SM-3). For the pristine BFO, the average of the staggered magnetic moment is 4.02 μB per Fe, which reduces to 3.95 μB and 3.74 μB for La and Sr doped BFO, respectively. Therefore, A-site dopants will overall suppress the magnetic moments in these systems. More importantly, the net magnetic moment for pristine BFO is 0 μB whereas net moments for the La, Sr cases are 0.004 μB and −0.630 μB, respectively.
Since calculations of spontaneous polarization demand the system to be perfectly insulating, we cannot report any polarization for Sr doped BFO. For the pristine BFO and 50% La doped BFO, the values of the polarization are 114.90 μC/cm2 and 122.43 μC/cm2 respectively. These are the largest reported polarizations of these systems in these specific geometric configurations. The change in polarization of R3 BiLaFe2O6 as compared to R3c pristine BiFeO3 is due to difference in ionic radii and local charge distribution of these A-site cations. For Bi (5d10 6s2 6p3) there are total 3 valence electrons whereas 3 for La (5s2 5p6 5d1 6s2) and 2 for Sr (4s2 4p6 5s2). For pristine BFO, there is a hybridization between 6s and 6p states that gives rise to active lone pair electrons. For La and Sr doped cases, the degree of Fe 3d-4p orbital mixing23 is reduced. This is due to the movements of local ions to a more symmetric position. This is further analyzed by Bader charge density approach69,70,71,72 as reported in Sec. III.C where the local charge distributions are compared for La and Sr doped BFO to that of pristine BFO. Because of these, the ionic and electronic contributions to the total polarization for La doped BFO are higher than those of the pristine BFO, leading to a higher spontaneous polarization.
Supercell
To observe and quantify the effects of dopants more rigorously, we have constructed 80-atom supercells with a = b = c = 11.37Å and αrh = 58.54 as shown in Fig. 1. The total electron density of states for both spin-resolved channels have been computed for 6%, 25%, and 50% La, Sr doped BFO. The results are plotted in Fig. 4 within specific energy ranges in comparison to that of the pristine BFO. Figure 4(b) shows that by introducing only 6% Sr doping, which amounts to only one Sr atom in the BFO supercell, the system goes to a metallic state73; while the La-doped BFO remains insulating. This behavior also suggests a p-type electrical behavior in Sr-doped BFO, where holes are the main charge carriers. As the dopant concentration is increased from 6% to 25% and 50%, these electronic properties are more pronounced as shown in Fig. 4(c–h). Even for 50% dopant concentration, La doped BFO maintains an insulating state.
For 6% dopant concentration, the Fe atom with the smallest distance 3.30 Å away from the dopant has the local magnetic moments of 4.03 μB for La and 3.98 μB for Sr cases, respectively; while the Fe atom with distance 3.11 Å away from the dopant has the local moment of −4.03 μB for La and −3.96 μB for Sr cases, respectively. In addition, the local moment on the other Fe atoms varies with their distance from the dopant site, suggesting a strong dependency on the atomic environment. The Fe atom with the farthest distance from the dopant has the largest local magnetic moments. We report local moments for each Fe atom along with its distance from the dopant atoms for both La and Sr cases in Supplementary Material (See SM-4). As the distance between the dopants to Fe atoms increases, the doped case behaves more like the pristine and the effects of the dopants are less pronounced. Similar behavior has been obtained for 25% and 50% dopant concentrations and the results are summarized in Table I. Overall, A-site dopants suppress magnetic moments. In our calculations, we obtained average magnetic moment of 4.04 μB (4.00) for 6% La (Sr) concentrations. For 25% La (Sr) concentrations, the average magnetic moments are 4.03 μB (3.78), 4.04 μB (3.88) and 4.03 μB (3.88) in Configuration I, II and III, respectively. For 50% La (Sr) concentrations, the average magnetic moments are 4.03 μB (3.75), 4.03 μB (3.76) and 4.03 μB (3.75) in Configuration I, II and III respectively. We remark that our results for 50% concentration in the Configuration III supercell calculations are consistent with those in primitive unit cells.
Overall, the difference in the highest and the lowest local moment for 6%, 25% and 50% dopant concentrations are listed in Table 1. The overall magnetic moment of Fe atoms is decreased as the dopant concentration is increased. The change is the greatest when BFO is doped with 50% Sr which suggests that the Sr dopant has a greater impact on the magnetic properties compared to La because of the dissimilar nature of its A-site cations as compared to pristine BFO.
We also report the polarizations (P) of pristine, 6%, 25%, 50% La-doped BFO as 115.61 μC/cm2, 116.59 μC/cm2, 118.71 μC/cm2 and 120.09 μC/cm2, respectively. There is a 7–10% change in polarization as is shown in Table 2. Again our results on the polarization for the 50% La-doped case in Configuration III is consistent with that reported with that reported for the primitive unit cell. We note that for the pristine BFO, the 0.6% difference in the polarization between the calculations with primitive unit cell and supercell could be attributed to the slight difference in the atomic positions during structural relaxation.
The relaxed cell volumes corresponding to each case are 1005.78 Å3 (pristine), 1023.58 Å3 (6% La-doped), 1010.38 Å3 (25% La-doped in Configuration III) and 1009.54 Å3 (50% La-doped in Configuration III), respectively which is used to calculate the true polarization. It is important to mention that these relaxed supercells still belong to the same rhombohedral R3 symmetry group family and thus the reference states for each of these cases are their corresponding cubic perovskites (undistorted) structures with equal volumes of the respective undistorted ones. Furthermore these computations are only performed for one specific structural configuration such as Configuration III since we do not expect major differences in this trend of enhanced spontaneous polarization as the distances between dopants sites are varied. There is no spontaneous polarization for Sr-doped BFO because they are metallic.
Discussion
From the previous sections, it is evident that the electronic properties of La doped BFO in each supercell is comparable to that of pristine BFO. The differences as shown in the comparative total electron density states in Fig. 4(c–h) arise due to reduction in anisotropy in Fe-O bond distances and local structural distortions as the dopants concentrations are increased. Moreover, for La-doped cases, the Fe 3d-4p orbital mixing and differences in electronegativities are the additional factors to enhance the spontaneous polarization and magnetic properties. Similarly, for the Sr case, the Fe ion in the FeO6 moves to a more symmetric position that gives rise to variation in electron densities. However, the electronegativity of Sr is quite low compared to Bi and the Fe-3d band upshift across the Fermi energy makes it non-insulating.
Partial density of states of Fe-3d orbitals on atoms closest to the (a) La and (b) Sr atoms for 6%, 25% and 50% (Configuration III) concentrations respectively. Total electron density of states for 6% doped (c), 25% doped (d–f) and 50% doped (g–i) BFO in all three configurations. Energy is measured with respect to the Fermi energy.
Here, we also provide a Bader charge analysis in Fig. 5 for pristine BFO as compared to the various doped cases. Bader analysis gives the electronic charge and density of atoms suitable to discuss electronic structure and ionic-covalent character of a compound. The normalization of volume as considered by this technique is necessary to highlight electronic structure modifications due to exact exchange.
The number of valence electrons included in each atomic species pseudo potential are 15e for Bi (5d10 6s2 6p3), 8e for Fe (3d7 4s1), 6e for O (2s2 2p4), 11e for La (5s2 5p6 5d1 6s2) and 10e for Sr (4s2 4p6 5s2). We only consider the valence electrons in this analysis since the effects of core electrons on the electronic behavior74 of these systems are expected to be minimal. Only one type of configuration (Configuration III) for 25% and 50% is considered here since the overall properties do not vary significantly for different configurations. The Bader charge volumes as represented in Fig. 5(a–d) are suggestive of more symmetric charge distributions around the A-site dopants in BFO, as described earlier. The average Bader charge for Bi cations is 12.32 electrons and 8.92 and 8.42 electrons for La and Sr cations, respectively. Therefore, the estimated valence charges of Bi, La and Sr are 2.68, 2.08 and 1.58 (cf. formal valence charges of 3, 3 and 2), respectively. Figure 5(e) shows the Bader charges of Fe atoms closest to the dopant atoms for varying concentrations. It also implies that valence charge of Fe is close to 2 + (8e −∼ 6e) for pristine and doped BFO compounds. Charges on oxygen atoms are also reduced to ∼1.4- (cf. formal valence charge of 2-) states for all systems to maintain charge neutrality. There is nominal difference in Fe valence states as compared between pristine and La-doped BFO supercells. There is overall ∼2% reduction in the local charges of Fe atoms between pristine and Sr doped BFO, which provides an explanation for the overall reduced moment in this case. Bader charges and volumes (Å3) for all the atoms for pristine, 6%, 25% and 50% La and Sr doped BFO (in Configuration III) are also given in Supplementary Material (See SM-5, SM-6 and SM-7 respectively). We observe the valence charge of the La dopant atoms is higher than that of Sr by 0.5 electrons. This analysis is also suggestive of mixed ionic-covalent character as observed in such compounds74.
Finally, we present the optical properties such as dielectric function as a function of frequency and refractive indices to provide a sufficient insight to how La and Sr can improve the energy loss. This computation was performed using Kramers-Kronig relation as implemented in VASP49,50. From Fig. 6(a,b), it is clear that both the phase lag and energy loss are improved as dopants are introduced in pristine BFO75,76. The dopant sites may no longer be considered as isolated sites in the presence of higher dopant concentrations, which may lead to a dielectric breakdown of such materials when subjected to intense electric fields. From the imaginary part of the dielectric functions, the transitions between O-p electron to unoccupied Fe-d states, O-p electron to p states high energy conduction bands and other inner electron excitations can also be identified in each case. The highest value of refractive index n for pristine BFO is reported as 2.88 at an energy of 2.22 eV. For 6% La and Sr doped cases these values shift to 2.82 at an energy of 1.4 eV and 2.84 at 2.12 eV. As the dopant concentration is increased to 25% and 50%, these values decrease to 2.34 and 2.67 at same energies, suggesting the same behavior of major absorption due to transition from valence to conduction bands as predicted by the frequency dependent dielectric functions.
Concluding Remarks
In conclusion, we have investigated systematically the La and Sr dopant effect on electronic and magnetic properties in BFO. We have found that La-doped BFO maintains an insulating state whereas adding Sr drives the system to be metallic. This behavior is evident from the band structure calculations. We have also obtained an enhancement of the total polarization in La-doped BFO by 4–8% over the pristine BFO, because of the variance in ionic radii, electronegativity and valence electrons in Bi3+ and La3+. The average magnetic moment of Fe atoms decreases as we increase dopant concentration. This behavior is also dependent on the local atomic environment. In the structural configuration where the distances between dopant atoms with respect to Fe atoms is the smallest, the variance is the highest for lowest local moments. The local charge distribution is responsible for these changes in electronic and magnetic properties. Variance in s and d orbitals occupancy for La and Sr and d orbital occupancy for the Fe-like transition metal ion may also contribute to changes in these properties.
The following remarks are in order: Our study gives an estimate of the magnetic moments in primitive unit cells and supercells as compared to pristine BFO. We note that we do not perform any structural relaxation for every supercell because the minimal changes in atomic positions will not affect the metallic or insulating states obtained for the doped system. We anticipate no substantial change in the electronic properties (density of states, band structures) if the impurity concentration is varied in La doped case. Structural relaxations were performed only for pristine BFO, 6%, 25% and 50% La doped BFO in Configuration III, for which the spontaneous polarization occurs. The interference caused by large concentration of dopants in BFO does not affect the polarization significantly. The net ferromagnetic component of La and Sr doped BFO is increased as compared to the pristine BFO. This increase gives the potential of ferromagnetic, ferroelectric coupling in at least La-doped BFO. The specific three structural configurations were chosen judiciously to quantify the effects of dopants with respect to wide change in the surrounding atomic environment. We reason that the use of the sample averaging technique77,78 for a large number of dopant atoms situated at every possible site may give us deeper insights into these effects. But such calculations will become extremely expensive for relatively large impurity configurations and are therefore beyond the scope of this paper. In addition, we expect that the electronic properties explored here in seven distinct structural configurations with 6%, 25% and 50% concentrations may not differ much compared to other possible structural configurations to cause significant variations in our predictions.
References
Michel, C., Moreau, J. M., Achenbach, G. D., Gerson, R. & James, W. J. The atomic structure of BiFeO3. Solid State Commun. 7(9), 701–704 (1969).
Kubel, F. & Schmid, H. Structure of a ferroelectric and ferroelastic monodomain crystal of the perovskite BiFeO3. Acta Cryst B. 46(6), 698–702 (1990).
Spaldin, N. A., Cheong, S. W. & Ramesh, R. Multiferroics: Past, present, and future. Phys. Today 63(10), 38–43 (2010).
Smolenski, G. A. & Chupis, I. E. Ferroelectromagnets. Phys.-Uspekhi 25(7), 475 (1982).
Schmid, H. Multi-ferroic magnetoelectrics. Ferroelectrics 162, 317–338 (1994).
Wang, J. et al. Epitaxial BiFeO3 multiferroic thin film heterostructures. Science 299(5613), 1719–1722 (2003).
Iakovlev, S., Solterbeck, C. H., Kuhnke, M. & Es-Souni, M. Multiferroic BiFeO3 thin films processed via chemical solution deposition: Structural and electrical characterization. J. Appl. Phys. 97(9), 094901 (2005).
Catalan, G. & Scott, J. F. Physics and applications of bismuth ferrite. Adv. Mater. 21, 2463 (2009).
Aksel, E. & Jones, J. L. Advances in lead-free piezoelectric materials for sensors and actuators. Sensors 10, 1935 (2010).
Teague, J. R., Gerson, R. & James, W. J. Dielectric hysteresis in single crystal BiFeO3. Solid State Commun. 8, 1073 (1970).
Martin, L. W., Chu, Y. H. & Ramesh, R. Advances in the growth and characterization of magnetic, ferroelectric, and multiferroic oxide thin films. Mater. Sci. Eng. R- Rep. 68, 89 (2010).
Selbach, S. M., Tybell, T., Einarsrud, M. A. & Grande, T. The ferroic phase transitions of BiFeO3. Adv. Mater. 20, 3692 (2008).
Yun, K. Y. et al. Structural and multiferroic properties of BiFeO3 thin films at room temperature. J. Appl. Phys. 96, 3399 (2004).
Qi, X., Dho, J., Tomov, R., Blamire, M. G. & MacManus-Driscoll, J. L. Greatly reduced leakage current and conduction mechanism in aliovalent-ion-doped BiFeO3. Appl. Phys. Lett. 86, 062903 (2005).
Singh, S. K., Ishiwara, H. & Maruyama, K. Room temperature ferroelectric properties of Mn-substituted BiFeO3 thin films deposited on Pt electrodes using chemical solution deposition. Jpn. J. Appl. Phys. 45, 3194 (2006).
Khomchenko, V. A. et al. Intrinsic nature of the magnetization enhancement in heterovalently doped Bi1−xAxFeO3(A = Ca, Sr, Pb, Ba) multiferroics. J. Phys. D 41, 102003 (2008).
Yang, C. H., Kan, D., Takeuchi, I., Nagarajan, V. & Seidel, J. Doping BiFeO3: approaches and enhanced functionality. Phys. Chem. Chem. Phys. 14, 15953 (2012).
Pan, D. F. et al. Local Magnetoelectric Effect in La-Doped BiFeO3 Multiferroic Thin Films Revealed by Magnetic-Field-Assisted Scanning Probe Microscopy. Nanoscale Res. Lett. 11, 1 (2016).
Du, Y. et al. Enhancement of ferromagnetic and dielectric properties in lanthanum doped BiFeO3 by hydrothermal synthesis. J. Alloys Compd. 490, 637 (2010).
Suresh, P. & Srinath, S. Effect of La substitution on structure and magnetic properties of sol-gel prepared BiFeO3. J. Appl. Phys. 113, 17D920 (2013).
Cheng, Z. X. et al. Structure, ferroelectric properties, and magnetic properties of the La-doped bismuth ferrite. J. Appl. Phys. 103, 07E507 (2008).
Khomchenko, V. A. et al. Synthesis and multiferroic properties of Bi0.8A0.2FeO3(A = Ca, Sr, Pb) ceramics. Appl. Phys. Lett. 90, 242901 (2007).
Lee, J. H. et al. Variations of ferroelectric off-centering distortion and 3d-4p orbital mixing in La-doped BiFeO3 multiferroics. Phys. Rev. B 82, 045113 (2010).
Martin, L. W. et al. Multiferroics and magnetoelectrics: thin films and nanostructures. J. Phys. Condens. Matter. 20, 434220 (2008).
Kharel, P. et al. Structural, magnetic, and electrical studies on polycrystalline transition-metal-doped BiFeO3 thin films. J. Phys. Condens. Matter. 21, 036001 (2008).
Lee, D., Kim, M. G., Ryu, S., Jang, H. M. & Lee, S. G. Epitaxially grown La-modified BiFeO3 magnetoferroelectric thin films. Appl. Phys. Lett. 86, 222903 (2005).
Jiang, Q. H., Nan, C. W. & Shen, Z. J. Synthesis and properties of multiferroic La-modified BiFeO3 ceramics. J. Am. Ceram. Soc. 89, 2123 (2006).
Yu, B. et al. Effects of ion doping at different sites on electrical properties of multiferroic BiFeO3 ceramics. J. Phys. D 41, 065003 (2008).
Lee, Y. H., Wu, J. M. & Lai, C. H. Influence of La doping in multiferroic properties of BiFeO3 thin films. Appl. Phys. Lett. 88, 042903 (2006).
Sharma, P. & Varshney, D. Effect of La and Pb substitution on structural and electrical properties of parent and La/Pb co doped BiFeO3 multiferroic. Adv. Mater. Lett. 5, 71 (2014).
Lin, F. et al. Effect of La/Cr codoping on structural transformation, leakage, dielectric and magnetic properties of BiFeO3 ceramics. J. Mater. Sci. 52(12), 7118–7129 (2017).
Liu, L. et al. Effects of (La, Sr) co-doping on electrical conduction and magnetic properties of BiFeO3 nanoparticles. Chin. Phys. B. 25(9), 097801 (2016).
Yu, B. et al. Enhanced electrical properties in multiferroic BiFeO3 ceramics co-doped by La3+ and V5+. J. Phys. D 41, 185401 (2008).
Kuo, J. H., Anderson, H. U. & Sparlin, D. M. Oxidation-reduction behavior of undoped and Sr-doped LaMnO3 nonstoichiometry and defect structure. J. Soild State Chem. 83, 52 (1989).
Hao, X., Zhai, J. & Yao, X. Improved energy storage performance and fatigue endurance of Sr-doped PbZrO3 antiferroelectric thin films. J. Am. Ceram. Soc 92, 1133 (2009).
Islam, M. R. et al. Correlation of charge defects and morphology with magnetic and electrical properties of Sr and Ta codoped BiFeO3. J. Alloys Compd. 688, 1186 (2016).
Ghosh, A., Ahmed, T., Yarotski, D. A., Nakhmanson, S. M. & Zhu, J. X. Oxygen vacancy effects on double perovskite Bi2FeMnO6: A first-principles study. EPL 116, 57002 (2017).
Chang, J. F. & Desua, S. B. Effects of dopants in PZT films. J. Mater. Res. 9, 955 (1994).
Tuttle, B. A. Electronic ceramic thin films: trends in research and development. MRS Bull. 12, 40 (1987).
Noguchi, Y., Miwa, I., Goshima, Y. & Miyayama, M. Defect control for large remanent polarization in bismuth titanate ferroelectrics-doping effect of higher-valent cations. Jpn. J. Appl. Phys. 39, L1259 (2000).
Maurya, D. et al. Soft phonon mode dynamics in Aurivillius-type structures. Phys. Rev. B 96, 134114 (2017).
Subramanyam, G. et al. Challenges and opportunities for multi-functional oxide thin films for voltage tunable radio frequency/microwave components. J. Appl. Phys. 114, 191301 (2013).
Wu, Y. et al. Doping effect in layer structured SrBi2Nb2O9 ferroelectrics. J. Appl. Phys. 90, 5296 (2001).
Dhir, G., Uniyal, P. & Verma, N. K. Multiferroic properties of Sr-doped BiFeO3 nanoparticles. PHYSICA B 531, 51–57 (2018).
Sharma, N., Kumar, S., Mall, A. K., Gupta, R. & Garg, A. Sr and Mn co-doped sol-gel derived BiFeO3 ceramics with enhanced magnetism and reduced leakage current. Mater. Res. Express 4, 015702 (2017).
Peng-Ting, L. et al. La-doped BiFeO3: Synthesis and multiferroic property study. Chin. Phys. B 23, 047701 (2014).
Xie, Y. J. et al. Preparation of La-doped BiFeO3 thin film and its photovoltaic properties. Journal of Inorganic Materials. 28, 436–440 (2013).
Zhang, X.Y., Qi, X.W., Qi, J.Q. & Wang, X. Preparation and Properties of Multiferroic La-Doped BiFeO3 Thin Film. In Adv. Mater. Res., 486 (Trans Tech Publ), 417–421 (2012).
Kresse, G. & Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 47, 558 (1993).
Kresse, G. & Furthmiller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169 (1996).
Neaton, J. B., Ederer, C., Waghmare, U. V., Spaldin, N. A. & Rabe, K. M. First-principles study of spontaneous polarization in multiferroic BiFeO3. Phys. Rev. B 71, 014113 (2005).
Lubk, A., Gemming, S. & Spaldin, N. A. First-principles study of ferroelectric domain walls in multiferroic bismuth ferrite. Phys. Rev. B 80, 104110 (2009).
Gavriliuk, A. G. et al. Another mechanism for the insulator-metal transition observed in Mott insulators. Phys. Rev. B: Condens. Matter Mater. Phys. 77, 155112 (2008).
Basu, S. R. et al. Photoconductivity in BiFeO3 thin films. Appl. Phys. Lett. 92, 091905 (2008).
Kumar, A. et al. Linear and nonlinear optical properties of BiFeO3. Appl. Phys. Lett. 92, 121915 (2008).
Kanai, T., Ohkoshi, S. & Hashimoto, K. Magnetic, electric, and optical functionalities of (PLZT)x(BiFeO3)1−x ferroelectric-ferromagnetic thin films. J. Phys. Chem. Solids 64, 391 (2003).
Gao, F. et al. Preparation and photoabsorption characterization of BiFeO3 nanowires. Appl. Phys. Lett. 89, 102506 (2006).
Zhao, H. J. et al. Effect of chemical and hydrostatic pressures on structural and magnetic properties of rare-earth orthoferrites: a first-principles study. J. Phys. Condens. Matter 25, 466002 (2013).
Zhao, H. J. et al. Creating multiferroics with large tunable electrical polarization from paraelectric rare-earth orthoferrites. J. Phys. Condens. Matter 26, 472201 (2014).
Monkhorst, H. J. & Pack, J. D. Special points for Brillouin-zone integrations. Phys. Rev. B 13, 5188 (1976).
King-Smith, R. D. & Vanderbilt, D. Theory of polarization of crystalline solids. Phys. Rev. B 47, 1651 (1993).
Resta, R. Macroscopic polarization in crystalline dielectrics: the geometric phase approach. Rev. Mod. Phys. 66, 899 (1994).
Hatt, A. J., Spaldin, N. A. & Ederer, C. Strain-induced isosymmetric phase transition in BiFeO3. Phys. Rev. B 81, 054109 (2010).
Jaya, S. M., Jagadish, R., Rao, R. S. & Asokamani, R. Electronic structure and magnetism of SrFeO3 and SrCoO3. Phy. Rev. B 43, 13274 (1991).
Matar, S. F. Ab initio investigations in magnetic oxides. Progress in solid state chemistry Prog. Solid State Chem. 31, 239–299 (2003).
Goodenough, J. B., Wold, A., Arnott, R. J. & Menyuk, N. Relationship between crystal symmetry and magnetic properties of ionic compounds containing Mn3+. Phys. Rev. 124, 373 (1961).
Goodenough, J.B. Magnetism and the chemical bond, Interscience monographs on chemistry: Inorganic chemistry section (1963).
Ahmed, T. et al. Magnetic, electronic, and optical properties of double perovskite Bi2FeMnO6. APL Mater. 5, 035601 (2017).
Tang, W., Sanville, E. & Henkelman, G. A grid-based Bader analysis algorithm without lattice bias. J. Phys. Condens. Matter 21, 084204 (2009).
Sanville, E., Kenny, S. D., Smith, R. & Henkelman, G. Improved grid-based algorithm for Bader charge allocation. J. Comput. Chem. 28, 899 (2007).
Henkelman, G., Arnaldsson, A. & Jonsson, H. A fast and robust algorithm for Bader decomposition of charge density. Comput. Mater. Sci 36, 354 (2006).
Yu, M. & Trinkle, D. R. Accurate and efficient algorithm for Bader charge integration. J. Chem. Phys. 134, 064111 (2011).
Li, M., Wang, Y., Wang, Y., Chen, F. & Xia, C. Bismuth doped lanthanum ferrite perovskites as novel cathodes for intermediate-temperature solid oxide fuel cells. CS Appl. Mater. Interfaces 6, 11286 (2014).
Stroppa, A. & Picozzi, S. Hybrid functional study of proper and improper multiferroics. Phys. Chem. Chem. Phys. 12, 5405–5416 (2010).
Wang, H., Zheng, Y., Cai, M. Q., Huang, H. & Chan, H. L. First-principles study on the electronic and optical properties of BiFeO3 Solid State. Commun. 149, 641 (2009).
Liu, K., Fan, H., Ren, P. & Yang, C. Structural, electronic and optical properties of BiFeO3 studied by first-principles. J. Alloys Compd. 509, 1901 (2011).
Ozaki, T. Variationally optimized atomic orbitals for large-scale electronic structures. Phys. Rev. B 67, 155108 (2003).
Seko, A., Koyama, Y. & Tanaka, I. Cluster expansion method for multicomponent systems based on optimal selection of structures for density-functional theory calculations. Phys. Rev. B 80, 165122 (2009).
Acknowledgements
Ayana Ghosh acknowledges the support of the Student Program at Los Alamos National Laboratory (LANL). This work was supported by the U.S. DOE Contract No. DE-AC52-06NA25396 through the LANL LDRD Program Code XWFL (A.G.) and the U.S. DOE BES Program Code E3B5 (J.-X.Z.). The work was in part supported by the Center for Integrated Nanotechnologies, a DOE BES user facility. Los Alamos National Laboratory, an affirmative action equal opportunity employer, is managed by Triad National Security, LLC for the U.S. DOE NNSA under Contract No. 89233218CNA000001. The authors acknowledge Dr. Sebastian E. Reyes-Lillo for his helpful discussion on polarization calculations in ferroelectrics.
Author information
Authors and Affiliations
Contributions
A.G. performed all theoretical computations and prepared all the figures. J.-X.Z. guided the project. D.P.T, H.C., S.M.N., S.P.A. participated in the discussion of the results. A.G. and J.-X.Z. wrote the paper with inputs from all co-authors.
Corresponding authors
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ghosh, A., Trujillo, D.P., Choi, H. et al. Electronic and Magnetic Properties of Lanthanum and Strontium Doped Bismuth Ferrite: A First-Principles Study. Sci Rep 9, 194 (2019). https://doi.org/10.1038/s41598-018-37339-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-018-37339-3
This article is cited by
-
Role of La substitution on structural, optical, and multiferroic properties of BiFeO3 nanoparticles
Applied Nanoscience (2023)
-
Multiferroic and Electrical Properties of Mg2+ Substituted Lead-Free Double Perovskite for Device-Based Utilizations
Journal of Inorganic and Organometallic Polymers and Materials (2023)
-
Magnetoresistive effect in the cobalt-doped bismuth ferrite films
Journal of Materials Science: Materials in Electronics (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.