Abstract
Anti-reflection coatings (ARCs) enable one to trap high dielectric spheres that may not be trappable otherwise. Through rigorously calculating the gradient and scattering forces, we directly showed that the improved trapping performance is due to the reduction in scattering force, which originates from the suppression of backscattering by ARC. We further applied ray optics and wave scattering theories to thoroughly understand the underlying mechanism, from which, we inferred that ARC only works for spherical particles trapped near the focus of an aplanatic beam, and it works much better for large spheres. For this reason, in contradiction to our intuition, large ARC-coated spheres are sometimes more trappable than their smaller counter parts. Surprisingly, we discovered a scattering force free zone for a large ARC-coated sphere located near the focus of an aplanatic beam. Our work provides a quantitative study of ARC-coated spheres and bridges the gap between the existing experiments and current conceptual understandings.
Similar content being viewed by others
Introduction
Optical tweezers1,2,3,4, which traps small particles using a tightly focused laser beam, have found fruitful applications across various scientific areas, ranging from physics5,6,7,8 to chemistry9,10, and to biology11,12. Particles in a laser beam are subject to both the optical scattering force Fs(x) and gradient force Fg(x)13,14,15,16,17,18. The former is divergence-less (∇ · Fs = 0) and tends to axially push the particle away from the focus, while the latter is curl-less (∇ × Fg = 0) and tends to attract the particle towards the focus. A particle can be trapped if the gradient force dominates2. Thus, optical trapping can be improved by either reducing the scattering force or enhancing the gradient force. So far, these two aspects are realized by either shaping the beam19,20,21,22 or customizing the morphology of the trapped object23,24. A simple and elegant example is to coat an anti-reflection coating (ARC) on a high dielectric spherical particle25,26,27, as shown in Fig. 1. While a bare high dielectric particle is highly reflective and thus not trappable, the ARC makes it trappable. Interestingly, such trapped ARC coated particle possesses a large transverse gradient force (up to a nano-Newton), which opens up new potentials for applications, such as protein unfolding, amyloid fibril disruption, cell adhesion and contraction26. It is commonly believed that ARC can reduce the scattering force, however, it was not rigorously proven. The difficulty partly lies in the fact that one cannot easily obtain the gradient and scattering force for Mie sized particles. Moreover, although the backward scattering is believed to be suppressed for ARC-coated particles, the mechanism was not well explained, especially from the perspective of wave scattering theory.
Here, we reinvestigate the optical trapping of ARC-coated spheres by explicitly calculating their gradient and scattering forces using the approach adopted by ref.18, and studying their scattering properties when illuminated by an aplanatic beam or a plane wave. The numerical results show clearly that the scattering force is reduced by several orders in magnitude near the focus when the sphere is coated by ARC, which directly verifies the conclusions in the previous work25. The scattering force is reduced due to the suppression of the backward scattering, which can be seen clearly from the scattering features. By analytically studying the Mie coefficients of the ARC-coated sphere, we find that the low order Mie coefficients satisfy the generalized Kerker condition that leads to the suppression of the backward scattering28,29. However, because the high order Mie coefficients do not satisfy the condition, the backward scattering can be suppressed only when the scattering is dominated by the low order scattering coefficients, which requires the incident beam to be an aplanatic beam whose beam shape coefficient decays as its order grows, but not a plane wave whose beam shape coefficient increases with its order. Also, the generalized Kerker condition is fulfilled for more orders as the particle size increases, implying that ARC works much better for the larger size spheres.
Results
The scattering and gradient forces acting on uncoated and ARC-coated spheres
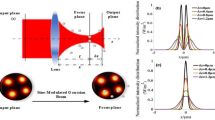
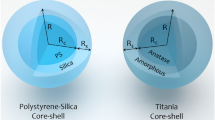
Consider the ARC-coated sphere shown in Fig. 1. It has inner and outer radii r1 and r2, respectively. Its core, coating, and surrounding have refractive indices of n1, n2, and n0, respectively. The ARC that coated on the sphere is similar to that of a planar surface, which is characterized by a refractive index \({n}_{2}\approx \sqrt{{n}_{1}{n}_{0}}\) and a thickness (r2 − r1) = λ/(4n2), where λ is the vacuum wavelength. We consider the same materials as in ref.26, namely, n0 = 1.33 (water), n1 = 2.3 (anatase titania), and n2 = 1.78 (amorphous titania), which approximately fulfill the ARC conditions30. The trapping beam is an x-polarized and z-propagating fundamental Gaussian beam with vacuum wavelength λ = 1.064 μm and is focused by a high numerical aperture (NA) objective lens with NA = 1.3, if not otherwise stated. As shown in Fig. 1, the origin of the coordinate system is chosen to be the beam focus.
The total optical force F(x) acting on the sphere can be calculated rigorously using the generalized Lorenz-Mie theory and the Maxwell stress tensor31,32,33,34. Such an approach makes no approximation within classical electrodynamics and is subject only to the numerical truncation error. The total force can then be numerically decomposed into the scattering force Fs(x) and gradient force Fg(x) using the approach presented in ref.18:
where \(\tilde{{\bf{F}}}({\bf{q}})\) is the Fourier transform of the total optical force, which is given by \(\tilde{{\bf{F}}}({\bf{q}})=\int \frac{{\bf{F}}({\bf{x}})}{{(2\pi )}^{3/2}}{e}^{-i{\bf{q}}\cdot {\bf{x}}}{d}^{3}{\bf{x}}.\)
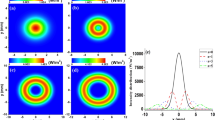
In Fig. 2, we plot the longitudinal (z direction) optical forces acting on uncoated (solid lines) and ARC-coated (dotted lines) spheres along the beam axis. Trapping equilibrium does not exist for the uncoated spheres, while stable axial trapping is possible after introducing the ARC, in agreement with refs25,26,27. The gradient and scattering forces on the xz-plane for spheres with and without the ARC are plotted in Fig. 3. Comparing the scattering force for the uncoated and coated spheres, i.e. comparing Fig. 3(a) with Fig. 3(e), and comparing Fig. 3(b) with Fig. 3(f), one can clearly see that the ARC significantly reduces the scattering force, especially near the focus as shown in the center blue spot in Fig. 3(f). Similarly, comparing Fig. 3(c and g), and comparing Fig. 3(d,h), it is clear that the gradient forces are enhanced. This is expected, as the particle size increases after coating. For a r1 = 5.0 μm sphere, the scattering and gradient forces are shown in Fig. 4. The scattering force is also greatly reduced, however, the gradient force is only enhanced slightly after coating, as illustrated in Fig. 5. For large particles, the relative volume of the ARC is smaller, therefore the enhancement in gradient force is also small. In short, ARC-coated spheres are trappable because of both the reduction in scattering force and enhancement in gradient force. As shown in Figs 3(f), 4(f) and 5(a), the scattering force is significantly diminished near the focus, especially for the larger particles. This is because the ARC effectively eliminated the reflection for a big sphere located at the focus. Intererstingly, this creates a zone where the conservative force dominates, which is useful when the scattering force is undesirable.
Gradient and scattering force for uncoated (left column) and ARC-coated (right column) spheres illuminated by an x-polarized Gaussian beam. The first, second, third, and fourth rows are, respectively, (Fs)x, (Fs)z, (Fg)x, and (Fg)z. The inner and outer radii of the sphere are r1 = 0.5 μm and r2 = 0.668 μm, respectively.
Gradient and scattering force for an uncoated (left column) and ARC-coated (right column) spheres illuminated by an x-polarized Gaussian beam. The first, second, third, and fourth rows are, respectively, (Fs)x, (Fs)z, (Fg)x, and (Fg)z. The unit of optical force is pN. The inner and outer radii of the sphere are r1 = 5.0 μm and r2 = 5.15 μm, respectively. Here, E0 = 106V/m.
The longitudinal component of scattering (a) and gradient (b) forces for uncoated (black) and ARC-coated (red) spheres. The parameters used are the same as in Fig. 4.
The scattering force is vanishing at the beam focus for the coated particle shown in Fig. 4(f). For this reason, the ARC-coated sphere is trapped close to the beam center, where the transverse gradient force reaches its maximum. This explains why a large trapping force is realized26. First, the gradient force is enhanced, mostly due to the increase in particle size. Second, the reduction of scattering force drives the equilibirum towards the focus, where the transverse gradient force is largest.
The working mechanism of ARC
The working mechanism of ARC in the large particle limit, can be captured by the ray optics, where the beam is decomposed into a bunch of rays13, as illustrated in Fig. 1(a). For a particle located at the focus, all incident rays are normal to the sphere’s surface. If the particle is sufficiently large such that the curvature of the sphere can be ignored, the rays will be fully transmitted without reflection, just as for a planar surface. The absence of reflection significantly reduces the longitudinal scattering force. However, when the particle is not at the focus, as illustrated in Fig. 1(b), the rays and the surface normal are not parallel, and the angle between them varies with position. Consequently, no ARC can be consistently matched to the position-dependent angle. Accordingly, the backward scattering is not suppressed, and the mechanism for reducing the scattering force no longer works. One can then infer that the ARC only works for an aplanatic beam trapping a particle near the focus, and not for other types of incident field such as a plane wave. We note that using high index dielectrics as the ARC can mitigate the problem35,36. By the Snell’s law, the refraction angle is small for high index coating. The rays inside the coating are almost normal to the surfaces, allowing the reflection to be suppressed by interference. Accordingly, ARC with a higher index works better for off-focus spheres, which also extends the scattering force free zone.
The ray optics theory is simple and elegant, yet it is inaccurate for small particles. Hereafter, we will apply a rigorous wave scattering theory. We introduce the normalized scattering intensity, which can describe the features of scattering37,38:
where (r, θ, ϕ) is the spherical coordinate system concentric with the particle, k is the wavenumber in the medium, and Es(r, θ, ϕ) is the scattered electric field. We shall only focus on the backward scattering (characterized by θ = π) for a particle located on the beam axis, where Eq. (2) has a succinct analytic expression (see detail in the method part):
where an and bn are the Mie coefficients of the coated sphere, and
are the beam shape coefficients of the Gaussian beam39, where \({l}_{0}=1/2k{w}_{0}^{2}\) is the Rayleigh diffraction length, w0 = n0λ/(π⋅NA) is the waist radius, and zc = l0 + iz with z being the location of the sphere.
The Mie coefficients of the coated sphere are25,26
where \({\psi }_{n}(x)=x{j}_{n}(x),{\chi }_{n}(x)=-\,x{y}_{n}(x),{\xi }_{n}(x)=x{h}_{n}^{(1)}(x)\) are Ricatti-Bessel functions, x = kr1 and y = kr2 are dimensionless size parameters for the core and shell, respectively, and \({\tilde{n}}_{1}\) = n1/n0 and \({\tilde{n}}_{2}\) = n2/n0 are normalized refractive indices. For ARC-coated spheres, \({\tilde{n}}_{1}={\tilde{n}}_{2}^{2}\) and 2\({\tilde{n}}_{2}\)(y − x) = π. We first consider the large particle limit with x → ∞. Here, the asymptotical formulae for the Ricatti-Bessel functions are introduced:
Using these expressions, the Mie coefficients reduce to a simple expression
Eq. (7) indicates that for a very large ARC-coated sphere, the Mie coefficients of all orders are the same. According to Eq. (3), the backward scattering becomes zero. For a sphere with finite size, although Eq. (7) is not exact, low order Mie coefficients can still be approximated by Eq. (7) and fulfill an ≈ bn, which can be seen from the numerical examples shown in Tables 1 and 2. Meanwhile, for the higher order terms, we note that for the Gaussian beam, (n + 1)gn decreases rapidly with n, so the contributions from the high order terms in Eq. (3) are not important. Because the low order Mie coefficients satisfy an ≈ bn, the total backward scattering intensity almost vanishes: see Eq. (3). One could have reached a similar conclusion by noting that an impedance-matched homogeneous sphere, with its permittivity equal to its permeability, will have an = bn, and its reflection is expected to be low. The condition an = bn is also called the generalized Kerker condition which leads to the directional emission28,29. To achieve the Kerker condition, particles fabricated are usually complex in structures and the frequency is tuned to support mutiple resonances simultaneously29,40,41,42,43. However, these methods are technically complicated, and the generalized Kerker condition is fulfilled only for a few orders. It is interesting to see that by coating an ARC on a large size sphere, many multiople orders will fulfill this condition without the need of resonances. If the scattering is dominated by the low orders which satisfy the generalized Kerker condition, unidirectional emmison is achieved. We can see that the ARC-coated large spheres have the potential for manipulating specific light fields.
Figure 6(a–c) plots the normalized scattering intensity for coated (blue dashed lines) and uncoated (red solid lines) spheres located at the Gaussian beam focus. Clearly, the uncoated high dielectric spheres have non-vanishing backward scatterings, leading to a strong forward scattering force. By applying ARCs on the spheres, though the total scattering efficiencies are not necessarily enhanced or reduced (see the amplitude of the scattering intensity), the backward scatterings are suppressed. In contrast, the ARC is not working for the plane wave incident case, as shown in Fig. 6(d). Because \((n+1){g}_{n}=(n+1)\sqrt{n+1}/2\) for the plane wave does not vanish for high orders, where the generalized Kerker condition is not fulfilled, the backward scattering cannot be suppressed.
ARC works better for large spheres
The axial forces for spheres illuminated by Gaussian beams with different NA are plotted in Fig. 7. For the 0.5-micron radius particle (vaccum wavelength is λ = 1.064 μm), a large NA is required for trapping even with the ARC, as shown in Fig. 7(a). In contrast, for the case of 5-micron radius partilce shown in Fig. 7(b), even for a small NA, the ARC can effectively reduces the forward forces, making the high dielectric particle trappable. Therefore, the ARC wokrs better for the larger size spheres. This seems to oppose our intuition that smaller particles are easier to trap, as the ratio of the gradient force to scattering force is much more favorable. Using Eq. (3), we can explain why the ARC works better for large spheres. For smaller NA, (n + 1)gn decreases slower as n grows, so that higher order Mie coefficients will contribute to the backward scattering. As fewer multipole orders fulfill an ≈ bn for smaller spheres, while more orders do so for larger spheres, the ARC reduces the backward scattering for larger spheres more efficiently: see also Fig. 6(a,c).
Conclusions
In summary, we have thoroughly addressed the problem of an ARC-coated sphere illuminated by an aplanatic beam. The ARC can reduce the scattering force when the sphere is located around the beam focus, so that the high dielectric spheres can be trapped close to the beam focus. This is especially useful when the particle size is large enough so that its curvature approaches that of the planar case. For small particles, the increase in size after coating with the ARC also leads to an enhancement in the optical force. Consequently, in agreement with previous studies, the trap stiffness is significantly enhanced. First, the gradient force increases as a consequence of the increase in particle size after coating. Second, the reduction in the forward scattering force due to the suppression of the backward scattering allows the particle to be trapped closer to the focus, where the transverse gradient force is stronger. The former effect is more significant for smaller spheres, while the latter is more significant for lager spheres. We have also analytically studied the scattering properties of the ARC-coated sphere, and found that its low order Mie coefficients satisfy the generalized Kerker condition while its high order ones do not. So the backward scattering can be suppressed only when an aplanatic beam incidents. This finding not only reveals the mechanism of the ARC using a rigorous wave scattering theory, but also may inspire the use of ARC-coated spheres in manipulating specific light fields. Finally, we remark that the reduced scattering force might also improve optical manipulation in whatever other areas where a conservative optical trap is needed.
Method
Derivation of the backward scattering intensity
The normalized scattering intensity can describe the scattering features of a particle illuminated by a beam37,38:
where (r, θ, ϕ) is the spherical coordinate system concentric with the particle, k is the wavenumber in the medium, and Es(r, θ, ϕ) is the scattered electric field. The incident and scattered fields can be written in vector spherical wave functions as37
where pmn and qmn are the beam shape coefficients31,32,33, amn and bmn are scattering coefficients given by37: amn = anpmn and bmn = bnqmn, and \({{\bf{N}}}_{mn}^{(J)}\) and \({{\bf{M}}}_{mn}^{(J)}\) are the vector spherical wave functions given by
where \({C}_{mn}=\sqrt{\frac{(2n+1)}{n(n+1)}\frac{(n-m)!}{(n+m)!}}\), ξn(kr) are the Ricatti-Bessel functions, which are ξn(kr) = (kr)jn(kr) when J = 1 and \({\xi }_{n}(kr)=(kr){h}_{n}^{(1)}(kr)\) when J = 3, and \({P}_{n}^{m}(\cos \,\theta )\) is the associated Legendre function of the first kind:
The two auxiliary angular functions \({\pi }_{mn}(\cos \,\theta )\) and \({\tau }_{mn}(\cos \,\theta )\) are defined as \({\pi }_{mn}(\cos \,\theta )={C}_{mn}\frac{m}{\sin \,\theta }{P}_{n}^{m}(\cos \,\theta ),\) \({\tau }_{mn}(\cos \,\theta )={C}_{mn}\frac{d}{d\theta }{P}_{n}^{m}(\cos \,\theta ),\)
which satisfy44
For a linearly polarized Gaussian beam, the beam shape coefficients can be written down analytically for a particle located on the beam axis39:
where \({l}_{0}=1/2k{w}_{0}^{2}\) is the Rayleigh diffraction length with w0 being the waist radius, and z = l0 − iz0 with z0 being the location of the beam center. As one can see from Eq. (12), for both pmn and qmn, only the azimuthal modes with m = ±1 contribute. Then, the scattered field in the far field (kr → ∞) is given by
Using the asymptotical formula for the Ricatti-Bessel functions for kr → ∞, ξn(kr) ∼ (−i)n+1eikr, \({\xi ^{\prime} }_{n}\)(kr) ∼ (−i)neikr = iξn(kr), Eq. (13) reduces to
For the backward direction, namely x = cosπ = −1, the auxiliary functions read
Then, substituting Eqs (14) and (15) into Eq. (8), we have the backward scattering intensity as
which is Eq. (3).
References
Ashkin, A. Acceleration and trapping of particles by radiation pressure. Phys. Rev. Lett. 24, 156–159 (1970).
Grier, D. G. A revolution in optical manipulation. Nature 424, 810–816 (2003).
Zhuang, X. Unraveling DNA condensation with optical tweezers. Science 305, 188–190 (2004).
Ashkin, A. Optical Trapping and Manipulation of Neutral Particles Using Lasers: areprint volume with commentaries (World Scientific, Singapore, 2006).
Tkachenko, G. & Brasselet, E. Optofluidic sorting of material chirality by chiral light. Nat. Commun. 5, 3577 (2014).
Tkachenko, G. & Brasselet, E. Helicity-dependent three dimensional optical trapping of chiral micrioparticles. Nat. Commun. 5, 4491 (2014).
Svoboda, K. & Block, S. M. Optical trapping of metallic Rayleigh particles. Opt. Lett. 19, 930–932 (1994).
Reece, P. J. et al. Characterization of semiconductor nanowires using optical tweezers. Nano Lett. 11, 2375–2381 (2011).
Larsen, A. E. & Grier, D. G. Like-charge attractions in metastable colloidal crystallites. Nature 385, 230–233 (1997).
Crocker, J. C., Matteo, J. A., Dinsmore, A. D. & Yodh, A. G. Entropic attraction and repulsion in binary colloids probed with a line optical tweezer. Phys. Rev. Lett. 82, 4352 (1999).
Yang, A. H. J. et al. Optical manipulation of nanoparticles and biomolecules in subwavelength slot waveguides. Nature 457, 71–75 (2009).
Zhang, H. & Liu, K. K. Optical tweezers for single cells. J. R. Soc. Interface 5, 671–690 (2008).
Ashkin, A. Forces of a single-beam gradient laser trap on a dielectric sphere in the ray optics regime. Biophys. J. 61, 569–582 (1992).
Wu, P., Huang, R., Tischer, C., Jonas, A. & Florin, E.-L. Direct measurement of the nonconservative force field generated by optical tweezers. Phys. Rev. Lett. 103, 108101 (2009).
Chen, J., Ng, J., Lin, Z. & Chan, C. T. Optical pulling force. Nature Photon. 5, 531–534 (2011).
Juan, M. L., Righini, M. & Quidant, R. Plasmon nano-optical tweezers. Nature Photon. 5, 349–356 (2011).
Divitt, S., Rondin, L. & Novotny, L. Cancellation of non-conservative scattering forces in optical traps by counter-propagating beams. Opt. Lett. 40, 1900–1903 (2015).
Du, J. et al. Tailoring optical gradient force and optical scattering and absorption force. Sci. Rep. 7, 18042 (2017).
Dholakia, K. & Čižmár, T. Shaping the future of manipulation. Nature Photon. 5, 335–342 (2011).
Padgett, M. & Bowman, R. Tweezers with a twist. Nature Photon. 5, 343–348 (2011).
Woerdemann, M., Alpmann, C., Esseling, M. & Denz, C. Advanced optical trapping by complex beam shaping. Laser Photon. Rev. 7, 839–854 (2013).
Taylor, M. A., Waleed, M., Stilgoe, A. B., Rubinsztein-Dunlop, H. & Bowen, W. P. Enhanced optical trapping via structured scattering. Nature Photon. 9, 669–673 (2015).
Glückstad, J. Optical manipulation: Sculpting the object. Nature Photon. 5, 7–8 (2011).
Bormuth, V. et al. Optical trapping of coated microspheres. Opt. Express 16, 13831–13844 (2008).
Hu, Y., Nieminen, T. A., Heckenberg, N. R. & Rubinsztein-Dunlop, H. Antireflection coating for improved optical trapping. J. Appl. Phys. 103, 093119 (2008).
Jannasch, A., Demirörs, A. F., van Oostrum, P. D. J., van Blaaderen, A. & Schäffer, E. Nanonewton optical force trap employing anti-reflection coated, high-refractive-index titania microspheres. Nature Photon. 6, 469–473 (2012).
Craig, D. et al. Enhanced optical manipulation of cells using antireflection coated microparticles. ACS Photon. 2, 1403–1409 (2015).
Kerker, M., Wang, D.-S. & Giles, C. L. Electromagnetic scattering by magnetic spheres. J. Opt. Soc. Am. 73, 765–767 (1983).
Alaee, R., Filter, R., Lehr, D., Lederer, F. & Rockstuhl, C. A generalized Kerker condition for highly directive nanoantennas. Opt. Lett. 40, 2645–2648 (2015).
Walheim, S., Schaffer, E., Mlynek, J. & Steiner, U. Nanophase-separated polymer films as high-performance antireflection coatings. Science 283, 520–522 (1999).
Gouesbet, G. Generalized Lorenz–Mie theories, the third decade: A perspective. J. Quant. Spectrosc. Radiat. Transf. 110, 1223–1238 (2009).
Gouesbet, G. & Grehan, G. Generalized Lorenz-Mie Theories (Springer, Berlin, 2011).
Gouesbet, G. & Lock, J. A. List of problems for future research in generalized Lorenz–Mie theories and related topics, review and prospectus [Invited]. Appl. Opt. 52, 897–916 (2013).
Wang, N., Chen, J., Liu, S. & Lin, Z. Dynamical and phase-diagram study on stable optical pulling force in Bessel beams. Phys. Rev. A 87, 063812 (2013).
Leem, J. W. & Yu, J. S. Broadband and wide-angle distributed Bragg reflectors based on amorphous germanium films by glancing angle deposition. Opt. Express 20, 20576–20581 (2012).
ElKabbash, M. et al. Iridescence-free and narrowband perfect light absorption in critically coupled metal high-index dielectric cavities. Opt. Lett. 42, 3598–3601 (2017).
Bohren, C. F. & Huffman, D. R. Absorption and Scattering of Light by Small Particles (Wiley and Sons, New York, 1983).
Wang, N., Lu, W., Ng, J. & Lin, Z. Optimized optical ‘tractor beam’ for core–shell nanoparticles. Opt. Lett. 39, 2399–2402 (2014).
Chen, J., Ng, J., Liu, S. & Lin, Z. Analytical calculation of axial optical force on a Rayleigh particle illuminated by Gaussian beams beyond the paraxial approximation. Phys. Rev. E 80, 026607 (2009).
Liu, W., Miroshnichenko, A. E., Neshev, D. N. & Kivshar, Y. S. Broadband unidirectional scattering by magneto-electric core-shell nanoparticles. ACS Nano 6, 5489–5497 (2012).
Fu, Y. H., Kuznetsov, A. I., Miroshnichenko, A. E., Yu, Y. F. & Lukyanchuk, B. Directional visible light scattering by silicon nanoparticles. Nat. Commun. 4, 1527 (2013).
Pors, A., Andersen, S. K. H. & Bozhevolnyi, S. I. Unidirectional scattering by nanoparticles near substrates: generalized Kerker conditions. Opt. Express 23, 28808–28828 (2015).
Yao, K. & Liu, Y. Controlling electric and magnetic resonances for ultracompact nanoantennas with tunable directionality. ACS Photon. 3, 953–963 (2016).
Xu, Y.-L. Electromagnetic scattering by an aggregate of spheres. Appl. Opt. 34, 4573–4588 (1995).
Author information
Authors and Affiliations
Contributions
All authors discussed extensively. N.W. did the simulation, analytical calculation, and interpreted the physics. Z.L. and J.N. developed the formalism and methodology. J.C. and X.L. contributed in the physical interpretation. J.N. initiated the research, interpreted the physics, and oversaw the project.
Corresponding author
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Wang, N., Li, X., Chen, J. et al. Gradient and scattering forces of anti-reflection-coated spheres in an aplanatic beam. Sci Rep 8, 17423 (2018). https://doi.org/10.1038/s41598-018-35575-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-018-35575-1
Keywords
This article is cited by
-
Enhancement of trapping efficiency by utilizing a hollow sinh-Gaussian beam
Scientific Reports (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.