Abstract
We present the first experimental realization of a quantum artificial life algorithm in a quantum computer. The quantum biomimetic protocol encodes tailored quantum behaviors belonging to living systems, namely, self-replication, mutation, interaction between individuals, and death, into the cloud quantum computer IBM ibmqx4. In this experiment, entanglement spreads throughout generations of individuals, where genuine quantum information features are inherited through genealogical networks. As a pioneering proof-of-principle, experimental data fits the ideal model with accuracy. Thereafter, these and other models of quantum artificial life, for which no classical device may predict its quantum supremacy evolution, can be further explored in novel generations of quantum computers. Quantum biomimetics, quantum machine learning, and quantum artificial intelligence will move forward hand in hand through more elaborate levels of quantum complexity.
Similar content being viewed by others
Introduction
As described by Deutsch, a quantum computer is a device that intends to fulfill the Deutsch-Church-Turing principle, namely, to efficiently simulate a finitely realizable physical system in the framework of quantum mechanics1. In this context, quantum supremacy would be reached when a quantum processor outperforms classical computers realizing a given task. Along these lines, several proposals to achieve quantum supremacy for a variety of quantum algorithms and quantum simulations have been proposed2,3,4,5,6,7.
The keyword “quantum” has overflowed the limits to which was initially constrained and, currently, incessantly spreads through the interdisciplinary scientific literature. Indeed, it is a source of inspiration for the breeding extensions of already existing models with their quantum counterparts8,9,10,11,12,13,14,15,16,17. Besides the appealing intellectual exercise, this hybridization is often motivated by a plausible improvement in the conditions and enhancement in the efficiency of the developed protocols. From all possible ramifications, including quantum machine learning and quantum artificial intelligence, our research in quantum biomimetics is concerned with the design of a framework for quantum algorithms based on the imitation of biological processes, belonging to the macroscopic classical complexity, and brought down by design to the microscopic quantum realm18,19,20,21,22,23,24,25,26. There may not always be a neat analogy between the physical models underlying our protocols and those used to describe real biological systems, but our proposed effective dynamics only partially aims at emulating core aspects of the mimicked process. From a wide perspective in the history of arts and science, close imitation is a natural first layer and wish in the aesthetic process. In this sense, plain simulation is a valid and fruitful engineering playground, where analogies abound and serve as communicating vessels between unconnected fields. Our central goal in quantum simulations and quantum computing is to go beyond it, through a higher creativity challenge, in the search of a second layer of a major art.
In the particular scenario of artificial life, simple models of organisms are able to undergo most common stages of life in a controlled virtual environment27,28,29. When extending this to the quantum realm, particularities of quantum physics, such as its limitation to linear dynamics, the no-cloning theorem, or the exponentially growing dimensionality of Hilbert spaces, play a relevant role. The quantum artificial life protocol we have engineered and implemented goes beyond the straightforward quantization of existing classical models. In this sense, and with similar spirit of other contributions30,31,32,33, it is noteworthy to mention that we leave open the question whether the origin of life is genuinely quantum mechanical. What we prove here is that microscopic quantum systems can efficiently encode quantum features and biological behaviours, usually associated with living systems and natural selection.
In this article, we report the first experimental implementation of a model for quantum artificial life20 into a quantum computer. To this end, we make use of the facilities provided by the IBM ibmqx4 quantum computing chip34. This work should be aligned with the ramping developments in classical and quantum machine learning and artificial intelligence: the development of algorithms and devices with the capacity to interpret and mimic human behaviors in order to solve useful problems and improve the interaction with human beings. Along these lines, we may foresee a future in which these idealized machines hybridize the knowledge in machine learning, artificial intelligence and artificial life, with an internal structure and dynamics following the laws of quantum physics, as is already happening in the classical domain35.
Results
We begin with a brief description of the model for quantum artificial life20, whose most important elements are the quantum living units or individuals. Each of them is expressed in terms of two qubits that we call genotype and phenotype. The genotype contains the information describing the type of living unit, an information that is transmitted from generation to generation. The state of the phenotype is determined by two factors: the genetic information and the interaction between the individual and its environment. This state, together with the information it encodes, is degraded during the lifetime of the individual.
The goal of the proposed model is to reproduce the characteristic processes of Darwinian evolution, adapted to the language of quantum algorithms and quantum computing. The self-replication mechanism is based on two partial quantum cloning events, an operation that entangles either the genotype or the phenotype with a blank state and copies a certain expectation value of the original qubit in both of the outcome qubits. In this set of experiments, the self-replication consists in duplicating the expectation value of σz in the genotype, in a blank state that will be transformed in the genotype of the individual in the next generation19. The process is completed by copying again σz of the new genotype in another blank state that will be transformed in the phenotype of the new individual. The next subprotocol in the algorithm is the interaction between the individuals and the environment, which emulates the aging of living units until an asymptotic state that represents its death. This evolution is encoded in a dissipative dynamics that couples a bath with each of the phenotype qubits, with σ = |0〉〈1| as Lindblad operator. The effective lifetime, i.e., the time the phenotype needs to arrive to the dark state of the Lindbladian up to a given error, depends implicitly on the genotype. The protocol also accounts for mutations, performed via random single qubit rotations in the genotype qubits or via errors in the self-replication process20. The final ingredient is the interaction between individuals, which conditionally exchange the phenotypes depending on the genotypes20. This behavior is achieved via a four-qubit unitary operation, where genotypes and phenotypes play the role of control and target qubits, respectively. The conjunction of these components leads to a minimal but consistent Darwinian quantum scenario. The protocol may be enriched when including spatial information, either quantum or classical, or increasing the model complexity by considering a larger set of observables.
The first step for this implementation is to express each of the building blocks of the previous paragraph in terms of the quantum gates available in the superconducting circuit architecture of IBM cloud quantum computer34. Since we have selected σz as the observable to clone, every partial quantum cloning event requires the realization of a UCNOT gate, that can be directly performed in the experiment. Regarding the interaction with the environment, we have adapted our protocol, because the experimental device does not allow to realize a conditional projection of the quantum state to the |0〉 in the phenotypes. The alternative we propose is to implement the transition between the basis states as a sequence of small rotations in σy for the phenotype qubits, \({e}^{-i{\sigma }_{y}\theta }\), with θ tuned according to the duration of each simulated time step. We have employed u2(ϕ, λ) and u3(θ, ϕ, λ) available in the experimental platform, to implement the single qubit gates.
The gate u3(θ, 0, 0) acting on genotype qubits can be used for the mutation events. Ideally, and in order to emulate their randomness both in the phase θ and in the presence or absence of the event, we could design the experimental runs following a classical program. For making the procedure tractable, we could discretize the range of θ in n values, and divide the total experimental runs in n + 1 groups to account for each of the different possibilities. The weight, or number of runs for each group, would depend on our selection for the mutation rate as well as on the random parameters obtained with the external program. However, constrained by the flexibility of the experimental device, we propose a less realistic but pragmatic procedure: assume that the mutations will only be of a specific θ and therefore eliminate a source of randomness and diversity in the protocol. The single-qubit gate accounting for the mutations will be σx. Regarding the randomness in the presence or absence of mutation events, we will have to adapt our algorithm to perform the mutations in groups of 1024 experimental runs, and achieve the mutation rate accordingly. The last subprotocol, the inter-individual interactions, requires the implementation of the interaction gate UI, whose effect is to exchange two pairs of quantum levels, while leaving the rest unaltered, as UI|xxyy〉 = |xyyx〉 and UI|xyyx〉 = |xxyy〉, for {x, y} ∈ {0, 1}. The challenge is to decompose UI in terms of the gates offered by the experimental setup. Our solution is given by \({U}_{I}={S}_{23}{U}_{12}({\mathbb{1}}\otimes F){U}_{12}{S}_{23}\), with \(F={U}_{43}{C}_{34}{C}_{24}{U}_{23}{C}_{34}^{\dagger }{U}_{43}{U}_{23}\). Here, the first and second subindices denote the control and target qubit respectively, U is the controlled-not gate, S is the SWAP gate and C is the controlled square root of not gate. These can be rewritten in terms of the controlled-not gate as Sij = UijUjiUij and \({C}_{12}=(T\otimes P{u}_{3}(\,-\,\pi /4,0,\mathrm{0)}){U}_{12}({\mathbb{1}}\otimes {u}_{3}(\pi \mathrm{/4,0,0)}){U}_{12}({\mathbb{1}}\otimes {P}^{\dagger })\), with \(P=\sqrt{{\sigma }_{z}}\) and \(T=\sqrt{P}\). An additional relation to point out is that the control target behavior in the controlled-not gate can be exchanged by introducing Hadamard gates, U21 = (H ⊗ H)U12(H ⊗ H). This is a useful formula for designing the quantum circuit in an experimental platform that only allows a single direction for the implementation of the UCNOT.
Experiments
Interaction between two individuals
We start with a quantum circuit designed for reproducing the dynamics of two interacting individuals. Two precursor genotypes are initialized in \(|\psi {\rangle }_{{g}_{1}}=\,\cos \,\frac{\pi }{8}\mathrm{|0}\rangle +\,\sin \,\frac{\pi }{8}\mathrm{|1}\rangle \) and \(|\psi {\rangle }_{{g}_{2}}=\,\cos \,\frac{3\pi }{8}\mathrm{|0}\rangle +\,\sin \,\frac{3\pi }{8}\mathrm{|1}\rangle \) with u3. Afterwards, both individuals are completed by copying the genotype qubits in blank states via UCNOT gate, \(|\psi {\rangle }_{1}=\,\cos \,\frac{\pi }{8}\mathrm{|00}\rangle +\,\sin \,\frac{\pi }{8}\mathrm{|11}\rangle \) and \(|\psi {\rangle }_{2}=\,\cos \,\frac{3\pi }{8}\mathrm{|00}\rangle +\,\sin \,\frac{3\pi }{8}\mathrm{|11}\rangle \). In terms of θ1 = π/8 and θ2 = 3π/8, the complete state, |ψ1〉 ⊗ |ψ2〉, reads
We now apply the interaction gate UI to conclude this building block,
Notice that the interaction fully exchanges the phenotypes, 〈σz〉2 and 〈σz〉4, that are now equal to the opposite genotype, \({\langle {\sigma }_{z}\rangle }_{1}={\cos }^{2}{\theta }_{1}-{\sin }^{2}{\theta }_{1}={\langle {\sigma }_{z}\rangle }_{4}\) and \({\langle {\sigma }_{z}\rangle }_{3}={\cos }^{2}{\theta }_{2}-{\sin }^{{\rm{2}}}\,{\theta }_{2}={\langle {\sigma }_{z}\rangle }_{2}\).
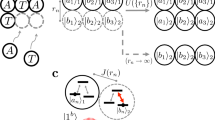
The experiment is planned to reduce the total errors induced by the use of two-qubit gates. Consequently, we have reordered the initial Hilbert space |g1p1g2p2〉, where gi is genotype and pi is phenotype, as |p2 g2p1g1〉 and assigned each of these qubits to the experimental ones |Q0Q1Q2Q3〉. See Fig. 1 for the remaining quantum circuit diagram.
Quantum circuit diagram for the protocol of two interacting individuals. Squares with a continuous line denote the phase values of u3 gate, while squares with a dashed line denote the phase values of u2 gate, both in units of π. When possible we reduce the expression to the value of θ and avoid writing the additional phases.
The results, in Table 1, agree with the ideal case with a 71.58% fidelity according to \(F(p,q)={\sum }_{j}\,\sqrt{{p}_{j}{q}_{j}}\), that compares the probability distribution obtained when measuring in the computational basis with the theoretical prediction. Therefore, this result is valid, but not equivalent to the one that is expected when the complete wave function is considered, which is hindered by the use of full tomography and computed via \(F({\rho }_{1},{\rho }_{2})={\rm{Tr}}\sqrt{\sqrt{{\rho }_{1}}{\rho }_{2}\sqrt{{\rho }_{1}}}\)36. The expectation values extracted from the data show a reasonable overlap between p1 and g2, as expected and a considerable distance between g1 and p2.
Interaction with the environment
In this round of experiments we test the combination of partial quantum cloning events and dissipation. A precursor genotype is initialized in \(|\psi {\rangle }_{{g}_{1}}=\,\cos \,\frac{\pi }{3}\mathrm{|0}\rangle +\,\sin \,\frac{\pi }{3}\mathrm{|1}\rangle \), and the individual completed with a first partial quantum cloning event via UCNOT and a blank state, \(|\psi {\rangle }_{1}=\,\cos \,\frac{\pi }{3}\mathrm{|00}\rangle +\,\sin \,\frac{\pi }{3}\mathrm{|11}\rangle \). Then, a single qubit rotation, u3(π/8, 0, 0), is applied in the phenotype, that substitutes the dissipation in a discrete manner, losing its exponential character. The course of time is simulated by this gate, by implementing one of them for every simulated time step. Subsequently, a second individual is created in a complete self-replication event with two partial quantum cloning operations. To conclude, u3(π/8, 0, 0), is implemented again on both genotypes associated with a next time step. We assign the Hilbert space of the simulating device as |Q0Q1Q2Q4〉 → |p2 g2 g1p1〉 to maximize the efficiency of the protocol. See Fig. 2 for the quantum circuit diagram. The results, shown in Table 2, account for similar probability distributions between the ideal and the real data with a fidelity of 91.18%, as before computed only for the computational basis.
The initialization of a genotype before three partial quantum cloning events. The first of these will produce an initial individual and the remaining two will replicate it into a second one. The protocol continues with single-qubit gates that emulate the dissipation. The squares denote u3(θ, ϕ, λ) gates where the number indicates the value of θ.
For the self-replication instance, there is an additional property of the model that only arises when measuring some purely quantum correlations of the system. The partial quantum cloning operation entangles the qubits which are involved on it, transmitting 〈σx〉 of the original state into 〈σx ⊗ σx〉. Note that this data can be extracted from the experiment when measuring on the σx basis, which is done by introducing a Hadamard gate in every entry before projecting. Therefore, one has to compute 〈σz ⊗ σz ⊗ σz ⊗ σz〉 in the new basis, to retrieve 〈σx ⊗ σx ⊗ σx ⊗ σx〉. This technique is based on the equality Tr[σxρ] = Tr[σzHρH], since σx = HσzH. Even if the calculation for the fidelity yields a satisfactory 93.45%, the value of 〈σx ⊗ σx ⊗ σx ⊗ σx〉 still shows a sizable error with respect to the ideal one, as we show in Table 3.
Even if this implementation does not coincide with the time evolution presented in the original model, it is able to emulate its results when only focusing on the σz or σx basis, but not to compare both measurements in general. Accordingly, if the lifetimes of each living qubits undergo a similar dynamics to the ones proposed in the model, the effect of the environment on the correlations cannot be correctly reproduced, and viceversa, unless the gates are specifically selected for a given precursor genotype. The theoretical value of 〈σx ⊗ σx ⊗ σx ⊗ σx〉 for a system that only undergoes self-replication events and dissipation decreases as \(\langle {\sigma }_{x}\rangle {e}^{-\gamma ({t}_{1}+{t}_{2})/2}\), with 〈σx〉 calculated over the precursor genotype and ti being the time between self-replication events. For the variant of the single qubit gates analyzed here, the theoretical value goes as 〈σx〉 cosθ1 cosθ2, where θi indicate the phase of each u3(θi, 0, 0). This part of the dissipative dynamics should match with the evolution of 〈σz〉, so the following set of equations should be fulfilled:
where a is the |0〉〈0| component in the precursor genotype. Given that there is no solution for θ1 and θ2 which is independent of a, the method of single-qubit gates for mimicking the dissipation is not valid as a general protocol, because it has to be tuned for each case. Nevertheless, the important quantum feature of the model, the existence of quantum correlations, and their role as witnesses of the interactions between quantum living units can correctly be represented with the approach followed here, even if their time dependence is different to the one presented in the original model.
In more practical terms, the implementations summarized in Tables 2 and 3 are realistic, but not compatible between them, because both can be associated to dissipative dynamics but with different representative parameters, as we have seen in Eq. (2). Furthermore, we believe that the ideal realization of the experiment will soon be feasible at least for a small number of individuals. Our proposal for introducing the dissipation is to exploit the natural decoherence present in quantum platforms and use error correction protocols only in the genotype qubits. This phenotype-genotype asymmetry in the decay probability is the key element in the emulation of the interaction between individuals and environment.
The implementation of mutations requires to combine the outcome of different designs of quantum circuit diagrams and, therefore, experimental runs. In this case, we consider that a mutation event, which can affect both individuals, is simulated with a σx. The complete result is achieved when gathering data from 4 different groups of experiments, that correspond to the cases of mutation on the first genotype, mutation on the second genotype, mutation on both genotypes and no mutation. We have performed 1024 experimental runs for each of the three cases with mutations and 8192 runs for the no-mutation rate. These results have been combined with the ones shown in Table 2, that coincide with the no-mutation case, with the goal of reducing the mutation rate for each individual, which takes a final value of 2/19. Table 4 contains the agreggated data of the mutation experiments. In IVb the mutation occurs before the self-replicating event, therefore affecting the second individual, in IVc the mutation can only occur after the second individual has been created, and IVd contains both mutations. See the illustration of this process in Fig. 3. See Table 4 for the measured data with a fidelity of 94.86% with respect to the ideal case in the σz basis.
Visualization of the ideal processes in experiments I and IV. We depict the individuals as combinations of two diamonds that represent the genotype and phenotype qubits. The color in the genotype qubit, the upper diamond of each pair, depends on the value of σz as indicated in the color bar. The color in the phenotype qubit is the same as in the genotype one, as the color is meant to be showing the genetic information. Moreover, the opacity of this color is modified according to the expectation value of σz being limited by the value of 1 that corresponds to the blank qubits. In both cases the right arrow separates two consecutive time steps. Following these clarifications, we can see the exchange of phenotypes in I and the self-replication followed by different mutation possibilities in IV.
Realization of the complete model of quantum artificial life
The last round of experiments is devoted to the reproduction of the aggregate of properties in the quantum artificial life algorithm. In order to maintain the fidelity in values that allow us to claim that the experiment is indeed behaving according to the protocol, we restrict our analysis to the case of two interacting individuals, which undergo mutations and dissipation. Then, the quantum circuit diagram, shown in Fig. 4, is an upgraded version of the one shown in Fig. 1 that includes u3(π/8, 0, 0) for simulating the dissipation in the phenotypes. For the mutations, we follow the same strategy as in the previous subsection, combining the data generated with different quantum circuit diagrams each of them emulating a specific case of the presence or absence of mutation instances. In particular, 3 rounds of 8192 runs emulating the no-mutation case and 1024 runs for each of the mutation cases determine a mutation rate of 2/27. The post-processing of the data, in Table 5, matches the ideal probability distribution in the computational basis with a fidelity of 93.94%.
Quantum circuit diagram for the complete quantum artificial life protocol. Squares with a continuous line denote the phase values of u3 gate, while squares with a dashed line denote the phase values of u2 gate, both in units of π. When possible we reduce the expression to the value of θ and avoid writing the additional phases.
Discussion
Quantum vs Classical
A natural method to evaluate the Quantum Artificial Life framework is to clearly describe on the similarities and differences between the quantum model and a classical analogue approach. On the one hand, all the indicators based in measurements on the 〈σz〉 basis can be reproduced by classical probability distributions. This means, that one can create a classical model of interacting individuals with identical ingredients, in which the single qubit results for each of the living units would be equal to the ones achieved in the quantum version. On the other hand, non-zero quantum correlations in particular, 〈σx ⊗ σx〉, and its generalization to more pairs of qubits, can only be achieved in the quantum case. These introduce a new feature when compared with the classical version of the model, as they can be interpreted as a time correlations between the quantum living units. Let this be illustrated with the following example. Suppose we have two pairs of quantum living units, all of them with the same value of 〈σz〉 in the genotype qubit but with different values for the phenotype, in a simplified system without mutations and interindividual interactions. When the individuals are not causally connected, the value of 〈σx ⊗ σx ⊗ σx ⊗ σx〉 in the four qubits of both individuals would yield a value of α2. However, if these individuals are related by a self-replication operation, the measurement would yield a value of α, where α accounts for 〈σx〉 in the precursor genotype. In other words, the nonzero quantum correlation between the subspaces of the first and second individuals allows to discriminate two different operations from the timeline perspective.
One can show that a classical counterpart of this model would not be able to store the information of the time correlations. The correlations we are interested in are originated in the initial nonzero value of 〈σx〉 the precursor genotype, and afterwards propagated in each partial quantum cloning event because of the property mentioned above. In order to validate our claim, let us assume that the precursor genotype is given by an incoherent mixture of states of the form ρ = a|0〉〈0| + (1 − a)|1〉〈1|. Already from this point, one can see that 〈σx〉 = 0, and therefore no information is going to be propagated to the global correlations when more than one qubit is present. In other words, the purely quantum information is produced by a quantum superposition state between the basis elements and afterwards propagated through the entanglement of quantum living units. The interpretation of this phenomenon is that the quantum model allows to keep track of the relation between the individuals without the need of introducing additional variables to the ones that describe the genotype and phenotype.
Experimental Errors
Regarding errors in the experimental protocol, even if the fidelities achieved are satisfactory, they do not correspond to the fidelities of the complete quantum state. In this sense, the prediction for the number of events to measure is done by simply multiplying the probability distribution by the number of events. These do not exactly match the experimental data (see Table 6 for all experimental outcomes). Indeed, the distances have to be properly weighed, since the probability distribution is the key quantity to be extracted (see Fig. 5). Moreover, the overlap between expectation values of observables in the measurement basis is lower than the fidelity of the probability distribution for all cases analyzed here.
Experimental and ideal probability distributions for all the cases analyzed. In each pair of columns the blue one in the left denotes the experimental value while the yellow one in the right denotes the ideal estimation. The labels in the subplots correspond to the tables for the different quantum artificial life instances.
In parallel, the assignment between the simulated and the simulating Hilbert spaces is designed to maximize the fidelity according to the calibration parameters provided by IBM. Nevertheless, the recalibration of the circuit changes the gate and readout errors, so we reevaluate our circuit according to the new parameters and adapt it when the fidelity outcome can be improved with a different labeling of qubits. Consequently, the performance of the different experiments is not directly comparable, since they have been implemented under unequal conditions.
Despite the different factors degrading the implementation, the performed experiments reproduce the characteristic properties of the sought quantum natural selection scenario. We have observed how the partial quantum cloning events allow us to inherit the information of 〈σz〉 from qubit to qubit, and use this property to encode the self-replication process. We have also seen how nonzero quantum correlations assure that both individuals have been part of a same event in their timelines, in this case self-replication. Another relevant characteristic of the analysis is the inclusion of mutations as a source of randomness that, counterintuitively, significantly improved the fidelity of the quantum algorithm outcome. Our explanation is that mutations tend to homogenize the probability distribution, which is the same effect as the one produced by the errors naturally present in the experimental platform. Surprisingly, in the classical realm, mutations also help the species to adapt to changing environments.
Scope of Quantum Artificial Life
Regarding the emergence of complexity, the route towards the scalability of our quantum algorithm is intrinsically related to the inclusion of more degrees of freedom in the description of quantum living units. These may be introduced by simply increasing the number of qubits, and making them part of the updated genotype and phenotype. A part of the dynamics would be adapted by repeating the partial cloning processes and extending the dissipation to the new phenotype qubits. Another part of the dynamics would deal with the properties introduced by the new degrees of freedom. In the same way as the genotype in the current model rules the individual-environment and inter-individual interactions, additional observables in the genotype would enable the exploration of more characteristics: different self-replication rates, independent lifetime and interaction role, or capacity to displace along the associated Hilbert space, all of them encoded in the genotype. An alternative is to encode the information in quantum states of higher dimensions. The general result of partial quantum cloning to qudits of any dimension makes this family of hypothetical models feasible, conditional to the availability of high dimensional entangling operations.
A different question is the scalability of the current model without including any modification. Notice that, in our protocol, the information about the lifetime and the predator-prey character is classical and encoded in the mean value 〈σz〉 of the phenotype and the genotype of the individual, respectively. Therefore, this partial dynamics can be predicted with a simpler classical analogue. However, the full quantum description of our protocol allows one to retrieve the connections between the quantum living units, linked through entanglement, which is a useful complement that is absent in the classical analogue. In other words, the extra free parameters available in the superposition and entanglement of quantum states are used for describing questions regarding the collective dynamics of individuals, and this is precisely the new source of complex behavior our algorithm is able to create. In this sense, the complexity of our quantum algorithm may only be reached by a larger quantum computer, currently being built in academic institutions and companies. This might yield unexpectedly interesting outcomes but, at the same time, will increase the sensitivity to decoherence during the self-replication process.
This experimental realization of the proposed quantum algorithm represents the consolidation of the theoretical framework of quantum artificial life. The improvement in scalable quantum computers will soon allow us for more accurate quantum emulations with growing complexity towards quantum supremacy, even considering spatial variables for the individuals and a mechanism for tracing out death living units. These future developments should lead towards an autonomous character of the set of individuals, i.e., the evolution will be an intrinsic property of the system, and the desired behavior will emerge without following the instructions of a previously designed quantum algorithm. In this context, the system would be transformed into an intelligent source of quantum complexity whose evolutionary plot for a large number of individuals may not be predicted classically and, consequently, has the capacity to produce unexpected results when scaled up. An interesting question to address is to establish the relation existing between the parameters defining the fundamental processes of the model, and the emergent multiqubit quantum state. Along these lines, and following the frame of artificial life oriented genetic algorithms37, we speculate about the idea of channeling this complexity to encode optimization problems by tuning the self-replication, mutation and dissipation rates that define the evolution. Furthermore, recent advances in quantum machine learning constitute a promising material to work with in the study of algorithms combining the properties of both fields, pursuing the design of intelligent and replicating quantum agents. Therefore, the creation of these quantum living units and their possible applications are expected to have deep implications in the community of quantum simulation and quantum computing in a variety of quantum platforms.
All in all, the experiments presented here entail the validation of quantum artificial life in the lab and, in particular, in cloud quantum computers as that of IBM. Still another interesting step would be the development of autonomous quantum devices following the theoretical and experimental results in quantum cellular automata38,39,40,41,42. Our quantum individuals are driven by an adaptation effort along the lines of a quantum Darwinian evolution, which effectively transfer the quantum information through generations of larger multiqubit entangled states. We believe that the presented results and vision, both in theory and experiments, should hoist this innovative research line as one of the leading banners in the future of quantum technologies.
References
Deutsch, D. Quantum theory, the Church-Turing principle and the universal quantum computer. Proc. Roy. Soc. London A 400, 97 (1985).
Feynman, R. P. Simulating physics with computers. Int. J. Theor. Phys. 21, 467 (1982).
Deutsch, D. & Josza, R. Rapid solutions of problems by quantum computation. Proc. Roy. Soc. London A 439, 553 (1992).
Grover, L. K. A fast quantum mechanical algorithm for database search, Proceedings, 28th Annual ACM Symposium on the Theory of Computing (STOC) 212 (1996).
Lloyd, S. Universal quantum simulators. Science 273, 1073 (1996).
Shor, P. W. Polynomial time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM J. Sci. Statist. Comput. 26, 1484 (1997).
Aaronson, S. & Arkhipov, A. The Computational Complexity of Linear Optics, Proceedings, 43rd Annual AMC Symposium on the Theory of Computing (STOC) 333 (2011).
Wiesner, S. Conjugate coding. SIGACT News 15, 78 (1983).
Bennett, C. H. & Brassard, G. Quantum cryptography: Public key distribution and coin tossing. In Proceedings of IEEE International Conference on Computers, Systems and Signal Processing, volume 175, page 8 (New York, 1984).
Ekert, A. K. Quantum cryptography based on Bells theorem. Phys. Rev. Lett. 67, 661 (1991).
Aharonov, Y., Davidovich, L. & Zagury, N. Quantum random walks. Phys. Rev. A 48, 1687 (1993).
Shenvi, N., Kempe, J. & Whaley, K. B. Quantum random-walk search algorithm. Phys. Rev. A 67, 052307 (2003).
Biamonte, J. et al. Quantum machine learning. Nature 549, 195 (2017).
Dunjko, V. & Briegel, H. J. Machine learning & artificial intelligence in the quantum domain. Rep. Prog. Phys. 81, 074001 (2018).
Schuld, M., Sinayskiy, I. & Petruccione, F. An introduction to quantum machine learning. Contemporary Phys. 56, 172 (2014).
Alvarez-Rodriguez, U., Lamata, L., Escandell-Montero, P., Martín-Guerrero, J. D. & Solano, E. Supervised Quantum Learning without Measurements. Scientific Reports 7, 13645 (2017).
Lamata, L. Basic protocols in quantum reinforcement learning with superconducting circuits. Scientific Reports 7, 1609 (2017).
Schrödinger, E. What is life? (Cambridge University Press, Cambridge, UK, 1944).
Alvarez-Rodriguez, U., Sanz, M., Lamata, L. & Solano, E. Biomimetic Cloning of Quantum Observables. Scientific Reports 4, 4910 (2014).
Alvarez-Rodriguez, U., Sanz, M., Lamata, L. & Solano, E. Artificial Life in Quantum Technologies. Scientific Reports 6, 20956 (2016).
Alvarez-Rodriguez, U., Di Candia, R., Casanova, J., Sanz, M. & Solano, E. Algorithmic quantum simulation of memory effects. Phys. Rev. A 95, 020301 (2017).
Alvarez-Rodriguez, U. et al. Advanced-Retarded Differential Equations in Quantum Photonic Systems. Scientific Reports 7, 42933 (2017).
Las Heras, U., Alvarez-Rodriguez, U., Solano, E. & Sanz, M. Genetic Algorithms for Digital Quantum Simulations. Phys. Rev. Lett. 116, 230504 (2016).
Pfeiffer, P., Egusquiza, I. L., Di Ventra, M., Sanz, M. & Solano, E. Quantum Memristors. Scientific Reports 6, 29507 (2016).
Salmilehto, J., Deppe, F., Di Ventra, M., Sanz, M. & Solano, E. Quantum Memristors with Superconducting Circuits. Scientific Reports 7, 42044 (2017).
Sanz, M., Lamata, L. & Solano, E. Quantum memristors in quantum photonics. APL Photonics 3, 080801 (2018).
Langton, C. G. Artificial Life: An overview. (MIT Press, Cambridge USA, 1997).
Gardner, M. The fantastic combinations of John Conway’s new solitaire game life. Sci. Am. 223, 120 (1970).
Ray, T. S. Ecology and Optimization of Digital Organisms. Santa Fe Institute Available at: http://samoa.santafe.edu/media/workingpapers/92-08-042.pdf (Accessed: 10th October 2017) (1992).
Martin-Delgado, M. A. On Quantum Effects in a Theory of Biological Evolution. Sci. Rep. 2, 302 (2012).
Abbott, D., Davies, P. C. W. & Pati, A. K. Quantum Aspects of Life. (Imperial College Press, London, 2008).
Arrighi, P. & Grattage, J. A Quantum Game of Life. Paper presented at Journées Automates Cellulaires, Turku, Finland (2010, December 15).
Bleh, D., Calarco, T. & Montangero, S. Quantum Game of Life. EPL 97, 20012 (2012).
IBM Quantum Experience, https://www.research.ibm.com/ibm-q/ (last accessed 10 October 2017).
Steels, L. The Artificial Life Roots of Artificial Intelligence. Artif. Life 1, 75 (1994).
Nielsen, M. A. & Chuang, I. L. Quantum Computation and Quantum Information. (Cambridge University Press, Cambridge, UK, 2000).
Mitchell, M. & Forrest, S. Genetic Algorithms and Artificial Life. Artif. Life 1, 267 (1994).
Lent, C. S., Tougaw, P. D., Porod, W. & Bernstein, G. H. Quantum cellular automata. Nanotechnology 4, 1 (1993).
Orlov, A. O., Amlani, I., Bernstein, G. H., Lent, C. S. & Snider, G. L. Realization of a Functional Cell for Quantum-Dot Cellular Automata. Science 277, 928 (1997).
Amlani, I. et al. Digital Logic Gate Using Quantum-Dot Cellular Automata. Science 284, 289 (1999).
Cowburn, R. P. & Welland, M. E. Room Temperature Magnetic Quantum Cellular Automata. Science 287, 1466 (2000).
Imre, A. et al. Majority Logic Gate for Magnetic Quantum-Dot Cellular Automata. Science 311, 205 (2006).
Acknowledgements
We thank Armando Pérez-Leija and Alexander Szameit for enthusiastic and enlightening discussions. We acknowledge the use of IBM Quantum Experience for this work. The views expressed are those of the authors and do not reflect the official policy or position of IBM or the IBM Quantum Experience team. We acknowledge support from Spanish MINECO/FEDER FIS2015-69983-P, UPV/EHU new PhD program, Basque Government Programa Posdoctoral de Perfeccionamiento de Personal Investigador Doctor, Basque Government IT986-16, and Ramón y Cajal Grant RYC-2012-11391.
Author information
Authors and Affiliations
Contributions
U.A.-R. performed the experiments on the IBM Quantum Experience. U.A.-R., M.S., L.L. and E.S. developed the model and analyzed the data. All authors contributed to writing the manuscript.
Corresponding author
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Alvarez-Rodriguez, U., Sanz, M., Lamata, L. et al. Quantum Artificial Life in an IBM Quantum Computer. Sci Rep 8, 14793 (2018). https://doi.org/10.1038/s41598-018-33125-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-018-33125-3
Keywords
This article is cited by
-
Asymmetric bidirectional cyclic controlled quantum teleportation in noisy environment
Quantum Information Processing (2023)
-
Quantum Teleportation of the Entangled Superconducting Qubits via LC Resonators
International Journal of Theoretical Physics (2023)
-
Comparison of the similarity between two quantum images
Scientific Reports (2022)
-
Self-replication of a quantum artificial organism driven by single-photon pulses
Scientific Reports (2021)
-
Demonstration of minisuperspace quantum cosmology using quantum computational algorithms on IBM quantum computer
Quantum Information Processing (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.