Abstract
One of the most important achievements in the field of spintronics is the development of magnetic tunnel junctions (MTJs). MTJs exhibit a large tunneling magnetoresistance (TMR). However, TMR is strongly dependent on biasing voltage, generally, decreasing with applying bias. The rapid decay of TMR was a major deficiency of MTJs. Here we report a new phenomenon at room temperature, in which the tunneling magnetocapacitance (TMC) increases with biasing voltage in an MTJ system based on Co40Fe40B20/MgO/Co40Fe40B20. We have observed a maximum TMC value of 102% under appropriate biasing, which is the largest voltage-induced TMC effect ever reported for MTJs. We have found excellent agreement between theory and experiment for the bipolar biasing regions using Debye-Fröhlich model combined with quartic barrier approximation and spin-dependent drift-diffusion model. Based on our calculation, we predict that the voltage-induced TMC ratio could reach 1100% in MTJs with a corresponding TMR value of 604%. Our work has provided a new understanding on the voltage-induced AC spin-dependent transport in MTJs. The results reported here may open a novel pathway for spintronics applications, e.g., non-volatile memories and spin logic circuits.
Similar content being viewed by others
Introduction
A new class of electronic devices based on the spin degrees of freedom has been extensively studied and it has given rise to the field of spintronics1,2,3,4,5,6,7. One of the most important achievements in this field is the development of magnetic tunnel junctions (MTJs), which has enabled the observation of a large tunneling magnetoresistance (TMR)3,4,8,9,10,11,12. Practical applications relying on this TMR effect range from data read heads in hard disk drives to highly sensitive magnetic sensors. The magnetic states of MTJs can also be manipulated by the current induced spin-transfer torque (STT) effect13,14,15,16,17. More applications have become possible, e.g., magnetic random access memories (MRAMs)18,19,20,21, logic-in-memory circuits22,23 and random number (RN) generators24,25. More recently, neuromorphic computing using spin-torque MTJ oscillators has been developed26. Thus, MTJs can serve as one of the most crucial building blocks of spintronics-based computing.
It is well known that TMR is strongly dependent on biasing voltage, generally, decreasing with applying bias27,28,29,30. One major challenge in MTJ research is to find ways to increase the half biasing voltage, V1/2, at which the total TMR ratio near zero biasing is halved. For MgO-based MTJs3, V1/2 is approximately 1 V. Normal electrical operations will always require certain applying biasing voltage, which renders TMR less optimal. Extensive efforts have been made to enhance V1/2, but progress has come very slowly. Recently, it has been demonstrated that V1/2 depends strongly on the interfacial structures between the ferromagnetic (FM) and the insulator layer. A high V1/2 can be obtained in MTJs with i) few misfit dislocations near the interfaces, ii) a small lattice strain inside the insulator or iii) well-defined sharp interfaces31,32,33,34,35. The value of V1/2 in lattice-matched Fe/spinel MgAl2O4/Fe(001) MTJs reaches +1.0 V (−1.3 V) for the positive (negative) bias31. In other studies, relatively high V1/2 values, ranging from 0.5 to 1.0 V, have also been reported in fully epitaxial Fe/MgO/GaOx/Fe32, NiFe(111)/AlOx/CoFe33, Fe(211)/AlOx/CoFe34 and epitaxial-Fe4N/MgO/CoFeB MTJs35.
Another approach to obtain a high V1/2 is to explore organic spin valves (OSVs), where carbon-based molecules are used between FM electrodes. The value of V1/2 for C60- and carbon nanotubes-based OSVs is approximately 0.2 V at 5 K36. In OSVs using tris(8-hydroxyquinolinate) aluminum (Alq3) or rubrene, the V1/2 has been reported to be 0.1−0.2 V at room temperature37,38,39. Interestingly, graphene-based OSVs show the robustness of spin polarization in a non-local scheme40. The normalized spin polarization reaches up to 0.8 at 1.2 V, which is inferior to MgO-based MTJs. Overall, efforts in increasing V1/2 have not been successful in MTJs or other spintronic devices.
Complementary to TMR effect, the tunneling magnetocapacitance (TMC) is also inherent to the capacitive MTJ structure41,42,43,44. Recently TMC has been increasingly studied due to their fascinating spin phenomena, such as spin capacitance45,46,47,48, frequency-dependent spin transport42,43,49 and potential applications41,50. Though TMC and TMR share some similar origins and are correlated, TMC is unique in many aspects. For example, TMC is peaked at a specific frequency43, but is weakly dependent on the temperature44. Furthermore, V1/2 of TMC is higher than that of TMR44,47. The highest V1/2 of TMC in MgO-based MTJs is 0.7 V, which is almost twice as high as that of TMR in the same device47. Therefore, TMC is more robust against biasing than TMR, and the mechanism of this robustness remains unclear. It is beneficial to understand this mechanism as the TMC effect may lead to more spintronics applications as well as insight into fundamental spintronic behavior.
In this work we report a new phenomenon at room temperature in which the TMC increases with applying biasing voltage in an MTJ system based on Co40Fe40B20/MgO/Co40Fe40B20. This result means an unprecedented enhancement of V1/2 with regard to TMC. We have observed a maximum TMC value of 102% under biasing, which is the largest voltage-induced TMC effect ever reported for MTJs. There is an excellent agreement between theory and experiment for the TMC in the bipolar bias regions using Debye-Fröhlich (DF) model combined with quartic barrier approximation (QBA) and spin-dependent drift-diffusion (SDD) model. Based on our calculations, we predict that the voltage-induced TMC ratio could reach 1100% in MTJs with a corresponding TMR ratio of 604%.
Results and Discussion
Device structure and TMR and TMC under no bias voltage
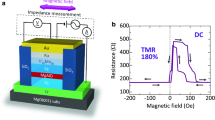
Figure 1a shows the device structure prepared by a magnetron sputtering system with a base pressure of 2 × 10−8 Torr, with the following layer sequence: SiO2/Ta(5)/Co50Fe50(2)/IrMn(15)/Co50Fe50(2)/Ru(0.8)/Co40Fe40B20(3)/MgO(2)/Co40Fe40B20(3)/contact layer (thickness in nm). Details of the device fabrication procedure are described in the Experimental Section. Using standard photolithography, we have patterned the multilayer MTJ stacks into a junction area of 1800 μm2 with an elliptical shape with Ar ion-milling and SiO2 insulation overlayer. The frequency characteristics and the bias voltage dependence of the TMR and TMC for MTJs were measured by an AC four-probe method at room temperature. The AC voltage was set to 2.6 mVrms. The magnetic field was applied along the magnetic easy-axis direction to 1.4 kOe.
Device structure and TMR and TMC under no bias voltage. (a) Schematic of an MgO-based MTJ, with the structure: SiO2/Ta(5 nm)/Co50Fe50(2 nm)/IrMn(15 nm)/Co50Fe50(2 nm)/Ru(0.8 nm)/Co40Fe40B20(3 nm)/MgO(2 nm)/Co40Fe40B20(3 nm)/contact layer. The measurement set-up for TMC and TMR is also shown. The magnetic field is applied along the magnetic easy-axis direction of Co40Fe40B20 layers. (b) TMR and (c) TMC curves of an MgO-based MTJ. The frequency is 60 Hz and the DC voltage is 0 V. Frequency dependence of (d) TMC and TMR and (e) the capacitance CP(AP)in the P(AP) configuration. The solid plots represent the experimental data and the solid lines represent the calculation results obtained by Debye-Fröhlich model, described by Eq. (2).
Figure 1b,c show the TMR and TMC curves at 60 Hz. The DC applied voltage is 0 V. Clear TMR and TMC effects are observed, i.e., RP < RAP and CP > CAP. Large TMR and TMC ratios of approximately 100% are obtained at room temperature. Figure 1d,e shows the frequency characteristics of TMC, TMR and CP(AP). We calculated the frequency characteristics of the TMC and CP(AP) using the DF model43,51. Based on the model, the capacitance \({C}_{{\rm{P}}({\rm{AP}})}^{{\rm{DF}}}({f})\) as a function of frequency f for the P(AP) configuration in MTJs can be expressed by
where C∞,P(AP) and C0,P(AP) are the high-frequency and static capacitances, τP(AP) is the relaxation time of electric dipoles, consisting of electrons and holes, formed near the interface between the FM layer and insulator, and βP(AP) is the exponent showing the distribution of the relaxation time, respectively, for the P(AP) configuration. After a straightforward calculation of Eq. (1), we can obtain
The relation between τP and τAP in FM/insulator/FM is given by \({\tau }_{{\rm{AP}}}={\tau }_{{\rm{P}}}(1+{P}_{{\rm{TMC}}}^{2})/(1-{P}_{{\rm{TMC}}}^{2})\), where PTMC is the spin polarization inside the FM layer43,51. Using these formula, we can calculate the frequency characteristics of the TMC ratio, defined by \({\rm{TMC}}({f})=({C}_{{\rm{P}}}^{{\rm{DF}}}({f})-{C}_{{\rm{AP}}}^{{\rm{DF}}}({f}))/{C}_{{\rm{AP}}}^{{\rm{DF}}}({f})\). From Fig. 1d,e, it is evident that the theoretical results of the TMC and CP(AP) fit the experimental data very well. The calculation was based on the following parameters: C∞,P(AP) = 1.45 (1.5) nF, C0,P(AP) = 630 (590) nF, βP(AP) = 0.998 (0.977), τP = 0.0071 s and PTMC = 0.46. As for the magnetoresistance, we calculated the TMR ratio using the Julliere formula52, assuming a spin polarization PTMR of 0.59. The difference between PTMC and PTMR is attributed to the different penetration lengths of spin-dependent carriers (inside Co40Fe40B20) contributing to TMC and TMR. Our previous paper reveals that the penetration length (λTMC) of TMC is longer than that (λTMR) of TMR43. Here, as is well known, the spin polarization of surface atoms in the FM layer or the interfacial FM atoms between FM/insulator is higher than that of inner atoms from the surface/interface due to the two-dimensional surface/interface effect53,54,55. This picture can be applied to our MTJ system. Namely, the spin polarization (Pinter) of the first interfacial atoms in Co40Fe40B20 layers is considered to be higher than that (Pinner) of inner atoms from the Co40Fe40B20/MgO interface (See Fig. S1). In fact, according to the first-principles calculation using the Vienna Ab Initio Simulation Package (VASP), the spin polarization at the Co terminated interface is higher than that of the inner Co and Fe atoms in CoFeB/MgO system56. From these spin-polarization behavior, it is found that PTMC is low for a long λTMC, and PTMR is high for a short λTMR. According to the above fitting results, PTMC is 0.46, and PTMR is 0.59. The spin polarization PTMR of 0.59 is in good agreement with the experimental value (0.57–0.65) of CoFeB alloy obtained by point-contact Andreev reflection57. Also, we herein note that a negative TMC, i.e., CP < CAP , is observed in the high-frequency region. This can be understood from the fitting results, i.e., C∞,P(AP) = 1.45 (1.5) nF, as well as the experimental results shown in Fig. 1d. This is due to the appearance of the spin capacitance originated from the accumulation of spin-polarized carriers at the two FM/insulator interfaces. The detailed results and discussion are described in the Supplementary Information section. The excellent agreement between theory and experiment reveals that the TMC shows a maximum value of 96% at 60 Hz. Hence, we will use operation frequency of 60 Hz to study the bias dependence of TMC effect. Here, it is noted that we reported a high TMC of 155% in our previous paper43. This result was obtained near zero bias voltage. In contrast, it is found that MTJs showing such high TMC tend to bring about the breakdown under the bias voltage. MTJs showing about 100% do not break down under the bias voltage, and the reproducibility is also good. From this reason, we have studied the bias dependence of TMC using MTJs with a TMC of about 100%.
Voltage-induced TMC and TMR
Figure 2 shows the bias dependence of TMC and TMR curves at 60 Hz. The TMC ratio under the applied bias voltage VDC at the frequency f is defined by \({\rm{TMC}}({f},{V}_{{\rm{DC}}})\)\(=({C}_{{\rm{P}}}(f,{V}_{{\rm{DC}}})-{C}_{{\rm{AP}}}(f,{V}_{{\rm{DC}}}))/{C}_{{\rm{AP}}}(f,{V}_{{\rm{DC}}})\). Interestingly, the TMC increases from 96% to 102% as the magnitude of bias voltage increases from 0 to 184 mV, whereas TMR rapidly decreases from 105% to 53%. As described earlier, the enhancement of \({V}_{1/2}^{{\rm{TMR}}}\) is an important issue in the development of high-performance TMR devices. The typical value of \({V}_{1/2}^{{\rm{TMR}}}\) is 0.1–1 V in MgO-based MTJs3,30,58,59. In our devices, \({V}_{1/2}^{{\rm{TMR}}}\) is 184 mV. In contrast, since the TMC does not decrease with the increasing bias voltage, the value of \({V}_{1/2}^{{\rm{TMC}}}\) cannot be defined. In fact, TMC remain robust against bias voltage which weakens the corresponding TMR quickly. Both the large TMC and its robustness are highly beneficial to spintronics applications associated with the TMC effect.
Modeling of voltage-induced TMC
Figure 3 shows the bias voltage dependence of RP(AP), CP(AP) and the modeling of the voltage-induced TMC. According to Zhang’s theory27, the tunnel conductance in FM/insulator/FM strongly depends on the bias voltage, especially within the order of a few hundred millivolts, due to hot electrons producing spin excitations. The conductance GP(AP) (VDC) at the bias voltage VDC in the P(AP) configuration can be expressed by \({G}_{{\rm{P}}({\rm{AP}})}({V}_{{\rm{DC}}})={G}_{{\rm{P}}({\rm{AP}})}^{0}({\rm{1}}+{\gamma }_{{\rm{P}}({\rm{AP}})}{V}_{{\rm{DC}}})\), where \({G}_{{\rm{P}}({\rm{AP}})}^{0}\) is the conductance at zero bias in the P(AP) configuration and γP(AP) is a parameter determined by the Curie temperatures of FM, the density of states (DOS) of itinerant electrons in FM, direct and spin-dependent transfers and spin quantum number within the framework of the transfer Hamiltonian. The resistance RP(AP)(VDC) can be calculated from \({R}_{{\rm{P}}({\rm{AP}})}({V}_{{\rm{DC}}})=1/{G}_{{\rm{P}}({\rm{AP}})}({V}_{{\rm{DC}}})\). As shown in Fig. 3a, the experimental data of RP(AP)(VDC) are in good agreement with the calculation using Zhang’s model, where γP(AP) is set to 0.0188 (1.87). This means that Zhang’s model is effective for explaining the bias dependence of TMR under both AC and DC mode.
Modeling of the voltage-induced TMC. DC voltage dependence of (a) the resistance RP(AP) in the P(AP) configuration. The calculation of RP(AP) is performed using Zhang’s theory. (b) Schematic of the electric potential profile of MTJs under DC voltage. The QBA is used to calculate the effective barrier thickness, which contributes to the measured capacitance. DC voltage dependence of (c) the capacitance CP in the P configuration. The CP is calculated using DF model under the QBA, described by Eq. (3). (d) Schematic of charge accumulation, contributing to \({C}_{{\rm{AP}}}^{{\rm{DF}}-{\rm{QBA}}}(f{,}\,{{V}}_{{\rm{DC}}})\) and \({C}_{{\rm{AP}}}^{{\rm{SDD}}}(f{,}\,{{V}}_{{\rm{DC}}})\), and the equivalent circuit in the AP configuration. \({C}_{{\rm{AP}}}^{{\rm{DF}}-{\rm{QBA}}}(f{,}\,{{V}}_{{\rm{DC}}})\) is described by the DF model combined with QBA under the DC voltage VDC at the frequency f [Eq. (6)]. \({C}_{{\rm{AP}}}^{{\rm{SDD}}}(f{,}\,{{V}}_{{\rm{DC}}})\) is obtained from the SDD model [Eq. (4)]. The equivalent circuit of the MTJ is modeled by the RC parallel network, consisting of the resistance RAP(VDC) and capacitance CAP(f, VDC). DC voltage dependence of (e) the capacitance CAP in the AP configuration.
The calculation of CP(f, VDC) is performed using the DF model combined with QBA. In the QBA, the potential profile of the barrier is assumed to be a quartic function, which is considered to be a good approximation to describe an AC tunneling transport51. The potential function \({\varphi }_{{\rm{P}}}(\eta )\) under the bias voltage VDC in the P configuration can be expressed by \({\varphi }_{{\rm{P}}}(\eta )=16{\varphi }_{0,{\rm{P}}}{\eta }^{4}-8{\varphi }_{0,{\rm{P}}}{\eta }^{2}+{\varphi }_{0,{\rm{P}}}+e{V}_{{\rm{D}}{\rm{C}}}(1-2\eta )/2\), where \({\rm{\eta }}=x/d\) is the reduced spatial variable, x is the distance from the center of the barrier, d and ϕ0,P are the barrier thickness and height in the absence of the bias voltage, respectively, and e is the electron charge. The potential profile is depicted in Fig. 3b. The solution of \({\varphi }_{{\rm{P}}}(\eta )=e{{V}}_{{\rm{DC}}}\) is η1 = −1/2, η2, η3 and η4 (for η2 < 0, η3 and η4 > 0, η3 < η4). Since the values of η2, η3 and η4 can be calculated by the Cardano’s method, the effective barrier thickness deff can be represented by deff = (1/2 + η3)d, where η3 depends on VDC and ϕ0,P. Therefore, CP(f, VDC) at the applied DC voltage in the P configuration can be written by
As shown in Fig. 3c, the measured capacitance CP(f, VDC) exhibiting a cusp-like behavior, is very well described by Eq. (3), using parameters of C∞,P = 1.45 nF, C0,P = 630 nF, βP = 0.998, τP = 0.0075 s, f = 60 Hz and ϕ0,P = 2.15 eV. Hence, the QBA is a good approximation for the expression of the potential-barrier profile in MTJs based on Co40Fe40B20/MgO/Co40Fe40B20 in calculating the bias dependence of CP under AC field.
The calculation of CAP(f, VDC) is performed using the DF model combined with QBA and SDD model. Based on the SDD model60, the accumulation of minority spins and the depletion of majority spins take place at the interface between the Co40Fe40B20 and MgO layers in the AP configuration. The spin accumulation causes a difference in the chemical potential between majority and minority spins, resulting in a different diffusion length in each spin. The difference in the diffusion length gives rise to the creation of tiny screening charge dipoles, which act as an additional serial capacitance, i.e., spin capacitance. The screening charge density is given by \(e{n}_{{\rm{AP}}}({x}_{i})=e{n}_{0,\mathrm{AP}}\,\exp (\,-\,{x}_{i}/\lambda )\), where xi is the distance from the interface between the Co40Fe40B20 and MgO, λ is a characteristic screening length and en0,AP is a screening charge density at the interface in the AP configuration. The spin capacitance can be expressed by \({{C}}_{{\rm{AP}}}^{{\rm{SDD}}}({V}_{{\rm{DC}}})={\rm{\Delta }}{Q}_{{\rm{AP}}}/{\rm{\Delta }}{V}_{{\rm{DC}}}\), where ΔQAP is the screening charge for the AP configuration and ΔVDC is the electrical potential difference applied in the charging space. Therefore, the spin capacitance can be obtained as \({{C}}_{{\rm{AP}}}^{{\rm{SDD}}}({V}_{{\rm{DC}}})=eS{n}_{{\rm{AP}}}({x}_{i})d{x}_{i}/d{V}_{{\rm{DC}}}({x}_{i})\), where S is a junction area and VDC(xi) is an electrical potential as a function of xi in the charging space, i.e., \({V}_{{\rm{DC}}}({x}_{i})={V}_{{\rm{eff}}}\,\exp (\,-\,{x}_{i}/\lambda )\). Veff is an effective applied voltage, which is expressed by κV, where κ is an adjustable positive parameter of much smaller than 1.0. Consequently, the spin capacitance can be represented by
Since this screening charge acts as a serial capacitance, the capacitance CAP(f, VDC) under the applied DC voltage VDC in the AP configuration,
where the capacitance \({C}_{{\rm{AP}}}^{\mathrm{DF}-\mathrm{QBA}}\) (f, VDC) based on the DF model combined with QBA in the AP configuration is represented by
The behavior of charge accumulation, contributing to \({{C}}_{{\rm{AP}}}^{\mathrm{DF}-\mathrm{QBA}}\) and \({{C}}_{{\rm{AP}}}^{{\rm{SDD}}}\), is illustrated in Fig. 3d. The bias voltage dependence of the capacitance CAP in the AP configuration is shown in Fig. 3e. The capacitance CAP increases at around zero bias and then it decreases at higher voltages. This behavior is in good agreement with the results calculated by Eqs (4)−(6) with parameters of C∞,AP = 1.5 nF, C0,AP = 590 nF, βAP = 0.977, τP = 0.0075 s, PTMC = 0.46, f = 60 Hz, κ = 0.1, S = 1800 μm2 and λ = 0.1 nm. ϕ0,AP is 0.144 (0.153) eV and n0,AP is 0.94 (0.92) × 1023 cm−3 for the positive (negative) bias region. The increase of CAP near zero bias is attributed to the decrease of the effective barrier thickness deff. As seen from the potential profile ϕP(x) of MTJs shown in Fig. 3b, deff decreases with increasing bias voltage VDC. This corresponds to the decrease of η3. According to our calculation, η3 is 0.5, 0.35 and 0.28 for VDC of 0, 50 and 100 mV, respectively. From Eq. (6), it is found that \({{C}}_{{\rm{AP}}}^{{\rm{DF}}-{\rm{QBA}}}(f,{V}_{{\rm{DC}}})\) increases with decreasing η3. Therefore, CAP(f, VDC) increases with increasing VDC. The reduction of CAP at higher voltages is attributed to the spin capacitance, described in Eq. (4), i.e., the spin capacitance decreases with increasing VDC.
Figure 4 shows the bias-voltage dependence of the TMC and TMR ratios. The calculation of the TMC is performed using Eqs (3–6) for setting the same parameters used in the calculation of CP(AP) (f, VDC) in Fig. 3c,e. The TMR is obtained from the Zhang formula. The calculation results of the TMC and TMR provide excellent fits to experimental data in bipolar bias regions. The reduction of TMR can be easily understood from the experimental results of both no significant change of RP (VDC) and the reduction of RAP (VDC) in higher voltages, as shown in Fig. 3a. In particular, the reduction of RAP (VDC) is due to the existence of hot electrons tunneling through the barrier, which brings about the decrease of TMR. The enhancement of TMC can also be clearly understood from the results of both the increase of CP (f, VDC) and the reduction of CAP (f, VDC) in higher voltages, as shown in Fig. 3c,e. The reduction of CAP (f, VDC) is attributed to the emergence of the spin capacitance, which promotes the increase of TMC. Thus, the spin capacitance gives a significant influence on TMC, and it will play an important role on future application.
Bias dependence of TMC and TMR ratio. The solid lines represent the calculation results performed using Eqs (3)−(6) for TMC and Zhang formula for TMR. The parameters used in this calculation are described in the main text. The TMC and TMR provide excellent fits to experimental data in bipolar bias regions.
Though the application of the interesting TMC effect is not well understood at this stage, we venture to discuss the application potential of TMC devices. As can be seen from Fig. 4, TMR is larger than TMC in the low bias region. In considering the application, the important factor in sensing is an electric sensitivity. The electric sensitivity is generally expressed by the signal-to-noise (S/N) ratio, which is defined as 20logVS/VN. Here VS is a signal voltage and VN is a noise voltage. In the case of TMR sensing under the applied voltage VDC, since VS is given by \(TMR\cdot {V}_{{\rm{DC}}}\) and VN is proportional to \(\sqrt{{V}_{{\rm{DC}}}}\), VS/VN is proportional to \(TMR\cdot \sqrt{{V}_{{\rm{DC}}}}\). Therefore, the increase of VDC is necessary for the improvement of the S/N ratio. In fact, magnetic read heads, sensors, or MRAMs are designed for operation under a bias of a few hundred mV61. Additionally, the enhancement of TMR at a higher voltage is of importance. As shown in Fig. 4, the TMR decreases with increasing VDC, whereas TMC increases at higher voltages. Since VS/VN is proportional to \(TMC\cdot \sqrt{{V}_{{\rm{DC}}}}\) in TMC sensing, the TMC is superior to TMR from the viewpoint of the S/N ratio. Furthermore, the impedance Z of TMC devices can be reduced in the high frequency region since the impedance of the capacitor is expressed as Z = 1/jωC, where ω is the angular frequency. This means that the noise voltage VN could be reduced. The high VS and low VN lead to the enhancement of the S/N ratio. Also, the AC technique allows for the performance of various functions such as modulation/demodulation, filtering, oscillation and resonance. In fact, magnetoimpedance devices using the AC technique have enabled the application to geomagnetic sensors or positioning sensors of GPS62,63,64,65. Also, a capacitive magnetic sensing, in which an RC parallel circuit module consisting semiconductor magnetoresistance device and capacitor was used in the feedback loop of a Hartley or Colpitts oscillator, has been proposed and demonstrated by our group66,67,68. In short, TMC devices may pave a new way for various applications to the next generation of magnetic read heads, MRAMs, logic circuits, and highly sensitive magnetic sensors (including geomagnetic sensors, positioning sensors, etc.).
Prediction of an extremely large voltage-induced TMC
Finally, the spin polarization dependence of the voltage-induced TMC is calculated for the prediction of an extremely large TMC. Figure 5a,b shows the calculated frequency dependence of the TMC under no bias voltage and the bias dependence of the TMC with varying P, respectively. Here, PTMC is assumed to be equal to PTMR, which is denoted by P. The assumed maximum value of P is 0.87, which is estimated experimentally for high-performance MgO-based MTJs at room temperature12. The parameters used in the calculation of the TMC are C∞,P(AP) = 1.45 (1.5) nF, C0, P(AP) = 184 (172) nF, β P(AP) = 0.998 (0.932) and τ P = 0.0033 s. As can be seen from Fig. 5a, the TMC ratio at VDC = 0 V shows the maximum value at f = 60 Hz for the P of 0.70, 0.79 and 0.87, respectively, and it increases from 273% to 995% with increasing P from 0.70 to 0.87. The maximum TMC of 273%, 505% and 995% are larger than TMR ratios of 192%, 325% and 604%, which are calculated from Julliere formula using P = 0.70, 0.79 and 0.87, respectively. The parameters used in the calculation of the bias dependence of TMC are f = 60 Hz, κ = 0.1, S = 1800 μm2 and λ = 0.1 nm. The barrier height ϕ0,P is 2.15 eV, and ϕ0,AP is 0.144 (0.153) eV in the positive (negative) bias voltage. The screening charge densities n0,AP are 0.312 (0.306), 0.208 (0.204) and 0.125 (0.123) × 1023 cm−3 in the positive (negative) bias voltage for the spin polarizations P of 0.70, 0.79 and 0.87, respectively. The TMC increases from 995% to 1119% with increasing VDC from 0 to 200 mV. Figure 5c shows the calculated frequency dependence of the TMC at VDC = 200 mV with varying τP. The maximum peak of the TMC is shifted to a high frequency region on the order of MHz for a short τP in the sub-μs scale. According to the DF model, τp can be tuned by changing the oscillation speed of electric dipoles formed near the FM/insulator interfaces; τp is short for a high oscillation speed. From the viewpoint of MTJ device structure, τp can be tuned by changing the thickness of the insulating barrier; τp could shorten in MTJs with a thinner barrier. Although this realization in MTJs is future work, the recent study using FeCo-MgF nanogranular films has demonstrated that the TMC peak is observed at a high frequency of 220 MHz, which corresponds to τp of 0.72 ns69. Our calculations predict that a large TMC of over 1100% could be possibly observed using MTJs with a realistic P of 0.87. Furthermore, this large TMC can be tuned from low to high frequencies by shortening τP.
Calculated frequency dependence of extremely large voltage-induced TMC. (a) Calculated frequency dependence of the TMC at VDC = 0 V in varying P. The TMC, showing the maximum value at f = 60 Hz, increases from 273% to 995% with increasing P from 0.70 to 0.87. (b) Calculated DC voltage dependence of the TMC. The calculation result predicts that the voltage-induced TMC could potentially reach 1100% in MTJs with a P of 0.87, which is within the realm of high-performance MTJs (See ref.12). (c) Calculated frequency dependence of the voltage-induced TMC with varying τP. The peak position of the TMC is shifted to a high frequency region for a short τP.
In summary, we observed a new phenomenon in which the TMC increases with the bias voltage in MgO-based MTJs at room temperature. The enhancement of TMC is attributed to the emergence of the spin capacitance in the AP configuration of MTJs. The voltage-induced TMC increases to 102%, which is the largest value ever reported for MTJs. We also found the voltage-induced TMC can be well explained by a newly proposed theoretical calculation using DF model combined with QBA and SDD model. This calculation predicts that the voltage-induced TMC could potentially reach 1100% in MTJs with a corresponding TMR value of 604%. These theoretical and experimental findings provide a deep insight into the voltage-induced AC spin transport in MTJs. We demonstrated that the complementary TMR and TMC effects must be treated on equal footing. The large TMC effect and the associated robustness against biasing may open up new avenues for spintronics applications and electrical modeling.
Methods
Preparation of the samples
The MTJs were prepared by using a magnetron sputtering system with a base pressure of 2 × 10−8 Torr. The MTJs have the following layer sequence: SiO2/Ta(5)/Co50Fe50(2)/IrMn(15)/Co50Fe50(2)/Ru(0.8)/Co40Fe40B20(3)/MgO(2)/Co40Fe40B20(3)/contact layer (thickness in nm). We deposited all the metallic layers in DC mode under a sputtering Ar gas pressure of 1.5 mTorr. The MgO layer was deposited with radio frequency (RF) magnetron sputtering at an Ar gas pressure of 1.1 mTorr. Using standard photolithography, we have patterned the multilayer MTJ stacks into a junction area of 1800 μm2 with an elliptical shape with Ar ion-milling and SiO2 insulation overlayer. Finally, we annealed the MTJs at 310 °C for 4 h in vacuum of 10−6 Torr under a uniform magnetic field of 4.5 kOe to define the pinning axis for the Co40Fe40B20 bottom electrode.
Measurements of the voltage-induced TMC
The frequency characteristics and the bias voltage dependence of the TMR and TMC for MTJs were measured by an AC four-probe method using an Agilent Technologies 4284 A LCR meter at room temperature. The frequency ranged from 50 Hz to 1 MHz and the bipolar bias voltage was applied up to 200 mV. The AC voltage was set to 2.6 mVrms. The magnetic field was applied along the magnetic easy-axis direction to 1.4 kOe.
References
Wolf, S. A. et al. Spintronics: A Spin-Based Electronics Vision for the Future. Science 294, 1488–1495 (2001).
Ney, A., Pampuch, C., Koch, R. & Ploog, K. H. Programmable computing with a single magnetoresistive element. Nature 425, 485–487 (2003).
Yuasa, S., Nagahama, T., Fukushima, A., Suzuki, Y. & Ando, K. Giant room-temperature magnetoresistance in single-crystal Fe/MgO/Fe magnetic tunnel junctions. Nat. Mater. 3, 868–871 (2004).
Parkin, S. S. P. et al. Giant tunneling magnetoresistance at room temperature with MgO (100) tunnel barriers. Nat. Mater. 3, 862–867 (2004).
Kent, A. D. & Worledge, D. C. A new spin on magnetic memories. Nat. Nanotechnol. 10, 187–191 (2015).
Parkin, S. & Yang, S.-H. Memory on the racetrack. Nat. Nanotechnol. 10, 195–198 (2015).
Matsukura, F., Tokura, Y. & Ohno, H. Control of magnetism by electric fields. Nat. Nanotechnol. 10, 209–220 (2015).
Miyazaki, T. & Tezuka, N. Giant magnetic tunneling effect in Fe/Al2O3/Fe junction. J. Magn. Magn. Mater. 139, L231–L234 (1995).
Moodera, J. S., Kinder, L. R., Wong, T. M. & Meservey, R. Large magnetoresistance at room temperature in ferromagnetic thin film tunnel junctions. Phys. Rev. Lett. 74, 3273–3276 (1995).
Butler, W. H., Zhang, X.-G., Schulthess, T. C. & MacLaren, J. M. Spin-dependent tunneling conductance of Fe|MgO|Fe sandwiches. Phys. Rev. B 63, 054416 (2001).
Mathon, J. & Umersky, A. Theory of tunneling magnetoresistance of an epitaxial Fe/MgO/Fe(001) junction. Phys. Rev. B 63, 220403R (2001).
Ikeda, S. et al. Tunnel magnetoresistance of 604% at 300 K by suppression of Ta diffusion in CoFeB/MgO/CoFeB pseudo-spin-valves annealed at high temperature. Appl. Phys. Lett. 93, 082508 (2008).
Slonczewski, J. C. Current-driven excitation of magnetic multilayers. J. Magn. Magn. Mater. 159, L1–L7 (1996).
Berger, L. Emission of spin waves by a magnetic multilayer traversed by a current. Phys. Rev. B 54, 9353–9358 (1996).
Albert, F. J., Emley, N. C., Myers, E. B., Ralph, D. C. & Buhrman, R. A. Quantitative Study of Magnetization Reversal by Spin-Polarized Current in Magnetic Multilayer Nanopillars. Phys. Rev. Lett. 89, 226802 (2002).
Diao, Z. et al. Spin transfer switching and spin polarization in magnetic tunnel junctions with MgO and AlOx barriers. Appl. Phys. Lett. 87, 232502 (2005).
Ikeda, S. et al. A perpendicular-anisotropy CoFeB–MgO magnetic tunnel junction. Nat. Mater. 9, 721–724 (2010).
Yoda, H. et al. High efficient spin transfer torque writing on perpendicular magnetic tunnel junctions for high density MRAMs. Curr. Appl. Phys. 10, e87–e89 (2010).
Lakys, Y. et al. Self-Enabled “Error-Free” Switching Circuit for Spin Transfer Torque MRAM and Logic. IEEE Trans. Mag. 48, 2403–2406 (2012).
Kang, W. et al. High reliability sensing circuit for deep submicron spin transfer torque magnetic random access memory. Electron. Lett. 49, 1283–1284 (2013).
Zhang, L. et al. A 16 Kb Spin-Transfer Torque Random Access Memory with Self-Enable Switching and Pre-Charge Sensing Schemes. IEEE Trans. Mag. 50, 1–7 (2014).
Wang, J., Meng, H. & Wang, J. P. Programmable Spintronics Logic Device Based on a Magnetic Tunnel Junction Element. J. Appl. Phys. 97, 10D509 (2005).
Yao, X. et al. Magnetic Tunnel Junction-Based Spintronic Logic Units Operated by Spin Transfer Torque. IEEE Trans. Nanotechnol. 11, 120–126 (2012).
Yuasa, S. et al. Future Prospects of MRAM Technologies. IEDM Tech. Dig. 3.1.1–3.1.4 (2013).
Fukushima, A. et al. Spin dice: A scalable truly random number generator based on spintronics. Appl. Phys. Exp. 7, 083001 (2014).
Torrejon, J. et al. Neuromorphic computing with nanoscale spintronic oscillators. Nature 547, 428–432 (2017).
Zhang, S., Levy, P. M., Marley, A. C. & Parkin, S. S. P. Quenching of magnetoresistance by hot electrons in magnetic tunnel junctions. Phys. Rev. Lett. 79, 3744–3747 (1997).
Lu, Y. et al. Bias voltage and temperature dependence of magnetotunneling effect. J. Appl. Phys. 83, 6515–6517 (1998).
Tezuka, N., Oogane, M. & Miyazaki, T. Applied voltage and temperature dependence of tunneling magnetoresistance. J. Magn. Magn. Mater. 198–199, 149–151 (1999).
Gao, L. et al. Bias Voltage Dependence of Tunneling Anisotropic Magnetoresistance in Magnetic Tunnel Junctions with MgO and Al2O3 Tunnel Barriers. Phys. Rev. Lett. 99, 226602 (2007).
Sukegawa, H. et al. Tunnel magnetoresistance with improved bias voltage dependence in lattice-matched Fe/spinel MgAl2O4/Fe(001) junctions. Appl. Phys. Lett. 96, 212505 (2010).
Matsuo, N., Doko, N., Takada, T., Saito, H. & Yuasa, S. High Magnetoresistance in Fully Epitaxial Magnetic Tunnel Junctions with a Semiconducting GaOx Tunnel Barrier. Phys. Rev. Applied 6, 034011 (2016).
Yu, J. H., Lee, H. M., Ando, Y. & Miyazaki, T. Electron transport properties in magnetic tunnel junctions with epitaxial NiFe (111) ferromagnetic bottom electrodes. Appl. Phys. Lett. 82, 4735–4737 (2003).
Yuasa, S. et al. Magnetic tunnel junctions with single-crystal electrodes: A crystal anisotropy of tunnel magneto-resistance. Europhys. Lett. 52, 344–350 (2000).
Komasaki, Y., Tsunoda, M., Isogami, S. & Takahashi, M. 75% inverse magnetoresistance at room temperature in Fe4N/MgO/CoFeB magnetic tunnel junctions fabricated on Cu underlayer. J. Appl. Phys. 105, 07C928 (2009).
Hueso, L. E. et al. Transformation of spin information into large electrical signals using carbon nanotubes. Nature 445, 410–413 (2007).
Xiong, Z. H., Wu, D., Vardeny, Z. V. & Shi, J. Giant magnetoresistance in organic spin-valves. Nature 427, 821–824 (2004).
Santos, T. S. et al. Room-Temperature Tunnel Magnetoresistance and Spin-Polarized Tunneling through an Organic Semiconductor Barrier. Phys. Rev. Lett. 98, 016601 (2007).
Shim, J. H. et al. Large Spin Diffusion Length in an Amorphous Organic Semiconductor. Phys. Rev. Lett. 100, 226603 (2008).
Shiraishi, M. et al. Robustness of Spin Polarization in Graphene-Based Spin Valves. Adv. Funct. Mater. 19, 3711–3716 (2009).
Kaiju, H., Fujita, S., Morozumi, T. & Shiiki, K. Magnetocapacitance effect of spin tunneling junctions. J. Appl. Phys. 91, 7430–7432 (2002).
Padhan, P., LeClair, P., Gupta, A., Tsunekawa, K. & Djayaprawira, D. D. Frequency-dependent magnetoresistance and magnetocapacitance properties of magnetic tunnel junctions with MgO tunnel barrier. Appl. Phys. Lett. 90, 142105 (2007).
Kaiju, H. et al. Large magnetocapacitance effect in magnetic tunnel junctions based on Debye-Fröhlich model. Appl. Phys. Lett. 107, 132405 (2015).
Parui, S. et al. Frequency driven inversion of tunnel magnetoimpedance and observation of positive tunnel magnetocapacitance in magnetic tunnel junctions. Appl. Phys. Lett. 109, 052401 (2016).
Zhang, S. Spin-dependent surface screening in ferromagnets and magnetic tunnel junctions. Phys. Rev. Lett. 83, 640–643 (1999).
Rondinelli, J. M., Stengel, M. & Spaldin, N. A. Carrier-mediated magnetoelectricity in complex oxide heterostructures. Nat. Nanotechnol. 3, 46–50 (2008).
Sahadevan, A. M., Gopinadhan, K., Bhatia, C. S. & Yang, H. Parallel-leaky capacitance equivalent circuit model for MgO magnetic tunnel junctions. Appl. Phys. Lett. 101, 162404 (2012).
Hoogdalem, K. A., Albert, M., Simon, P. & Loss, D. Proposal for a quantum magnetic RC circuit. Phys. Rev. Lett. 113, 037201 (2014).
Chui, S. T. & Hu, L. ac transport in ferromagnetic tunnel junctions. Appl. Phys. Lett. 80, 273–275 (2002).
Kuo, K. M. et al. Influence of frequency and DC bias on magneto-impedance behaviors in double-MgO magnetic tunnel junctions. Solid State Commun. 150, 1856–1859 (2010).
Kobayashi, N., Masumoto, H., Takahashi, S. & Maekawa, S. Giant dielectric and magnetoelectric responses in insulating nanogranular films at room temperature. Nat. Commun. 5, 4417 (2014).
Julliere, M. Tunneling between ferromagnetic films. Phys. Lett. 54A, 225–226 (1975).
Fullerton, E. E. et al. Structure and magnetism of epitaxially strained Pd(001) films on Fe(001): Experiment and theory. Phys. Rev. B 51, 6364–6378 (1995).
Fujii, Y., Komine, T., Kai, T. & Shiiki, K. A theoretical study of interfacial structure of Co/Cu and Co/Pd multilayers. J. Phys.: Condens. Matter 11, 9601–9609 (1999).
Shiiki, K., Sakaguchi, N. & Kaiju, H. Effect of unoxidized residual Al at the boundary of Co/Al-oxide/Co junction on TMR estimated by LMTO band calculation. Thin Solid Films 505, 64–66 (2006).
Burton, J. D., Jaswal, S. S., Tsymbal, E. Y., Mryasov, O. N. & Heinonen, O. G. Atomic and electronic structure of the CoFeB/MgO interface from first principles. Appl. Phys. Lett. 89, 142507 (2006).
Huang, S. X., Chen, T. Y. & Chien, C. L. Spin polarization of amorphous CoFeB determined by point-contact Andreev reflection. Appl. Phys. Lett. 92, 242509 (2008).
Djayaprawira, D. D. et al. 230% room-temperature magnetoresistance in CoFeB/MgO/CoFeB magnetic tunnel junctions. Appl. Phys. Lett. 86, 092502 (2005).
Wang, W., Sukegawa, H., Shan, R., Mitani, S. & Inomata, K. Giant tunneling magnetoresistance up to 330% at room temperature in sputter deposited Co2FeAl/MgO/CoFe magnetic tunnel junctions. Appl. Phys. Lett. 95, 182502 (2009).
Lee, T.-H. & Chen, C.-D. Probing spin accumulation induced magnetocapacitance in a single electron transistor. Sci. Rep. 5, 13704 (2015).
Hall, M. J., Gruev, V. & Chamberlain, R. D. Performance of a Resistance-To-Voltage Read Circuit for Sensing Magnetic Tunnel Junctions. Proc. of 55th International Midwest Symposium on Circuits and Systems, 639–642 (2012).
Beach, R. S. & Berkowitz, A. E. Giant magnetic field dependent impedance of amorphous FeCoSiB wire. Appl. Phys. Lett. 64, 3652–3654 (1994).
Panina, L. V., Mohri, K., Bushida, K. & Noda, M. Giant magneto-impedance and magneto-inductive effects in amorphous alloys. J. Appl. Phys 76, 6198–6203 (1994).
Mohri, K., Panina, I. V., Uchiyama, T., Bushida, K. & Noda, M. Sensitive and Quick Response Micro Magnetic Sensor Utilizing Magneto-Impedance in Co-rich Amorphous Wires. IEEE Trans. Magn. 31, 1266–1275 (1995).
Mohri, K., Uchiyama, T., Panina, L. V., Yamamoto, M. & Bushida, K. Recent Advances of Amorphous Wire CMOS IC Magneto-Impedance Sensors: Innovative High-Performance Micromagnetic Sensor Chip. Journal of Sensors 2015, 718069 (2015).
Kaiju, H., Saisho, K. & Shiiki, K. Highly sensitive magnetic sensing method using magnetoresistance devices. Jpn. J. Appl. Phys. 43, 5600–5603 (2004).
Kaiju, H. & Shiiki, K. Oscillation controlled magnetic sensing by using spinelectronics devices. Comp. Comm. Cont. Tech. Proc. 2, 31–34 (2005).
Kaiju, H. & Shiiki, K. Magnetic sensor utilizing magnetoresistance effect, method for driving magnetic sensor utilizing magnetoresistance effect and magnetic recording systems. US Patent 6975110 (2005).
Ikeda, K., Kobayashi, N., Arai, K.-I. & Yabukami, S. Magnetoelectric effect in nanogranular FeCo-MgF films at GHz frequencies. J. Magn. Magn. Mater. 446, 80–86 (2018).
Acknowledgements
This research was supported by the Grant-in-Aid for Scientific Research (B) (under Grant No. 15H03981) and Challenging Exploratory Research Program (No. 17K19019) funded by the Japan Society for the Promotion of Science (JSPS), the Dynamic Alliance for Open Innovation Bridging Human, Environment and Materials and the Cooperative Research Program of “Network Joint Research Center for Materials and Devices” funded by the Ministry of Education, Culture, Sports, Science, and Technology (MEXT), Research Project funded by the Center for Spintronics Research Network (CSRN) at Tohoku University, and the US National Science Foundation at Brown University (under Grant No. DMR-1307056).
Author information
Authors and Affiliations
Contributions
H.K. and G.X. conceived and designed the experiments using the help of other authors. G.X. performed the sample preparation and structural analysis. H.K., T.M. and T.N. performed dc measurements. H.K., M.F. and J.N. performed ac impedance measurements. H.K., G.X., T.K. and O.K. performed the theoretical analysis and calculation. All the authors contributed to analyzing and interpreting the data, and to writing the manuscript.
Corresponding author
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kaiju, H., Misawa, T., Nagahama, T. et al. Robustness of Voltage-induced Magnetocapacitance. Sci Rep 8, 14709 (2018). https://doi.org/10.1038/s41598-018-33065-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-018-33065-y
Keywords
This article is cited by
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.