Introduction

Metamaterials with fascinating radiative properties not found in nature have drawn increased attention as of late1,2,3. They have been tested in many applications from increasing energy harvesting efficiency through near-field radiation4, radiative cooling5, to visual optics that exceed the diffraction limit6. They consist of nanoscale three-dimensional periodic assemblies whose properties are determined by the specific size, geometry, material, and orientation of the structures. Arrays consisting of nanorods (NRs) in a dielectric host form simple yet versatile arrangements that show promise for applications involving tunable properties of thermal emission and absorption4,7,8. In addition, metallic NRs can also exhibit hyperbolic dispersion in certain wavelengths9 and hold promise in both energy conversion10 and plasmonic devices11. However, the analysis of the radiative properties of these NR array structures is made more complex due to their inherent geometrically induced anisotropy and inhomogeneous nature.

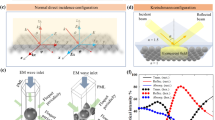
Theoretical methods require the use of estimation techniques such as the effective medium theory (EMT) to describe the field-averaged dielectric function of array-like structures by treating them as effectively homogeneous media. However, due to the geometry-induced anisotropic nature, the effective radiative properties (i.e., reflectance, transmittance, or absorptance) of such structures are predominantly calculated for samples with specifically controlled angles of incidence and structural orientations (see details in the “Methods” section)12,13. In such cases, the polarizations of anisotropic electromagnetic (EM) wave propagation through these complex media are decoupled. For example, incidence of transverse electrical (TE, also s-polarization) or transverse magnetic (TM, also p-polarization) polarized light will generate only ordinary or extraordinary waves, respectively, in an anisotropic medium, depending on the structural orientation (refer to Fig. 1). To make this EMT-based approach applicable to array-like structures for more universal scenarios, such as s- or p-polarized incident light exciting both ordinary and extraordinary wave propagation in the array-like structures, a generalized solution is necessary for such polarization-coupled cases.

Figure 1
figure 1

(a) Local axes of the single metallic nanorod. The ordinary modes have the electrical field in the a-b plane while the extraordinary mode has the electric field parallel to the \(\hat{c}\) axis. (b) Schematic depicting the relationship between the global coordinates (x, y, and z) and the local coordinates defined by the primary optical axis of the NRs (\(\hat{c}\)). The direction of the incident EM wave is determined by the incidence angle (θi) and the azimuthal angle (ψ). The geometry of the tilted metallic nanorod array is determined by the tilt angle (θt) and the volume fraction (f), which can be found by the spacing between nanorods in the x and y directions (s1 and s2 respectively).

Full size image

Herein, we analytically derive a solution to predict the effective radiative properties of array-like anisotropic media that can be extended to the scenarios of polarization coupling. This analytical solution agrees well with finite-difference time-domain (FDTD) simulations when the wavelength is about 10 times greater than the critical dimension of considered structures (which depends on the incident polarization, to be discussed in detail in the “Results” section). The final solution can be readily applied to material systems that contain multiple components and polarization-dependent response to the incident EM waves.

The geometry and related parameters of the array-like structure are depicted in Fig. 1. In the EMT calculation, we conduct a coordinate transform from a local coordinate system (defined by the individual nanorod in Fig. 1a to a global coordinate system in Fig. 1b for the ease of tracing the light propagation. For validation of the EMT calculation, an FDTD simulation is performed to model how the light interacts with the surface of a tilted nanorod system. In the present work, a commercial software, Lumerical FDTD Solutions, is employed. Several studies investigate the optical properties of absorbing nanorod arrays with metallic behaviors8,13,14,15,16,17,18,19,20, however, these studies focused on specific conditions with nanorods that are only slightly tilted14 or vertically aligned8,13,15,16,17 such that the boundaries of the simulation domain can be simply set as periodic boundary conditions in FDTD. Additionally, several literature studies only analyzed the behavior of the electric field at a very localized area around several nanorods with a finite thickness, which is straightforward to be modeled in an FDTD simulation18,19,20. On the other hand, in the present study, we eliminate the effects of thin-film interference in highly tilted metallic nanorod arrays and actually model the entire nanorod array that extends to the semi-infinite regime using FDTD. Notice that the exact calculation of a semi-infinite metallic nanorod array is crucial for validating the EMT formulation. Details regarding the procedures of EMT and FDTD calculation are provided in the “Methods” section.

Results

Decoupled case: wavelength dependence

We have conducted FDTD simulations (see details in the “Methods” section) for a decoupled case (i.e., the optical axis of the nanorods in the plane of incidence) to justify the validity of our EMT calculation of silver nanorods. In the calculation, the optical constants of silver were taken from the tabulated data in Palik’s handbook21. Figure 2 shows the comparison of the predicted reflectance from FDTD and EMT as a function of wavelength for an array of Ag nanorods. It can be clearly seen from Fig. 2 that the EMT generally follows the exact results by FDTD for both polarizations with either normal or oblique incidence (θi = ±30°). While the agreement between EMT and FDTD is excellent for long wavelengths, EMT cannot capture the short-wavelength behavior due to the major assumption for EMT validation, which requires that λ is ~10 times the characteristic dimension of the material system of interest (as discussed in the “Methods” section). For cases with s-polarized light (i.e., the electric field oscillates parallel to the y-axis), EMT begins to agree with FDTD at λ ≈ 800 nm for both θi = 0° and θi = ±30° incidences (Fig. 2c). This is because the electric field in the s-polarized case always interacts with a constant nanorod diameter, which does not change with θi. It is worthwhile to mention that the FDTD results for θi = −30° and 30° show different behavior at shorter wavelength region, but become identical at λ ≈ 800 nm when the EMT starts to agree with the FDTD. The situation is different for the p-polarized case (i.e., the electric field oscillates in the x-z plane at an angle of θi with respect to the z-axis), where the critical wavelength now depends on the projection of the nanorod seen by the electric field. For larger θt, the wavelength at which the EMT starts to agree with FDTD is much longer than the s-polarized case and shifts to slightly smaller wavelengths at oblique incidences. For example, when θt = 73°, the comparison between FDTD and EMT suggests a critical dimension of approximately 2000 nm for the p-polarized case.

Figure 2
figure 2

Comparison of the reflectance found from FDTD and EMT as a function of wavelength for Ag nanorods with D = 100 nm, f = 0.20 (s1 = 480 nm and s2 = 280 nm), and θt = 73°. The left panel is for the s polarization and the right panel is for the p polarization.

Full size image

Coupled case: angular dependence

For polarization-coupled situations, it can be shown that the azimuthal angle ψ (refer to Fig. 1) will greatly affect the resulting reflectance. In addition to the s- and p-polarized reflectance (Rss and Rpp), the cross-polarized reflectances (i.e., Rsp and Rps corresponding to the fraction of s-polarized incident light that is reflected as p-polarized and vice versa) must be accounted for. These terms can be calculated from EMT through the Fresnel coefficients rsp and rps (see Supplementary Information); however, determining the coupled reflectivity through the FDTD simulation is a non-trivial task (see “Methods” section for details).

Figure 3 shows the dependence of ψ on the polarization-resolved reflectance for the oblique incidence of θi = 30° and λ = 2000 nm, where the EMT agrees well with FDTD for both polarizations. When ψ = 0°, the two polarizations are decoupled, and the resulting Rss is smaller than Rpp. Rotating the nanorods to ψ = 90° provides the opposite behavior (larger Rss than Rpp), which is captured by both the trends of FDTD and EMT. When the polarization coupling effect appears (i.e., ψ ≠ 0), the EMT calculation agrees excellently with the FDTD simulation. Similarly to the relation between Rss and Rpp, Rsp and Rps exhibit similar azimuthal angle dependence; that is, Rsp at ψ corresponds to Rps at ψ + 90°.

Figure 3
figure 3

Coupled reflectance from an Ag nanorod structure (D = 100 nm, f = 0.20, s1 = 480 nm, s2 = 280 nm, and θt = 73°) at λ = 2000 nm and θi = 30°. Results from EMT are shown as black lines and FDTD results are shown as red circles with a dashed red line to guide the eye. Rs (or Rp) indicates the total reflectance from incident s-polarized (or p-polarized) light; that is, Rs = Rss + Rsp (or Rp = Rpp + Rps).

Full size image

Parametric study

Figures 2 and 3 clearly verify that our EMT formulation can successfully predict the radiative properties of tilted nanorod arrays by considering polarization coupling. In order to better understand the impact of the interface reflectance from nanorod arrays, a parametric study has been conducted using the EMT to show the impact of the filling fraction, the nanorod material, the material of surrounding medium, and the azimuthal angle. Notice that the geometric parameters of nanorod arrays, such as the diameter, s1, and s2, are not considered hereafter because the EMT is proven to be valid in the chosen wavelength region (1.5–3 μm).

Filling fraction

One of the most critical parameters to understand for nanorod arrays is the filling fraction. Small inter-wire spacing often leads to enhanced radiation transport through surface plasmons, which are thought to be the reason for enhanced Raman signals seen by silver nanorods22. Figure 4 shows the coupled calculation at the interface between air and Ag NRs with f = 0.1 and 0.3. Although Ag is highly reflective in the near-infrared (NIR) spectral region, the Ag NR array with f = 0.1 shows greatly suppressed reflection (total reflectance is about 0.1), as shown in Fig. 4a. Interestingly, a large cross-polarization term (Rsp) exists in the considered spectral region. This term is largely dependent on both the magnitude of the single polarization terms and the azimuthal angle. Increasing the filling fraction results in an increase in s- and p-polarized reflectance over the NIR region, but a decrease in the magnitude of the cross-polarization terms (see Fig. 4c). For the dependence of reflectance on the incident angle depicted in Fig. 4b and d, Rss and Rsp follow the typical trend of polarized light incident on a semi-infinite medium; that is, Rss increases monotonically with θi, while Rpp exhibits a minimum at a pseudo-Brewster angle. An increase in the volume fraction shifts the Brewster angle to a larger θi. The cross-polarization terms remain relatively small for the entire range of θi.

Figure 4
figure 4

Spectral and angular reflectance at the interface between air and an Ag nanorod array with varying filling fraction. (a) and (c) show the spectral reflectance from 1.5 to 3.0 μm for f = 0.10 and f = 0.30, respectively, and θi = 45°, θt = 45°, and ψ = 45°. (b) and (d) show reflectance as a function of incidence angle θi, with θt = 45°, ψ = 45°, and λ = 2000 nm for f = 0.10 and 0.30, respectively.

Full size image

Impact of nanorod materials

While Ag nanorods are one of the most prevalent tilted nanorod systems, glancing angle deposition (dynamic shadowing growth) is able to create nanorod arrays from a variety of materials, including metals, semiconductors, and various metal-oxides23. Our proposed EMT approach considering the polarization coupling effect can be readily applied for such versatile systems with a great flexibility and ease of computation. Figure 5 shows the reflectance of an array of titanium (Ti) nanorods as a function of wavelength and incidence angle for two filling fractions of f = 0.1 and 0.3, respectively. As shown by Fig. 5a, the TiNRs exhibit extremely low reflectance (less than 10% of incident intensity is reflected). Since the nanorods are assumed to be semi-infinite (i.e., their length is much longer than the optical penetration depth), the absorptance of TiNRs would approach the optical properties of vertically aligned carbon nanotubes23. Similar to AgNRs, an increase of the filling fraction from 0.1 to 0.3 will increase s− and p−polarized reflectance while decreasing the cross-polarization terms of Rsp and Rps (Fig. 5c). Comparing TiNRs to AgNRs in the same conditions (Fig. 4), the reflectance of TiNRs is nearly constant as opposed to decreasing when the wavelength increases (such as in AgNR). This difference is because Ti is lossier (i.e., the imaginary part of its dielectric function is greater) than Ag in the considered wavelength region24.

Figure 5
figure 5

Spectral and angular reflectance at the interface between air and a Ti nanorod array with varying filling fraction. (a) and (c) show the spectral reflectance from 1.5 to 3.0 μm for f = 0.10 and f = 0.30, respectively, and θi = 45°, θt = 45°, and ψ = 45°. (b) and (d) show reflectance as a function of incidence angle θi, with θt = 45°, ψ = 45°, and λ = 2000 nm for f = 0.10 and 0.30, respectively.

Full size image

Surrounding medium materials

In all of the previously discussed simulations, the material surrounding the nanorods is treated as air, but taking this term to be non-unity (n ≠ 1) will result in noticeable changes to the optical properties of the interface between the incident medium and the array structure. Figure 6a is produced using the same parameters as Fig. 4, but with the addition of polymethyl methacrylate (PMMA) as the surrounding medium. PMMA is chosen as a representative surrounding material in this work, based on the following reasons: (1) optical polymers, including PMMA, generally have dielectric behaviors with similar indices of refraction (n  ≈  1.4–1.5 and κ = 0) that are relatively wavelength independent over the spectral regime of interest in this work25; and (2) spin coating of PMMA is a common practice that can be easily applied as the host medium for nanorod array structure. Comparison of Figs 4a and 6a suggests that the refractive index of the surrounding medium greatly affects the Rss and Rpp such that s- and p-polarized reflectance of the metallic nanorods in PMMA are higher than those of the case in air. However, the cross-polarization terms, Rsp and Rps exhibit little variation with respect to the change of the surrounding medium, suggesting that cross-polarized reflectance may mainly be induced by the geometrical effect of the tilted nanorod array. Figure 6b also shows a behavior in that p-polarization term approaches zero at a pseudo-Brewster angle which results in an even greater ratio of the reflected s-polarized light to any other polarization.

Figure 6
figure 6

Spectral and angular reflectance of an optically opaque array of Ag nanorods with a surrounding medium of PMMA. Calculation parameters are (a) f = 0.10, θi = 45°, θt = 45°, and ψ = 45°; (b) f = 0.10, θt = 45°, ψ = 45°, and λ = 2000 nm.

Full size image

Azimuthal angle

All coupled derivations include the azimuthal angle, which is the main difference between coupled and decoupled models. This term leads to cross polarizations that greatly complicate the predicted reflectance, but once the model has been made, the impact of azimuthal rotation can be plotted, as illustrated in Fig. 7. In the decoupled limit (ψ = 0°), the cross-polarization terms go to zero, which is another verification of the robustness of this model. Due to the nature of the coordinate system transform, the cross-polarization terms are equal, but seen at angles 180° offset from each other. This behavior could be used to determine the direction of the nanorod array simply by looking at the magnitude of cross-polarization terms. While these terms are typically small (as shown in Fig. 7) compared to the Rss and Rpp terms, there are conditions when they can be large, such as in Fig. 6, where the Rsp dominates over Rpp in a small wavelength window. The magnitudes of these cross-polarization terms are always maximized at ψ = 45°, 135°, 225°, and 315°.

Figure 7
figure 7

Reflectance as a function of azimuthal angle ψ at λ = 2000 nm. (a) and (b) show the behavior of varying Ag filling fractions, f = 0.10 and 0.30 respectively. (c) shows the behavior in the case of Ag nanorods (f = 0.10) in a surrounding medium of PMMA. (d) plots the calculation results for an array of Ti nanorods in air with a filling fraction of f = 0.10.

Full size image

Conclusion

In this work, we investigate the polarization-coupled radiative properties of metallic nanorod arrays by combining EMT and anisotropic wave propagation. The Maxwell-Garnett EMT is utilized to obtain ordinary and extraordinary relative permittivities. A coordinate transform of the local permittivity results in a global permittivity tensor that can be used to calculate the Fresnel coefficients. The exact results computed by FDTD simulation justify the validity of EMT with polarization coupling taken into account.

Parametric studies have also been conducted to examine the effects of wavelength, filling fraction, incidence angle, nanorod material, and azimuthal angle. Increasing the filling fraction tends to enhance the s- and p-polarized reflectance while decreasing the cross-polarized reflectances (i.e., Rsp and Rps). Changing the nanorod material from silver to titanium can greatly change the optical behavior, even at low filling fraction, resulting in a much more absorbing material that is also less dependent on incidence angle. The final study showed that changing the surrounding medium to a polymer infill will increase the impedance mismatch at the air/array interface and thus increase Rss and Rpp of the array structure, while keeping Rsp and Rps relatively small. This indicates that the geometry of the nanorod array has a large impact on the cross-polarized reflectance.

The theoretical simulation results presented point to the potential of metallic nanorod arrays as optical gratings, Brewster windows, and other optical instruments. Further work is needed to explore a larger range of nanorod materials and geometries and to better understand the light path in the event of multiple interfaces as seen in thin-film optics. Because this is a single interface with an effective medium assumption, it is a relatively simple calculation compared to other simulation methods (e.g., FDTD in this work) that are computationally expensive while capable of simulating more complicated material structures.

Methods

Effective medium theory

Analytical derivation of the reflectance of small embedded particles requires the consideration of multiple reflections within the structure. The EMT has been widely used to approximate the effective properties of a medium consisting of two or more components. Two main approximations have been widely used to predict the effective permittivity based on volume-averaged fields. In the case of two component materials, both the Maxwell-Garnett (MG)26 approximation and the Bruggeman27 approximation consider a filler material (a) embedded in a host material (b) and compute an effective relative permittivity as a function of the relative permittivity of each material, a volumetric filling fraction (f), and a depolarization factor (g). The MG approximation is given as

$${\varepsilon }_{eff}={\varepsilon }_{b}+{\varepsilon }_{b}\frac{f({\varepsilon }_{a}-{\varepsilon }_{b})}{g(1-f)({\varepsilon }_{a}-{\varepsilon }_{b})+{\varepsilon }_{b}}$$
(1)

and is used typically for low filler concentration (f < 30%). In Eq. (1), g is the depolarization factor that is shape-specific for the filler materials dispersed as particles in the host media. The depolarization factor of filler particles with random shape can be rather complicated to calculate. However, for the case of NRs which can be treated as a prolonged ellipse with a uniaxial geometry (cigar-like, Fig. 1a), two of the axes along the radial directions are equivalent, degenerating to the “ordinary” state leaving the third axis along the axial direction being the “primary extraordinary” state (also called the optical axis of the uniaxial medium to be discussed later). This simplification gives two depolarization factors corresponding to “primary extraordinary” and “ordinary”, respectively:

$${g}_{{\rm{E}}}=\frac{1-{e}^{2}}{{e}^{2}}[\frac{1}{2e}\,\mathrm{ln}(\frac{1+e}{1-e})-\,1]\,{\rm{and}}\,{g}_{{\rm{O}}}=\frac{1}{2}(1-{g}_{{\rm{E}}})$$
(2)

Both gE and gO depend on the eccentricity of the prolonged ellipsoidal NR:

$$e=\sqrt{1-{(D/L)}^{2}}$$
(3)

where D and L correspond respectively to the diameter and length of the NR. The degeneration of g results in two distinctive effective permittivities for a NR: the “ordinary permittivity” (εO) along the radial direction calculated by using gO and the “extraordinary permittivity” (εE) along the axial direction calculated by using gE.

For spherical particles with εE ≈ εO, the system behaves as an effectively isotropic material. Whereas for aligned NRs, the difference in εE and εO results in an effective uniaxial medium consisting of NRs and air. This uniaxial medium has a single optical axis parallel to the axial direction of the aligned NRs as denoted by in Fig. 1. This shape-induced uniaxial feature leads to anisotropic wave propagation in the aligned NRs that is highly dependent on the orientation of the optical axis and the direction of incident light.

For reasonable predictions on the effective radiative properties of aligned NR array using the EMT, it is also important that the characteristic dimension of the structure should be much less than the wavelength of the incident light. In this case, the incident EM wave does not see individual NRs, but rather, it interacts with an effectively homogeneous medium with properties averaged over all components. The application for EMT typically requires that λ is at least 10 times longer than the critical dimension. Because of the ease of application, these theories are sometimes used for parameter extraction in situations that do not meet the characteristic dimension requirement, as discussed by Smith et al.28. However, EMT can provide a first estimation of the optical properties even for cases like these.

Using previously discussed formulas29, this permittivity tensor can be used to calculate Fresnel coefficients, including: rss (the Fresnel coefficient corresponding to s-polarized light that is reflected as s-polarized light), rsp (s-polarized light that is reflected as p-polarized light), rps (p-polarized light that is reflected as s-polarized light), and rpp (p-polarized light that is reflected as p-polarized light).

Note that for isotropic cases, or cases where the optical axis is inside the plane of incidence (ψ = 0), the cross-polarization terms (rsp and rps) will reduce to zero. In these special situations, there is no coupling between electric fields for the ordinary and extraordinary cases and they are thus are decoupled cases. For these decoupled cases, β = 0, which causes the permittivity tensor to simplify to an admittance and impedance approach as described by Gaylord et al.30, resulting in rss and rpp being equivalent to r12s and r12p as defined by Wang et al.12.

Finite-difference time-domain simulation

In order to calculate the reflectance of arrays of tilted nanorods, a three-dimensional simulation domain with a mesh of 5-nm cubes was created, and periodic boundary conditions in the x- and y-direction, and a perfect matching layer (PML) in the z-direction were set. The auto shutoff ratio is set to be 10−6. In general, a semi-infinite medium can be approximated by a thin (i.e., finite thickness) opaque layer. Since the metallic nanorod array can be either highly absorbing or highly transparent, depending on the polarization state, we cannot make it opaque for both polarizations. Furthermore, the FDTD simulation will be unstable when a metallic structure penetrates or overlaps the PML31. Therefore, a special trick is applied to simulate the reflectance of a semi-infinite metallic nanorod array. In the simulation, we actually employ a free standing metallic nanorod array with the finite thickness of 30 μm, which is much greater than the wavelength of incident light. Therefore, there must be reflected waves from the bottom interface between the nanorod array and air. To avoid collecting the reflected energy from the bottom interface, we adjust the simulation time so that the calculation is finished before the reflected beam from the bottom interface arrives at the monitor. In our simulation, the time that the wave was initially emitted by the source initially reaches the top surface of the nanorod array and the time that the reflected wave from the top surface of the nanorod array reaches the monitor is 2 fs. An additional 20 fs is also required for the fluctuation of the light source to be stabilized, which means that at least 22 fs is required to collect the reflected beam from the top surface of the nanorod array. To assure numerical convergence, we set the system to allow a total simulation time of 200 fs (i.e., about 10 times the minimum required time). To satisfy this criterion, the thickness of the tilted nanorod array should be at least 30 μm so that the reflected light from the bottom interface cannot reach the monitor before 200 fs. Although it is not shown here, the reflectance of a semi-infinite material with a refractive index of 1.4 is calculated by the aforementioned trick and compared with the analytical solution using the Fresnel coefficient. The relative error of the FDTD simulation is found to be less than 1%.

Regarding the coupled case, since the Fresnel coefficient is defined as the electric field of the reflected light relative to the electric field of the incident light, in order to calculate the cross-polarization terms (rsp and rps) the electric field of the reflected light must be analyzed in the coordinate system of the incident light. Therefore, in order to calculate the cross-polarization terms, the electric field detected at the monitor in the FDTD coordinate system should converted into the coordinate system of the incident light. Since the incident light has both the azimuthal angle ψ and the incidence angle θi, we extract the x-, y-, and z-components of the electric field, and use the Euler angle transform to convert the coordinate system. It can be seen that after the transformation is performed, the electric field of the reflected light is represented by only two components of s- and p-polarization on the incident light coordinate system. The cross-polarization terms were calculated through the ratio of the polarized reflected electric field to that of the polarized incidence. By taking average of the Fresnel reflection coefficient over the unit cell of the nanorod array in the near field, one can estimate the reflectance32.