Abstract
Micro-computed tomography (µCT) is a standard method for bone morphometric evaluation. However, the scan time can be long and the radiation dose during the scan may have adverse effects on test subjects, therefore both of them should be minimized. This could be achieved by applying iterative reconstruction (IR) on sparse projection data, as IR is capable of producing reconstructions of sufficient image quality with less projection data than the traditional algorithm requires. In this work, the performance of three IR algorithms was assessed for quantitative bone imaging from low-resolution data in the evaluation of the rabbit model of osteoarthritis. Subchondral bone images were reconstructed with a conjugate gradient least squares algorithm, a total variation regularization scheme, and a discrete algebraic reconstruction technique to obtain quantitative bone morphometry, and the results obtained in this manner were compared with those obtained from the reference reconstruction. Our approaches were sufficient to identify changes in bone structure in early osteoarthritis, and these changes were preserved even when minimal data were provided for the reconstruction. Thus, our results suggest that IR algorithms give reliable performance with sparse projection data, thereby recommending them for use in µCT studies where time and radiation exposure are preferably minimized.
Similar content being viewed by others
Introduction
Micro-computed tomography (µCT) has long been considered as the ‘gold standard’ method for structural bone analysis due to its ability of retrieving high-resolution volumetric data in a non-invasive manner, and providing optimal contrast between bone and soft tissue1. Other applications of µCT include small animal imaging for phenotyping of disease models, evaluating pre-clinical study outcomes, and developing of drug and treatment interventions2,3. The imaging times in µCT vary from a few minutes for in vivo scans to several hours for high-resolution (<2 µm) in vitro scans. Long scan times are associated with high radiation exposure and movement induced imaging artifacts4,5. In extreme cases, the radiation dose is so high that it affects tissue metabolism and produces unwanted tissue changes. Such changes are of special concern in longitudal in vitro studies6, for example in digital volume correlations used for in situ mechanical testing7. Furthermore, harmful radiation effects, such as burns, radiation sickness, or cancer, are of scientific and ethical concern2,3,6.
In µCT, a cone-beam X-ray geometry and a radiation detector are used to gather projected images from different angles around the test object2,3,8. These images are reconstructed mathematically to obtain the 3-dimensional structure within the object. Traditionally, reconstructions are made using methods that are based on filtered back-projection (FBP), such as the three-dimensional cone-beam reconstruction algorithm developed by Feldkamp, Davis and Kress in 1984 (FDK)9. FBP- or FDK-based methods are robust and computationally efficient but are limited in that they require vast amounts of X-ray projection data, otherwise image reconstructions are plagued by imaging artefacts, such as streaking, stretching, blurring, partial volume effects, low resolution, or noise4,10.
CT reconstruction is an inverse problem. Projection data measured with a known X-ray setup (forward problem) are used to retrieve the attenuation information from within the imaged object (inverse problem). With the help of inversion mathematics, images of sufficiently good quality (minimal artefacts and noise) can be computed iteratively from a limited amount of attenuation data10,11,12, reducing the imaging time and radiation dose12,13. Simple iterative reconstruction (IR) algorithms, such as the simultaneous algebraic reconstruction technique (SART)14, or simultaneous iterative reconstruction technique (SIRT)15, use an algebraic solver to minimize the Euclidean norm, L2, of the residual of the reconstruction. By using iterative techniques, the radiation dose can be reduced up to 76% while still obtaining image quality comparable to FBP-based methods11. Accordingly, a better image quality can be achieved by using IR instead of FBP with the same amount of radiation dosage13. The inverse problems associated with sparse X-ray tomography data reconstructions often do not have stable and unique solutions and require a priori knowledge about the object to converge to a reliable solution16,17. This so-called regularization consists of iterative algorithms aimed at solving an optimization problem (e.g. the minimization of the L2 norm) with a penalty term containing prior information. Some well-known examples are the Tikhonov regularization and the total variation (TV) regularization, which take advantage of information about the smoothness and edges within the target object17. In the context of µCT imaging, IR or regularizing methods could enable the acquisition of a large number of high-resolution scans, thereby increasing reliability of many biologically relevant µCT studies while simultaneously reducing movement artefacts and harmful radiation exposure. However, due to their iterative nature, these algorithms are associated with high computational demands. However, the computational power of commercially available workstations has increased to a level where IR is a viable option, and the major clinical CT vendors have already implemented IR algorithms into their imaging systems10,13. In clinical applications, IR techniques are usually applied with a certain amount of FBP to reduce blotchy image appearance obtained with full IR11,13. Further reasons why IR is not more widely used in clinical CT include the limited accessibility to corrected raw data, the problems with intellectual property rights, and the communication barrier between mathematicians and engineers18. With high-performance GPUs, IR can be performed even for high-resolution µCT datasets that are considerably larger than those obtained in clinical CT.
Since µCT achieves high spatial resolution and contrast between bone and soft tissues, it has become an important tool for various musculoskeletal diseases, such as osteoarthritis (OA). OA is a progressive joint disease causing pain and stiffness in synovial joints, and may cause disability in middle aged and old people. Risk factors for OA include age, excessive weight, joint instability, mechanical impacts, large torsional loads, and injury19. Because OA is a progressive disease with little or no symptoms in its early stage, only severe and symptomatic cases are usually studied in human patients. Different animal models have been studied alongside the human disease to obtain a better understanding of OA20,21,22,23. OA is associated with degradation of the extracellular matrix and changed chondrocyte function, causing degeneration and disturbed repair of articular cartilage19,24,25. OA-related damage is not only present in the articular cartilage, but also the subchondral bone which also undergoes structural changes with increasing OA severity26. Osteoarthritic trabecular bone often has coarser and discontinuous microstructure, resulting in decreased stiffness, which can be quantified by changes in structural parameters such as trabecular bone volume fraction, and the thickness and separation of trabeculae27,28,29.
The standard method of obtaining quantitative information on bone structure is via quantitative bone morphometry, in which bone data acquired with µCT is analyzed mathematically30,31. First, the data are segmented into bone and other tissues, after which morphometric parameter analyses are performed to obtain information about the size and shape of specific bone compartments. The minimal set of variables to be reported in such analyses are bone volume fraction (BV/TV), trabecular number (Tb.N), trabecular thickness (Tb.Th) and trabecular separation (Tb.S)32. Along with these parameters, structural model index (SMI) has also been calculated to quantify as a degree of anisotropy in trabecular structure. However, it is known that SMI has limitations, such as not accounting for concave bone surfaces33, and recently the ellipsoid factor (EF) has been introduced in its place with convincing results34. In the light of these findings, EF is used instead of SMI in this study to assess the geometric composition of our bone samples. Furthermore, the thickness of the subchondral bone plate (Pl.Th) is also quantified. This set of parameters provides a quantitative overview of the structure of the bone and how it changes with the progression of OA.
The aim of this study was to test the performance of different image reconstruction algorithms in a µCT setting. The algorithms are tested using quantitative parameter analysis related to the biomedical imaging studies of OA, and the results are compared against those given by FDK reconstruction.
Materials and Methods
Sample acquisition
Six female New Zealand white rabbits (Oryctolagus cuniculus, age 14 months at the end of the experiments, weight 4.5 ± 0.3 kg) underwent unilateral anterior cruciate ligament transection (ACLT) surgery to a randomized knee to induce the onset of OA. A control group (n = 4, age 14 months at the end of the experiments, weight 4.8 ± 0.3 kg) was left unoperated. After 8 weeks, the animals were euthanized and the femoral condyles (both medial and lateral) were harvested from the operated knees of the ACLT group and both knees of the control group. All procedures were approved by the Committee on Animal Ethics at the University of Calgary and were carried out according to the guidelines of the Canadian Council on Animal Care (certificate of animal use protocol approval #AC11-0035). Femoral condyles were wrapped in moisturized tissue paper and placed in a plastic container to prevent drying and movement, respectively. From these samples (N = 12 and N = 16 for ACLT and control groups, respectively), subchondral bone properties were analyzed quantitatively using different image reconstruction algorithms. The medial and lateral condyles were pooled for statistical power because of the small number of samples.
Micro-computed tomography
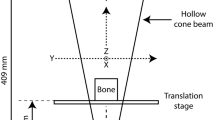
Projection data were acquired using a SkyScan 1272 high-resolution cone-beam µCT scanner (Bruker micro-CT, Kontich, Belgium) with 50 kV source voltage, 200 µA source current, focal spot size of <5 µm at 4 W power, and additional 0.5 mm aluminum filtering. Each projection image was taken with 2016 ms exposure time, 4 × 4 binning, and 2 frames (rays) per projection averaging. Datasets of 260 projection images were measured from 181.3° angle of view with 0.7° angular step size and isotropic 9 µm camera pixel size. The image size of projections was 1008 × 672.
Image reconstruction
The tomographic datasets were reconstructed into a 500 × 500 × 600 volume of interest (VOI) with isotropic 25 µm voxel side length in several ways. First, an FDK reconstruction (Hamming filter, α = 0.54) of the full (260 projections) dataset was obtained. Then, the projection data was reduced to half, one-fourth and approximately one-sixth of the original amount of the projection images (130, 65 and 44 projections, respectively). All projection data were pre-processed in the NRecon software (Bruker micro-CT, Kontich, Belgium) to correct for beam hardening, post-alignment and ring artifacts for improved image quality. The reduced datasets were then reconstructed with three different iterative reconstruction methods; the least squares implementation of the conjugate gradient method (CGLS)35, the total variation regularization method (TV)36, and the discrete algebraic reconstruction method (DART)37. The CGLS algorithm was chosen for its computational efficiency and applicability in solving large-scale linear systems38. TV regularization was chosen because of its edge-preserving properties that can be useful in X-ray tomography36,39, and the Barzilai-Borwein minimization40 was used for large scale TV regularization. The regularization parameter was chosen with the L-curve method41, which was supported by visual evaluation of image quality. The DART algorithm was chosen because it incorporates a priori information about the grayscale values of the data in the reconstruction. As bone samples have highly distinguishable values for different materials, such knowledge can be powerful when working with severely limited amount of projection data37,42. The a priori grayscale and thresholds values for bone, soft tissue and background classification were chosen manually from the histograms of the corresponding CGLS reconstructions. In each DART iteration, a pre-set amount of iterations of a chosen algebraic reconstruction method (ARM) is run, after which the algorithm performs segmentation and fixation steps to restrict the boundaries of the next update37. We chose the ARM to be CGLS with 10 iterations, and 25 CGLS iterations were used to obtain the initial reconstruction. All reconstruction methods were run with 25 base iterations.
All reconstructions were calculated in the MATLAB 2016b programming environment (MathWorks, Natick, MA, USA) with the help of the ASTRA toolbox (iMinds-Vision Lab, University of Antwerp, Belgium)43,44,45, and the Spot toolbox46. ASTRA provides a programming and simulation environment for various CT geometries, as well as some popular image reconstruction functions and algorithms. Furthermore, the Spot toolbox and the opTomo operator of ASTRA wrap linear operators (such as forward- and back-projection in computed tomography) to MATLAB objects, resulting in fast and efficient computation with GPU memory47. Image reconstruction in the aforementioned frameworks was implemented as follows: (1) generation of projection and volume geometries, (2) computation of the system matrix as per the previously generated geometry objects, (3) running the chosen optimization algorithm on the given projection data, and (4) retrieval of reconstructed image data for further analysis.
Algorithm runtimes were measured in MATLAB as the time it takes for each reconstruction function to perform its computation, omitting the time needed for loading data and preprocessing. As a measure of absolute image quality, contrast-to-noise ratio (CNR) was calculated from the middle slice of the datasets by subtracting the mean value of a background region of interest (ROI) from a homogeneous bone ROI and dividing the result with the standard deviation of the background ROI.
Segmentation and image processing
The reconstructed µCT data were analyzed in the CT Analyzer (CTAn, v.1.16) software (Bruker micro-CT, Kontich, Belgium). From the data, 2 × 2 × 4 mm3 (80 × 80 × 160 voxels) VOIs were chosen from the weight-bearing regions of the femoral condyles, similarly to what has been done previously in the rabbit ACLT model22. Trabecular bone and subchondral bone plate regions were manually segmented to obtain masks for parameter analyses. Bone tissue was segmented from other tissues in the µCT data using an automated Otsu thresholding algorithm in 3D48. Prior to the thresholding, the images were processed with median (radius = 1) and unsharping (radius = 1, amount = 50%) filters, and after thresholding a despeckling filter (sweep in 3D) was applied to the images to include only the largest object in the volume. Furthermore, for subchondral bone plate thickness analyses, another despeckling filter was run to remove the pores within the plate, and the pores in the edges of the plate were removed with morphological closing.
Quantitative bone morphometry
After the pre-processing, the structural parameters (Table 1) were calculated from the processed images. All computations were performed with direct 3D methods in CT Analyzer, except for the ellipsoid factor (EF), which was calculated from the binarized image stacks with the BoneJ plugin (v.1.4.2)49 for the ImageJ software (v. 1.51n, National Institutes of Health, Bethesda, Maryland, USA)50. Furthermore, all of the calculated bone parameter values were statistically tested using Mann-Whitney testing for two independent datasets to see whether there were statistically significant differences between the ACLT and control groups. Mann-Whitney non-parametric testing was chosen because of the small sample sizes, and as it does not require assumption of normally distributed data. In addition, the relative errors (%) of the parameters calculated from IR data to the parameters calculated from the reference FDK reconstruction were calculated and averaged for each algorithm and sparsity level. All statistical analyses were performed using SPSS software (v.24, IBM Analytics, New York, USA).
Results
In the reference FDK reconstruction, BV/TV, Tb.Th, Tb.N and EF were lower in the ACLT group compared to the control group, and Pl.Th and Tb.S were higher in the ACLT group compared to the control group (Table 2). Three of these parameters (BV/TV, Tb.Th and EF) were significantly different.
Results obtained for CGLS, TV and DART are presented in Table 3. Out of the iterative algorithms, DART performed best when compared to the results of the full data FDK reconstruction for all reduced datasets. CGLS and TV performed well with half of the original projections, but further reduction resulted in great differences from the reference bone parameter values. DART was the only iterative algorithm that preserved the statistical significance in BV/TV, Tb.Th and EF across all reduced datasets. Example reconstructions of all algorithms are presented in Fig. 1, and the segmented binary images of those reconstructions (used for parameter analyses) are presented in Fig. 2.
Example images of reconstructed data, shown as one 80 × 160 pixel image from the 80 × 80 × 160 voxel volume of interest. FDK = Feldkamp, David and Kress algorithm, CGLS = conjugate gradient least squares algorithm, TV = total variation regularization and DART = discrete algebraic reconstruction technique. The number of projection images used in reconstruction is denoted by n.
The binarized slice images corresponding to the data in Fig. 1. FDK = Feldkamp, David and Kress algorithm, CGLS = conjugate gradient least squares algorithm, TV = total variation regularization and DART = discrete algebraic reconstruction technique. The number of projection images used in reconstruction is denoted by n.
Mean relative errors per algorithm and parameter are presented in Fig. 3. Out of the three algorithms, DART performed best with little errors (2–8%) across all reduced data. Although CGLS and TV gave slightly better results for some parameters with half of the projection data, DART was far superior with reductions to one-quarter or one-sixth of the original data.
The mean relative error of the used iterative algorithms with regards to reference data in quantitative bone morphometry analysis. The number below each bar trio corresponds to the number of used projection images. The bar height indicates the mean and the error bars indicate the standard deviation of the data. The analyzed morphometric parameters were BV/TV = bone volume fraction, Pl.Th = plate thickness, EF = ellipsoid factor, Tb.S = trabecular separation, Tb.Th = trabecular thickness and Tb.N = trabecular number. FDK = Feldkamp, David and Kress algorithm, CGLS = conjugate gradient least squares algorithm, TV = total variation regularization and DART = discrete algebraic reconstruction technique.
Mean CNR values and their standard deviations are presented in Fig. 4. Across all reduced datasets, TV had the highest value of CNR. For CGLS, CNR was slightly better than the reference (FDK) value, and for DART, it was slightly worse.
Contrast-to-noise ratio (CNR) as a function of used projection images. For iterative algorithms, the bar height indicates the mean and the error bars indicate the standard deviation in the data. For FDK, the continuous line refers to the mean (reference level) and the dashed lines indicate the standard deviation in the data. FDK = Feldkamp, David and Kress algorithm, CGLS = conjugate gradient least squares algorithm, TV = total variation regularization and DART = discrete algebraic reconstruction technique.
Finally, the algorithm runtimes are presented in Table 4. DART and TV had longer runtimes than CGLS. Furthermore, reduction of projection data did not reduce the reconstruction times of TV as efficiently as it did for DART and CGLS.
Discussion
ACLT in rabbits resulted in statistically significant alterations of the subchondral bone structure, indicative of OA, after 8 weeks of surgery. Reduction of bone volume, thinning of trabeculae, and a shifting of trabecular alignment to more oblate configuration were statistically significant. Furthermore, thickening of the subchondral bone plate, increase of trabecular separation, and a reduction in trabecular number were observed, although these changes were not statistically significant. In Florea et al.22 similar changes in bone volume, trabecular thickness, and trabecular separation were seen in rabbits after 4 weeks of ACLT surgery. However, unlike in our study, the subchondral bone plate was thinned significantly in the medial side and SMI was analyzed instead of EF. Apart from that, our findings on changes to the trabecular bone agree with previous observations in the rabbit model of OA22,51.
Out of the three algorithms tested in this study, DART performed best when compared to the reference data, as it gave good results even with severely reduced projection dataset. DART incorporates a priori information about the grayscale distribution of the data by strong enforcement of a pre-specified finite set of attenuation values that are the only possible ones in the target of imaging. Actually, very few optimization algorithms for tomographic reconstruction implement this, although other optimization algorithms exist as well in the field of discrete tomography. In our case, the grayscale values in bone datasets can be pre-classified into three values: background, soft tissue (or water), and bone, by just looking at the dataset’s histogram. Therefore, it is possible to estimate the a priori values for the aforementioned materials from a test reconstruction, although an automated procedure for estimation exists as well52. The easiest of the methods to implement, CGLS, does not use any a priori information but only minimizes the L2-norm of the residual with a gradient-based optimization algorithm. Therefore, one would not expect it to give good results with highly reduced datasets, even though it showed good performance with only half of the projection data, and is expected to perform really well with a complete projection dataset. The third algorithm, TV regularization, assumes that the total variation of the grayscale values in the final reconstruction is small, and the contribution of this assumption is controlled via the magnitude of the regularization parameter. Even though TV regularization is known to be robust in noise removal while preserving edge information in sparse data reconstructions, it causes the resulting image to appear blurred because of the way it performs its computation. This blurring affects the performance of the segmentation algorithm, especially for greatly reduced data with lots of noise to regularize. This is likely the reason why parameters obtained with TV regularization were not as close to the reference data as those obtained with DART. As such, the a priori knowledge used by TV regularization may not be ideal for µCT imaging of bone, where a lot of small details need to be preserved. Due to the ill-posed nature of tomographic reconstruction, some a priori knowledge is needed in very sparse cases, as can be seen from the poor performance of CGLS for extreme cases. The discrete a priori knowledge incorporated by DART seems to be strongly preferable in this application, in which the data itself is nearly discretely distributed to several classes.
DART was the only algorithm capable of preserving the statistically significant differences in BV/TV, Tb.Th and EF across all data reduction levels, and it did not give rise to extra parameters becoming significantly different. However, the Tb.Th values with one-fourth and one-sixth of the original data became significant also with the two-tailed test, while they were only significant with the one-tailed test in the original data. With CGLS and TV, significant differences were only preserved for BV/TV and EF when the original dataset was reduced to half. Reduction to one-quarter of the data preserved the statistically significant differences in BV/TV and EF with CGLS, and only in EF with TV. Additionally, TV generated unwanted statistically significant results for Tb.N. For a reduction to one-sixth of the original projection data, CGLS and TV both preserved the significant difference in EF, but generated incorrect significant differences in Tb.N. These results support the notion that DART was the most reliable of the three IR algorithms analyzed in this study.
The IR algorithms take more computing time than the FDK algorithm. For CGLS, the computational times were almost two times the computing times of FDK when handling half of the projection data, but remained in an acceptable range because they were still in the order of tens of seconds with our workstation. However, when using TV and DART, the computations took considerably longer. Time inefficiency may be tolerated, though, since TV and DART require much less input data for successful reconstruction of bone geometry, resulting in reductions of imaging time and radiation dose. Furthermore, less data storage is required, which may be of value for some situations. For these reasons, IR methods facilitate the imaging of large sample series, as more scientifically relevant data can be acquired per unit of time and computer memory.
Regarding CNR, TV expressed the highest values across all reduced datasets. The texture in TV reconstructed images is typically smooth and contains little noise, so it is expected to have better values in basic metrics of image quality compared to CGLS and DART. CGLS and DART performed similarly to FDK, with DART having slightly lower CNR values. The lower CNR values are likely caused by the appearance of small speckles in the background sometimes seen in DART reconstructions. This artifact did not occur in the segmentation results. It should be noted that achieving high absolute image quality was not the primary aim of this research, therefore traditional image quality metrics may not be the best way in drawing conclusions from our data. Instead, we wanted to obtain reconstructions of sufficient quality so that reliable segmentations of bone and other tissues are possible, and quantitative bone analyses can be performed reliably from reduced datasets.
While the results suggest that collection of less projection data in µCT is feasible when the reconstruction is done iteratively, the study had the following limitations. While we chose data reconstructed with FDK as the reference method in our study, it should be noted that it does not output exact ‘ground truth’ data due to approximation errors caused by the cone-beam imaging geometry. It is, however, the most commonly used reconstruction algorithm in µCT studies as commercial scanners routinely output FDK data. Since we studied limited-data solutions to µCT imaging, using FDK as the reference is a rational and practical choice. Furthermore, the reconstruction framework we used assumed a point source in computing the system matrix for reconstruction. The scanner we used, however, has a nonzero focal spot size, thus the assumption may have produced minor error in the computations. Finally, although we used an analytical method and three distinct iterative algorithms in this study, there remain many different algorithms that could have been used. In the future, additional methods could be tested that are not discussed here, including but not limited to entropy methods53, multiplicative algebraic methods54, statistical inversion55, and deep-learning based approaches56.
In conclusion, we demonstrated that iterative and regularizing image reconstruction algorithms applied to reduced projection data are sufficiently reliable when used for morphological bone analysis involving segmentation. Furthermore, we were able to quantify changes in bone structure in early OA using sparse projection data. Thus, there is the potential for iterative reconstruction algorithms to replace the algorithms presently considered the gold-standard in micro-structural analyses of bone. In particular, discrete methods, such as DART, seem promising in quantitative parameter analyses requiring segmented data. By reconstructing data with iterative methods, the amount of projection data needed can be drastically lowered, thereby reducing imaging times and radiation doses associated with µCT imaging. This would allow for a larger number for imaged samples in in vitro studies, and prevent harmful radiation effects in in vivo studies.
References
Boutroy, S., Bouxsein, M. L., Munoz, F. & Delmas, P. D. In vivo assessment of trabecular bone microarchitecture by high-resolution peripheral quantitative computed tomography. J. Clin. Endocrinol. Metab. 90, 6508–15 (2005).
Holdsworth, D. W. & Thornton, M. M. Micro-CT in small animal and specimen imaging. Trends Biotechnol. 20, 34–39 (2002).
Schambach, S. J., Bag, S., Schilling, L., Groden, C. & Brockmann, M. A. Application of micro-CT in small animal imaging. Methods 50, 2–13 (2010).
Boas, F. E. & Fleischmann, D. CT artifacts: causes and reduction techniques. Imaging Med. 4, 229–240 (2012).
Schulze, R. et al. Artefacts in CBCT: A review. Dentomaxillofacial Radiol. 40, 265–273 (2011).
Willekens, I. et al. Evaluation of the radiation dose in micro-CT with optimization of the scan protocol. Contrast Media Mol. Imaging 5, 201–207 (2010).
Dall’Ara, E. et al. Precision of digital volume correlation approaches for strain analysis in bone imaged with micro-computed tomography at different dimensional levels. Front. Mater. 4, 31 (2017).
Li, H., Zhang, H., Tang, Z. & Hu, G. Micro-computed tomography for small animal imaging: Technological details. Prog. Nat. Sci. 18, 513–521 (2008).
Feldkamp, L. A., Davis, L. C. & Kress, J. W. Practical cone-beam algorithm. J. Opt. Soc. Am. A 1, 612–619 (1984).
Beister, M., Kolditz, D. & Kalender, W. A. Iterative reconstruction methods in X-ray CT. Phys. Medica 28, 94–108 (2012).
Willemink, M. J. et al. Iterative reconstruction techniques for computed tomography Part 1: Technical principles. Eur. Radiol. 23, 1623–1631 (2013).
Geyer, L. L. et al. State of the Art: Iterative CT Reconstruction Techniques. Radiology 276, 339–357 (2015).
Willemink, M. J. et al. Iterative reconstruction techniques for computed tomography part 2: Initial results in dose reduction and image quality. Eur. Radiol. 23, 1632–1642 (2013).
Andersen, A. H. & Kak, A. C. Simultaneous algebraic reconstruction technique (SART): a superior implementation of the ART algorithm. Ultrason. Imaging 6, 81–94 (1984).
Trampert, J. & Leveque, J.-J. Simultaneous iterative reconstruction technique: physical interpretation based on the generalized least squares solution. J. Geophys. Res. Solid Earth 95, 12553–12559 (1990).
Demoment, G. Image reconstruction and restoration: overview of common estimation structures and problems. IEEE Trans. Acoust. 37, 2024–2036 (1989).
Mueller, J. L. & Siltanen, S. Linear and nonlinear inverse problems with practical applications. (SIAM, 2012).
Pan, X., Sidky, E. Y. & Vannier, M. Why do commercial CT scanners still employ traditional, filtered back-projection for image reconstruction? Inverse Probl. 25, 123009 (2009).
Buckwalter, J. A. & Mankin, H. J. Articular cartilage: degeneration and osteoarthritis, repair, regeneration, and transplantation. Instructional course lectures 47, 487–504 (1998).
Sniekers, Y. H. et al. A role for subchondral bone changes in the process of osteoarthritis; a micro-CT study of two canine models. BMC Musculoskelet. Disord. 9, 20 (2008).
Botter, S. M. et al. Quantification of subchondral bone changes in a murine osteoarthritis model using micro-CT. Biorheology 43, 379–388 (2006).
Florea, C. et al. Alterations in subchondral bone plate, trabecular bone and articular cartilage properties of rabbit femoral condyles at 4 weeks after anterior cruciate ligament transection. Osteoarthr. Cartil. 23, 414–422 (2015).
Batiste, D. L. et al. High-resolution MRI and micro-CT in an ex vivo rabbit anterior cruciate ligament transection model of osteoarthritis. Osteoarthr. Cartil. 12, 614–626 (2004).
Layton, M. W. et al. Examination of subchondral bone architecture in experimental osteoarthritis by microscopic computed axial tomography. Arthritis Rheum. 31, 1400–1405 (1988).
Pritzker, K. P. H. et al. Osteoarthritis cartilage histopathology: Grading and staging. Osteoarthr. Cartil. 14, 13–29 (2006).
Finnilä, M. A. J. et al. Association between subchondral bone structure and osteoarthritis histopathological grade. J. Orthop. Res. 35, 785–792 (2017).
Day, J. S. et al. A decreased subchondral trabecular bone tissue elastic modulus is associated with pre-arthritic cartilage damage. J. Orthop. Res. 19, 914–918 (2001).
Kamibayashi, L., Wyss, U. P., Cooke, T. D. V. & Zee, B. Trabecular microstructure in the medial condyle of the proximal tibia of patients with knee osteoarthritis. Bone 17, 27–35 (1995).
Chappard, C. et al. Subchondral bone micro-architectural alterations in osteoarthritis: A synchrotron micro-computed tomography study. Osteoarthr. Cartil. 14, 215–223 (2006).
Müller, R., Hahn, M., Vogel, M., Delling, G. & Rüegsegger, P. Morphometric analysis of noninvasively assessed bone biopsies: comparison of high-resolution computed tomography and histologic sections. Bone 18, 215–220 (1996).
Müller, R. et al. Morphometric analysis of human bone biopsies: a quantitative structural comparison of histological sections and micro-computed tomography. Bone 23, 59–66 (1998).
Bouxsein, M. et al. Guidelines for assessment of bone microstructure in rodents using micro-computed tomography. J. Bone Miner. Res. 25, 1468–1486 (2010).
Salmon, P. L., Ohlsson, C., Shefelbine, S. J. & Doube, M. Structure model index does not measure rods and plates in trabecular bone. Front. Endocrinol. (Lausanne). 6, 1–10 (2015).
Doube, M. The ellipsoid factor for quantification of rods, plates, and intermediate forms in 3D geometries. Front. Endocrinol. (Lausanne). 6, 1–5 (2015).
Hestenes, M. M. R. & Stiefel, E. Methods of conjugate gradients for solving linear systems. J. Res. Natl. Bur. Stand. (1934). 49, 409-436 (1952).
Hämäläinen, K. et al. Total variation regularization for large-scale X-ray tomography. Int. J. Tomogr. Simul. 25, 1–25 (2014).
Batenburg, K. J. & Sijbers, J. DART: A practical reconstruction algorithm for discrete tomography. IEEE Trans. Image Process. 20, 2542–2553 (2011).
Björck, Å., Elfving, T. & Strakos, Z. Stability of conjugate gradient and Lanczos methods for linear least squares problems. 19, 720–736 (1998).
Tian, Z., Jia, X., Yuan, K., Pan, T. & Jiang, S. B. Low-dose CT reconstruction via edge-preserving total variation regularization. Phys. Med. Biol. 56, 5949–5967 (2011).
Barzilai, J. & Borwein, J. M. Two-point step size gradient methods. IMA J. Numer. Anal. 8, 141–148 (1988).
Hansen, P. C. Analysis of discrete ill-posed problems by means of the L-curve. SIAM Rev. 34, 561–580 (1992).
van de Casteele, E., Perilli, E., van Aarle, W., Reynolds, K. J. & Sijbers, J. Discrete tomography in an in vivo small animal bone study. J. Bone Miner. Metab. 36, 40–53 (2017).
Palenstijn, W. J., Batenburg, K. J. & Sijbers, J. The ASTRA tomography toolbox. In 13th International Conference on Computational and Mathematical Methods in Science and Engineering, CMMSE 2013 4, 1139–1145 (2013).
van Aarle, W. et al. Fast and flexible X-ray tomography using the ASTRA toolbox. Opt. Express 24, 25129 (2016).
van Aarle, W. et al. The ASTRA Toolbox: A platform for advanced algorithm development in electron tomography. Ultramicroscopy 157, 35–47 (2015).
van den Berg, E. & Friedlander, M. P. Spot-a linear-operator toolbox. http://www.cs.ubc.ca/labs/scl/spot (2018).
Bleichrodt, F. et al. Easy implementation of advanced tomography algorithms using the ASTRA toolbox with Spot operators. Numer. Algorithms 71, 673–697 (2016).
Otsu, N. N. A threshold selection method from Gray-level. IEEE Trans. Syst. Man. Cybern. 9, 62–66 (1979).
Doube, M. et al. BoneJ: Free and extensible bone image analysis in ImageJ. Bone 47, 1076–1079 (2010).
Abràmoff, M. D., Magalhães, P. J. & Ram, S. J. Image processing with imageJ. Biophotonics Int. 11, 36–41 (2004).
Wang, S. X., Laverty, S., Dumitriu, M., Plaas, A. & Grynpas, M. D. The effects of glucosamine hydrochloride on subchondral bone changes in an animal model of osteoarthritis. Arthritis Rheum. 56, 1537–1548 (2007).
van Aarle, W., Batenburg, K. & Sijbers, J. Automatic parameter estimation for the Discrete Algebraic Reconstruction Technique (DART). IEEE Trans. Image Process. 21, 4608–4621 (2012).
Skilling, J. & Bryan, R. K. Maximum entropy image reconstruction - general algorithm. Mon. Not. R. Astron. Soc. 211, 111–124 (1984).
Mishra, D., Muralidhar, K. & Munshi, P. A robust mart algorithm for tomographic applications. Numer. Heat Transf. Part B Fundam. 35, 485–506 (1999).
Siltanen, S. et al. Statistical inversion for medical x-ray tomography with few radiographs: I. General theory. Phys. Med. Biol. 48, 1437–1463 (2003).
Wang, G. A Perspective on Deep Imaging. IEEE Access 4, 8914–8924 (2016).
Acknowledgements
J.H.K. acknowledges the support from Business Finland grant (project 1392/31/2016). R.K.K. acknowledges the support from the Academy of Finland (grant no. 286526) and the Sigrid Juselius Foundation. W.H. acknowledges the support from the Canadian Institutes of Health Research (Foundation Scheme Grant, FDN-143341), the Canada Research Chairs Program (950-230603), and the Killam Foundation. S.Sa. acknowledges the support from the Academy of Finland (grant nos. 268378 and 303786), the European Research Council under the European Union’s Seventh Framework Programme (FP/2007-2013, ERC grant agreement no. 336267), and the Sigrid Juselius Foundation.
Author information
Authors and Affiliations
Contributions
J.H.K. performed the data reconstruction and wrote the manuscript; J.H.K., S.S.K. and M.A.J.F. performed the data analysis; J.H.K. and M.A.J.F. performed the µCT measurements; M.A.J.F., R.K.K. and W.H. collected the samples; S. Si. and M.T.N. contributed to the study design; S. Sa. contributed at each stage and supervised the project. All authors reviewed the manuscript.
Corresponding author
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ketola, J.H., Karhula, S.S., Finnilä, M.A.J. et al. Iterative and discrete reconstruction in the evaluation of the rabbit model of osteoarthritis. Sci Rep 8, 12051 (2018). https://doi.org/10.1038/s41598-018-30334-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-018-30334-8
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.