Abstract
The dynamics of social networks is a complex process, as there are many factors which contribute to the formation and evolution of social links. While certain real-world properties are captured by the degree-driven preferential attachment model, it still cannot fully explain social network dynamics. Indeed, important properties such as dynamic community formation, link weight evolution, or degree saturation cannot be completely and simultaneously described by state of the art models. In this paper, we explore the distribution of social network parameters and centralities and argue that node degree is not the main attractor of new social links. Consequently, as node betweenness proves to be paramount to attracting new links – as well as strengthening existing links –, we propose the new Weighted Betweenness Preferential Attachment (WBPA) model, which renders quantitatively robust results on realistic network metrics. Moreover, we support our WBPA model with a socio-psychological interpretation, that offers a deeper understanding of the mechanics behind social network dynamics.
Similar content being viewed by others
Introduction
Despite the widespread use of the Gaussian distribution in science and technology, many social, biological, and technological networks are better described by a power-law (Zipf) distribution of nodes degree (the node degree is the number of links incident to a node). The Barabasi-Albert (BA) model, based on the degree-driven preferential attachment, generates such scale free networks with a power-law distribution of node degree P(k) = k−λ. In fact, degree preferential attachment (DPA) is widely considered to be one of the main factors behind complex network evolution (the scale-free topologies generated with the BA model are able to capture other real-world social network properties such as a low average path length L)1,2. However, recent research challenges the idea that the scale free property is prevalent in complex networks3. Additionally, the degree-driven preferential attachment model has well-known limitations to accurately describe social networks (i.e., complex networks where nodes represent individuals or social agents, and links represent social ties or social relationships), owing to the following considerations:
-
People are physically and psychologically limited to a maximum number of real-world friendships; this imposes a saturation limit on node degree4,5. Conversely, in the BA model no such limit exists.
-
People have weighted relationships, i.e., not all ties are equally important: an average person knows roughly 350 persons, can actively befriend no more than 150 people (Dunbar’s number)4, and has only a few very strong social ties (links)6. The BA model does not account for such link weights7.
-
The structure and dynamics of communities in social networks are not accurately described with DPA7,8,9,10,11.
To address these issues, recent research has combined the DPA model with properties derived directly from empirical data. For instance, there exist proposals which add the small-world property to scale-free models (e.g., Holme-Kim model12, evolving scale-free networks13) or the power-law distribution to small-worlds (e.g., the Watts-Strogatz model with degree distribution14, multistage random growing small-worlds15, evolving small-worlds16, random connectivity small-worlds17). Other research proposals extend Milgram’s experiment18, e.g., static-geographic19 and cellular20 models. However, all these models are still not accurate enough when compared against real-world social networks.
To better understand the real-world accuracy problem, we perform a topological analysis on a variety of real-world network datasets and show that node betweenness (which expresses the node quality of being “in between” communities) is power-law distributed and–at the same time–correlated with link weight distributions. Our empirical findings align well with previous research in some particular cases11,21. Such empirical pieces of evidence suggest that, for social networks, the node degree is not the main driver of preferential attachment; therefore other centralities may be better attractors of social ties. We conclude that node betweenness–as opposed to node degree or any other centrality metric–is the key attractor for new social ties.
Consequently, as the main theoretical contribution, we introduce the new Weighted Betweenness Preferential Attachment (WBPA) model, which is a simple yet fundamental mechanism to replicate real-world social networks topologies more accurately than other state-of-the-art models. More precisely, we show that the WBPA model is the first social network model that is able to replicate community structure while it simultaneously: (i) explains how link weights evolve, and (ii) reproduces the natural saturation of degree in hub nodes.
Finally, we further interpret WBPA from a socio-psychological perspective, which may explain why node betweenness is such an important factor behind social network formation and evolution.
Results
Centrality statistics
We investigate the distributions of node betweenness on a variety of social network datasets: Facebook users (590 nodes), Google Plus users (638 nodes), weighted co-authorships in network science (1589 nodes), weighted online social network (1899 nodes), weighted Bitcoin web of trust (5881 nodes), unweighted Wikipedia votes (7115 nodes), weighted scientific collaboration network (7343 nodes), unweighted Condensed Matter collaborations (23 K nodes), weighted MathOverflow user interactions (25 K nodes), unweighted HEP citations (28 K nodes), POK social network (29 K nodes), unweighted email interaction (37 K nodes), IMDB actors (48 K nodes), Brightkite OSN users (58 K nodes), Facebook - New Orleans (64 K nodes), respectively Epinions (76 K nodes), Slashdot (82 K nodes) and Timik (364 K nodes) on-line platforms. To improve the robustness of our analysis, we ensure data diversity by considering network datasets with different sizes, weighted and unweighted, and representing various types of social relationships (see Methods).
Our first observation is that, in all datasets, node degree, node betweenness, link betweenness, and link weights (for datasets with weighted links) are power-law distributed. Moreover, the power-law slope of degree distribution is steeper in comparison with node betweenness distribution. More precisely, as presented in Fig. 1a, the average degree slope is γdeg = 2.097 (standard deviation σ = 0.774) and the average betweenness slope is γbtw = 1.609 (σ = 0.431), meaning that γdeg is typically 30.3% steeper than γbtw across all datasets (details in SI.1. Social network datasets statistics). Also, for all considered datasets there is a significant non-linear (polynomial or exponential) correlation between node betweenness and node degree (see Fig. 1b); this further suggests that node betweenness may be the source of imbalance in node degree distribution. The statistics for the entire dataset collection are presented in SI.1.
(a) Overview of centrality distribution slopes for all empirical datasets; the average slopes are highlighted for node degree (blue) and node betweenness (red). (b) Non-linear correlation of node betweenness and node degree in a representative weighted on-line social network (OSN)22 with 1899 nodes. These results show that, in social networks, degree and betweenness have a power-law distribution (with a steeper slope for degree), and that there is a non-linear correlation between the two centralities.
The second observation is that–unlike node degree–node betweenness is significantly more correlated with the weights of the incident links. After assessing the correlation between both node betweenness and node degree with the weighted sum of all adjacent links, we argue that betweenness acts as an attractor for stronger ties. For example, for the co-authorships weighted network with 1589 nodes23, the top 5% links accumulate 27.4% of the total weight in the graph; these top 5% links are incident to nodes which amass 80.2% of the total node betweenness, but only 14.9% of the total node degree (see Fig. 2–further numerical details in SI.1, Table 2). In all analyzed weighted datasets, node betweenness correlates with incident link weights by ratios that are 2.5–9 times higher than node degree–link weights associations (additional details in SI.1, Fig. 2).
The accumulated fitness (expressed as Degree D and Betweenness B centralities) of nodes incident to links with weights within the top 1% to 100% percentiles (a) in the Geom network (7343 nodes, 11898 links), and (b) in the Co-authorships network (1589 nodes, 2742 links). The Betweenness/Degree ratios (B/D) range between 2.5–9, highlighting that top link weights are predominantly incident to high betweenness nodes, rather than high degree nodes.
The first observation indicates a significant correlation between node degree and node betweenness but it does not necessarily imply causation. However, the second observation is that betweenness attracts stronger links which, in turn, triggers more imbalance in degree distribution; this suggests that node betweenness is behind networks evolution, while the power-law degree distribution is only a by-product. The importance of node betweenness is further supported by the analysis of centrality dynamics. To this end, we provide the example of an on-line social network, UPT.social, which was intended to facilitate social interaction between students and members of faculty at University Politehnica of Timişoara, Romania24. Right after its launch in 2016, UPT.social attracted hundreds of users, and the entire dynamical process of new links formation was recorded as snapshots of the first 6 weeks (T0 − T5). As exemplified in Fig. 3 (and further detailed in SI.3, Fig. 6), the nodes with high betweenness become the principal attractors of new social ties; we also note that the top 3 nodes attracting new edges at time snapshot T2 are the ones which maximize their betweenness beforehand, and then trigger a subsequent degree increase. As shown, once node degree begins to saturate (T3 − T5), node betweenness drops, as nodes fulfill their initial bridging potential.
Betweenness preferential attachment (BPA)
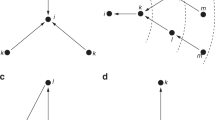
In what follows, we propose the betweenness preferential attachment model (BPA) and conjecture that–for social networks–it is more realistic than the degree preferential attachment (DPA) model. The fundamental difference between the degree-driven and betweenness-driven preferential attachment is illustrated in Fig. 4; the upper panel shows that, under the DPA rule, the nodes with high degree (colored in orange) gain an even higher degree. In contrast, the lower panel in Fig. 4 shows that, under the BPA rule, the nodes with high betweenness (orange) attract more links and increase their degrees; in turn this decreases their betweenness via a redistribution process, thus limiting the number of new links for high-degree nodes as a second order effect. This may explain why, in real-world networks, the number of new links is limited for high degree nodes (i.e., degree saturation).
The mechanisms of degree preferential attachment (DPA) versus betweenness preferential attachment (BPA) depicted in terms of acquiring new links and limiting the (excessive) accumulation of degree over time. In DPA, nodes with high degree attract even more links, and thus node degree increases ad infinitum. Conversely, in BPA, nodes attracting new links because of their high betweenness will eventually lose their betweenness in favor of their neighboring nodes, thus limiting the acquired degree.
WBPA model
Besides validating the BPA mechanism, we also realize that all the empirical network data gathered in a real-world context is weighted, even if the information about link weights is not always available. For example, there is no link weight information in our Facebook and Google Plus datasets, yet these networks are clearly part of a weighted social context in which each link has a distinct social strength. Realistic networks evolve according to a mechanism which considers link weights, therefore we develop the weighted BPA (WBPA) algorithm to characterize the social network evolution.
The WBPA algorithm for link weight assignment according to the fitness-weight correlation is given in Fig. 5 and discussed below. In the case of WBPA, the fitness f is node betweenness. Note that even though link weights wij are not used directly during the growth phase, they have a significant second order impact: Betweenness depends on the shortest paths in the graph, which in turn are highly dependent on link weights. Link weights are updated in step 3 of the WBPA algorithm, and whenever a weight becomes ≤0, the corresponding link is removed.
Network evolution according to the Weighted BPA algorithm. (a) All bidirectional links E in graph G are initialized with weights wij and wji, respectively. Each outgoing link weight of node v1 is proportional to the fitness function (indicated as \(w\sim f\)) of the target neighbor nodes, and then normalized such that the sum of outgoing weights is 1. (b) New node v6 connects to existing ones v1–v5 based on probabilities that are proportional to the normalized fitness (\(p\sim f\)) of the target nodes. Say, v6 connects only to v1 based on fitness f1. (c) Once v6 and v1 connect, node v1 assigns a weight w1−6 on the new link that is proportional to fitness f6. As such, a proportional weight ratio of w1−6/4 is subtracted (indicated with a minus sign) from the four already existing links. If any of the newly resulting weights drop below 0, the corresponding link is removed from node v1. According to the BPA principle, the fitness f is represented by the node betweenness centrality.
Weighted BPA Algorithm (WBPA)
-
1)
Distribute weights: Begin with an arbitrarily connected graph G with nodes V and bidirectional links E (i.e., for ∀eij ∃ eji). A weight wij is added for each link eij in the graph, so that wij is proportional to fitness fj of the target node vj. For each node vi, all incident link weights wij are normalized so that the outgoing weighted degree is 1.
-
2)
Growth (BPA): At every step, a new node vk is introduced; the new node tries to connect to n (1 ≤ n ≤ V) existing nodes in G. The probability pi that vk becomes connected to an existing node vi is proportional to fitness fi. Therefore, we have \({p}_{i}={f}_{i}/{\sum }_{j\in V}\,{f}_{j}\) where the sum is made over all nodes in the graph.
-
3)
Dynamic weight redistribution: Once a new node vk becomes connected to an existing node vi, weights wki and wik are initialized with the normalized fitnesses fi and fk respectively. As the weighted outgoing degree of node vi increases by wik, every other weight wij is rescaled with −wik/n, where n is the previous number of neighbors of node vi.
Assessing the realism of WBPA
WBPA defines complex interactions between link weights and node centralities, hence we expect emerging phenomena such as n-order effects. Therefore, a mathematical analysis of WBPA would be cumbersome and beyond the scope of our paper. Instead, as validation strategy, we test WBPA against several preferential attachment (PA) models to explore which one produces the most realistic social network topology. To this end, we quantify preferential attachment according to a fitness function f which expresses the capability of individual nodes to attract new connections (e.g., if f is chosen to be node degree Deg, then we reproduce the classic BA model2). We consider f as one of the following network centralities: degree Deg (DPA model), betweenness Btw (WBPA model), eigenvector centrality EC (ECPA model), closeness Cls (ClsPA model), and clustering coefficient CC (CCPA model). Each node centrality is defined in the Methods section. The comparison between synthetic and real-world networks is done through topological similarity assessment supported by the statistical fidelity metric25, alongside standard deviation and p-values. Fidelity takes values φ ∈ [0, 1] with 1 representing a network that is identical with the reference network (see the Methods section for more details).
We also make use of the following graph metrics to characterize and compare networks: average degree (AD), average path length (APL), average clustering coefficient (ACC), modularity (Mod), graph diameter (Dmt), and graph density (Dns). We start by measuring the distributions of these six metrics on the 18 selected real-word datasets. To assess which centrality is the most appropriate as fitness function, we start by generating networks according to each PA model, of increasing sizes: N = {1K, 2K, 5K, 10K, 50K, 100K} nodes; the full statistical results are presented in SI.2. Best fitness for preferential attachment. Aggregating the statistical results from SI.2–Fig. 4 (real-world data) and Fig. 5 (PA networks), we provide an intuitive visual comparison in Fig. 6 between the averaged evolution of the six graph metrics on the real-world data (N = 590 to N = 364 K nodes), and on the degree-driven and betweenness-driven PA networks.
To better illustrate the comparisons between the synthetic PA networks and the real-world datasets, we present the trend lines for each graph metric in Fig. 6; for the real-world data networks the trend line is green-dotted, for Btw fitness networks is blue, and for Deg fitness networks is red. On close inspection, we uncover the following:
-
AD in real data evolves differently than in PA networks.
-
APL evolution in real data resembles Btw networks much better than Deg networks. We measure a statistical fidelity of φBtw = 0.925 and φDeg = 0.853.
-
ACC evolution in real data resembles Btw more than Deg, with statistical fidelities of φBtw = 0.665 and φDeg = 0.515.
-
Mod evolution in real data resembles both networks very well, with statistical fidelities of φBtw = 0.814 and φDeg = 0.812 (a slight advantage for the Btw networks).
-
Dmt evolution in real data resembles Deg more than Btw. Even though we see the same type of increase, Deg produces longer diameters as seen in the majority of real-word data. The measured statistical fidelities are φBtw = 0.796 and φDeg = 0.836.
-
Dns evolution in real data resembles both networks, with statistical fidelities of φBtw = 0.634 and φDeg = 0.634.
Distribution of the six fundamental graph metrics (a–f) for increasing networks sizes (N = 1 K to N = 100 K nodes) for the real world datasets (green), and the synthetic Preferential Attachment (PA) networks driven by Btw (blue) and Deg (red). The min-max intervals for each set of measurements are marked with error bars.
For simplicity, Fig. 6 includes only Deg and Btw PA networks in the comparison with real-world data; the full numerical data–with all PA network models–are detailed in Table 1. All these results demonstrate the superior realism provided by the WBPA in comparison to the classic DPA principle, as well as in comparison to PA driven by other node centralities such as eigenvector, closeness or clustering coefficient.
We strengthen our analysis by presenting several direct comparisons between real networks and synthetic PA networks, generated with the same node sizes as the real-world reference networks. The comparisons are made using the fidelity metric φ, as well as by comparing individual graph metrics (one by one), to show that WBPA is superior to the other PA networks. To this end, we select the Facebook (FB), Google Plus (GP), Online social network (OSN), and IMDB real-world datasets, and provide the full statistical results in Table 2; here, each sub-table contains the reference real-world network and its graph metrics on the first row, while the remaining lines contain the averaged graph metrics for 10 synthetic networks generated according to preferential attachment driven by each centrality (Deg, Btw, EC, Cls, CC). Additionally, we provide measurements for a Null model (Random network) to serve as baseline. The standard deviation for each synthetic dataset metric is symbolized with a ± sign.
The mechanism of preferential attachment which we adopt in our paper is a fundamental, yet generic and simple framework. State of the art studies which are specifically aimed at creating realistic topologies propose algorithms with a far increased complexity. Therefore, intuitively, it is expected that state of the art models like Cellular (Cell)20, Home-Kim (HK)12, Toivonen (TV)26, or Watts-Strogatz with degree distribution (WSDD)14 etc., will generate more realistic topologies in terms of the six discussed graph metrics. To test this hypothesis, we further generate such synthetic networks of size N = 10,000 and compare them with WBPA, DPA networks and several real-world datasets. The results are provided in Table 3, showing that not only is WBPA superior to DPA and PA models driven by other centralities but, in most cases (i.e., 10 out of 13), it outperforms the other synthetic models in terms of topological fidelity as well. For readability purposes we did not add information about the standard deviations of each synthetic model here; this information may be found in SI.4, Tables 4 and 5.
To offer the diversity required by a robust test of our model, we also include unweighted networks in our collection. A fair comparison between WBPA networks (which are all weighted) and the large and unweighted example networks, requires that all weights on our WBPA algorithm output be discarded. In this comparison, we start by generating WBPA networks of 10,000 nodes, then make all weights \({w}_{ji} > 0\) become 1, thus obtaining unweighted BPA networks.
The upper half of Table 3 contains the average fidelities of WBPA, DPA and the two null model networks, towards the real-world reference networks. The lower half of Table 3 contains the other state of the art synthetic networks. Our WBPA obtains the highest fidelity towards most empirical references, e.g., 13–68% higher φFB, 21–81% higher φOSN, 4–47% higher φTK than all other synthetic models. As such, we prove the increased realism of our model in comparison with some elaborated state-of-the-art models (briefly described in SI.4, and quantified in SI.4, Table 4). Compared to DPA, our model produces networks with higher fidelity values; when averaged over all empirical networks we obtain: \({\overline{\varphi }}_{Btw}=0.831\) and \({\overline{\varphi }}_{Deg}=0.777\).
We note that the WBPA model produces a specific distribution of the Betweenness/Degree (B/D) ratio. To this end, we measure B/D distributions on all datasets (weighted and unweighted), as well as on our synthetic WBPA-generated networks, using the Gini coefficient (a Gini coefficient takes values between 0 and 1, with values closer to 0 representing a more uniform dispersion of data) to evaluate data dispersion27. The Gini values obtained on the empirical data are given in Table 4: all empirical datasets, whether weighted or unweighted, have their Gini coefficients within a similar range, i.e., the average real-world Gini is greal = 0.5193 ± 0.071. Indeed, for WBPA networks with 10,000 nodes, we have an average Gini coefficient of gWBPA = 0.4962 ± 0.0282, which is very close to the real-world B/D Gini values (−4.5%). Additionally, we generate 10 of each random, small world, and PA networks of 10,000 nodes. For these synthetic networks we obtain the corresponding Gini values in Table 4. The PA networks (except WBPA) produce an average gPA = 0.7784 ± 0.0128, whereas the random network produces an average Gini grand = 0.9374 ± 0.0013. These results point out two key aspects: (i) the B/D dispersion in other PA and other state-of-the-art synthetic models differs significantly from real-world social networks, and (ii) WBPA produces networks with B/D distributions that are closer to the real-world.
Two specific B/D distributions are exemplified in Fig. 7a,b for the Google Plus and POK users networks, respectively. Figure 7c,d present the B/D distribution for the DPA and WBPA networks. The visual similarity inspection reveals WBPA as the only synthetic model capable of reproducing the real-world B/D ratios (see SI.1, Fig. 3 for additional examples).
Distributions of betweenness/degree (B/D) ratios in empirical and synthetic social networks characterized by Gini coefficients g. (a) Google Plus users network28 (gGP = 0.4820). (b) POK users network29 (gPK = 0.4879). (c) DPA network2 (gDPA = 0.7828 ± 0.0182) (d) WBPA network (gWBPA = 0.4962 ± 0.0282). The B/D distribution in our WBPA network model, as opposed to the DPA network, is very similar to that found in real-world networks.
The WBPA realism is also backed up by the centrality distribution analysis. The power-law slopes for degree and betweenness distributions in WBPA (γdeg = 1.391 and γbtw = 1.171) are very similar to the real-world distributions from the Centrality statistics section (see Fig. 1) and SI.1, Table 1, meaning that the degree slope is steeper than the betweenness slope (with 18.8%). Similar to the real-world cases, we obtain a polynomial fit for the node betweenness-degree correlation in WBPA (y = 0.246x2 + 329.8x − 3569.4, with correlation coefficient R2 = 0.9977).
Discussion and a Socio-Psychological Interpretation
From a computational standpoint, node betweenness is significantly more complex to compute in comparison with node degree. However, when individuals make assessments of social attractiveness in real-world situations–which is essential for driving preferential attachment and establishing new social links–they do not rely on executing algorithms or other types of quantitative evaluations. Instead, individuals make decisions based on qualitative perceptions30. In light of the quality over quantity hypothesis proposed by social psychology31, we argue that node betweenness is a far better indicator of social attractiveness than node degree, because the quality of being “in between” can be easily and quickly perceived, due to the fact that humans are better at observing qualitative aspects (e.g., differences and diversity) than quantitative ones32. This idea is supported by an experimental study on how people favor investing in fewer qualitative social ties, rather than numerous lower quality ties32. Our results indicate that WBPA provides a more accurate social network topological model, being able to reproduce real-world community structure as well as to explain degree saturation and link weight evolution.
We believe that the WBPA model transcends the mere topological perspective on social relationships evolution. As such, in the field of social psychology, individuals are perceived as social creatures who strive for social recognition, validation, approval and fame7,19,33,34. Indeed, individuals tend to connect to two types of other nodes: individuals who are popular in their communities (i.e., typically they have high degree), and individuals who connect multiple communities (having high betweenness). While the former type of interconnection is mostly related to the popularity of individuals within local communities, it appears to be an epiphenomenon of the latter.
Also, state of the art has previously identified that social networks have apparent (degree) assortative mixing, while, technological and biological networks appear to be disassortative in nature34,35. The study in35 explains this as most networks have a tendency to evolve, unless otherwise constrained, towards their maximum entropy state–which is usually disassortative. A similar debate was introduced by Borondo et al. based on the concepts of meritocracy versus topocracy36. The authors discuss the critical point at which social value changes from being based on personal merit, to being based on social position, status, and acquaintances. In the context of social networks, we interpret this issue as follows: in our ego-networks the balance between friends with less influence and ones with more influence than us translates into betweenness assortativity. Indeed, connecting to persons with high betweenness and increasing our tie strength with them (through, say, a stable social relationship), we ourselves become, in turn, more influential social bridges. This propagation of influence determines other persons, with lower betweenness, to interact with us and direct more tie strength towards us.
Towards this end, we introduce the concept of social evolution cycle, which revolves around betweenness assortativity rather than degree assortativity34,35,37. According to our approach, individuals become more influential over time by increasing their own betweenness. Therefore, the exhibition of one individual’s desire to increase his/her betweenness is two-fold: it attracts new ties (i.e., increase in degree), and it creates stronger ties (i.e., increase in link weight); this process continues for the next generation of individuals who aspire to climb the social ladder. As shown, this conclusion is supported by the evolution of networks generated with WBPA.
We envision two ways of improving an individual’s social status. The first choice relies on forcing tie strengths inside the existing neighborhood to increase first, followed by an increase in influence. The second choice relies on increasing influence first by broadening the neighborhood to influential agents (BPA principle), which will in turn trigger an increase in tie strengths. We consider the second choice as the more plausible social process, as detailed and explained in Fig. 8.
An intuitive explanation of the social evolution cycle. All nodes are colored and sized proportional to their betweenness centrality (influence). (a) A non-influential individual (grey) initiates social contact (link) with other individuals equal or more influential than himself. (b) This action leads to a natural increase of the individual’s influence (betweenness). (c) Other nodes with less influence start connecting to the initial individual. At this point, the initial node has become a predominant receiver of new ties, as emphasized by the new violet links.
We conclude that the WBPA model is quantitatively more robust than DPA, as it can reproduce more accurately a wide range of real-world social networks. Such a conclusion means that node degree is not the main driver in social network dynamics. Instead, node betweenness is a much better indicator of social attractiveness, because it drives the formation of new social bonds, as well as the evolution of social status of individuals. From a socio-psychological standpoint, individuals (intuitively) perceive node’s betweenness as the capacity of bridging communities, irrespective of its degree. As shown, WBPA is a subtle mechanism at work that is able to replicate the social network community structure. Also, WBPA explains the dynamic accumulation of degree and link weights, as well as the eventual degree saturation, as a second order effect. Consequently, we believe our work paves the way for a new and deeper understanding of the mechanisms that lie behind the dynamics of complex social networks.
Methods
Real-world datasets
All data used in this study were selected to facilitate a thorough analysis of node betweenness and degree, as well as measuring the realism of synthetic networks. The real-world datasets have been chosen based on diversity of both context and network size. Prior studies confirm that data mining from sources such as Facebook or Google Plus is reliable for realistic social network research38,39, and indicate a strong correlation between the real-world and virtual friendships of people40,41.
Table 5 provides the graph metric measurements used for the realism assessment of our WBPA model, as presented in the Results section. Our real-world datasets comprise the following social networks (ordered by network size, from N = 590 to N = 364K nodes): Facebook (FB) users41, Google Plus (GP) users28, weighted co-authorships (CoAu) in network science23, weighted on-line social network (OSN)22, trade network using Bitcoin OTC platform (BTC)42, votes for Wikipedia administrators (WkV)43, weighted scientific collaboration network in Computational Geometry (Geom)44, Condensed Matter collaboration network from arXiv (CM)45, weighted interactions on the stack exchange web site MathOverflow (MOvr)46, High-Energy Physics citation network (HEP)47, POK online social network29, Enron email (EmE) communication network48, IMDB adult actors co-appearances, Brightkite online social network (BK)49, Facebook-New Orleans (FBNO)50, Epinions online social network (EP)51, Slashdot online social network (SL)48, and Timik online platform (TK)52.
Information about the nature of nodes and links, as well as direct URLs for each dataset are provided in SI.5 Datasets availability, Table 6. In the main manuscript, Table 6 presents the natural ranges for the graph metrics that are provided in Table 5, as they are measured across the entire range of considered real-world on-line social networks41.
Network centralities
All graphs are generated and visualized using Gephi53; the graph centralities are analyzed using the poweRlaw package distributed with R according to the methodology described in54. Full details for the topological analysis of data are given in SI.1. Furthermore, to quantify the specific distributions of B/D ratios introduced in this paper we made use of the Gini coefficient–borrowed from the area of economics where it is used to evaluate data dispersion27.
In SI.2 we present the preferential attachment analysis based on combinations of two and three node centralities. Given a graph G = (V, E), with nodes vi ∈ V and links eij ∈ E, we define the basic graph centralities and metrics used throughout the paper. We represent the adjacency matrix as W = {wij}, which contains either the weight of the link for any link eij, or 0, if no link exists. If the network is unweighted, then each wij = 1.
The degree ki of a node vi (also denoted as D) is defined as \({k}_{i}=\sum {w}_{ij}\). In case of directed networks, there is a differentiation between in-degree and out-degree, but that is beyond the scope of this subsection. The average degree AD of the graph is calculated over all nodes as1:
The clustering coefficient CCi measures the fraction of existing links in the vicinity Vi of a node, and is formally defined as55:
with ki being the degree of node vi, and ejk the set of links connecting two friends in the vicinity of node vi, all divided by the maximum number of links in vicinity Vi. Consequently, the average clustering coefficient ACC of the entire graph is the average of all CCi over all nodes.
Considering d(vi, vj) as the shortest path between two nodes in G, the average path length APL is defined as1:
If there is no path between two nodes, then that particular distance is considered 0; n is the total number of nodes |V| in G.
The diameter of a graph is defined as the longest geodesic56, namely the longest shortest distance between any two nodes: Dmt = max(d(vi, vj)).
Graph density is simply defined as the ratio between number of links and maximum possible number of links, if the graph were complete56. For undirected graphs, it is defined as:
Modularity is a measure for quantifying the strength of division of a graph into modules, or clusters, and is often used in detection of community structure57. Modularity Mod is the fraction of the links which lie within a given group minus the expected fraction if links were distributed at random. Values for Mod range between [−1/2, 1). If it is positive, then the number of links within a cluster exceeds the expected number. Also, a high overall modularity means dense connections between the nodes within modules and sparse connections between nodes in different modules. We use the algorithm of Blondel et al. to compute modularity58.
Betweenness centrality is commonly defined as the fraction of shortest paths between all node pairs that pass through a node of interest1, and is defined as59:
where σjk(vi) is the number of shortest paths in G which pass through node vi, and σjk is the total number of shortest paths between all pairs of two nodes vj and vk from G.
Closeness centrality is defined as the inverse of the sum of geodesic distances to all other nodes in G1,56, and can be considered as a measure of how long it will take to spread information from a given node to other reachable nodes in the network:
where d(vi, vj) is the distance (number of hops) between the two nodes vi and vj.
The most common centrality based on the random walk process is the Eigenvector centrality (EC), which assumes that the influence of a node is not only determined by the number of its neighbors, but also by the influence of each neighbor23. The centrality of any node is proportional to the sum of neighboring centralities1. Considering a constant λ, the EC is formally defined as:
Assessing network fidelity
In order to assess the structural realism of the generated social networks, we used the statistical fidelity φ, which is proven to offer reliable insights on complex network topologies25. The fidelity metric φ numerically captures the similarity between any graph topology G* with respect to another reference graph G (i.e., a complex network G = (V, E)). More precisely, by measuring and comparing their common individual graph metrics, a maximum fidelity of 1 represents complete similarity, while a minimum fidelity of 0 represents complete dissimilarity between the two compared topologies. Of note, the fidelity is not dependent on the choice of metrics of interest, however it is customizable to allow a weighted comparison. Depending on the context of the problem, any numerical value (i.e. metric) that is representative for the model can be used. The definition and proof of statistical fidelity φ are detailed in25.
Definition 1. Given a reference topology G, and any other network G* being compared to G, the arithmetic fidelity \({\phi }_{A}^{\ast }\), which expresses the similarity between G* and G, is defined as:
In equation 8, i is the index of the metric which describes the two networks being compared, and n is the total number of metrics used in the comparison. In this paper we compute the fidelity between multiple synthetic topologies and the empirical social network references. These reference datasets are chosen because they have typical real-life social network features. The fidelity comparison is made relative to the set of relevant network metrics (indexed by i).
In this paper, fidelity is measured by taking into consideration the following topological characteristics: average degree AD, average path length APL, average clustering coefficient ACC, modularity Mod, diameter Dmt, and density Dns.
References
Wang, X. F. & Chen, G. Complex networks: small-world, scale-free and beyond. Circuits and Systems Magazine, IEEE 3, 6–20 (2003).
Barabási, A.-L. & Albert, R. Emergence of scaling in random networks. science 286, 509–512 (1999).
Broido, A. D. & Clauset, A. Scale-free networks are rare. arXiv preprint arXiv:1801.03400 (2018).
Dunbar, R. I. Neocortex size as a constraint on group size in primates. Journal of Human Evolution 22, 469–493 (1992).
Brashears, M. E. Humans use compression heuristics to improve the recall of social networks. Scientific reports 3 (2013).
Krackhardt, D. The strength of strong ties: The importance of philos in organizations. Networks and organizations: Structure, form, and action 216, 239 (1992).
Adamic, L., Buyukkokten, O. & Adar, E. A social network caught in the web. First monday 8 (2003).
Strogatz, S. H. Exploring complex networks. Nature 410, 268–276 (2001).
Newman, M. Networks: an introduction (Oxford University Press, 2009).
Burt, R. S. Attachment, decay, and social network. Journal of Organizational Behavior 22, 619–643 (2001).
Abbasi, A., Hossain, L. & Leydesdorff, L. Betweenness centrality as a driver of preferential attachment in the evolution of research collaboration networks. Journal of Informetrics 6, 403–412 (2012).
Holme, P. & Kim, B. J. Growing scale-free networks with tunable clustering. Physical Review E 65, 026107 (2002).
Fu, P. & Liao, K. An evolving scale-free network with large clustering coefficient. In Control, Automation, Robotics and Vision, 2006. ICARCV'06. 9th International Conference on, 1–4 (IEEE, 2006).
Chen, Y., Zhang, L. & Huang, J. The watts–strogatz network model developed by including degree distribution: theory and computer simulation. Journal of Physics A: Mathematical and Theoretical 40, 8237 (2007).
Jian-Guo, L., Yan-Zhong, D. & Zhong-Tuo, W. Multistage random growing small-world networks with power-law degree distribution. Chinese Physics Letters 23, 746 (2006).
Wang, J. & Rong, L. Evolving small-world networks based on the modified ba model. In Computer Science and Information Technology, 2008. ICCSIT'08. International Conference on, 143–146 (IEEE, 2008).
Zaidi, F. Small world networks and clustered small world networks with random connectivity. Social Network Analysis and Mining 1–13 (2013).
Milgram, S. The small world problem. Psychology today 2, 60–67 (1967).
Lazer, D. et al. Life in the network: the coming age of computational social science. Science (New York, NY) 323, 721 (2009).
Tsvetovat, M. & Carley, K. M. Generation of realistic social network datasets for testing of analysis and simulation tools. Tech. Rep. DTIC Document (2005).
Leydesdorff, L. Betweenness centrality as an indicator of the interdisciplinarity of scientific journals. Journal of the American Society for Information Science and Technology 58, 1303–1319 (2007).
Opsahl, T. & Panzarasa, P. Clustering in weighted networks. Social networks 31, 155–163 (2009).
Newman, M. E. Finding community structure in networks using the eigenvectors of matrices. Physical review E 74, 036104 (2006).
Topirceanu, A., Garcia, J. & Udrescu, M. Upt. social: The growth of a new online social network. In Network Intelligence Conference (ENIC), 2016 Third European, 9–16 (IEEE, 2016).
Topirceanu, A. & Udrescu, M. Statistical fidelity: a tool to quantify the similarity between multi-variable entities with application in complex networks. International Journal of Computer Mathematics 94, 1787–1805 (2017).
Toivonen, R., Onnela, J.-P., Saramäki, J., Hyvönen, J. & Kaski, K. A model for social networks. Physica A: Statistical Mechanics and its Applications 371, 851–860 (2006).
Xie, Y. & Zhou, X. Income inequality in today’s china. Proceedings of the National Academy of Sciences 111, 6928–6933 (2014).
McAuley, J. J. & Leskovec, J. Learning to discover social circles in ego networks. NIPS 2012, 548–56 (2012).
Takac, L. & Zabovsky, M. Data analysis in public social networks. In International Scientific Conference and International Workshop Present Day Trends of Innovations, 1–6 (2012).
Tversky, A. & Kahneman, D. Advances in prospect theory: Cumulative representation of uncertainty. Journal of Risk and uncertainty 5, 297–323 (1992).
Rowatt, W. C., Nesselroade, K., Beggan, J. K. & Allison, S. T. Perceptions of brainstorming in groups: The quality over quantity hypothesis. The Journal of Creative Behavior 31, 131–150 (1997).
Shirado, H., Fu, F., Fowler, J. H. & Christakis, N. A. Quality versus quantity of social ties in experimental cooperative networks. Nature communications 4, 2814 (2013).
Plous, S. The psychology of judgment and decision making. (Mcgraw-Hill Book Company, 1993).
McPherson, M., Smith-Lovin, L. & Cook, J. M. Birds of a feather: Homophily in social networks. Annual review of sociology 415–444 (2001).
Johnson, S., Torres, J. J., Marro, J. & Munoz, M. A. Entropic origin of disassortativity in complex networks. Physical review letters 104, 108702 (2010).
Borondo, J., Borondo, F., Rodriguez-Sickert, C. & Hidalgo, C. To each according to its degree: The meritocracy and topocracy of embedded markets. Scientific reports 4 (2014).
Zhou, D., Stanley, H. E., DAgostino, G. & Scala, A. Assortativity decreases the robustness of interdependent networks. Physical Review E 86, 066103 (2012).
Hossmann, T., Legendre, F., Nomikos, G. & Spyropoulos, T. Stumbl: Using facebook to collect rich datasets for opportunistic networking research. In World of Wireless, Mobile and Multimedia Networks (WoWMoM), 2011 IEEE International Symposium on a, 1–6 (IEEE, 2011).
Ferrara, E. & Fiumara, G. Topological features of online social networks. arXiv preprint arXiv:1202.0331 (2012).
Valenzuela, S., Park, N. & Kee, K. F. Is there social capital in a social network site?: Facebook use and college students’ life satisfaction, trust, and participation1. Journal of Computer-Mediated Communication 14, 875–901 (2009).
Topirceanu, A., Udrescu, M. & Vladutiu, M. Genetically optimized realistic social network topology inspired by facebook. In Online Social Media Analysis and Visualization, 163–179 (Springer, 2014).
Kumar, S., Spezzano, F., Subrahmanian, V. & Faloutsos, C. Edge weight prediction in weighted signed networks. In Data Mining (ICDM), 2016 IEEE 16th International Conference on, 221–230 (IEEE, 2016).
Leskovec, J., Huttenlocher, D. & Kleinberg, J. Signed networks in social media. In Proceedings of the SIGCHI conference on human factors in computing systems, 1361–1370 (ACM, 2010).
Batagelj, V. & Mrvar, A. Pajek-program for large network analysis. Connections 21, 47–57 (1998).
Leskovec, J., Kleinberg, J. & Faloutsos, C. Graph evolution: Densification and shrinking diameters. ACM Transactions on Knowledge Discovery from Data (TKDD) 1, 2 (2007).
Paranjape, A., Benson, A. R. & Leskovec, J. Motifs in temporal networks. In Proceedings of the Tenth ACM International Conference on Web Search and Data Mining, 601–610 (ACM, 2017).
Leskovec, J., Kleinberg, J. & Faloutsos, C. Graphs over time: densification laws, shrinking diameters and possible explanations. In Proceedings of the eleventh ACM SIGKDD international conference on Knowledge discovery in data mining, 177–187 (ACM, 2005).
Leskovec, J., Lang, K. J., Dasgupta, A. & Mahoney, M. W. Community structure in large networks: Natural cluster sizes and the absence of large well-defined clusters. Internet Mathematics 6, 29–123 (2009).
Cho, E., Myers, S. A. & Leskovec, J. Friendship and mobility: user movement in location-based social networks. In Proceedings of the 17th ACM SIGKDD international conference on Knowledge discovery and data mining, 1082–1090 (ACM, 2011).
Viswanath, B., Mislove, A., Cha, M. & Gummadi, K. P. On the evolution of user interaction in facebook. In Proceedings of the 2nd ACM workshop on Online social networks, 37–42 (ACM, 2009).
Richardson, M., Agrawal, R. & Domingos, P. Trust management for the semantic web. In The Semantic Web-ISWC2003, 351–368 (Springer, 2003).
Jankowski, J., Michalski, R. & Bródka, P. A multilayer network dataset of interaction and influence spreading in a virtual world. Scientific Data 4, sdata2017144 (2017).
Bastian, M., Heymann, S. & Jacomy, M. Gephi: an open source software for exploring and manipulating networks. In ICWSM (2009).
Gillespie, C. S. Fitting heavy tailed distributions: the powerlaw package. arXiv preprint arXiv:1407.3492 (2014).
Watts, D. J. & Strogatz, S. H. Collective dynamics of small-world networks. Nature 393, 440–442 (1998).
Newman, M., Barabasi, A.-L. & Watts, D. J. The structure and dynamics of networks (Princeton University Press, 2011).
Newman, M. E. Modularity and community structure in networks. Proceedings of the National Academy of Sciences 103, 8577–8582 (2006).
Blondel, V. D., Guillaume, J.-L., Lambiotte, R. & Lefebvre, E. Fast unfolding of communities in large networks. Journal of statistical mechanics: theory and experiment 2008, P10008 (2008).
Newman, M. E. The structure and function of complex networks. SIAM review 45, 167–256 (2003).
Author information
Authors and Affiliations
Contributions
A.T., M.U., and R.M. designed research, analyzed data and wrote the paper; A.T. and M.U. designed algorithms; A.T. performed simulations.
Corresponding author
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Topirceanu, A., Udrescu, M. & Marculescu, R. Weighted Betweenness Preferential Attachment: A New Mechanism Explaining Social Network Formation and Evolution. Sci Rep 8, 10871 (2018). https://doi.org/10.1038/s41598-018-29224-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-018-29224-w
This article is cited by
-
Emergence of a mutual-growth mechanism in networks evolved by social preference based on indirect utility
Scientific Reports (2023)
-
Decentralizing the lightning network: a score-based recommendation strategy for the autopilot system
Applied Network Science (2023)
-
Emergence and evolution of social networks through exploration of the Adjacent Possible space
Communications Physics (2021)
-
A Graph Theory approach to assess nature’s contribution to people at a global scale
Scientific Reports (2021)
-
Explaining the emergence of complex networks through log-normal fitness in a Euclidean node similarity space
Scientific Reports (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.