Abstract
In this paper, we present two novel dual-band bandpass filters based on surface plasmon polariton-like (SPP-like) propagation induced by structural dispersion of substrate integrated waveguide (SIW). Both filters are realized as a three-layer SIW where each layer represents a sub-SIW structure with intrinsic effective permittivity that depends on its width and filling dielectric material. The layers are designed to have effective permittivities of opposite signs in certain frequency ranges, which enables SPP-like propagation to occur at their interfaces. Since three layers can provide two distinct SPP-like propagations, the filters exhibit dual-band behaviour. A detailed theoretical and numerical analysis and numerical optimization have been used to design the filters, which were afterwards fabricated using standard printed circuit board technology. The independent choice of geometrical parameters of sub-SIWs and/or the corresponding dielectric materials provide a great freedom to arbitrarily position the passbands in the spectrum, which is a significant advantage of the proposed filters. At the same time, they meet the requirements for low-cost low-profile configuration since they are realized as SIW structures, as well as for excellent in-band characteristics and selectivity which is confirmed by the measurement results.
Similar content being viewed by others
Introduction
Surface plasmon polaritons (SPP) present electromagnetic waves that occur at the interface of a dielectric and conductor due to the coupling of light to collective electron oscillations1. Owing to the specific nature, SPPs allow for breaking the diffraction limit and the localization of light into subwavelength dimensions, ultimately enabling strong field enhancements. As such, SPPs have been applied in various fields including optical communications, photonics, and sensing2,3,4,5.
The advantageous properties of SPPs such as slow-wave behaviour and field confinement are also very desirable in frequency regimes other than optical since they open up possibilities for significant improvement of components and devices. Since SPPs naturally occur at optical frequencies, there have been proposed different concepts to engineer SPP phenomenon in other frequency ranges including microwaves and terahertz.
One of the concepts that effectively mimics SPPs are spoof or designer surface plasmon polaritons6,7, which have been widely used in different microwave circuits including transmission lines8,9,10,11,12,13,14,15,16, filters17,18,19,20,21,22,23,24,25,26, antennas27, couplers28, splitters29, absorbers30, and circulators31. Unlike genuine SPPs, spoof SPPs are supported by specifically designed structures, predominantly by grooved strips whose geometrical properties are used to tailor the behaviour of spoof SPPs.
Recently, a novel “natural” SPP-like concept in microwave regime has been proposed, which is based on exploitation of the well-known structural dispersion of the electromagnetic modes in parallel-plate waveguide structure filled only with materials with positive permittivity32,33. Namely, if a parallel-plate waveguide is divided into two parts by an array of wires placed along the plane normal to the plates, and if the parts are filled with different materials, then the two parts exhibit effective permittivities of opposite signs in a certain frequency range, which allows for SPP to occur at their interface. This methodology was applied in somewhat different waveguide structure - substrate integrated waveguide (SIW), and the realized configuration demonstrated potential for filtering applications at microwave frequencies34.
It is well-known that the rapid growth of communication systems imposes the requirements for high-performance, low-cost, low-profile components that operate at two or more non-harmonically related frequencies. Taking into consideration those demands and the potential of the proposed concept, in this paper we propose two novel dual-band filters that employ “natural” SPP-like phenomenon, to achieve operation at two non-harmonically related microwave frequencies. Besides slow-wave behaviour and field confinement, SPP-like propagation also provides a transmission zero in spectral response, capable to clearly separate a passband in the spectrum, which is the underlying idea of filtering operation based on SPP-like propagation.
The proposed filters are realized as a microstrip-fed three-layer SIW where each layer represents a sub-SIW structure with intrinsic structural dispersion depending on its geometry and dielectric material. One filter comprises sub-SIW structures of the same width but with different dielectric materials, whilst the other one is comprised of three sub-SIWs which are filled with the same dielectric material, but have different widths. Since the layers are designed to have effective permittivities of opposite signs in certain frequency ranges, two distinct SPP-like propagations occur at the interfaces between the top and middle sub-SIWs and the middle and bottom sub-SIWs, which ultimately provides two passbands in the filters’ response.
To the best of authors’ knowledge, the two filters are first dual-band microwave filters based on “natural” SPP-like concept. The independent choice of geometrical parameters of sub-SIWs and/or the corresponding dielectric materials provide a great freedom to arbitrarily position the passbands in the spectrum, which is a significant advantage of the proposed configurations. At the same time, they meet the requirements for excellent in-band characteristics and selectivity as well as the requirements for low-cost low-profile configuration since they are realized as SIW structures.
In the following sections, a detailed theoretical background of the filters’ design will be presented, followed by the numerical analysis and discussion on their performance. The fabrication process will be described, and the measurement results of the fabricated circuits will be presented to confirm the high potential of the proposed filters.
Results
Theoretical analysis
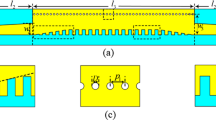
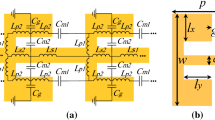
The layout of the proposed filters is shown in Fig. 1 together with the corresponding geometrical parameters. The filters are based on a substrate integrated waveguide that is fed by tapered microstrip lines. Being bounded by metal walls on the top and bottom sides, and by arrays of vias on lateral sides, SIW represents a waveguide structure whose dominant propagating mode is TE10, whilst TM modes are not supported. The effective dielectric constant of TE10 mode can be defined as35:
where f is frequency, c is the speed of light, a is the width, and ε r dielectric constant of the material that fills the SIW. The cut-off frequency is defined as
and below it the effective dielectric constant is negative, i.e. the wave propagation is not allowed, whilst above it the propagation is allowed. Such structural dispersion of SIW indicates that SPP-like propagation can be achieved by coupling of two TE10 modes, providing the modes have effective dielectric constants of opposite signs. In other words, SPP-like propagation can be achieved at the interface of two SIWs in the frequency range in which the two have effective dielectric constants of opposite signs, and this is the underlying idea of the proposed filters.
To achieve SPP-like propagation in the proposed configuration, the SIW is divided into three layers, i.e. there are three sub-SIWs in the proposed structure, Fig. 1. In general case, the three sub-SIWs have different widths a1, a2, and a3 and they are filled with different dielectric materials whose dielectric constants are ε1, ε2, and ε3, respectively. Since effective dielectric constant of a sub-SIW depends on its width and the filling dielectric material, by the proper choice of those parameters we can tailor the frequency ranges in which the three sub-SIWs have desirable sign of the effective dielectric constant.
If we consider that the top sub-SIW has the lowest, and the bottom sub-SIW the highest cut-off frequency, then Fig. 2 summarizes the four frequency ranges according to the signs of the effective dielectric constants of TE10 mode in the three sub-SIWs. Whilst the first frequency range entirely forbids propagation, and the fourth allows conventional propagation typical for a SIW, the second and the third ranges are of a particular interest for the filters’ design. Namely, in the second range the top and the middle sub-SIWs exhibit effective dielectric constants of opposite signs, thus allowing for SPP-like propagation at their interface. By the same token, in the third frequency range SPP-like propagation occur at the interface between the middle and the bottom sub-SIWs.
Since the proposed structure can support SPP-like propagation in two different frequency ranges, this opens up possibility to design dual-band filtering operation. To further explain how the passbands are actually formed, the dispersion relation of the structure should be considered. Although not partially filled waveguide per se, for the sake of theoretical analysis the whole SIW can be considered in that manner. The wavenumber in the three sub-SIWs can be defined as36,37:
where β is the propagation constant in the z direction, k0 is the wavenumber in vacuum, k yi is the wavenumber in the y direction, ε ei effective dielectric constant, whilst i take the values 1, 2, and 3, denoting the top, middle, and bottom layer, respectively. Without loss of generality, the losses are omitted to simplify the explanation.
The dispersion relation for the overall structure can be obtained by solving the wave equation and imposing boundary conditions:
where d, τ, and b are the geometrical parameters of the structure as shown in Fig. 1(a), and k iy are the wave-vector components along y direction in each layer. A detailed derivation of the Eq. (4) and explanation of the parameter Ψ are given in the Supplementary Material.
To illustrate the behaviour of the propagation constant and the overall SIW, Fig. 2 also shows the dispersion curve of the proposed structure. One can distinguish the four frequency ranges that were previously discussed – in the first range all sub-SIWs have negative effective permittivity and thus there is no propagation, whilst in the fourth frequency range conventional propagation occurs which is indicated by the propagation constant curve positioned on the right side of the light line. In the second and the third frequency ranges, the propagation constant has similar trend, i.e. it exhibits the same behaviour as the genuine SPPs, being positioned on the right side of the light line and going to infinity at specific frequencies called surface-plasmon frequencies fSP1 and f SP2 . These frequencies play an important role in filters design since they are spectral positions at which β goes to the infinity, which causes propagation suppression and a sharp transmission zero in the structure’s response. We note the region marked with lines in the second range, in which the effective dielectric constant of the middle layer is still negative, however its absolute value is smaller than that of the top layer. Thus, the propagation constant does not go to infinity nor SPP-like nor conventional propagation occurs, i.e. the region represents a stopband range. The same explanation can be applied to the region marked with lines in the third frequency range.
In other words, once an SPP-like propagation is established at the interface between the top and middle layers, propagation exists in the second frequency range, which is interrupted at f SP1 and forbidden in the region marked with lines. Propagation is established again once an SPP-like occurs at the interface between the bottom and middle layers, which is interrupted at f SP2 and forbidden in the corresponding region marked with lines. These transmission zeros together with the described stopband regions are capable to clearly separate passbands in the spectrum, and this is the main principle of the filters’ design.
The surface-plasmon frequencies f SP1 and f SP2 , spectral width of the ranges in which propagation does not occur and consequently the bandwidths of the passbands, can be controlled by the sub-SIWs parameters – dielectric constant and the width. Figure 3(a) shows the theoretically obtained dispersion relations for different values of a 1 and a3, when ε r1 = εr2 = ε r3 = 5 and a 2 = 20 mm, whilst Fig. 3(b) shows the theoretically obtained dispersion relations for different values of εr1 and ε r3 , when εr2 = 5 and a 1 = a 2 = a3 = 20 mm. Other geometrical parameters are kept constant. The parameter a1 affects only f SP1 and the region marked with lines in the second frequency range, i.e. the first passband, whilst a3 affects only f SP2 and the region marked with lines in the third frequency range, i.e. the second passband. Similarly, εr1 and ε r3 affect only the first and the second passband, respectively. Therefore, the widths and dielectric constants of sub-SIWs represent mechanisms to independently control the passbands’ positions and bandwidths, which is of crucial importance in dual-band filter design.
Filter design
To demonstrate the potential of the SPP-like propagation and the three-layer SIW structure for dual-band filtering operation, two dual-band filters have been designed. Since the sub-SIWs’ width and dielectric constants are mechanisms for independent control of the passbands, theoretically there are six degrees of freedom in filter design. However, it should be noted that the top sub-SIW should have the lowest cut-off frequency and the bottom one the highest cut-off frequency or vice versa, to achieve dual-band operation. Otherwise, the two SPP-like propagation would overlap and only one passband would be formed. Also, to further simplify the procedure and simultaneously keep the design freedom it is judicious to use either the same width or the same dielectric constant for the three sub-SIWs.
Therefore, the first filter that we propose comprises three sub-SIWs of the same width filled with different dielectric materials. The dielectric constant of the middle layer and its width have been chosen to position its cut-off frequency in the range 2.7–3.2 GHz to be able to position the passbands around 2.4 and 3.5 GHz. We note that these frequencies correspond to the IEEE standards, but in general they are arbitrarily chosen. Afterwards, the dielectric constants of the top and bottom sub-SIWs have been chosen to obtain the passbands at the desired frequencies. Since the three layers have different dielectric materials they are realized using the following dielectric substrates: Rogers TMM10i with relative permittivity εr1 = 9.8, dielectric loss tanδ 1 = 0.002, and thickness t 1 = b-d-τ = 1.27 mm, Neltec NH9450 with relative permittivity εr2 = 4.5, dielectric loss tanδ 2 = 0.0027, and thickness τ = 0.768 mm, and Rogers RT5880 with relative permittivity ε r = 2.2, dielectric loss tanδ = 0.0009, and thickness d = 0.51 mm. Also, it should be noted that using of the commercially available substrates somewhat limit the range of the available dielectric constants, and consequently the design freedom. However, this does not affect the overall idea and this limitation can be overcome by variation of the widths.
After the three sub-SIWs are designed based on theoretical analysis, numerical simulations are used to finely tune the structure’s response. Although the theory can very precisely determine the positions and bandwidths of the passbands, the filter needs to be numerically optimized since the theoretical model cannot predict minute mutual couplings between the layers that affect the filter response. Also, good impedance matching in the whole range of interest is very important for filter performance and thus the microstrip-to-SIW transition has to be optimized.
We note here that the sub-SIWs are mutually coupled through arrays of wires as indicated in Fig. 1, since the wires provide that there are no other modes which would interfere with TE10 mode and disturb the field distribution at the interfaces. Also, the wires support accumulation of electric charges and consequently provide that the normal components of the electric field at the interfaces are opposite to each other. If there were not wires, then the whole structure would behave as a conventional partially filled waveguide which cannot provide SPP propagation but only conventional propagation. In other words, the interface itself is not sufficient to achieve the coupling between two TE10 modes, but the SPP-like propagation has to be reinforced through the array of wires.
The final geometrical parameters of the filter are the following: a = 22 mm, L = 40 mm, L T = 12.5 mm, W in = 4.5 mm, W t = 5 mm, w w = 0.2 mm, dw1 = 1 mm, n w1 = 33, d w2 = 0.4 mm, n w2 = 65, d via = 0.8 mm, p via = 1.1 mm, where d via represents the diameter of the via, p via the spacing between the vias, whilst n w1 and n w2 represent the number of wires at the interface between neighbouring materials.
Since the actual configuration of the filters employs the arrays of wires, which were not considered in the theoretical analysis, at this point we would like to show that the introduction of the wires, instead of ideal SPP interfaces, does not significantly influence the SPP-like propagation. To that end, Fig. 3 also shows the comparison of the theoretically predicted dispersion relations with those in which the wires are taken into account. The latter dispersion relations have been obtained using numerical analysis, which is explained in the section Methods, and the geometrical parameters of the wires are those given for the final filter. One can note an excellent agreement between the theoretically and numerically obtained dispersion relations, which confirms that the introduction of wires does not influence the control mechanisms for the filter response.
However, one may argue that different periodicity of the wires and their geometrical parameters can influence the overall structure behaviour. To avoid any doubt, Fig. 4 shows numerically obtained dispersion relations for different values of the parameters d w1 , dw2, and w w . The dispersion relations exhibit very similar trend and values, particularly in the region in which β goes to the infinity, which means that the geometrical parameters practically do not influence the positions of the transmission zeros induced by the SPP-like propagation. Certainly, the previous claim is valid as far as the periodicity of the wires is significantly smaller than the operational wavelength.
Nevertheless, the geometrical parameters of the wires at the two interfaces differ, since they have been optimized to achieve minimal loss in the filter response, i.e. to achieve the sufficiently good impedance matching.
Figure 5(a) shows the response of the filter. The central frequencies of the two passbands are positioned at 2.4 and 3.5 GHz, and their 3-dB bandwidths are 10.3% and 15.8%, respectively. The insertion losses are 1.1 and 1.2 dB, whereas the return losses are below 13 and 11 dB, respectively. The passbands are characterized by the excellent selectivity which is primarily due to transmission zeros that occur at surface-plasmon frequencies.
(a) Simulation response of first proposed filter. (b) Theoretically and numerically obtained dispersion relations of the first proposed filter. (c) Theoretically and numerically calculated propagation length of the first SPP-like mode. (d) Theoretically and numerically calculated propagation length of the second SPP-like mode.
Theoretically and numerically obtained dispersion diagrams of the structure are shown in Fig. 5(b). The theoretically obtained dispersion diagram confirms the validity of the theoretical model since the passbands, stopbands, and transmission zeros in the response excellently agree with the model. This is further supported by the numerically obtained dispersion diagram, which shows a very good agreement with the theoretical one.
In addition, Fig. 5 shows the analytically and numerically obtained propagation length of the SPP-like modes around the central frequencies of the two passbands, both of which have been calculated using the expression38:
The parameter v g is the group velocity obtained as derivative of the dispersion relation, ω is the complex eigenfrequency, β propagation constant, and Q is the quality factor of SPP-like mode calculated as Q = Re(ω)/2Im(ω). Theoretical and numerical results show an excellent agreement. Also, both SPP-like modes exhibit relatively long propagation lengths, with the greatest values equal to 117.1 and 43.2 cm, respectively.
The SPP-like behaviour is also confirmed in Fig. 6 that shows the electric field distribution at the interfaces at the frequencies denoted in Fig. 5. Whilst E-field distribution at f 1 and f4 is very similar to that of the conventional SIW, at f2, f3, f5, and f6 the wavelength is significantly smaller implying increase of β and its approaching to the infinity. At f1 and f4 the absolute values of dielectric constants in the corresponding layers are still sufficiently different, whilst at f2 and f5, and particularly at f3 and f6 they have practically the same absolute values causing β to abruptly increase.
The second filter that we propose comprises three sub-SIWs with different widths and same dielectric constants. To that end, the dielectric substrate Neltec NH9450 with relative permittivity εr2 = 4.5, dielectric loss tanδ 2 = 0.0027, and thickness τ = 0.768 mm, has been used. The widths a1, a2, and a3 have been determined to achieve the passbands around the frequencies 4.7 and 5.5 GHz. Following the theoretical model, numerical analysis and simulations have been performed to optimize the filter response in terms of impedance matching and suppressing non-desirable coupling. To that end, the microstrip-to-SIW transmission has been optimized and strips between the arrays of vias in different layers added. As in the previous case, the sub-SIWs are mutually coupled through the array of wires to achieve the SPP-like propagation. The final geometrical parameters of the filter are the following: a1 = 16 mm, a2 = 13.8 mm, a3 = 12.4 mm, L = 25 mm, L T = 5 mm, W in = 4.5 mm, W t = 9 mm, w w = 0.25 mm, dw1 = 0.25 mm, n w1 = 45, dw2 = 0.375 mm, n w2 = 30, d via = 0.5 mm, p via = 0.8 mm.
Figure 7 shows the response of the filter together with the theoretically and numerically obtained dispersion diagram of the structure and propagation lengths of the SPP-like modes. The central frequencies of the two passbands are positioned at 4.7 and 5.5 GHz, and the 3-dB bandwidths are 4.5% and 4.1%, respectively. The insertion losses are equal to 1.58 and 1.77 dB, whereas the return losses are below 18 and 17 dB, respectively. The passbands are also characterized by the excellent selectivity. The theoretical dispersion diagram confirms the validity of the theoretical model, which is further confirmed by the numerical dispersion diagram. Besides an excellent agreement between the theoretically and numerically obtained propagation lengths, one can note that the propagation lengths of SPP-like modes are somewhat shorter than those in the previous filter, which is due to the higher dielectric losses in the second filter. Figure 8 shows the electric field distribution at the interfaces at the frequencies denoted in Fig. 7, which clearly confirms SPP-like behaviour of the proposed structure.
(a) Simulation response of second proposed filter. (b) Theoretically and numerically obtained dispersion relations of the second proposed filter. (c) Theoretically and numerically calculated propagation length of the first SPP-like mode. (d) Theoretically and numerically calculated propagation length of the second SPP-like mode.
Measurement results and discussion
To validate the designed filters, they have been fabricated using standard printed circuit board (PCB) technology, which is explained in detail in the section Methods. Photographs of the fabricated circuits are shown in Fig. 9, whilst the photographs of the individual layers of the filters are shown in Supplementary Material.
As it is explained in the section Methods, the three layers of each filter are fabricated separately and afterwards assembled into the final structure using screws, which causes small air gaps between the layers. Since SPP-like propagation is confined to the interface between the layers, it is very sensitive to the existence of small disturbances around the interface. Therefore, the air gaps, although very thin, can influence the spectral positions of the passbands. Although their thickness cannot be precisely determined, the air gaps have been approximated by the thickness of the copper layer, i.e. 0.035 mm, which might be taken as the limit by which the layers can be screwed.
In accordance with the previous approximation, Fig. 10 shows the simulation results that correspond to the designed structures in which the air gaps between the layers are taken into account. If these simulation results are compared to those in Figs 5 and 7, the same trend of the curves can be noted, except for the spectral shifts of around 0.2 GHz. The comparison of the measurement and simulation results in Fig. 10 reveals a good agreement except for slight differences in the bandwidths which can be attributed to the tolerance of the manufacturers related to the dielectric constant, as well as to a slight misalignment of the via arrays in fabrication process.
The first filter exhibit two passbands at 2.65 and 3.75 GHz, with insertion loss of 1.47 and 1.69 dB, and the 3-dB bandwidths of 8.7% and 13.3%, respectively. The central frequencies of the second filter are 4.8 and 5.7 GHz, their insertion losses 2.22 and 2.17 dB, and the 3-dB bandwidths 5.2% and 8.2%, respectively. Both filters are characterized by good in-band and out-of-band performance as well as by excellent selectivity owing to the transmission zeros. The difference in the insertion losses between the first and the second filter can be attributed to the fact that the first filter comprises three different substrates whose dielectric losses are tanδ 1 = 0.002, tanδ 2 = 0.0027, and tanδ3 = 0.0009, respectively, whilst in the second proposed filter only the substrate with tanδ2 = 0.0027 has been used. Therefore, the losses in dielectric are more pronounced in the second proposed filter, which results in higher insertion losses.
The proposed filters are first dual-band filters based on the “natural” SPP-like concept, and they are characterized by good overall performance and possibility for independent control of the passbands in terms of position and bandwidth. Moreover, they meet requirements for low-cost and low-profile configuration since they are realized as SIW structures. As such, they can be considered as very promising candidates for dual-band filtering operation at microwave frequencies.
Conclusion
In this work, we proposed novel microwave dual-band filters employing SPP-like propagation based on structural dispersion of SIW. The filters are realized as a SIW that consists of three sub-SIW structures, tailored to exhibit effective permittivities of opposite signs in certain frequency ranges. Such configuration provides two distinct SPP-like propagations to occur, ultimately providing two passbands in the filters’ responses.
A detailed theoretical and numerical analysis of the structures’ behaviour have been presented and they showed how the choice of the geometrical parameters and dielectric constants of sub-SIWs can provide arbitrarily positioning of the passbands in the spectrum.
To demonstrate the potential of the proposed ideas, we have designed two dual-band filters operating at 2.65/3.75 and 4.8/5.7 GHz, respectively, which are characterized by excellent in-band characteristics and selectivity. The designed filters have been fabricated using standard PCB technology, and the measurements results agree well with the simulated ones.
The proposed filters are first dual-band microwave filters based on SPP-like propagation and they are excellent candidates for dual-band filtering applications since they provide independent control of the passbands, excellent performance, and low-cost fabrication.
Methods
Design optimization
The responses of the structures were simulated and optimized using FEM method employed in the commercial software package CST. Both structures were simulated using frequency domain solver and tetrahedral mesh in the frequency ranges from 2 to 5 GHz and 4 to 6 GHz, respectively.
To properly configure the feeding of the filters and achieve appropriate impedance matching, in the initial step we determined the optimal widths of the microstrip lines W in and SIW feeding lines W t using quasi-static expressions39,40,41. Since there is a difference between the widths W in and W t , a microstrip taper is used and configured to have a smooth transition from one width to another. Due to the complexity of the structure and the dual-band operation, in the final step the analytically designed feeding scheme was numerically optimized to achieve a good impedance matching in both passbands.
Dispersion curves have been numerically obtained using unit cell configuration and eigenmode solver in which periodic boundary conditions were used in the direction of propagation. Unit cells comprise the three dielectric layers and a wire for each interface between the layers. The eigenmode analysis was conducted using both CST and COMSOL Multiphysics solvers.
Fabrication
The first structure has been fabricated using standard printed circuit board (PCB) technology. The three layers have been realized using the commercially available substrates Rogers TMM10i with relative permittivity εr1 = 9.8, dielectric loss tanδ1 = 0.002, and thickness t 1 = b – d – τ = 1.27 mm, Neltec NH9450 with relative permittivity εr2 = 4.5, dielectric loss tanδ 2 = 0.0027, and thickness τ = 0.762 mm, and Rogers RT5880 with relative permittivity εr3 = 2.2, dielectric loss tanδ 3 = 0.0009, and thickness b = 0.51 mm. Metallic parts of each layer were etched according to the design and the three layers have been assembled using six nylon screws. In the final step, SMA connectors have been mounted on the structure.
The second filter has been fabricated using the same technology. Three layers of the substrate Neltec NH9450 with relative permittivity εr2 = 4.5, dielectric loss tanδ 2 = 0.0027 have been used to realize the filter. Metallic parts of each layer were etched according to the design and the three layers have been assembled using four nylon screws. In the final step, SMA connectors have been mounted on the structure.
Measurements
The responses of the fabricated structures were measured using Vector Network Analyzer E5071C two-port measurements. Measurements were performed with the resolution of 1601 points in the frequency range from 2 to 5 GHz and from 4 to 6.5 GHz, respectively.
References
Maier, S. Plasmonics: fundamentals and applications. Springer Science & Business Media (2007).
Li, Y. Plasmonic optics: Theory and applications. SPIE Press (2017).
Xiangang, L. & Lianshan, Y. Surface plasmon polaritons and its applications. IEEE Photon. J. 4, 590–595 (2012).
Wang, J. et al. Surface plasmon resonance sensors on raman and fluorescence spectroscopy. Sensors 17, 2719 (2017).
Singh, P. SPR Biosensors: Historical perspectives and current challenges. Sens Actuators B 229, 110–130 (2016).
Pendry, J. Mimicking surface plasmons with structured surfaces. Science 305, 847–848 (2004).
Sambles, R., Hibbins, A. & Lockyear, M. Manipulating microwaves with ‘spoof’ surface plasmons. SPIE Newsroom (2009).
Zhu, J., Liao, S., Li, S. & Xue, Q. Half-spaced substrate integrated spoof surface plasmon polaritons based transmission line. Sci. Rep. 7, (2017).
Zhang, D., Zhang, K., Wu, Q., Ding, X. & Sha, X. High-efficiency surface plasmonic polariton waveguides with enhanced low-frequency performance in microwave frequencies. Opt. Exp. 25, 2121 (2017).
Tian, L. et al. Compact spoof surface plasmon polaritons waveguide drilled with L-shaped grooves. Opt. Exp. 24, 28693 (2016).
Ye, L. et al. Strongly confined spoof surface plasmonp waveguiding enabled by planar staggered plasmonic waveguides. Sci. Rep. 6, (2016).
Chen, C. A new kind of spoof surface plasmon polaritons structure with periodic loading of T-shape grooves. AIP Adv. 6, 105003 (2016).
Kianinejad, A., Chen, Z. & Qiu, C. Low-loss spoof surface plasmon slow-wave transmission lines with compact transition and high isolation. IEEE Trans. Microwave Theory Tech. 64, 3078–3086 (2016).
Li, Z. et al. High-contrast gratings based spoof surface plasmons. Sci. Rep. 6 (2016).
Liu, X., Zhu, L., Wu, Q. & Feng, Y. Highly-confined and low-loss spoof surface plasmon polaritons structure with periodic loading of trapezoidal grooves. AIP Adv. 5, 077123 (2015).
Wan, X. & Cui, T. Guiding spoof surface plasmon polaritons by infinitely thin grooved metal strip. AIP Adv. 4, 047137 (2014).
Zhao, S., Zhang, H., Zhao, J. & Tang, W. An ultra-compact rejection filter based on spoof surface plasmon polaritons. Sci. Rep. 7, (2017).
Zhou, Y. & Xiao, Q. Electronically controlled rejections of spoof surface plasmons polaritons. J. Appl. Phys. 121, 123109 (2017).
Hu, M. et al. Ultra-wideband filtering of spoof surface plasmon polaritons using deep subwavelength planar structures. Sci. Rep. 6, (2016).
Zhao, L. et al. A novel broadband band-pass filter based on spoof surface plasmon polaritons. Sci. Rep. 6, (2016).
Zhang, Q., Zhang, H., Yin, J., Pan, B. & Cui, T. A series of compact rejection filters based on the interaction between spoof SPPs and CSRRs. Sci. Rep. 6, (2016).
Xu, B. et al. Bandwidth tunable microstrip band-stop filters based on localized spoof surface plasmons. J. Opt. Soc. Am. B 33, 1388 (2016).
Liu, X., Zhu, L. & Feng, Y. Spoof surface plasmon-based bandpass filter with extremely wide upper stopband. Chin. Phys. B 25, 034101 (2016).
Zhang, Q., Zhang, H., Wu, H. & Cui, T. A hybrid circuit for spoof surface plasmons and spatial waveguide modes to reach controllable band-pass filters. Sci. Rep. 5, (2015).
Xu, B. et al. Tunable band-notched coplanar waveguide based on localized spoof surface plasmons. Opt. Lett. 40, 4683 (2015).
Wu, J. et al. Bandpass filter based on low frequency spoof surface plasmon polaritons. Electron. Lett. 48, 269 (2012).
Guan, D. et al. A wide-angle and circularly polarized beam-scanning antenna based on microstrip spoof surface plasmon polariton transmission line. IEEE Antennas Wireless Propag. Lett. 16, 2538–2541 (2017).
Meng, Y. et al. Broadband spoof surface plasmon polaritons coupler based on dispersion engineering of metamaterials. Appl. Phys. Lett. 111, 151904 (2017).
Gao, X. et al. Ultra-wideband surface plasmonic Y-splitter. Opt. Exp. 23, 23270 (2015).
Li, S. et al. Hybrid metamaterial device with wideband absorption and multiband transmission based on spoof surface plasmon polaritons and perfect absorber. Appl. Phys. Lett. 106, 181103 (2015).
Qiu, T., Wang, J., Li, Y., Wang, J. & Qu, S. Broadband circulator based on spoof surface plasmon polaritons. J. Phys. D. Appl. Phys. 49, 355002 (2016).
Della Giovampaola, C. & Engheta, N. Plasmonics without negative dielectrics. Phys. Rev. B. 93, (2016).
Prudêncio, F., Costa, J., Fernandes, C., Engheta, N. & Silveirinha, M. Experimental verification of ‘waveguide’ plasmonics. New J. Phys. 19, 123017 (2017).
Li, Z. et al. Effective surface plasmon polaritons induced by modal dispersion in a waveguide. Phys. Rev. Appl. 7, (2017).
Rotman, W. Plasma simulation by artificial dielectrics and parallel-plate media. IRE Trans. Antennas and Propagation 10, 82–95 (1962).
Balanis, C. Advanced engineering electromagnetics, 2nd ed., J. Wiley & Sons, New York (2012).
Collin, R. Foundations for microwave engineering, 2nd ed., Wiley-IEEE Press, New York, (2001).
Liu, L. et al. Ultra-low-loss high-contrast gratings based spoof surface plasmonic waveguide. IEEE Trans. Microwave Theory Tech. 65, 2008–2018 (2017).
Wan Ali, W. K. A theoretical development to simplify the analysis of rectangular patch microwave sensor built on multi-layer substrate. 2003 Asian Conference on Sensors, 257–262 (2003).
Hong, J., Lancaster, M. Microstrip filters for RF/microwave applications, J. Wiley & Sons, New York (2001).
Deslandes, D. Design equations for tapered microstrip-to-substrate integrated waveguide transitions. 2010 IEEE MTT-S International Microwave Symposium, 704-707 (2010).
Acknowledgements
This work is supported in part by the Ministry of Education, Science, and Technological Development of the Republic of Serbia through the project III44006.
Author information
Authors and Affiliations
Contributions
N.C. partially conceived the idea, performed theoretical analysis, and contributed to the manuscript drafts. Z.S. performed numerical analysis and design optimization, contributed to the fabrication and measurements, and to the manuscript drafts. G.K. contributed to the design optimization, carried out the measurements, and contributed to the manuscript drafts. V.C.B. contributed to the design optimization and to the manuscript drafts. N.J. partially conceived the idea, supervised the research, and prepared the manuscript drafts.
Corresponding author
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Cselyuszka, N., Sakotic, Z., Kitic, G. et al. Novel Dual-band Band-Pass Filters Based on Surface Plasmon Polariton-like Propagation Induced by Structural Dispersion of Substrate Integrated Waveguide. Sci Rep 8, 8332 (2018). https://doi.org/10.1038/s41598-018-26705-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-018-26705-w
This article is cited by
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.