Abstract
In Hebbian plasticity, neural circuits adjust their synaptic weights depending on patterned firing. Spike-timing-dependent plasticity (STDP), a synaptic Hebbian learning rule, relies on the order and timing of the paired activities in pre- and postsynaptic neurons. Classically, in ex vivo experiments, STDP is assessed with deterministic (constant) spike timings and time intervals between successive pairings, thus exhibiting a regularity that differs from biological variability. Hence, STDP emergence from noisy inputs as occurring in in vivo-like firing remains unresolved. Here, we used noisy STDP pairings where the spike timing and/or interval between pairings were jittered. We explored with electrophysiology and mathematical modeling, the impact of jitter on three forms of STDP at corticostriatal synapses: NMDAR-LTP, endocannabinoid-LTD and endocannabinoid-LTP. We found that NMDAR-LTP was highly fragile to jitter, whereas endocannabinoid-plasticity appeared more resistant. When the frequency or number of pairings was increased, NMDAR-LTP became more robust and could be expressed despite strong jittering. Our results identify endocannabinoid-plasticity as a robust form of STDP, whereas the sensitivity to jitter of NMDAR-LTP varies with activity frequency. This provides new insights into the mechanisms at play during the different phases of learning and memory and the emergence of Hebbian plasticity in in vivo-like activity.
Similar content being viewed by others
Introduction
Long-term changes in synaptic efficacy between neurons are thought to underlie learning and memory1 and can be assessed with a synaptic Hebbian paradigm such as spike timing-dependent plasticity (STDP)2,3,4,5,6,7,8. In STDP, the occurrence of timing-dependent-long-term potentiation (tLTP) or -depression (tLTD) is the result of three factors. The two first ones are the two coincident activity patterns on either side of the synapse, which depends on (1) the relative timing between pre- and postsynaptic spikes (ΔtSTDP)4,8, (2) the dendritic and axonal propagation delays9, (3) the number of paired spikes (Npairings)10,11,12,13, (4) the frequency of the paired spikes (Fpairings)6,7,10,11,14 and (5) membrane depolarization14,15; the third factor involves in STDP expression mainly refers to neuromodulators16,17 and glial cells18.
STDP has been attracting a lot of interest in computational and experimental neurosciences because it relies on spike correlation and has emerged as a candidate mechanism for experience-dependent changes in neural circuits, including map plasticity8,19,20,21,22,23. STDP is classically investigated using regular repetitions of the same spike timing and fixed intervals between successive paired stimulations. A typical experimental protocol consists in pairing pre- and postsynaptic stimulations with a fixed ΔtSTDP (ranging from −30 to +30 ms for plasticity induction); ΔtSTDP < 0 when the postsynaptic stimulation occurs before the paired presynaptic one (post-pre pairings), whereas ΔtSTDP > 0 when the presynaptic stimulation occurs before the postsynaptic one (pre-post pairings). These pairings are then repeated between 15 and 200 times (between 0.1 and 5 Hz) with the spike timing and the time interval between successive pairings being kept constant.
Regular stimulation paradigms produce patterns of activity that are likely to differ from the variability expected in in vivo-like firing. In vivo paired natural visual stimulations with postsynaptic action potential lead to Hebbian STDP with specific characteristics when compared to ex vivo STDP (broader membrane potential changes and STDP window), which can be explained by jittered presynaptic inputs occurring in vivo22. A theoretical study has started to explore naturalistic stimulations and showed that when neurons fire irregularly, the impact of spike timing in plasticity becomes weaker than the influence of the firing rate24. However, whether STDP emergence and maintenance is robust against biological variability remains to be investigated. To address this question, it is important to take into account various forms of STDP, involving distinct intracellular signal transduction pathways, i.e. NMDAR-, mGluR- or endocannabinoid(eCB)-mediated STDP25,26,27,28,29 (for reviews see8,30,31). It is thus expected that those various STDP forms might exhibit different robustness to spike train variability.
Here, we show with patch-clamp recordings and mathematical modeling that corticostriatal NMDAR- and eCB-STDP do not exhibit the same sensitivity to noisy spike timings: eCB-plasticity (eCB-tLTD and eCB-tLTP) appeared robust to jittering whereas NMDAR-tLTP was fragile. However, increasing the number or frequency of pairings improved NMDAR-tLTP robustness. Our results further indicate that the robustness of NMDAR-tLTP to jitter is also strengthened by the irregularity of the spike-train stimulations.
Results
Corticostriatal synapses exhibit a bidirectional STDP in which NMDAR-tLTP, eCB-tLTD29,32,33,34 or eCB-tLTP12,13 are induced depending on the number of pairings (Npairings) and the spike timing (ΔtSTDP). While STDP is classically investigated using fixed ΔtSTDP, we examine here the effect of noisy ΔtSTDP, closer to in vivo-like firing. Here, we define the Inter-Pairing-Interval (IPI) as the time interval between two consecutive presynaptic stimulations, whereas ΔtSTDP is the time interval between the post- and the presynaptic stimulation times within a given paired stimulation (in a “standard” STDP protocol both IPIs and ΔtSTDP are constant).
NMDAR- and eCB-mediated STDP triggered with fixed ΔtSTDP
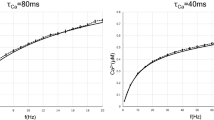
We observed bidirectional asymmetric STDP in MSNs (Fig. 1a): 100 post-pre pairings (ΔtSTDP < 0) induced tLTP whereas 100 pre-post pairings (ΔtSTDP > 0) induced tLTD. An example of the tLTP induced by 100 post-pre pairings with fixed ΔtSTDP (Fig. 1b) is illustrated in Fig. 1c1. The input resistance Ri remained stable over this period. Although we fixed the values of ΔtSTDP, they slightly vary from one pairing to another (Fig. 1b). This low jitter can be written formally as ΔtSTDP = mΔt + ξΔt, were mΔt is the mean spike timing and ξΔtis a random variable with mean 0 and standard deviation σΔt. Overall, 100 post-pre pairings induced tLTP (mean EPSC amplitude recorded 60 min after protocol induction: 149 ± 13% of baseline, p = 0.0028, n = 13) (Fig. 1c2). σΔt was 1.4 ± 0.2 ms (Fig. 1c3). This tLTP was NMDAR-mediated since prevented by D-AP5 (50 μM), a NMDAR antagonist, (88 ± 12%, p = 0.375, n = 5; p < 0.0001 when compared with tLTP in control) (Fig. 1c2). Conversely, pre-post pairings induced tLTD, as shown in the example in Fig. 1d1. Overall, 100 pre-post pairings induced tLTD (76 ± 7%, p = 0.0070, n = 10) (Fig. 1d2). σΔt was 1.4 ± 0.2 ms (Fig. 1d3). This tLTD was CB1R-mediated since prevented by AM251 (3 μM), a CB1R specific inhibitor (99 ± 2%, p = 0.816, n = 5; p < 0.0001 when compared with tLTD in control) (Fig. 1d2). We thus find an anti-Hebbian polarity for corticostriatal STDP. We previously showed that GABA operates as a Hebbian/anti-Hebbian switch at corticostriatal synapses34,35 and corticostriatal STDP polarity depends on the presence32,33 or the absence12,29,36,37 of GABAA receptor antagonists.
NMDAR- and eCB-mediated STDP induced with fixed ΔtSTDP. (a) STDP protocol: a single postsynaptic spike was paired with a single cortical stimulation, 10 or 100 times at 1 Hz. (b) Example of 5 successive pairings (#4–8, from c1) exhibiting relatively fixed ΔtSTDP (#4–8: −8.0, −7.8, −7.4, −8.8 and −8.0 ms). Plotting the successive ΔtSTDP illustrates their low variance σΔt (2.6 ms). (c) Corticostriatal NMDAR-tLTP induced by 100 post-pre pairings with fixed ΔtSTDP. (c1) Example of tLTP induced by 100 post-pre pairings (mΔt = −9 ms, σΔt = 2.6 ms). The mean baseline EPSC amplitude, 95 ± 3 pA, increased by 77% to 168 ± 6 pA 45 minutes after pairings. Upper panel, time course of Ri (baseline: 172 ± 2 MΩ and 35–45 min after pairings: 170 ± 3 MΩ; change of 1%) and holding current (Ihold). Inset: distribution of the 100 ΔtSTDP. (c2) Averaged time-courses of tLTP induced by 100 post-pre pairings; this tLTP was NMDAR-mediated because prevented by D-AP5 (50 μM). (c3) Relationship between the STDP magnitude and the STDP jitter for each of the recorded neurons. (d) Corticostriatal eCB-tLTD induced by 100 pre-post pairings with fixed ΔtSTDP. (d1) Example of tLTD induced by 100 pre-post pairings (mΔt = +21 ms, σΔt = 2.1 ms); the mean baseline EPSC amplitude, 206 ± 4 pA, decreased by 25%, to 154 ± 8 pA, 45 minutes after pairings. Upper panel, time course of Ri (baseline: 195 ± 1 MΩ and 45–55 min after pairings: 196 ± 2 MΩ; change <1%) and Ihold. Inset: distribution of the 100 ΔtSTDP. (d2) Averaged time-courses of tLTD induced by 100 pre-post pairings; this tLTD was CB1R-mediated because prevented by AM251 (3 μM). (d3) Relationship between the STDP magnitude and the jitter. (e) Corticostriatal eCB-tLTP induced by 10 post-pre pairings with fixed ΔtSTDP. (e1) Example of tLTP induced by 10 post-pre pairings (mΔt = −11 ms, σΔt = 3.1 ms); the mean baseline EPSC amplitude, 147 ± 3 pA, increased by 43% to 209 ± 9 pA 45 minutes after pairings. Upper panel, time course of Ri (baseline: 227 ± 2 MΩ and 45–55 min after pairings: 239 ± 2 MΩ; change of 5%) and Ihold. Inset: distribution of the 10 ΔtSTDP. (e2) Averaged time-courses of tLTP induced by 10 post-pre pairings; this tLTP was CB1R-mediated because prevented by AM251. (e3) Relationship between the STDP magnitude and the jitter. (c1-d1-e1) Insets: average of 12 successive EPSC amplitude at baseline (black traces) and at 40–50 min after pairings (grey traces). (f) Predictions of the mathematical model in the absence of added jitter. The model expresses the biochemical pathways schematized in (f1). (f2) Changes of Wtotal with various ΔtSTDP and Npairings. (f3) Removing NMDAR/CaMKII signaling suppresses the tLTP observed for ΔtSTDP > 0 and Npairings > 50. (f4) Removing CB1R suppresses the tLTP observed for ΔtSTDP > 0 and Npairings < 20 and the tLTD observed for ΔtSTDP < 0.
Besides this bidirectional STDP (NMDAR-tLTP and eCB-tLTD) induced for 100 pairings, we reported that low numbers of pairings (Npairings = 5–15) induce an eCB-tLTP, dependent on the activation of CB1R12,13. Figure 1e1 shows an example of tLTP induced by 10 post-pre pairings. Overall, 10 post-pre STDP pairings induced tLTP (145 ± 9%, p = 0.0005, n = 15), which was prevented by AM251 (3 μM) (76 ± 10%, p = 0.080, n = 4; p < 0.0001 when compared with tLTP in control) (Fig. 1e2) as recently reported12. σΔt for 10 post-pre parings STDP was 1.8 ± 0.3 ms (n = 15) (Fig. 1e3). Note that there was no difference between the σΔt measured for NMDAR-tLTP, eCB-tLTD and eCB-tLTP (one way ANOVA, p = 0.4094).
A computer model emulates NMDAR- and eCB-mediated STDP
To help interpret our experimental results, we used a mathematical model of the signaling pathways implicated in corticostriatal STDP, including NMDAR- and CB1R-plasticity12,29,32,33 (Fig. 1f1). The model is detailed in S1 Text, with parameter values listed in S1 and S2 Tables. We include in the Supporting Information a thorough description of the mechanisms by which eCB- and NDMAR-plasticity are expressed in the model when STDP protocol (Npairings = 100) is applied (S3 Text). Figure 1f2 shows the value of the total synaptic weight (Wtotal) predicted by the model with various Npairings and ΔtSTDP. In agreement with the experimental data, with small σΔt (3 ms), the model features three main plasticity regions: tLTD was observed for short pre-post pairings (0 < ΔtSTDP < +30 ms), whereas short post-pre pairings (−30 < ΔtSTDP < 0 ms) induced a first tLTP region for low numbers of pairings (3 < Npairings < 25) and a second tLTP region emerging for Npairings > 50. Blocking the NMDAR-CaMKII pathway in the model (Fig. 1f3) suppresses the second tLTP region whereas blocking CB1R activation (Fig. 1f4) prevents the expression of tLTD and of the first tLTP region. Therefore, the model emulates both CB1R-tLTD and -tLTP, in agreement with the eCB-tLTD and eCB-tLTP illustrated in the experimental data of Fig. 1d and e, respectively. The model also faithfully emulates the appearance of NMDAR-tLTP for Npairings > 50.
Predicting the effects of jittered STDP with a mathematical model
The small jitter observed in the above experiments was the result of biological variability inherent to the experimental setup. Our next goal was to extend this study to larger jitters (3 < σΔt < 10 ms) that we controlled experimentally. We first used constant intervals between two consecutive pairings (Inter-Pairing Interval, IPI) and used the same definition as above for jittered ΔtSTDP (Methods): ΔtSTDP = mΔt + ξΔt, where ξΔt is a random variable with zero mean and mΔt is the expected value of the spike timing ΔtSTDP over the Npairings. Next, we adjusted the probability distribution function and the variance of ξΔt to perform a parametric exploration of the impact of jitter.
In Fig. 2, the jitter ξΔt was sampled from a uniform distribution in [−σΔt, +σΔt] (Fig. 2a1). STDP in the model was globally not robust to jitter, since the three forms of plasticity vanished when σΔt was large enough (Fig. 2a2). However, the model delivered the prediction that the three forms of plasticity do not display the same sensitivity to jitter. In particular, NMDAR-tLTP is predicted to be very fragile when subjected to σΔt: its amplitude decreases as soon as σΔt > 2 ms and completely vanishes for σΔt > 4 ms (Fig. 2a2 and b2). In contrast, eCB-plasticity is much less sensitive: eCB-tLTP is still present for jitters as large as 7–8 ms and eCB-tLTD is still expressed with σΔt = 10 ms (Fig. 2b3).
The mathematical model predicts that NMDAR-tLTP is less robust to jitter than eCB-tLTP and eCB-tLTD. (a) Using a jittered STDP protocol combining uniformly-distributed jitter of the spike timing with deterministic IPIs at 1 Hz (a1), the amplitudes of NMDAR-tLTP, eCB-tLTD and eCB-tLTP decrease with increasing jitter amplitudes σΔt (a2). eCB-tLTP (red full line) was triggered with 10 pairings of average spike timing mΔt = −15 ms and eCB-tLTD (blue full line) with 100 pairings of mΔt = +20 ms. NMDAR-tLTP (red dashed line) corresponded to 100 pairings of mΔt = −15 ms. eCB-tLTD and eCB-tLTP are weakly affected by the jitter. NMDAR-tLTP is less robust. Full and dashed lines show averages and light swaths show ± 1 sem. (b) Evolution of NMDAR-tLTP, eCB-tLTD and eCB-tLTP domains for σΔt = 0 (b1), 5 (b2) and 10 ms (b3) for the STDP protocol of (a). Note the persistence of the eCB-tLTD domain (blue box) while eCB-tLTP (red box) and NMDAR-tLTP domain (red dashed box) disappeared for 5 and 10 ms, respectively. (c–e) Similar results are obtained with other jitter distributions, including Gaussian-distributed jitter (c) and triangularly-distributed jitter (d). We also considered a combination of triangularly-distributed jitter with random IPIs distributed according to an exponential distribution with refractory period τ r = 0.95 s (see Methods) in (e). The plots of the amplitude of NMDAR-tLTP, eCB-tLTD and eCB-tLTP for increasing jitter amplitude σΔt (c2, d2, e2) show similar profiles and are similar to panel (a2), indicating that the model predictions are not qualitatively modified by the probability distribution function of the jitter.
We next evaluated the validity of this prediction when the probability distribution function of the jitter changes. Figure 2 illustrates the results we obtained with Gaussian (Fig. 2c) or triangular (Fig. 2d) distributions of σΔt (see Methods). In both cases, the profiles of the robustness curves (Fig. 2c2 and d2) are almost identical to each other and similar to the robustness curves obtained with a uniform distribution (Fig. 2a2). In Fig. 2e, we combined a triangular distribution for σΔt with random IPIs, i.e. in this case, stochasticity is applied not only to the timing between the two stimulations of a given pairing, but also to the time interval between two consecutive pairings: IPI distribution was Poisson with refractory period τ r and rate λ (see Methods). Despite this increased stochasticity, we found that eCB-tLTD was again more robust, tolerating jitters up to 6–7 ms (eCB-tLTP) or 10 ms (eCB-tLTD) whereas NMDAR-tLTP was fragile, vanishing for σΔt > 4 ms (Fig. 2e2). Therefore, according to our model, the observation that eCB-STDP is more robust to jitter than NMDAR-tLTP could be a general property of the response of the signaling pathways to noisy paired stimulations.
Differential effect of jitter on NMDAR- and eCB-mediated plasticity
Based on the model predictions, we next investigated experimentally the sensitivity to jitter of NMDAR-tLTP induced by 100 post-pre pairings (Fig. 3a), using stochastic ΔtSTDP, distributed according to Fig. 2c1. As aforementioned, NMDAR-tLTP can be induced with a σΔt < 3 ms (Fig. 1c3). Increasing σΔt beyond 3 ms was sufficient to obliterate tLTP for 100 post-pre pairings. As exemplified (Fig. 3b and c1), 100 post-pre pairings with σΔt = 7.9 ms and centered on mΔt = −18 ms failed to induce plasticity. Overall, we did not observe tLTP expression for σΔt > 3 ms (92 ± 2%, p = 0.560, n = 7; p < 0.0001 when compared with tLTP observed without jitter) (Fig. 3c2 and c3) in agreement with the model prediction (Fig. 2c2).
Differential effect of jitter on NMDAR- and eCB-mediated plasticity. (a) STDP protocol; ΔtSTDP indicates the time between pre- and postsynaptic stimulations. ΔtSTDP < 0 and ΔtSTDP > 0 refer to post-pre and pre-post pairings, respectively. (b) Example of 5 successive pairings (#5–9, from c1) exhibiting jittered values of ΔtSTDP (#5–9: −10.3, −15.2, −30.5, −20.7 and −17.3 ms); these pairings are indicated with the grey frame within the 100 pairings displaying jittered ΔtSTDP. The distribution of the successive ΔtSTDP illustrate their standard deviation σΔt = 7.9 ms. (c) NMDAR-tLTP is prevented with σΔt > 3 ms. (c1) Example of the absence of plasticity after 100 post-pre pairings with mΔt = −18 ms and σΔt = 7.9 ms; the mean baseline EPSC amplitude, 194 ± 3 pA, did not show significant change 45 minutes after pairing, 186 ± 4 pA. Upper panel, time course of Ri (baseline: 198 ± 2 MΩ and 45–55 min after pairings: 194 ± 2 MΩ; change of 2%) and holding current (Ihold). Inset: distribution of the 100 ΔtSTDP. (c2) Averaged time-courses of the absence of plasticity after 100 post-pre pairings with 3 < σΔt < 10 ms. (c3) Relationship between the STDP magnitude and the jitter. (d) eCB-tLTD is not affected by 3 < σΔt < 10 ms. (d1) Example of tLTD induced by 100 pre-post pairings with mΔt = +18 ms and σΔt = 7.1 ms; the mean baseline EPSC amplitude, 160 ± 3 pA, decreased by 50%, to 81 ± 5 pA, 45 minutes after pairings. Upper panel, time course of Ri (baseline: 112 ± 1 MΩ and 35–45 min after pairings: 118 ± 1 MΩ; change of 5%) and Ihold. Inset: distribution of the 100 ΔtSTDP. (d2) Averaged time-courses of tLTD induced by 100 pre-post pairings with 3 < σΔt < 10 ms. (d3) Relationship between the STDP magnitude and the jitter. (e) eCB-tLTP is not affected by 3 < σΔt < 10 ms. (e1) Example of tLTP induced by 10 post-pre pairings with mΔt = −21 ms and σΔt = 6.4 ms; the mean baseline EPSC amplitude, 113 ± 2 pA, increased by 115% to 243 ± 6 pA 45 minutes after pairings. Upper panel, time course of Ri (baseline: 185 ± 1 MΩ and 45–55 min after pairings: 197 ± 2 MΩ; change of 6%) and Ihold. Inset: distribution of the 10 ΔtSTDP. (e2) Averaged time-courses of tLTP induced by 10 post-pre pairings with 3 < σΔt < 10 ms. (e3) Relationship between the STDP magnitude and the jitter. Insets: average of 12 successive EPSC amplitude at baseline (black trace) and at 40–50 min after STDP pairings (grey trace). Error bars represent the SEM.
We next investigated the robustness of the eCB-tLTD to the variability of ΔtSTDP. We observed potent tLTD even with large values of σΔt. As shown in Fig. 3d1, 100 pre-post pairings with σΔt = 7.0 ms centered on mΔt = +18 ms induced a large tLTD. Overall, we observed that tLTD was still induced for 100 pre-post pairings with 3 < σΔt < 10 ms (70 ± 6%, p < 0.0001, n = 14; p = 0.1661 when compared with tLTD observed without jitter) (Fig. 3d2 and d3). The mean value of tLTD, observed for 3 < σΔt < 10 ms, was not different from the one observed in control, i.e. for 0 < σΔt < 3 ms (p = 0.400).
Finally, we investigated the robustness of the eCB-tLTP to the variability of ΔtSTDP and observed potent tLTP even with large values of jitter, i.e. up to σΔt ~ 8 ms. An example of tLTP induced by 10 post-pre pairings with σΔt = 6.4 ms centered on mΔt = −21 ms is illustrated in Fig. 3e1. In summary, tLTP could be induced even for σΔt = 8 ms (160 ± 12%, p = 0.0021, n = 9; p = 0.0732 when compared with tLTP observed without jitter) (Fig. 3e2 and e3); the mean value of tLTP was not different from the one observed in control (p = 0.1660).
We ensured that the mΔt absolute values were not different in control and jittered conditions for 100 post-pre pairings (18 ± 2 ms, n = 13, vs 21 ± 3 ms, n = 7, p = 0.4711), 100 pre-post pairings (21 ± 2 ms, n = 10, vs 21 ± 2 ms, n = 14, p = 0.8984), 10 post-pre pairings (17 ± 2 ms, n = 15, vs 20 ± 2 ms, n = 9, p = 0.2297) or between these different STDP protocols (one-way ANOVA: p = 0.4851) (Supplementary Fig. 1).
In conclusion, in agreement with our model prediction, whereas NMDAR-tLTP appears fragile against the variability of ΔtSTDP, eCB-plasticity (eCB-tLTD as well as eCB-tLTP) exhibits a large robustness for the temporal imprecision of ΔtSTDP.
Model-based analysis of the effects of jittering
The above experimental results provide us with a validation of our mathematical model. We next used this validated model as a tool to investigate the molecular mechanisms behind these differences of robustness.
We have shown in a previous study that eCB-tLTP was expressed when the amount of eCBs produced was large enough that the fraction of activated CB1R, yCB1R, overcomes a threshold \({\theta }_{{\rm{LTP}}}^{{\rm{start}}}\)13. In the absence of added noise, σΔt = 0, our experimental data shows that as few as 5 pairings at 1 Hz and ΔtSTDP = −15 ms are enough to trigger eCB-tLTP12. Accordingly, our model produces large amounts of eCBs in the first 5–10 pre-post pairings so that yCB1R reaches \({\theta }_{{\rm{LTP}}}^{{\rm{start}}}\) after as few as 5 pairings (Fig. 4a1). When σΔt = 5 ms jitter was added to mΔt = −15 ms, some of the pairings failed to deliver yCB1R transients of maximal amplitude (Fig. 4a2). But for σΔt < 7–8 ms, a number of yCB1R transients still had sufficient amplitude to overcome \({\theta }_{{\rm{LTP}}}^{{\rm{start}}}\), which was enough to trigger eCB-tLTP (Fig. 4a2). When σΔt was large though (e.g. 10 ms), the yCB1R transients failed to reach the LTP zone and eCB-tLTP was not expressed (Fig. 4a3).
Model-based analysis of the effects of jittering. Model-predicted time-courses of (a) CB1R activation yCB1R and (b) the concentration of active CaMKII during a protocol with jitter amplitude σΔt = 0 (a1,b1), 5 (a2,b2) or 1 0 (a3,b3) ms. The STDP protocol was the same as Fig. 2a1 i.e. uniformly-distributed jitter of the spike timing and deterministic IPIs at 1 Hz. eCB-tLTP (a, red full line) and NMDAR-tLTP (b, red dashed line) were triggered with average spike timing mΔt = −15 ms and eCB-tLTD (a, blue full line) with mΔt = +20 ms. In (a) the shaded boxes locate the areas where yCB1R triggers eCB-tLTP or eCB-tLTD. Those areas are defined by the thresholds \({\theta }_{{\rm{LTP}}}^{{\rm{start}}}\,\,\)and (\({\theta }_{{\rm{LTD}}}^{{\rm{start}}}\), \({\theta }_{{\rm{LTD}}}^{{\rm{stop}}}\)), respectively (see Methods). For mΔt = −15 ms (red), increasing jitter amplitudes progressively hinders the build up of the yCB1R transients. yCB1R still reaches the LTP area for 5–25 pairings with σΔt = 0 (a1) and 5 ms (a2) thus triggering eCB-tLTP but fails to do so for σΔt = 10 ms (a3). Conversely, eCB-tLTD is robust to jitter because yCB1R remains in the LTD region for most of the pairings with mΔt = +20 ms (blue), for all tested jitter amplitudes. In (b), with mΔt = −15 ms (red) the switch from the low activation to the high activation state of CaMKII is obtained in the absence of jittering σΔt = 0 ms (b1). The progressive build up of activated CaMKII is efficiently suppressed as soon as σΔt = 5 ms (b2) thus effectively suppressing NMDAR-tLTP (b3).
In experiments without added jitter, eCB-tLTD progressively accumulates when Npairings increases and starts to be significant for Npairings > 2512. In the model with mΔt = +20 ms and σΔt = 0, the yCB1R transients remain in the LTD area for the most part of the STDP pairings (Fig. 4a3). To account for the progressive accumulation of eCB-tLTP with Npairings, each transient in the model contributes a small decrease of the synaptic weight. Even with large amounts of jitter (see e.g. σΔt = 5 or 10 ms in Fig. 4a2,a3) yCB1R transients remain mostly inside LTD area so eCB-tLTD remains expressed even with large jitter.
The robustness of NMDAR-tLTP is predicted to be frequency-dependent
Experimentally, NMDAR-tLTP (mΔt = −15 ms and σΔt = 0) was observed at Fpairings = 1 Hz when Npairings > 50, beyond which its amplitude did not depend much on Npairings13. To account for this feature, the steady-state concentration of activated CaMKII, that sets Wpost in the model, is bistable: 45 min after the stimulation, CaMKII was either almost fully inactivated (“no plasticity” state) or almost fully activated (“LTP” state)13,38. When the frequency of post-pre pairings (−30 < ΔtSTDP < 0 ms) was large enough (i.e. Fpairings ≥ 1 Hz), the IPI was smaller than the decay time of the CaMKII activation transient triggered by each post-pre pairings (Fig. 4b1). As a result, in the absence of added noise (σΔt = 0), the CaMKII activation transients progressively built up on top of each other. The accumulated CaMKII activation overcomes the threshold between the “no plasticity” and the “LTP” states only for Npairings > 50 (Fig. 4b1)13. With jitter (e.g. σΔt = 5 ms in Fig. 4b2 or 10 ms in Fig. 4b3), many of the IPIs were either too long or too short to trigger maximal amplitude transients of activated CaMKII. As a result, CaMKII activation never reached the threshold, thus explaining the fragility of NMDAR-tLTP with respect to jittering (at 1 Hz).
A major indication from the above analysis is the importance of the IPI frequency for the robustness of NMDAR-tLTP to jitter. Figure 5 compares the robustness to jitter for constant IPI with Fpairings = 1 Hz (Fig. 5a) and 1.05 Hz (Fig. 5b). The size of the green area that locates eCB-tLTD on Fig. 5a2,b2 was not much altered by the increase of the pairing frequency. Likewise, the size of the red area that locates eCB-tLTP in Fig. 5a1,b1 did not vary much when the frequency was increased. However, the size of the red area locating NMDAR-tLTP increased drastically with frequency (Fig. 5a2,b2). Therefore, our model predicts that NMDAR-tLTP should become more robust to jitter at larger frequencies, whereas eCB-tLTP and eCB-tLTD are not significantly changed.
Model-based analysis of the change of robustness with frequency. (a) Summary of the robustness of the model plasticity at 1 Hz. The jittered STDP protocol combined uniformly-distributed jitter of the spike timing and constant IPIs at 1 Hz. Two-dimensional maps show alterations of the plasticity obtained with 10 (a1) or 100 (a2) pairings, when the average spike timing mΔt and the jitter amplitude σΔt are changed. The locations of the plasticity blotches are indicated with horizontal lines: full red for eCB-tLTP, full blue for eCB-tLTD and dashed red for NMDAR-tLTP. The length of each of these blotches along the y-axis reflects their robustness to jitter. (a3) A cross-section along the dashed and full horizontal lines of (a1,a2) illustrates the robustness of NMDAR-tLTP, eCB-tLTD and eCB-tLTP. (b) Robustness of the model with larger frequency (1.05 Hz) and same jittered STDP protocol as in (a). Note the distortion between the pairing frequency in the model and in the experiments. The behavior of the model for Fpairings = 1.05 Hz corresponds to experimental results with Fpairings ≈ 3 Hz13. The two-dimensional maps for 10 (b1) or 100 (b2) pairings as well as the cross-sections (b3) predict that for frequencies larger than 1 Hz, the robustness changes, with NMDAR-tLTP becoming more robust.
Several aspects of glutamate signaling at the corticostriatal synapse are known to display complex frequency-dependence39. Our model is calibrated with experimental data at 1 Hz and features none of the above frequency dependencies. Therefore, we cannot expect a precise quantitative match between experiments and model when frequency is varied below or above 1 Hz. However, the model still yields correct predictions of the main qualitative trends observed in the experiments, since the effects of a small change of Fpairings in the model (1.00 to 1.05 Hz) were similar to the effects of larger changes (1 to 3 Hz) in the experiments13. Therefore, in the experiments, we expect to observe a change of robustness pattern similar to Fig. 5b, around Fpairings = 3 Hz rather than 1.05 Hz.
Increasing F pairings and N pairings stabilized NMDAR-tLTP against jitter
We next tested experimentally whether an increase from 1 to 3 Hz of STDP pairings would protect the NMDAR-tLTP against jitter, as predicted by the model. As shown in Fig. 6a1, 100 post-pre pairings at 3 Hz with σΔt = 9 ms and centered on mΔt = −22 ms induced tLTP. Overall, we observed tLTP for 100 post-pre pairings applied at 3 Hz with 4 < σΔt < 9 ms (181 ± 30%, p = 0.0274, n = 9) (Fig. 6a2 and a3); the mean value of these tLTP observed at 3 Hz with 4 < σΔt < 9 ms were not significantly different from the one observed with stimulation-related σΔt < 3 ms at 1 Hz (p = 0.520). When we plotted the magnitude of plasticity against σΔt for 100 post-pre pairings at 3 Hz, we observed that tLTP was still induced even for σΔt = 9 ms (Fig. 6a3). We observed different synaptic efficacy changes following 100 post-pre pairings at 1 Hz with and without jitter and at 3 Hz with jitter (ANOVA, p < 0.0001). The NMDAR-tLTP thus acquires certain robustness to the variability of ΔtSTDP with increasing frequency of pairings.
Increasing frequency and N pairings stabilized NMDAR-tLTP against jitter. (a) 100 post-pre pairings at 3 Hz induced a tLTP, which is not affected by 3 < σΔt < 10 ms. (a1) Example of tLTP induced by 100 post-pre pairings at 3 Hz with mΔt = −22 ms and σΔt = 9 ms; the mean baseline EPSC amplitude, 194 ± 4 pA, increased by 212%, to 606 ± 7 pA, 45 min after pairings. Upper panel, time course of Ri (baseline: 123 ± 1 MΩ and 45–55 min after pairings: 138 ± 1 MΩ; change of 12%) and Ihold for this cell. Inset: distribution of ΔtSTDP for the 100 pairings. (a2) Averaged time-courses of tLTP induced by 100 post-pre pairings at 3 Hz with 3 < σΔt < 10 ms. (a3) Relationship between the STDP magnitude and the jitter for each of the recorded neurons after 100 pairings at 1 Hz (n = 7; blue circles) or at 3 Hz (n = 10; red circles). (b) 250–300 post-pre pairings induced tLTP, which is not affected by 3 < σΔt < 10 ms. (b1) Example of tLTP induced by 250 post-pre pairings with mΔt = −20 ms and σΔt = 5 ms; the mean baseline EPSC amplitude, 126 ± 3 pA, increased by 57% to 198 ± 4 pA 45 minutes after pairings. Upper panel, time course of Ri (baseline: 65 ± 1 MΩ and 45–55 min after pairings: 65 ± 2 MΩ; change < 1%) and Ihold. Inset: distribution of ΔtSTDP for the 250 pairings. (b2) Averaged time-courses of tLTP induced by 250–300 post-pre pairings with 3 < σΔt < 10 ms. (b3) Relationship between the STDP magnitude and the jitter for each of the recorded neurons after 100 (n = 7; blue circles), 200 (n = 6; black circles) or 250–300 (n = 7; red circles) post-pre pairings. Insets: average of 12 successive EPSC amplitude at baseline (black trace) and at 40–50 min after STDP pairings (grey trace). Error bars represent the SEM.
We next investigated whether a higher Npairings would secure the expression of NMDAR-tLTP even with σΔt > 3 ms (Fig. 6b). When we doubled Npairings we did not observe expression of significant tLTP. Indeed, 200 post-pre pairings (−30 < mΔt < 0 ms with 3 < σΔt < 10 ms) did not induce plasticity (112 ± 9%, p = 0.236, n = 6; Fig. 6b3) but when we increased Npairings up to 250–300, tLTP was reliably observed with σΔt > 3 ms. Figure 6b1 shows an example of tLTP induced by 250 pairings with σΔt = 5 ms and centered on −20 ms. Overall, 250–300 post-pre STDP pairings (−30 < mΔt < 0 ms with 3 < σΔt < 10 ms) induced tLTP (170 ± 10%, p = 0.0012, n = 6; Fig. 6b2 and b3); the mean values of these tLTP observed for Npairings = 250–300 at 1 Hz with 4 < σΔt < 9 ms were not different compared to tLTP induced with 100 post-pre pairings at 1 Hz with σΔt < 3 ms (p = 0.1952). We observed different synaptic efficacy changes following 100, 200 and 250–300 post-pre pairings (ANOVA, p < 0.0001).
Transitions from spike-timing- to frequency-dependent plasticity
We next tested with our mathematical model whether the robustness of STDP to jitter of the spike timing depends on the regularity of the spike train. In Fig. 2e, we show an example of the combination of stochastic spike timings (triangular distribution) with stochastic IPIs (Poisson distributed) with a constant and relatively large refractory period τ r (see Methods- Mathematical model, Protocol 4). However, when τ r decreases, short IPIs are more frequently sampled and the train of presynaptic stimulation becomes more irregular. Therefore, through variations of the refractory period τ r , the presynaptic stimulation can be progressively switched from highly irregular to regular spike trains.
Figure 7 shows model predictions for the alteration of the robustness curves when τ r varies. With high refractory period, i.e. when τ r ≈ Fpairings, the IPIs are weakly noisy, so one recovers the robustness curves of Fig. 2e, with eCB-STDP being more robust than NMDAR-tLTP. However, when τ r is 70% of Fpairings, the robustness of both eCB-tLTP and NMDAR-tLTP increases and both exhibit similar robustness. With even smaller values of τ r , NMDAR-tLTP becomes more robust than eCB-tLTP. Moreover, eCB-tLTD (Fpairings = 1 Hz, mΔt = +20 ms, Npairings = 100) progressively stops triggering LTD when τ r decreases, even inducing LTP for very low τ r . Hence, when the presynaptic spike train is progressively switched from regular to very irregular spike trains, two main changes occur: (i) the three plasticity forms (NMDAR-tLTP, eCB-tLTD and eCB-tLTP) become increasingly robust to jittering (at the limit of highly irregular spike trains, jittering hardly affects plasticity amplitudes), and (ii) eCB-tLTD is progressively changed to LTP, so that highly irregular paired stimulations with Fpairings = 1 Hz only produce LTP regardless of the sign of the spike timing.
The robustness of plasticity depends on the regularity of the presynaptic spike train. The figure shows the robustness of the model plasticity (eCB-tLTP with red, eCB-tLTD with blue and NMDAR-tLTP with dashed red) with the jittered STDP protocol of Fig. 2e1, i.e. exponentially-distributed IPIs with refractory period τ r and triangularly-distributed jitter ξΔt. From right to left, the refractory period τ r is gradually decreased. When τ r → 1/Fpairings where Fpairings = 1 Hz is the average pairings frequency, one gets regular presynaptic spike trains, similar to classical STDP protocols. In this case (see e.g. τ r = 0.95/Fpairings), the robustness pattern is similar to the previous observations at 1 Hz: eCB-STDP is robust, whereas NMDAR-tLTP is fragile. However, when τ r → 0, the presynaptic spike train becomes highly irregular. In this case, the robustness patterns changes totally, with NMDAR-LTP becoming the most robust, and eCB-tLTD turning into a LTP. Hence, irregular presynaptic spike trains are predicted to produce robust LTP at the expense of LTD.
Discussion
Here, we have introduced jittered STDP protocols as noisy variants of STDP protocols where the spike timing, i.e. the delay between a presynaptic and paired postsynaptic stimulation (or vice-versa), is a random variable. Our results show that the magnitude of variability that STDP can tolerate varies depending on the pairing frequency and on the STDP form, i.e. NMDAR-tLTP, eCB-tLTP or eCB-tLTD. At 1 Hz pairing frequency, eCB-STDP (eCB-tLTD and eCB-tLTP) is much more robust than NMDAR-dependent tLTP. However, this robustness depends on the number and frequency of pairings. Indeed, increasing the average pairing frequency to 3 Hz improved the robustness of NMDAR-tLTP. We observed a similar improvement of the robustness of NMDAR-tLTP to jitter when the number of pairings increased more than two folds.
These results have wide-ranging implications for STDP expression in in vivo-like firing. They indicate that eCB-STDP could be more likely responsible for fast learning involving few trials (eCB-tLTP) or for learning at lower activity frequency than NMDAR-STDP. NMDAR-STDP could however take part in learning for larger frequencies or when the same spike timing recurs a large number of times during sustained activity. It also implies that in synapses where NMDAR is the main coincidence detector for tLTD or tLTP3,5,6,40,41,42, a high degree of precision of the spike timing, and/or an increased number or frequency of pairings, are required for the emergence of the NMDAR-mediated plasticity. This can be viewed as a mechanism preventing the occurrence of spurious plasticity for noisy neural network activity. At synapses in which NMDAR and endocannabinoids are both involved in STDP expression12,13,25,26,27,33,43 and in which eCB-LTP can occur, as it is the case in the striatum12,13, the hippocampus44,45,46,47,48 or the neocortex49 the emergence of STDP would be possible even in noisy conditions and could thus serve subsequently as a priming for the subsequent expression of NMDAR-tLTP.
In the present study, we explored the robustness of STDP when noise affects not only the spike timing but also the inter-pairing interval (IPI), i.e. the delay between two successive pairings. In the absence of jitter of the spike timing, our model predicts that IPI irregularity tends to consolidate tLTP at the expense of tLTD. This prediction that irregular IPIs strengthen tLTP when the spike timing is constant confirms the result obtained independently and with different mathematical models7,19,22,24. When IPIs are regular, adding jitter of the spike timing in our model progressively suppresses STDP. However, with more irregular IPIs our model predicts that the three STDP forms should exhibit larger robustness to noise. Therefore our result suggests that jittering of the spike timing has larger impact on STDP when the IPIs are regular, but that jittering has much less consequence with irregular IPIs. Experimental testing of this model prediction would greatly improve our understanding of the induction and maintenance of STDP in in vivo-like firing.
Subthreshold postsynaptic depolarization is a key factor in the induction of plasticity50. The existence of plasticity induced by STDP-like protocols without postsynaptic spikes (subthreshold-depolarization-dependent plasticity, SDDP) has been reported in the neocortex51, striatum52 and hippocampus53. In the striatum, SDDP differs from STDP on two aspects: (i) SDDP was induced in a larger temporal window (−100 < ΔtSTDP < +100 ms) and (ii) tLTP and tLTD were induced regardless of the spike timing. Therefore, the action potential would not be necessary for plasticity induction, but determinant for the STDP polarity and the width of the ΔtSTDP. The effects of jitter remain to be determined on SDDP, i.e. subthreshold events.
The polarity of plasticity depends greatly on the frequency of stimulus presentation. Indeed, prolonged firing activity at low and high frequency promote LTD and LTP, respectively, at the same synapses in hippocampus54,55,56. However, alteration of a regular low-frequency stimulation (900 stimulations at 1 Hz) with Poisson-distributed interstimulus intervals (as an approximation of naturalistic patterns) prevents LTD expression in the neocortex57. Interestingly, this LTD induced with regular low-frequency stimulation has been reported to be NMDAR-mediated58, and we show here that NMDAR-plasticity is fragile to jitter especially for low firing rate (1 Hz). It remains thus to investigate in a rate-based paradigm whether Poisson stimulation would erase LTD induced by higher firing rate (3–5 Hz54). Various forms of naturalistic patterns as an attempt to mimic in vivo activity have been experimentally tested for plasticity expression: from single burst of dendritic spikes, which induced NMDAR-LTP in hippocampus59 and NMDAR-LTD in neocortex60, to noisy STDP-like protocols7,19,20,22 and burst-timing-dependent plasticity paradigms61. Based on data harvested in the neocortex, a phenomenological computer modeling showed that for constant frequencies but random spiking, LTP wins over LTD with increasing frequency7. Activity patterns recorded in vivo during specific behavioral tasks have been replayed ex vivo to test their ability to induce plasticity19,56,62. When sequences of spike trains recorded in vivo from visual cortex of the anaesthetized cat in response to natural scenes were replayed ex vivo in layer 2/3 pyramidal cells of rat visual cortex, both LTP and LTD was observed experimentally and modeling suggested the importance of suppressive interactions between spikes19. In the dentate gyrus, in vivo patterns recorded in granule cell during a task of delayed nonmatch-to-sample were able in most of the cases to induce LTP at mossy fibers56. Similarly, when hippocampal place cells activity recorded in vivo were replayed ex vivo, NMDAR-LTP (also dependent on cholinergic tone) was observed62. Natural stimuli recruit various neuronal circuits leading to presynaptic jitter, which can have important physiological consequences. Indeed, in vivo visually driven presynaptic inputs induce presynaptic jitter leading to broader membrane potential events, and can consequently promote a spatial reorganization of the responses of neurons to neighboring stimuli within a receptive field, as demonstrated in the rat visual cortex22.
The debate about the nature of the neural coding, i.e. rate versus time codes63,64,65, is prominent when studying STDP. It remains to be tested with mathematical models and experiments whether activity patterns of various vigilance states differently result in the emergence of spike- or rate-coding plasticity. At most of the synapses both rate and time codes co-exist; for example at CA1 synapses, stimuli induced LTD at 2–3 Hz, no plasticity at 10 Hz and LTP at 50 Hz demonstrating a rate code54, and time codes are also supported as illustrated by the expression of various forms of STDP at the same synapse11. An answer to this debate could be that both rate and time codes work together for plasticity expression, as recently shown in the somatosensory cortex66, but their relative contribution in vivo would depend on the ongoing activity (low or high), the cerebral structures, the noise level, the neuromodulatory systems at play and the signaling pathways involved in plasticity expression (as shown in the present study). Briefly, it appears that STDP can emerge form low frequency activity whereas rate codes would take over for higher frequency ranges7,19,20,22.
A major conclusion from our present work is that the robustness of STDP to jitter depends on the underlying signaling pathways. For instance, the robustness of NMDAR-tLTP in our model is dependent on the amplitude of the activated CaMKII transients triggered by each post-pre pairings or on alterations of the ratio between the decay time of these transients and the IPIs. The robustness of STDP to jitter could be similarly controlled by quantitative variations in the underlying pathways. Such variations are expected to occur between two neuronal subtypes or brain regions but also as a result of the activation of a neuromodulatory pathway. Therefore, our work suggests that the expression of STDP in in vivo-like firing might appear or disappear as a result of modulations of its robustness to jitter, depending on the properties of the incoming patterns (reflecting for example fast learning or heavy training), but also on the brain region and, more transiently, on the activation of neuromodulatory pathways.
Methods
Animals and brain slice preparation
OFA (Oncins France Strain A) rats (Charles River, L’Arbresle, France) were used at postnatal day 25–32 for brain slice electrophysiology. All experiments were performed in accordance with the guidelines of the local animal welfare committee (Center for Interdisciplinary Research in Biology Ethics Committee) and the EU (directive 2010/63/EU). The experimental protocol (ref. 2017–02 N° 2016120110255176) was approved by the Ethics Committee in Charge of Animal Experimentation (Paris Centre et Sud). Every precaution was taken to minimize stress and the number of animals used in each series of experiments. Animals were housed in standard 12 hours light/dark cycles and food and water were available ad libitum. Horizontal brain slices containing the somatosensory cortical area and the corresponding corticostriatal projection field were prepared as previously described36. Corticostriatal connections (between somatosensory cortex layer 5 and the dorso-lateral striatum) are preserved in the horizontal plane. Brain slices (330 µm-thick) were prepared with a vibrating blade microtome (VT1200S, Leica Microsystems, Nussloch, Germany). Brains were sliced in an ice-cold cutting solution (125 mM NaCl, 2.5 mM KCl, 25 mM glucose 25 mM NaHCO3, 1.25 mM NaH2PO4, 2 mM CaCl2, 1 mM MgCl2, 1 mM pyruvic acid) through which 95% O2/5% CO2 was bubbled. The slices were transferred to the same solution at 34 °C for one hour and then to room temperature.
Patch-clamp recordings
Patch-clamp recordings were performed as previously described12,18. Briefly, for whole-cell recordings in borosilicate glass pipettes of 5–7 MΩ resistance were filled with (in mM): 122 K-gluconate, 13 KCl, 10 HEPES, 10 phosphocreatine, 4 Mg-ATP, 0.3 Na-GTP, 0.3 EGTA (adjusted to pH 7.35 with KOH). The composition of the extracellular solution was (mM): 125 NaCl, 2.5 KCl, 25 glucose, 25 NaHCO3, 1.25 NaH2PO4, 2 CaCl2, 1 MgCl2, 10 μM pyruvic acid bubbled with 95% O2 and 5% CO2. Signals were amplified using EPC10–2 amplifiers (HEKA Elektronik, Lambrecht, Germany). All recordings were performed at 34 °C (Bath-controller V, Luigs&Neumann, Ratingen, Germany) and slices were continuously superfused with extracellular solution, at a rate of 2 ml/min. Slices were visualized under microscope (BX51WI Olympus, Rungis, France), with a 4x/0.13 objective for the placement of the stimulating electrode and a 40x/0.80 water-immersion objective for the localization of cells for whole-cell recordings. Current- and voltage-clamp recordings were filtered at 5 kHz and sampled at 10 kHz, with the Patchmaster v2 × 32 program (HEKA Elektronik).
Spike timing-dependent plasticity protocols: regular and jittered patterns
Electrical stimulations were performed with a concentric bipolar electrode (Phymep, Paris, France) placed in layer 5 of the somatosensory cortex. Electrical stimulation was monophasic, at constant current (ISO-Flex stimulator, AMPI, Jerusalem, Israel). Cortical stimulations evoked glutamatergic excitatory postsynaptic currents (EPSCs) (inhibited by CNQX 10 μM and D-AP5 50 μM, n = 6) and not significantly affected by GABAergic events; Indeed, blocking GABAARs with picrotoxin (50 μM) did not significantly affect EPSC amplitude at corticostriatal synapses (123 ± 31 pA before and 118 ± 26 pA after picrotoxin, p = 0.500, n = 5). MSNs were kept at their resting membrane potential (−74.6 ± 0.6 mV, n = 90) and repetitive control stimuli were applied at 0.1 Hz. Currents were adjusted to evoke 50–200 pA EPSCs. STDP protocols consisted of pairings of pre- and postsynaptic stimulations (at 1 Hz) separated by a specific time interval (ΔtSTDP). The paired stimulations were applied at 1 Hz throughout the study except in Fig. 6a1 and a2 in which 3 Hz stimulations were tested. Presynaptic stimulations corresponded to cortical stimulations and the postsynaptic stimulation of an action potential evoked by a depolarizing current step (30 ms duration) in MSNs. ΔtSTDP < 0 ms for post-before-pre pairings, and ΔtSTDP > 0 ms for pre-before-post pairings. Neuronal recordings on neurons were made over a period of 10 minutes at baseline, and for at least 60 minutes after the STDP protocols. EPSC baseline stability was assessed by comparing the average of the EPSC magnitude of the two first and the two last minutes of baseline; if the variation of amplitude exceeded 10%, the experiment was discarded4. Recordings were stopped if the injected current was larger than 50 or 100–150 pA during the baseline and after pairings, respectively. We individually measured and averaged the amplitude of 60 successive EPSCs from both baseline and 45–55 minutes after STDP protocol, in which the latter was normalized by the former to calculate long-term synaptic efficacy changes. Neuron recordings were made in voltage-clamp mode during baseline and for the 60 minutes of recording after the STDP protocol, and in current-clamp mode during STDP protocol. Experiments were excluded if the input resistance (Ri), measured every 10 sec all along the experiment, varied by more than 20% during the very same time period where the EPSC amplitude were measured for plasticity assessment: 10 minutes of baseline and the 10 last minutes of the recording (generally 45–55 minutes after pairings). After recording of 10 min control baseline, drugs were applied in the bath. A new baseline with drugs was recorded after a time lapse of 10 min (to allow the drug to be fully perfused) for 10 min before the STDP protocol. Drugs were present until the end of the recording. All chemicals were purchased from Tocris (Ellisville, MO, USA), except for picrotoxin (Sigma). DL-2-amino-5-phosphono-pentanoic acid (D-AP5; 50 μM) and 6-cyano-7-nitroquinoxaline-2,3-dione (CNQX; 10 μM) were dissolved directly in the extracellular solution and bath applied. N-(piperidin-1-yl)-5-(4-iodophenyl)-1-(2,4-dichlorophenyl)-4-methyl-1H-pyrazole-3-carboxamide (AM251; 3 μM) and picrotoxin (50 μM) were dissolved in ethanol and added to the external solution, such that the final concentration of ethanol was 0.01–0.1%.
For the jittered ΔtSTDP patterns, we used the following algorithm (see Protocol 2, below). We note \({t}_{{{\rm{pre}}}_{i}}\) and \({t}_{{{\rm{post}}}_{i}}\) the times of the presynaptic and postsynaptic stimulations in the paired stimulation number i, respectively. To set them, we first fixed the times of each presynaptic stimulation using the pairing frequency, i.e. \({t}_{{{\rm{pre}}}_{i}}=\frac{i}{{F}_{{\rm{pairings}}}}\). The postsynaptic times were then chosen randomly according to \({t}_{{{\rm{post}}}_{i}}\) = \({t}_{{{\rm{pre}}}_{i}}\) + mΔt + ξΔt,i where mΔt is the average spike timing and ξΔt is a random variable with mean 0 and variance \({\sigma }_{{\rm{\Delta }}t}^{2}\). We defined the Inter-Pairing-Interval (IPI) as the time interval between the presynaptic stimulation times of two consecutive paired stimulations (\({{\rm{IPI}}}_{i}={t}_{{{\rm{pre}}}_{i+1}}-{t}_{{{\rm{pre}}}_{i}}\)), whereas the spike timing \(\xi t\) is the time interval between the postsynaptic and the presynaptic stimulation times within a given paired stimulation (\({\rm{\Delta }}{t}_{{{\rm{STDP}}}_{i}}={t}_{{{\rm{post}}}_{i}}-{t}_{{{\rm{pre}}}_{i}}\)). In a standard STDP protocol both the spike timing and the IPI are constant. The above algorithm yields constant IPIs and stochastic spike timings.
Electrophysiological data analysis
Off-line analysis was performed with Fitmaster (Heka Elektronik) and Igor-Pro 6.0.3 (Wavemetrics). Statistical analysis was performed with Prism 5.02 software. In all cases “n” refers to an experiment on a single cell from a single slice. All results are expressed as mean ± SEM in the text and as mean ± SD in the figures. Statistical significance was assessed in unpaired t tests, one way ANOVA, or in one-sample t tests, as appropriate, using the indicated significance threshold (p).
Mathematical model
Jittered STDP protocols
In the model, we define the spike timing as \({\rm{\Delta }}{t}_{{{\rm{STDP}}}_{i}}=\) \({t}_{{{\rm{post}}}_{i}}-{t}_{{{\rm{pre}}}_{i}}+\delta \) where δ accounts for the time elapsed between the onset of the postsynaptic step current and the action potential it triggers (~3 ms in MSNs). In agreement with the experiment protocol above, we introduced stochasticity of the spike timing by adding a random jitter ξΔt to the spike timing: ΔtSTDP = mΔt + ξΔt, were mΔt is the average spike timing and ξΔt is a random variable whose distribution is given by the STDP protocol. Here, we explored five STDP protocols:
-
(1)
Protocol 0 consisted of pairings with no jittering, i.e. \({{\rm{IPI}}}_{i}=\frac{1}{{F}_{{\rm{pairings}}}}\) and ξΔt = 0.
-
(2)
Protocol 1 consisted of deterministic IPIs and uniformly distributed spike timings (Fig. 2a1), i.e. \({{\rm{IPI}}}_{i}=\frac{1}{{F}_{{\rm{pairings}}}},\,\forall i\), and the probability distribution function of the jitter is given by
$$P({\xi }_{{\rm{\Delta }}t})=\{\begin{array}{cc}\frac{1}{2{\sigma }_{{\rm{\Delta }}t}} & {\rm{i}}{\rm{f}}\,|{\xi }_{{\rm{\Delta }}t}| < {\sigma }_{{\rm{\Delta }}t},\\ 0 & {\rm{o}}{\rm{t}}{\rm{h}}{\rm{e}}{\rm{r}}{\rm{w}}{\rm{i}}{\rm{s}}{\rm{e}}\end{array}$$(1)In eq. (1), σΔt defines the maximal jitter amplitude i.e. the level of noise in the protocol. To simulate Protocol 1, we first set each presynaptic stimulation time using \({t}_{{{\rm{pre}}}_{i}}=\frac{i}{{F}_{{\rm{pairings}}}}\). Postsynaptic times were then fixed by \({t}_{{{\rm{p}}{\rm{o}}{\rm{s}}{\rm{t}}}_{i}}\) = \({t}_{{{\rm{pre}}}_{i}}\) + mΔt + ξΔt,i − δ.
-
(3)
Protocol 2 (Fig. 2c1) shared the same definition as Protocol 1, except that the jitter followed a normal distribution with zero mean and variance \({\sigma }_{{\rm{\Delta }}t}^{2}\): \(P({\xi }_{{\rm{\Delta }}t})=\,{\mathscr{N}}(0,\,{\sigma }_{{\rm{\Delta }}t}^{2})\).
-
(4)
For Protocol 3 (Fig. 2d1), we used a triangular distribution of the jitter by adding uniformly distributed jitter to both presynaptic and postsynaptic times. We set \({t}_{{{\rm{pre}}}_{i}}=\frac{i}{{F}_{{\rm{pairings}}}}+{\zeta }_{{\rm{pre}},i}\) and \({t}_{{{\rm{post}}}_{i}}=\frac{i}{{F}_{{\rm{pairings}}}}+{m}_{{\rm{\Delta }}t}+{\zeta }_{{\rm{post}},i}-\delta \), where ζpre and ζpost are i.i.d. random variables with the uniform distribution of eq. (1). The resulting spike timing is ΔtSTDP = mΔt + ξΔt where ξΔt = ζpost − ζpre has a triangular distribution. Note that in this case, one still has \({{\rm{IPI}}}_{i}\approx \frac{1}{{F}_{{\rm{pairings}}}}\,\forall i\) as long as 2|mΔt|Fpairings ≪ 1, which can safely be assumed here since we used |mΔt| < 50 ms and Fpairings < 2 Hz.
-
(5)
Protocol 4 includes both a stochastic spike timing and stochastic IPIs (Fig. 2e1). We first sampled Npairings IPIs according to an exponential distribution with rate λ and refractory period τ r : P(IPI) = Θ (IPI − τ r )λ exp (−λ(IPI − τ r )), where Θ(x) is the Heaviside function Θ (x) = 1 if x ≥ 0; 0 otherwise. The spike trains defined with protocol 4 are thus Poisson process. We used these IPIs to fix the stimulation times, adding a triangularly distributed jitter as in Protocol 3 above: \({t}_{{{\rm{pre}}}_{i}}={\sum }_{j < i}{{\rm{IPI}}}_{j}+{\zeta }_{{\rm{pre}},i}\) and \({t}_{{{\rm{post}}}_{i}}={\sum }_{j < i}{{\rm{IPI}}}_{j}+{m}_{{\rm{\Delta }}t}+{\zeta }_{{\rm{post}},i}-\delta \). To keep the average stimulation frequency at 1/Fpairings, we constrained the value of the rate λ as λ = (1/Fpairings − τ r )−1.
Stimulations
A detailed account of our mathematical model can be found in S1 Text. We modeled glutamate concentration in the synaptic cleft, G(t), as a train of exponentially-decaying impulses triggered by presynaptic stimuli at time \({t}_{{{\rm{pre}}}_{i}}\). We modeled the electrical response to these stimulations in a postsynaptic element considered as a single isopotential compartment with AMPAR, NMDAR, VSCC and TRPV1 conductances:
where V is membrane potential; gL and VL are leak conductance and reversal potential respectively; IAMPAR, INMDAR, IVSCC and ITRPV1 are currents through AMPAR, NMDAR, L-type VSCC (v1.3) and TRPV1 respectively. Iaction is the action current resulting from the postsynaptic stimulation (backpropagating action potential on top of a 30 ms depolarization). Details about the analytical expressions of these currents are given in S1 Text.
Biochemical signaling
We modeled the kinetics of the biochemical pathways activated by the above electrical stimulations using the model of ref.13. We give below a quick overview of this model and refer to S1 Text for the details. Free cytosolic calcium is one of the main signaling actors in the model. To model its dynamics, we assumed calcium can be transferred from/to two main sources: (i) extracellular calcium, via the plasma membrane channels of eq. (2) above and (ii) the endoplasmic reticulum (ER), via the IP3-dependent calcium-induced calcium release system. These calcium transients activated a network of biochemical pathways that collectively set the synaptic weight. Hence, in this model, the synaptic weight is entirely fixed by the underlying biochemical signaling network13. More precisely, we assumed that the total synaptic weight is the product of a pre- and a postsynaptic contribution Wtotal = WpreWpost. Postsynaptic plasticity was based on the activation by calcium of calmodulin and CaMKII67,68. We assumed that postsynaptic plasticity is directly proportional to the calcium-dependent activation of CaMKII:
where CaMKII* and \(CaMKI{I}_{{\rm{\max }}}^{\ast }\) are the current concentration of activated (phosphorylated) CaMKII and its maximum value.
Our model also accounts for the biochemical pathways leading to the production of the endocannabinoids 2-arachidonoylglycerol (2-AG) and AEA, and their subsequent activation of CB1R (see S1 Text for further details). In our model, CB1R activation (yCB1R) controls the presynaptic weight Wpre according to the following rule:
and
Details about model implementation and numerics are given in the supplementary information.
References
Takeuchi, T., Duszkiewicz, A. J. & Morris, R. G. M. The synaptic plasticity and memory hypothesis: encoding, storage and persistence. Philos. Trans. R. Soc. Lond., B, Biol. Sci. 369, 20130288 (2014).
Debanne, D., Gähwiler, B. H. & Thompson, S. M. Bidirectional associative plasticity of unitary CA3-CA1 EPSPs in the rat hippocampus in vitro. J. Neurophysiol. 77, 2851–2855 (1997).
Magee, J. C. & Johnston, D. A synaptically controlled, associative signal for Hebbian plasticity in hippocampal neurons. Science 275, 209–213 (1997).
Markram, H., Lübke, J., Frotscher, M. & Sakmann, B. Regulation of synaptic efficacy by coincidence of postsynaptic APs and EPSPs. Science 275, 213–215 (1997).
Bi, G. & Poo, M. Synaptic Modifications in Cultured Hippocampal Neurons: Dependence on Spike Timing, Synaptic Strength, and Postsynaptic Cell Type. J. Neurosci. 18, 10464–10472 (1998).
Zhang, L. I., Tao, H. W., Holt, C. E., Harris, W. A. & Poo, M. A critical window for cooperation and competition among developing retinotectal synapses. Nature 395, 37–44 (1998).
Sjöström, P. J., Turrigiano, G. G. & Nelson, S. B. Rate, timing, and cooperativity jointly determine cortical synaptic plasticity. Neuron 32, 1149–1164 (2001).
Feldman, D. E. The spike-timing dependence of plasticity. Neuron 75, 556–571 (2012).
Madadi Asl, M., Valizadeh, A. & Tass, P. A. Dendritic and Axonal Propagation Delays Determine Emergent Structures of Neuronal Networks with Plastic Synapses. Sci Rep 7, 39682 (2017).
Froemke, R. C., Tsay, I. A., Raad, M., Long, J. D. & Dan, Y. Contribution of individual spikes in burst-induced long-term synaptic modification. J. Neurophysiol. 95, 1620–1629 (2006).
Wittenberg, G. M. & Wang, S. S.-H. Malleability of spike-timing-dependent plasticity at the CA3-CA1 synapse. J. Neurosci. 26, 6610–6617 (2006).
Cui, Y. et al. Endocannabinoids mediate bidirectional striatal spike-timing-dependent plasticity. J. Physiol. (Lond.) 593, 2833–2849 (2015).
Cui, Y. et al. Endocannabinoid dynamics gate spike-timing dependent depression and potentiation. Elife 5, e13185 (2016).
Sjöström, P. J. & Häusser, M. A Cooperative Switch Determines the Sign of Synaptic Plasticity in Distal Dendrites of Neocortical Pyramidal Neurons. Neuron 51, 227–238 (2006).
Clopath, C., Büsing, L., Vasilaki, E. & Gerstner, W. Connectivity reflects coding: a model of voltage-based STDP with homeostasis. Nat. Neurosci. 13, 344–352 (2010).
Pawlak, V., Wickens, J. R., Kirkwood, A. & Kerr, J. N. D. Timing is not Everything: Neuromodulation Opens the STDP Gate. Front Synaptic Neurosci 2 (2010).
Frémaux, N. & Gerstner, W. Neuromodulated Spike-Timing-Dependent Plasticity, and Theory of Three-Factor Learning Rules. Front Neural Circuits 9, 85 (2015).
Valtcheva, S. & Venance, L. Astrocytes gate Hebbian synaptic plasticity in the striatum. Nat Commun 7 (2016).
Froemke, R. C. & Dan, Y. Spike-timing-dependent synaptic modification induced by natural spike trains. Nature 416, 433–438 (2002).
Celikel, T., Szostak, V. A. & Feldman, D. E. Modulation of spike timing by sensory deprivation during induction of cortical map plasticity. Nat. Neurosci. 7, 534–541 (2004).
Morrison, A., Diesmann, M. & Gerstner, W. Phenomenological models of synaptic plasticity based on spike timing. Biol Cybern 98, 459–478 (2008).
Pawlak, V., Greenberg, D. S., Sprekeler, H., Gerstner, W. & Kerr, J. N. D. Changing the responses of cortical neurons from sub- to suprathreshold using single spikes in vivo. Elife 2, e00012 (2013).
Abbott, L. F. & Nelson, S. B. Synaptic plasticity: taming the beast. Nat. Neurosci. 3(Suppl), 1178–1183 (2000).
Graupner, M., Wallisch, P. & Ostojic, S. Natural Firing Patterns Imply Low Sensitivity of Synaptic Plasticity to Spike Timing Compared with Firing Rate. J. Neurosci. 36, 11238–11258 (2016).
Sjöström, P. J., Turrigiano, G. G. & Nelson, S. B. Neocortical LTD via coincident activation of presynaptic NMDA and cannabinoid receptors. Neuron 39, 641–654 (2003).
Bender, V. A., Bender, K. J., Brasier, D. J. & Feldman, D. E. Two Coincidence Detectors for Spike Timing-Dependent Plasticity in Somatosensory Cortex. J Neurosci 26, 4166–4177 (2006).
Nevian, T. & Sakmann, B. Spine Ca2+ signaling in spike-timing-dependent plasticity. J. Neurosci. 26, 11001–11013 (2006).
Banerjee, A. et al. Double dissociation of spike timing-dependent potentiation and depression by subunit-preferring NMDA receptor antagonists in mouse barrel cortex. Cereb. Cortex 19, 2959–2969 (2009).
Fino, E. et al. Distinct coincidence detectors govern the corticostriatal spike timing-dependent plasticity. J. Physiol. (Lond.) 588, 3045–3062 (2010).
Sjöström, P. J., Rancz, E. A., Roth, A. & Häusser, M. Dendritic excitability and synaptic plasticity. Physiol. Rev. 88, 769–840 (2008).
Korte, M. & Schmitz, D. Cellular and System Biology of Memory: Timing, Molecules, and Beyond. Physiol. Rev. 96, 647–693 (2016).
Pawlak, V. & Kerr, J. N. D. Dopamine receptor activation is required for corticostriatal spike-timing-dependent plasticity. J. Neurosci. 28, 2435–2446 (2008).
Shen, W., Flajolet, M., Greengard, P. & Surmeier, D. J. Dichotomous dopaminergic control of striatal synaptic plasticity. Science 321, 848–851 (2008).
Paille, V. et al. GABAergic circuits control spike-timing-dependent plasticity. J. Neurosci. 33, 9353–9363 (2013).
Valtcheva, S. et al. Developmental control of spike-timing-dependent plasticity by tonic GABAergic signaling in striatum. Neuropharmacology 121, 261–277 (2017).
Fino, E., Glowinski, J. & Venance, L. Bidirectional activity-dependent plasticity at corticostriatal synapses. J. Neurosci. 25, 11279–11287 (2005).
Schulz, J. M., Redgrave, P. & Reynolds, J. N. J. Cortico-striatal spike-timing dependent plasticity after activation of subcortical pathways. Front Synaptic Neurosci 2, 23 (2010).
Graupner, M. & Brunel, N. STDP in a Bistable Synapse Model Based on CaMKII and Associated Signaling Pathways. PLOS Computational Biology 3, e221 (2007).
Goubard, V., Fino, E. & Venance, L. Contribution of astrocytic glutamate and GABA uptake to corticostriatal information processing. J. Physiol. (Lond.) 589, 2301–2319 (2011).
Markram, H., Wang, Y. & Tsodyks, M. Differential signaling via the same axon of neocortical pyramidal neurons. PNAS 95, 5323–5328 (1998).
Fino, E., Deniau, J.-M. & Venance, L. Cell-specific spike-timing-dependent plasticity in GABAergic and cholinergic interneurons in corticostriatal rat brain slices. J. Physiol. (Lond.) 586, 265–282 (2008).
Froemke, R. C., Poo, M.-M. & Dan, Y. Spike-timing-dependent synaptic plasticity depends on dendritic location. Nature 434, 221–225 (2005).
Tzounopoulos, T., Rubio, M. E., Keen, J. E. & Trussell, L. O. Coactivation of Pre- and Postsynaptic Signaling Mechanisms Determines Cell-Specific Spike-Timing-Dependent Plasticity. Neuron 54, 291–301 (2007).
Xu, J.-Y., Zhang, J. & Chen, C. Long-lasting potentiation of hippocampal synaptic transmission by direct cortical input is mediated via endocannabinoids. J. Physiol. (Lond.) 590, 2305–2315 (2012).
Wang, W. et al. A Primary Cortical Input to Hippocampus Expresses a Pathway-Specific and Endocannabinoid-Dependent Form of Long-Term Potentiation. eNeuro 3, ENEURO.0160–16.2016 (2016).
Zhu, P. J. & Lovinger, D. M. Persistent synaptic activity produces long-lasting enhancement of endocannabinoid modulation and alters long-term synaptic plasticity. J. Neurophysiol. 97, 4386–4389 (2007).
Lin, Q.-S. et al. Hippocampal endocannabinoids play an important role in induction of long-term potentiation and regulation of contextual fear memory formation. Brain Res. Bull. 86, 139–145 (2011).
Carlson, G., Wang, Y. & Alger, B. E. Endocannabinoids facilitate the induction of LTP in the hippocampus. Nat. Neurosci. 5, 723–724 (2002).
Maglio, L. E., Noriega-Prieto, J. A., Maraver, M. J. & Fernández de Sevilla, D. Endocannabinoid-Dependent Long-Term Potentiation of Synaptic Transmission at Rat Barrel Cortex. Cereb. Cortex 1–14, https://doi.org/10.1093/cercor/bhx053 (2017).
Lisman, J. & Spruston, N. Questions about STDP as a General Model of Synaptic Plasticity. Front. Synaptic Neurosci. 2 (2010).
Sjöström, P. J., Turrigiano, G. G. & Nelson, S. B. Endocannabinoid-dependent neocortical layer-5 LTD in the absence of postsynaptic spiking. J. Neurophysiol. 92, 3338–3343 (2004).
Fino, E., Deniau, J.-M. & Venance, L. Brief subthreshold events can act as Hebbian signals for long-term plasticity. PLoS ONE 4, e6557 (2009).
Brandalise, F. & Gerber, U. Mossy fiber-evoked subthreshold responses induce timing-dependent plasticity at hippocampal CA3 recurrent synapses. Proc. Natl. Acad. Sci. USA 111, 4303–4308 (2014).
Dudek, S. M. & Bear, M. F. Homosynaptic long-term depression in area CA1 of hippocampus and effects of N-methyl-D-aspartate receptor blockade. Proc. Natl. Acad. Sci. USA 89, 4363–4367 (1992).
Mulkey, R. M. & Malenka, R. C. Mechanisms underlying induction of homosynaptic long-term depression in area CA1 of the hippocampus. Neuron 9, 967–975 (1992).
Mistry, R., Dennis, S., Frerking, M. & Mellor, J. R. Dentate gyrus granule cell firing patterns can induce mossy fiber long-term potentiation in vitro. Hippocampus 21, 1157–1168 (2011).
Perrett, S. P., Dudek, S. M., Eagleman, D., Montague, P. R. & Friedlander, M. J. LTD induction in adult visual cortex: role of stimulus timing and inhibition. J. Neurosci. 21, 2308–2319 (2001).
Massey, P. V. et al. Differential roles of NR2A and NR2B-containing NMDA receptors in cortical long-term potentiation and long-term depression. J. Neurosci. 24, 7821–7828 (2004).
Remy, S. & Spruston, N. Dendritic spikes induce single-burst long-term potentiation. PNAS 104, 17192–17197 (2007).
Holthoff, K., Kovalchuk, Y., Yuste, R. & Konnerth, A. Single-shock LTD by local dendritic spikes in pyramidal neurons of mouse visual cortex. J. Physiol. (Lond.) 560, 27–36 (2004).
Butts, D. A., Kanold, P. O. & Shatz, C. J. A burst-based ‘Hebbian’ learning rule at retinogeniculate synapses links retinal waves to activity-dependent refinement. PLoS Biol. 5, e61 (2007).
Isaac, J. T. R., Buchanan, K. A., Muller, R. U. & Mellor, J. R. Hippocampal place cell firing patterns can induce long-term synaptic plasticity in vitro. J. Neurosci. 29, 6840–6850 (2009).
Shmiel, T. et al. Neurons of the cerebral cortex exhibit precise interspike timing in correspondence to behavior. PNAS 102, 18655–18657 (2005).
London, M., Roth, A., Beeren, L., Häusser, M. & Latham, P. E. Sensitivity to perturbations in vivo implies high noise and suggests rate coding in cortex. Nature 466, 123–127 (2010).
Brette, R. Philosophy of the Spike: Rate-Based vs. Spike-Based Theories of the Brain. Front. Syst. Neurosci. 9 (2015).
Zuo, Y. et al. Complementary contributions of spike timing and spike rate to perceptual decisions in rat S1 and S2 cortex. Curr. Biol. 25, 357–363 (2015).
Lindskog, M., Kim, M., Wikström, M. A., Blackwell, K. T. & Kotaleski, J. H. Transient calcium and dopamine increase PKA activity and DARPP-32 phosphorylation. PLoS Comput. Biol. 2, e119 (2006).
Fernandez, E., Schiappa, R., Girault, J.-A. & Le Novère, N. DARPP-32 is a robust integrator of dopamine and glutamate signals. PLoS Comput. Biol. 2, e176 (2006).
Acknowledgements
We thank the L.V. lab members for helpful suggestions and critical comments, in particular Sebastien Valverde for proofreading of the manuscript. This work was supported by grants from INSERM, Collège de France, the Agence Nationale pour la Recherche (Grant Dopaciumcity ANR-14-NEUC-0003), INRIA, CNRS, and the Ecole des Neurosciences de Paris.
Author information
Authors and Affiliations
Contributions
L.V. and H.B. designed the study; Y.C. and A.M. performed electrophysiological experiments and analysis; H.B. carried out the conception and the design of the mathematical model; H.B. and I.P. performed the acquisition and analysis of data from the mathematical model; H.B. and L.V. wrote the manuscript and all authors have edited and corrected the manuscript; L.V. supervised the whole study.
Corresponding authors
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Cui, Y., Prokin, I., Mendes, A. et al. Robustness of STDP to spike timing jitter. Sci Rep 8, 8139 (2018). https://doi.org/10.1038/s41598-018-26436-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-018-26436-y
This article is cited by
-
Environmental enrichment shapes striatal spike-timing-dependent plasticity in vivo
Scientific Reports (2019)
-
Dopamine–endocannabinoid interactions mediate spike-timing-dependent potentiation in the striatum
Nature Communications (2018)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.