Abstract
Organic/polymer transistors can enable the fabrication of large-area flexible circuits. However, these devices are inherently temperature sensitive due to the strong temperature dependence of charge carrier mobility, suffer from low thermal conductivity of plastic substrates, and are slow due to the low mobility and long channel length (L). Here we report a new, advanced characterization circuit that within around ten microseconds simultaneously applies an accurate large-signal pulse bias and a small-signal sinusoidal excitation to the transistor and measures many high-frequency parameters. This significantly reduces the self-heating and therefore provides data at a known junction temperature more accurate for fitting model parameters to the results, enables small-signal characterization over >10 times wider bias I–V range, with ~105 times less bias-stress effects. Fully thermally-evaporated vertical permeable-base transistors with physical L = 200 nm fabricated using C60 fullerene semiconductor are characterized. Intrinsic gain up to 35 dB, and record transit frequency (unity current-gain cutoff frequency, fT) of 40 MHz at 8.6 V are achieved. Interestingly, no saturation in fT − I and transconductance (gm − I) is observed at high currents. This paves the way for the integration of high-frequency functionalities into organic circuits, such as long-distance wireless communication and switching power converters.
Similar content being viewed by others
Introduction
Organic electronics is expected to provide a technology platform for emerging applications which require large-area mechanically-flexible light-weight circuits. For instance, organic light-emitting devices have been demonstrated on plastic substrate for flexible and unbreakable displays1. Furthermore, organic devices can be made ultra-thin2,3, stretchable4, and can conformally interface with the skin and moving internal organs such as uneven heart tissue5, making them suitable for health monitoring and artificial electronic skins6. The use of organic transistors has also been demonstrated for ferroelectric memories7 and sophisticated electrical circuits. E.g. using inductively-coupled coil antennas, organic RFID tags can be employed for short distance (2–5 cm) wireless communication8, or a fully-printed bendable audio system has been demonstrated9, consisting of a 128 cm2 piezo-polymer loudspeaker and a self-biased organic audio amplifier.
While compact device modeling is a key requirement for complex circuit simulation and system design, accurate device characterization and parameter extraction is a prerequisite for fine tuning and optimization of model parameters. In this regard, the characterization and modeling of organic transistors is for two reasons particularly difficult: Firstly, there are unusual physical effects in organic transistors that cause serious difficulties when extracting static modeling parameters such as charge carrier mobility or gate-source capacitance. For example, when using conventional long-channel Field-Effect Transistor (FET) equations for calculating the charge carrier mobility, the presence of a kink in the transfer I–V characteristic can cause significant mobility overestimation10,11; large contact or source/drain electrode resistances result in large mobility underestimation12,13; or measuring the gate capacitance at high frequencies and using this value for extracting the mobility from DC, i.e. near 0 Hz, I–V measurements brings an additional error if there is a strong gate capacitance frequency dependence13.
Secondly, there are also time-dependent processes happening in organic transistors such as self-heating and bias-stress so that the dynamic behavior of organic FETs is insufficiently described by state-of-the-art DC parameter models.
Self-heating is an important physical effect which occurs during the device characterization at high DC I× V points and has two major drawbacks. First, it results in an unknown device junction temperature if the junction-to-substrate thermal resistance is not known, making the measured data unsuitable for fitting any compact models into it. Second, junction burning or breakdown limits the maximum I–V point at which the device can be characterized, whereas in some real circuits such as digital logic gates and super regenerative oscillators only a very high transient pulse current is passing through the device during the switching or on time.
Self-heating is an issue in all semiconductor-based devices, but organic transistors are inherently more sensitive to it because their charge carrier mobility strongly increases with temperature14,15, and their source/drain metal electrode to polymer channel contact resistance rapidly decreases with it15. In addition, these devices are mostly intended for flexible plastic substrates, which are in general very poor thermal conductors resulting in large junction to substrate thermal resistance. This problem is partly alleviated by low current densities in organic devices. However, these devices generally work instead at relatively higher voltage levels, and the current density will increase by development of higher mobility organic semiconductors in the future.
Device measurement can be divided into two general domains of large-signal and small-signal measurements. For the large-signal I–V characterization, the self-heating can be suppressed by applying short pulses instead of long-time DC biasing14. This can be easily done using existing commercial equipment such as the Keysight Precision Source/Measure Unit B2912A. However, for the case of small-signal measurements this is absolutely not straightforward and has not been done so far. All existing small-signal measurement techniques work based on the principle of long-time DC biasing of the device at a known I–V point, and then superimposing a known small-signal voltage/current on this DC bias at one input terminal of the device, and measuring the output small-signal voltage/current at another terminal of the device. For example, this approach has been used in our previous works13,16 for measuring the transconductance (gm), intrinsic gain (Av0), gate/base impedance, and current gain (h21); for S-parameter measurement17; and for transit frequency (fT) measurement18,19,20.
In this context, DC biasing of the device also has a third drawback. Most organic transistors still suffer from the bias-stress effect, which is due to the trapping of charge carries, and causes dynamic shift of the threshold voltage as well as the electric field inside the device21,22. Therefore, applying a DC bias during long-time measurements changes the characteristics of the device and reduces the accuracy and repeatability of the results.
In order to overcome the above-mentioned problems, we present in this paper for the first time an advanced pulse-biasing characterization circuit, which can turn on the organic transistor and apply an accurate bias I–V to it in less than ten microseconds, then apply a small sinusoidal signal to the device and measure several small-signal parameters such as h21, fT, gm and Av0, and then quickly turn off the device again. This approach significantly reduces the junction temperature increase, and allows measurements at much higher bias currents. In addition, the new setup can be used for measuring the temporal evolution of stress and self-heating effects over a μs to ms time scale.
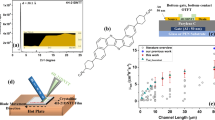
As a case study, we characterized the fully-thermally-evaporated n-type vertical Organic Permeable-Base Transistor (OPBT)23, shown in Fig. 1. The OPBT is a promising low-voltage high-current high-speed device, fabricated solely using low-resolution low-cost shadow masks. This transistor resembles triodes and bipolar junction transistors, but here we have a thin metal base layer that contains naturally occurring pores. The native aluminum oxide of this electrode leads to a channel formation around it and the fact that the base potential controls the electrons flowing from emitter to collector. Space charge limited current (SCLC) in the undoped C60 fullerene layers is the main limitation of this transistor24, whereas electron injection is very efficient due to the thin n-doped C60 layer. Details of the device fabrication and operation mechanism, DC I–V characteristics, SCLC and device simulation can be found in other publications23,24, as well as the methods section.
This manuscript is organized in the following way. Firstly, we demonstrate the pulse-biasing measurement results of an OPBT device including the small-signal performance, and the temporal evolution of the charge distribution and self-heating effects occurring in the device. Secondly, we focus on the characterization circuit and small-signal parameter extraction techniques. Finally, we discuss the consequences of our findings on the context of real circuit applications.
Case Study Measurement Results
Measurements are performed at a controlled room temperature of ~25 °C, on the samples shown in Fig. 1, with an active area of Aact = 200 μm × 200 μm, at three low/moderate/high collector-to-base voltages of VCB = 0.1 V/1.0 V/3.3 V, respectively.
Transfer large-signal pulse I–V characteristics of the OPBT are shown in Fig. 1(c), reaching a peak current of IE = 200 mA at a total voltage of VCE = VCB + VBE = 8.6 V. This corresponds to a current density of 5 μA/μm2 in the Aact. At VCE = 1.0 V, the device can still drive 47 nA/μm2.
Transit Frequency (fT)
The small-signal current gain (h21) is defined as the ratio of the small-signal collector current (ic) over the small-signal base current (ib) measured when both emitter and collector are small-signal AC ground.
An example of the magnitude of h21 as a function of frequency at a pulse bias IE = 1.0 mA at three different VCB is shown in Fig. 2(a). The h21 is decreasing ~20 dB per decade (i.e. proportional to 1/f) as known for conventional transistors. fT is defined as the frequency at which the extrapolation from the low frequency part of h21 falls to unity. It is an important figure of merit of a transistor, indicating the frequency range in which the device can amplify the input current signal.
Measured small-signal performance of the OPBT with Aact = 200 μm × 200 μm. (a) Current gain at 1 mA pulse bias versus frequency. (b) Transit frequency versus pulse-biased emitter current. (c) Transconductance versus pulse-biased emitter current. (d) Intrinsic voltage gain Av0 versus pulse-biased emitter current.
Measured fT versus pulse bias emitter current is shown in Fig. 2(b), reaching fT = 40 MHz at pulse IE = 200 mA; i.e. current density of 5 μA/μm2; at VCB = 3.3 V, VBE = 5.3 V and VCE = 8.6 V; measured at the shortest possible pulse duration of ~10 μs. To the best of our knowledge, this is the highest measured fT for an organic transistor so far. As a comparison, fT = 27.7 MHz at around three times higher voltage of VDS = 25 V for C60, and 11.4 MHz for Pentacene at 25 V were previously reported for planar transistors on glass substrate19, fabricated using high-resolution patterning techniques such as photolithography and lift-off process. fT = 20 MHz at 30 V was achieved using laser sintering of high resolution electrodes on glass18. In vertical structures, fT = 1.5 MHz was reported for step edge devices25, and fT = 20 MHz at 15 V for a 3D transistor structure20.
Transconductance (gm)
The effective transconductance versus pulse bias current is shown in Fig. 2(c) and is calculated as the ratio of the ic to the small-signal base-emitter voltage; measured below the frequency of fT/10. Interestingly, no saturation of the gm-eff at high current densities is observed. This indicates that the parasitic emitter resistance RE is small, otherwise gm-eff = gm/(1 + gm × RE) would eventually saturate to 1/RE at high currents. The small RE means that the electrode resistance is small and the n-C60 doped layer is making low impedance interfaces to both Cr and intrinsic-C60 layers.
Considering the equation fT ≈ gm/(2π × (Cbe + Cbc)), increasing the VCB bias from 0.1 V to 3.3 V at fixed IE in Fig. 2(c) improves the transconductance, however, the amount of the corresponding fT or h21 improvement at the same IE in Fig. 2(b or a) is always higher, e.g. X2 is 89% more than X1. This is because of the fact that increasing the VCB depletes the collector-base C60 layer from the charge carriers, and this also reduces the Cbc and therefore further improves the fT.
Intrinsic Gain (Av0)
Intrinsic gain is the maximum small-signal voltage gain that a device can provide, and is equal to gm × rout, where rout = ∂VCE/∂IC is the output resistance of the device. Basically a transistor with Av0 less than one, i.e. 0 dB, is a useless device, because it cannot perform any amplification.
In general, Av0 decreases with scaling down the channel length. However, as shown in Fig. 2(d), OPBT can provide a good gain of 35 dB at low currents and a fairly acceptable gain of 16 dB at the fT = 40 MHz bias point, i.e. IE = 200 mA, with a short physical L = 200 nm. With Av0 = 16 dB, one can make an amplifier with a gain of 10 dB per stage by means of the bootstrapping technique16.
A diffusion-driven organic transistor was recently reported26, which can even provide 57 dB of intrinsic gain at W/L = 100 μm/12.5 μm. However, this transistor can drive less than 200 nA at tens of volt, and therefore is only suitable for very low-current low-speed applications.
Temporal Evolution of Charge Distribution, Self-Heating and Bias-Stress
The charge carrier mobility in organic semiconductors is known to improve with temperature. In addition, polymeric materials as used for plastic substrates are generally weak thermal conductors. For these reasons, gradual self-heating of organic devices at high I × V points has a large impact on the device characteristics.
As will be explained in the next section, the developed pulse-biasing setup can also accurately monitor the variations of VBE, i.e. ΔVBE after applying a fixed IE to the device. Measuring the temporal evolution of this ΔVBE allows to study the effect of self-heating with the highest sensitivity, because in case of self-heating, this ΔVBE would be proportional to the increase of the device temperature, i.e. ΔT, and therefore to the power dissipated in the device. This fact is because organic semiconductors have usually strongly increasing mobility with temperature14,15. Further, the contact resistance strongly decreases simultaneously15, resulting in a lower required VBE, i.e. negative ΔVBE, at fixed IE. This ΔVBE would be linearly proportional to ΔT when ΔT is small, but in general it is a nonlinear function.
For the purposes of comparison and verification of this method, ΔVBE of a general purpose, silicon Bipolar Junction Transistor (BJT) is measured at two different IE × VCE products of 100 mW and 200 mW, and is shown in Fig. 3(a). Conventional BJT is also a vertical device, but the silicon substrate conducts heat around 10 times better than the glass. In this experiment, tracking of the VBE variation is started 90 μs after turning on the device. The VBE variation during the initial 90 μs was smaller than the accuracy of the measurement setup. 200 mW is applied one time by doubling the current and one time by doubling the voltage. As expected, in both cases ΔVBE is nearly two times that of the 100 mW. This confirms that here we only have self-heating, but no stress effects.
VBE change due to self-heating, lateral diffusion of charge carriers and bias-stress. (a) Self-heating in a standard silicon bipolar junction transistor, 2N3904. (b) The OPBT at low-current, only showing lateral diffusion of charge carriers. (c) The OPBT at high-current, showing both self-heating and lateral diffusion of charge carriers. (d) Long-time bias-stress in the OPBT.
Similar experiments are performed on the OPBT at two low and high current levels as shown in Fig. 3(b and c). The VBE and VCE given in this figure are average values over the measurement time. In Fig. 3(b), although we have a considerable amount of ΔVBE at 1 mA × 1.6 V, surprisingly, doubling the VCE does not affect the ΔVBE, whereas doubling the current increases it by ~60%. This proves that in this case the observed effect is not self-heating.
As shown in Fig. 1(a), although the emitter window is 200 μm × 200 μm, the underneath base and collector electrodes are wider. Therefore we speculate that this effect is induced by the lateral diffusion of some of the electrons accumulated around the base oxide towards the outside of this window. This diffusion gradually increases the effective active area of the channel, and therefore decreases the required VBE at the fixed IE = 1 mA by the amount of ~9% after 200 ms in Fig. 3(b). Increasing the collector voltage has a small impact on the charge in the C60 layer of the emitter side, whereas increasing the IE largely affects this charge density and the required VBE.
At a 15 times higher IE × VCE shown in Fig. 3(c), doubling the current increases the ΔVBE ~95%, but here doubling the voltage also increases it ~66%. This indicates that in this case in addition to the lateral diffusion of the charge carriers, self-heating is also occurring and is important. Since self-heating has a considerable impact after hundreds of μs at 10 mA, obviously at 100 mA range it would already have an impact after tens of μs. In order to circumvent this effect, the pulse-biasing circuit developed here can turn on and apply an accurate bias to the device under test within few μs, and immediately start doing small-signal analysis afterwards.
Figure 3(d) shows a long-time DC stress measurement, performed using the Keysight B2912A Precision SMU, at a very low current of 100 μA at which self-heating would be negligible. The ΔVBE tracking is started ~200 ms after turning on the device. Here, we clearly see different mechanisms occurring in different directions. The ΔVBE initially goes negative due to the lateral charge diffusion, but finally starts increasing due to the bias-stress effect. Surprisingly, the lateral charge diffusion seems to be the dominant effect for an incredibly long time of ~1000 s. This might really be the case, because far away from the Aact there is no lateral electric field, and the undoped C60 layer could be extremely resistive causing very slow diffusion of electrons. However, other unknown mechanisms might also be the reason, such as very slow changes in the morphology of C60 or base-oxide under the electric field. We cannot provide a concrete explanation for the observed behavior. Anyway, it is a very slow and small effect in the mV range.
Pulse-Biasing Small-Signal Characterization Circuit
Figure 4 shows the simplified schematic of the new measurement setup. Examples of the waveforms are illustrated in Fig. 5. An accurate 1 V reference is generated using the LT1004 voltage reference, and is used for defining the pulse IE passing through RE1 = 1 V/IE as shown in Fig. 5(b). DC voltage at the base electrode is zero. ME3 forces VE = 0 V when there is no VG pulse, keeping the OPBT off. The 10 V low-duty-cycle gating pulse VG turns on ME2 on its rising edge to start the pulse bias current IE, and turns off ME3. The small-signal excitation comes from the sinusoidal source 2 × Vin*, while CE1 and CC2 keep both emitter and collector at small-signal AC ground. Applying and stabilizing of the bias point at different nodes is done over the time interval of 0 to ~6 μs. Circuit parameters such as VD1, VE1 and RC1 are manually tuned to minimize this initialization time. The small-signal measurements are carried out afterwards.
Signal waveforms of the characterization setup at pulse IE = 10 mA and bias VCB = 1 V, RE1 = 100 Ω, CE1 = 0.35 μF, CE2 = 0.1 μF, CC2 = 0.22 μF, LC1 = 5 μH, RC2 = 50 Ω, RB1 = 4.7 kΩ, RB4 = 1 MΩ and frequency = 1 MHz. (a–h) Signals are measured concurrently at Vin = 600 mVrms. (i) Vout is measured at Vin = 0 Vrms.
At the base side, we have RB4 ≫ RB1 ≫ 50 Ω, and the input base impedance |Zb| ≈ 1/Cbω<<RB1 at the measurement frequency. The diode DB1 has less than 0.3 pF parasitic capacitance and is completely off during the small-signal measurement time.
h21 and gm Measurement Circuitry
The small-signal sinusoidal excitation comes from a differential signal generator. The invert of Vin arrives at the oscilloscope, and then Vin is calculated from it. The Cables 1–4 are 50 Ω, i.e. Vin and VinB are slightly delayed versions of Vin*. Since RB1 ≫ 50 Ω we have |VinB| ≈ |Vin*| = |Vin|. ic/ib/ie are small-signal currents into the collector/base/emitter, respectively. As long as RB1 > 7/Cbω, |ib| can be estimated as |Vin|/RB1 with less than 1% error. However, by measuring the signal amplitude at VB using a high-impedance probe, as shown in Fig. 5(g), we can calculate the input base capacitance Cb and then calculate |ib| even more precisely.
At the collector side, the large-bandwidth op-amp O1 forces n3 to be ground and the large coupling capacitor CC2 keeps the collector to be AC ground. LC1 provides a path for the pulse IE bias current, and LC1ω ≫ 1/CC2ω, i.e. most of the ic passes through CC2, but CC2 is so large that the small-signal voltage amplitude at the collector is much smaller than the signal at the base. It is possible to calculate the exact value of |ic| using the equation given in Fig. 4. Since IE is a pulse, it is important to make sure that LC1–CC2 do not cause additional ringing on the Vout. This is assured by tuning RC1 ≈ 2 × sqrt(LC1/CC2). As shown in Fig. 5(i), when IE pulse is applied but Vin is zero, no ringing appears on the Vout after Time = 6 μs. A 50 pF capacitor is added to the feedback loop around O1 to improve the stability.
Cable1 is intentionally twice the length of Cables 2 and 3; so that the signal delay from Vin* to VinB plus the signal delay from n4 at the output of the op-amp O1 to Vout would be equal to the delay along Cable1. In this way, we could also measure the phase of h21 by measuring the phase difference between Vin and Vout on the oscilloscope. However, only the magnitude of h21 is needed to extract the fT, and |h21| = |ic|/|ib|.
At the emitter side, a very large CE1, in the μF range, is needed to keep the emitter at AC ground during the small-signal measurement after Time = 6 μs. On the other hand, a time much larger than T0 = VBE × CE1/IE would be needed for VE to reach its required value; with the parameter values given in Fig. 5, this would be T0 = 57 μs. In order to significantly speed up this initialization time, the power switch ME4 is added. During the long off time, i.e. VG = 0 V, CE2 is charged to a tunable voltage VD1 in the range of 0–30 V, and then on the rising edge of VG, a very large transient current up to VD1/1.5 Ω is sunk through CE2 and as shown in Fig. 5(c) this current quickly charges CE1 to a VBE that enables an OPBT current exactly equal to the IE. However, this is true only if after this initialization time, no part of the IE passes through CE1,2,4. In other words, the gradual slope of VE should become zero.
To accurately monitor the gradual slope and variations of VE after its sharp falling edge, VG turns on ME5 for the first 1–3 μs, and during this time the small capacitor CE4 is charged to the initial emitter voltage. Then the kΩ resistor RE2 quickly pulls n1 to 0 V, turning off ME5, resulting in a >4 GΩ resistance across ME5,6. Because of the large time constant of CE4 × RDS-ME5,6, any further mV variations at VE will be directly tracked at n2 and VS. VD1 is manually tuned to have ~0 mV/μs gradual slope at VS over the small-signal measurement interval. Comparing Fig. 5(c to d), the VS circuitry is providing ~25X zoom on the VE for accurate tuning of VD1. ME6 just forces n2 to ground on the falling edge of VG.
On the falling edge of VE, a large RB1 × Cb time constant can slow down the charging of the base-emitter capacitance and increase the required initialization time. To make this faster, on the rising edge of VG, a certain amount of charge is injected into the base through CB1-RB2-DB1. VE1 is a negative DC voltage that controls the amount of this charge, and turns off the DB1 afterwards. VE1 is manually tuned to keep VB around 0 V.
DC leakage current into the base, IB, is usually negligible. However, in case of a large IB, RB4 can be added, and VD2 controls the DC current injected into the base.
Intrinsic Gain Measurement Method
For measuring the intrinsic gain, VE is accurately measured at two slightly different collector voltages, but with equal pulse IE. Then we would have gm × ΔVBE = ΔVCE/rout. Therefore Av0 = gm × rout = ΔVCE/ΔVBE is obtained. For this measurement VB is grounded, CE1,2 are not needed, and VC is shorted to VDD.
Measurement Limits
The low-leakage BS170 MOSFET used as ME1,2 current source can drive up to ~300 mA into the OPBT. Larger MOSFETs with higher current drive capabilities, and accurate resistors down to 100 mΩ range for RE1 are widely available in the market. Therefore, accurate IE pulses up to 10 A should be feasible with the proposed circuit, but it was not needed in our case study. At IE < 1 μA range, the gate leakage through ME1,2 can cause bias inaccuracies; therefore ultra-low leakage MOSFETs would be needed for this case. The maximum bias voltages VCB and VBE are basically controlled by the VDD and VEE; there is no specific limit in this regard.
The shortest measurement pulse width is mainly limited by the required initialization time for reaching the steady state (~6 μs in Fig. 5); afterwards, the small-signal information can be extracted in principle even from one sinusoidal signal cycle. As can be seen in Fig. 5(b), the IE pulse settles in less than 2 μs. The charge injector circuitry ME4-CE2 has a very short R-C time constant of <160 ns. However, the OPBT capacitances and the frequency of the sinusoidal signal impose the main limitations on the initialization time. Although the charge injector path CB1-RB2-DB1 significantly speeds up the charging of the base capacitance Cb, as can be seen in Fig. 5(g), still some time (~3 μs) proportional to RB1 × Cb is needed for the VB to reach the steady state after DB1 turns off. On the collector side, CC2 should be more than 20 × 20 times larger than Cb to keep the small-signal voltage at VC twenty times smaller than VB at the frequency where |h21| = 20 is measured. We recommend LC1CC2ω2 > 10 so that the inaccuracy of the L-C components does not make large error in the ic equation in Fig. 4. Taking all these points into account, practically we found that by optimizing the circuit parameters, the initialization time can be minimized to 5–7 periods of the sinusoidal signal.
Further Discussions and Conclusion
The proposed pulse-biasing small-signal measurement circuit enables analog characterization of the device over >10 times wider I–V range comparing to the simple DC biasing approach13,23, and provides a much better control on the junction temperature by adjusting the pulse duration. It can also precisely track the ΔVBE at different power densities for better understanding of the self-heating effects.
For the ~12 μs measurement shown in Fig. 5, if we repeat the pulse every 1.2 s, the waveforms can still be well monitored on the oscilloscope, while the bias-stress rate in the device decreases by a factor of ~105 comparing to the DC biasing method. Therefore, many more measurements can be performed on the same fresh device during several days, providing reliable data for device modeling.
The OPBT currently suffers from a low charge carrier mobility in the vertical direction ~0.06 cm2/V.s23. However, the study presented in this work proved that despite this very low mobility, it can already reach the record fT of 40 MHz and the intrinsic gain of 35 dB at VCE = 8.6 V thanks to the short channel length. There is certainly a large room for further improvement of this speed by developing organic semiconductors which can provide higher mobility in the vertical direction. This can be better understood by considering the fact that in FETs, above the threshold region gm and therefore fT are proportional to sqrt(μ × IE). This gm − IE trend can be seen in Fig. 2(c), and more importantly, no gm or fT saturation is observed at high currents, confirming the room for reaching higher speeds. A higher mobility will also result in a lower bias voltage, power and self-heating for reaching the same IE. In planar organic FETs, mobility in the range of 3–30 cm2V−1s−1 has been reported by several groups12,27,28,29. Device simulations also predict sub-nano-second intrinsic switching delay for OPBTs with a mobility of 10 cm2/V.s30.
A fT ≥ 40 MHz can pave the way for integrating new functionalities into organic circuits and systems. Long-distance wireless communication is the first example, because in this case the key challenge is the extremely large size of the antenna required to have electromagnetic wave radiation in MHz regime. For example, an electrically-small single-turn loop antenna has a radiation resistance, and therefore efficiency, roughly proportional to frequency4 × D4, where D is the diameter of the loop; an antenna with D = 1 m radiates with an efficiency of 18% at 10.1 MHz31. Therefore, we can expect ~7% RF power radiation at 40 MHz with D = 20 cm which is a reasonable size for integration onto human body or cloth, or toys. Wireless communication can also be done in pulse mode. For example, super regenerative receivers, which are in use since 1940s32, turn on an oscillator just for a few μs, receive the data, and then turn it off again for a long time, similar to how we operated the device in this work.
As the second example, inductor-based switching power converters can be mentioned. Power supply is an essential part of any electronic system, and inductor-based switching power converters are the most energy efficient circuits widely used in up/down DC–DC converters and battery chargers. Key elements of such circuits are FET switches, diodes, inductors and capacitors. A typical switching circuit working with <1 μs pulses would require spiral inductors in the 10 μH range which can be easily fabricated by inkjet printing or evaporating a single metal layer on a plastic substrate with outer diameter <10 cm. Organic rectifying diodes already can work at tens of MHz33,34. Printed flexible 10 μF range multi-layer capacitors for power conversion applications have been demonstrated35 and show a high relative dielectric constant of 15–22 up to 10 MHz. In addition to the high fT, the high current drive capability of the OPBT is also an advantage for compatibility with this application. In this context, it also worth to mention that flexible batteries and organic solar cells are also already developed and even commercialized.
The pulse measurement results are also relevant for digital logic circuits in which we only have transient currents in the transistors.
Methods
The OPBT presented here is built in a single chamber UHV-tool. The glass substrate is previously cleaned with N-Methylpyrrolidone, distilled water, ethanol, and an Ultra Violet Ozone Cleaning System. By using thermal vapor deposition at high vacuum conditions (p < 10−7 mbar), the OPBT stack layers are deposited through laser-cut, stainless steel shadow masks. The layer stacks, evaporation rates, and treatments are: Al 100 nm (1.0 Å/s); Cr 10 nm (0.1 Å/s); i-C60 100 nm (1.0 Å/s); Al 15 nm (1 Å/s); 15 min oxidation at air; i-C60 100 nm; 2 times (perpendicular to each other) SiO 100 nm with a free stripe of 200 μm (1.0 Å/s); n-C60 20 nm (0.4 Å/s) co-evaporating C60 with W2(hpp)4 (purchased from Novaled GmbH, Dresden) with 1 wt%; Cr 10 nm (0.1 Å/s); Al 100 nm (1.0 Å/s); encapsulation in a nitrogen atmosphere using UV cured epoxy glue without UV exposure on the active area; annealing for 2 h at 150 °C in a nitrogen glove-box on a heat plate, for positively affecting both current-transmission through the base and regeneration of the air-exposed C6036,37.
The 50 pF capacitor across the op-amp O1 is a mica capacitor, but other capacitors in the circuit are polypropylene or polyester film capacitors. For CE1,2,4 polypropylene is preferred.
Figure 1(a) has been taken using the Nikon microscope ECLIPSE LV 100 ND. Dot lines are added around the base electrode and the active area. This photo is not recolored; base and collector look colorful because of the materials deposited on top of them; emitter electrode looks white because it is on the top.
Data availability
All data generated or analysed during this study are included in this published article.
References
Lee, S. M., Kwon, J. H., Kwon, S. & Choi, K. C. A Review of flexible OLEDs toward highly durable unusual displays. IEEE Transactions on Electron Devices 64, 1922–1931, https://doi.org/10.1109/TED.2017.2647964 (2017).
Fukuda, K. et al. Free-standing organic transistors and circuits with sub-micron thicknesses. Scientific Reports 6, 27450, https://doi.org/10.1038/srep27450 (2016).
Takeda, Y. et al. Fabrication of ultra-thin printed organic TFT CMOS logic circuits optimized for low-voltage wearable sensor applications. Scientific Reports 6, 25714, https://doi.org/10.1038/srep25714 (2016).
Oh, J. Y. et al. Intrinsically stretchable and healable semiconducting polymer for organic transistors. Nature 539, 411–415, https://doi.org/10.1038/nature20102 (2016).
Sekitani, T. et al. Ultraflexible organic amplifier with biocompatible gel electrodes. Nature Communications 7, 11425, https://doi.org/10.1038/ncomms11425 (2016).
Schwartz, G. et al. Flexible polymer transistors with high pressure sensitivity for application in electronic skin and health monitoring. Nature Communications 4, 1859, https://doi.org/10.1038/ncomms2832 (2013).
Katsouras, I. et al. Controlling the on/off current ratio of ferroelectric field-effect transistors. Scientific Reports 5, 12094, https://doi.org/10.1038/srep12094 (2015).
Fiore, V. et al. An integrated 13.56-MHz RFID tag in a printed organic complementary TFT technology on flexible substrate. IEEE Transactions on Circuits and Systems I: Regular Papers 62, 1668–1677, https://doi.org/10.1109/TCSI.2015.2415175 (2015).
Kheradmand-Boroujeni, B. et al. A fully-printed self-biased polymeric audio amplifier for driving fully-printed piezoelectric loudspeakers. IEEE Transactions on Circuits and Systems I: Regular Papers 63, 785–794, https://doi.org/10.1109/TCSI.2016.2538060 (2016).
Bittle, E. G., Basham, J. I., Jackson, T. N., Jurchescu, O. D. & Gundlach, D. J. Mobility overestimation due to gated contacts in organic field-effect transistors. Nature Communications 7, 10908, https://doi.org/10.1038/ncomms10908 (2016).
McCulloch, I., Salleo, A. & Chabinyc, M. Avoid the kinks when measuring mobility. Science 352, 1521–1522, https://doi.org/10.1126/science.aaf9062 (2016).
He, D. et al. Ultrahigh mobility and efficient charge injection in monolayer organic thin-film transistors on boron nitride. Science Advances 3, e1701186, https://doi.org/10.1126/sciadv.1701186 (2017).
Kheradmand-Boroujeni, B. et al. Small-signal characteristics of fully-printed high-current flexible all-polymer three-layer-dielectric transistors. Organic Electronics 34, 267–275, https://doi.org/10.1016/j.orgel.2016.04.037 (2016).
Fischer, A. et al. Self-heating, bistability, and thermal switching in organic semiconductors. Physical Review Letters 110, 126601, https://doi.org/10.1103/PhysRevLett.110.126601 (2013).
Hamadani, B. H. & Natelson, D. Temperature-dependent contact resistances in high-quality polymer field-effect transistors. Applied Physics Letters 84, 443–445, https://doi.org/10.1063/1.1639945 (2004).
Kheradmand-Boroujeni, B. et al. Analog Characteristics of Fully Printed Flexible Organic Transistors Fabricated with Low-Cost Mass-Printing Techniques. IEEE Transactions on Electron Devices 61, 1423–1430, https://doi.org/10.1109/TED.2014.2315038 (2014).
Zaki, T. et al. S-parameter characterization of submicrometer low-voltage organic thin-film transistors. IEEE Electron Device Letters 34, 520–522, https://doi.org/10.1109/LED.2013.2246759 (2013).
Perinot, A. et al. Direct-written polymer field-effect transistors operating at 20 MHz. Scientific Reports 6, 38941, https://doi.org/10.1038/srep38941 (2016).
Kitamura, M. & Arakawa, Y. High current-gain cutoff frequencies above 10 MHz in n-Channel C60 and p-Channel pentacene thin-film transistors. Japanese Journal of Applied Physics 50, 01BC01, https://doi.org/10.1143/JJAP.50.01BC01 (2011).
Uno, M., Cha, B.-S., Kanaoka, Y. & Takeya, J. High-speed organic transistors with three-dimensional organic channels and organic rectifiers based on them operating above 20 MHz. Organic Electronics 20, 119–124, https://doi.org/10.1016/j.orgel.2015.02.005 (2015).
Zschieschang, U., Weitz, R. T., Kern, K. & Klauk, H. Bias stress effect in low-voltage organic thin-film transistors. Applied Physics A 95, 139–145, https://doi.org/10.1007/s00339-008-5019-8 (2009).
Mathijssen, S. G. J. et al. Dynamics of threshold voltage shifts in organic and amorphous silicon field-effect transistors. Advanced Materials 19, 2785–2789, https://doi.org/10.1002/adma.200602798 (2007).
Klinger, M. P. et al. Organic power electronics: transistor operation in the kA/cm2 regime. Scientific Reports 7, 44713, https://doi.org/10.1038/srep44713 (2017).
Kaschura, F. et al. Operation mechanism of high performance organic permeable base transistors with an insulated and perforated base electrode. Journal of Applied Physics 120, 094501, https://doi.org/10.1063/1.4962009 (2016).
Kudo, K., Takano, T., Yamauchi, H., Iizuka, M. & Nakamura, M. High-speed operation of step-edge vertical-channel organic transistors with pentacene and 6,13-Bis(triisopropyl-silylethynyl) pentacene. Japanese Journal of Applied Physics 49, 04DK03, https://doi.org/10.1143/JJAP.49.04DK03 (2010).
Torricelli, F., Colalongo, L., Raiteri, D., Kovács-Vajna, Z. M. & Cantatore, E. Ultra-high gain diffusion-driven organic transistor. Nature Communications 7, 10550, https://doi.org/10.1038/ncomms10550 (2016).
Chen, H. et al. Dithiopheneindenofluorene (TIF) semiconducting polymers with very high mobility in field-effect transistors. Advanced Materials 29, 1702523, https://doi.org/10.1002/adma.201702523 (2017).
Iino, H. & Hanna, J. Liquid crystalline organic semiconductors for organic transistor applications. Polymer Journal 49, 23–30, https://doi.org/10.1038/pj.2016.101 (2017).
Pauli, Md, Zschieschang, U., Barcelos, I. D., Klauk, H. & Malachias, A. Tailoring the dielectric layer structure for enhanced carrier mobility in organic transistors: the use of hybrid inorganic/organic multilayer dielectrics. Advanced Electronic Materials 2, 1500402, https://doi.org/10.1002/aelm.201500402 (2016).
Chen, W., So, F. & Guo, J. Intrinsic delay of permeable base transistor. Journal of Applied Physics 116, 044505, https://doi.org/10.1063/1.4891231 (2014).
Boswell, A., Tyler, A. J. & White, A. Performance of a small loop antenna in the 3-10 MHz band. IEEE Antennas and Propagation Magazine 47, 51–56, https://doi.org/10.1109/MAP.2005.1487778 (2005).
MacFarlane, G. G. & Whitehead, J. R. The theory of the super-regenerative receiver operated in the linear mode. Journal of the Institution of Electrical Engineers - Part III: Radio and Communication Engineering 95, 143–157, https://doi.org/10.1049/ji-3-2.1948.0032 (1948).
Steudel, S. et al. 50 MHz rectifier based on an organic diode. Nature Materials 4, 597–600, https://doi.org/10.1038/nmat1434 (2005).
Higgins, S. G., Agostinelli, T., Markham, S., Whiteman, R. & Sirringhaus, H. Organic diode rectifiers based on a high-performance conjugated polymer for a near-field energy-harvesting circuit. Advanced Materials, 1703782, https://doi.org/10.1002/adma.201703782 (2017).
Tassell, B. V. et al. Metacapacitors: printed thin film, flexible capacitors for power conversion applications. IEEE Transactions on Power Electronics 31, 2695–2708, https://doi.org/10.1109/TPEL.2015.2448529 (2016).
Fischer, A., Scholz, R., Leo, K. & Lüssem, B. An all C60 vertical transistor for high frequency and high current density applications. Applied Physics Letters 101, 213303, https://doi.org/10.1063/1.4767391 (2012).
Matsushima, T., Yahiro, M. & Adachi, C. Estimation of electron traps in carbon-60 field-effect transistors by a thermally stimulated current technique. Applied Physics Letters 91, 103505, https://doi.org/10.1063/1.2779240 (2007).
Acknowledgements
This work was funded by the German Research Foundation (DFG) Priority Programme FFlexCom under the project ‘Flexible Active Radar Backscatter Tag in Organic Electronics’ (FlexART, EL 506/22-1), and in part by the DFG project ‘Low-Voltage High-Frequency Vertical Organic Transistors’ (HFOE, EL 506/13-1 and LE 747/48-1), and in part by the organic/polymer path of the DFG Cluster of Excellence ‘Center for Advancing Electronics Dresden’ (cfaed, EXC 1506/1), and in part by the DFG project ‘Electrothermal feedback in organic devices’ (EFOD, RE 3198/6-1).
Author information
Authors and Affiliations
Contributions
B.K.B. designed and fabricated the characterization circuit, performed the measurements, and wrote the manuscript with the help of M.P.K., A.F., and H.K.; M.P.K. designed the transistor. A.F. and H.K. contributed to the analysis and interpretation of the measured data. K.L and F.E. motivated and supervised the work. All authors reviewed the manuscript. The OPBT samples were fabricated at the IAPP and measured at the CCN.
Corresponding author
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kheradmand-Boroujeni, B., Klinger, M.P., Fischer, A. et al. A Pulse-Biasing Small-Signal Measurement Technique Enabling 40 MHz Operation of Vertical Organic Transistors. Sci Rep 8, 7643 (2018). https://doi.org/10.1038/s41598-018-26008-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-018-26008-0
This article is cited by
-
Crystalline order offers access to high speeds for organic transistors
Nature (2022)
-
Organic bipolar transistors
Nature (2022)
-
MXene based saturation organic vertical photoelectric transistors with low subthreshold swing
Nature Communications (2022)
-
Organic Devices: Fabrication, Applications, and Challenges
Journal of Electronic Materials (2022)
-
Organic circuits reach new heights
Nature Electronics (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.