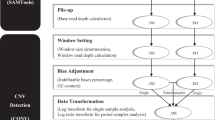
Abstract
Currently a few tools are capable of detecting genome-wide Copy Number Variations (CNVs) based on sequencing of multiple samples. Although aberrations in mate pair insertion sizes provide additional hints for the CNV detection based on multiple samples, the majority of the current tools rely only on the depth of coverage. Here, we propose a new algorithm (MSeq-CNV) which allows detecting common CNVs across multiple samples. MSeq-CNV applies a mixture density for modeling aberrations in depth of coverage and abnormalities in the mate pair insertion sizes. Each component in this mixture density applies a Binomial distribution for modeling the number of mate pairs with aberration in the insertion size and also a Poisson distribution for emitting the read counts, in each genomic position. MSeq-CNV is applied on simulated data and also on real data of six HapMap individuals with high-coverage sequencing, in 1000 Genomes Project. These individuals include a CEU trio of European ancestry and a YRI trio of Nigerian ethnicity. Ancestry of these individuals is studied by clustering the identified CNVs. MSeq-CNV is also applied for detecting CNVs in two samples with low-coverage sequencing in 1000 Genomes Project and six samples form the Simons Genome Diversity Project.
Similar content being viewed by others
Introduction
Copy Number Variation (CNV) and balanced rearrangements such as inversions and translocations are types of the large structural variations in the human genome and other organisms. In Copy Number Variation, a gene or a genomic region appears in different number of copies in different individuals or even in different cells of the same individual. CNVs are generally referred to as a duplication or deletion of a genomic region with at least 1 kb in length. However, several clinically important CNVs are shorter than 1 kb in length. CNV results in having variations in the gene expressions and abnormalities in the human phenotypes1. Moreover, CNV is envisaged to be associated with many human diseases such as autoimmune disease2, autism1 and developmental disabilities3, diabetes, schizophrenia4, cancer3 and obesity.
In the last decade, CNVs are studied via Microarray-based Comparative Genomic Hybridization (aCGH) methods5,6,7,8,9,10. However, the current aCGH platforms which benefit of more than 1 million genomic probes have a lower detection limit of CNVs of length ~5 kb to 25 kb11,12. In the recent years, Next Generation Sequencing (NGS) has provided new opportunities for the CNV studies with an unprecedented resolution13,14,15. In NGS, millions of single end or mate pair reads are generated from the sample genomes with shotgun sequencing. CNVs are then detected based on the frequency of the reads (read depth) or aberrations in the mate pairs, after mapping the short reads to the reference genome.
The majority of the current CNV detection tools analyze only one sample genome, at a time. These tools which are not capable of the simultaneous analysis of multiple samples rely either on read depth data e.g. CNV-seq14, rSW-seq16, m-HMM17, BIC-seq18, EWT19, SegSeq20, CNVwire21 and ReadDepth22 or on mate pair/split reads23,24,25,26,27,28,29,30,31,32,33,34. However, there are benefits in having the capability to analyze several sequencing samples, simultaneously.
Multiple sequencing reduces the effect of the systematic errors and artifacts which are attributed to the library-preparation protocol or individual sample genome characteristics35. There are common CNVs which are shared by complex diseases36 and can be detected from sequencing of multiple samples. Simultaneous analysis of multiple samples allows detecting read counts variations occurring due to the noise across samples, even in genomic positions with constant copy numbers.
Therefore, to increase the detection power, more samples should be sequenced with a low sequencing coverage rather than for sequencing a few samples with high-coverage sequencing. Indeed, CNV detection methods which rely on a low-coverage sequencing data are more relevant in the future studies37,38. Currently, many individuals are sequenced with a low genome-wide coverage. For example, the 1000 genomes project carried out the whole-genome shotgun sequencing of 179 individuals with 2× to 4× coverages39,40,41.
Currently, there are a few tools which are capable of the simultaneous analysis of several sequenced samples37,42,43. However, a major drawback of these tools is relying only on read depth data which results in suffering from a low power or a high false positive rate, due to the large noise in read depth signals. Moreover, these tools do not take the observed aberrations in the mate pair reads into account. Indeed, besides read depth, mate pair insertion sizes provide another source of information for the genome-wide CNV detection with an increased resolution.
In this paper, MSeq-CNV is proposed for detecting recurrent genomic deletions and duplications across multiple individuals, by the simultaneous analysis of samples. To the best of our knowledge, MSeq-CNV is the first computational tool which takes both read depth and insertion size signals in several individuals into account. The MSeq-CNV applies a mixture density to model the distribution of the read counts and the distribution of the number of mate pairs with aberrations in insertion size.
Each component in the mixture density applies a Binomial distribution to model the number of mate pairs with insertion size aberrations and a Poisson distribution to model the read counts, in each genomic region. After estimating the model parameters based on Expectation-Maximization (EM) algorithm, the posterior probability of the digitized copy number of each segment in the sample genomes is computed. The resolution of the MSeq-CNV is evaluated on a set of samples with implanted CNVs, which are constructed based on the human reference genome. Compared to the other state of the art methods, MSeq-CNV has reached an unprecedented precision and recall values which allows detecting recurrent genomic variants, accurately.
The MSeq-CNV is also applied for the CNV detection in a set of six HapMap individuals with high-coverage sequencing, including a CEU trio of European ancestry (NA12891, NA12892, and NA12878) and a YRI trio of Yoruba Nigerian ethnicity (NA19238, NA19239, and NA19240).
Methods
Assume that there are k sample genomes which are sequenced using a Next Generation Sequencing platform and mate pair reads are generated. After mapping mate pairs, the reference genome is divided into T segments of length L. Here, we aim at estimating the copy number of each genomic segment in samples 1 to k. To estimate the copy number of each sample in the tth genomic segment where t = 1, 2, …, T, this paper relies on two signals: i) number of reads which are mapped to the segment, and ii) information from the mate pair whose insertion (un-sequenced) region is passing the tth genomic segment and its reads are flanking the corresponding genomic segment.
Here, number of reads which are generated from the jth sample and are mapped to the tth segment of reference genome (studied segment) is denoted by \({f}_{j}\). Also, \({n}_{j}\) denotes the number of mate pairs which are generated from the jth sample and their insertion region is passing the tth segment, after mapping to it.
Signal characteristics in different genomic states
The studied segment in the jth sample has one of the following copy number states i.e. {homozygous deletion, heterozygous deletion, diploid and duplications}. In each state, the characteristics of the read counts and mate pair signals which are used for the mathematical modeling are described below:
Diploid
in this state, jth sample carries two copies of the corresponding segment in the reference genome. Here, a mate pair which is generated from the jth sample aligns to the reference genome with a normal insertion size, distributed with the clone library insertion size distribution. Also, number of reads which are mapped to the corresponding segment in the reference genome i.e. \({f}_{j}\) is assumed to have a Poisson distribution with parameter \(\lambda \).
Heterozygous deletion
in this state, the jth sample carries only one allele of the corresponding segment in the reference genome. Therefore, some mate pairs which are generated from the jth sample align to the reference with a normal insertion size, distributed with the clone library insertion size distribution. Other mate pairs align to the reference genome much further apart than expected. In this state, read counts are also distributed with a Poisson distribution with a parameter of \(\frac{\lambda }{2}\).
Homozygous deletion
in this state, both alleles are deleted from the jth sample. Therefore, a high percentage of the mate pairs which are generated from this region will map to the reference genome much further apart than the expected insertion size distribution in the clone library. Also, we consider a Poisson distribution with a parameter of \(\varepsilon \lambda \) for the read counts, where \(\varepsilon \) is assumed to be a very small value.
Duplication
in this state, the sample genome carries more than two copies of the corresponding segment in the reference genome. However, mate pairs which are generated from duplicated regions will map to the reference with the insertion size distribution of the clone library. Read counts are also distributed with a Poisson distribution with a parameter of \(i\,{\rm{\lambda }}/2\), for the samples carrying i copies.
Mathematical modeling of mate pair insertion sizes and read counts
Consider a segment of the reference genome whose copy number in the jth sample is of interest, j = 1, 2, …, k. Also, let \({n}_{j}\) denote the total number of mate pairs which are generated from the jth sample and align to the reference genome with condition ii, as mentioned before. Also, \({n}_{j1}\,\)denotes the number of mate pairs which are mapped to the reference with the insertion size distribution of the clone library and \({n}_{j2}\) denotes the number of mate pairs which are mapped to the reference much further apart, compared to the insertion sizes in the clone library. Clearly, \({n}_{j}={n}_{j1}+{n}_{j2}\). Here, we assumed that \({n}_{j1}\) is binomially distributed as follows:
where, \({n}_{j1}=1,2,\ldots ,{n}_{j}\). In the above distribution, \({\beta }_{i}\) indicates the probability of observing a mate pair mapped to the reference with a clone library insertion size distribution, when sample genome is in the ith CNV state. Where, i = 0, 1, 2, 3, …, m corresponds to {homozygous deletion, heterozygous deletion, diploid and duplications}. Also, the maximum copy number of a genomic segment is denoted by m, i.e. \(i\le m\).
When jth sample has i copies of the studied segment of the reference genome, read count \({f}_{j}\) follows a Poisson distribution with a parameter of \({\theta }_{i}\lambda \):
where, \({{\rm{\theta }}}_{0}={\rm{\varepsilon }}{\rm{\lambda }}\), and \({{\rm{\theta }}}_{{\rm{i}}}=i{\rm{\lambda }}/2\), for \({\rm{i}}\ge 1\).
Also, from a total number of k samples, let \({{\rm{\alpha }}}_{{\rm{i}}}\) denote the percentage of samples which have i copies of the studied segment of the reference genome. Taking the above descriptions into account, the probability of observing \(({f}_{j},{n}_{j1},{n}_{j2})\) in the jth sample genome can be written as follows:
However, it should be added that in the above formulations \({n}_{j1}\) and \({n}_{j2}\) are not known and they depend on the unknown parameter \({\beta }_{i}\). Also, the estimation of \({n}_{j1}\) and \({n}_{j2}\), requires estimating the probability of each insertion size to be distributed with the clone library insertion size distribution. For this purpose, let \({o}_{jr}\) denote insertion size of the rth mate pair which was generated from the jth sample and was mapped to the studied segment of the reference genome. Where \(r=1,\,2,\,\ldots ,\,\,{n}_{j}\) and j = 1, 2, …, k. Consequently, a random variable \({z}_{jr}\) is corresponded to each mate pair insertion size \({o}_{jr}\):
where, \({n}_{j1}=\sum _{r=1}^{{n}_{j}}{z}_{jr}\) and \({n}_{j2}=\sum _{r=1}^{{n}_{j}}(1-{z}_{jr})\). To estimate the expected value of \({n}_{j1}\) and \({n}_{j2}\), we calculate the probability of having a \({z}_{jr}\) equal to 1, for \(r=1,\,2,\,\ldots ,\,\,{n}_{j}\) and \(j=1,\,2,\,\ldots ,\,\,k\), see Supplementary file 1 for a detailed description.
Now, a Dirichlet prior distribution is defined for the parameter vector \({\boldsymbol{\alpha }}=({\alpha }_{0},\,{\alpha }_{1},\,\ldots ,\,{\alpha }_{m})\):
where, \({\alpha }_{0}=1-\sum _{i=1}^{m}{\alpha }_{i}\,\)and \({\gamma }_{s}=\sum _{i=0}^{m}{\gamma }_{i}\). Also, the prior of each \({\beta }_{i}\) is considered to be a beta distribution as follows:
where, i = 0, 1, 2, …, m. Moreover, the prior distribution of \(\lambda \) is considered to be a uniform distribution, over the interval of \((0,t)\), where t is large enough.
Model parameters
There are a number of parameters in the above mathematical model which have to be estimated. These parameters include \(\lambda \), the average read counts in a genomic segment of diploid state. The parameter vector \({\boldsymbol{\alpha }}=({\alpha }_{0},\,{\alpha }_{1},\,\ldots ,\,{\alpha }_{m})\) represents the percentage of samples with copy numbers 0, 1, …, m of the studied segment of the reference genome. Also, for a sample genome with copy number state i, \({\beta }_{i}\) indicates the proportion of the mate pairs which are mapped to the reference genome much further apart than expected under the clone library insertion size distribution.
The parameters of the prior distribution over \({\boldsymbol{\alpha }}=({\alpha }_{0},\,{\alpha }_{1},\,\ldots ,\,{\alpha }_{m})\) are given values based on information from genome-wide CNV percentage. Since a high percentage of genomic segments in each sample are expected to be in diploid state, \({\gamma }_{2}\) is given a value much higher than \({\gamma }_{i}\), \(i\ne 2\). Also, a beta distribution is defined as a prior distribution over each \({\beta }_{i}\), i = 0, 1, 2, …, m. The parameters of the beta distribution i.e. \({\nu }_{i1}\) and \({\nu }_{i2}\) are given values based on the expected number of mate pairs which are mapped to the reference much further apart, compared to the clone library insertion size distribution. In genomic diploid state and segments with an elevated number of copies \({\nu }_{i1}\gg {\nu }_{i2}\), for i = 2, 3, …, m. In genomic segments with heterozygous deletion \({\nu }_{11}\cong {\nu }_{12}\) and in genomic segments with homozygous deletions \({\nu }_{01}\ll {\nu }_{02}\).
Parameter estimation
MSeq-CNV applies the Expectation-Maximization (EM) algorithm, for parameter estimation. The parameter estimation details are given in Supplementary file 1.
Parameter initialization in EM algorithm
\(\lambda \) is initialized based on the number of reads that are expected to be generated from a genomic segment with diploid state, after taking the sequencing coverage into account. For example, for a coverage of 5×, a read length of 100 bp and genomic segments of length 100 bp, \(\lambda \) is initialized with a value of 20. Also, \({\alpha }_{2}=0.90\), \({\alpha }_{i}=0.02\) for i = 0, 1, 3, 4, 5, and \({\beta }_{2}={\beta }_{3}={\beta }_{4}={\beta }_{5}=1\), \({\beta }_{0}=0\), and \({\beta }_{1}=0.5\) are taken as the start point of the parameters in the EM algorithm. In the jth sample, \({\mu }_{j1},{\mu }_{j2}\) are initialized by comparing the mate pair insertion sizes with the clone library insertion size distribution.
In this study, we have considered a segment size of 150 bps in the simulated data analysis and a segment size of 100 bps in the real data analysis. Considering a longer segment size decreases the running time of the algorithm, with the cost of lower resolution. The methods which are compared to MSeq-CNV are also implemented with the same segment size, as MSeq-CNV. However, there are other methods which are specialized in detecting genomic rearrangements and tandem duplications using paired reads which get the nucleotide resolution breakpoint25,29.
Data availability
BAM (Binary Alignment/Map) files of the alignment of the mate pair reads to the build 36 (hg18) of the human reference genome are available at ftp://ftp-trace.ncbi.nih.gov/1000genomes/ftp/. R program of MSeq-CNV and a detailed procedure for its running is available at https://github.com/CNVdetection/MSeq-CNV. The list of detected CNVs in the studied individuals is also submitted to this webpage.
Results
Implementation To Real Data of The Human Reference Chromosome
We have constructed 40 sample genomes with implanted CNVs, from chromosome 3 of the human reference genome. After duplicating chromosome 3 of the reference genome, it was altered with implanted CNVs of length 250 bp, 500 bp, 750 bp, 1 kb, 1.5 kb, 2 kb, 2.5 kb, 3 kb, 3.5 kb, 4 kb, 4.5 kb, 5 kb. The position of each CNV is randomly chosen so that CNVs do not overlap along chromosome. After determining the CNV positions on the reference genome, CNVs are implanted into each sample genome.
Indeed, for each CNV region which is implanted in the reference genome, distributions and characteristics of CNVs across sample genomes are determined based on a previous analysis of the HapMap individuals.
Based on the characteristics of the HapMap individuals, 80% of the implanted CNVs were of type loss in which deletions occurs in some sample genomes. Also, 15% of the CNV regions were of type gain in which some sample genomes have an elevated number of copies. The other 5% of the implanted CNV regions were of type mixed in which sample genomes may either have copy loss or copy gain.
In each CNV region, the copy number of each sample was also drawn from the copy number distribution in HapMap individuals. For a genomic loss region, a sample has copy numbers 2, 1, and 0 with probabilities 0.8, 0.15 and 0.05, respectively. For a genomic gain region, a sample has copy numbers 2, 3, 4, and 5 with probabilities 0.85, 0.08, 0.06 and 0.01, respectively. Also, for a CNV region of type mixed, a sample has copy numbers 0, 1, 2, 3, 4 with probabilities 0.04, 0.16, 0.67, 0.11 and 0.02, respectively.
After constructing the sample genomes, MAQ is applied for generating mate pair reads from each sample genome. Mate pairs are then mapped to the human reference genome. After dividing the human reference genome into segments of length 150 bp, MSeq-CNV is applied for detecting CNVs in the corresponding segments of the constructed sample genomes. In Table 1, the performance of MSeq-CNV is reported for each CNV state i.e. homozygous deletion, heterozygous deletion, and duplications, for a genome-wide sequencing coverage of 10×.
The performance of MSeq-CNV is also compared to the central CNV detection tools i.e. rSW-seq, CNV-seq and cnMOPS. These tools are selected for comparisons because of their high resolution and their capability in detecting both genome-wide deletions and duplications37. It should be added that rSW-seq and CNV-seq are not capable of detecting the digitized copy number of genomic regions i.e. these tools do not discriminate heterozygous deletions from homozygous deletions. However, MSeq-CNV resembles cn.MOPS in detecting the digitized copy number of each CNV region.
For calculating precisions and recalls, the whole simulation study was repeated five times for each setting and the average results across five repeats are summarized in Table 2. In this table, for a genome-wide sequencing coverage of 1×, 5×, 10×, MSeq-CNV is compared to the other tools in each genomic state i.e. homozygous deletion, heterozygous deletion, diploid and duplications. The F-score which is the harmonic mean of the precision and recall values are also calculated in Table 2, for each CNV state.
As shown in Table 2, for all coverage values and according to the F-score, the performance of MSeq-CNV has been superior to the compared tools in detecting genomic regions with deletions and duplications. In regions with diploid copies, MSeq-CNV outperformed the compared tools for a coverage of 1×. Also for a coverage of 5× and 10×, MSeq-CNV and CNV-seq are both ranked as the best tools in detecting regions with diploid copies.
In Table 3, the overall performance of MSeq-CNV is compared to the other tools. To calculate the overall performance of each tool in estimating the correct copy number state, number of nucleotides whose states were correctly predicted is divided by the genome length. As indicated in Table 3, the overall performance of the MSeq-CNV is superior to rSW-seq, CNV-seq and cnMOPS, for a coverage of 1× and 5×. Also, MSeq-CNV and CNV-seq outperformed rSW-seq and cn.MOPS with an overall accuracy of 0.98, for a 10× coverage.
Performance of MSeq-CNV is also evaluated in terms of allele frequency of CNVs. As shown in Table 4, in CNV regions with copy loss, accuracy does not change with an increase in allele frequency i.e. MSeq-CNV is accurate in detecting genomic deletions. However, in CNV regions of type copy gain or mixed, overall accuracies decrease with an increase in allele frequency. This is associated with lower accuracies in detecting genomic duplications, compared to the other genomic regions.
Figure 1 shows the RAM usage, running time and overall accuracy of MSeq-CNV in terms of sequence numbers, i.e. number of individuals which are compared to each other, for 10× sequencing coverage. To obtain these results, 4 computer cores were applied for running the parallel programming version of the MSeq-CNV, on a 64-bit windows operating system with Intel Core(TM) i7-4710HQ CPU @3.5 GHz processor. As shown in Fig. 1A,B, RAM usage and running time of MSeq-CNV both increase, with an increase in sequence numbers. However, as shown in Fig. 1C, analyzing more sample genomes at a time has a positive effect on the overall accuracy of MSeq-CNV.
Ram usage, run time and accuracy of MSeq-CNV is reported, in terms of sequence numbers, in a 5 Mega bp of the genomic region and for a coverage of 10×. These results are achieved using parallel programming version of the MSeq-CNV on a 64-bit windows operating system with Intel Core(TM) i7-4710HQ CPU @3.5 GHz processor. (A) Ram usage of MSeq-CNV in terms of sequence numbers. (B) Run time of MSeq-CNV in terms of sequence numbers. (C) The overall accuracy of MSeq-CNV, in terms of number of analyzed individuals.
Results From The High-Coverage Data of The 1000 Genomes Project
MSeq-CNV is applied for the CNV detection in the genome of six HapMap individuals. These genomes which are sequenced with a high coverage as part of the 1000 Genomes Project (http://www.1000genomes.org) consist of a CEU trio of European ancestry (NA12891, NA12892 and NA12878) and a YRI trio of Yoruba Nigerian ethnicity (NA19238, NA19239 and NA19240).
BAM (Binary Alignment/Map) files of the alignment of the mate pair reads to the build 36 (hg18) of the human reference genome are downloaded from ftp://ftp-trace.ncbi.nih.gov/1000genomes/ftp/. Mate pair reads with low mapping qualities (Q < 25) are then filtered out using SAMtools (samtools.sourceforge.net). Then, MSeq-CNV is applied for detecting deletions and duplications in the genome of CEU and YRI individuals, simultaneously.
In past studies44, to reduce the false discovery rate, CNVs’ callset were heavily pre-filtered and only a high confident set of CNVs were reported. In our Bayesian framework, to reduce the false positive rate, we report a set of CNVs with high posterior probabilities. Indeed, those CNVs with posterior probabilities lower than a fixed threshold i.e. 0.5 are filtered out from the callset.
In Table 5, number of CNVs and their total size (in Mega bp) are reported for deletion and duplication calls with at least 1 kb in size. As indicated in Table 5, numbers of CNVs in CEU trio NA12891, NA12892 and NA12878 are respectively 249, 404 (421.284 Mega bp), 248, 889 (390.479 Mega bp) and 249, 162 (410.194 Mega bp). Also, numbers of CNVs in YRI trio NA19238, NA19239 and NA19240 are respectively 278, 027 (459.610 Mega bp), 246, 229 (453.394 Mega bp) and 251, 269 (488.895 Mega bp). Also, similar to previous estimations45, CNV calls in NA12891, NA12892, NA12878, NA19238, NA19239 and NA19240 respectively cover 13.02%, 12.07%, 12.68%, 14.21%, 14.02% and 15.11% of the human genome.
The average number of CNVs in YRI trio i.e. 258, 508 (467.300 Mega bp) is slightly higher than the average calls in CEU i.e. 249, 152 (407.319 Mega bp). Also, as indicated in Table 5, the average number of deletion and duplication calls in YRI individuals (91, 609 and 166, 899) are both more than CEU trio (83, 778 and 165, 374), indicating the increased diversity of the African individuals in comparison with CEUs46. Moreover, in the studied individuals genomic deletions are less common compared to duplications44,46,47.
Total number of CNV calls in each chromosome is plotted in Fig. 2A, for each HapMap individual. Numbers of deletion and duplication calls are also given in Table S.1, for each chromosome. See Table S.2 for the size (in Mega bp) of deletion and duplication calls.
Number of CNV calls which are made by MSeq-CNV. (A) In the high-coverage sequencing data of HapMap individuals NA12891, NA12892, NA12878, NA19238, NA19239 and NA19240, from 1000 Genomes Project. (B) In the low-coverage sequencing data of NA12761 and NA12762, from 1000Genomes Project. (C) In the six individuals from the Simons Genome Diversity Project (SGDP).
To investigate the validity of the CNV calls, their overlap with the Database of Genomic Variants (DGV)48, http://dgv.tcag.ca/dgv/ is studied. DGV includes 8, 599 CNVs from 40 HapMap individuals which are validated experimentally using aCGH methods.
The overlap of the detected CNVs with DGV are determined by the number of calls and also by the size of overlap, in base pairs. CNV calls in CEU trio NA12891, NA12892 and NA12878 overlap with DGV respectively with a ratio of 0.61, 0.62 and 0.61, for the number of calls. Also, a base which is called as a CNV in NA12891, NA12892 and NA12878 overlap with a base in DGV respectively with a ratio of 0.60, 0.61 and 0.61. The YRI individuals NA19238, NA19239 and NA19240 overlap with DGV respectively with a ratio of 0.62, 0.61 and 0.62 for the number of calls, and 0.61, 0.59 and 0.60 for the base pairs. Therefore, more than a half of CNV calls which are made by MSeq-CNV are previously validated using aCGH methods.
Size distribution of CNVs are also shown in Fig. 3A,B, respectively for the deletion and duplication calls. Clearly, the numbers of deletion and duplication calls decrease exponentially, with an increase in CNV size. As shown in Fig. 3A, deletion size distributions almost overlap in all studied individuals. Duplication size distributions are also very similar in all individuals, with CEU individuals having more CNVs of smaller sizes.
Moreover, we applied the hierarchical clustering algorithm to the matrix of CNV regions which are identified in the genome of six HapMap individuals. As shown in Fig. 4, although no information about the individual’s identities are used in the hierarchical clustering, the algorithm has correctly segregated the ancestry of the six individuals in two groups. While one group includes the CEU individuals NA12891, NA12892 and NA12878 with European ancestry, the other group includes YRI individuals NA19238, NA19239 and NA19240 with Nigerian ancestry.
The hierarchical clustering algorithm is applied to the matrix of CNV regions which are detected using MSeq-CNV in the genome of HapMap individuals NA12891, NA12892, NA12878, NA19238, NA19239 and NA19240. Based on the CNV information, the hierarchical clustering algorithm has correctly segregated the ancestry of the six individuals in two groups i.e. a group includes CEU trio and a group includes YRI trio.
Results From The Low-Coverage Data of The 1000 Genomes Project
MSeq-CNV is also applied for the CNV detection form the low-coverage data of two individuals i.e. NA12761 and NA12762, from 1000 Genome project. After downloading BAM files of the alignment of mate pair reads to the human reference genome, mate pairs with low mapping qualities (Q < 25) are filtered out.
MSeq-CNV called a total number of 145, 462 (191.495 Mega bp) and 119, 074 (169.339 Mega bp) CNVs in the genomes of NA12761 and NA12762, respectively. Also, in both individuals, genomic deletions are less common compared to the duplications44,46,47. Details of deletion and duplication calls are given in Table 5 and Table S.3.
The low number of CNV calls in the genome of NA12761 and NA12762 is potentially associated with lower accuracies in detecting genomic CNVs, especially duplications, from low-coverage sequencing data of NA12761 and NA12762 (see Table 2).
The overall number of detected CNVs in each chromosome is shown in Fig. 2B, for NA12761 and NA12762. Detected CNVs in NA12761 and NA12762 overlap with DGV respectively with a ratio of 0.65 and 0.66 for the number of calls, and 0.66 and 0.67 for base pairs.
Results From The Simons Genome Diversity Project (SGDP)
MSeq-CNV is also applied for CNV detection in the genome of six individuals from the Simons Genome Diversity Project49 i.e. LP6005592-DNA_H03 (USA), LP6005442-DNA_E07 (Taiwan), LP6005443-DNA_G05 (Taiwan), LP6005519-DNA_A04 (India), LP6005519-DNA_A05 (India), and LP6005592-DNA_D01 (Finland).
As indicated in Table 5, in the analyzed individuals from SGDP, the lowest number of CNVs are called in the LP6005592-DNA_H03 (USA)46 (171, 410 CNVs with a total size of 303.064 Mega bp). Two East Asian individuals LP6005443-DNA_G05, LP6005442-DNA_E07(form TAIWAN) and West Eurasian individual LP6005592-DNA_D01 (from FINLAND) are the next, respectively with a total number of 183, 439 (317.397 Mega bp), 197, 435 (323.638 Mega bp), 185, 837 (323.829 Mega bp) calls.
The highest number of CNVs are detected in the South Asian individuals LP6005519-DNA_A04 and LP6005519-DNA_A05 (from INDIA) respectively with a total number of 262, 405 (431.409 Mega bp) and 341, 909 (545.435 Mega bp) calls. Extensive CNVs in Indian individuals, which is as many as YRI trio, were also previously reported in the admixed Indian population of African ancestry47,50, to adopt with environmental conditions.
Details of deletion and duplication calls are given in Table S.4 and Table S.5. The overall number of detected CNVs in each chromosome is shown in Fig. 2C, for each individual.
Detected CNVs in LP6005592-DNA_H03, LP6005442-DNA_E07, LP6005443-DNA_G05 LP6005519-DNA_A04 and LP6005519-DNA_A05, and LP6005592-DNA_D01 overlap with DGV respectively with a ratio of 0.61, 0.62, 0.61, 0.60, 0.62, and 0.62, for the number of calls and 0.60, 0.60, 0.59, 0.60, 0.59, and 0.61, for the base pairs.
Applications and Limitations
The MSeq-CNV can be applied for detecting the recurrent genome-wide CNVs from NGS data in the diploid genome of human and other organisms, as well. However, the current version of MSeq-CNV is not capable of detecting CNVs in the sequencing data of a haploid genome. The input NGS data for the MSeq-CNV are possibly the mate pair reads which are collected from sequencing with multiple platforms, multiple individuals and experimental conditions.
Although the current version of the MSeq-CNV is limited to the whole genome shotgun sequencing, further work is in progress to adopt MSeq-CNV with the exome or gene panel sequencing data.
Also, as mentioned above, the other attractive feature of the MSeq-CNV is in constructing the ancestry of the sequenced individuals, based on the detected CNV matrix.
Discussion
In this article we proposed MSeq-CNV as a new tool for detecting genome-wide deletions and duplications from sequencing of multiple samples. Simultaneous analysis of multiple samples allows detecting common CNVs which are shared by complex diseases. Also, read count variations which occur due to the sequencing noise can be detected by the analysis of several samples together. MSeq-CNV applies a novel probabilistic framework for modeling the read depth and insertion size signals, together.
The overall performance of MSeq-CNV has been superior to the central CNV detection tools such as rSW-seq, CNV-seq and cnMOPS. Specially, for a coverage of 1× which is fairly low, the overall performance MSeq-CNV has been considerably higher than the compared tools. Reaching a high performance in low coverage data is an advantage of MSeq-CNV. In future, CNV detection tools which rely on a low-coverage sequencing are more relevant37,38. Indeed, a low coverage sequencing is common in many individuals e.g. in the 1000 Genomes Project the shotgun sequencing of 179 individuals is carried out with a coverage of 2× to 4×41.
The MSeq-CNV works with the empirical distribution of the insertion sizes in clone library. Therefore, MSeq-CNV is robust to deviations from the theoretical insertion size distribution which occurs due to several artifacts, attributed to the library-preparation protocols.
References
Stankiewicz, P. & Lupski, J. R. Structural variation in the human genome and its role in disease. Annu Rev Med 61, 437–455, https://doi.org/10.1146/annurev-med-100708-204735 (2010).
Aitman, T. J. et al. Copy number polymorphism in Fcgr3 predisposes to glomerulonephritis in rats and humans. Nature 439, 851–855, https://doi.org/10.1038/nature04489 (2006).
Albertson, D. G. & Pinkel, D. Genomic microarrays in human genetic disease and cancer. Hum Mol Genet 12(Spec No 2), R145–152, https://doi.org/10.1093/hmg/ddg261 (2003).
Cook, E. H. Jr. & Scherer, S. W. Copy-number variations associated with neuropsychiatric conditions. Nature 455, 919–923, https://doi.org/10.1038/nature07458 (2008).
Fridlyand, J., Snijders, A. M., Pinkel, D., Albertson, D. G. & Jain, A. N. Hidden Markov models approach to the analysis of array CGH data. Journal of Multivariate Analysis 90, 132–153, https://doi.org/10.1016/j.jmva.2004.02.008 (2004).
Marioni, J. C., Thorne, N. P. & Tavare, S. BioHMM: A heterogeneous Hidden Markov model for segmenting array CGH data. Bioinformatics (Oxford, England) 22, https://doi.org/10.1093/bioinformatics/btl089 (2006).
Shah, S. P., Lam, W. L., Ng, R. T. & Murphy, K. P. Modeling recurrent DNA copy number alterations in array CGH data. Bioinformatics (Oxford, England) 23, i450–458, https://doi.org/10.1093/bioinformatics/btm221 (2007).
Ding, J. & Shah, S. A robust hidden semi-Markov model with application to aCGH data processing. Int J Data Min Bioinform 8, 427–442 (2013).
Zhang, Q. et al. CMDS: a population-based method for identifying recurrent DNA copy number aberrations in cancer from high-resolution data. Bioinformatics (Oxford, England) 26, 464–469, https://doi.org/10.1093/bioinformatics/btp708 (2010).
Park, C., Ahn, J., Yoon, Y. & Park, S. A Multi-Sample Based Method for Identifying Common CNVs in Normal Human Genomic Structure Using High-Resolution aCGH Data. PLoS ONE 6, e26975, https://doi.org/10.1371/journal.pone.0026975 (2011).
McCarroll, S. A. et al. Integrated detection and population-genetic analysis of SNPs and copy number variation. Nat Genet 40, 1166–1174, http://www.nature.com/ng/journal/v40/n10/suppinfo/ng.238_S1.html (2008).
Cooper, G. M., Zerr, T., Kidd, J. M., Eichler, E. E. & Nickerson, D. A. Systematic assessment of copy number variant detection via genome-wide SNP genotyping. Nat Genet 40, 1199–1203, https://doi.org/10.1038/ng.236 (2008).
Weischenfeldt, J., Symmons, O., Spitz, F. & Korbel, J. O. Phenotypic impact of genomic structural variation: insights from and for human disease. Nat Rev Genet 14, 125–138, https://doi.org/10.1038/nrg3373 (2013).
Xie, C. & Tammi, M. T. CNV-seq, a new method to detect copy number variation using high-throughtput sequencing. BMC Bioinformatics 10, https://doi.org/10.1186/1471-2105-10-80 (2009).
Zhao, M., Wang, Q., Wang, Q., Jia, P. & Zhao, Z. Computational tools for copy number variation (CNV) detection using next-generation sequencing data: features and perspectives. BMC Bioinformatics 14, S1, https://doi.org/10.1186/1471-2105-14-s11-s1 (2013).
Kim, T. M., Luquette, L. J., Xi, R. & Park, P. J. rSW-seq: algorithm for detection of copy number alterations in deep sequencing data. BMC Bioinformatics 11, 432, https://doi.org/10.1186/1471-2105-11-432 (2010).
Wang, H., Nettleton, D. & Ying, K. Copy number variation detection using next generation sequencing read counts. BMC Bioinformatics 15, 1–14, https://doi.org/10.1186/1471-2105-15-109 (2014).
Xi, R. et al. Copy number variation detection in whole-genome sequencing data using the Bayesian information criterion. Proc Natl Acad Sci USA 108, E1128–1136, https://doi.org/10.1073/pnas.1110574108 (2011).
Yoon, S., Xuan, Z., Makarov, V., Ye, K. & Sebat, J. Sensitive and accurate detection of copy number variants using read depth of coverage. Genome research 19, 1586–1592, https://doi.org/10.1101/gr.092981.109 (2009).
Chiang, D. Y. et al. High-resolution mapping of copy-number alterations with massively parallel sequencing. Nat Methods 6, https://doi.org/10.1038/nmeth.1276 (2009).
McCallum, K. J. & Wang, J. P. Quantifying copy number variations using a hidden Markov model with inhomogeneous emission distributions. Biostatistics 14, 600–611, https://doi.org/10.1093/biostatistics/kxt003 (2013).
Miller, C. A., Hampton, O., Coarfa, C. & Milosavljevic, A. ReadDepth: a parallel R package for detecting copy number alterations from short sequencing reads. PLoS One 6, e16327, https://doi.org/10.1371/journal.pone.0016327 (2011).
Chen, K. et al. BreakDancer: an algorithm for high-resolution mapping of genomic structural variation. Nat Methods 6, 677–681, https://doi.org/10.1038/nmeth.1363 (2009).
Abyzov, A. & Gerstein, M. AGE: defining breakpoints of genomic structural variants at single-nucleotide resolution, through optimal alignments with gap excision. Bioinformatics (Oxford, England) 27, 595–603, https://doi.org/10.1093/bioinformatics/btq713 (2011).
Rausch, T. et al. DELLY: structural variant discovery by integrated paired-end and split-read analysis. Bioinformatics (Oxford, England) 28, i333–i339, https://doi.org/10.1093/bioinformatics/bts378 (2012).
Yavas, G., Koyuturk, M., Gould, M. P., McMahon, S. & LaFramboise, T. DB2: a probabilistic approach for accurate detection of tandem duplication breakpoints using paired-end reads. BMC Genomics 15, 175, https://doi.org/10.1186/1471-2164-15-175 (2014).
Layer, R. M., Chiang, C., Quinlan, A. R. & Hall, I. M. LUMPY: a probabilistic framework for structural variant discovery. Genome Biol 15, R84, https://doi.org/10.1186/gb-2014-15-6-r84 (2014).
Korbel, J. O. et al. PEMer: a computational framework with simulation-based error models for inferring genomic structural variants from massive paired-end sequencing data. Genome Biol 10, R23, https://doi.org/10.1186/gb-2009-10-2-r23 (2009).
Ye, K., Schulz, M. H., Long, Q., Apweiler, R. & Ning, Z. Pindel: a pattern growth approach to detect break points of large deletions and medium sized insertions from paired-end short reads. Bioinformatics (Oxford, England) 25, 2865–2871, https://doi.org/10.1093/bioinformatics/btp394 (2009).
Abel, H. J. et al. SLOPE: a quick and accurate method for locating non-SNP structural variation from targeted next-generation sequence data. Bioinformatics (Oxford, England) 26, 2684–2688, https://doi.org/10.1093/bioinformatics/btq528 (2010).
Sindi, S. S., Onal, S., Peng, L. C., Wu, H. T. & Raphael, B. J. An integrative probabilistic model for identification of structural variation in sequencing data. Genome Biol 13, R22, https://doi.org/10.1186/gb-2012-13-3-r22 (2012).
Zhang, Z. D. et al. Identification of genomic indels and structural variations using split reads. BMC Genomics 12, 375, https://doi.org/10.1186/1471-2164-12-375 (2011).
Sindi, S., Helman, E., Bashir, A. & Raphael, B. J. A geometric approach for classification and comparison of structural variants. Bioinformatics (Oxford, England) 25, i222–230, https://doi.org/10.1093/bioinformatics/btp208 (2009).
Malekpour, S. A., Pezeshk, H. & Sadeghi, M. MGP-HMM: Detecting genome-wide CNVs using an HMM for modeling mate pair insertion sizes and read counts. Mathematical biosciences 279, 53–62, https://doi.org/10.1016/j.mbs.2016.07.006 (2016).
Ratan, A. et al. Comparison of Sequencing Platforms for Single Nucleotide Variant Calls in a Human Sample. PLoS ONE 8, e55089, https://doi.org/10.1371/journal.pone.0055089 (2013).
Moreno-De-Luca, D. et al. Deletion 17q12 is a recurrent copy number variant that confers high risk of autism and schizophrenia. American journal of human genetics 87, 618–630, https://doi.org/10.1016/j.ajhg.2010.10.004 (2010).
Klambauer, G. et al. cn.MOPS: mixture of Poissons for discovering copy number variations in next-generation sequencing data with a low false discovery rate. Nucleic acids research 40, e69, https://doi.org/10.1093/nar/gks003 (2012).
Le, S. Q. & Durbin, R. SNP detection and genotyping from low-coverage sequencing data on multiple diploid samples. Genome research 21, 952–960, https://doi.org/10.1101/gr.113084.110 (2011).
The Genomes Project, C. An integrated map of genetic variation from 1, 092 human genomes. 491, 56, https://doi.org/10.1038/nature11632, https://www.nature.com/articles/nature11632#supplementary-information (2012).
The Genomes Project, C. A global reference for human genetic variation. 526, 68, https://doi.org/10.1038/nature15393 https://www.nature.com/articles/nature15393#supplementary-information (2015).
A map of human genome variation from population-scale sequencing. Nature 467, 1061–1073, http://www.nature.com/nature/journal/v467/n7319/abs/10.1038-nature09534-unlocked.html#supplementary-information (2010).
Duan, J., Deng, H. W. & Wang, Y. P. Common copy number variation detection from multiple sequenced samples. IEEE transactions on bio-medical engineering 61, 928–937, https://doi.org/10.1109/tbme.2013.2292588 (2014).
Magi, A., Benelli, M., Yoon, S., Roviello, F. & Torricelli, F. Detecting common copy number variants in high-throughput sequencing data by using JointSLM algorithm. Nucleic acids research 39, https://doi.org/10.1093/nar/gkr068 (2011).
Sudmant, P. H. et al. An integrated map of structural variation in 2, 504 human genomes. Nature 526, 75, https://doi.org/10.1038/nature15394 https://www.nature.com/articles/nature15394#supplementary-information (2015).
Redon, R. et al. Global variation in copy number in the human genome. Nature 444, 444–454, https://doi.org/10.1038/nature05329 (2006).
Sudmant, P. H. et al. Global diversity, population stratification, and selection of human copy-number variation. Science (New York, N.Y.) 349, aab3761, https://doi.org/10.1126/science.aab3761 (2015).
Veerappa, A. M. et al. Global Spectrum of Copy Number Variations Reveals Genome Organizational Plasticity and Proposes New Migration Routes. PLOS ONE 10, e0121846, https://doi.org/10.1371/journal.pone.0121846 (2015).
MacDonald, J. R., Ziman, R., Yuen, R. K., Feuk, L. & Scherer, S. W. The Database of Genomic Variants: a curated collection of structural variation in the human genome. Nucleic Acids Res 42, D986–992, https://doi.org/10.1093/nar/gkt958 (2014).
Mallick, S. et al. The Simons Genome Diversity Project: 300 genomes from 142 diverse populations. 538, 201, https://doi.org/10.1038/nature18964 https://www.nature.com/articles/nature18964#supplementary-information (2016).
Narang, A. et al. Extensive copy number variations in admixed Indian population of African ancestry: potential involvement in adaptation. Genome biology and evolution 6, 3171–3181, https://doi.org/10.1093/gbe/evu250 (2014).
Acknowledgements
Hamid Pezeshk and Seyed Amir Malekpour would like to thank department of research affairs at University of Tehran. Hamid Pezeshk is also grateful to School of Biological Sciences at IPM for their supports. Some parts of this study were completed when he was visiting the Department of Mathematics and Statistics of Concordia University during a sabbatical leave. The authors would also like to thank the excellent comments and suggestions of two anonymous referees. The financial support of INSF (No. 95834244) is gratefully acknowledged.
Author information
Authors and Affiliations
Contributions
The data analysis and calculations are done by S.A.M., H.P. and M.S. were involved in the scientific discussions. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Malekpour, S.A., Pezeshk, H. & Sadeghi, M. MSeq-CNV: accurate detection of Copy Number Variation from Sequencing of Multiple samples. Sci Rep 8, 4009 (2018). https://doi.org/10.1038/s41598-018-22323-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-018-22323-8
This article is cited by
-
A snapshot neural ensemble method for cancer-type prediction based on copy number variations
Neural Computing and Applications (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.