Introduction

Nonclassical states1,2, as a very fundamental and practical application in quantum optics and quantum information processing, have attracted extensive attention. One of the most essential quantum states is the squeezed state1,3,4, in a harmonic oscillator, which can be defined as the reduction of uncertainty in one quadrature below the standard quantum limit at the expense of the corresponding enhanced uncertainty in the other, such that the Heisenberg uncertainty relation is not violated5,6,7,8. Since then, the schemes for producing and performing squeezed states have been intensively investigated via theoretical proposals and experimental implementations9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34.

Following the development of laser cooling of mechanical oscillators35,36,37,38, the preparations of mechanical squeezed states10 were widely used to study the applicability of quantum mechanics and the precision of quantum measurements11,12. In particular, the theoretical schemes for generation of the mechanical squeezing were proposed by amplitude-modulated driving field16,17,18, quantum measurement plus feedback19,20, two-tone driving21, injection of squeezed light22, or quadratic optomechanical coupling23,24,25,26,27,28,29,30. On the experimental side, the mechanical squeezing has been realized via reservoir engineering technique32, or parametric modulation33. The above-mentioned methods for preparation of the mechanical squeezing are based on optomechanical systems10,11,12,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,32,33,34, where via the radiation-pressure force, a laser-driven optical cavity is used to control a mechanical oscillator.

In this paper, we present an alternative scheme to effectively prepare strong mechanical squeezing in an electromechanical system, where via the Coulomb force, the coupling between a charged mechanical oscillator and two fixed charged bodies leads to the strong mechanical squeezing. Our proposed scheme in the electromechanical system has an important advance: the adjustment of the voltage of the bias gate could produce the large Coulomb force sufficient for the realization of the strong mechanical squeezing. The present results are applicable to generate the strong position squeezing of the mechanical oscillator, with presently available experimental capabilities.

Results

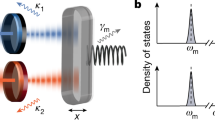
As shown schematically in Fig. 1, our model consists of a charged mechanical oscillator in the middle which is coupled to two fixed charged bodies on the left and right sides. The charged mechanical oscillator is subject to the Coulomb force due to the nearby charged bodies. The Hamiltonian describing the vibration of the charged mechanical oscillator is given by

$$H={H}_{0}+{H}_{{\rm{int}}},$$
(1)

with

$${H}_{0}=\frac{1}{2}m{\omega }_{m}^{2}{\hat{x}}^{2}+\frac{{\hat{p}}^{2}}{2m},$$
(2)

and39,40,41,42,43,44

$$\begin{array}{rcl}{H}_{{\rm{int}}} & = & {H}_{{\rm{int}}}^{(1)}+{H}_{{\rm{int}}}^{(2)}\\ & = & \frac{{C}_{0}{{\rm{U}}}_{0}^{2}}{2(1+\hat{x}/{r}_{1})}+\frac{{C}_{0}{{\rm{U}}}_{0}^{2}}{2(1-\hat{x}/{r}_{2})},\end{array}$$
(3)

here, H0 is the free Hamiltonian with \(\hat{x}\) and \(\hat{p}\) being the position and momentum operators for the vibration of the charged mechanical oscillator, with frequency ω m and mass m, and \({H}_{{\rm{int}}}^{(l)}\) describes the Coulomb interaction between the charged mechanical oscillator and the lth (l = 1, 2) charged body. C0U0 is the positive charge on the charged mechanical oscillator, with C0 and U0 being the equilibrium capacitance and the voltage of the bias gate. r l represents the equilibrium distance between the charged mechanical oscillator and the lth charged body.

Figure 1
figure 1

Schematic representation of the electromechanical system via the Coulomb force.

Full size image

In the case of \(\hat{x}\ll {r}_{1},{r}_{2}\), the Coulomb interaction Hamiltonian \({H}_{{\rm{int}}}^{(1)}\) and \({H}_{{\rm{int}}}^{(2)}\) can be expanded to the second order of \(\hat{x}/{r}_{l}\) as \(\frac{{C}_{0}{{\rm{U}}}_{0}^{2}}{2}[1-\frac{\hat{x}}{{r}_{1}}+\frac{{\hat{x}}^{2}}{{r}_{1}^{2}}]\) and \(\frac{{C}_{0}{{\rm{U}}}_{0}^{2}}{2}[1+\frac{\hat{x}}{{r}_{2}}+\frac{{\hat{x}}^{2}}{{r}_{2}^{2}}]\)45,46. Considering r1 = r2 = r0 and omitting the constant term, we then obtain a simple form \({H}_{{\rm{int}}}=\frac{{C}_{0}{{\rm{U}}}_{0}^{2}}{{r}_{0}^{2}}{\hat{x}}^{2}\).

After defining dimensionless annihilation and creation operators for the vibration mode of mechanical oscillator using the position and momentum operators of the oscillator, \(\hat{x}={[\hslash /(2m{\omega }_{m})]}^{\mathrm{1/2}}({\hat{b}}^{\dagger }+\hat{b})\) and \(\hat{p}=i{[\hslash m{\omega }_{m}\mathrm{/2}]}^{\mathrm{1/2}}({\hat{b}}^{\dagger }-\hat{b})\), we rewrite the Hamiltonian H as

$$H^{\prime} =\hslash {\omega }_{m}{\hat{b}}^{\dagger }\hat{b}+\hslash g{({\hat{b}}^{\dagger }+\hat{b})}^{2},$$
(4)

where \(g=\frac{{C}_{0}{{\rm{U}}}_{0}^{2}}{2m{\omega }_{m}{r}_{0}^{2}}\) is the effective mechanical coupling constant. In Eq. (4), we have neglected the zero-point energy from the first term. The second term is quadratic in position quadrature \(\hat{x}\) of mechanical oscillator, which can produce quadrature squeezing through a unitary evolution on any initial state of mechanical mode. Note that the quadratic Hamiltonian H′ is similar to that of optomechanical systems for generating squeezing of the mechanical oscillator23,24,25,26,27,28,29,30. However in the quadratic optomechanical systems, the optomechanical coupling depends on average photons in the optical cavity. As the large photon numbers in the cavity tend to faster decay out of the cavity, the squeezing of the mechanical oscillator in refs23,24,25,26,27,28,29,30 is limited by the cavity decay.

Next, we consider the mechanical squeezing in the different temperatures of the environment. The state of the mechanical oscillator in thermal equilibrium with an environmental temperature T is described by means of the density matrix \(\rho ={\sum }_{n}\,{p}_{n}|n\rangle \langle n|\), where \({p}_{n}=\mathrm{(1}-\exp [-\hslash {\omega }_{m}/{k}_{B}T])\,\exp (-n\hslash {\omega }_{m}/{k}_{B}T)\) represents the population in phonon number state |n〉 with k B being the Boltzmann constant. In order to extract the squeezing properties of the mechanical mode, we need to calculate the mean square fluctuations 〈ΔQ(t)〉2 and 〈ΔP(t)〉2 20,30 in the position and momentum of the mechanical oscillator. Let 〈ΔQ(t)〉2 = 〈Q(t)2〉 − 〈Q(t)〉2 and 〈ΔP(t)〉2 = 〈P(t)2〉 − 〈P(t)〉2, where \(Q=1/\sqrt{2}({\hat{b}}^{\dagger }+\hat{b})\) and \(P=i/\sqrt{2}({\hat{b}}^{\dagger }-\hat{b})\), satisfying the commutation relation [Q, P] = i. In Heisenberg picture, the operator b can evolve as the time-dependent operator30

$$b(t)=\exp [iH^{\prime} t/\hslash ]b\,\exp [-iH^{\prime} t/\hslash ]=rb\mathrm{(0)}+s{b}^{\dagger }\mathrm{(0)},$$
(5)

where exp[iH′t/ħ] is the time evolution operator, \(r=\,\cos \,(qt)-\frac{if}{q}\,\sin \,(qt)\), \(s=-\frac{2ig}{q}\,\sin \,(qt)\) with f = 2g + ω m and \(q=\sqrt{{f}^{2}-4{g}^{2}}\). Thus we can obtain \({\langle {\rm{\Delta }}Q(t)\rangle }^{2}=\frac{V}{2}[1-\frac{4g}{4g+{\omega }_{m}}\,{\sin }^{2}\,(qt)]\) and \({\langle {\rm{\Delta }}P(t)\rangle }^{2}=\frac{V}{2}\,[1+\frac{4g}{{\omega }_{m}}\,{\sin }^{2}\,(qt)]\), where \(V=2{\bar{n}}_{th}+1\) with \({\bar{n}}_{th}={[\exp (\hslash {\omega }_{m}/{k}_{B}T)-1]}^{-1}\) being the mean number of thermal excitation phonons. At qt = π/2, 〈ΔQ(t)〉2 and 〈ΔP(t)〉2 become minimum and maximum as \(\frac{V}{2}\frac{{\omega }_{m}}{4g+{\omega }_{m}}\) and \(\frac{V}{2}\frac{4g+{\omega }_{m}}{{\omega }_{m}}\), respectively. Note that the product of the mean square fluctuations (〈ΔQ(t)〉2)min and (〈ΔP(t)〉2)max is V 2/4. In the particular case of the vacuum state, the position and momentum variances \({\langle {\rm{\Delta }}Q\rangle }_{vac}^{2}\) and \({\langle {\rm{\Delta }}P\rangle }_{vac}^{2}\) are 1/2. The degree of the squeezing S in units of decibel (dB) can be calculated by \(-10\,{\mathrm{log}}_{10}\frac{{({\langle {\rm{\Delta }}Q(t)\rangle }^{2})}_{{\rm{\min }}}}{{\langle {\rm{\Delta }}Q\rangle }_{vac}^{2}}=-10\,{\mathrm{log}}_{10}\frac{V}{1+4g/{\omega }_{m}}\)47. Clearly, the squeezing is primarily controlled through the coupling constant g, the mechanical frequency ω m , and the temperature T.

Discussion

The degree of the squeezing S as functions of the mechanical frequency (ω m  = 5 MHz–5 GHz) and the voltage of the bias gate (U0) for different temperatures of the environment T = 0 K, 1 mK, 0.1 K, 1 K when C0 = 5 nF, r0 = 4 μm, and the elastic coefficient \(k=m{\omega }_{m}^{2}=22\) N/m is shown in Fig. 2. It is observed that at low temperature, the adjustment of the voltage of the bias gate could yield the strong squeezing in the high frequency. For example, we choose the realistic parameters corresponding to the experiment ω m  = 5.6 MHz and m = 0.7 ng44. Using C0 = 5 nF, U0 = 10 V, and r0 = 4 μm, we obtain S ≈ 14.8 dB at the equilibrium temperature T = 1 mK and the evolution time t = π/(2q) ≈ 5.2 ns. According to ref.13, there exists a critical time \({t}_{diss}=\mathrm{1/}(\gamma {\bar{n}}_{tot})\), here γ is the mechanical damping rate and \({\bar{n}}_{tot}\approx {\sinh }^{2}\,\mathrm{(2}\xi )+{\bar{n}}_{th}\) is the total phonon number with ξ being the squeeze parameter. Choosing the damping rate γ = 204 Hz44, we get t diss  ≈ 0.16 ms, which satisfies the condition \(t\ll {t}_{diss}\), and thus the decoherence of the mechanical oscillator could be negligible.

Figure 2
figure 2

The degree of the squeezing S versus the frequency and the voltage for different temperatures of the environment T = 0 K, 1 mK, 0.1 K, 1 K when C0 = 5 nF, r0 = 4 μm, and the elastic coefficient \(k=m{\omega }_{m}^{2}=22\) N/m.

Full size image

Conclusion

In summary, we have proposed an effective method to generate the mechanical squeezing in the electromechanical system. This is realized through the Coulomb interaction acting on the charged mechanical oscillator and two charged bodies, implementing the strong squeezing of the mechanical oscillator. It is found that at low temperature, the squeezing can be enhanced by moderately increasing the voltage of the bias gate. Our proposed scheme would contribute to the experimental study of fundamental aspects in the macroscopic quantum effects and the precision of quantum measurements with mechanical oscillators.