Introduction

In clinical routine, up to now solely the attenuation of x-rays interacting with matter has been employed to form the image. In addition, a variety of promising phase-sensitive methods evolved, which rely on the refraction of x-rays1,2. Yielding improved soft tissue contrast3, a major shortcoming of conventional attenuation-based imaging, those methods have been extensively investigated with regard to medical applications4,5,6. Among others, x-ray grating-based phase-contrast imaging7,8,9 is a imaging modality that has been expanded to medical tubes of low brilliance10, as well. Simultaneously, a conventional attenuation image, a differential phase-contrast image, and a dark-field image is calculated from a reference measurement without object and an object measurement with the object in place. Thereby, the dark-field image provides complementary information about the subpixel-size structures of a granular object11,12,13,14,15, whereas information about the orientation of the substructure is included16,17,18.

The method raised interest due to a number of promising medical applications, such as mammography19,20,21, lung imaging22,23,24, and imaging of the joints25,26,27. Scaling the method from laboratory setups to human-size specimen in a preclinical setup, several challenges have to be overcome: the transition towards higher x-ray energies suitable for medical imaging of larger parts of the human body, the increment of the size of possible measurable specimens, and the realization of sufficient image quality at low doses to enable in vivo imaging in combination with fast data acquisition.

Regarding medical applications carried out using a medical x-ray tube with large focal spot size and a polychromatic x-ray spectrum at higher acceleration voltages above 50 kV, a first measurement has been reported with a CT measurement of a human cervical spine28. Recently, a radiographic measurement of a human knee has been published revealing signatures of chondrocalcinosis of the medial meniscus applying a dose that is comparable to conventional attenuation-based devices29. The tube voltage has been 70 kV for both measurements.

While typical sizes of the field of view have been in the range of a few centimeters, recently progress towards larger specimens has been reported by either increasing the grating sizes up to 200 mm × 200 mm by stitching of smaller gratings30,31,32 or the realization of scanning radiographic devices33,34,35, which means that the object is scanned by an interferometer with sufficient size to capture the object at once in one dimension. Additionally, the transition to a scanning setup overcomes the time-consuming phase-stepping procedure9, as the phase-stepping curve can then be measured by continuously moving the object through the scanner, if the phase image of the reference measurement comprises at least a complete fringe of the Moiré pattern in scanning direction36. A scanning interferometer has also been reported for an edge-illumination setup, recently37,38.

In vivo measurement of small animals has been demonstrated for a radiographic measurement by Bech et al.39 using a multiple image small-animal scanner operated at 31 kV tube voltage, which proved that the retrieval of the differential phase-contrast and dark-field image is still possible despite the object motion. The realization of a gantry-type small-animal CT-setup and its challenges towards Talbot-Lau imaging have been described by Tapfer et al.40. As an alternative to conventional iodine-based angiography, the application of microbubbles commonly used in ultrasound imaging has been reported as a scattering contrast agent in the dark-field image for Talbot-Lau imaging41 and diffraction enhanced imaging42,43. Regarding Talbot-Lau imaging, the ex vivo CT-measurement aiming at the depiction of the microbubble contrast agent has been performed using the same small-animal CT-setup as an additionally reported in vivo CT-measurement of mice by Velroyen et al.44. Further small-animal studies comprise imaging of emphysema45, pneumothoraces46, and lung cancer47 of murine lungs.

With the report of an in vivo dark-field chest radiography of a pig’s lung carried out at 70 kV within 40 s by Gromann et al.34 a major milestone, covering all of the aforementioned demands, has been achieved. Thereby, the applied dose of 80 μSv for a human-sized specimen is clinically acceptable indicating the possible transition from “bench to bedside”.

However, signal extraction remains challenging taking in mind the small grating periods, typically in the range of a few microns. Hence, the mechanical robustness of the interferometer is key together with sophisticated image retrieval algorithms that correct for artifacts caused by mismatches in grating alignment40 and phase-step position48,49,50,51. An alternative to phase-stepping is especially important for CT-measurements, as a continuously rotating gantry is a requirement for clinical applications. Recently, a robust data acquisition protocol that reduces the necessary number of measurements to a single image for each projection has been published52,53, which represents important progress.

Regarding the realization of setups that aim at clinical imaging, a prototype dedicated to the diagnosis of rheumatoid arthritis in human finger joints has been reported by Tanaka et al.54 and Momose et al.55 which is operated in vivo in a clinical environment. Thereby, the field of view is restricted to 49 mm × 49 mm, though, and the dose is quite high with about 5 mGy at a limited tube voltage of 40 kV. Nevertheless, the depiction of cartilage confirms the clinical potential. Additionally, considerations with regard to the development of a device aimed at mammography have been summarized by Roessl et al.56 which led to the development of a slit-scanning mammography device33. Further investigations for the optimization of interferometer specifications aiming at a clinical mammography setup have been reported57. Experimental studies have been carried out by Li et al.58 concerning a tomosynthesis setup.

In general, additional restrictions apply to a clinical Talbot-Lau imaging device in comparison to a laboratory setup. The interferometer’s length is restricted for practical reasons in a hospital and because of the quadratic decline of the flux with increasing distance from the source, which leads to an intolerable boost of exposure time. A vertical oriented optical axis is favorable regarding patient positioning and the interferometer can’t be operated on an optical table, which yields a disturbance of the measurement by mechanical vibrations and may cause the appearance of artifacts due to unstable Moiré fringes. Of course, the entailing costs of a transition towards the clinics have to be held at a bearable amount, as well.

Altogether, these reasons favor the implementation of a Talbot-Lau interferometer in a yet existing clinical device. An interferometer designed to operate at high tube voltages between 50 kV and 125 kV has been mounted on a c-arm identical to a clinical system and tested for feasibility regarding Talbot-Lau imaging.

With the possibility to angulate the c-arm arm and thus change the optical axis around a patient lying on the table, a c-arm offers high flexibility in interventional medical imaging. Thereby, the inherent restrictions with regard to mechanical stability of a c-arm, the medical tube with a rotating anode, which induces vibrations to the c-arm and gratings, and mechanical deformation of the interferometer provide a challenging scenario for interferometric imaging. Experimental studies have been performed to assess the feasibility of the prototype system.

Results

Demonstration of feasibility

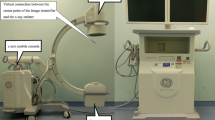
A sketch of the used c-arm prototype is shown in Fig. 1(a). A regular Talbot-Lau interferometer has been used consisting of a polychromatic medical x-ray tube with an extended focal spot S10, a flat-panel scintillating x-ray detector D, and the three gratings G0, G1, and G2. The Talbot-Lau interferometer has been mounted to a conventional clinically used c-arm floor-mounted angiography setup. A c-arm platform can be used flexibly in a variety of medical imaging and surgical procedures, as it features the possibility to take images from a broad range of angles59. The used c-arm offers two independent modes of angulation, which differ in the direction of motion of the detector from the perspective of the patient. The detector can be moved in cranial/caudal (CRAN/CAUD) direction of rotation, as well as in left/right anterior oblique (LAO/RAO) direction. Thereby, a cranial/caudal angulation means that the c-arm is angulated in such a way that the direction of propagation is changed head-wards/foot-wards. On the contrary a left/right anterior oblique rotation means that the x-rays are emitted from the right/left hand side towards the left/right hand side of the patient lying on the table. Figure 1(b–g) illustrates the different modes of angulation.

Figure 1
figure 1

(a) C-arm Talbot-Lau prototype based on Siemens Healthineers Artis one floor-mounted system. (b) Sketch of frontal view of a c-arm in parking position. (c) Sketch of frontal view of a c-arm in 30° LAO-angulation. (d) Sketch of frontal view of a c-arm in 30° RAO-angulation. (e) Sketch of frontal view of a c-arm in parking position. (f) Sketch of side view of a c-arm in 30° CRAN-angulation. (g) Sketch of side view of a c-arm in 30° CAUD-angulation.

Full size image

The c-arm device works in conjunction with the patient table which can be moved to a suitable height and position, therefore increasing the flexibility of the device. In the case of Talbot-Lau imaging, the patient should be moved as close as possible to G1 to maximize sensitivity60,61.

For reasons of comparison, the mean visibilities achieved by the Talbot-Lau interferometer used have been determined for various tube voltages with the interferometer consisting of the same gratings either mounted to the c-arm or placed on an optical table. The result is given in Fig. 2(a) for tube voltages between 50 kV and 125 kV. At 60 kV, where the measurements have been carried out, the mean visibility met 21.4%. Both setups show a similar behavior, whereas the visibilities for the tabletop setup slightly surpasses the c-arm. A reduction of the visibility for the c-arm setup is expected due to high-frequency vibrations of the gratings. This effect can be quantified by an analytical model resulting in Eq. 5, which is described in the methods section in more detail. The differences between the measured mean visibilities of both setups fall within 2% in most cases, which is expected according to the model. Additionally, the calculated reduced visibilities applying the model to the measured visibilities of the tabletop setup are drawn for comparison.

Figure 2
figure 2

(a) Measured mean visibilities over the field of view for various acceleration voltages for both the interferometer mounted to the c-arm and placed in a laboratory tabletop setup. Additionally, calculated visibilities applying the visibility reduction model to the measured visibilities of the tabletop setup are shown. (b) Relative reduction of the visibility due to high-frequency vibrations of the gratings as a function of the oscillation amplitude relative to p2. The red dashed line marks the worst case scenario of the introduced model assuming Aeff/p2 = 0.077, as described in section methods.

Full size image

Figure 2(b) shows the calulated relative reduction of the visibility due to high-frequency vibrations depending on the effective oscillation amplitude Aeff in relation to the analyzer grating period p2. Thereby, Aeff is determined by the oscillation amplitudes and the phase between the oscillations of the source grating and the phase grating. The oscillation amplitudes of both gratings have been measured to be below 0.2 μm in phase-stepping direction. A worst case scenario with the two vibrations being opposite in phase is marked by the red dashed line for Aeff/p2 = 0.077 and reveals a relative reduction of 5.8%, which yields 1.3% as an absolute reduction for a visibility of 22.7% of the tabletop setup at 60 kV. Thereby, the calculated reduction matches the gap between both measured mean visibilities. A realignment of the interferometer and the variance of measured visibilities may yield an additional offset of the measured visibilities, which is of a similar scale, though.

As a demonstration of feasibility, a non-inflated stent with a dilatation catheter has been placed in a water bath with a height of 13 mm. The stent of type Cordis Presillion is made of cobalt-chromium (CoCr) and features both cells with wide (60–70 μm) and narrow (30–35 μm) strut thicknesses62. It has an non-inflated length of 9 mm, while the diameter measures 1.78 mm. Due to inflation it expands to a diameter of 4 mm. The images are included in Fig. 3(a–f) applying two different reconstruction algorithms.

Figure 3
figure 3

Non-inflated stent with a dilatation catheter placed in a water bath with a height of 13 mm. The dose has been 0.54 mGy measured as air kerma. (a–c) From left to right: attenuation, differential phase-contrast, and dark-field image using a standard reconstruction algorithm applying a Fourier transform with respect to the phase-steps. Due to phase drift effects Moiré fringe artifacts are visible in the images. (d–f) From left to right: Attenuation, differential phase-contrast, and dark-field image of the stent using an advanced reconstruction algorithm adjusting the phase-step positions. The algorithm is able to remove the fringe artifacts.

Full size image

Displaced gratings cause a shift of the Moiré pattern yielding a deviation from the intended position while measuring a phase-step and lead to the formation of fringe artifacts in the reconstructed images. Thereby, the phase-drift effects are caused by thermal influences on the interferometer and mechanical instabilities of the c-arm, which change the imprinted Moiré pattern on a time scale that is longer than the time of measurement of a single phase-step. With the source grating G0 being integrated in the collimator next to the tube source the interferometer is subject to heating of the tube. Figure 3(a–c) shows the resulting images using a standard reconstruction method applying a Fourier transform with regard to the phase-step positions giving rise to the formation of Moiré artifacts. On the contrary, Fig. 3(d–f) proves the removal of the artifacts using an improved reconstruction algorithm, which adjusts the phase-step positions51.

The images reveal that the non-inflated stent is clearly visible in the dark-field image due to the sharp edges of the mesh. This result can be explained by the additionally generated visibility contrast for objects with unresolvable edges in the differential phase-contrast image, as shown by Yashiro and Momose63. Concerning the attenuation image, the highest signal is measured for the radiopaque markers made of platinum iridium, whereas in the dark-field image the stent struts themselves cause the highest signal. The dose of the measurement has been 0.54 mGy measured as air kerma.

Angulation

The core feature of a c-arm device is the possibility to angulate the c-arm meaning a change of the optical axis from the x-ray source to the detector. The normal position of a c-arm is with a vertically oriented optical axis, labeled as parking position. By angulation, a mechanical shake is caused to the c-arm and the c-arm is deformed due to a change in the impact of gravity. The deformation provokes a misalignment of the interferometer. Hence, the shape of the Moiré pattern is changed and the visibility is reduced.

In order to assess the feasibility of measurements with the c-arm in an angulated position, a series of reference measurements has been carried out with the c-arm driven to various positions. Thereby, the interferometer has not been realigned after angulation and the phase-stepping curves have been measured after a pause of 1–3 s to allow for a relaxation of vibrations caused by angulation. Figure 4(a) shows the measured mean visibilities over the field of view for a LAO-/RAO-angulated c-arm. A decrease is visible towards higher angulation angles. It is evident that the decrease slows down for angles higher than 50° for both LAO- and RAO-angulation. Thereby, the maximum reduction is caused from 21% to 17% for 90° in both directions. The mean visibilities of CRAN-/CAUD-angulation are displayed in Fig. 4(b). Towards higher angles in caudal direction even a slight increase of mean visibility is noticeable, which means that the interferometer has not been adjusted to an optimal state in the parking position. With a difference of 1% in visibility compared to the parking position this offset is minor, though. Altogether, the mean visibilities comprise values from 16% to 22% at 60 kV tube voltage.

Figure 4
figure 4

(a) Measured mean visibilities for a LAO-/RAO-angulated c-arm depending on angulation angle. Positive angles correspond to LAO-angulation. (b) Measured mean visibilities for a CRAN-/CAUD-angulated c-arm depending on angulation angle. Positive angles correspond to CRAN-angulation. (c) Gradients of the fitted polynomial of first degree to the phase ramps created by LAO-/RAO-angulation. Positive angles correspond to LAO-angulation. (d) Gradients of the fitted polynomial of first degree to the phase ramps created by CRAN-/CAUD-angulation. Positive angles correspond to CRAN-angulation. (e) Visualization of phase distributions of reference measurements for various angulated positions of the c-arm.

Full size image

In addition to the influence on visibility, angulation changes the phase distribution, whereas a misalignment of the interferometer causes an increase of the frequency of the Moiré pattern. Figure 4(e) visualizes the phase distributions of reference measurements for various angulated positions of the c-arm comprising a value range from −π to π. If the position of the c-arm differs in between a reference and an object measurement, the mismatch in the reference phase distribution overlays the actual differential phase-contrast image formed by the specimen. This artifact can be corrected by an algorithm based on fitting a polynomial of first degree to the unwrapped phase images. The method has been described by Seifert et al.49 in more detail applying a fit of polynomials of higher degree to correct for instable reference phase distributions over time. Figure 4(c) shows the gradients of the polynomial for LAO-/RAO-angulation and (d) for CRAN-/CAUD angulation. The highest gradients have been determined for a c-arm angulated by 90° in LAO- or RAO-direction with a gradient exceeding 0.2 rad/pixel in y-direction, which means in the direction perpendicular to the phase-stepping. As the Moiré fringe pattern is created by line gratings along the y-axis and the fringe pattern arises in a perpendicular direction, the theory of Moiré effect indicates a rotation of the gratings in relation to each other around the optical axis64. The gradients in x-direction are less pronounced. A corrected differential phase-contrast image is then given by the difference of the residuals of the object and reference measurement eliminating the phase ramps.

Correction of artifacts resulting from angulation

Angulation leads to a misalignment of the gratings, which gives rise to a reduction of visibility and causes an increase in the frequency of the Moiré pattern. If a reference measurement and a measurement with the object in place are carried out at different angulated positions of the c-arm, the phase shift remains visible in the differential phase-contrast image deteriorating image quality, which is shown in Fig. 5(a). Therefore, without any further post-processing a new reference measurement would be an obligation after each movement of the c-arm. In clinical routine, this requirement would reduce the possible throughput and potentially prevent the use of a Talbot-Lau c-arm in a medical procedure.

Figure 5
figure 5

(a) Differential phase-contrast image calculated with the c-arm in the parking position for the reference measurement and in 50° RAO-angulated position for the object measurement. (b) Compared to (a) the ramp artifacts have been removed by subtraction of the fitted polynomials to the reference and object measurement. The image is calculated by the difference of the residuals. Artifacts due to displaced grating structures are still visible. (c) Calibration image calculated by the difference of the residuals of two reference measurements carried out in the parking position and in 50° RAO-angulated position. (d) Final corrected image.

Full size image

Hence, we propose additional post-processing steps to maintain image quality in the differential phase-contrast image. Firstly, a 2-D Constantini-unwrapping65 is performed to the phase image of both the reference and object measurement. Afterwards, a polynomial of first degree according to Φ(xpixel,ypixel) = Φ0 + gx ⋅ xpixel + gy ⋅ ypixel is fitted to the unwrapped data. A preliminary differential phase-contrast image can then be determined by calculating the difference between the residuals of both fits. In doing so, Fig. 5(b) proves the removal of the phase ramps due to angulation. This approach is similar to the adaptive differential phase recovery method described by Tapfer et al.40 and identical to the image reconstruction routine described by Seifert et al.49. However, after subtraction of the fitted polynomial from a phase image the residuals still contain information about grating structures and their position relative to the detector pixels. As the residuals of reference measurements carried out at different angulations were found to be different, a calibration measurement consisting of reference measurements for every possible angulation angle is performed prior to the actual imaging procedure. Afterwards, the difference of the residuals is calculated for every possible combination and saved for post-processing. Exemplary, the calibration image consisting of the difference of two residuals of reference measurements with the c-arm in the parking position and in 50° RAO-angulated position is shown in Fig. 5(c). Since residuals for reference measurements at the same angulated position of the c-arm were found to be stable despite an intermediate movement of the c-arm, the difference of the calibration measurement can be subtracted from the difference of the actual object and reference measurement yielding the final corrected differential phase-contrast image depicted in Fig. 5(d).

As the mean visibility, the distribution of visibilities and the contribution of the specimen holder to measured attenuation changes with angulation, a similar prior calibration measurement has been performed for the attenuation and dark-field image, as well. Thereby, the attenuation and dark-field images have been calculated between reference measurements with the c-arm in parking position and in different angulated positions. Later-on the calibration images can be subtracted from the uncalibrated images without the necessity of subtracting fitted polynomials in a previous step.

Demonstration of a specimen measurement for different angulated c-arm states

A proof-of-concept measurement has been executed measuring a chili from different angulation angles and applying the proposed image correction algorithm. Even though not representing a clinical application, the sample is sufficient to examine the robustness of the setup and the proposed algorithm. As the residuals of two reference measurements from different angulations disagree, indicating a shift of grating structures in relation to the pixel matrix, the proposed calibration measurement has been carried out consisting of a series of reference measurements with the c-arm driven to every position. Afterwards, the c-arm has been re-positioned in the parking position and the actual reference measurement has been performed, which is used to calculate the three images of Talbot-Lau imaging. Finally, the object measurements have been carried out at the different angulated positions of the c-arm without measuring further reference measurements. Hence, the c-arm has been angulated in between every object measurement and the used reference measurement.

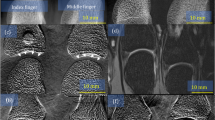
As an example, Fig. 6(a–d) show the resulting attenuation, (e)–(h) the differential phase-contrast, and (i)–(l) the dark-field images. For the measurement at 90° RAO-angulation, the specimen holder made of metal came in the field of view, which is visible in the right part of the images. The images display only a minor amount of artifacts proving the successful application of the correction algorithm and the feasibility of Talbot-Lau interferometry using a clinical c-arm setup, which is angulated in between the reference and object measurement. Thereby, the dose has been 0.36 mGy for each projection, measured as air kerma.

Figure 6
figure 6

Measurement of a chili for different projections angulating the c-arm. Each measurement has been carried out at a dose level of 0.36 mGy measured as air kerma. For all images the described correction algorithm has been used. A single reference measurement was carried out with the c-arm in the parking position (0° RAO). The position of the c-arm is given by the title. (a–d) Attenuation image. (e–h) Differential phase-contrast image. (i–l) Dark-field image.

Full size image

Discussion

The measurements prove the successful implementation of a Talbot-Lau interferometer in a clinically used c-arm angiography setup. The prototype reached a mean visibility of 21.4% at a tube voltage of 60 kV and sufficient visibility up to 125 kVp to perform Talbot-Lau imaging. A method to estimate the reduction of visibility due to high-frequency grating vibrations has been introduced and experimentally validated. An improved reconstruction algorithm adjusting phase-step positions has been tested for a setup being subject to phase-drift effects to a greater extent in comparison to a laboratory setup. The algorithm was shown to be able to remove visible Moiré artifacts.

The setup was found to be mechanically robust against deformation caused by angulation due to only a minor reduction of the visibility. Hence, a measurement without a realignment of the interferometer after angulation is feasible. Artifacts formed by a misalignment of the gratings could be successfully corrected by the applied algorithm, allowing for repeated object measurements at different c-arm positions without the need for a new reference measurement after every angulation. This is a requirement for a potential clinical application of a Talbot-Lau interferometer mounted to a c-arm.

We experienced a shift of grating structures in relation to the pixel matrix caused by a movement of the gratings relative to the detector. In the constructive design of future prototypes a more proper fixation of the gratings is necessary, as even slight deviations are visible when comparing measurements with an intermediate movement of the setup.

The usability of the prototype is hold back by its grating sizes. In fact, the additional restriction due to shadowing further limits the size of the field of view to 17 mm × 46 mm, which is too small for most clinical applications. However, shadowing can be corrected by bending of the gratings66,67 and recently the advance towards larger grating sizes has been reported by stitching of smaller gratings31,32. Both, bent gratings and the usage of larger gratings, can be transferred from a laboratory setup to a c-arm platform. Therefore, in a next step towards the clinics, recent progress with regard to the ability of measuring larger specimens due to larger gratings or a scanning approach34,35,38 at a time span that allows for in vivo measurement has to be combined with medical equipment, e.g. a gantry, a c-arm or a conventional radiography system. In addition, for an angiography system methods for real-time fluoroscopic phase-contrast imaging need to be developed.

The doses applied have been 0.54 mGy for the measurement of the stent and 0.36 mGy for the measurement of the chili. Considering the size of the samples, the doses are higher compared to clinical radiographs. However, the parameters have been chosen to examine the mechanical robustness of the setup without further optimization regarding dose. In general, compared to a laboratory setup the same considerations with regard to dose apply for the prototype with except of the small reduction of visibility due to high-frequency vibrations, which results in increased noise68,69. Recently, two publications reported measurements carried out at a dose level that is comparable to the clinics29,34. Using the same interferometer specifications, the findings could be transferred to a c-arm platform.

The successful implementation of a grating-based phase-contrast imaging setup in a clinical device proving sufficient mechanical robustness for interferometric imaging represents progress in the research aiming at the translation towards clinical practice.

Methods

Talbot-Lau interferometry

A regular Talbot-Lau interferometer has been used consisting of a polychromatic medical x-ray tube with an extended focal spot S10, a flat-panel scintillating x-ray detector D, and three gratings. The phase grating G1 imprints a periodical phase-shift to the wave-front produced by the x-ray tube, which leads to a downstream intensity fringe pattern matching the shape of G1 at certain distances due to the Talbot effect. In addition, the source grating G0 is needed to satisfy the requirements regarding spatial coherence by a partition of the focal spot in several slit sources each fulfilling the coherence requirement and producing its own intensity pattern. As the slit sources are mutually incoherent, the parameters of G0 have to be chosen leading to matching positions of each intensity pattern. An object in the beam path modifies the intensity pattern and may lead to a reduction of the mean intensity, a local change of the position of the fringes caused by deflection and an alternation of the amplitude of the fringes. Accordingly, the attenuation image, differential phase-contrast image, and the dark-field image can be calculated by a comparison of a reference measurement without object and an object measurement with the object in place. As the period of the intensity pattern typically is below the pixel pitch of the detector, an additional analyzer grating G2 is used to sample the intensity pattern by a phase-stepping technique9. The resulting phase-stepping curve in dependence of the phase-step position x measured for each pixel is described by

$$I(x)={I}_{0}[1+{V}_{0}\,\sin (\frac{2\pi }{{p}_{{\rm{G}}2}}x+\varphi )],$$
(1)

where I0 is the mean intensity, V0 the visibility defined by V0 = (Imax − Imin)/(Imax + Imin), and Φ the local offset of the position. The attenuation image Γ, the differential phase-contrast image ΔΦ, and the dark-field image Σ can then be calculated according to

$$\begin{array}{ccc}{\rm{\Gamma }}=-\mathrm{ln}(\frac{{I}_{0}^{{\rm{obj}}}}{{I}_{0}^{{\rm{ref}}}}), & {\rm{\Delta }}{\rm{\Phi }}={{\rm{\Phi }}}_{{\rm{obj}}}-{{\rm{\Phi }}}_{{\rm{ref}}}, & {\rm{and}}\,\,{\rm{\Sigma }}=-\mathrm{ln}(\frac{{V}_{0}^{{\rm{obj}}}}{{V}_{0}^{{\rm{ref}}}}).\end{array}$$
(2)

Description of the setup

The Talbot-Lau interferometer has been mounted to a Siemens Artis one, which is a conventional clinically used floor-mounted c-arm angiography setup. The G0 grating has been integrated between X-ray source and collimator. A unit consisting of the G1, G2 grating and detector is replacing the conventional detector. The interferometer consisted of three gratings manufactured by Microworks: the source grating G0 with the period p0 = 11.54 μm and the height h0 = 270 μm, the phase grating G1 with the period p1 = 3.39 μm and the height h1 = 6.37 μm imprinting a phase shift of π/2 at the grating bars at the design energy of 62.5 keV, and the analyzer grating G2 with the period p2 = 4.8 μm and the height h2 = 160 μm. All grating have been made of gold with a duty cycle of 0.5. G1 has been placed l = 986 mm away from G0. The distance between G1 and G2 amounted to dT = 410 mm.

As x-ray source a medical x-ray tube of type Siemens Megalix CAT Plus 125/40/90 with a rotating anode made of tungsten has been used, which can be driven at acceleration voltages between 40 kV and 125 kV. The focal spot size has been 0.4 (IEC 60336), respectively 0.6 mm × 0.85 mm (H×V) at 15% of the maximum value. The x-rays have been detected using an integrating flat panel detector PerkinElmer Dexela 1512 with 74.8 μm pixel size and a 600 μm thick CsI scintillation layer. The x-ray spectrum has been filtered with a 0.3 mm thick copper plate to suppress x-ray photon energies below 30 keV.

The images have been acquired at 60 kV tube voltage reaching a visibility of 21.4±1.8% over the field of view. The size of the field of view at the position of G1 has been restricted to 17 mm × 46 mm due to shadowing in phase-stepping direction. Every phase-stepping curve has been measured with a tube current of 50 mA. The number of phase-steps and the acquisition time of each phase-step varied between the measurements. The chili has been measured at 17 phase-step positions with an acquisition time of 250 ms per phase-step. The measurement of the stent has been performed at 32 positions with an acquisition time of 200 ms per phase-step.

Reduction of visibility due to high-frequency grating vibrations

The x-ray tube with a rotating anode is mounted to the c-arm. In consequence, vibrations are transferred to the c-arm and the fixed interferometer. Measurements regarding the amplitude and frequency of occurring vibrations with an operating tube have been carried out using triaxial piezoelectric accelerometers, which revealed that vibrations are mainly originating from the anode rotating with a frequency of 156 Hz. The acceleration amplitudes at gratings are typically ≤200 mm/s2 corresponding to displacement amplitudes of about 0.2 μm in phase-stepping direction for a frequency of 156 Hz. Consequently, as the vibration period is much shorter than the acquisition time for one phase step the vibrations lead to a reduction of the visibility due to smearing of the phase-stepping curves. The reduction of the visibility can be quantified according to the following considerations.

The visibility V0 is usually given by V = (Imax − Imin)/(Imax + Imin) with Imax and Imin being the intensity at the maximum, respectively the minimum of the phase-stepping curve. The phase-stepping curve itself is described by Eq. 1. Due to the grating vibrations x = x(t) is depending on the time t. It is assumed that the analyzer grating’s position, which samples the phase-stepping curve, is fixed and the intensity pattern created by the gratings G1 and G2 performs a sinusoidal oscillation caused by the vibrations of both gratings. The position of the intensity pattern then changes over time according to

$$x(t)={x}_{0}+{A}_{{\rm{eff}}}\,\sin (\frac{2\pi }{T}t+{\varphi }_{{\rm{t}}})\mathrm{.}$$
(3)

As the initial position of the phase-stepping curve is arbitrary regarding visibility, the phase ϕ = 0 may be set to zero without a loss in generality. With tacq being the acquisition time of each phase-step it is assumed \(T\ll {t}_{\mathrm{acq}}\). Hence, the phase ϕt = 0 is neglected and the intensity pattern is expected to perform an integer amount of repetitions of the oscillation. Consequently, the average intensity of the phase-step \({\hat{I}}_{\max }\) at the maximum position xmax = g2/4 is given by

$$\begin{array}{rcl}{\hat{I}}_{{\rm{\max }}} & = & \frac{1}{T}{\int }_{0}^{T}{I}_{0}[1+{V}_{0}\,\sin (\frac{2\pi }{{p}_{G2}}({x}_{{\rm{\max }}}+{A}_{\mathrm{eff}}\,\sin (\frac{2\pi }{T}t)))]{\rm{d}}t\\ & = & {I}_{0}+{I}_{0}{V}_{0}\,{J}_{0}(2\pi \frac{{A}_{{\rm{eff}}}}{{p}_{{\rm{G}}2}}),\end{array}$$
(4)

where J0 is the Bessel function of the first kind. Similar calculations result in \({\hat{I}}_{{\rm{\min }}}={I}_{0}-{I}_{0}{V}_{0}\,{J}_{0}[(2\pi {A}_{{\rm{eff}}})/{p}_{{\rm{G}}2}]\). In summary, the relative reduction of the visibility by the oscillations using \({V}_{{\rm{red}}}=({\hat{I}}_{{\rm{\max }}}-{\hat{I}}_{{\rm{\min }}})/({\hat{I}}_{{\rm{\max }}}+{\hat{I}}_{{\rm{\min }}})\) is given by

$$\frac{{V}_{{\rm{red}}}}{{V}_{0}}=|{J}_{0}(2\pi \frac{{A}_{{\rm{eff}}}}{{p}_{{\rm{G}}2}})|\mathrm{.}$$
(5)

Thereby, it was taken into account that the mean intensity at the former phase-step position of the maximum may become the minimum and vice versa by taking the absolute value. The effective amplitude Aeff depends on the phase ϕosc between the oscillations of G0 and G1. The worst case scenario is given for ϕosc = π meaning both oscillations occur in opposing directions increasing the vibration amplitude. Assuming oscillation amplitudes of AG0 = AG1 = 0.2 μm for each grating and considering the magnification, the effective amplitude is calculated by

$${A}_{{\rm{eff}}}=\frac{{d}_{{\rm{T}}}}{l}({A}_{G0}+{A}_{G1})+{A}_{G1},$$
(6)

resulting in Aeff/p2 = 0.077 for the prototype.

Data availability

The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.