Abstract
It is of great fundamental and practical interest to develop effective means of modulating the magnetic hystereses of magnetic materials and their heterostructures. A notable example is the exchange bias (EB) effect between an antiferromagnet or ferrimagnet and a ferromagnet, which has been widely employed to manipulate magnetic anisotropy in spintronic devices and artificial magnets. Here, we report the design, synthesis and characterization of a synthetic perpendicularly-magnetized ferrimagnet based on [Mn2.9Ga/Co2MnSi]n superlattices, which attains thermal stability above 400 K and a coercive field up to 45 kOe through a mechanism of magnetic compensation. The structure is incorporated into a prototype Heusler alloy and MgO barrier based magnetic tunnel junction, which demonstrates high dynamic range linear field responses and an unusual in-plane EB effect. With increasing temperature, the coercive field reaches beyond 70 kOe at 400 K in this device due to the increasing degree of magnetic moment compensation in the superlattice. The results demonstrate that the compensation mechanism can be utilized to achieve simultaneous thermal robustness and high coercivity in realistic spintronic devices.
Similar content being viewed by others
Introduction
The magnetic hysteresis is a signature characteristic of a ferromagnet and the basis for most of its applications. The abilities to control the magnitude and position of the coercive field of a ferromagnet are critical for a variety of magnetic material and device functionalities. A prominent example is the exchange bias (EB) effect1, which is ubiquitous at antiferromagnet/ferromagnet (AFM/FM) and hard ferrimagnet/ferromagnet (FIM/FM) interfaces. EB is widely employed to produce unidirectional magnetic anisotropy in AFM/FM or FIM/FM bilayers; it shifts the magnetic hysteresis loop of the FM, resulting in an increase or decrease of the coercive field at either side of the hysteresis. EB has been utilized to engineer artificial hard magnets free of rare earth elements2, and to produce a pinned FM layer in spin valves and magnetic tunnel junctions (MTJs)3,4,5. For the latter, the EB in an AFM/FM bilayer is often used in combination with the exchange coupling in an artificial AFM, e.g. in Co/Ru(Cu)/Co/IrMn6, in order to minimize the magnetostatic interactions in spin-valve and MTJ devices, and to amplify the exchange bias field significantly beyond the typical values in AFM/FM bilayers4. Besides the AFM/FM heterostructures, EB is also widely observed in FIM/FM hybrid structures7,8,9,10,11. The FIM/FM systems offer an additional advantage that both the coercivity and EB field may be significantly modulated via the compensation state of the FIM12,13. However, the EB field is normally below a few kOe in AFM/FM, while the thermal stability is often poor in FIM/FM structures. More recently, ferromagnets with large perpendicular magnetic anisotropy (PMA) have gained increasing relevance in high-density magnetic recording media and spin transfer torque magnetic random access memory (STT-MRAM), due to their superior thermal and magnetic stability over their in-plane magnetized counterparts. Therefore, perpendicularly-magnetized compensated FIMs with near zero net magnetization, such as Sm0.974Gd0.026Al2 14, DyCo4 12, DyCo5 15, TbCo13, TbFe16, DO3-Mn3Ga17 and Mn2.4Pt0.6Ga18, have attracted much recent attention, and they have been used as the base layer for creating perpendicularly-magnetized FIM/FM bilayers including SmAl2/Sm0.974Gd0.026Al2 7, DyCo5/Ta/Fe76Gd24 9, [Co/Ni]n/TbCo10, TbFe/[Co/Pt]n 11. However, there are a couple of important drawbacks with these materials. The first is the low compensation temperatures, which would limit the utility in practical applications at room temperature or higher. And, with the exception of the compensated Heusler alloys (e.g., the ideal DO3-Mn3Ga), the spin polarization is very low, which essentially precludes direct use of these perpendicularly-magnetized compensated FIMs as a spin polarized electrode19. Therefore, a pertinent question is: Is it possible to design and synthesize an artificial FIM which simultaneously exhibits PMA, high spin polarization, very large coercivity, and superior thermal stability?
Inspired by the compensated FIM compounds and artificial AFMs, we propose a perpendicular hard artificial FIM based on AFM-coupled [FM1/FM2]n superlattices, whose compensation temperature can be flexibly tuned by the thickness ratio of FM1/FM2. Previously, a superlattice FIM of [MnGa/Co2FeAl]n was reported by Q. Ma et al., and the magnetic properties were tuned by adjusting the thickness of MnGa layer20. Here, we realized a thermally robust, perpendicular hard artificial FIM based on perpendicularly-magnetized, AFM-coupled [Mn2.9Ga/Co2MnSi]n superlattices (we describe the form of Mn2.9Ga as MnGa for simplicity from the outset). The mechanism of the AFM coupling in this type of MnGa/Co2MnSi (Co2FeAl) bilayers may originate from an AFM-coupled MnGa/Co interface rooted in the Pauli exclusion effect20,21,22. MnGa is a perpendicularly magnetized ferromagnet with a large magnetocrystalline anisotropy (K u) up to 21.7 Merg/cm3, and tunable saturation magnetization (M s) via variation of the composition and/or growth conditions23,24. An ultralow damping constant of 0.008 was determined from optical pump-probe measurement25, and a spin polarization of 58% as well as a Curie temperature of 730 K was also observed26,27. These features make it an attractive candidate for modern magnetic information storage devices at sub-10 nm nodes. On the other hand, Co2MnSi is a well-known Heusler alloy with 100% spin polarization and a high Curie temperature near 1000 K28; it has been widely studied for applications in spin valve and MTJ structures29,30,31. Recently, MnGa/Co2MnSi bilayers were synthesized and the exchange coupling was studied32,33. Although at a thickness of 20 nm the Co2MnSi exhibits in-plane magnetic anisotropy, in an applied perpendicular magnetic field higher than its demagnetization field, perpendicular AFM coupling between MnGa and Co2MnSi was observed. Here, by reducing the Co2MnSi thickness to 1 nm, we successfully realized AFM-coupled [MnGa/Co2MnSi]n superlattices with full PMA, which presents a model system of perpendicularly-magnetized hard FIM with near zero net magnetization at tunable temperatures. We demonstrate that by properly setting the compensation point, a very high perpendicular coercivity is realized at room temperature, and it continues to increase up to 45 kOe with increasing temperature up to 400 K, which is opposite to the temperature dependence in a conventional FM. The compensation temperature is limited by the individual Curie temperatures of the AFM-coupled FM layers, hence the [MnGa/Co2MnSi]n superlattices have the potential for achieving a compensation temperature much higher than 400 K. Furthermore, we incorporate the [MnGa/Co2MnSi]n into a prototypical MTJ stack of GaAs/Co2MnSi/ [MnGa/Co2MnSi]n/MgO/CoFe/Pd, which yields an appreciable tunneling magnetoresistance (TMR) of 31% at room temperature. With increasing temperature, the coercive field reaches beyond 70 kOe at 400 K in this device due to the increasing degree of magnetic moment compensation in the superlattice. The results demonstrate that the compensation mechanism can be utilized to achieve simultaneous thermal robustness and high coercivity in realistic spintronic devices.
Results
Design of perpendicular hard AFM-coupled [FM2/FM1]n FIM superlattices
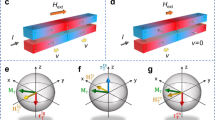
Figure 1 (a) depicts an analytical model for the AFM-coupled FM1/FM2 bilayer system. In this structure, the thickness of each individual layer is smaller than the exchange length, and the soft ferromagnetic film FM2 is strongly AFM-coupled with the PMA hard ferromagnetic film FM1. The total free energy per unit area of a bilayer system can be expressed as
Analytical model and principal compensation mechanism in AFM-coupled bilayers. (a) Schematic drawing of an FM1/FM2 AFM-coupled bilayer structure, and magnetization M 1 (M 2) and magnetic anisotropy field H K1 (H K2) directions of FM1 (FM2). (b) Schematic diagram depicting different scenarios of magnetic moment (m) versus temperature (T). The AFM-coupled ferromagnetic films FM1 and FM2 have Curie temperature T c1 and T c2 respectively. When m of FM1 is greater than that of FM2 (solid line), there is no intersection point between the two m-T curves. At a smaller m of FM1, the m-T curve of FM1 (dash line) will cross the m-T curve of FM2 at a compensation temperature of T comp. (c) The two scenarios in (b) result in two distinct M net - T curves at temperature below T comp: One has decreasing m with increasing T, and the other is opposite.
where K 1 is the perpendicular anisotropy of the perpendicular hard magnet FM1, K 2 is the in-plane uniaxial anisotropy of the soft magnet FM2, M 1 (M 2) and t 1 (t 2) are the saturation magnetization and thickness of FM1 (FM2) respectively, θ 1 (θ 2) is the angle between M 1 (M 2) and the film normal, and J ex is the exchange coupling constant between M 1 and M 2. Magnetic field H is applied perpendicular to the film plane. For very strong AFM coupling, the exchange coupling field is much larger than the out-of-plane demagnetizing field of FM2 and the coercive field of FM1, so there is a simple relation θ 2 = θ 1 − π. By setting \(\partial E/\partial {\theta }_{1}=0\), and θ 1 = 0, we obtain the coercive field of the bilayer
where
and
This indicates that the coercive field of the AFM-coupled bilayer could be effectively tuned by changing the net magnetization (M net) via the thickness ratio of FM1/FM2. Figure 1b,c) depicts schematically the temperature-dependent magnetic moment (magnetization) of the individual FM layers (the AFM-coupled bilayer). FM1 and FM2 have different Curie temperatures of T c1 and T c2. As illustrated in Fig. 1b and c, depending on the thickness ratio, there are two distinct net magnetization (M net ) states with different temperature dependencies. In the first state, the m-T curves for FM1 and FM2 have no intersection point, so the M net increases with increasing temperature. Upon decreasing the thickness of FM1, the two m-T curves cross at an intersection point T comp, and the M net decreases with increasing temperature up to T comp. For a strongly AFM-coupled FM1/FM2 bilayer, its coercivity is mainly determined by K eff/M net. Therefore, for the case of a bilayer or superlattice in which M net decreases with increasing temperature, the coercivity would increase with increasing temperature, which is opposite of the behavior of a conventional FM. By choosing a suitable FM1/FM2 thickness ratio and setting a proper compensation temperature T comp, one could obtain an artificial perpendicularly-magnetized FIM, in which the coercive field increases with increasing temperature.
Magnetic properties of superlattices of [MnGa/Co2MnSi]n
We have grown three samples of [MnGa/Co2MnSi]n superlattices by molecular-beam epitaxy (MBE). For all three samples, the thickness of the Co2MnSi layer is fixed at 1.0 nm, while the MnGa thicknesses are chosen as 3.75, 4.5, and 5.6 nm. The number of period is n = 5. The temperature dependence of M net, and the magnetic hysteresis at 280 K were measured by a superconducting quantum interference device (SQUID) magnetometer. As shown in Fig. 2(a), for the sample with the thickest MnGa layer of 5.6 nm (sample C), there is no compensated state in the entire measurement temperature range, and the M net increases with increasing temperature, consistent with the first case depicted in Fig. 1(a). As the MnGa thickness decreases to 4.5 nm (sample B), the M net (T) shows qualitatively different behavior: The M net decreases with increasing temperature, indicating the existence of a compensated state at a higher temperature. Further decreasing the thickness of MnGa to 3.75 nm (sample A), the \({M}_{{\rm{net}}}\) shows similar temperature dependence as that of sample B, but has a higher value at the same temperature. It should be noted that the results in Fig. 2a are consistent with a Curie temperature for the ultrathin (1 nm) Co2MnSi layer much reduced from its bulk value, to lower than that of MnGa, because if the Curie temperature of MnGa is lower than that of Co2MnSi, the crossover of the m(T) curves should occur larger, rather than smaller, MnGa thicknesses, which is contrary to the experimental data. Consequently, the compensation state was achieved in the optimal temperature range in sample B. Figure 2b shows the hystereses for the three samples at T = 280 K (the hysteresis loop of a single MnGa layer is shown in the section I of Supplementary Information for comparison). Two important aspects of the data are worth noting. First, although the magnetization dynamics of a hard ferromagnet is expected to be controlled primarily by the internal nucleation or pinning processes, the coercivity of sample B, which has the smallest \({M}_{{\rm{net}}}\) at room temperature, shows a marked enhancement over those of the other two samples. Second, despite that sample C has a much smaller M net than sample A at the same temperature, they have essentially the same coercivity. These observations imply that the magnetization dynamics of the AFM-coupled superlattices can be controlled by the degree of compensation thanks to the lowered system Zeeman energy, as long as the thickness of each layer is smaller than a critical value. In these samples, although the Co2MnSi thickness is always smaller than its critical length; if the MnGa thickness is larger than the critical value, the magnetization dynamics will be similar to that of a single layer MnGa film even if the net magnetic moment of the bilayer is close to the compensation point. The critical length should be related to the exchange length, which is defined by \(\sqrt{\frac{A}{{K}_{{\rm{eff}}}}}\), where A is the exchange stiffness and K eff is the effective anisotropy constant. For MnGa, we assume A and K eff have typical values of 10 pJ/m and 1 MJ/m3, respectively, resulting in an exchange length of 3 nm. For the superlattices of [MnGa/Co2MnSi]5, the thickness of the MnGa layer should be much less than 6 nm considering the double interfaces for each MnGa layer. Therefore, the temperature dependence of the coercive field for the three samples provides a model system to ascertain the effects of the magnetic compensation mechanism in the AFM-coupled superlattices.
Magnetic properties of [MnGa (t nm)/Co2MnSi]5 superlattices. (Sample A: t = 3.75 nm, red circles; sample B: t = 4.5 nm, black squares; sample C: t = 5.6 nm, blue up triangles). (a) Net magnetization (M net) versus temperature (T) for samples A, B and C from 50 to 350 K. (b) Hystereses of samples A, B and C measured in a magnetic field range from −50 to +50 kOe at 280 K.
As one approaches the compensation temperature, it becomes increasingly challenging to measure the magnetic hysteresis and determine the coercivity of a compensated FIM by SQUID magnetometry. Fortunately, for our systems, the anomalous Hall effect (AHE) coefficients of MnGa and Co2MnSi are different and of opposite signs34,35. Consequently, for the MnGa dominated sample C, the AHE coefficient is positive, while for the Co2MnSi dominated sample A, it is negative, as shown in Fig. 3a. It is well established that the AHE signal is directly proportional to the magnetization of the sample36. Therefore, the temperature dependence of the coercivity of these superlattices can be measured by the AHE precisely as the temperature increases all the way to the compensation point. Figure 3a shows the Hall resistance (R Hall, in which the AHE makes the predominant contribution here) loops for samples A and C at two representative temperatures, and Fig. 3b shows the resulting coercivity H c(sl) for the two samples at various temperatures. For the MnGa dominated sample C, the temperature dependence of the H c(sl) is similar to that of a single MnGa layer; in contrast, for the Co2MnSi dominated sample A, its temperature dependence is not monotonic, and for temperatures higher than 100 K, the H c(sl) actually increases with increasing temperature. At 50 K, the nucleation/pinning mechanism is likely to be dominant and also leads to enhancement of H c(sl). These features are consistent with the SQUID measurements and the conclusion that the magnetic compensation modulates the magnetization dynamics in the thinner samples.
Hall resistance at different temperatures for [MnGa (t nm)/Co2MnSi]5 superlattices. (Sample A: t = 3.75 nm, red circles; sample C: t = 5.6 nm, blue up triangles). (a) R Hall for samples A and C at two representative temperatures of 100 K (open) and 350 K (solid) in a magnetic field range from −85 to + 85 kOe. (b) Coercivity of superlattices versus temperature (H c(sl) − T) curves from 50 to 350 K.
For sample B, with MnGa thickness of 4.5 nm and closest to the compensation point at high temperatures, the anomalous Hall resistances show an interesting new feature. As is evident in Fig. 4a, there are two hystereses attached to each Hall resistance sweep, suggesting two distinct magnetic switchings in the superlattice. The opposite signs of the AHE coefficients for MnGa and Co2MnSi provide a rare situation in which the coercivity of the superlattice (H c(sl)), the exchange coupling field between MnGa and Co2MnSi (H ex), and the coercivity of the MnGa (H c(MnGa)) can be uniquely determined from the switching fields in the Hall traces. The schematic diagram accompanying Fig. 4a shows four different magnetic states (red arrows for Co2MnSi, and blue arrows for MnGa); the transitions between these states are marked by numbers from 1 to 4 for the down-sweep (positive to negative). In the low field range, the AFM-coupled MnGa and Co2MnSi produce anomalous Hall voltages of the same sign, and switch together as the applied magnetic field increases to H c(sl) (from state 2 to 3). As the applied magnetic field further increases, the magnetic moment of the MnGa layers switches from being antiparallel to parallel with the magnetic field (from state 3 to 4), and their contributions to the anomalous Hall voltage switch sign, leading to a decrease in the AHE signal. The AHE was measured at different temperatures from 50 to 400 K, which yields H c(MnGa), H ex, and H c(sl) at these temperatures, as plotted in Fig. 4b and c. H c(MnGa) and H ex show the normal trend, decreasing from 8.0 to 5.7 kOe and 72.5 to 56.0 kOe respectively from 50 to 400 K. However, in the same temperature range, the coercivity of the superlattice as a whole (H c(sl)) increases significantly from 33 to 45 kOe, and the rate of increase appears to accelerate as the compensation point is approached. In contrast, the enhancement is much weaker for sample A with thinner MnGa layers, implying that the compensation mechanism in the compensated natural FIM compounds is effective in this synthetic AFM-coupled superlattice. The perpendicular magnetic anisotropy K 1 was deduced to be about 1 Merg/cm3 by a linear fitting of the H c ∝ K eff/M net curve. This implies that the hysteresis loop of this superlattice can be described by the Kronmüller equation, where the nucleation and pinning processes are two determining factors for the coercive field. The outstanding characteristics of this artificial FIM promise a variety of applications in artificial hard magnets, high density magnetic recording and, in particular, because of the high spin polarization of Co2MnSi, it may be used directly as a reference layer in perpendicular MTJs without the use of AFM EB pinning.
Hall resistance at different temperatures for [MnGa(t nm)/Co2MnSi]5 superlattice (sample B, t = 4.5 nm). (a) The R Hall curves at different temperatures from 50 to 400 K. Four different magnetic states are depicted (red arrows for Co2MnSi, blue arrows for MnGa), and the transitions between them are indicated by numbers from 1 to 4 for a down-sweep (positive to negative: the green line with arrows). \({H}_{{\rm{C}}}^{-}\) and \({H}_{{\rm{C}}}^{+}\) are the coercive fields of the superlattice as a whole. \({H}_{{\rm{C}}({\rm{MnGa}})}^{+}\) and \({H}_{{\rm{C}}({\rm{MnGa}})}^{-}\) are the coercive fields for the MnGa layers biased by the exchange coupling field from the Co2MnSi layers in the superlattice. (b) The coercivity of the MnGa layers, determined by \({H}_{{\rm{c}}({\rm{MnGa}})}=\,({H}_{{\rm{C}}({\rm{MnGa}})}^{+}-{H}_{{\rm{C}}({\rm{MnGa}})}^{-})/2\). (c) The exchange coupling field \({H}_{{\rm{ex}}}[{H}_{{\rm{ex}}}=({H}_{{\rm{C}}({\rm{MnGa}})}^{+}+{H}_{{\rm{C}}({\rm{MnGa}})}^{-})/2]\) and the coercivity of the superlattices \({H}_{{\rm{c}}({\rm{s}}{\rm{l}})}[{H}_{{\rm{c}}({\rm{s}}{\rm{l}})}=({H}_{{\rm{C}}}^{+}-{H}_{{\rm{C}}}^{-})/2]\) as functions of temperature.
Synthesis and characterization of MTJ incorporating [MnGa/Co2MnSi]n synthetic FIM
To demonstrate the efficacy of the MnGa/Co2MnSi synthetic FIM as the reference electrode of an MTJ, we have fabricated an epitaxial heterostructure of GaAs/Co2MnSi/[MnGa/Co2MnSi]n/MgO/CoFe/Pd and evaluated its TMR. The microstructure of this heterostructure was examined by cross-section high-resolution transmission electron microscopy (HRTEM). As shown in Fig. 5a, a periodical structure of multilayers was seen clearly. The thicknesses of the Co2MnSi and MnGa layers are about 0.9 nm and 4.5 nm respectively. The entire MTJ stack is single crystalline with an epitaxial relationship Co2MnSi (001) (110)//MnGa (001) (100), which was confirmed by in-situ reflection high-energy electron diffraction (RHEED) patterns. None of the layers is much below 1 nm thick, in contrast to other metal multilayers such as Co/Pt where the layer thickness are typically a few angstroms; as a result, the structure should be amenable to wafer-scale fabrication of spintronic devices.
HRTEM image of the MTJ stack and a schematic of the MTJ device structure. (a) Transmission electron microscopy image showing the sharp interfaces between GaAs, [MnGa/Co2MnSi]4 superlattice, MgO and CoFe layers. Each layer is readily distinguishable. (b) Schematic of the prototype MTJ device with a [MnGa/Co2MnSi]4 superlattice as a reference layer, and CoFe as a sensing layer.
The heterostructure is patterned into an MTJ device, as schematically shown in Fig. 5b, via photolithography and ion milling. The TMR of this superlattice-based MTJ was measured at different temperatures from 10 to 370 K, and the results are shown in Fig. 6a. The junction resistance versus perpendicular magnetic field (R-H) has a basic symmetrical butterfly shape at temperatures below 250 K, beyond which an asymmetry gradually develops. Figure 6b shows schematically the four different magnetic states corresponding to the TMR, with the magnetic switchings marked by numbers 1 to 4 for a down-sweep MR curve (positive to negative magnetic field); the magnetic moment rotation of the CoFe from state 2 to 3 is depicted, which results in a linear TMR response within its demagnetizing field (H D to - H D). At 280 K and above, an asymmetry in the TMR becomes evident, clearly indicated by a decrease of \({H}_{{\rm{C}}}^{-}\) and increase of \({H}_{{\rm{C}}}^{+}\). The increase of \({H}_{{\rm{C}}}^{+}\) beyond + H D leads to a null response of the junction resistance to increasing applied field (a plateau). At the highest measurement temperatures (350 K and 370 K), \({H}_{{\rm{C}}}^{+}\) is so high that in applied field beyond 59.3 kOe, the junction resistance decreases with increasing field. The prominent exchange bias evident in the TMR traces at high temperatures is unexpected since it is not observed in the AHE measurements of the unpatterned [MnGa(t nm)/Co2MnSi(1 nm)]5 superlattices (Fig. 4a). We surmise that the surprising effect in the MTJ originates from an in-plane EB coupling between the MnGa/Co2MnSi directly under the MTJ and that in the surrounding area defined by the ion milling. The initialization and evolution of such an exchange-biased state for a similar MTJ are presented in Section II of the Supplementary Information. The corresponding R-H curves at high temperatures (350 K and 300 K) following an unusual field warming process show pronounced asymmetries indicative of the in-plane exchange bias effect, with EB fields of 25 kOe and 17.5 kOe respectively.
TMR in an MTJ with a [MnGa(4.5 nm)/Co2MnSi(0.9 nm)]4 reference electrode. (a) Resistance of the MTJ versus applied perpendicular magnetic field (R-H) measured at temperatures from 10 to 370 K. (b) Schematic depiction of the four different magnetic states for the MTJ in a down-sweep (positive to negative magnetic field: dash line and black arrows). The switchings between the magnetic states are marked by numbers 1 to 4. The magnetic moment rotation of the CoFe from state 2 to 3 is depicted separately. (c) TMR, coercivity H c, and the exchange bias field H EB at different temperatures. The TMR is defined as \(({R}_{{\rm{state}}3}-{R}_{{\rm{state}}1})/{R}_{{\rm{state}}1}\), H c and H EB are determined by \(({H}_{{\rm{C}}}^{+}-{H}_{{\rm{C}}}^{-})/2\) and \(({H}_{{\rm{C}}}^{+}+{H}_{{\rm{C}}}^{-})/2\), respectively.
Outside the junction area, the ion milling etches into the [MnGa/Co2MnSi]4 superlattice (Fig. 5b). The different thicknesses of the MnGa/Co2MnSi multilayer under the MTJ and outside of it result in different degrees of magnetic moment compensation. However, in the etched area, the magnetic compensation mechanism remains effective, which we verified by SQUID magnetometry measurements on a reference sample obtained by dry-etching a piece of the heterostructure for an MTJ without any resist mask during the ion milling step of the MTJ mesa fabrication. As presented in Section III of the Supplementary Information, the coercivity of the uniformly etched reference sample increases as temperature increases, and the H C shows a negative correlation with the net areal magnetization of the sample; both are indicators of the magnetic compensation. Furthermore, the ion bombardment induced damages to the etched area may also alter its magnetization dynamics. Hence, the MnGa/Co2MnSi multilayers in the two different areas may well have different coercive fields (H c) with different temperature dependencies, which could lead to the unusual in-plane EB effect. As evident in the TMR curve, at 370 K neither H c nor the EB field (H EB) is reached at an external magnetic field of 70 kOe. Microscopically, we speculate that EB stems from the exchange coupling at the boundary between the MnGa/Co2MnSi electrode directly under the MTJ and that in the surrounding area.
As shown in Fig. 6c, the TMR decreases from 65.0% to 24.4% with increasing temperature. The values are much lower than the TMR of Co2MnSi based MTJs, probably due to poor interfacial quality caused by large lattice mismatch between the superlattice electrodes and MgO barrier and/or diffusion of Mn atoms into the MgO barrier. Nevertheless, both H c and H EB increase with increasing temperature above 200 K. This feature is in good agreement with the trend revealed in the AHE measurements in a similar temperature range on a single [MnGa (4.5 nm)/Co2MnSi(1 nm)]4 superlattice. For the H c versus temperature curve of the MTJ, there is a peak at 280 K, and H c continue to rise after 310 K due to the dramatically increased EB field. It is worth noting that the unusual temperature dependence of the \({H}_{{\rm{EB}}}\) implies that the orientation of H EB can be changed by a field warming process, which is distinct from the traditional procedure for building an exchange bias field in FM/AFM systems. These results indicate that this [MnGa(4.5 nm)/Co2MnSi(0.9 nm)]4 superlattice alone serves as a reference electrode in the perpendicular MTJ device with exceptional thermal and magnetic stability.
Discussion
As is evidenced in intrinsic FIMs such as TbxCo1−x, DyCo5, and Sm0.972Gd0.028Al2 etc., magnetic compensation is a most important condition for large exchange bias effect in FM/FIM multilayers; we have adopted this concept in the design and synthesis of an artificial perpendicularly-magnetized FIM. By using an ultrathin Co2MnSi layer and choosing the appropriate MnGa/Co2MnSi thickness ratio, we have engineered the compensation state of an AFM-coupled MnGa/Co2MnSi superlattice and realized a high compensation temperature well beyond 400 K. Hence a thermally robust, perpendicularly magnetized synthetic FIM was successfully demonstrated. Both the as-grown superlattice and the subsequently fabricated MTJ exhibit H C which increases with increasing temperature, a strong indicator of compensation-induced exchange coupling. Meanwhile, the high spin polarization in Co2MnSi is also preserved as evidenced by the large TMR. In the lithographically patterned MTJ device, an unexpected exchange bias effect emerges, which is absent in a similar unpatterned superlattice. The effect is attributed to an in-plane EB effect between the MnGa/Co2MnSi multilayers under the tunnel junction and in its surrounding areas. This in-plane EB effect can reach tens of kOe, which is large enough for a variety of applications. It should be noted that the H c and H EB are impacted by the device fabrication process, to which much attention should be paid for optimal and consistent device performance. A similar strategy of compensation point engineering may be applicable to a broad set of AFM-coupled bilayers of a PMA hard ferromagnet and a thin soft FM layer, such as MnAl/Co37, MnGa/Co21,22, MnGa/Co2FeSi38.
In conclusion, a thermally robust PMA synthetic FIM with a high compensation temperature beyond 400 K was successfully realized in the AFM-coupled [MnGa/Co2MnSi]n superlattices. A prototype device for high field sensing with a structure of GaAs/Co2MnSi/[MnGa/Co2MnSi]n/MgO/CoFe/Pd was fabricated which demonstrated high thermal and magnetic stability beyond 370 K and 70 kOe simultaneously. The design method of this artificial hard perpendicular FIM can be adapted to a variety of AFM-coupled multilayer systems as well as functional spintronic devices.
Methods
Growth and characterization
[Mn2.9Ga (t)/Co2MnSi(1 nm)]5 was epitaxially grown on GaAs (001) substrates at 250 °C with different Mn2.9Ga thicknesses (t A = 3.75, 4.5, 5.6 nm) in a VG80 molecular-beam epitaxy system, and annealed in-situ at 250 °C for 10 minutes. The atomic ratio of Mn/Ga in the MnGa was calibrated to be about 2.9/1.0 by energy-dispersive spectrometry. For the MTJ structure, besides the periodical Mn2.9Ga/Co2MnSi bilayers, near the MgO barrier one more Co2MnSi layer was deposited for better TMR ratio. MgO was deposited by an electron-beam evaporator at room temperature, and the CoFe layer was deposited at 200 °C. The entire growth process was monitored in-situ by reflection high-energy electron diffraction (RHEED). The RHEED patterns showed 1/2-order superlattice reflections along the [110]Co2MnSi direction, indicating a L21 phase39. The MTJ device structures were characterized by cross-sectional high-resolution transmission electron microscopy (HRTEM, Tecnai G2 F30). The magnetic properties of the superlattices were characterized by SQUID magnetometry with a maximum applied field of ±5 T. The MTJ with a junction size of 50 × 50 μm2 and Hall devices with an active area of 100 × 300 μm2 were fabricated by UV lithography and ion milling processes. The transport properties were measured by a Quantum Design PPMS with an applied magnetic field up to 9 T using the four-terminal DC method with a current of 10 μA. More measurement and device information could be found in Supporting Information.
Data availability
The data sets generated during measurements and/or analysed during the current study are available from the corresponding author upon request.
References
Nogués, J. & Schuller, I. K. Exchange bias. J. Magn. Magn. Mater. 192, 203–232 (1999).
Giri, S., Patra, M. & Majumdar, S. Exchange bias effect in alloys and compounds. Journal of Physics-Condensed Matter 23, 23 (2011).
Kools, J. C. S. Exchange-biased spin-valves for magnetic storage. IEEE Trans. Magn. 32, 3165–3184 (1996).
Parkin, S. et al. Magnetically engineered spintronic sensors and memory. Proc. IEEE 91, 661–680 (2003).
Ikeda, S. et al. Magnetic tunnel junctions for spintronic memories and beyond. IEEE Trans. Electron Devices 54, 991–1002 (2007).
Huai, Y. et al. Spin-valve heads with synthetic antiferromagnet CoFe/Ru/CoFe/IrMn. J. Appl. Phys. 85, 5528–5530 (1999).
Ungureanu, M. et al. Using a zero-magnetization ferromagnet as the pinning layer in exchange-bias systems. Phys. Rev. B 82, 174421 (2010).
Kulkarni, P. D., Dhar, S. K., Provino, A., Manfrinetti, P. & Grover, A. K. Self-magnetic compensation and shifted hysteresis loops in ferromagnetic samarium systems. Phys. Rev. B 82, 144411 (2010).
Radu, F., Abrudan, R., Radu, I., Schmitz, D. & Zabel, H. Perpendicular exchange bias in ferrimagnetic spin valves. Nature Communications 3, 1728 (2012).
Tang, M. H. et al. Interfacial exchange coupling and magnetization reversal in perpendicular [Co/Ni]N/TbCo composite structures. Sci. Rep. 5, 10863 (2015).
Romer, S. et al. Temperature dependence of large exchange-bias in TbFe-Co/Pt. Appl. Phys. Lett. 101, 222404 (2012).
Chen, K. et al. Observation of an atomic exchange bias effect in DyCo4 film. Sci. Rep. 5(8), 18377 (2015).
Tang, M. H., Zhang, Z. Z. & Jin, Q. Y. Manipulation of perpendicular exchange bias effect in [Co/Ni]N/(Cu,Ta)/TbCo multilayer structures. Aip Advances 5, 076105 (2015).
Adachi, H. & Ino, H. A ferromagnet having no net magnetic moment. Nature 401, 148–150 (1999).
Unal, A. A. et al. Ferrimagnetic DyCo5 Nanostructures for Bits in Heat-Assisted Magnetic Recording. Physical Review Applied 5, 064007 (2016).
Schubert, C. et al. Interfacial exchange coupling in Fe-Tb/ Co/Pt heterostructures. Phys. Rev. B 87, 054415 (2013).
Sabine, W., Hem, C. K. & Gerhard, H. F. & Claudia, F. Valence electron rules for prediction of half-metallic compensated-ferrimagnetic behaviour of Heusler compounds with complete spin polarization. J. Phys.: Condens. Matter 18, 6171 (2006).
Nayak, A. K. et al. Design of compensated ferrimagnetic Heusler alloys for giant tunable exchange bias. Nat. Mater. 14, 679–684 (2015).
Da Silva, M. et al. Finite tunnel magnetoresistance at the compensation point of Sm1−xGdxAl2, a ferromagnetic electrode with zero magnetization. Appl. Phys. Lett. 98, 232504 (2011).
Ma, Q. L., Zhang, X. M., Miyazaki, T. & Mizukami, S. Artificially engineered Heusler ferrimagnetic superlattice exhibiting perpendicular magnetic anisotropy. Scientific Reports 5, 7863 (2015).
Ma, Q. et al. Abrupt Transition from Ferromagnetic to Antiferromagnetic of Interfacial Exchange in Perpendicularly Magnetized L10-MnGa/FeCo Tuned by Fermi Level Position. Phys. Rev. Lett. 112, 157202 (2014).
Xiao, J. X. et al. Tailoring the interfacial exchange coupling of perpendicularly magnetized Co/ L10 -Mn1.5Ga bilayers. J. Phys. D: Appl. Phys. 49, 245003 (2016).
Zhu, L. J. et al. Multifunctional L10-Mn1.5Ga Films with Ultrahigh Coercivity, Giant Perpendicular Magnetocrystalline Anisotropy and Large Magnetic Energy Product. Adv. Mater. 24, 4547–4551 (2012).
Mizukami, S. et al. Composition dependence of magnetic properties in perpendicularly magnetized epitaxial thin films of Mn-Ga alloys. Phys. Rev. B 85, 014416 (2012).
Mizukami, S. et al. Long-Lived Ultrafast Spin Precession in Manganese Alloys Films with a Large Perpendicular Magnetic Anisotropy. Phys. Rev. Lett. 106, 117201 (2011).
Balke, B., Fecher, G. H., Winterlik, J. & Felser, C. Mn3Ga, a compensated ferrimagnet with high Curie temperature and low magnetic moment for spin torque transfer applications. Appl. Phys. Lett. 90, 152504–152503 (2007).
Kurt, H., Rode, K., Venkatesan, M., Stamenov, P. & Coey, J. M. D. High spin polarization in epitaxial films of ferrimagnetic Mn3Ga. Phys. Rev. B 83, 020405 (2011).
Jourdan, M. et al. Direct observation of half-metallicity in the Heusler compound Co2MnSi. Nat Commun 5, 4974 (2014).
Liu, H.-x et al. Giant tunneling magnetoresistance in epitaxial Co2MnSi/MgO/Co2MnSi magnetic tunnel junctions by half-metallicity of Co2MnSi and coherent tunneling. Appl. Phys. Lett. 101, 132418 (2012).
Sakuraba, Y. et al. Giant tunneling magnetoresistance in Co2MnSi/Al-O/Co2MnSi magnetic tunnel junctions. Appl. Phys. Lett. 88, 192508 (2006).
Iwase, T. et al. Large Interface Spin-Asymmetry and Magnetoresistance in Fully Epitaxial Co2MnSi/Ag/Co2MnSi Current-Perpendicular-to-Plane Magnetoresistive Devices. Applied Physics Express 2, 063003 (2009).
Ranjbar, R. et al. Structural and magnetic properties of cubic and tetragonal Heusler alloy bilayers. Materials & Design 96, 490–498 (2016).
Ranjbar, R. et al. Antiferromagnetic coupling in perpendicularly magnetized cubic and tetragonal Heusler bilayers. Mater. Lett. 160, 88–91 (2015).
Schneider, H., Vilanova, E., Balke, B., Felser, C. & Jakob, G. Hall effect in laser ablated Co2(Mn,Fe)Si thin films. J. Phys. D: Appl. Phys. 42, 084012 (2009).
Zhu, L. J., Pan, D. & Zhao, J. H. Anomalous Hall effect in epitaxial L10Mn1.5Ga films with variable chemical ordering. Phys. Rev. B 89, 220406 (2014).
Nagaosa, N., Sinova, J., Onoda, S., MacDonald, A. H. & Ong, N. P. Anomalous Hall effect. Rev. Mod. Phys. 82, 1539–1592 (2010).
Bruynseraede, C. et al. Strong anti-ferromagnetic coupling in tau MnAl/Co perpendicular magnetic superlattices on GaAs. IEEE Trans. Magn. 34, 861–863 (1998).
Ranjbar, R. et al. Interfacial exchange coupling in cubic Heusler Co2FeZ (Z = Al and Si)/tetragonal Mn3Ga bilayers. J. Appl. Phys. 117, 17A332 (2015).
Li, G. F. et al. Effect of nonstoichiometry on the half-metallic character of Co2MnSi investigated through saturation magnetization and tunneling magnetoresistance ratio. Phys. Rev. B 89, 014428 (2014).
Acknowledgements
The work was supported by the National Program on Key Basic Research Project [MOST, Grant Nos. 2015CB921500], National High-tech R&D Program of China [MOST, Grant Nos. 2014AA032904], Key Research Project of Frontier Science of Chinese Academy of Science [Grant Nos. QYZDY-SSW-JSC015], and the National Natural Science Foundation of China [NSFC, Grant Nos. 61334006, 11304307, 11474273]. P. X. acknowledges support by NSF grant DMR-1308613.
Author information
Authors and Affiliations
Contributions
J.H.Z. coordinated the project. J.L. and S.W.M. performed the sample fabrication and basic characterization. P.X., J.L., S.W. M., X.P.Z., X.L.W., J.B.X., J.L. and J.H.Z. analyzed the data and wrote the manuscript. All authors contributed to the discussion of the results.
Corresponding authors
Ethics declarations
Competing Interests
The authors declare that they have no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Lu, J., Mao, S., Zhao, X. et al. Design and Synthesis of an Artificial Perpendicular Hard Ferrimagnet with High Thermal and Magnetic Field Stabilities. Sci Rep 7, 16990 (2017). https://doi.org/10.1038/s41598-017-16761-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-017-16761-z
This article is cited by
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.