Abstract
The marine invertebrate fossil record provides the most comprehensive history of how the diversity of animal life has evolved through time. One of the main features of this record is a modest rise in diversity over nearly a half-billion years. The long-standing view is that ecological interactions such as resource competition and predation set upper limits to global diversity, which, in the absence of external perturbations, is maintained indefinitely at equilibrium. However, the effect of mechanisms associated with the history of the seafloor, and their influence on the creation and destruction of marine benthic habitats, has not been explored. Here we use statistical methods for causal inference to investigate the drivers of marine invertebrate diversity dynamics through the Phanerozoic. We find that diversity dynamics responded to secular variations in marine food supply, substantiating the idea that global species richness is regulated by resource availability. Once diversity was corrected for changes in food resource availability, its dynamics were causally linked to the age of the subducting oceanic crust. We suggest that the time elapsed between the formation (at mid-ocean ridges) and destruction (at subduction zones) of ocean basins influences the diversity dynamics of marine invertebrates and may have contributed to constrain their diversification.
Similar content being viewed by others
Introduction
Based primarily on the metazoan fossil record, two models of clade diversification, equilibrium and non-equilibrium, have been proposed to explain the evolution of taxonomic diversity since the Cambrian (~541 million years, Myr, ago)1,2,3,4,5. The equilibrium model predicts that, for a given amount of resource availability and ecospace occupation, diversity cannot exceed a global carrying capacity and, as a consequence, diversity eventually reaches an equilibrium level1,6. At equilibrium, the origination and settling of new species are balanced by the failure and extinction of earlier taxa in what has been termed an evolutionary arms race. The non-equilibrium model, in contrast, predicts that diversity may rise or fall as abiotic forcing mechanisms such as tectonic, eustatic, climatic and/or oceanographic contingencies promote either lineage splitting or termination, respectively7,8,9,10. Alternatively, a non-equilibrium, innovation-driven model has been put forward to account for instances of unconstrained diversity growth in the absence of abiotic forcing mechanisms11. In all cases, diversity levels are expected to track changes in food resource availability12,13,14, making it difficult to select the model that best explains the diversity dynamics of marine animals. For instance, enhanced food supply relieves biological communities from resource limitation, which is the main control on diversity expansion in equilibrium models15,16. Alternatively, enhanced food supply could promote diversification, if tectonic processes facilitated habitat fragmentation8 or, alternatively, if evolutionary innovation led to novel mechanisms for resource exploitation17,18. Whereas increased resource supply is an essential requirement for the growth of diversity in equilibrium models, resource limitation does not necessarily preclude the growth of diversity in non-equilibrium diversification models. As a consequence, an increase of diversity under conditions of constant resource supply should be indicative of abiotic forcing mechanisms or new ecospace occupation. Here we correct marine invertebrate diversity for changes in marine food supply through Phanerozoic time (~541 Myr ago to present), thereby revealing the signal of diversity dynamics related to factors other than food resource availability. Then, we use a state-of-the-art statistical method for causal inference to unveil the mechanisms responsible for changes in corrected diversity. In particular, we explore the effect of mechanisms associated with the history of the seafloor (i.e. biome age), and their influence on the creation and destruction of marine benthic habitats using data derived from a geodynamic model.
Results
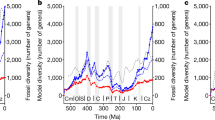
Global estimates of the organic carbon (C) burial rate, extracted from the long-term C and sulphur (S) cycle GEOCARBSULF model19, were used as a proxy for food supply. Not all sources of detrital organic matter were accessible to marine consumers. C and S isotope mass balance analyses show a maximum of O2 centred around 300 Myr ago, which was caused by the expansion of terrestrial vascular plants20 combined with a combination of climatic and palaeogeographic factors that enhanced plant-derived organic C preservation and coal formation21. It is possible to estimate the rate of organic C burial in marine environments through time using the worldwide weight ratio of organic C to pyrite-S (C/S) in sedimentary organic matter (see Methods). Whereas abundant sulphate reduction and pyrite formation in marine euxinic environments leads to sedimentary organic matter with low C/S ratios22, the burial of organic C in freshwater environments such as forest swamps and peatlands results in high C/S ratios because of their comparatively lower sulphate content22. The resulting marine organic C burial rate curve showed a cyclical pattern during the Palaeozoic (541–252 Myr ago) and Early Mesozoic (252–175 Myr ago) superimposed on a long-term decline, followed by a secular increase across the Mid-Late Mesozoic (175–66 Myr ago) and Cenozoic (66 Myr ago-present) (Fig. 1a). We compared estimates of organic C burial rate against sampling-standardized estimates of marine invertebrate diversity based on the shareholder quorum subsampling method, SQS, and classical rarefaction, CR. Sampling standardization is recommended because sampling effort per time interval in fossil databases is skewed toward recent records23. The organic C burial rate curve was remarkably coincident with the diversity dynamics of marine invertebrates (Fig. 1a), substantiating the idea that global species richness is largely regulated by resource limitation15,16. The disparity of the sources from which diversity and organic C burial rate estimates were obtained emphasizes the significance of such a remarkable correspondence.
Phanerozoic trends in marine organic C burial rate and the global diversity of marine invertebrates. (a) Organic C burial rate after subtracting the fraction of organic C buried in non-marine environments (solid line) (see Methods). Marine invertebrate diversity estimates based on the shareholder quorum subsampling method (SQS) and the classical rarefaction (CR) (dashed and dotted line, respectively). For representation purposes, diversity estimates were normalized to the maximum value of the series. (b) Diversity corrected for changes in marine organic C burial rate through time for SQS and CR diversity estimates (solid and dashed line, respectively). ME1-5 denotes the temporal distribution of mass extinction events.
We corrected diversity curves for changes in marine food supply through time as inferred from a resource-associated proxy variable such as the marine organic C burial rate (i.e. sampling-standardized diversity in a given time bin divided by the rate of marine organic C burial in the same bin) (Fig. 1b). The resultant variable represents an estimate of the number of lineages supported by a given rate of marine food supply and underlines the signal of diversity dynamics related to factors other than food resource availability (i.e. equivalent to the hypothetical scenario of constant food supply through time). We first observed that the corrected diversity curves still showed a pattern of peaks and troughs across the entire Phanerozoic superimposed on a long-term secular trend (Fig. 1b). To investigate the cause/s for the variability of corrected diversity, we tested for causality using convergent cross mapping (CCM), a statistical test for cause-and-effect relationships based on the dynamical systems theory and the concept of state space reconstruction24. If variable X causes Y, then the values of X can be reconstructed from the state information of Y via cross mapping based on a training dataset recorded in the corresponding shadow manifold, but not vice versa (i.e. Y xmap X ≠ X xmap Y) (see Methods). CCM analyses revealed significant causal relationships between estimates of corrected diversity and the mean age of the subducting oceanic crust (Fig. 2a,b). These results were robust to changes in embedding dimension, a critical parameter in cross mapping methodology (Fig. 2a,b and Supplementary Fig. S1). However, our analysis showed that neither changes in global shelf area nor sea level height were primary determinants of corrected diversity through time (Fig. 2c,d and Supplementary Fig. S2).
Convergent cross mapping for detecting causality. Maximum cross-mapping skill at different embedding dimensions for the relationships between (a,b) mean age of the subducting crust (SubAge) and corrected diversity (cSQS and cCR), and (c,d) global shelf area (ShelfAr) and corrected diversity (cSQS and cCR). The 95th percentile of the corresponding cross mapping skill for 1000 surrogate time series from the Ebisuzaki phase shift null model71 is also shown (dashed lines). Cross-mapping skill and causality were considered significant if the Sugihara’s correlation coefficient (rho) for the cross-mapping of time series X to Y exceeded the 95th percentile of the corresponding estimate for the surrogates (e.g., X xmap Y means that Y causes X) (see Methods).
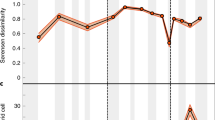
The age of the subducting oceanic crust is adjusted by the rates of seafloor spreading and subduction, and can be used as a proxy for the longevity of ocean basins. For instance, low rates of seafloor spreading and subduction increase the time elapsed between the formation and destruction of ocean basins, thereby allowing more time for the growth of diversity. Conversely, high rates of crustal recycling shorten the history of the seafloor and hence the time available for the development of diversity. On average, corrected diversity and the age of the subducting oceanic crust increased towards the present (Fig. 3a), presumably associated with an overall reduction in the speed of plate motions25,26.
A tectonically-driven model of marine invertebrate diversification. (a) Corrected diversity (cSQS and cCR) through the Phanerozoic with colour code depicting the mean age of the subducting oceanic crust. Corrected diversity estimates were normalized to the mean value of each time series. (b) Uncorrected diversity estimates (SQS and CR) plotted against marine organic C burial rate. Diversity and organic C burial rate estimates were normalized to the mean value of each time series. Data points above the 1:1 line indicate that global diversity becomes dominated by lineages with a smaller per capita share of food resources relative to the normalization factor, and vice versa for data points falling below the 1:1 line.
Finally, for a given amount of food, an increase of uncorrected diversity would imply a finer partitioning of food resources among taxa. Simply, there is the same amount of food for a larger number of taxa. We compared estimates of uncorrected diversity and marine organic C burial rate in order to investigate the extent to which the per-capita share of food resources varied through time (Fig. 3b). In this plot, data points above the 1:1 linear relationship indicate that global diversity became dominated by lineages with a smaller per capita share relative to the normalization factor (i.e. the mean value of the time series), and vice versa for data points falling below the 1:1 line. Our analysis indicates that, on average, modern faunas exhibit lower levels of per-capita share than their Palaeozoic counterparts (Fig. 3b), largely reflecting an increased degree of faunal provinciality.
Discussion
We have reported a statistically significant positive relationship between the rate of organic C burial and diversity using model estimates of organic C burial rate and marine invertebrate fossil data spanning the entire Phanerozoic eon (Fig. 1a, 3b). To the extent that organic C burial rate represents a proxy for food resource availability, our results substantiate the idea that resource limitation imposes fundamental limits to the global increase of marine invertebrate diversity1,6,15,16. Once diversity was corrected for changes in organic C burial rate, we found a strong causal linkage between diversity and the mean age of the subducting oceanic crust (Fig. 2a,b), suggesting a role for plate tectonics in regulating evolutionary rates.
Sedimentary data and satellite-derived estimates of ocean net primary production suggest that the vast majority of organic burial takes place on and immediately adjacent to continental shelves27,28. It has been estimated that, at present, 0.13–0.16 Pg C y−1 are buried in the oceans, with 80–85% of this occurring along continental shelves and deltas29. Likewise, the shallow continental shelf is where the vast majority of marine diversity and productivity of benthos is located30,31. Thus, we speculate that variations in organic C burial rate through time primarily influenced the biodiversity of highly productive continental margins, which represent the locus of major organic C burial. This observation does not preclude a role for food resource limitation in regulating the diversity of deep sea benthic communities. Rather, owing to the more homogeneous delivery of organic matter into the deep sea, we suggest a comparatively minor role for resource fluctuations in regulating the evolutionary rates and diversity dynamics of deep sea faunas.
The age of the subducting oceanic crust was computed from global palaeogeographic reconstructions generated by the University of Lausanne (UNIL) geodynamic model (v.2011, © Neftex) (Fig. 2a,b). The UNIL model predicts a long-term reduction in the global average rate of seafloor spreading and subduction, and the ensuing progressive aging of the oceanic basins over the last 600 Myr26,32. On the other hand, the observation of a linear decrease in the area of preserved oceanic lithosphere per unit time with increasing age has led to the hypothesis of a constant destruction (and therefore production) rate of the oceanic crust through time33. The extent to which this relative stability of tectonic plate motion is extensible to the Palaeozoic era is not straightforward. Spreading rates calculated thanks to preserved magnetic anomalies have varied strongly since Jurassic times34,35, and model simulations indicate that the wavelength of predicted variations is much longer than 80 Myr26. For the Cretaceous, the results of the UNIL model are in good agreement with previous studies on accretion36,37 and subduction rates38. Indeed, comparing average plate velocities stemming from the UNIL model to seafloor spreading rates resulting from other geodynamic models for Palaeozoic and Mesozoic times25,39,40, we found consistently a long-term decrease in the rates of seafloor spreading and subduction through the Palaeozoic and Mesozoic (Supplementary Fig. S3).
The role of plate tectonics and Earth system evolution in regulating the diversity dynamics of marine animals has long been associated with the demarcation of geographic provinces (e.g. assembly-disassembly of continental masses)8,41, tectonic enhancement of nutrient weathering fluxes42, the impact of continental configuration on global climate43, and changes in sea level9, shelf redox conditions9 or volcanism44,45,46. Our analysis suggests that the slowdown of plate tectonics further increased the global diversity of marine invertebrates. We interpret this causal connection between plate kinematics and the diversity dynamics of marine invertebrates as a result of the positive relationship between seafloor age and number of geographical barriers to dispersal, which represents a major control on marine animal diversification47,48. Separate analyses on specific taxonomic groups (bivalves, gastropods, etc) might potentially unveil additional controls on diversity49,50.
In summary, our analysis suggests that rates of seafloor spreading and subduction influenced the diversity dynamics of marine invertebrates throughout the Phanerozoic. According to these results, a tectonically-driven non-equilibrium model of marine invertebrate diversification is proposed. In our model, diversity increases in response to the intensification of continental weathering and the slowdown of plate tectonics, which increase, respectively, the productivity and age of oceanic basins. This route of diversity expansion entails an increase in the number of geographical discontinuities or provinciality, an increase in geographic disparity; an index of the compositional similarity among the biotas of a given stratigraphic interval with respect to their geographic distances from one another51,52 and an increase in the time lag between lineage splitting and their subsequent expansion53. Conversely, intervals of diversity loss most likely reflect phases of food shortage and rapid crustal recycling. Our results suggest that the relative stability of marine invertebrate diversity through the Phanerozoic might not be a result, at least exclusively, of ecological constraints on diversity growth1,3,5,6,16, but a consequence of the continuous recycling and deformation of the oceanic crust, which sets another fundamental limit to the global increase of marine animal diversity.
Methods
Data
The time series of sampling-standardized marine invertebrate diversity1,50, organic carbon (C) burial rates19,54, sea level55,56, mean age of the subducting oceanic crust26 and global shelf area57 through the Phanerozoic were extracted from previous reports by graph digitization using GetData Graph Digitizer v2.26. Additionally, estimates of organic C burial rate in marine environments and corrected diversity were derived from digitized data. The following sections describe the methods used in the papers depicting the graphs digitized here.
Diversity data
Sampling effort per time interval in fossil databases is skewed toward recent records. To correct for differences in sampling effort across the time series, sampling-standardized estimates of the number of taxa are commonly used23. The classical rarefaction (CR) method uses randomised subsampling protocols that seek to hold each time interval to a uniform sample quota or number of taxonomic occurrences23,58. This method, and in general those based on fixed quotas, effectively sample only those taxa with a relatively high frequency (i.e. the bulk of rare taxa are more difficult to detect and frequently missed in datasets). The shareholder quorum subsampling (SQS) method represents an advance in this regard over quota methods. This method calculates the expected number of taxa by sampling a given, fixed coverage of the frequency curve of species occurrences, where coverage is the sum of the frequencies of the species sampled50,59. The SQS method produces relative diversity estimates with fair but uneven sampling such that taxa with relatively low frequencies are equally well represented in estimates as dominant ones. Typically, diversity estimates are tabulated from large numbers of pseudorandom datasets generated under the subsampling routines described above (i.e. item quota and fixed coverage, respectively). For representation purposes, CR and SQS diversity estimates were normalized to the maximum (Fig. 1a) or mean value (Fig. 3) of the time series.
Organic C burial rate
Global organic C burial rates are calculated by models such as GEOCARBSULF, a long-term C and sulphur (S) cycle model19,54, which estimates atmospheric carbon dioxide (CO2) and oxygen (O2) levels by reconstructing long-term sources and sinks through time. GEOCARBSULF tracks the multi-million-year transfer of C and S between surface reservoirs (atmosphere, ocean, soil, living biomass) and rock reservoirs, mainly organic C, carbonate C and pyrite S. As for C, volcanic degassing constitutes the primary input of C to the surface reservoirs, whereas silicate weathering and subsequent biogenic sedimentation as carbonate C and organic C dominates removal60,61,62. S is released from geological sources through the weathering of continental rocks, volcanic degassing and hydrothermal emanation of S-bearing gases and fluids. Once S is exposed to subaerial conditions, it combines with O2 to form sulphate. Plants and microbes assimilate sulphate and convert it into organic compounds. The burial of anhydrite (calcium sulphate, CaSO4) and pyrite (iron sulphide, FeS) in the oceanic crust exceeds its removal. Organic C and pyrite-S are isotopically lighter than the CO2 and sulphate they are derived from due to biological fractionation during photosynthesis and sulphate reduction. Because the timescale of integration is sufficiently long (typically >10 Myr), the model presumes that the surface reservoirs are in a “quasi” steady-state (i.e. input fluxes of C and S to the surface reservoirs must be balanced in mass and isotopic value by output fluxes)63. Hence, the model calculates organic C, carbonate C and pyrite-S burial rates through time by isotope mass balance, a technique in which burial rates are inferred in order to match known isotope records.
The relative contribution of marine and non-marine organic C burial to the sedimentary organic C reservoir is critical to quantify the amount of food resources available for marine invertebrates. It is possible to distinguish the relative contribution of marine and freshwater environments to organic C burial by looking at the patterns of sedimentary pyrite formation through time27,64. The rationale is founded on the observation of an inverse relationship between δ13C and δ34S, which results from a positive covariance of organic C and pyrite-S contents in marine sediments22. The main reason of this relationship lies in the fact that a fraction of marine organic matter is mineralised by sulphate-reducing bacteria in marine environments (primarily euxinic). Conversely, enhanced deposition of organic material in freshwater environments (e.g. forest swamps) results in a negative covariance of organic C and pyrite-S because of the relatively lower sulphate content of freshwater systems, where pyrite formation is comparatively negligible. We used the worldwide burial ratio of organic C to pyrite S (C/S) in sediments65,66 as a proxy for changes in the dominant locus of organic C deposition through time. Whereas abundant sulphate reduction and pyrite formation in Early Palaeozoic marine environments gave rise to sedimentary organic matter with low C/S values22, i.e. prior to the expansion of terrestrial plants, present-day values are the result of both terrestrial and marine organic C sources22. Thus, we calculated the rate of marine organic C burial through time as a function of C/S by assuming that min(max) C/S values correspond to min(max) terrestrial organic C burial rates. Then, the terrestrial organic C burial rate curve through time was calculated accordingly. This method is analogous to those based on C and S isotope mass balance analyses64,67, which calculate marine organic C burial rate as a function of pyrite burial.
Geodynamic data
The mean age of the subducting oceanic crust was calculated by using a global geodynamic model following true plate tectonic principles and covering the whole surface of the Earth (i.e. continental and oceanic realms)26. The model was constructed by assembling regional-scale tectonic reconstructions developed at the University of Lausanne (UNIL) over the past 20 years26,32 (v.2011, © Neftex). These reconstructions were generated by the analysis of elementary units, also named geodynamic units (GDUs). A GDU describes the present-day smallest continental/oceanic fragment that underwent the same geodynamic evolution through time. The Earth’s history is reconstructed by redistributing the GDUs through space and time. The GDUs position is controlled by palaeogeographic data and geological data of geodynamic interest such as rift zone, passive margin, active margin, collision zone, etc32. Knowing the positions of the GDUs and the timing of major geodynamic events (e.g. continental break-up, collision, subduction initiation or reversal, etc.), one can trace the motion of plates. For disappeared oceans, the exact shape of mid-oceanic ridges is not known. However, during continental break-up, if plate velocities and geometries are known, the space between the detaching and the left-over fragments (into which the new ridge formed) can be constrained. The reconstruction work is carried out from 600 Myr ago to present. Crustal material is added/removed in divergent/convergent areas marked by newly defined plate boundaries. From one reconstruction to the next, plate positions are interpolated and former plate polygons are first preserved to identify the diverging (gaps) and converging (overlaps) areas. The UNIL model comprises 48 reconstructions extending back to 600 Myr ago every 5–20 Myr ago. Using a specific software, these global age map reconstructions were then used to compute the mean age of the oceanic crust along subduction zones26.
Data processing
The time series were arranged into continuous curves using both linear and cubic splines interpolation methods. The former assumes a linear point-to-point connection through the series data, while in the latter the interpolated value at a query point is based on cubic interpolation of the values at neighbouring grid points in each respective dimension68. Among all the time series extracted, the time series of diversity (CR and SQS) were the most limited in length. Since CR and SQS are central variables in our study, we considered their sampled time points as our base time array. Consequently, we projected (downsampled) all other time series onto that target time vector using the aforementioned interpolation methods. Subsequent analyses revealed that the interpolation of raw data did not play any significant role so as to modify quantitatively our findings, and therefore we chose the simpler piecewise linear interpolation method as our data estimator throughout the study (Supplementary Dataset).
Detecting causality between time series: Convergent Cross Mapping
The interplay between key variables was further analysed by considering potential cause and effect combinations. Causal interactions cannot be directly assessed from plain correlations (even in its first differences form) and are not straightforward to evaluate in general. Sugihara and co-workers24 proposed the Convergent Cross Mapping (CCM) technique, which relies on central statements in the theory of nonlinear dynamical systems; namely, the delay embedding theorem (also known as Takens’ theorem) and the concept of state space reconstruction. By means of the historical observations of two given coupled variables (X and Y) evolving in time (t), one can construct for a dynamical system the arrays M X = {X(t), X(t-τ}, X(t-2τ}, …, X(t-Eτ)} and equivalently M Y (for the time series Y), where E is an integer denoted as the embedding dimension and τ is the time delay. M X and M Y conform lagged coordinate embeddings of X and Y, respectively. The theorem dictates generically that these vectors, considered as new coordinates in a (E + 1)-dimensional space, can in fact be used to reconstruct shadow versions of the original system’s manifold M or state space, from which X and Y series are nearly just time projections of the manifold dynamics onto corresponding coordinate axes. Moreover, and crucially, the scheme of a state space reconstruction ensures that each M X and M Y manifolds are in one-to-one mapping to the state of the original dynamical system, which “lives” in the manifold M (state space) expanded by X(t), Y(t) and eventually other variables Z i (t), while also preserving the topology and other essential mathematical properties. The reconstructed shadow manifolds M X and M Y , each produced from lags of a single variable, can be therefore used to recover states of the original dynamic system. If X and Y, belonging to the same dynamic system, are two variables causally related, so are thus their shadow manifolds M X and M Y , since they are in a one-to-one correspondence to each other (through M). CCM exploits the fact that points that are nearby on the manifold M X correspond to points that are also nearby on M Y , as a necessary condition for causality between X and Y. By finding nearest neighbour points in M X , say coordinates P X , and the corresponding points by same time indexing in M Y , from which to estimate a new set \({P}_{{X|M}_{Y}}\) using simplex projection69, one can tell about causation if the set \({P}_{{X|M}_{Y}}\) actually resembles the real nearest neighbours P X in M X (just by computing standard Pearson correlation coefficients between both sets). The technique is therefore called cross mapping and is denoted in this case as “Y xmap X”, meaning that “X is causally influencing Y”.
The CCM analyses were performed using the rEDM package (https://cran.r-project.org/package=rEDM) written in R programming language. Because of the short-length time series, the delay time lag τ was always set to 1 time step (~11 Myr). In order to determine the best embedding dimension E, false nearest neighbour tests with parameters of R tol and A tol of 15 and 2 respectively70 were performed on each time series independently. An optimum overall embedding dimension of E = 3 was obtained from these tests for most of the cases involved, although other embedding dimensions were examined as an extra check on parameters dependency (Fig. 2 and Supplementary Fig. S1). At each library size (ranging up to such 45 points), leave-one-out cross validation constructed from 200 different randomly-chosen library samples was employed to avoid any bias in the calculations. The averaged cross map skill at each library size was plotted as the result (Supplementary Fig. S1). For the sake of simplicity, the maximum skill is plotted in Fig. 2. Causal tests for the whole set of variables investigated were carried out at three different embedding dimensions (Supplementary Fig. S2).
Statistical significance of the results was verified by surrogates data testing using the Ebisuzaki phase shift null model71. A null distribution of 1000 generated surrogate time series was set to perform this check. Outcomes from CCM calculations were then considered significant if the Sugihara’s correlation coefficient (rho) for the cross-mapping of time series X to Y exceeded the 95th percentile of the corresponding estimates for the surrogates.
Uncertainty in organic C burial rate estimates
Global organic C (and reduced S) burial rates can be estimated from models computing the input of nutrients via weathering fluxes (e.g. COPSE model)72 or, alternatively, by comparing geological C and S isotope records to the isotopic composition of modelled sediments assuming steady-state (isotope mass balance)54. There is considerable quantitative uncertainty regarding estimates of global (and marine) organic C burial rates during the past 200 Myr19,54,72,73. For instance, isotope mass balance analyses predict estimates of atmospheric O2 concentration and organic C burial rates well below those predicted by nutrient-weathering models73. Taking as valid marine organic C burial rate estimates computed from COPSE (in its original configuration), which does not support for relatively low productivity and organic C burial rates during the past 200 Myr, our analysis suggests a significant causal relationship between the mean age of subducting crust and corrected CR diversity (i.e. cCR(copse) xmap SubAge, Supplementary Fig. S2), but non-significant for corrected SQS diversity.
References
Alroy, J. et al. Phanerozoic trends in the global diversity of marine invertebrates. Science 321, 97–100 (2008).
Benton, M. J. The Red Queen and the Court Jester: species diversity and the role of biotic and abiotic factors through time. Science 323, 728–732 (2009).
Sepkoski, J. J. A kinetic model of Phanerozoic taxonomic diversity I. Analysis of marine orders. Paleobiology 4, 223–251 (1978).
Stanley, S. M. An Analysis of the History of Marine Animal Diversity. Paleobiology 33, 1–55, https://doi.org/10.1666/06020.1 (2007).
Raup, D. M. Taxonomic Diversity during the Phanerozoic. Science 177, 1065–1071, https://doi.org/10.1126/science.177.4054.1065 (1972).
Sepkoski, J. J. A Kinetic Model of Phanerozoic Taxonomic Diversity II. Early Phanerozoic Families and Multiple Equilibria. Paleobiology 5, 222–251 (1979).
Benton, M. J. Models for the diversification of life. Trends in Ecology & Evolution 12, 490–495 (1997).
Valentine, J. & Moores, E. Plate-tectonic regulation of faunal diversity and sea level: a model. Nature 228, 657–659 (1970).
Hannisdal, B. & Peters, S. E. Phanerozoic Earth system evolution and marine biodiversity. Science 334, 1121–1124 (2011).
Peters, S. E. Geologic constraints on the macroevolutionary history of marine animals. Proceedings of the National academy of Sciences of the United States of America 102, 12326–12331 (2005).
Benton, M. J. The origins of modern biodiversity on land. Philosophical Transactions of the Royal Society B: Biological Sciences 365, 3667–3679, https://doi.org/10.1098/rstb.2010.0269 (2010).
Allmon, W. D. & Martin, R. E. Seafood through time revisited: the Phanerozoic increase in marine trophic resources and its macroevolutionary consequences. Paleobiology 40, 256–287 (2014).
Bambach, R. K. Seafood through time: changes in biomass, energetics, and productivity in the marine ecosystem. Paleobiology 19, 372 (1993).
Martin, R. E. Secular increase in nutrient levels through the Phanerozoic: implications for productivity, biomass, and diversity of the marine biosphere. Palaios, 209–219 (1996).
Rabosky, D. L. & Hurlbert, A. H. Species richness at continental scales is dominated by ecological limits. The American Naturalist 185, 572–583 (2015).
Alroy, J. Geographical, environmental and intrinsic biotic controls on Phanerozoic marine diversification. Palaeontology 53, 1211–1235, https://doi.org/10.1111/j.1475-4983.2010.01011.x (2010).
Vermeij, G. J. The Mesozoic marine revolution: evidence from snails, predators and grazers. Paleobiology 3, 245–258 (1977).
Bambach, R. K., Bush, A. M. & Erwin, D. H. Autecology and the filling of ecospace: key metazoan radiations. Palaeontology 50, 1–22 (2007).
Berner, R. A. Phanerozoic atmospheric oxygen: New results using the GEOCARBSULF model. American Journal of Science 309, 603–606 (2009).
Berner, R. A. & Canfield, D. E. A new model for atmospheric oxygen over Phanerozoic time. American Journal of Science 289, 333–361 (1989).
Nelsen, M. P., DiMichele, W. A., Peters, S. E. & Boyce, C. K. Delayed fungal evolution did not cause the Paleozoic peak in coal production. Proceedings of the National Academy of Sciences 113, 2442–2447, https://doi.org/10.1073/pnas.1517943113 (2016).
Berner, R. A. & Raiswell, R. Burial of organic carbon and pyrite sulfur in sediments over Phanerozoic time: a new theory. Geochimica et Cosmochimica Acta 47, 855–862 (1983).
Alroy, J. et al. Effects of sampling standardization on estimates of Phanerozoic marine diversification. Proceedings of the National Academy of Sciences 98, 6261–6266, https://doi.org/10.1073/pnas.111144698 (2001).
Sugihara, G. et al. Detecting causality in complex ecosystems. Science 338, 496–500 (2012).
Matthews, K. J. et al. Global plate boundary evolution and kinematics since the late Paleozoic. Global and Planetary Change 146, 226–250 (2016).
Vérard, C., Hochard, C., Baumgartner, P. O., Stampfli, G. M. & Liu, M. Geodynamic evolution of the Earth over the Phanerozoic: Plate tectonic activity and palaeoclimatic indicators. Journal of Palaeogeography 4, 167–188 (2015).
Berner, R. A. Burial of organic carbon and pyrite sulfur in the modern ocean: its geochemical and environmental significance. Am. J. Sci.;(United States) 282 (1982).
Muller-Karger, F. E. et al. The importance of continental margins in the global carbon cycle. Geophysical Research Letters 32, n/a–n/a, https://doi.org/10.1029/2004GL021346 (2005).
Hedges, J. I. & Keil, R. G. Sedimentary organic matter preservation: an assessment and speculative synthesis. Marine chemistry 49, 81–115 (1995).
Gray, J. et al. Coastal and deep-sea benthic diversities compared. Marine ecology progress series, 97-103 (1997).
Sanders, H. L. Marine benthic diversity: a comparative study. The American Naturalist 102, 243–282 (1968).
Stampfli, G. M. & Borel, G. D. A plate tectonic model for the Paleozoic and Mesozoic constrained by dynamic plate boundaries and restored synthetic oceanic isochrons. Earth and Planetary Science Letters 196, 17–33 (2002).
Rowley, D. B. Rate of plate creation and destruction: 180 Ma to present. Geological Society of America Bulletin 114, 927–933 (2002).
Müller, R. D., Sdrolias, M., Gaina, C. & Roest, W. R. Age, spreading rates, and spreading asymmetry of the world’s ocean crust. Geochemistry, Geophysics, Geosystems 9, n/a–n/a, https://doi.org/10.1029/2007GC001743 (2008).
Larson, R. Latest pulse of Earth: Evidence for a mid-Cretaceous superplume. Geology 19, 547–550 (1991).
Gaffin, S. Ridge volume dependence on seafloor generation rate and inversion using long term sealevel change. American Journal of Science 287, 596–611 (1987).
Müller, R. D., Sdrolias, M., Gaina, C., Steinberger, B. & Heine, C. Long-term sea-level fluctuations driven by ocean basin dynamics. science 319, 1357–1362 (2008).
Engebretson, D. C., Kelley, K. P., Cashman, H. & Richards, M. A. 180 million years of subduction. GSA today 2, 93–100 (1992).
Domeier, M. & Torsvik, T. H. Plate tectonics in the late Paleozoic. Geoscience Frontiers 5, 303–350, https://doi.org/10.1016/j.gsf.2014.01.002 (2014).
Zahirovic, S., Müller, R. D., Seton, M. & Flament, N. Tectonic speed limits from plate kinematic reconstructions. Earth and Planetary Science Letters 418, 40–52, https://doi.org/10.1016/j.epsl.2015.02.037 (2015).
Zaffos, A., Finnegan, S. & Peters, S. E. Plate tectonic regulation of global marine animal diversity. Proceedings of the National Academy of Sciences 114, 5653–5658, https://doi.org/10.1073/pnas.1702297114 (2017).
Cardenas, A. L. & Harries, P. J. Effect of nutrient availability on marine origination rates throughout the Phanerozoic eon. Nature Geosci 3, 430–434, http://www.nature.com/ngeo/journal/v3/n6/suppinfo/ngeo869_S1.html (2010).
Davis, K. E., Hill, J., Astrop, T. I. & Wills, M. A. Global cooling as a driver of diversification in a major marine clade. Nature Communications 7, 13003, https://doi.org/10.1038/ncomms13003 (2016).
Vermeij, G. J. Economics, volcanoes, and Phanerozoic revolutions. Paleobiology 21, 125–152 (1995).
Rich, J. E., Johnson, G. L., Jones, J. E. & Campsie, J. A significant correlation between fluctuations in seafloor spreading rates and evolutionary pulsations. Paleoceanography 1, 85–95, https://doi.org/10.1029/PA001i001p00085 (1986).
McLean, D. M. Deccan Traps mantle degassing in the terminal Cretaceous marine extinctions. Cretaceous Research 6, 235–259 (1985).
Kiessling, W. Evolution: Promoting marine origination. Nature Geosci 3, 388–389 (2010).
Briggs, J. C. Biogeography and plate tectonics. Vol. 10 (Elsevier, 1987).
Mondal, S. & Harries, P. J. The Effect of Taxonomic Corrections on Phanerozoic Generic Richness Trends in Marine Bivalves with a Discussion on the Clade’s Overall History. Paleobiology 42, 157–171, https://doi.org/10.1017/pab.2015.35 (2015).
Alroy, J. The shifting balance of diversity among major marine animal groups. Science 329, 1191–1194 (2010).
Miller, A. I. et al. Phanerozoic trends in the global geographic disparity of marine biotas. Paleobiology 35, 612–630 (2009).
Valentine, J. W., Foin, T. C. & Peart, D. A Provincial Model of Phanerozoic Marine Diversity. Paleobiology 4, 55–66 (1978).
Foote, M. Contingency and Convergence. Science 280, 2068–2069, https://doi.org/10.1126/science.280.5372.2068 (1998).
Berner, R. A. GEOCARBSULF: A combined model for Phanerozoic atmospheric O2 and CO2. Geochimica et Cosmochimica Acta 70, 5653–5664, https://doi.org/10.1016/j.gca.2005.11.032 (2006).
Haq, B. U. & Schutter, S. R. A Chronology of Paleozoic Sea-Level Changes. Science 322, 64–68, https://doi.org/10.1126/science.1161648 (2008).
Miller, K. G., Mountain, G. S., Wright, J. D. & Browning, J. V. A 180-million-year record of sea level and ice volume variations from continental margin and deep-sea isotopic records. Oceanography 24, 40–53 (2011).
Walker, L. J., Wilkinson, B. H. & Ivany, L. C. Continental drift and Phanerozoic carbonate accumulation in shallow-shelf and deep-marine settings. The Journal of Geology 110, 75–87 (2002).
Miller, A. I. & Foote, M. Calibrating the Ordovician radiation of marine life: implications for Phanerozoic diversity trends. Paleobiology 22, 304–309 (1996).
Alroy, J. Accurate and precise estimates of origination and extinction rates. Paleobiology 40, 374–397 (2014).
Walker, J. C., Hays, P. & Kasting, J. F. A negative feedback mechanism for the long‐term stabilization of Earth’s surface temperature. Journal of Geophysical Research: Oceans 86, 9776–9782 (1981).
Berner, R. Atmospheric carbon dioxide levels over Phanerozoic time. Science 249, 1382–1386 (1990).
Holland, H. D. The Chemical Evolution of the Atmosphere and Oceans (Princeton Univ. Press, 1984).
Berner, R. A. The Phanerozoic Carbon Cycle: CO 2 and O 2 . (Oxford University Press, 2004).
Kump, L. R. in Interactions of C, N, P and S Biogeochemical Cycles and Global Change 475-490 (Springer, 1993).
Berner, R. A. The long-term carbon cycle, fossil fuels and atmospheric composition. Nature 426, 323–326 (2003).
Berner, R. A. Modeling atmospheric O2 over Phanerozoic time. Geochimica et Cosmochimica Acta 65, 685–694 (2001).
Garrels, R. M. & Lerman, A. Coupling of the sedimentary sulfur and carbon cycles; an improved model. American Journal of Science 284, 989–1007 (1984).
De Boor, C., De Boor, C., Mathématicien, E.-U., De Boor, C. & De Boor, C. A practical guide to splines. Vol. 27 (Springer-Verlag New York, 1978).
Sugihara, G. & May, R. M. Nonlinear forecasting as a way of distinguishing chaos from. Nature 344, 6268 (1990).
Kennel, M. B. & Abarbanel, H. D. False neighbors and false strands: a reliable minimum embedding dimension algorithm. Phys Rev E Stat Nonlin Soft Matter Phys 66, 026209, https://doi.org/10.1103/PhysRevE.66.026209 (2002).
Ebisuzaki, W. A method to estimate the statistical significance of a correlation when the data are serially correlated. Journal of Climate 10, 2147–2153 (1997).
Bergman, N. M., Lenton, T. M. & Watson, A. J. COPSE: A new model of biogeochemical cycling over Phanerozoic time. American Journal of Science 304, 397–437, https://doi.org/10.2475/ajs.304.5.397 (2004).
Mills, B. J., Belcher, C. M., Lenton, T. M. & Newton, R. J. A modeling case for high atmospheric oxygen concentrations during the Mesozoic and Cenozoic. Geology 44, 1023–1026 (2016).
Acknowledgements
P.C. was supported by a Ramón y Cajal contract from the Spanish Government. This research was funded by the Spanish Government through research grant CTM2014-54926-R.
Author information
Authors and Affiliations
Contributions
P.C., M.J.B and O.P. designed the research. P.C. and O.P. performed statistical analyses and analysed data. C.V. provided geodynamic data. All authors were involved in writing the manuscript and all gave final approval for its publication.
Corresponding author
Ethics declarations
Competing Interests
The authors declare that they have no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Cermeño, P., Benton, M.J., Paz, Ó. et al. Trophic and tectonic limits to the global increase of marine invertebrate diversity. Sci Rep 7, 15969 (2017). https://doi.org/10.1038/s41598-017-16257-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-017-16257-w
This article is cited by
-
Empirical dynamic modelling and enhanced causal analysis of short-length Culex abundance timeseries with vector correlation metrics
Scientific Reports (2024)
-
Onset of Late Cretaceous diversification in Europe’s freshwater gastropod fauna links to global climatic and biotic events
Scientific Reports (2022)
-
Timing and periodicity of Phanerozoic marine biodiversity and environmental change
Scientific Reports (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.