Abstract
We study the possibility for the extraction of the Rashba spin-orbit coupling constant for a two-dimensional electron gas with the conductance microscopy technique. Due to the interplay between the effective magnetic field due to the Rashba spin-orbit coupling and the external magnetic field applied within the plane of confinement, the electron backscattering induced by a charged tip of an atomic force microscope located above the sample leads to the spin precession and spin mixing of the incident and reflected electron waves between the QPC and the tip-induced 2DEG depletion region. This mixing leads to a characteristic angle-dependent beating pattern visible in the conductance maps. We show that the structure of the Fermi level, bearing signatures of the spin-orbit coupling, can be extracted from the Fourier transform of the interference fringes in the conductance maps as a function of the magnetic field direction. We propose a simple analytical model which can be used to fit the experimental data in order to obtain the spin-orbit coupling constant.
Similar content being viewed by others
Introduction
Spin-orbit (SO) coupling in semiconductor nanostructures1 besides its direct effects in spin relaxation and dephasing2,3,4, induce appearance of a number of extensively studied phenomena, including spin Hall effects5,6,7, persistent spin helix states8,9,10, or Majorana fermions11 in contacts with superconductors. Moreover, the SO interactions allow for construction of spin-active elements of spintronic devices, e.g. spin transistors12,13,14,15,16, exploiting the precession of the electron spin in the SO effective magnetic field17 or spin-filters based on quantum point contacts (QPCs)15,18.
In the two-dimensional electron gas (2DEG) formed at the semiconductor heterojunctions a strong Rashba spin-orbit interaction appears as a consequence of electric fields present within the confinement layer. The latter results from the electrostatic potential of the ionized donor layer that provide the charge to the 2DEG, which produces the the Rashba SO coupling19. The characterization of the Rashba interaction strength is of an elementary importance for the design of spin devices and description of the SO transport phenomena. Measurements of the SO coupling usually employ the Shubnikov-de Haas20,21,22,23,24,25,26,27 oscillations or antilocalization in the magnetotransport28. Optical procedures using photocurrents29 or precession of optically polarized electron spins17 are also employed. The spin-orbit coupling constant for a disordered sample can be extracted from QPC conductance for rotated external magnetic field30.
The Rashba SO coupling produces a shift of the spin-up and spin-down dispersion relations along the wave vector axis1 that is a linear function of the SO coupling constant. In this paper we propose a way to extract the structure of the dispersion relation near the Fermi level1 using spin-dependent scattering and the resulting interference with the scanning gate microscopy31,32 (SGM) applied to systems with QPCs33,34. In this technique, the tip acts as a floating perturbation of the potential landscape as seen by the Fermi level electrons. As a result the recorded SGM images contain interference fringes due to the incident and backscattered electron waves35,36. In presence of an in-plane magnetic field the fringes form beating pattern due to spin-dependence of the Fermi wavelengths37. In this paper we analyze the beating patterns that appear for SO-coupled high-mobility systems. The electron – when scattered – experiences precession of its spin due to rotation of the momentum-dependent effective magnetic field17, and the interference of the incident and reflected electron waves potentially involves spin-mixing effects. However, we find that in the absence of the external magnetic field the backscattering involves a pure inversion of the effective field with no precession effects. The latter are triggered by an external in-plane magnetic field, and lead to an appearance of the dependence of the beating patterns on the orientation of the magnetic field. We demonstrate that the shape of the Fermi level structure and thus the SO coupling constant can be traced back from the beating patterns by the Fourier transform analysis.
The dispersion relation including the spin-orbit coupling effects for the 2DEG confined at the metal surface38,39,40,41,42,43,44, or graphene45 can be experimentally determined by well established techniques of the scanning tunneling spectroscopy (STS)38,39,45, or angle-resolved photoemission spectroscopy (ARPES)40,41,42,43,44. The advantage of using the SGM technique over STS and ARPES is that SGM exploits the long-range perturbation of the electrostatic potential introduced by the charged probe and does not require the electrons from 2DEG to leave the surface of the system. For that reason SGM is not limited to the surface 2DEG and can be used for the electron gas burried at a distance from the surface, e.g. within the semiconductor heterostructure31,33,34,35,36,37, at a depth of about 50 nm.
Theory
The theoretical approach46,47 applied in this paper has been recently verified in interpretation of the experimental SGM maps for QPCs in both disordered and high-mobility samples46. Below we present a proposal of a procedure for extraction of the Rashba constant using rotation of the external magnetic field within the plane of 2DEG confinement followed by a Fourier transform post-treatment.
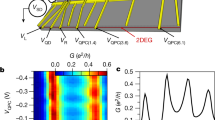
We consider Fermi level transport in a 2DEG within In0.5Ga0.5As with a local constriction forming the QPC as depicted in Fig. 1. The Fermi level electrons travel from the electron reservoir placed at x < 100 nm through a channel modeled with an infinite potential step and an additional potential tuned by gates (gray areas of the scheme). A negatively charged tip acts as a backscatterer to the right of the QPC. The conductance maps as functions of the tip position resolve the coherent interference fringes as observed in a number of experiments48,33,35,36,49. The part of the system to the right of the QPC is considered open such that electron may freely propagate without reflections. Transparent boundary conditions for the electron flow are introduced with a method described in ref.50.
Sketch of system. The electrons come from the reservoir on the left of the QPC. The computational box starts at x = 0 nm. The QPC gates form a gap of size 200 nm × 100 nm centered at (200 nm, 600 nm). The gates are located at 50 nm above the 2DEG layer51. Dashed lines show the potential energy isolines for which eV ext = E F in leads. The SGM tip is located at \({r}_{{\rm{tip}}}=({x}_{{\rm{tip}}},{y}_{{\rm{tip}}},50\,{\rm{nm}})\mathrm{.}\) The blue map shows (the square root of) the scattering electron density obtained for the QPC tuned to the first conductance plateau [G = 2G 0 with \({G}_{{\rm{0}}}=\frac{{e}^{2}}{h}\)] for electrons incident from the left lead for B = 0. The inset presents the standard conductance quantization as a function of gate voltage V g in case without and with in-plane magnetic field.
We adopt a standard two-dimensional model assuming that all the electrons of 2DEG occupy a strongly localized lowest-energy state of the vertical quantization. The Hamiltonian accounts for the Rashba SO interaction and a presence of the external magnetic field applied within the plane of confinement
with \(k=-i\nabla -e{\boldsymbol{A}}\), \({\boldsymbol{B}}=({B}_{{\rm{x}}},{B}_{{\rm{y}}}\mathrm{,0})\), and σ is the vector of Pauli matrices. The external potential V ext is a superposition of two components: (i) V QPC – the QPC gate potential modeled with analytical formulas for a rectangle gate adapted from ref.51, and (ii) V tip – the electrostatic potential created by the charged tip of the scanning probe. The tip potential is modeled by the Lorentzian profile given by \({V}_{{\rm{tip}}}={d}_{{\rm{tip}}}^{2}{V}_{{\rm{t}}}/[{(x-{x}_{{\rm{tip}}})}^{2}+{(y-{y}_{{\rm{tip}}})}^{2}+{d}_{{\rm{tip}}}^{2}],\) with effective width d tip = 50 nm, which is of order of the distance between 2DEG and surface of the sample, and V t that depends on the voltage applied to the tip. This form of the potential results from the screening of the tip charge by 2DEG52,53. The Rashba Hamiltonian \({{\boldsymbol{H}}}_{{\rm{rsb}}}=\gamma \{{{\boldsymbol{\sigma }}}_{x}{k}_{y}-{{\boldsymbol{\sigma }}}_{y}{k}_{x}\}\) in Eq. (1) comes from the electrostatic confinement of the 2DEG in the growth direction54. We apply the symmetric gauge \({\boldsymbol{A}}=({B}_{y}z,{B}_{x}z,\mathrm{0)}\). By choosing the plane of the 2DEG confinement to be located at z = 0, we get A = 0, thus the magnetic field enters the Hamiltonian only via the spin Zeeman term.
Results and Discussion
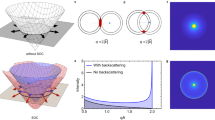
Figure 2 shows the spin density for electrons incident to the system from the positive S y mode of the QPC, i.e. for electrons with a spin initially set to \({S}_{y}=\hslash \mathrm{/2}\). In presence of SO interaction, this initial spin state is not conserved, but instead evolves during the electron propagation by precessing around the total magnetic field, which is the sum of the local SO field and the uniform external field. In absence of external magnetic field [Fig. 2(a–c)], the local SO field is almost aligned with the initial spin along the y-axis, and the initial spin is then almost conserved during the electron propagation. For wave vectors which are off the axis of the system however, the local SO field is not exactly aligned with the initial spin, and the resulting spin precession causes the appearance of small S x and S z spin components. In presence of an external magnetic field oriented along the x-axis [Fig. 2(d–f)], the direction of the total field is far from the direction of the initial spin state, and the resulting spin precession produces large S x and S z spin components which are interlaced with the S y component. Note that the total field is drastically changed when the electron leaves the lateral confinement of the QPC due to the increase of the wave vector. The direction of the total magnetic field is then different within the constriction and outside. For a system containing only a QPC, the spin precession has no effect on conductance, since the electrons keep moving away from the constriction. When the SGM tip is added to the system however, the spin precession superposes on the backscattering ripples. In the following, we explain how the SGM measurement allows for extraction of the spin modulation for the backscattered electron wave.
Figure 3(a–f) show spatial derivatives of SGM images \(dG/d{x}_{{\rm{tip}}}\) obtained from the solution of the quantum scattering problem for QPC depicted in Fig. 1 tuned to the first QPC conductance plateau. For B = 0, γ = 0 [Fig. 3(a)] a pronounced interference pattern of the incident and backscattered wave is observed33,34,35,36, with the period of \({\lambda }_{F}\mathrm{/2}\) for both γ = 0 [Fig. 3(a)] and \(\gamma \ne 0\) [Fig. 3(b)]. A beating pattern37 appears at non-zero B [Fig. 3(c)], which depends on the orientation of the in-plane field for \(\gamma \ne 0\) (Fig. 3(d–f)).
Derivatives of simulated SGM images (\(dG/d{x}_{{\rm{tip}}}\)) obtained for QPC tuned to the first plateau in arb. units. \(dG/d{x}_{{\rm{tip}}}\) map obtained in absence of external magnetic field and SO interaction (a), with SO coupling (γ = 12 meVnm) at B = 0 (b), for in-plane magnetic field B = 5 T and without SO interaction (c). (d–f) \(dG/d{x}_{{\rm{tip}}}\) images obtained for in-plane magnetic field B = 5 T and γ = 12 meVnm. The arrows show the in-plane direction of the B vector.
The beating pattern observed in Fig. 3(d) qualitatively reproduces the spin precession shown in Fig. 2(f) for a magnetic field applied along the x-axis. Both phenomena have indeed the same origin: the precession effect is the dynamical evolution of a spin in the total effective field, and the beating pattern in the SGM map results from the mixing of the eigenmodes calculated for the same total effective field.
Same as on Fig. 3 but calculated from simple model discussed in this paper.
In order to explain quantitatively the results of Fig. 3 we consider a simple model for SGM images in presence of in-plane magnetic field and SO interaction. The electron wave which leaves the QPC55,56,57,58 is approximated by a plane wave e ikr (an inverse of the square root of the distance from the QPC is neglected as slowly varying). The schematics of the considered scattering process is presented in Fig. 5. The electron wave which leaves the QPC (not shown in the diagram) propagates through the device until it is backscattered by the potential barrier created by the SGM tip with probability 1. We fix the origin at the scattering point. For a given incoming spin state \(|{k}_{\sigma }^{+}\rangle \) the scattering wave function can be expanded in terms of the possible scattering modes
where \({k}_{\sigma }^{\pm }r=|{{\boldsymbol{k}}}_{\sigma }^{\pm }\cdot {\boldsymbol{r}}|\) and \({k}_{\sigma }^{\pm }\) denotes the absolute value of the wave vector of an electron in spin state σ. The sign in the superscript indicates the electron incoming from left+ or backscattered by the tip −. The values of the scattering amplitudes \({a}_{\sigma \sigma ^{\prime} }\) depend on a specific situation. For SO coupling and magnetic field simultaneously present, the Hamiltonian for a free electron can be written
where \({\alpha }_{x/y}=\frac{1}{2}g{\mu }_{B}{B}_{x/y}\) and \({{\boldsymbol{E}}}_{{\rm{kin}}}=\frac{{\hslash }^{2}{{\boldsymbol{k}}}^{2}}{2{m}_{{\rm{eff}}}}\). Plane wave solution for the Schröedinger equation gives two eigenvalues
where \({{\boldsymbol{p}}}^{\pm }=(\gamma {k}_{{\rm{y}}}^{\pm }+{\alpha }_{{\rm{x}}},-\gamma {k}_{{\rm{x}}}^{\pm }+{\alpha }_{{\rm{y}}})\), with \(\sigma =\{+,-\}\) and
are eigenvectors for incoming + and outgoing directions − of an electron, with \({p}^{\pm }\) being the length of \({{\boldsymbol{p}}}^{\pm }\) vector. Due to the assumed infinite potential generated by the SGM tip, the scattering wave function in Eq. (2) has to vanish at r = 0 (see Fig. 5)
By substituting Eq. (5) to this equation one evaluates the scattering amplitudes \({a}_{\sigma \sigma ^{\prime} }\).
Sketch of considered scattering process. The electron wave leaves QPC in one of two spin states, propagates to the right and is backscattered at position r = (0, 0) by the potential barrier induced by the SGM tip. Here we assume a hard wall potential profile (i.e. \({V}_{{\rm{tip}}}=+\infty \) inside the circle).
For the special case when SO interaction and magnetic field are not present in the Hamiltonian (3) the propagating modes in Eq. (5) reduce to
with \({k}_{\sigma }^{\pm }=k\) and scattering amplitudes \({a}_{\sigma \sigma ^{\prime} }=-{\delta }_{\sigma \sigma ^{\prime} }\), hence backscattering does not change the spin orientation. The scattering wave function from Eq. (2) is then
and the scattering density is given by \({\rho }_{\sigma }=\langle {{\rm{\Psi }}}_{\sigma }|{{\rm{\Psi }}}_{\sigma }\rangle \propto cos(2kr),\) and the variation of the G map follows the pattern of the density55. The SGM conductance pattern can be approximated by \(G({r}_{\mathrm{tip}})\,\propto {\cos }({2{kr}}_{\mathrm{tip}})\). The SGM image obtained with this model is presented in Fig. 4(a) and is consistent with the simulated image obtained in Fig. 3(a).
For B = 0 and \(\gamma \ne 0\) one may easily check that the propagating modes [Eq. (5)] still satisfy orthogonality relations \(\langle {k}_{\sigma ^{\prime} }^{+}|{k}_{\sigma }^{-}\rangle ={\delta }_{\sigma \sigma ^{\prime} }\) and \(|{k}_{\sigma }^{+}\rangle =|{k}_{\sigma }^{-}\rangle \), which leads to the spin conserving reflection \({a}_{\sigma \sigma ^{\prime} }=-{\delta }_{\sigma \sigma ^{\prime} }\). However, in this case \({k}_{\sigma }^{+}\ne {k}_{\sigma }^{-}\) and the scattering wave function is given by \(|{{\rm{\Psi }}}_{\sigma }\rangle =({e}^{i{k}_{\sigma }^{+}r}-{e}^{-i{k}_{\sigma }^{-}r})|{k}_{\sigma }^{+}\rangle \). The electron density is then proportional to \({\rho }_{\sigma }\propto cos([{k}_{\sigma }^{+}+{k}_{\sigma }^{-}]r)\). Since \({k}_{\sigma }^{\pm }={k}^{\pm }+\sigma \frac{\gamma {m}_{{\rm{eff}}}}{{\hslash }^{2}}\) 59 we get the same expression as for γ = 0 i.e. \({\rho }_{\sigma }\propto \,\cos (2kr)\), which does not depend on electron spin. Hence the SO effect vanishes for the backscattering process which leads to the same SGM image [Fig. 4(b)] as in case of γ = 0 [Fig. 4(a)].
The third possible configuration of parameters i.e. γ = 0 and \(B\ne 0\) was recently discussed in ref.37. In this case the same orthogonality relation is still satisfied \(\langle {k}_{\sigma ^{\prime} }^{+}|{k}_{\sigma }^{-}\rangle ={\delta }_{\sigma \sigma ^{\prime} }\), and \({a}_{\sigma \sigma ^{\prime} }=-{\delta }_{\sigma \sigma ^{\prime} }\). However, the resulting electron density is now proportional to \({\rho }_{\sigma }\propto \,\cos (2{k}_{\sigma }r)\) and depends on the spin via the Zeeman term inducing shifts of \({k}_{\sigma }\). The approximated SGM map \(G={G}_{{\rm{0}}}{\sum }_{\sigma }{T}_{\sigma }\,\cos \,(2{k}_{\sigma }r)\) gives a signal being a superposition of two frequencies \({\omega }_{\sigma }=2{k}_{\sigma }\) resulting in the beating pattern visible in Fig. 4(c). The present reasoning explains the findings of ref.37.
In a general case of \(B\ne 0\) and \(\gamma \ne 0\) the eigenvalues [Eq.(4)] depend on both the direction of the magnetic field and the propagation vector, thus the spin will not be conserved anymore during the backscattering process, since the orthogonality relations between the incident and backscattered modes no longer hold \(\langle {k}_{{\sigma }^{^{\prime} }}^{+}|{k}_{\sigma }^{-}\rangle \ne {\delta }_{\sigma {\sigma }^{^{\prime} }}\), and \({a}_{\sigma {\sigma }^{^{\prime} }}\ne -{\delta }_{\sigma {\sigma }^{^{\prime} }}\). The resulting electron density will be then a composition of four different possible superpositions of the Fermi wave vectors \({k}_{i}=\{{k}_{+}^{+}+{k}_{+}^{-},{k}_{+}^{+}+{k}_{-}^{-},{k}_{-}^{+}+{k}_{+}^{-},{k}_{-}^{+}+{k}_{-}^{-}\}\). The SGM images obtained for this general case for three different orientation of magnetic field \(\alpha =\{{0}^{\circ },\,{45}^{\circ },\,{90}^{\circ }\}\) are depicted in Fig. 4(d–f). Although, the images differ somewhat from Fig. 3 (d–f), still both the model and the full simulation allow for extraction of the wave vectors and their dependence on the orientation of the magnetic field in the Fourier analysis (see below).
The form of Eq. (3) indicates that rotation of a SGM tip position along the arc centered at the QPC entrance is equivalent to a rotation of the in-plane magnetic field (in an opposite direction) for a fixed tip position. For a practical implementation of an experiment it should be more efficient to perform a SGM scan along a straight line, where the longest electron branch48,49 is present and rotate the magnetic field instead (see Fig. 6(a)).
(a) Conductance as a function of the tip position moving along the x axis (with y tip = 600 nm) and the angle that the magnetic field vector forms with the x axis. The inset shows a zoomed part in the area denoted by the black square. The simulation was performed for 5 T and γ = 12 meVnm with the simple analytical model. (b) Fourier transform (FT) of (a) remapped from k space to \(\lambda =2\pi /k\). Dashed lines were calculated from the dispersion relation defined by Eq. (4) as \({\lambda }_{i}=2\pi /{k}_{i}\) with \({k}_{i}=\{{k}_{+}^{+}+{k}_{+}^{-},{k}_{+}^{+}+{k}_{-}^{-},{k}_{-}^{+}+{k}_{+}^{-},{k}_{-}^{+}+{k}_{-}^{-}\}\). The inset shows the same image but in the k space for a large range of wave vectors values. (c) Same as (b) but for the full numerical simulation taken at G = G 0. The finite size of the SGM tip potential leads to a shift of all lines towards higher frequencies. Quantum mechanical simulation reveals also the higher harmonics in the inset denoted by 1st and 2nd arrows.
In Fig. 6(b,c) we present the Fourier transform (FT) of the conductance signal calculated from the \(dG/d{x}_{{\rm{tip}}}\) map for the tip moving along the QPC axis, as a function of the magnetic field direction B for B = 5 T. The results are plotted on the wavelength scale calculated as \(\lambda =2\pi /k\). The dashed lines in Fig. 6(b,c) were plotted for backscattering processes that are explained in Fig. 7(a) and calculated numerically from the condition \({E}_{F}={E}_{\sigma }\) with the latter given by Eq. (4). Note, that due to the smooth and extended shape of the tip potential in the full simulation the resonance lines in Fig. 6(c) are slightly shifted to the left by 0.8 nm (in comparison to model Fig. 6(b)). We accordingly shifted the dashed lines in Fig. 6(c) to coincide with the FT image. In the inset in Fig. 6(c) one observes also higher harmonics, which result from the possible multiple reflections between the tip and QPC (not present in the model, see inset in Fig. 6(b)).
(a–c) Fermi level surface calculated from Eq. (4) obtained for three directions of magnetic field ϕ = {0°, 45°, 90°} (for B = 5T) denoted by arrows. Green dashed lines show the direction of scattering process i.e. k = (k x, 0). Dashed arrows on (a) represent four different possible backscattering processes. However, due to the symmetry of the scattering process two of them lead to the same frequency in FT image, hence three lines are observed in Fig. 6(b,c) for \(\varphi =0\) and π. This is no more valid for (b) and (c), which imply four different lines in Fig. 6 for other values of ϕ.
The backscattering taken along the axis of the QPC involves k y = 0 and we find in general four various values of k i visible as four lines in FT images. However, when B y = 0, Eq. (4) reduces to
which is symmetric with respect to electron reflection \({E}_{\sigma }({k}_{{\rm{x}}})={E}_{\sigma }(-{k}_{{\rm{x}}})\), which implies the symmetry of scattering process that \({k}_{\sigma }^{+}={k}_{\sigma }^{-}\equiv {k}_{\sigma }\) (see Fig. 7(a)), and thus reducing the number of resonance lines in FT image to three. For other cases presented in Fig. 7(b,c) this symmetry is not satisfied and all four frequencies are visible.
One could expect that there should be another symmetry point when magnetic field is oriented along the SO effective magnetic field i.e. for α = 90°. However, for this case α x = k y = 0 thus we get \({E}_{\sigma }=\frac{{\hslash }^{2}{k}_{{\rm{x}}}^{2}}{2m}+\sigma |{\alpha }_{{\rm{y}}}-\gamma {k}_{{\rm{x}}}|\) which in consequence leads to four different spinors \(|{k}_{\sigma }^{\pm }\rangle \) (5) and \({a}_{\sigma \sigma ^{\prime} }\ne -{\delta }_{\sigma \sigma ^{\prime} }\). Four different scattering processes leading to four different frequencies are then allowed which thus produces the four resonances observed in FFT images.
Note, that in our previous work30 we indicated that for disordered sample with multiple random scatterers the spin-orbit coupling can be estimated by the QPC conductance in the rotated magnetic field. The present paper indicates a solution that is suitable for clean high-mobility two-dimensional electron gas, where the scanning probe experiment induces the backscattering. The beating of conductance due to the spin-orbit coupling modification of the dispersion relation and its modification by the in-plane magnetic field are used for determination of the spin-orbit coupling constant.
Summary
In summary, we have shown that SGM imaging can be used to extract the Fermi surface properties by Fourier analysis of the beatings due to the SO interaction and an in-plane magnetic field. The analysis allows for deduction of the Rashba constant from the real space measurement of conductance as a function of the tip position involving spin-scattering in a crossed external and built-in magnetic fields.
Methods
The scattering problem is solved within the finite difference approach46,47, with spatial discretization \({\rm{\Delta }}x={\rm{\Delta }}y=6\) nm using the wave function matching (WFM) method60. Then we calculate conductance \(G\) using the Landauer approach by evaluating \(G={G}_{{\rm{0}}}{\sum }_{\sigma }{T}_{\sigma }\) at the Fermi level (with \({G}_{{\rm{0}}}=\frac{{e}^{2}}{h}\)). For simplicity, we consider the case of a single mode being transmitted through the QPC (\(G\le 2{G}_{{\rm{0}}}\)) (see the inset to Fig. 1). We set E F = 20 meV (for γ = 0 the Fermi wavelength is \({\lambda }_{{\rm{F}}}=40\) nm), and the tip potential V t = 40 meV for which a strict depletion of the electron density below the tip is obtained (see the dashed circle in Fig. 1). Landé factor is assumed to be g = 9 and effective mass m eff = 0.0465 m 0 as for InGaAs.
Data availability
All data generated or analysed during this study are included in this published article.
References
Manchon, A., Koo, H. C., Nitta, J., Frolov, S. M. & A., D. R. New perspectives for Rashba spin-orbit coupling. Nat. Mater. 14, 871–882 (2015).
Ohno, Y., Terauchi, R., Adachi, T., Matsukura, F. & Ohno, H. Spin relaxation in GaAs(110) quantum wells. Phys. Rev. Lett. 83, 4196–4199 (1999).
D’yakonov, M. I. & Perel, V. I. Possibility of orienting electron spins with current. JETP Lett. 13, 467 (1971).
Kainz, J., Rössler, U. & Winkler, R. Temperature dependence of Dyakonov-Perel spin relaxation in zinc-blende semiconductor quantum structures. Phys. Rev. B 70, 195322 (2004).
Hirsch, J. E. Spin Hall effect. Phys. Rev. Lett. 83, 1834–1837 (1999).
Sinova, J. et al. Universal intrinsic spin Hall effect. Phys. Rev. Lett. 92, 126603 (2004).
Kato, Y. K., Myers, R. C., Gossard, A. C. & Awschalom, D. D. Observation of the spin Hall effect in semiconductors. Science 1910, 306 (2004).
Bernevig, B. A., Orenstein, J. & Zhang, S.-C. Exact SU(2) symmetry and persistent spin helix in a spin-orbit coupled system. Phys. Rev. Lett. 97, 236601 (2006).
Koralek, J. D. et al. Emergence of the persistent spin helix in semiconductor quantum wells. Nature 458, 610–613 (2009).
Walser, M. P., Reichl, C., Wegscheider, W. & Salis, G. Direct mapping of the formation of a persistent spin helix. Nature Phys. 8, 757–762 (2012).
Mourik, V. et al. Signatures of Majorana fermions in hybrid superconductor-semiconductor nanowire devices. Science 336, 1003–1007 (2012).
Datta, S. & Das, B. Electronic analog of the electrooptic modulator. Appl. Phys. Lett. 56, 665–667 (1990).
Schliemann, J., Egues, J. C. & Loss, D. Nonballistic spin-field-effect transistor. Phys. Rev. Lett. 90, 146801 (2003).
Žutić, I., Fabian, J. & Das Sarma, S. Spintronics: Fundamentals and applications. Rev. Mod. Phys. 76, 323–410 (2004).
Chuang, P. et al. All-electric all-semiconductor spin field-effect transistors. Nat Nano 10, 35–39 (2015).
Bednarek, S. & Szafran, B. Spin rotations induced by an electron running in closed trajectories in gated semiconductor nanodevices. Phys. Rev. Lett. 101, 216805 (2008).
Meier, L. et al. Measurement of Rashba and Dresselhaus spin-orbit magnetic fields. Nature Phys. 3, 650–654 (2007).
Debray, P. et al. All-electric quantum point contact spin-polarizer. Nature Nanotech. 4, 759–764 (2009).
Bychkov, Y. & Rashba, E. Effect of k-linear terms on electronic properties of 2D systems. J. Phys. C 17, 6039 (1984).
Nitta, J., Akazaki, T., Takayanagi, H. & Enoki, T. Gate control of spin-orbit interaction in an inverted In0.53Ga0.47As/In0.52Al0.48As heterostructure. Phys. Rev. Lett. 78, 1335–1338 (1997).
Engels, G., Lange, J., Schäpers, T. & Lüth, H. Experimental and theoretical approach to spin splitting in modulation-doped InxGa1−xAs/InP quantum wells for B → 0. Phys. Rev. B 55, R1958–R1961 (1997).
Lo, I. et al. Spin splitting in modulation-doped Al x Ga1−x N/GaN heterostructures. Phys. Rev. B 65, 161306 (2002).
Kwon, J. H., Koo, H. C., Chang, J., Han, S.-H. & Eom, J. Channel width effect on the spin-orbit interaction parameter in a two-dimensional electron gas. Appl. Phys. Lett. 90, 112505 (2007).
Grundler, D. Large Rashba splitting in InAs quantum wells due to electron wave function penetration into the barrier layers. Phys. Rev. Lett. 84, 6074–6077 (2000).
Kim, K.-H., Kim, H.-J., Koo, H. C., Chang, J. & Han, S.-H. Spin-orbit coupling in double-sided doped InAs quantum well structures. Appl. Phys. Lett. 97, 012504 (2010).
Das, B. et al. Evidence for spin splitting in InxGa1−xAs/In0.52Al0.48AS heterostructures as B→0. Phys. Rev. B 39, 1411–1414 (1989).
Ho Park, Y. et al. Separation of Rashba and Dresselhaus spin-orbit interactions using crystal direction dependent transport measurements. Appl. Phys. Lett. 103, 252407 (2013).
Koga, T., Nitta, J., Akazaki, T. & Takayanagi, H. Rashba spin-orbit coupling probed by the weak antilocalization analysis in InAlAs/InGaAs/InAlAs quantum wells as a function of quantum well asymmetry. Phys. Rev. Lett. 89, 046801 (2002).
Ganichev, S. D. et al. Experimental separation of Rashba and Dresselhaus spin splittings in semiconductor quantum wells. Phys. Rev. Lett. 92, 256601 (2004).
Kolasinski, K., Sellier, H. & B. S. Conductance measurement of spin-orbit coupling in two-dimensional electron systems with an in-plane magnetic field. Phys. Rev. B 94, 121304(R) (2016).
Sellier, H. et al. On the imaging of electron transport in semiconductor quantum structures by scanning-gate microscopy: successes and limitations. Semicond. Sci. Technol. 26, 064008 (2011).
Ferry, D. K. et al. Open quantum dots-probing the quantum to classical transition. Sem. Sci. Tech. 26, 043001 (2011).
Topinka, M. A. et al. Coherent branched flow in a two-dimensional electron gas. Nature 410, 183–186 (2001).
Schnez, S. et al. Imaging the lateral shift of a quantum point contact using scanning gate microscopy. Phys. Rev. B 84, 195322 (2011).
Jura, M. P. et al. Unexpected features of branched flow through high-mobility two-dimensional electron gases. Nature Phys. 3, 841–845 (2007).
Jura, M. P. et al. Electron interferometer formed with a scanning probe tip and quantum point contact. Phys. Rev. B 80, 041303 (2009).
Kleshchonok, A., Fleury, G., Pichard, J.-L. & Lemarié, G. Scanning gate microscopy of quantum contacts under parallel magnetic field: Beating patterns between spin-split transmission peaks or channel openings. Phys. Rev. B 91, 125416 (2015).
Ast, C. R. et al. Local detection of spin-orbit splitting by scanning tunneling spectroscopy. Phys. Rev. B 75, 201401 (2007).
Steinbrecher, M., Harutyunyan, H., Ast, C. R. & Wegner, D. Rashba-type spin splitting from interband scattering in quasiparticle interference maps. Phys. Rev. B 87, 245436 (2013).
Ast, C. R. et al. Giant spin splitting through surface alloying. Phys. Rev. Lett. 98, 186807 (2007).
Bareille, C. et al. Two-dimensional electron gas with six-fold symmetry at the (111) surface of ktao3. Sci. Rep. 4, 3586 (2014).
King, P. D. C. et al. Subband structure of a two-dimensional electron gas formed at the polar surface of the strong spin-orbit perovskite ktao3. Phys. Rev. Lett. 108, 117602 (2012).
Santander-Syro, A. F. et al. Orbital symmetry reconstruction and strong mass renormalization in the two-dimensional electron gas at the surface of ktao3. Phys. Rev. B 86, 121107 (2012).
Santander-Syro, A. F. et al. Two-dimensional electron gas with universal subbands at the surface of srtio3. Nature 469, 189 (2011).
Leicht, P. et al. Rashba splitting of graphene-covered au(111) revealed by quasiparticle interference mapping. Phys. Rev. B 90, 241406 (2014).
Kolasiński, K., Szafran, B., Brun, B. & Sellier, H. Interference features in scanning gate conductance maps of quantum point contacts with disorder. Phys. Rev. B 94, 075301 (2016).
Kolasiński, K., Mreńca-Kolasińska, A. & Szafran, B. Transconductance and effective Landé factors for quantum point contacts: Spin-orbit coupling and interaction effects. Phys. Rev. B 93, 035304 (2016).
Topinka, M. A. et al. Imaging coherent electron flow from a quantum point contact. Science 289, 2323–2326 (2000).
Kozikov, A. A. et al. Mode specific backscattering in a quantum point contact. Nano Lett. 15, 7994–7999 (2015).
Nowak, M. P., Kolasiński, K. & Szafran, B. Signatures of spin-orbit coupling in scanning gate conductance images of electron flow from quantum point contacts. Phys. Rev. B 90, 035301 (2014).
Davies, J. H., Larkin, I. A. &Sukhorukov, E. V. Modeling the patterned two dimensional electron gas: electrostatics. J. Appl. Phys 77, 4504 (1995). We apply the formula for the finite rectangle gate, given by equation V QPC/V g = g(x − L, y − B) + g(x − L, T − y) + g(R − x, y − B) + g(R − x, T − y), where g (u, v) = 1/2π arctan uv/dR, R = √v 2+u 2+d 2 with L = 100 nm, R = 300 nm, B = −100 nm, T = 1300 nm and, d = 50 nm.
Kolasiński, K. & Szafran, B. Simulations of imaging of the local density of states by a charged probe technique for resonant cavities. Phys. Rev. B 88, 165306 (2013).
Steinacher, R. et al. Scanning-gate-induced effects and spatial mapping of a cavity. New J. Phys. 17, 043043 (2015).
Bhandari, N. et al. Steps toward an all-electric spin valve using side-gated quantum point contacts with lateral spin-orbit coupling. Adv. Nat. Sci: Nanosci. Nanotechnol. 4, 013002 (2013).
Kolasiński, K., Szafran, B. & Nowak, M. P. Imaging of double slit interference by scanning gate microscopy. Phys. Rev. B 90, 165303 (2014).
Kolasiński, K. & Szafran, B. Electron paths and double-slit interference in the scanning gate microscopy. New J. Phys. 17, 063003 (2015).
Jalabert, R. A., Szewc, W., Tomsovic, S. & Weinmann, D. What is measured in the scanning gate microscopy of a quantum point contact? Phys. Rev. Lett. 105, 166802 (2010).
Khatua, P., Bansal, B. & Shahar, D. Single-slit electron diffraction with Aharonov-Bohm phase: Feynman’s thought experiment with quantum point contacts. Phys. Rev. Lett. 112, 010403 (2014).
Bercioux, D. & Lucignano, P. Quantum transport in Rashba spin-orbit materials: a review. Rep. Prog. Phys. 78, 106001 (2015).
Zwierzycki, M. et al. Calculating scattering matrices by wave function matching. Phys. Stat. Sol. 245, 623–640 (2008).
Acknowledgements
This work was supported by National Science Centre according to decision DEC-2015/17/N/ST3/02266, and by PL-Grid Infrastructure.
Author information
Authors and Affiliations
Contributions
K.K. performed the calculations. H.S. and B.S. analysed the calculated results. All the authors contributed to writting and finalizing the paper.
Corresponding author
Ethics declarations
Competing Interests
The authors declare that they have no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kolasiński, K., Sellier, H. & Szafran, B. Extraction of the Rashba spin-orbit coupling constant from scanning gate microscopy conductance maps for quantum point contacts. Sci Rep 7, 14935 (2017). https://doi.org/10.1038/s41598-017-14380-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-017-14380-2
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.