Abstract
Understanding the influence of changes in solar activity on Earth’s climate and distinguishing it from other forcings, such as volcanic activity, remains a major challenge for palaeoclimatology. This problem is best approached by investigating how these variables influenced past climate conditions as recorded in high precision paleoclimate archives. In particular, determining if the climate system response to these forcings changes through time is critical. Here we use the Wiener-Granger causality approach along with well-established cross-correlation analysis to investigate the causal relationship between solar activity, volcanic forcing, and climate as reflected in well-established Intertropical Convergence Zone (ITCZ) rainfall proxy records from Yok Balum Cave, southern Belize. Our analysis reveals a consistent influence of volcanic activity on regional Central American climate over the last two millennia. However, the coupling between solar variability and local climate varied with time, with a regime shift around 1000–1300 CE after which the solar-climate coupling weakened considerably.
Similar content being viewed by others
Introduction
A very important problem in climate science is to understand and evaluate the relative contributions of natural factors to the observed global and regional climate variations on decadal to centennial time scales. Because instrumental records do not extend beyond the last three centuries, they cannot inform us on the low-frequency part of these climate variations and their links to external and internal climate forcings. Therefore, any link between climate change and types of forcings needs to be extracted from palaeoclimate archives, such as ice cores, tree rings, or stalagmites1. On decadal and multi-decadal time scales, changes in solar irradiance2, 3 and volcanic activity4,5,6 are the most potent drivers of natural variability in the natural climate system.
The influence of solar irradiance and volcanic activity on natural climate variability has been subject of intensive research (e.g. refs 7,8,9,10) including directional coupling estimation from instrumental records over the last 150 years (see Supplementary Section 1 and references therein). Until now however, specific methods for inferring directional couplings from observational data were not systematically used to analyze the causal interrelationships between climate and solar or volcanic activity on longer (centennial to millennial) time scales. The latter is necessary, for example, to quantify the variable effects and individual contributions of solar and volcanic forcings through time, to better understand the forcing mechanisms and to improve predictive climate models. There has been considerable interest in how extended periods of low solar activity are linked to climatic changes11, 12 and what this implies for the future13, 14. A notable example is the 17th-century grand solar Maunder Minimum15 and its link to a period of intense cold within the Little Ice Age in the Northern Hemisphere16. Recent research suggests that the particular cold spell around the time of the Maunder Minimum was triggered by a series of volcanic eruptions and sustained by atmospheric and oceanic feedbacks rather than changes in solar irradiance17, 18. Indeed, evidence from a network of tree-ring chronologies from the North American taiga suggests a drastic regime shift to lower summer temperatures following a series of tropical eruptions in the late 13th century19.
Furthermore, systematic investigations of causal relations between natural forcings and global and regional climate can shed light on potential variations of these links over time and space20. It is often implicitly assumed that causal couplings remained constant through time. A rigorous analysis of the time-dependence of these couplings however is vital for a deeper understanding of the complex influence of solar and volcanic activity on global and regional climate, especially if lessons for present-day conditions are inferred from past climatic changes.
In this study, we investigate the temporal evolution of the regional influence of solar and volcanic activity on paleorainfall in southern Belize using an extended, temporally resolved Wiener-Granger causality analysis of a 2000 year long rainfall proxy record derived from Yok Balum Cave in southern Belize, Central America. The stable isotope record from stalagmite YOK-I6, 21 represents one of the most highly resolved and best dated datasets available from Central America for the last two millennia (Fig. 1b). The YOK-I stable oxygen (δ18O) and carbon (δ13C) isotope ratio time series give detailed insights in local rainfall and infiltration changes in southern Belize with near-annual temporal resolution. This proxy record is well suited for the study of dynamic link changes between forcing and regional terrestrial climatic response, due to its exceptional chronological control, high proxy resolution and location near the northern limit of modern summer Intertropical Convergence Zone (ITCZ) extent. In southern Belize, rainfall is driven by the annual migration of the ITCZ, which reaches its northernmost extent during the boreal summer months. Stronger summer insolation results in a warmer Northern Hemisphere and higher Belizean rainfall totals due to northward displacement of the ITCZ. Enhanced volcanic activity (and consequently higher atmospheric aerosol content) in the Northern Hemisphere, on the other hand, leads to atmospheric cooling and a southward shift of the ITCZ, resulting in lower rainfall over southern Belize6. By analyzing the YOK-I rainfall proxy data we are able to obtain quantitative empirical estimates of the strength of these relationships and to reveal their temporal variation.
We focus on the causal links between solar activity, volcanic forcing, and climatic changes documented in the YOK-I record, and on possible variability of the strength of these links through time. For this analysis, solar activity changes over the last 2000 years are inferred from a reconstruction of total solar irradiance (TSI) from 10Be concentrations in Greenland ice cores22 (Fig. 1c). To assess the influence of volcanic aerosols the most recent ice core-based estimate of natural (volcanic) atmospheric aerosol loadings (sulfate accumulation) is used8 (Fig. 1a). To unravel the hidden link dynamics, we employ the specialized Wiener-Granger causality analysis and assess the associated uncertainties using both Fisher’s F-criterion and a Monte Carlo-based significance test (see Section “Data and Methods” below). We compare the results with a more widely known and less specific approach to coupling analysis based on the cross-correlation function (CCF).
As a measure of the influence of an observed process y (solar or volcanic activity) on another observed process x (local climate proxy), we use the Wiener-Granger causality characteristic \({G}_{y\to x}\) which assesses how strongly the future of x depends on the past of y given the past of x 23. This measure is defined as prediction improvement of the autoregressive models fitted to the data from x only or from both x and y. To account for possible dating errors, we calculate \({G}_{y\to x}(s)\) where s stays for a trial time shift of the signal x to the past by s years, and \({G}_{y\to x,{\rm{\max }}}\) is the value maximal over an appropriate range of s. The results are compared to Pearson cross correlation function (CCF) \({K}_{yx}(l)\) where positive lags l indicate that y leads x, and the absolute CCF value maximized over an appropriate range of l is \(|{K}_{yx}{|}_{\max }\). Further details including assessment of the statistical significance levels (p-levels, both pointwise and corrected for multiple testing) are given in “Data and Methods” below.
Results
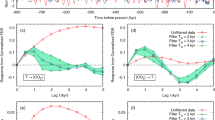
The Wiener-Granger causality test confirms the causal influence of solar irradiance on regional moisture availability in southern Belize as reflected in the YOK-I δ18O time series (Fig. 2). The maximal link strength is found at a time lag of YOK-I δ18O of –15 years. This lag corresponds to an (illogical) situation of proxy leading the forcing, like that found in an earlier study comparing solar activity and speleothem based paleoclimate variation24. This lag is in the range of dating uncertainties in the time series involved and most likely results from uncertainties in the TSI age model. The lag is therefore considered only as resulting from these uncertainties, and we use the logical interpretation of the forcing towards the proxy (and not vice versa) without over-interpreting the exact value of the lag. The coupling is significant at (asymptotic) Bonferroni-corrected p < 0.05. Using the ice core-based volcanic sulfate data, the Wiener-Granger analysis also confirms a robust influence of volcanic activity on regional moisture availability in southern Belize, with a maximum volcanic influence at a time lag of 1 to 2 years and a significance level lower than p = 0.003 according to the F-test. Such 1 to 4 years lagged regional response to volcanic forcing is commonly found in paleoclimate records, e.g. ref. 19. The dating uncertainties in the volcanic forcing data are lower than in the solar proxy record. In order to identify the latitudinal range with the strongest impact of volcanic forcing on southern Belizean rainfall, we separated the test into volcanic activity in the tropics, Northern, and Southern Hemisphere, using the volcanic forcing reconstruction of Sigl et al.8. Our analysis corroborates earlier findings25 that tropical eruptions have the strongest impact on Central American climate (p < 0.05), whereas eruptions originating in the Northern and Southern Hemisphere have only slight influences (vanishing significance, p > 0.05). Interestingly, the regional hydroclimate seems to respond to tropical volcanic forcing somewhat later compared to Northern Hemisphere forcing. We note that an earlier study on volcanic forcing of rainfall at Yok Balum Cave6 categorized eruptions slightly differently, by not considering tropical eruptions as a separate category but instead attributed them to either the Northern Hemisphere or Southern Hemisphere. This current study complements Ridley et al.6 by also assessing how the latitude of the eruption affected the climate response, but does not distinguish the hemisphere of low latitude eruptions.
Coupling between Central American regional climate (represented by YOK-I δ18O) and solar forcing (left) and volcanic forcing (right) as estimated by a Granger causality analysis. Asymptotic point-wise significance level (left, red line) of the Granger causality estimates (left, blue line) indicate a significant influence of the solar forcing on the regional climate with a lag of −15 yr due to dating errors (Bonferroni-corrected significance level of p = 0.05 is marked by grey dashed line). The point-wise significance level for the volcanic forcing (right) indicates influences from the global volcanic activities and topical eruptions, but no significant influence from volcanoes of the Northern or Southern Hemisphere (grey dashed line: Bonferroni-corrected significance level of p = 0.05).
To extract information on the variation of the causal coupling over time, we calculated the coupling characteristics within 1000-year moving windows and use the Wiener-Granger statistic \({G}_{y\to x,{\rm{\max }}}\). The window length represents a compromise between statistical robustness and temporal resolution of the Wiener-Granger technique and the maximum lag is considered sufficient to cover both physical delays between forcing and climate as well as dating uncertainties. The analysis applied on the solar data reveals a significant change of the influence of solar irradiance occurring between 1000 and 1300 CE (Fig. 3a). Before this period (50 BCE to 1050 CE), the Wiener-Granger causality test shows a strong influence of solar irradiance on regional moisture (pointwise significant at p < 0.001 according to F-test). After 1300 yr CE, this influence diminished to being barely significant (pointwise p ≈ 0.1). Plotting the values of \({G}_{y\to x,{\rm{\max }}}\) for moving windows of different lengths L versus the window endpoint W (Fig. 4a, solid lines) helps to justify the localization of the transition interval. The dashed lines in Fig. 4a represent the Monte-Carlo based 0.95-percentile for the quantity \({G}_{y\to x,{\rm{\max }}}\) maximized over all windows within the entire 2020-years interval, and we can again reject the hypothesis of no coupling at p < 0.05 since \({G}_{y\to x,{\rm{\max }}}\) exceeds that percentile for any window length in the range from 700 to 1000 yrs. The largest, significant values of \({G}_{y\to x,{\rm{\max }}}\) are observed for several early time windows (in particular, 100 CE to 1100 CE). The transition interval between stronger and weaker couplings in terms of W appears the same (1000 CE to 1300 CE) for any moving window length in the above range, i.e. \({G}_{y\to x,{\rm{\max }}}\) starts to decrease only when the data later than 1000 CE start to fall into the time window used for the estimation. This is evidence for a change of the coupling strength taking place in the latest part of the time interval (0–1300 CE), i.e. within the interval of [1000 CE – 1300 CE]. If the coupling would have changed in earlier parts, e.g. (0 CE – 300 CE), the decrease of \({G}_{y\to x,{\rm{\max }}}\) for different window lengths L would have been apparent at different W (at smaller W for smaller L).
Temporal variation of the forcing on the regional climate represented by δ18O. (a) Wiener-Granger causality for TSI forcing YOK-I (blue line), and (b) Wiener-Granger causality for volcanic aerosols forcing YOK-I (blue line) versus the moving window endpoint W. The red curves in (a) and (b) represent the p-values as derived from the F-test, revealing a more or less constant highly significant volcanic forcing of the climate, but solar forcing decreasing after around 1300 CE.
The Wiener-Granger causality estimates for the TSI and δ18O variations (a) and maximal CCF between these processes (b) in moving windows of different lengths. The dashed lines show the corresponding Monte Carlo-based 0.95-percentiles for the quantities maximized over all subsequent time windows within a 2020 yr interval for the uncoupled model (1).
The fact that significant coupling estimates are obtained for earlier time windows (roughly, in the first millennium CE) and insignificant for later windows (in the second millennium CE) is a sign of change in coupling strength, but not direct evidence for the statistical significance of such change. The latter might be a result of statistical fluctuations due to short window lengths, i.e. insignificant coupling estimate for the second millennium CE might be due to noise effect rather than due to weaker coupling. To address this question directly, we performed a Monte Carlo test against the model (1) with constant parameters by calculating the range \({\rm{\Delta }}{G}_{y\to x,{\rm{\max }}}\) over all W at fixed L (see “Data and Methods”). It allowed rejection of the hypothesis of constant parameters and, hence, to infer a statistically significant decrease in coupling strength at the significance level of p = 0.1. This result provides statistically robust (“very probable” using the IPCC nomenclature26) support for the hypothesized regime shift over the time interval of interest.
Similar results are found for the YOK-I δ13C time series (Fig. 5a); although not as clearly as for δ18O (Fig. 5b), these results confirm previous studies suggesting that solar forcing and YOK-I δ13C become decoupled around 1250 CE27. The discrepancy between δ13C and δ18O may result from multiple controls on δ18O, including moisture source, moisture amount, and height of the convective column28.
To test the robustness of the results, we performed the same analysis using another solar reconstruction based on the Δ14C data compiled from various sources (IntCal13, Supplementary Figure S7)29. Overall, the same qualitative conclusion about solar influence decreasing during the interval 1000 to 1300 CE can be drawn (Supplementary Section S5). Moreover, the maximal WG causality for early windows is achieved at physically meaningful positive lag of 10 yr (Supplementary Figure S9) in contrast to the negative lag for the above TSI reconstruction (Fig. 2) supporting the hypothesis of the possible dating error in the TSI record. Still, statistical significance of the results for the Δ14C data is worse than for TSI, which is partly explained by the presence of strong slow components (time scales of several hundreds of years) in the Δ14C data. Removal of such trends would not be straightforward and may introduce statistical artefacts. Comparison with other solar reconstructions and other speleothem data from Central America is not currently possible since other available proxy records do not satisfy the conditions of sufficiently long duration (at least 2000 years), high temporal resolution (sampling interval not greater than 5 yrs) and stationarity (no strong slow components with time scales of 500 yrs or longer). To our knowledge, these requirements are currently met only by the used YOK-I and TSI data.
The windowed analysis does not reject the hypothesis that the influence of volcanic activity on climate remains invariant through time (Fig. 3b). This conclusion is based on the Monte Carlo tests with the model (2) and window length L = 1000 yrs. Although the hypothesis of no coupling is confidently rejected at the level of p < 0.001, the hypothesis of constant parameters is not rejected at any reasonably small significance level suggesting that the volcanic influence on climate remains more constant in time than the detected time-changing solar influence. For a vivid comparison, note that the value of \({G}_{y\to x,{\rm{\max }}}\) changes between the first millennium CE and the second millennium CE by the factor of four for the solar activity (Fig. 3a) and only twice for the volcanic activity (Fig. 3b). This indicates a quite robust response of regional atmospheric circulation and the regional hydroclimate to volcanic aerosol forcing, supporting previous interpretations6.
These results regarding the presence and decrease of coupling between solar activity and climate are confirmed by common CCF analysis. Namely, the CCF reveals an overall general correlation at a Bonferroni-corrected significance level of p = 0.04 and indicates a decreasing correlation between the TSI and YOK-I δ18O (Fig. 4b) as well as δ13C with time. For example, the window length of 700 years shows that starting around 800 CE the maximal correlation \(|{K}_{yx}{|}_{\max }\) gradually decreases from 0.7 to values below 0.3 at around 1400 CE (Fig. 4b). However, the change is more gradual than that of the Wiener-Granger causality reflecting the lower sensitivity of CCF analysis to changes in coupling strength. Thus, the CCF analysis identifies the time interval of change less clearly, explainable by the fact that CCF does not specifically detect coupling direction and consequently the CCF value as a characteristic of the causal coupling strength is ambiguous. Over the same period, the correlation between global volcanic activity and δ18O remains relatively constant (Supplementary Figure S12d). Further details are given in Supplementary Sections S3.1, S3.2, S4.1 and S6.
Discussion and Conclusions
The intriguing weakening of the influence of solar irradiance on rainfall over southern Belize following the advent of the Little Ice Age strongly suggests that the impact of solar insolation on the regional hydroclimatic dynamics in tropical Belize was not constant during the last two millennia. Increased solar insolation enhances Northern Hemisphere warming, resulting in northward ITCZ displacement and consequently more rainfall in the study region. Enhanced atmospheric aerosol concentrations (volcanic or anthropogenic) cool the NH sufficiently to force the ITCZ southward6. ITCZ position reflects a delicate balance between the opposing effects of solar and (mainly) volcanic forcing. The geographical location of the Yok Balum Cave at the northern realm of the ITCZ makes proxy records from this cave sensitive to changes in the meridional position of the ITCZ. Our study reveals a rather constant influence of volcanic forcing, but a changing influence of the solar forcing (according to our rigorous statistical analysis over 800–1000 yrs intervals). Large volcanic eruptions are not uncommon, and the clustering in time of large eruptions over the last 2000 years is largely down to chance. These volcanic effects are superimposed on atmospheric conditions that are otherwise modulated by solar forcing. Before 1200 CE, solar forcing significantly contributed to the regional climate variability, resulting in enhanced rainfall over the Caribbean region, including southern Belize. With the onset of the Little Ice Age around 1200 CE, the solar influence decreased, resulting in drier regional climate conditions. The influence of volcanic aerosols stems mainly from tropical eruptions, with less severe impact of volcanic activity in both the Northern and Southern Hemispheres. Our results emphasize the importance of potential changes of the strength of the solar impact, relative to other forcings, on climate when interpreting paleoclimate variability.
In this study we introduce Wiener-Granger causality adjusted for possible dating errors as a method for inferring directional coupling, and develop an appropriate significance test for use on palaeoclimate datasets. This approach reveals a changing solar influence on rainfall in southern Belize, with the solar influence considerably decreasing after approximately 1300 CE. In contrast, the impact of volcanic activity on the regional rainfall remains consistent over the last two millennia, thus increasing its importance relative to solar forcing after 1300 CE. The technique is promising, and future studies should use similar approaches to further deconstruct seemingly complex couplings involving multiple possible forcings.
Data and Methods
Data
In our analysis, we use previously published δ18O and δ13C data from stalagmite YOK-I from Yok Balum Cave, southern Belize6, 21, 30. Stalagmite δ18O at this cave site has previously been interpreted as reflecting rainfall amount and the δ18O of precipitation21, 28. Hydroclimate in southern Belize is driven by the seasonal migration of the ITCZ, resulting in distinct rainfall seasonality (wet summers, dry winters). Moisture at Yok Balum Cave is predominantly derived from the adjacent Gulf of Honduras and the Caribbean Sea, with increasingly important contributions from more distal moisture sources (i.e., tropical Atlantic) during the boreal summer months21. The influence of large storm cells and high intensity rain during the summer rainy season results in more depleted δ18O values registered in surface waters and in a clear “amount effect”21, 31. Changes in moisture source have some influence on rainfall δ18O over the course of the year, with enhanced Rayleigh distillation of moisture in more distally sourced storms during the summer months, contributing to the summer depletion in δ18O. However, the amount effect appears to be the dominant driver of precipitation variability, and stalagmite δ18O can thus be interpreted as a proxy for rainfall amount21, 31.
Stalagmite δ13C largely reflects the effective rainfall amount at the site, and hydrological conditions in the karst system6, 27. Dry conditions in southern Belize result in less negative δ13C values, due to reduced soil bioproductivity, increased prior calcite precipitation and cave ventilation, and a higher proportion of bedrock carbon to the dripwater. Conversely, more negative δ13C values reflect wetter conditions at the site. By validating the analysis performed on YOK-I δ18O with δ13C, we can confirm that the proxy response to solar/volcanic forcing is indeed reflecting a reduction in precipitation at the study site, and not simply a change in moisture source isotopic composition upstream of the cave (as suggested for caves in China, e.g. refs 32,33,34).
Data availability
YOK-I data30: http://doi.org/10.5880/pik.2017.004. TSI data22: ftp://ftp.ncdc.noaa.gov/pub/data/paleo/climate_forcing/solar_variability/steinhilber2009tsi.txt. Volcanic forcing data8: http://www.nature.com/nature/journal/v523/n7562/abs/nature14565.html#supplementary-information.
Methods
The concept of Wiener-Granger causality was originally developed for mathematics35 and econometrics23, but is becoming widely used for characterizing directional coupling in physical and other research disciplines36,37,38. Influence of a process y on a process x is usually quantified by comparing prediction errors of autoregressive (AR) predictive models fitted to the data from x only or from both x and y (see Eqs (S1) and (S2) in Supplementary Section S3.3). Below we construct one-step-ahead AR models where the time “step” is the sampling interval Δt, which is equal to 5 years in our study. To estimate the Wiener-Granger causality in the direction y → x, we find the least possible mean-squared prediction error \({\sigma }_{x}^{2}\) of the individual AR model for x (where the next x value is predicted based on the history of x) and the error \({\sigma }_{x,y}^{2}\) of a joint AR model, where the next x value is predicted based on the histories of both x and y. The normalized prediction improvement \({G}_{y\to x}=({\sigma }_{x}^{2}-{\sigma }_{x,y}^{2})/{\sigma }_{x}^{2}\) is the basic measure of coupling “strength”. If \({G}_{y\to x}\) is significantly greater than zero, the influence y → x can be inferred. Statistical significance can be estimated via an (asymptotic) F-test (see Supplementary Section S3.3) if the time series is sufficiently long. This model-based approach often enhances the sensitivity of the coupling analysis as compared to the CCF or traditional regression analysis, since the internal dynamics of the studied processes are considered in \({G}_{y\to x}\).
To incorporate the possible (mean) dating error, we shift the signal x by s years (positive s means shifting x to the past) and calculate \({G}_{y\to x}(s)\) searching for its maximum. Without dating errors, only positive lags of the maximum are expected, corresponding to an influence of solar or volcanic activity on the regional climate (represented by the paleoclimate proxy x). However, considering relative dating uncertainties complicates the situation by moving the maximum in any direction from its physically justified location at \(s\ge 0\). Errors associated with even the earliest dates within the YOK-I record are less than 20 years, compared with basic time scales of the considered processes of no more than 25 to 30 years (Supplementary Section S2) that lead to the respective statistical fluctuations of the maximum point. Combined, these two factors could shift the maximum of \({G}_{y\to x}(s)\) by no more than 50 yrs. Maximization over the appropriate range of s provides \({G}_{y\to x\max }=\mathop{\max }\limits_{-50yr\le s\le 50yr}{G}_{y\to x}(s)\) and reduces the effects of dating errors as large as those expected for the data under study. More details on this adjustment of the method are given in39.
We compare the Wiener-Granger causality estimation results with the standard approach for correlation analysis by calculating the Pearson cross correlation coefficient \({K}_{yx}(l)\) between the local climate proxy (x) and solar or volcanic activity (y) for different lags l. Positive values for l indicate that y leads x. Statistical significance of K yx different from zero at given l can be estimated via an (asymptotic) Z-test assuming zero-mean Gaussian distribution of the CCF estimator (see e.g. ref. 40). Incorporating possible dating errors described above, we use mainly the maximal CCF value \(|{K}_{yx}{|}_{\max }=\mathop{\max }\limits_{-50yr\le l\le 50yr}|{K}_{yx}(l)|\).
Models and procedure for Monte Carlo significance testing
Along with the asymptotic F-test and Z-test including the Bonferroni correction for multiple testing41, we use Monte Carlo tests based on specific models in the form of first-order stochastic differential equations and random impulse processes, which reproduce basic statistical properties of the observed data. With these models, we get typical estimator values for the same time series length, sampling frequencies, and dating errors as those in the data under study, without the requirement of infinitely (or at least very) long time series as would be necessary for the asymptotic F-test. Moreover, these models allow simulations of different coupling conditions and testing against the hypothesis of constant coupling in addition to the no coupling scenario. Using moving windows of the length ranging from 500 to 1200 yrs, we test for potential changes in the coupling through time.
Such a bivariate model for the joint δ18O and solar activity variations reads
where Y represents the solar activity underlying the observed signal y n (TSI data), X represents the climate process underlying the observed signal x n (δ18O variations), τ x , τ y are relaxation times, c is the coupling coefficient, \(d\xi (t)\) and \(d\eta (t)\) are mutually independent Wiener processes with variances \(2{D}_{\xi }dt\) and \(2{D}_{\eta }dt\), respectively (\({D}_{\xi }\) and \({D}_{\eta }\) are diffusion coefficients which determine the noise intensities). Replacing dt with the finite time interval Δt = 1 month, setting τ x = 20 yrs, τ y = 25 yrs, \(2{D}_{\xi }{\rm{\Delta }}t=2{D}_{\eta }{\rm{\Delta }}t=0.0004\), introducing irregular time sampling of X in accordance with the observed sampling frequency (see Supplementary Figure S1c), and performing the Gaussian kernel averaging of X with σ = 2.5 years and of Y with σ = 5 years (see Supplementary Section S2), we get the behavior of the model (1) quite close to the observed properties of the data. Since the decorrelation times of the processes are artificially increased by about 5 yrs due to the kernel averaging, we try the relaxation times for the underlying process in the range 20–25 yrs in the model (1). Setting the coupling coefficient cΔt = 0, we simulate the case of uncoupled processes. Setting cΔt=const > 0, we simulate a nonzero constant coupling.
For each set of the parameter values, dating errors, time series length, and settings of the sampling procedure, we generate an ensemble of 1000 time series of the length of 2020 yrs with a time step of 5 yrs and perform CCF and Wiener-Granger causality estimation exactly as for the paleoclimate data above. Then, we compare the estimates obtained for the paleoclimate data with percentiles of the distribution estimated from the respective 1000-member ensemble. Thereby, we reject or do not reject the hypothesis of no coupling or of constant coupling under which the model time series are simulated. Such an approach avoids any assumptions of a very long time series. Therefore, it is a useful complementary tool to assess reliability of the conclusions.
In the Monte Carlo tests for significance of volcanic activity influence, we use a model of the type (1) where the y variable mimics the properties of the observed volcanic data summarized in Supplementary Figure S3c,d. Namely, we take y to be the sum of Gaussian impulses and finally get the model
where t k are random instants of pulses with inter-pulse distance taken at random from the fit to the distribution in Supplementary Figure S3d, amplitudes of pulses A k are taken at random from the fit to the distribution in Supplementary Figure S3c, and the kernel width is σ = 2.5 years.
References
Masson-Delmotte, V. M. et al. Information from Paleoclimate Archives, in Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change (ed. Stocker, T. F., et al.) 383–464 (Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA, 2013).
Gray, L. J. et al. Solar influences on climate. Rev. Geophys. 48(4), RG4001, doi:10.1029/2009RG000282 (2010).
Lockwood, M. Solar Influence on Global and Regional Climates. Surv. Geophys. 33(3-4), 503–534, doi:10.1007/s10712-012-9181-3 (2012).
Robock, A. Volcanic eruptions and climate. Rev. Geophys. 38(2), 191–219, doi:10.1029/1998RG000054 (2000).
Iles, C. E. & Hegerl, G. C. Systematic change in global patterns of streamflow following volcanic eruptions. Nat. Geosci. 8(11), 838–842, doi:10.1038/ngeo2545 (2015).
Ridley, H. E. et al. Aerosol forcing of the position of the intertropical convergence zone since ad 1550. Nat. Geosci. 8, 195–200, doi:10.1038/ngeo2353 (2015).
Goswami, B., Marwan, N., Feulner, G. & Kurths, J. How do global temperature drivers influence each other? – A network perspective using recurrences. European Physical Journal – Special Topics 222, 861–873, doi:10.1140/epjst/e2013-01889-8 (2013).
Sigl, M. et al. Timing and Climate Forcing of Volcanic Eruptions for the Past 2,500 Years. Nature 523, 543–549, doi:10.1038/nature14565 (2015).
Eroglu, D. et al. See–saw relationship of the Holocene East Asian–Australian summer monsoon. Nature Communications 7, 12929, doi:10.1038/ncomms12929 (2016).
Lovejoy, S. & Varotsos, C. Scaling regimes and linear/nonlinear responses of last millennium climate to volcanic and solar forcings. Earth Syst. Dynam. 7, 133–150, doi:10.5194/esd-7-133-2016 (2016).
Crowley, T. J. Causes of Climate Change Over the Past 1000 Years. Science 289(5477), 270–277, doi:10.1126/science.289.5477.270 (2000).
Feulner, G. Are the most recent estimates for Maunder Minimum solar irradiance in agreement with temperature reconstructions? Geophys. Res. Lett. 38(16), L16706, doi:10.1029/2011GL048529 (2011).
Feulner, G. & Rahmstorf, S. On the effect of a new grand minimum of solar activity on the future climate on Earth, Geophys. Res. Lett. 37(5), doi:10.1029/2010GL042710 (2010).
Meehl, G. A., Arblaster, J. M. & Marsh, D. R. Could a future “grand Solar Minimum” like the Maunder Minimum stop global warming? Geophys. Res. Lett. 40(9), 1789–1793, doi:10.1002/grl.50361 (2013).
Eddy, J. A. The Maunder Minimum. Science 192(4245), 1189–1202, doi:10.1126/science.192.4245.1189 (1976).
Matthews, J. A. & Briffa, K. A. The “Little Ice Age”: Re-evaluation of an evolving concept. Geogr. Ann. 87, 17–36, doi:10.1111/j.0435-3676.2005.00242.x (2005).
Miller, G. H. et al. Abrupt onset of the Little Ice Age triggered by volcanism and sustained by sea-ice/ocean feedbacks, Geophys. Res. Lett. 39(2), doi:10.1029/2011GL050168 (2012).
Schleussner, C. F. & Feulner, G. A volcanically triggered regime shift in the subpolar North Atlantic Ocean as a possible origin of the Little Ice Age Instrumentation. Clim. Past 9, 1321–1330, doi:10.5194/cp-9-1321-2013 (2013).
Gennaretti, F., Arseneault, D., Nicault, A., Perreault, L. & Begin, Y. Volcano-induced regime shifts in millennial tree-ring chronologies from northeastern North America. P. Natl. Acad. Sci. USA 111, 10077–10082 (2014).
Runge, J. et al. Identifying causal gateways and mediators in complex spatio-temporal systems. Nature Communications 6, 8502, doi:10.1038/ncomms9502 (2015).
Kennett, D. J. et al. Development and Disintegration of Maya Political Systems in Response to Climate Change. Science 338(6108), 788–791, doi:10.1126/science.1226299 (2012).
Steinhilber, F., Beer, J. & Fröhlich, C. Total solar irradiance during the Holocene. Geophys. Res. Lett. 36, L19704, doi:10.1029/2009GL040142 (2009).
Granger, C. W. J. Investigating Causal Relations by Econometric Models and Cross-spectral Methods. Econometrica 37(3), 424–438, doi:10.2307/1912791 (1969).
Steinhilber, F. et al. 9,400 years of cosmic radiation and solar activity from ice cores and tree rings. Proceedings of the National Academy of Sciences 109(16), 5967–5971, doi:10.1073/pnas.1118965109 (2012).
Winter, A. et al. Persistent drying linked to volcanic forcing. Nature Communications 6, 7627, doi:10.1038/ncomms8627 (2015).
Stocker, T. F. et al. (eds) Summary for Policymakers. In: Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change (Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA, 2013).
Lechleitner, F. A. et al. Hydrological and climatological controls on radiocarbon concentrations in a tropical stalagmite. Geochimica et Cosmochimica Acta 194, 233–252, doi:10.1016/j.gca.2016.08.039 (2016).
Baldini, L. M. et al. Persistent northward North Atlantic tropical cyclone track migration over the past five centuries. Scientific Reports 6, 37522, doi:10.1038/srep37522 (2016).
Reimer, P. J. et al. Intcal 13 and Marine 13 Radiocarbon Age Calibration Curves 0–50,000 Years Cal BP. Radiocarbon 55(4), 1869–1887, doi:10.2458/azu_js_rc.55.16947 (2013).
Kennett, D. J. et al. Yok Balum Cave, Belize 2000 Year Stalagmite Stable Isotope. Data. V. 2. GFZ Data Services. doi:10.5880/pik.2017.004 (2017).
Lachniet, M. S. & Patterson, W. P. Oxygen isotope values of precipitation and surface waters in northern Central America (Belize and Guatemala) are dominated by temperature and amount effects. Earth and Planetary Science Letters 284, 435–446 (2009).
Pausata, F. S., Battisti, D. S., Nisancioglu, K. H. & Bitz, C. M. Chinese stalagmite δ 18O controlled by changes in the Indian monsoon during a simulated Heinrich event. Nat. Geosci. 4, 474–480 (2011).
Maher, B. A. & Thompson, R. Oxygen isotopes from Chinese caves: records not of monsoon rainfall but of circulation regime. J. Quaternary Sci. 27, 615–624 (2012).
Tan, M. Circulation effect: response of precipitation δ18O to the ENSO cycle in monsoon regions of China. Clim. Dyn. 42, 1067–1077 (2014).
Wiener, N., Theory of prediction, In Modern Mathematics for the Engineer, ed. Beckenbach, E. F. (McGraw-Hill, New York, 1956).
Pereda, E., Quian Quiroga, R. & Bhattacharya, J. Nonlinear multivariate analysis of neurophysiological signals. Prog. Neurobiol. 77, 1–37, doi:10.1016/j.pneurobio.2005.10.003 (2005).
Hlaváčková-Schindler, K., Paluš, M., Vejmelka, M. & Bhattacharya, J. Causality detection based on information-theoretic approaches in time series analysis. Phys. Rep. 441, 1–46, doi:10.1016/j.physrep.2006.12.004 (2007).
Prokopenko, M. & Lizier, J. T. Transfer Entropy and Transient Limits of Computation. Sci. Rep. 4, 5394, doi:10.1038/srep05394 (2014).
Smirnov, D. A., Marwan, N., Breitenbach, S. F. M., Lechleitner, F. & Kurths, J. Coping with dating errors in causality estimation. Europhys. Lett. 117, 100004, doi:10.1209/0295-5075/117/10004 (2017).
von Storch, H., Zwiers, F. Statistical Analysis in Climate Research (New York: Cambridge Univ. Press, 1999).
Lehmann, E. L. Testing Statistical Hypotheses (New York: Springer, 1986).
Acknowledgements
The design of this study and all coupling estimations from palaeoclimate data were done under the financial support of the Government of the Russian Federation (Agreement No. 14.Z50.31.0033 with the Institute of Applied Physics RAS). The Russian Science Foundation (grant No. 14–12–00291) supported the method-development part of this study which included the adjustment of the Wiener-Granger method to the case of possible dating errors (Section “Data and methods”, Subsection “Methods”) and Monte Carlo studies of its properties in numerical simulations (Supplementary Section S4). The collection and initial preparation of the palaeoclimate data for this study were supported by the European Union’s Horizon 2020 Research and Innovation programme under the Marie Skłodowska-Curie grant agreement No 691037 (RISE project QUantitative palaeoEnvironments from SpeleoThems QUEST) and the Swiss National Science Foundation (grant P2EZP2_172213).
Author information
Authors and Affiliations
Contributions
J.K., N.M, and D.A.S. designed the study. D.A.S. performed the adjustment of the Wiener-Granger causality method and the estimation of couplings from the palaeoclimate data and wrote the Supplementary text. N.M. prepared the figures for the main text. S.F.M.B., F.A.L., N.M., and K.M.P. selected, collected and initially prepared the palaeoclimate data for this study. J.B., G.F., and J.K. interpreted the results. D.A.S., N.M., S.F.M.B., G.F., J.B., and J.K. wrote the paper. All authors reviewed the paper.
Corresponding author
Ethics declarations
Competing Interests
The authors declare that they have no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Smirnov, D.A., Breitenbach, S.F.M., Feulner, G. et al. A regime shift in the Sun-Climate connection with the end of the Medieval Climate Anomaly. Sci Rep 7, 11131 (2017). https://doi.org/10.1038/s41598-017-11340-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-017-11340-8
This article is cited by
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.