Abstract
The ability to predict hidden phases under extreme conditions is not only crucial to understanding and manipulating materials but it could also lead to insight into new phenomena and novel routes to synthesize new phases. This is especially true for Ruddlesden-Popper perovskite phases that possess interesting properties ranging from superconductivity and colossal magnetoresistance to photovoltaic and catalytic activities. In particular, the physical properties of the bilayer perovskite Sr3Ru2O7 at the surface are intimately tied to the rotation and tilt of the RuO6 octahedra. To take advantage of the extra degree of freedom associated with tilting we have performed first principles hybrid density functional simulations of uniaxial pressure applied along the c-axis of bulk Sr3Ru2O7 where we find that the octahedra become tilted, leading to two phase transitions. One is a structural transition at \(\simeq \)1.5 GPa, and the other is from a ferromagnetic (FM) metal to an antiferromagnetic (AFM) insulator at \(\simeq \)21 GPa whose AFM spin configuration is different from the AFM state near the FM ground state.
Similar content being viewed by others
Introduction
Understanding and exploiting materials in extreme environments is crucial not only to address global energy challenges, but also to control and tailor the materials response to enhance performance, lifetime, and enable new technologies. Thus, a central goal of the materials community is to understand and control the behavior of materials that are either driven far from their equilibrium or placed in extreme conditions such as high pressure, temperature, strain or under high magnetic or electric fields. The response of a material exposed to such environments provides information on its internal structure and dynamics. To be able to assess global and local materials stability between competing structures will enable the design of new synthetic routes for stabilizing hidden metastable phases that contain highly desirable properties.
The search for hidden phases in complex materials is of central interest since it could lead to new materials that display fundamentally interesting and technologically desirable properties such as high strength, ductility or hardness and others such as colossal magnetoresistance, high temperature superconductivity or ferroelectricity. These phases may be accessed and controlled by tuning a number of parameters such as high pressure, high magnetic field, etc. The emergence of new properties is due to the intimate coupling between charge, lattice, and spin degrees of freedom. A possible approach to access new phases is the manipulation of this coupling through changes in the structural, electronic, and magnetic properties by inducing broken symmetry at the surface, interface, or local symmetries in the bulk.
Our hypothesis is that understanding the phases at the surface of a complex multi-component transition-metal compound presents a window on hidden phases in the bulk, especially under extreme conditions. Here we show for the first time that theory can explain the surface structure and electronic properties of Sr3Ru2O7. Our success in calculating the surface properties led us to explore the effect of applying uniaxial pressure along the c-axis, which lead to the emergence of new structural phases. The first transition is observed at \(\simeq \)1.5 GPa where octahedral tilts produce a structural transition from Bbcb to Bbmm orthorhombic symmetries. At an uniaxial pressure of \(\simeq \)21 GPa the second transition occurs transforming the metallic ferromagnetically (FM) ordered bulk into an AFM insulator. Although the total energy difference between the FM and AFM states as a function of octahedral rotation in the bulk is quite small, the large uniaxial pressure necessary to drive the transition indicates that a significant energy barrier exists between these two states, thereby indicating a strong lattice-spin coupling. Remarkably, the hidden AFM phase is an A-type AFM (AFM-A) where Ru atoms are ferromagnetically coupled in-plane and antiferromagnetically coupled out-of-plane in each bilayer, whereas the lowest energy AFM structure at 0 GPa (AFM-I)1 occurs when all Ru atoms in each bilayer are coupled ferromagnetically and coupled antiferromagnetically between bilayers.
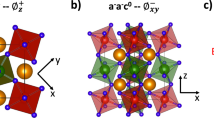
Sr3Ru2O7 is the bilayered member of the Ruddlesden-Popper (RP) family of strontium ruthenates. The system is formed by two layers of RuO6 octahedra connected by an apical oxygen and interleaved by two SrO layers (Fig. 1)2, 3. The octahedra in the bilayer are twisted with one octahedron rotated clockwise by 8.05° about the c axis while the neighboring octahedra are rotated counter-clockwise by the same amount and contains no octahedral tilt. In its ground state, Sr3Ru2O7 is a paramagnetic (PM) metal4, 5 that is highly susceptible to external parameters such as pressure, composition, temperature, or magnetic field6,7,8, and defects that can produce diverse electronic and magnetic properties along with a variety of phase transitions9,10,11,12,13,14 including metamagnetism15, 16 and electron nematic phases17. Understanding the competing interactions in this system is key to understanding the underlying mechanisms responsible for this wide array of observed phenomena and for engineering the electronic and magnetic properties of this system.
Side and top views of the orthorhombic Sr3Ru2O7 structure. (a) Model used in our calculations. Surface planes are indicated by the LYX nomenclature where X is the surface plane position. (b) Top view of the relaxed surface. The RuO6 octahedra are rotated alternately clockwise and counter-clockwise. Darker octahedra refer to the surface bilayer. (c) Calculated tilt and rotations observed in the surface bilayer.
Our experimental investigation revealed that octahedral tilt emerges when creating a (001) surface, which only occurs within the first surface bilayer18. Using a combination of low-energy electron diffraction (LEED) and high-resolution electron energy loss spectroscopy (HREELS) analysis, we observed more distorted RuO6 octahedra at the surface than in the bulk18, 19. These distortions are characterized by a higher rotation angle of \(\simeq \)10.5° ± 3° and a tilt angle of 2.6° ± 0.8° producing a surface symmetry-breaking that leads to a reduced conducting state relative to the bulk. Our computational results reproduce these structural parameters and the reduction in the conductivity. Thereby, RuO6 octahedral tilt is an interesting degree of freedom that can be used to investigate new phases in the bulk or at the surface.
As we will show, inducing octahedral tilt via uniaxial pressure results in a new broken symmetry that stabilizes either a new FM metallic structure or an AFM insulating phase in bulk Sr3 Ru2O7 depending on the pressure applied. In fact, our studies found that the charge density displays local symmetry breaking when octahedral tilt develops in the system. This symmetry breaking along with the strong FM-AFM competition in the bulk provides necessary information to postulate that the use of uniaxial pressure could trigger the FM metallic to AFM insulating transition.
Results and Discussion
Our simulations yield two kinds of RuO6 octahedra tilt where the apical O atoms are pointing in opposite directions (Fig. 1). We note that while O and Sr atoms experience large displacements, the Ru atoms barely move. Our calculations yield Θ1 and Θ2 tilt angles of 1.89° and 2.00° respectively and rotation angles, Φ1 and Φ2, equal to 11° and 9.25° (see Table 1). The experimental and calculated tilts and rotation angles are in very good agreement where an enhancement of Φ1 and reduction of Φ2 relative to bulk are observed2, 18. The difference between Ru1-O and Ru2-O distances increased from 0 Å in the bulk to 0.033 Å at the surface indicating a symmetry breaking.
These results show that surface symmetry breaking results from the creation of two distinct Ru environments characterized by different octahedral distortion, which causes difference in the charge density of these two sites that can clearly be seen in Fig. 2. The two different Ru environments will be referred to as Ru1O6 and Ru2O6. The Ru1O6 exhibits an in-plane compression and an out-of-plane elongation, resulting in a gain of charge of 0.055e and a magnetic moment equal to 1.44 μ B. In contrast, the Ru2O6 octahedron is stretched in-plane with an increase of the in-plane Ru2-O bond distance and a compressed out-of-plane. This leads to a loss of charge of 0.055e and a magnetic moment equal to 1.59 μ B whereas, the bulk structure has only one type of Ru atom by symmetry with a magnetic moment equal to 1.41 μ B. It should be noted that the next RuO2 layer (LY4) shows smaller difference in Ru3-O/Ru4-O bond distances (\(\simeq \)0.005 Å) and, unlike LY2, it does not produce any appreciable changes in the electronic properties as compared to the bulk (see Fig. 2). These results clearly show that the symmetry breaking is purely localized.
To gain additional insight on the effects of symmetry breaking on the electronic properties at the surface, the density of states for tilted and untilted RuO2 layers along with the corresponding bulk density of states (DOS) are shown in Fig. 3. The SrO contributions around the Fermi energy (E F ) are insignificant with the majority of electronic states coming from the RuO2 layers. As expected, bulk and non-tilted structures produce similar DOS. However, when the octahedra are tilted the total energy of the system is reduced by 11.6 meV per formula unit where a significant reduction of the states around E F occurs. Specifically, the partial DOS yields different Ru1 and Ru2 4d xy states at the surface due to symmetry breaking. The 4d xy level of the Ru1 atom (compressive in-plane octahedra) becomes unoccupied due to a stronger coupling between O and Ru producing a larger splitting of the d xy orbital, whereas the 4d xy level in Ru2 is occupied. As a consequence there is a reduction of electronic states crossing E F , leading to a reduction in metallicity at the surface as compared to the bulk.
Non-tilted and tilted structures have similar octahedral rotation in the surface bilayer, which could indicate that rotation is not strongly coupled with electronic or magnetic properties. This result is in agreement with our previous simulations on bulk Sr3Ru2O7 1, where we found that electronic and magnetic properties do not depend on the octahedral rotation. The difference in the electronic properties of both structures is due to tilt and therefore, octahedral tilt plays an important role in the observed properties of Sr3Ru2O7.
In our previous investigation on bulk Sr3Ru2O7 1, we did not have the capability to treat the PM state. Thus, we found the FM state to always be the ground-state but it does become nearly degenerate with the AFM-I phase by −0.5 meV per formula unit. Here, we find that this competition disappears for the surface tilted structure where the FM state is favored with a total energy difference of 22 meV per formula unit.
Both experiment and theory show that RuO6 octahedral tilt reduces the metallicity of the system at the surface. The obvious extension of this finding is to calculate the effect on the bulk by the application of a uniaxial pressure along the c axis. Uniaxial pressure should induce tilt and change the delicate balance between FM-AFM spin states. We observe that the application of \(\simeq \)2% compressive strain (correspondent to \(\simeq \)1.5 GPa) produces a 8.6° octahedral tilt accompanied by a large reduction of rotation from 9.7° to 2.1° in the bulk. This point is marked by an arrow in Fig. 4a. However, the system still exhibits the FM ground state. By increasing the uniaxial pressure to \(\simeq \)21 GPa the system transforms to an AFM insulating ground state, marked by the second arrow in Fig. 4a.
(a) Phase diagram of Sr3Ru2O7 showing the evolution of the ΔE and bandgap as a function of c cell parameter. The structural insets show the octahedra tilts in the ground-state structure and in the AFM-A insulator phase. The α + β density of states at c = 18.5 Å and AFM-A configuration are also displayed. (b) Evolution of RuO6 tilt and rotation as a function of c cell parameter.
Figure 4a displays the calculated bandgap as well as the difference in total energy between the FM and AFM-A states as a function of uniaxial pressure (along the c direction). For each uniaxial compressive strain a constrained geometry relaxation was performed where the atoms, a and b lattice parameters were allowed to relax while holding the c lattice parameter fixed. For high pressures the resulting AFM state is different from the lowest energy AFM-I phase found in the ground state bulk structure. This AFM insulating state obtained at 21 GPa, with c = 18.5 Å is an AFM-A state with a band gap of 0.35 eV. Further increasing uniaxial pressure does not significantly increase the band gap. Tilt of octahedra are \(\simeq \)12° similar to that found in the AFM insulator Ca3Ru2O7 14. This provides additional evidence that the local structure is strongly coupled with spin and charge degrees of freedom. Finally, the mechanism associated with the AFM-A insulating phase transition can be understood via the inverse Goodenough-Kanamori interaction20. The application of uniaxial pressure forces the O atoms to move, resulting in the Ru-O-Ru intrabilayer angle (along the c axis) decreasing below 180° (i.e. tilt) along with a reduction of the corresponding Ru-O bond lengths. This produces a reduction of the magnetic coupling that satisfies the Goodenough-Kanamori rules21, 22 ultimately, leading to the FM-AFM phase transition.
Figure 4b shows the resulting tilt and rotation as the c axis reduces due to uniaxial pressure. It is clear that there are two first order phase transitions, one between the FM metallic (a = b) and the distorted FM metallic (a ≠ b) phases and the other, under higher uniaxial pressure, from the FM metallic to AFM insulator. Therefore, our calculations reveal two different hidden phase transitions in the bulk.
Conclusion
By applying uniaxial pressure we have discovered a hidden AFM insulating phase in bulk of Sr3Ru2O7. The hypothesis of using uniaxial pressure to uncover this phase was motivated by our experimental and computational investigations on the structure property relationship due to: (1) The effects of RuO6 octahedra tilts on the electronic and magnetic properties of the first surface bilayer in Sr3Ru2O7 and (2) The strong FM-AFM competition found in the bulk phase. We observe that there is a strict relation between octahedral tilts and reduction of metallicity on the Sr3Ru2O7 surface as compared to the bulk. By applying \(\simeq \)21 GPa of uniaxial compressive strain along the c axis we predict a phase transition from FM metal to an AFM-A insulator whose AFM structure is different from the lowest energetically AFM ground-state structure (AFM-I). Furthermore, the mechanism that leads to the AFM-A state is based on the inverse Goodenough-Kanamori interaction and Goodenough-Kanamori rules.
Methods
We have performed first principles DFT calculations based on PBES-10 hybrid functional. This functional is based on a mixing of 10% Hartree-Fock exchange with 90% PBESol exchange potential23, which has been shown to accurately capture the properties of Sr3Ru2O7 1. For an additional explanation of this particular mixing the reader can be referred to ref. 24. We used the CRYSTAL14 computational package25, 26 which uses atom-centered Gaussian-type orbital (GTO) basis sets to build Bloch functions and thus expand the one-electron crystalline orbitals. The GTOs and calculation parameters used in this investigation have been reported in ref. 1. Surface Sr3Ru2O7 structures were modeled using slabs symmetrically terminated along the (001) direction (Fig. 1). The system under study has 25 layers with five RuO6 octahedral bilayers totaling 120 atoms. For atomic relaxation, the first 8 atomic layers, which includes two RuO6 bilayers were included in the relaxation process while the remaining atoms were fixed to the calculated bulk parameters1. To obtain a better understanding of the coupling between surface and octahedral distortion, and to determine the ground-state surface structure, simulations were performed with and without tilt. The total energy difference between tilted and untilted RuO6 octahedra is −11.6 meV per formula unit, indicating that having RuO6 tilted octahedra in the 1st surface bilayer is the preferred ground-state surface structure.
References
Rivero, P., Meunier, V. & Shelton, W. Half-metallic ferromagnetism in Sr3Ru2O7. Phys. Rev. B 95, 195106, doi:10.1103/PhysRevB.95.195106 (2017).
Huang, Q., Lynn, J. W., Erwin, R. W., Jarupatrakorn, J. & Cava, R. J. Oxygen displacements and search for magnetic order in Sr3Ru2O7. Phys. Rev. B 58, 8515–8521, doi:10.1103/PhysRevB.58.8515 (1998).
Shaked, H., Jorgensen, J., Chmaissem, O., Ikeda, S. & Maeno, Y. Neutron diffraction study of the structural distortions in Sr3Ru2O7. Journal of Solid State Chemistry 154, 361–367, doi:10.1006/jssc.2000.8796 (2000).
Ikeda, S.-I. & Maeno, Y. Magnetic properties of bilayered Sr3Ru2O7. Physica B Condensed Matter 259, 947–948 (1999).
Perry, R. S. et al. Hall effect of Sr3Ru2O7. Physica B: Condensed Matter 284–288, Part 2, 1469–1470 (2000).
Ikeda, S.-I. et al. Uniaxial-pressure induced ferromagnetism of enhanced paramagnetic Sr3Ru2O7. Journal of the Physical Society of Japan 73, 1322–1325, doi:10.1143/JPSJ.73.1322 (2004).
Grigera, S. A. et al. Angular dependence of the magnetic susceptibility in the itinerant metamagnet Sr3Ru2O7. Phys. Rev. B 67, 214427, doi:10.1103/PhysRevB.67.214427 (2003).
Stone, M. B. et al. Temperature-dependent bilayer ferromagnetism in Sr3Ru2O7. Phys. Rev. B 73, 174426, doi:10.1103/PhysRevB.73.174426 (2006).
Steffens, P. et al. Incommensurate magnetic ordering in ti-doped Sr3Ru2O7. Phys. Rev. B 79, 054422, doi:10.1103/PhysRevB.79.054422 (2009).
Hooper, J. et al. Competing magnetic fluctuations in Sr3Ru2O7 probed by ti doping. Phys. Rev. B 75, 060403, doi:10.1103/PhysRevB.75.060403 (2007).
Li, G. et al. Atomic-scale fingerprint of mn dopant at the surface of Sr3(Ru1-xMnx)2O7. Sci. Rep. 3, 2882 (2013).
Hu, B. et al. Structure-property coupling in Sr3(Ru1-xMnx)2O7. Phys. Rev. B 84, 174411, doi:10.1103/PhysRevB.84.174411 (2011).
Mathieu, R. et al. Impurity-induced transition to a mott insulator in Sr3Ru2O7. Phys. Rev. B 72, 092404, doi:10.1103/PhysRevB.72.092404 (2005).
Peng, J. et al. Interplay between the lattice and spin degrees of freedom in (Sr1−xCa x )3Ru2O7. Phys. Rev. B 82, 024417, doi:10.1103/PhysRevB.82.024417 (2010).
Perry, R. S. et al. Metamagnetism and critical fluctuations in high quality single crystals of the bilayer ruthenate Sr3Ru2O7. Phys. Rev. Lett. 86, 2661–2664, doi:10.1103/PhysRevLett.86.2661 (2001).
Grigera, S. A. et al. Magnetic field-tuned quantum criticality in the metallic ruthenate Sr3Ru2O7. Science 294, 329–332, doi:10.1126/science.1063539 (2001).
Borzi, R. A. et al. Formation of a nematic fluid at high fields in Sr3Ru2O7. Science 315, 214–217, doi:10.1126/science.1134796 (2007).
Chen, C. et al. Hidden phases revealed at the surface of double-layered Sr3(Ru1−x Mn x )2O7. Phys. Rev. B 94, 085420, doi:10.1103/PhysRevB.94.085420 (2016).
Hu, B. et al. Surface and bulk structural properties of single-crystalline Sr3Ru2O7. Phys. Rev. B 81, 184104, doi:10.1103/PhysRevB.81.184104 (2010).
Yamaguchi, K. et al. Magnetically induced ferroelectricity in TbMnO3: inverse Goodenough–Kanamori interaction. J. Phys.: Condens. Matter 21, 064203 (2009).
Goodenough, J. B. Theory of the role of covalence in the perovskite-type manganites [La,M(II)]MnO3. Phys. Rev. 100, 564–573, doi:10.1103/PhysRev.100.564 (1955).
Kanamori, J. Superexchange interaction and symmetry properties of electron orbitals. Journal of Physics and Chemistry of Solids 10, 87–98, doi:10.1016/0022-3697(59)90061-7 (1959).
Wu, Z. et al. More accurate generalized gradient approximation for solids. Phys. Rev. B 73, 235116–235121, doi:10.1103/PhysRevB.73.235116 (2006).
Rivero, P. et al. Electronic, structural, and magnetic properties of LaMnO3 phase transition at high temperature. Phys. Rev. B 93, 024111–024120, doi:10.1103/PhysRevB.93.024111 (2016).
Dovesi, R. et al. CRYSTAL14: A program for the ab initio investigation of crystalline solids. Int. J. Quantum Chem. 114, 1287 (2014).
Dovesi, R. et al. CRYSTAL14 User’s Manual (University of Torino, Torino, 2014).
Acknowledgements
The computational work conducted by P.R. and W.A.S. is supported by the U.S. Department of Energy under EPSCoR contract No. DE-SC0012432 with additional support from the Louisiana Board of Regents and by an allocation of computing time from the Louisiana State University High Performance Computing center. E.W.P., R.J., and C.C. were supported by the National Science Foundation Grant DMR-1504226. V.M. acknowledges support by New York State under NYSTAR program C080117.
Author information
Authors and Affiliations
Contributions
P.R. and W.S. conceived the calculations. P.R., R.J., C.C., V.M., E.W.P., and W.S. analyzed the results and reviewed the manuscript.
Corresponding author
Ethics declarations
Competing Interests
The authors declare that they have no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Rivero, P., Jin, R., Chen, C. et al. Predicting hidden bulk phases from surface phases in bilayered Sr3Ru2O7 . Sci Rep 7, 10265 (2017). https://doi.org/10.1038/s41598-017-10780-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-017-10780-6
This article is cited by
-
Strain control of a bandwidth-driven spin reorientation in Ca3Ru2O7
Nature Communications (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.