Abstract
We have produced a superconducting binary-elements intercalated graphite, CaxSr1−xCy, with the intercalation of Sr and Ca in highly-oriented pyrolytic graphite; the superconducting transition temperature, T c, was ~3 K. The superconducting CaxSr1−xCy sample was fabricated with the nominal x value of 0.8, i.e., Ca0.8Sr0.2Cy. Energy dispersive X-ray (EDX) spectroscopy provided the stoichiometry of Ca0.5(2)Sr0.5(2)Cy for this sample, and the X-ray powder diffraction (XRD) pattern showed that Ca0.5(2)Sr0.5(2)Cy took the SrC6-type hexagonal-structure rather than CaC6-type rhombohedral-structure. Consequently, the chemical formula of CaxSr1−xCy sample could be expressed as ‘Ca0.5(2)Sr0.5(2)C6’. The XRD pattern of Ca0.5(2)Sr0.5(2)C6 was measured at 0–31 GPa, showing that the lattice shrank monotonically with increasing pressure up to 8.6 GPa, with the structural phase transition occurring above 8.6 GPa. The pressure dependence of T c was determined from the DC magnetic susceptibility and resistance up to 15 GPa, which exhibited a positive pressure dependence of T c up to 8.3 GPa, as in YbC6, SrC6, KC8, CaC6 and Ca0.6K0.4C8. The further application of pressure caused the rapid decrease of T c. In this study, the fabrication and superconducting properties of new binary-elements intercalated graphite, CaxSr1−xCy, are fully investigated, and suitable combinations of elements are suggested for binary-elements intercalated graphite.
Similar content being viewed by others
Introduction
Some graphite intercalation compounds show superconductivity, and have attracted serious attention because of their high superconducting transition temperatures (T c’s). The highest-onset superconducting transition temperature, T c onset, is currently 11.5 K at ambient pressure (0 GPa)1, 2 and 15.1 K at 7.5 GPa for CaC6 3. However, despite much effort to make new graphite superconductors, no graphite superconductors with higher T c onset values than 11.5 K have been synthesized. In fact, the T c values of graphite superconductors prepared by the intercalation of alkali metal atoms thus far were 136 mK for KC8 4, 5 and 23 mK for RbC8 4. The graphite superconductors prepared by alkali earth or lanthanide atoms were SrC6 (T c = 1.65 K)6, BaC6 (T c = 65 mK)7 and YbC6 (T c = 6.5 K)1. Furthermore, binary-elements intercalated graphite was first achieved in KHgC8 (T c = 1.9 K)8. Subsequently, some binary-elements intercalated graphite superconductors were realized such as RbHgC8 (T c = 1.44 K)9, KTl1.5C4 (T c = 2.7 K)10, KTl1.5C8 (T c = 2.5 K)10, CsBi0.55C5 (T c = 4.05 K)11, Li3Ca2C6 (T c = 11.15 K)12. Recently, our group succeeded in synthesis of CaxK1−xC8 (6.5 – 11.5 K) for 0.33 ≤ x ≤ 113. Thus, binary-element intercalation has provided a family of superconductive graphites.
A positive pressure dependence of T c onset was observed in CaC6, and the maximum T c onset reached 15.1 K at 7.5 GPa3. At higher pressure, the T c onset suddenly dropped. Such a pressure dependence was also observed for other metal-intercalated graphite superconductors. The maximum T c onset values were 7.1 K at 1.8 GPa for YbC6 14, 2 K at 1 GPa for SrC6 6, and 1.7 K at 1.5 GPa for KC8 15. Such a pressure dependence is characteristic of graphite superconductors. The increase in T c onset for CaC6 was assigned to the softening of the in-plane Ca-Ca phonon and the hardening of the Ca-C phonon3, 16. Moreover, the rapid decrease in T c is attributed to the order-disorder transition relating to a large softening of the lattice under pressure17. Similar behavior under pressure was also observed for binary-elements intercalated graphite Ca0.6K0.4C8, showing a maximum T c of 11.6 K at 3.3 GPa13.
The mechanism of superconductivity has been extensively discussed based on the theoretical calculation18, 19. Calandra and Mauri18 suggested clearly that the supecondsuctivity in CaC6 is due to an electron-phonon mechanism, and carriers are mostly electrons in the Ca Fermi surface which couples with in-plane Ca-Ca phonon and out-of plane C-C phonons. They suggested the importance of Ca Fermi surface (not π* band of graphite) for the superconductivity. On the other hand, Yang et al. experimetally showed the opening of a superconducting gap in the π* band of graphite19, suggesting that the superconductivity cannot be assigned to only interlayer band but interaction of π* and interlayer bands. Thus, the mechanism is still under debate. Furthermore, the superconductivity of metal-doped graphene has recently been pursued from theretical and experimental points of view20,21,22. The study on metal-doped graphene may lead to the elucidation of superconductivity in metal-intercalated graphite, since graphene is a thin limit of graphite.
The X-ray diffraction (XRD) patterns of CaxK1−xCy (x ≠ 1) suggested a KC8-type structure13 (face-centered orthorhombic, space group No. 70, Fddd)23, rather than a CaC6-type structure (rhombohedral, space group No. 166, R \(\bar{3}\)m)2. The former (KC8 structure) shows ‘AαAβAγAδ’, where ‘A’ refers to the graphene sheet, and α, β, γ, and δ refer to the four sites occupied by the metal atoms. On the other hand, the latter (CaC6-structure) shows ‘AαAβAγ’ in which metal occupies three different sites. The most interesting point is that in CaxK1−xCy the T c is much higher than that of KC8 despite the KC8-type structure.
In this study, we discovered a new binary-elements intercalated graphite superconductor through the intercalation of Ca and Sr. The T c values of CaxSr1−xCy with x = 0.8 or 0.9 were ~3 K in the metal-intercalation to highly-oriented pyrolytic graphite (HOPG). Energy dispersive X-ray (EDX) spectroscopy showed the chemical composition of the prepared CaxSr1−xCy. The XRD pattern of CaxSr1−xCy showed that the crystal structure is SrC6-type (hexagonal, space group No. 194, P63/mmc)24. Therefore, the CaxSr1−xCy sample was finally expressed ‘CaxSr1−xC6’. The pressure dependence of the XRD pattern of CaxSr1−xC6 showed monotonic shrinkage of the lattice up to 20 GPa. The pressure dependence of T c for CaxSr1−xC6 showed a positive pressure dependence at 0–8.3 GPa, and a sudden drop in T c was observed with applied pressure above 8.3 GPa. The magnetic characteristics of the R – T plot for CaxSr1−xC6 were also studied at 0.80, 4.3 and 8.5 GPa.
Results
Preparation and characterization of superconducting CaxSr1−xCy sample through metal doping of HOPG
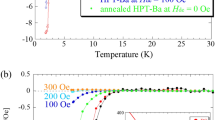
The temperature (T) dependence of magnetic susceptibility, M/H, (M/H – T plot) measured in zero-field cooling (ZFC) mode in CaxSr1−xCy (x = 0.8) prepared by the intercalation of Sr and Ca to HOPG, which is expressed ‘Ca0.8Sr0.2Cy’, is shown in Fig. 1a; M and H refer to magnetization and applied magnetic field, respectively. The optical image of Ca0.8Sr0.2Cy sample is shown in Fig. 2a, which was bright-gold colour.
(a) M/H – T plots in ZFC and FC modes for Ca0.8Sr0.2Cy. (b) M/H – T plot in ZFC and FC modes for SrC6. (c) M – H plot at 2 K for Ca0.8Sr0.2Cy. (d) M/H - T plots at different H’s for Ca0.8Sr0.2Cy, measured in ZFC mode. Inset of (a) shows how to determine the T c. The inset of Fig. 1(c) shows the M – H plot in the low-H range. Inset of (d): H c2 – T plot for Ca0.8Sr0.2Cy determined from (d). Stoichiometry of Ca0.8Sr0.2Cy refers to the experimental nominal value, and all samples were made by the intercalation of Ca and Sr in HOPG.
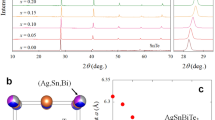
(a) Optical image (left) of the Ca0.8Sr0.2Cy sample and microscope image (right) of the sample set in the DAC. (b) EDX spectrum of Ca0.8Sr0.2Cy. (c) XRD pattern of Ca0.5(2)Sr0.5(2)Cy. The XRD pattern was measured with synchrotron radiation of λ = 0.68841 Å at room temperature. Patterns shown in (c) for Ca0.5Sr0.5C6, SrC6, CaC6, graphite and LiC6 were simulated using the VESTA program, using structural data from refs 2, 24, 25 and 26, respectively.
A rapid drop in M/H is observed below ~3.0 K, and T c is 3.2 K; how to determine T c is shown in the inset of Fig. 1a. The T c onset is 4.0 K from the M/H – T plot in ZFC mode. The M/H – T plot in field-cooling (FC) mode is shown in Fig. 1a, and the T c was also estimated to be 3.2 K. The shielding fraction was estimated to be 100% at 2 K from the M/H – T plot in ZFC mode. Thus, the Ca0.8Sr0.2Cy sample is quite simply a bulk superconductor. On the other hand, we prepared the SrC6 sample by the intercalation of Sr in HOPG, which did not show superconductivity down to 2 K, as seen from Fig. 1b. As the T c onset of SrC6 is 1.65 K, the absence of superconductivity is reasonable, suggesting that the Ca0.8Sr0.2Cy sample is not SrC6 but Ca/Sr co-doped graphite (CaxSr1−xCy).
In this study, we changed nominal x value from 0 to 0.9 in CaxSr1−xCy. For CaxSr1−xCy at x ≥ 0.7, the superconductivity was observed. The CaxSr1−xCy sample with nominal x of 0.9, Ca0.9Sr0.1Cy, provided both phases of CaC6 (T c ≈ 11 K) and CaxSr1−xCy (T c ≈ 4 K), while that with nominal x of 0.7, Ca0.7Sr0.3Cy, showed smaller fraction of superconductivity (T c ≈ 2.5 K). For the CaxSr1−xCy sample at nominal x of 0.9, we measured the EDX spectra at eight different positions, which showed three different stoichiometry, Ca0.98(1)Sr0.02(1)Cy (four points), Ca0.58(6)Sr0.42(6)Cy (three points) and Ca0.35Sr0.65Cy (only one point), consistent with two superconducting phases (T c ≈ 11 K and T c ≈ 4 K) as described above; the Ca0.35Sr0.65Cy is probably lower T c than 4 K. Furthermore, for the CaxSr1−xCy sample at nominal x of 0.7, the EDX spectra were measured at five different positions, showing a single phase, Ca0.2(1)Sr0.8(1)Cy. This result is consistent with the observation of a single phase exhibiting a small superconducting volume fraction (T c ≈ 2.5 K). Thus, owing to the observation of a very large shielding fraction (T c = 3.2 K) as shown in Fig. 1a, we investigated the CaxSr1−xCy sample prepared with nominal value of x = 0.8 throughout this study. Finally, we may stress the validity of stoichiometry determined from EDX, based on the consistency between the EDX results and magnetic properties of the CaxSr1−xCy samples.
The M – H plot of Ca0.8Sr0.2Cy at 2 K is shown in Fig. 1c, which shows typical superconducting M – H behaviour. The lower critical filed, H c1, was determined to be 20 Oe (see inset of Fig. 1c). This H c1 is much smaller than 500 Oe (at 6 K) of CaC6 2. The M/H – T plots at different H’s are shown in Fig. 1d. The H c2 – T plot obtained from M/H – T plots (Fig. 1d) is shown in the inset of Fig. 1d, and the H c2 at 0 K, H c2(0), was determined to be 200 Oe from the H c2 – T plot using the Werthamer-Helfand-Hochenberg (WHH) formula, H c2(0) = −0.693T c(dH c2/dT) T=Tc, indicating that the London penetration depth (λ) and Ginzburg Landau coherent length (ξGL) are 215 and 130 nm, respectively. The H c2 value is much smaller than 7000 Oe of CaC6 2. Here, it should be noted that the H c2 predicted from the M – H plot at 2 K (Fig. 1c) seems to be higher than 4000 Oe. This is probably due to the contribution from a CaC6 phase, because this sample contains a trace of CaC6, as seen from Fig. 1a. This scenario would be reasonable because the H c2(0) of CaC6 is 7000 Oe2.
The EDX of Ca0.8Sr0.2Cy is presented in Fig. 2b, and shows peaks due to Sr, Ca, O and C atoms. The presence of O atoms must be due to the oxidation of Ca0.8Sr0.2Cy because the sample used for the EDX spectrum was once treated under atmospheric conditions before the EDX measurement, i.e., the contamination of O originates from an extrinsic factor. Therefore, the EDX spectrum suggests that the chemical composition of the Ca0.8Sr0.2Cy sample can be expressed ‘CaxSr1−xCy’; the contamination of Li could not be confirmed by the EDX spectrum because the energy of the Li Kα peak is too low. The stoichiometry of Ca0.8Sr0.2Cy was estimated to be Ca0.5(2)Sr0.5(2)Cy from the area intensity of the peaks in the EDX spectrum. Here we can point out that since each peak is substantially resolved in the EDX spectrum (Fig. 2b), the area intensity is obtained with high accuracy. The estimated standard deviation (e.s.d.) of the chemical composition shown above was somewhat large when a large grain of Ca0.8Sr0.2Cy was used for the EDX measurement, indicating that the sample was slightly inhomogeneous. From here, we use the chemical formula, Ca0.5(2)Sr0.5(2)Cy, for the Ca0.8Sr0.2Cy sample.
Structure of superconducting Ca0.5Sr0.5Cy
The XRD pattern of Ca0.5(2)Sr0.5(2)Cy at around 0 GPa is shown in Fig. 2c, indicating that the main peaks can be assigned to the SrC6-type structure, which is P63/mmc (No. 194)24. Simulation spectra (powder pattern) of LiC6, CaC6, SrC6 and graphite are also shown in Fig. 2c; the simulation was made using the crystal structures of LiC6 25, CaC6 2 SrC6 24, and graphite26. Furthermore, as seen from Fig. 2c, the relative intensity of the peaks observed is quite similar to that of SrC6. Notably, the XRD pattern was measured with synchrotron radiation (wavelength λ = 0.68841 Å), in which the sample is introduced into a diamond anvil cell (DAC). The pressure was determined to be 0 GPa from the fluorescence of ruby, but the exact pressure may be 0–0.2 GPa.
The lattice constant, a, was determined to be 4.32 Å from the 100 and 110 peaks, while the lattice constant, c, was determined to be 9.82 Å from the 112 peak using the above a value. Furthermore, the values of a and c were evaluated using iterative approximation. In the iterative approximation, firstly we roughly estimated the a value from 100 and 110 peaks. Secondly, the c value was estimated from all peaks and the a value determined roughly in the first process. Finally the a value was estimated from the all peaks and the c determined in the second process. The a and c were 4.31(1) and 9.85(8) Å, respectively. The Le Bail fitting was also tried for determination of a and c. The a and c determined by Le Bail fitting were 4.3077(3) and 9.883(1) Å, respectively. Actually, because of the impurity peaks, the Le Bail fitting was difficult. Therefore, these values are for reference. The a and c values determined by all ways are consistent each other, implying that the a and c determined were reliable.
It is easy to assume that only 00 l reflections will be measured, if the ab-plane of metal-intercalated HOPG sample is completely aligned to the sample holder. However, all reflections are observed as seen from indices of XRD pattern shown in Fig. 2c, indicating that the metal-intercalated HOPG sample is not completely aligned to the sample holder. Therefore, the XRD pattern observed is powder-like with preferred orientation. Consequently, we could successfully obtained both values of a and c. As seen from Fig. 2c, the XRD pattern of Ca0.5Sr0.5Cy was simulated using a = 4.31(1) and c = 9.85(8) Å (iterative approximation) and assuming that the 50% of Ca and 50% of Sr randomly occupy the 2c site in the space group (No. 194, P63/mmc) of SrC6-type crystal. As seen from the comparison between the experimenmtal XRD pattern and the simulated pattern of Ca0.5Sr0.5C6 (Fig. 2c), most of peaks in the experimental XRD pattern for Ca0.5(2)Sr0.5(2)Cy sample were assigned to those of Ca0.5Sr0.5C6 simulated with SrC6 structure. Thus, the indices for most of peaks were provided at SrC6 structure, but some peaks were assigned to those of CaC6 and graphite. Moreover, some of peaks were not assigned. The difference in relative intensities was found between the experimental XRD pattern and the simulated one of Ca0.5Sr0.5C6, but the conclusion that the sample takes SrC6 structure is supported. Furthermore, it should be noticed that to completely reproduce the relative intensities observed in the experimental XRD pattern is difficult, because it shows a powder-like pattern affected by strong preferred orientation, as described above.
The a and c values are almost the same as those (a = 4.316 Å and c = 9.88 Å) of SrC6 24, and the simulated pattern of Ca0.5Sr0.5Cy at SrC6 structure is consistent with the experimental XRD pattern. As a results, all XRD results support that the stoichiometry of Ca0.5(2)Sr0.5(2)Cy can be expressed ‘Ca0.5(2)Sr0.5(2)C6’. The fact that the Ca/Sr binary-elements intercalated graphite takes the SrC6 structure may be reasonable because the ionic radius of Sr2+ (1.18 Å for six coordination) is larger than that of Ca2+ (1.0 Å for six coordination). Namely, the Ca atoms may be intercalated into the crystal lattice of graphite separated by Sr atoms because of the larger ionic radius of Sr2+. In this crystal, the metal atoms occupy two different sites of α and β, and the graphite layer shows AAA stacking. The stacking form, AαAβAα, of SrC6 is different from that, AαAβAγAα, of CaC6. The distance, d AA, between graphenes in SrC6 is 4.94 Å (d AA = c/2), which is larger than the d AA = 4.524 Å (d AA = c/3) in CaC6, indicating that the Ca intercalation into SrC6 (or CaxSr1−xCy) may not affect the lattice constant c. In fact, the c value of Ca0.5(2)Sr0.5(2)C6 is almost the same as that of SrC6, as described above. Thus, despite the SrC6 structure, we could obtain the 3 K superconducting phase in Ca0.5(2)Sr0.5(2)C6.
Finally, we must comment upon the peaks that cannot be assingned to Ca0.5Sr0.5C6. Some of peaks were assigned to CaC6 and pure graphite, as seen from Fig. 2c, indicating the presence of small amount of pure graphite in the sample. This may be the origin of the significant diamagnetic background observed in M – H plot (Fig. 1c). As described previously, the presence of CaC6 in the Ca0.5(2)Sr0.5(2)C6 sample was suggested from the M/H – T plot at ZFC mode shown in Fig. 1a. Here, it should be noticed that the M/H – T at FC mode (Fig. 1a) did not show any trace of CaC6. This may imply that the CaC6 phase is not bulky but surface (thin layer). As seen from Fig. 2c, some of weak peaks in the XRD pattern were assigned to CaC6, indicating the presence of CaC6, which is consistent with the observation of a trace of CaC6-superconductivity.
Pressure dependence of superconductivity and structure in Ca0.5Sr0.5C6
Microscope image of Ca0.5(2)Sr0.5(2)C6 sample and four electrodes set in DAC is shown in Fig. 2a, in which four electrodes are contacted to the sample. The sample shows bright-gold color. Figure 3a and b show the temperature dependence of resistance (R – T plots) of Ca0.5(2)Sr0.5(2)C6 at different pressures. The former shows the R – T plots at 2–300 K, and the latter shows the expanded plots (2–9 K). The pressure dependence of T c in Ca0.5(2)Sr0.5(2)C6 is shown in Fig. 3c; the T c was determined from the cross point of the R – T plot at normal state and that exhibiting the drop, in the same manner as the inset of Fig. 1a. The T c increased with increasing pressure up to 8.3 GPa, then suddenly decreased. This behaviour is similar to that of CaC6 3 and Ca0.6K0.4C8 13. Such a positive pressure dependence of T c in Ca0.5(2)Sr0.5(2)C6 may also be due to the softening of in-plane Ca(Sr)-Ca(Sr) phonons, as suggested in CaC6 3. The highest T c was 5.4 K at 8.3 GPa. The values of dT c/dp and dT c onset /dp were determined to be 0.34(4) K GPa−1 and 0.42(1) K GPa−1, respectively, from the T c – p and T c onset – p plots at 0–8.3 GPa, consistent with those of SrC6 and CaC6 (dT c/dp (SrC6) = 0.35 K GPa−1 and dT c onset /dp (CaC6) = 0.39 K GPa−1)6, 27. The sudden drop of T c is found in CaC6 and Ca0.6K0.4C8 which was assigned to the order-disorder transition originating from random off-center displacement of Ca(K) atoms in the ab-plane with accompanying lattice-softening3, 17. Therefore, the T c drop in the pressure range above 8.3 GPa for Ca0.5(2)Sr0.5(2)C6 may be assigned to the above order-disorder transition.
R – T plots for Ca0.5(2)Sr0.5(2)C6 at different pressures in T range of (a) 2–300 K and (b) 2–9 K. (c) T c – p and (d) R – p plots for Ca0.5(2)Sr0.5(2)C6; R in (d) means the R value at 280 K. Inset of (c): T c – p plot for the Ca0.9Sr0.1Cy sample below 1.5 GPa, which was determined from M/H – T plots at different pressures; this sample’s stoichiometry is shown in the text.
The R – T plots at H’s of 0 and 500 Oe were measured at 0.80 GPa (Fig. 4a), indicating the suppression of superconductivity at 500 Oe. Furthermore, the R – T plots at different H values were measured at 4.3 and 8.5 GPa. Figure 4b shows the R – T plots at different H values at 8.5 GPa. The H c2 – T plot determined from the graph shown in Fig. 4b is depicted in the inset of Fig. 4b. The H C2(0) at 8.5 GPa was evaluated to be 3100 Oe from the WHH formula. This value is larger than that, 200 Oe, evaluated from M/H – T plots at 0 GPa (inset of Fig. 1d). Notably, as seen from Fig. 3a, the behavior of the R – T plot in the normal state was metallic up to 12 GPa, i.e., the R decreased with decreasing temperature. But at 14 and 15 GPa, the R increased slightly with decreasing temperature below 90 K, suggestive of a change in electric transport in the normal state at around 14 GPa (Fig. 3a). The M/H – T plots at different pressures (0–1.3 GPa) for Ca0.9Sr0.1Cy are shown in Fig. 1S of Supplementary Information, showing the positive pressure dependence. This sample contained three diffrenet phases, Ca0.98(1)Sr0.02(1)Cy, Ca0.58(6)Sr0.42(6)Cy and Ca0.35Sr0.65Cy, as shown previously, but the stoichiometry exhibiting the T c’s determined from the M/H – T plots (Figure S1) would be Ca0.58(6)Sr0.42(6)Cy which is almost the same as Ca0.5(2)Sr0.5(2)Cy. The T c – p plot obtained from M/H – T at 0–1.3 GPa is shown in the inset of Fig. 3c. Figure 3d shows the pressure dependence of R at 280 K for Ca0.5(2)Sr0.5(2)C6. The R rapidly increases above 10 GPa, which may be correlated with the change in electric transport above 12 GPa shown in Fig. 3a.
Figure 5a–c show the pressure dependence of three representative peaks of Ca0.5(2)Sr0.5(2)C6 in the XRD pattern. These peaks shifted to higher 2θ with an increase in pressure, indicating shrinkage of the unit cell. The 100 peak was observed up to 20 GPa, but suddenly disappeared above 20 GPa, while the 110 peak was clearly observed across the entire range of applied pressure (0–31 GPa). Moreover, the 112 peak quickly disappeared above 8.6 GPa. In Ca0.6K0.4C8, the 004 peak completely disappeared at 16 GPa13, which was assigned to the structural change from the KC8 structure to a non-graphite type structure. The disappearance of the 112 peak at 10 GPa would be attributed to the vanishing of the long-range order of graphite, such as the graphite – non-graphite transition found at around 16 GPa in Ca0.6K0.4C8 13. Furthermore, the change of electric transport (Fig. 3a) and the rapid increase in R (Fig. 3d) may be explained by considering a structural transition at around 10 GPa.
The pressure dependence of lattice constants a and c is plotted in Fig. 5d and e; the a was determined up to 20 GPa, while c determined up to 8.6 GPa because of the rapid disappearance of the 112 peak around 10 GPa. Both plots show a monotonic shrinkage of the unit cell with increasing pressure. The pressure dependence of d AA in Ca0.6K0.4C8 and Ca0.5(2)Sr0.5(2)C6 is shown in Fig. 6; that of Ca0.6K0.4C8 is taken from ref. 13. The behaviour of d AA – p is similar in both. Namely, the d AA approaches the d AA (=4.524 Å) of CaC6 with increasing pressure, and any Bragg peak disappears when reaching that d AA (above 13.7 GPa for Ca0.6K0.4C8 and above 8.6 GPa for Ca0.5(2)Sr0.5(2)C6). To sum up, any structural transition may take place when the d AA reaches the threshold value of d AA.
Discussion
In this paper, the most important issue is that a new class of superconducting binary-elements intercalated graphite was prepared by the intercalation of Sr and Ca. These are alkali-earth elements, and their ionic radii differ slightly (Sr2+: 1.18 Å for six coordination and Ca2+: 1.0 Å for six coordination). The ionic radii of some elements which can be intercalated to graphite are shown in Table 1, in which they were taken form ref. 28. On the other hand, the crystal structure is different between CaC6 and SrC6, in which the former takes the rhombohedral structure (space group No. 166, R \(\bar{3}\)m)2, while the latter takes the hexagonal structure (space group No. 194, P63/mmc)24. In both crystals, the graphene sheets stack in AAA form, but location of Ca or Sr is different; AαAβAγA for CaC6, and AαAβA for SrC6. Previously, we successfully made the superconducting CaxK1−xCy materials which consist of alkali and alkali earth elements. The ionic radii of Ca and K are 1.0 Å (for six coordination) and 1.38 Å (for six coordination), respectively, which are quite different. The crystal of KC8 takes face-centered orthorhombic structure (space group No. 70, Fddd), in which the stacking form is AαAβAγAδA, different from that of CaC6. Regardless of such a large difference between CaC6 and KC8, CaxK1−xCy was successfully formed.
On the other hand, we tried to fabricate CaxYb1−xCy, but the M/H – T plot showed a complete phase separation of CaC6 (T c = 11.5 K) and YbC6 (T c = 6.7 K), as seen from Fig. 7. The crystal structure of YbC6 is the same as that of SrC6. The ionic radius of Yb is 1.02 Å for six coordination, which is the same as that of Ca. Nevertheless, the CaxYb1−xCy could not be realized thus far. The liquid alloy method has been used for the preparation of binary-elements intercalated graphites, and the YbC6 and CaC6 phases were separately generated in the preparation of CaxYb1−xCy, suggesting both elements are melted. Therefore, we can rule out the possibility of no melting of either element.
Here, we focus on the fact that the element with the larger ionic radius dominates the crystal structure, i.e., the SrC6 structure in CaxSr1−xCy and the KC8 structure in CaxK1−xCy. Furthermore, the d AA in binary-elements intercalated graphite is the same as that of a crystal lattice consisting solely of an element with larger ionic radius; the d AA (=c /2 = 4.91 Å (c = 9.81 Å) or 4.925 Å (c = 9.85(8) Å) of CaxSr1−xCy is the same as that (=c/2 = 4.95 Å) of SrC6, and the d AA = (c /4 = 5.40 Å) of CaxK1−xC8 is the same as that (=c/4 = 5.35 Å)23 of KC8, as seen from Fig. 2 of ref. 23. These facts may point to a scenario in which the crystal lattice formed by the element with larger ionic radius is subsequently doped with the other element with smaller ionic radius. Based on this scenario, we can propose suitable combinations for the superconducting binary-elements or ternary-elements intercalated graphites, i.e., the binary-elements graphites must be realized using Cs and Ca, or Cs and Yb, because of the larger difference in ionic radii (Cs+: 1.67 Å for six coordination), and for the ternary-elements superconductors the combination of Ca (or Yb), Sr (or K) and Cs are probably suitable. The crystal structure of the binary- and ternary-elements intercalated graphites suggested above would be the CsC8-type structure, because the CsC8 phase is formed with the CsC8 structure29.
Methods
Sample preparation and characterization
The CaxSr1−xCy samples were prepared using the liquid-alloy method. Ca and Sr metals were mixed in appropriate molar ratios and placed in an iron vessel with Li. The molar ratio of Li was the same as the sum of Ca and Sr. The vessel was then heated to 350 °C, at which temperature the Ca/Sr/Li alloy was completely melted. The HOPG was immersed in the molten Ca/Sr/Li alloy for approximately one week. The whole preparation was performed in an Ar-filled glove box (O2 and H2O concentrations were maintained below 0.1 ppm). The M/H – T curves of the CaxSr1−xCy samples were measured with a SQUID magnetometer (Quantum Design, MPMS2). All XRD patterns at 0–31 GPa were measured at 295 K using synchrotron radiation (λ = 0.68841 Å) at BL12B2 of SPring-8. The simulated XRD patterns for LiC6, CaC6 and SrC6 made using the VESTA program30 were employed for the analyses of XRD patterns.
The diamond anvil cell was used for the measurements, and the Ca0.5(2)Sr0.5(2)C6 sample was placed in the diamond anvil cell without any exposure of the sample to air, as is described below. A 300-μm-thick stainless steel gasket with a 160-μm diameter hole was placed on a diamond with a 400-μm culet, and the sample was introduced into the hole. The sample was covered with daphne oil (Idemitsu Co., Ltd., Daphne 7373) as the pressure medium. Finally the sample was pressed by another diamond. The pressure was monitored by the fluorescence peak of a piece of ruby set in the DAC. The pressure dependence of the M/H – T plot for CaxSr1−xCy was measured using the above SQUID equipment in which the sample was placed in a piston-cylinder cell; the pressure medium was the same daphne oil as above. Meanwhile, the pressure dependence of the R – T plots was measured in four-terminal measurement mode; the used sample was identified to be Ca0.5(2)Sr0.5(2)C6. The sample was placed in a diamond anvil cell (DAC); the pressure medium was NaCl. Details of sample-setting for the M/H – T and R – T measurements at high pressure are described elsewhere13. The R was recorded using an AC resistance-bridge (Lakeshore, 370-type Resistance Bridge), limiting the applied current to less than 100 µA. The sample was cooled using liquid He, and the temperature was controlled with a temperature controller (Oxford, ITC503 Temperature Controller).
References
Weller, T. E., Ellerby, M., Saxena, S. S., Smith, R. P. & Skipper, N. T. Superconductivity in the intercalated graphite compounds C6Yb and C6Ca. Nat. Phys. 1, 39–41 (2005).
Emery, N. et al. Superconductivity of bulk CaC6. Phys. Rev. Lett. 95, 087003 (2005).
Gauzzi, A. et al. Enhancement of superconductivity and evidence of structural instability in intercalated graphite CaC6 under high pressure. Phys. Rev. Lett. 98, 067002 (2007).
Hannay, N. B. et al. Superconductivity in graphitic compounds. Phys. Rev. Lett. 14, 225–226 (1965).
Koike, Y., Suematsu, H., Higuchi, K. & Tanuma, S. Superconductivity in graphite-alkali metal intercalation compounds. Physica 99B, (503–508 (1980).
Kim, J. S., Boeri, L., O’Brien, J. R., Razavi, F. S. & Kremer, R. K. Superconductivity in heavy alkaline-earth intercalated graphites. Phys. Rev. Lett. 99, 027001 (2007).
Heguri, S. et al. Superconductivity in the graphite intercalation compound BaC6. Phys. Rev. Lett. 114, 247201 (2015).
Alexander, M. G. & Goshorn, D. P. Synthesis and low temperature specific heat of the graphite intercalation compounds KHgC4 and KHgC8. Synth. Met. 2, 203–211 (1980).
Pendrys, L. A. et al. Superconductivity of the graphite intercalation compounds KHgC8 and RbHgC8. Solid. State. Commun. 38, 677–681 (1981).
Wachnik, R. A., Pendrys, L. A., Vogel, F. L. & Lagrange, P. Superconductivity of graphite intercalated with thallium alloys. Solid. State. Commun. 43, 5–8 (1982).
Lagrange, P., Bendriss-Rerhrhaye, A., Mareche, J. F. & Mcrae, E. Systhesis and electrical properties of some new ternary graphite intercalation compounds. Synth. Met. 12, 201–206 (1985).
Emery, N. et al. Superconductivity in Li3Ca2C6 intercalated graphite. J. Solid. State. Chem. 179, 1289–1292 (2006).
Nguyen, H. T. L. et al. Fabrication of new superconducting materials, CaxK1−xCy (0 < x < 1). Carbon 100, 641–646 (2016).
Akrap, A. et al. C6Yb and graphite: A comparative high-pressure transport study. Phys. Rev. B 76, 045426 (2007).
Delong, L. E. et al. Observation of anomalies in the pressure dependence of the superconducting transition temperature of potassium-based graphite intercalation compounds. Phys. Rev. B 26, 6315–6318 (1982).
Kim, J. S., Boeri, L., Kremer, R. K. & Razavi, F. S. Effect of pressure on superconducting Ca-intercalated graphite CaC6. Phys. Rev. B 74, 214513 (2006).
Gauzzi, A. et al. Maximum T c at the verge of a simultaneous order-disorder and lattice-softening transition in superconducting CaC6. Phys. Rev. B 78, 064506 (2008).
Calandra, M. & Mauri, F. Theoretical explanation of superconductivity in C6Ca. Phys. Rev. Lett. 95, 237002 (2005).
Yang, S.-L. et al. Superconducting graphene sheets in CaC6 enlabled by phonon-mediated interband interactions. Nat. Commun. 5, 3493 (2014).
Rahnejat, K. C. et al. Charge density waves in the graphene sheets of the superconductor CaC6. Nat. Commun. 2, 558 (2011).
Profeta, G., Calandra, M. & Mauri, F. Phonon-mediated superconductivity in graphene by lithium deposition. Nat. Phys. 8, 131–134 (2012).
Chapman, J. et al. Superconductivity in Ca-doped graphene laminates. Sci. Rep. 6, 23254 (2016).
Hérold, A., Billaud, D., Guérard, D., Lagrange, P. & Makrini, M. E. Intercalation of metals and alloys into graphite. Physica B 105, 253–260 (1981).
Guérard, D. & Hérold, A. Chimie Macromoléculaire. Synthèse directe de composés d’insertion du strontium dans le graphite. C. R. Seances Acad. Sci. C 280, 729–730 (1975).
Kganyago, K. R. & Ngoepe, P. E. Structural and electronic properties of lithium intercalated graphite LiC6. Phys. Rev. B 68, 205111 (2003).
Zhao, Y.-X. & Spain, I. L. X-ray diffraction data for graphite to 20 GPa. Phys. Rev B 40, 993–987 (1989).
Debessai, M. et al. Superconductivity for CaC6 to 32 GPa hydrostatic pressure. Phys. Rev. B 82, 132502 (2010).
Shannon, R. D. Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides. Acta Cryst. A 32, 751–767 (1976).
Guerard, D., Lagrange, P., Mohamed, E. M. & Hérold, A. Etude structurale du graphiture I de cesium. Carbon 16, 285–290 (1978).
Momma, K. & Izumi, F. An integrated three-dimensional visualization system VESTA using wxWidgets. Commission on Crystallogr. Comput. 7, 106–119 (2006).
Acknowledgements
This study was partly supported by Grants-in-aid (26105004, 26400361 and 15K05477) from MEXT and by the Program for Promoting the Enhancement of Research Universities. This work was partly supported by JST ACT-C Grant Number JPMJCR12YW, Japan. The XRD measurements were performed at the proposal of 2016B4131 of SPring-8.
Author information
Authors and Affiliations
Contributions
Y.K. suggested the idea for this research, and designed this study with S.N., who prepared and characterised all of the CaxSr1−xCy samples with the assistance of X.M. and T.T. The X-ray diffraction of the sample was measured at BL12B2 of SPring-8 by T.T., H.Y., H.I., Y.-F.L. and Y.K; the diamond anvil cell used for pressure-dependent X-ray diffraction was designed by H.Y. The pressure-dependent M/H – T measurement was done by S.N. and T.M. EDX measurement was done by S.N. and X.Y. Pressure-dependent R – T measurement was made by H.F., M.H., K.S., T.K. and S.N.; the experimental setup for R – T measurement was designed by K.S. and T.K. All data were analysed by S.N., T.T. and X.Y. under continuous discussion with Y.K. and H.G. The manuscript was prepared by Y.K. with discussions with all authors.
Corresponding author
Ethics declarations
Competing Interests
The authors declare that they have no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Nishiyama, S., Fujita, H., Hoshi, M. et al. Preparation and characterization of a new graphite superconductor: Ca0.5Sr0.5C6 . Sci Rep 7, 7436 (2017). https://doi.org/10.1038/s41598-017-07763-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-017-07763-y
This article is cited by
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.