Introduction

Blind quantum computation (i.e. BQC)1,2,3,4,5,6,7 is still a challenging research field, where a client has not enough quantum computability, and delegates her quantum computing to the servers who have full-advanced quantum computers. In long-distance BQC, quantum entanglement plays an important role and three mainly blind entangled states have already been studied which are blind brickwork state1, blind topological state2 and Affleck-Kennedy-LiebTasaki (i.e. AKLT) state3. Some BQC protocols1, 4,5,6 are based on the blind brickwork state which is proposed by Broadbent et al.1. Later, Barz et al.7 demonstrated the blindness of the brickwork state. Broadbent et al.1 in 2009 proposed a single-server BQC protocol based on single-qubit states and double-server BQC protocol based on the entanglement swapping of Bell states. However, the quantum entanglement of Bell states in double-server BQC protocol1 will suffer quantum channel loss due to the influence of noisy channel. To solve this problem, Morimae and Fujii4 proposed a method of entanglement distillation to extract high-fidelity Bell states, meanwhile its security can also be guaranteed. Li et al.5 proposed a triple-server BQC protocol based on Bell states. Sheng and Zhou6 proposed a double-server BQC protocol based on Bell states, where the deterministic entanglement distillation can remove the noise that transforms pure entangled states into mixed entangled states. As we can see that the aims of BQC protocols1, 4,5,6 are all to obtain the single-qubit states \(|{\pm }_{{\theta }_{i}}\rangle \) with \({\theta }_{i}\in \{0,\frac{\pi }{4},\frac{2\pi }{4},\ldots ,\frac{7\pi }{4}\}\) to create the blind brickwork states1. The other two blind graph states2, 3 can also be used to perform BQC successfully. The Raussendorf-Harrington-Goyal (i.e. RHG) lattice2, which the blindness is guaranteed in a topological manner, is used to perform four quantum measurements {X, Y, Z, T} only known by clients. Compared with the cluster states, AKLT states can be prepared efficiently and simply in linear optics with biphotons8. Recently, more and more interesting BQC protocols are proposed9,10,11,12,13,14,15,16,17,18. In BQC, the quantum channel noise is still an urgent problem. Previous works4, 6, 14 have studied quantum channel noises in BQC protocols. For example, Takeuchi et al.14 proposed three BQC protocols based on decoherence-free subspace (i.e. DFS) to resist the collective noise of quantum channel.

The new BQC protocol is based on maximally GHZ entangled states, where there are three participants (a client Alice, two servers Bob and Charlie). The BQC protocol is divided into four steps. First, Bob prepares initial GHZ states, remains one photon and sends other two photons to Alice. Alice disturbs the orders of two photons and sends to Charlie. Second, Bob and Charlie perform entanglement concentration to get ideal maximally entangled states, where two identical less-entangled states can be used to concentrate a maximally entangled state by two-step parity check and project measurements. Third, Bob performs Pauli operations on his photons under Alice’s instruction. Then Charlie performs measurement on one photon with the basis {|0〉, |1〉}. Alice randomly chooses θ i \((\in \,\{\mathrm{0,}\frac{\pi }{4},\ldots ,\frac{7\pi }{4}\})\) and sends to Charlie. Charlie performs measurement on the other photon and Bob gets the single-qubit. Finally, Alice and Bob perform single-server BQC protocol.

This BQC protocol has four contributions. First, two servers can communication with each other without degrading the security. Second, it does not need a trusted center. The task of preparing initial entangled states can be assigned to Bob. Third, Bob and Charlie don’t need to exchange their classical information. If they collude, they don’t know any information about Alice’s inputs, outputs and algorithms. The last one, entanglement concentration can be used to remove the channel noise.

Results

BQC protocol based on maximally GHZ entangled states

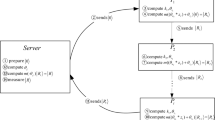
Photons are the best physical systems for the long-distance transmission of entangled states, thus entangled photons states are used as quantum information carriers in BQC. In this BQC protocol, we use |0〉 and |1〉 to express photons. In entanglement concentration, we use |H〉 and |V〉 to express photons, where |H〉 is equal to |0〉 and |V〉 is equal to |1〉. In this section, we propose the BQC protocol based on maximally GHZ photons entangled states \({|GHZ\rangle }_{{A}_{j}{B}_{j}{C}_{j}}=\frac{1}{2}(|001\rangle +|010\rangle +|100\rangle +|111\rangle )\) (\(j=1,2,\ldots ,n\)) (Fig. 1). The cross-Kerr nonlinear can be used to construct a CNOT gate in ref. 19. There are also many other methods to realize it19,20,21,22,23. In the BQC protocol, we suppose that these quantum devices are all ideal. The client owns quantum channels with two servers and quantum disturbing device.

  • Bob generates enough maximally GHZ entangled states \({|GHZ\rangle }_{{A}_{j}{B}_{j}{C}_{j}}\), where the subscripts A j , B j and C j represents photons A j , B j and C j . Bob keeps photons sequences S B  = [B 1, B 2, …, B n ] and sends photons sequences S A  = [A 1, A 2, …, A n ] and S C  = [C 1, C 2, …, C n ] to Alice successively. After receiving photons sequences, Alice disturbs the order of photons sequences S A and S C . The reordered photons sequences are rewritten as S A′ = [\({A}_{1}^{\prime}\), \({A}_{2}^{\prime}\), …, \({A}_{n}^{\prime}\)] and S C′ = [\({C}_{1}^{\prime}\), \({C}_{2}^{\prime}\), …, \({C}_{n}^{\prime}\)], meanwhile \({|GHZ\rangle }_{{A}_{j}{B}_{j}{C}_{j}}\) is remarked as \({|GHZ\rangle }_{{A}_{{t}_{2}}^{{\prime}}{B}_{j}{C}_{{t}_{1}}^{{\prime}}}({t}_{1},{t}_{2}\in \{1,2,\cdots ,n\})\). The orders of photons sequences S A′ and S C′ are different and only known by Alice. Then Alice sends photons sequences S A′ and S C′ to Charlie. Due to the effect of quantum channel noise, the maximally entangled states \({|GHZ\rangle }_{{A}_{{t}_{2}}^{\prime }{B}_{j}{C}_{{t}_{1}}^{\prime }}\) evolve into less-entangled states \({|GHZ^{\prime} \rangle }_{{A}_{{t}_{2}}^{\prime }{B}_{j}{C}_{{t}_{1}}^{\prime}}=\alpha |001\rangle +\beta |010\rangle +\delta |100\rangle +\eta |111\rangle \), where |α|2 + |β|2 + |δ|2 + |η|2 = 1. In order to get states \({|GHZ\rangle }_{{A}_{{t}_{2}}^{\prime }{B}_{j}{C}_{{t}_{1}}^{\prime }}\), Bob and Charlie firstly perform entanglement concentration.

  • Bob performs one of four operations {I, σ x , iσ y , σ z } randomly chosen by Alice on photons B j and \({|GHZ\rangle }_{{A}_{{t}_{2}}^{\prime }{B}_{j}{C}_{{t}_{1}}^{\prime }}\) states evolve into one of four states \(\{{|GH{Z}_{1}\rangle }_{{A}_{{t}_{2}}^{\prime }{B}_{j}{C}_{{t}_{1}}^{\prime }}\), \({|GH{Z}_{2}\rangle }_{{A}_{{t}_{2}}^{\prime }{B}_{j}{C}_{{t}_{1}}^{\prime }}\), \({|GH{Z}_{3}\rangle }_{{A}_{{t}_{2}}^{\prime }{B}_{j}{C}_{{t}_{1}}^{\prime }}\), \({|GH{Z}_{4}\rangle }_{{A}_{{t}_{2}}^{\prime }{B}_{j}{C}_{{t}_{1}}^{\prime }}\}\).

$$\begin{array}{rcl}\mathop{\to }\limits^{I}{|GH{Z}_{1}\rangle }_{{A}_{{t}_{2}}^{\prime }{B}_{j}{C}_{{t}_{1}}^{\prime }} & = & \frac{1}{2}(|001\rangle +|010\rangle +|100\rangle +|111\rangle )\\ & = & \frac{1}{2\sqrt{2}}({|{\psi }^{+}\rangle }_{{A}_{{t}_{2}}^{\prime }{B}_{j}}{|0\rangle }_{{C}_{{t}_{1}}^{\prime }}+{|{\varphi }^{+}\rangle }_{{A}_{{t}_{2}}^{\prime }{B}_{j}}{|1\rangle }_{{C}_{{t}_{1}}^{\prime }}),\\ \mathop{\to }\limits^{{\sigma }_{x}}{|GH{Z}_{2}\rangle }_{{A}_{{t}_{2}}^{\prime }{B}_{j}{C}_{{t}_{1}}^{\prime }} & = & \frac{1}{2}(|011\rangle +|000\rangle +|110\rangle +|101\rangle )\\ & = & \frac{1}{2\sqrt{2}}({|{\varphi }^{+}\rangle }_{{A}_{{t}_{2}}^{\prime }{B}_{j}}{|0\rangle }_{{C}_{{t}_{1}}^{\prime }}+{|{\psi }^{+}\rangle }_{{A}_{{t}_{2}}^{\prime }{B}_{j}}{|1\rangle }_{{C}_{{t}_{1}}^{\prime }}),\\ \mathop{\to }\limits^{i{\sigma }_{y}}{|GH{Z}_{3}\rangle }_{{A}_{{t}_{2}}^{\prime }{B}_{j}{C}_{{t}_{1}}^{\prime }} & = & \frac{1}{2}(-\,|011\rangle +|000\rangle -|110\rangle +|101\rangle )\\ & = & \frac{1}{2\sqrt{2}}({|{\varphi }^{-}\rangle }_{{A}_{{t}_{2}}^{\prime }{B}_{j}}{|0\rangle }_{{C}_{{t}_{1}}^{\prime }}-{|{\psi }^{-}\rangle }_{{A}_{{t}_{2}}^{\prime }{B}_{j}}{|1\rangle }_{{C}_{{t}_{1}}^{\prime }}),\\ \mathop{\to }\limits^{{\sigma }_{z}}{|GH{Z}_{4}\rangle }_{{A}_{{t}_{2}}^{\prime }{B}_{j}{C}_{{t}_{1}}^{\prime }} & = & \frac{1}{2}(|001\rangle -|010\rangle +|100\rangle -|111\rangle )\\ & = & \frac{1}{2\sqrt{2}}(-\,{|{\psi }^{-}\rangle }_{{A}_{{t}_{2}}^{\prime }{B}_{j}}{|0\rangle }_{{C}_{{t}_{1}}^{\prime }}+{|{\varphi }^{-}\rangle }_{{A}_{{t}_{2}}^{\prime }{B}_{j}}{|1\rangle }_{{C}_{{t}_{1}}^{\prime }}).\end{array}$$
(1)

Since the orders of sequences S A′, S B and S C′ are different, both Bob and Charlie cannot know which state \({|GH{Z}_{u}\rangle }_{{A}_{{t}_{2}}^{\prime }{B}_{j}{C}_{{t}_{1}}^{\prime }}\) (u∈{1, 2, 3, 4}) they shared.

  • Charlie performs measurement on photons \({C}_{{t}_{1}}^{\prime }\) using the basis {|0〉, |1〉} under the guidance of Alice. Alice randomly chooses \({\theta }_{i}\in \{0,\pi \mathrm{/4},2\pi \mathrm{/4},\ldots ,7\pi \mathrm{/4}\}\) and sends to Charlie. Charlie performs measurement on the basis \(\{|0\rangle \pm {e}^{-i{\theta }_{i}}|1\rangle \}\) and Bob obtains photons states \(|{\pm }_{{\theta }_{i}+{c}_{i}\pi }\rangle \), where c i (∈{0, 1}) is Charlie’s measurement outcome. Because the orders of \({A}_{{t}_{2}}^{\prime }\) and B j are different, Bob can not know anything even if Charlie tells the value of θ i to Bob.

  • Alice, Bob and Charlie repeat (1–3) steps such that Bob obtains single-photon states \(\underset{i=1}{\overset{n}{\bigotimes }}|{\pm }_{{\theta }_{i}+{c}_{i}\pi }\rangle \) successfully. The remaining steps are the same as steps (2–3) of the BFK protocol1 or steps (2–5) of blind topological BQC protocol2. The blindness of graph states and the correctness of quantum computation have already been exhibited in refs 1 and 2 in detail.

Figure 1
figure 1

Schematic diagram of BQC protocol is based on maximally GHZ entangled states with z-basis ({|0〉, |1〉}) measurement M 1, basis \(|0\rangle \pm {e}^{-i{\theta }_{i}}|1\rangle \) measurement M 2, Pauli operations U, Bell measurement BM, Charlie’s measurement outcome c i . The order of photons sequences A j and C j (\(j\in \{1,2,3,\ldots ,n\}\)) are disturbed and rewritten as \({A}_{{t}_{2}}^{\prime }\) and \({C}_{{t}_{1}}^{\prime }\) (t 1, \({t}_{2}\in \{1,2,3,\ldots ,n\}\)). Photons \({A}_{{t}_{2}}^{\prime }\) and \({C}_{{t}_{1}}^{\prime }\) belong to Charlie, and B j belongs to Bob, where \({A}_{{t}_{2}}^{\prime }\), B j and \({C}_{{t}_{1}}^{\prime }\) (t 1 ≠ t 2 ≠ j) belong to a GHZ state.

Full size image

In the step 1 of this BQC, entanglement concentration is used to remove the noise. In the following, the process of entanglement concentration is showed with optical system.

Entanglement concentration of pure maximally GHZ entangled state

In a practical transmission, there exist two kinds of quantum channel noises, i.e. pure maximally entangled states evolve into mixed states or less-entangled states. Entanglement purification24,25,26,27,28 is applied to extract high-fidelity maximally entangled states from mixed entangled states. Entanglement concentration29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45 is often used to distill less-entangled states into pure maximally entangled states by local operations and classical communication (i.e. LOCC). Bennett et al.29 firstly proposed an entanglement concentration protocol by using Schmidt projection. In 2003, Zhao et al.42 not only demonstrated the entanglement concentration scheme in ref. 30 but also verified a quantum repeater in experiment. Li et al.39 proposed two protocols to concentrate hyper-entangled GHZ states by using a single-photon state of two freedoms and two less-entangled states respectively. Sheng et al.32 proposed to concentrate arbitrary W states by using two steps. Afterwards, a universal concentration scheme of an arbitrary less-entangled N-photon W state is proposed in ref. 43. Here, we consider a special quantum channel noise, i.e. pure maximally entangled states evolve into less-entangled states, which can be distilled by entanglement concentration. In the following, we give the entanglement concentration of GHZ states that were experimentally prepared in refs 46,47,48.

The first round of entanglement concentration

In the BQC, the maximally GHZ states can be rewritten in the form of

$${|GHZ\rangle }_{{a}_{1}{b}_{1}{c}_{1}}=\frac{1}{2}(|HHV\rangle +|HVH\rangle +|VHH\rangle +|VVV\rangle ),$$
(2)

where we define |H〉 = |0〉 and |V〉 = |1〉. The subscripts a 1, b 1 and c 1 represent the spatial-mode of photons \({A}_{{t}_{2}}^{\prime }\), B j and \({C}_{{t}_{1}}^{\prime }\). We consider the noisy model that pure maximally entangled states evolve pure less entangled states. Suppose less-entangled pure photons states are

$${|GHZ^{\prime} \rangle }_{{a}_{1}{b}_{1}{c}_{1}}=\alpha |HHV\rangle +\beta |HVH\rangle +\delta |VHH\rangle +\eta |VVV\rangle ,$$
(3)

where four real numbers α, β, δ, η satisfy |α|2 + |β|2 + |δ|2 + |η|2 = 1.

Two identical less-entangled states, which the parameters are all unknown, can distill a maximally entangled state in Eq. (2). The schematic of entanglement concentration is shown in Fig. 2. Here, only Alice knows whether entanglement concentration is successful and the correct orders of \({A}_{{t}_{2}}^{{\prime }}\), B j and \({C}_{{t}_{1}}^{{{\rm{\prime }}}}\).

Figure 2
figure 2

The schematic diagram of polarization-entanglement concentration. The sources is used to produce polarization-entangled states. Photons a 1(a 2) and c 1(c 2) belong to Charlie, where Bob retains photons b 1(b 2). HWP is half-wave plate which HWP 90° flips the horizontal and vertical polarization states. HWP 45° just likes a Hadamard operation to rotate horizontal and vertical polarization states. The polarizing beam splitters (PBSs) are used to transmit horizontal polarization |H〉 and reflect vertical polarization |V〉. QND i (with i = 1, 2, 3) represents quantum nondemolition detections. Detectors \({D}_{{B}_{1}}\) and \({D}_{{B}_{2}}\) belong to Bob, \({D}_{{A}_{1}}\), \({D}_{{A}_{2}}\), \({D}_{{C}_{1}}\) and \({D}_{{C}_{2}}\) belong to Charlie.

Full size image

After passing HWP 90°, the state \({|GHZ^{\prime} \rangle }_{{a}_{1}{b}_{1}{c}_{1}}\) evolves to

$${|GHZ^{\prime} \rangle }_{{a}_{2}{b}_{2}{c}_{2}}=\alpha |VVH\rangle +\beta |VHV\rangle +\delta |HVV\rangle +\eta |HHH\rangle ,$$
(4)

where polarization photons a 1, b 1 and c 1 are flipped and relabeled as a 2, b 2 and c 2.

The entanglement concentration is divided into two steps. In the first step, the system composed of six photons is

$$\begin{array}{rcl}{|{\rm{\Psi }}\rangle }_{{a}_{1}{b}_{1}{c}_{1}{a}_{2}{b}_{2}{c}_{2}} & = & {|GHZ^{\prime} \rangle }_{{a}_{1}{b}_{1}{c}_{1}}\otimes {|GHZ^{\prime} \rangle }_{{a}_{2}{b}_{2}{c}_{2}}\\ & = & [{\alpha }^{2}|HHVVVH\rangle +{\beta }^{2}|HVHVHV\rangle \\ & & +{\delta }^{2}|VHHHVV\rangle +{\eta }^{2}|VVVHHH\rangle ]\\ & & +[\alpha \beta (|HHVVHV\rangle +|HVHVVH\rangle )\\ & & +\delta \eta (|HHVHVV\rangle +|VHHVVH\rangle )]\\ & & +[\alpha \delta (|HVHHHH\rangle +|VVVVHV\rangle )\\ & & +\beta \eta (|VHHHHH\rangle +|VVVHVV\rangle )]\\ & & +[\alpha \eta |HHVHHH\rangle +|VVVVVH\rangle \\ & & +\beta \delta (|HVHHVV\rangle +|VHHVHV\rangle )]\end{array}$$
(5)

After both a 1 and a 2 (b 1 and b 2, c 1 and c 2) pass parity check device (Fig. 3), Bob and Charlie can get some specific quantum state by choosing phase shifts. Here, we suppose that Bob and Charlie are honest to perform the entanglement concentration. The concrete process of the parity check device is given in Methods.

Figure 3
figure 3

Schematic diagram of QND49. ±θ = χt represents the cross-Kerr nonlinearity media that introduces the phase shift θ when photons pass through the media. |χ〉 〈χ| is homodyne measurement that can distinguish different phase shifts. The signal photons |α 1〉, |α 2〉 and |α 3〉 are related to a 1 and a 2, b 1 and b 2, c 1 and c 2 respectively. Here x 1 and x 2 can be specifically expressed as a 1 and a 2 (b 1 and b 2, c 1 and c 2).

Full size image

For b 1 and b 2, a 1 and a 2, c 1 and c 2, if Bob and Charlie all choose ±2θ phase shifts of odd-parity check states, the state is

$$\begin{array}{rcl}{|{\phi }_{1}\rangle }_{{a}_{1}{b}_{1}{c}_{1}{a}_{2}{b}_{2}{c}_{2}} & = & {\alpha }^{2}|HHV\rangle |VVH\rangle +{\beta }^{2}|HVH\rangle |VHV\rangle \\ & & +{\delta }^{2}|VHH\rangle |HVV\rangle +{\eta }^{2}|VVV\rangle |HHH\rangle \end{array}$$
(6)

with the probability \({p}_{11}^{1}={\alpha }^{4}+{\beta }^{4}+{\delta }^{4}+{\eta }^{4}\), where \({p}_{vj}^{m}\) represents the probability of obtaining \({|{\phi }_{1}\rangle }_{{a}_{1}{b}_{1}{c}_{1}{a}_{2}{b}_{2}{c}_{2}}\) with the number of rounds v \((v=1,2,3,\ldots ,k)\), the number of steps j (j = 1, 2) in vth round and the quantum state m (m = 1, 2, 3, 4) in jth step of vth round.

If Bob chooses 0 phase shift of even-parity check states for b 1 and b 2, Charlie chooses 0 phase shift of even-parity check states for c 1 and c 2, and ±2θ phase shift of odd-parity check states for a 1 and a 2, the state is

$$\begin{array}{rcl}{|{\phi }_{2}\rangle }_{{a}_{1}{b}_{1}{c}_{1}{a}_{2}{b}_{2}{c}_{2}} & = & \alpha \beta (|HHV\rangle |VHV\rangle +|HVH\rangle |VVH\rangle )\\ & & +\delta \eta (|VHH\rangle |HHH\rangle +|VVV\rangle |HVV\rangle )\end{array}$$
(7)

with the probability \({p}_{11}^{2}=\mathrm{2(}{\alpha }^{2}{\beta }^{2}+{\delta }^{2}{\eta }^{2})\).

If Bob chooses ±2θ phase shift of odd-parity check states for b 1 and b 2, Charlie chooses 0 phase shifts of even-parity check states for a 1 and a 2, c 1 and c 2, the state is

$$\begin{array}{rcl}{|{\phi }_{3}\rangle }_{{a}_{1}{b}_{1}{c}_{1}{a}_{2}{b}_{2}{c}_{2}} & = & \alpha \delta (|HHV\rangle |HVV\rangle +|VHH\rangle |VVH\rangle )\\ & & +\beta \eta (|HVH\rangle |HHH\rangle +|VVV\rangle |VHV\rangle )\end{array}$$
(8)

with the probability \({p}_{11}^{3}=\mathrm{2(}{\alpha }^{2}{\delta }^{2}+{\beta }^{2}{\eta }^{2})\).

If Bob chooses 0 phase shift of even-parity check state for b 1 and b 2, Charlie chooses ±2θ phase shift of odd-parity check states for c 1 and c 2, and 0 phase shift of even-parity check states for a 1 and a 2, the state is

$$\begin{array}{rcl}{|{\phi }_{4}\rangle }_{{a}_{1}{b}_{1}{c}_{1}{a}_{2}{b}_{2}{c}_{2}} & = & \alpha \eta (|HHV\rangle |HHH\rangle +|VVV\rangle |VVH\rangle )\\ & & +\beta \delta (|HVH\rangle |HVV\rangle +|VHH\rangle |VHV\rangle )\end{array}$$
(9)

with the probability \({p}_{11}^{4}=\mathrm{2(}{\alpha }^{2}{\eta }^{2}+{\beta }^{2}{\delta }^{2})\).

We give an example for PBSs measurement. After passing through HWP 45°, \({|{\phi }_{1}\rangle }_{{a}_{1}{b}_{1}{c}_{1}{a}_{2}{b}_{2}{c}_{2}}\) evolves into

$$\begin{array}{ll}\to & {({\alpha }^{2}|HHV\rangle +{\beta }^{2}|HVH\rangle +{\delta }^{2}|VHH\rangle +{\eta }^{2}|VVV\rangle )}_{{a}_{1}{b}_{1}{c}_{1}}\\ & \times {(|HHH\rangle +|VVV\rangle )}_{{a}_{2}{b}_{2}{c}_{2}}\\ & +{({\alpha }^{2}|HHV\rangle -{\beta }^{2}|HVH\rangle -{\delta }^{2}|VHH\rangle +{\eta }^{2}|VVV\rangle )}_{{a}_{1}{b}_{1}{c}_{1}}\\ & \times {(|HHV\rangle +|VVH\rangle )}_{{a}_{2}{b}_{2}{c}_{2}}\\ & +{(-{\alpha }^{2}|HHV\rangle +{\beta }^{2}|HVH\rangle -{\delta }^{2}|VHH\rangle +{\eta }^{2}|VVV\rangle )}_{{a}_{1}{b}_{1}{c}_{1}}\\ & \times {(|HVH\rangle +|VHV\rangle )}_{{a}_{2}{b}_{2}{c}_{2}}\\ & +{(-{\alpha }^{2}|HHV\rangle -{\beta }^{2}|HVH\rangle +{\delta }^{2}|VHH\rangle +{\eta }^{2}|VVV\rangle )}_{{a}_{1}{b}_{1}{c}_{1}}\\ & \times {(|HVV\rangle +|VHH\rangle )}_{{a}_{2}{b}_{2}{c}_{2}}.\end{array}$$
(10)

If the detectors \({D}_{{A}_{1}}\), \({D}_{{B}_{1}}\), \({D}_{{C}_{1}}\) (or \({D}_{{A}_{2}}\), \({D}_{{B}_{2}}\), \({D}_{{C}_{2}}\)) are triggered, we will get

$${|{\phi }_{11}^{\mathrm{(1)}}\rangle }_{{a}_{1}{b}_{1}{c}_{1}}^{1}={\alpha }^{2}|HHV\rangle +{\beta }^{2}|HVH\rangle +{\delta }^{2}|VHH\rangle +{\eta }^{2}|VVV\rangle ,$$
(11)

where \({|{\phi }_{vj}^{(\gamma )}\rangle }_{{a}_{1}{b}_{1}{c}_{1}}^{m}\) represents the quantum state with the number of rounds v \((v=1,2,3,\ldots ,k)\), the number of steps j (j = 1, 2) in vth round, the quantum state m (m = 1, 2, 3, 4) in jth step of vth round, and the quantum state (γ) (γ = 1, 2, 3, 4) of PBSs measurement for the states \({|{\phi }_{\varepsilon }\rangle }_{{a}_{1}{b}_{1}{c}_{1}{a}_{2}{b}_{2}{c}_{2}}\) (ε = 1, 2, 3, 4).

If the detectors \({D}_{{A}_{1}}\), \({D}_{{B}_{1}}\), \({D}_{{C}_{2}}\) (or \({D}_{{A}_{2}}\), \({D}_{{B}_{2}}\), \({D}_{{C}_{1}}\)) are triggered, we get

$${|{\phi }_{11}^{\mathrm{(2)}}\rangle }_{{a}_{1}{b}_{1}{c}_{1}}^{1}={\alpha }^{2}|HHV\rangle -{\beta }^{2}|HVH\rangle -{\delta }^{2}|VHH\rangle +{\eta }^{2}|VVV\rangle .$$
(12)

Bob and Charlie perform unitary transformation \({\sigma }_{z}^{B}\otimes {\sigma }_{z}^{A}\) on photons a 1 and b 1 of state \({|{\phi }_{11}^{\mathrm{(2)}}\rangle }_{{a}_{1}{b}_{1}{c}_{1}}^{1}\) to get \({|{\phi }_{11}^{\mathrm{(1)}}\rangle }_{{a}_{1}{b}_{1}{c}_{1}}^{1}\).

If the detectors \({D}_{{A}_{1}}\), \({D}_{{B}_{2}}\), \({D}_{{C}_{1}}\) (or \({D}_{{A}_{2}}\), \({D}_{{B}_{1}}\), \({D}_{{C}_{2}}\)) are triggered, we will get

$${|{\phi }_{11}^{\mathrm{(3)}}\rangle }_{{a}_{1}{b}_{1}{c}_{1}}^{1}=-{\alpha }^{2}|HHV\rangle +{\beta }^{2}|HVH\rangle -{\delta }^{2}|VHH\rangle +{\eta }^{2}|VVV\rangle .$$
(13)

Charlie performs unitary transformation \({\sigma }_{z}^{A}\otimes {\sigma }_{z}^{C}\) on photons a 1 and c 1 of state \({|{\phi }_{11}^{\mathrm{(3)}}\rangle }_{{a}_{1}{b}_{1}{c}_{1}}^{1}\) to get \({|{\phi }_{11}^{\mathrm{(1)}}\rangle }_{{a}_{1}{b}_{1}{c}_{1}}^{1}\).

If the detectors \({D}_{{A}_{1}}\), \({D}_{{B}_{2}}\), \({D}_{{C}_{2}}\) (or \({D}_{{A}_{2}}\), \({D}_{{B}_{1}}\), \({D}_{{C}_{1}}\)) are triggered, we will get

$${|{\phi }_{11}^{\mathrm{(4)}}\rangle }_{{a}_{1}{b}_{1}{c}_{1}}^{1}=-{\alpha }^{2}|HHV\rangle -{\beta }^{2}|HVH\rangle +{\delta }^{2}|VHH\rangle +{\eta }^{2}|VVV\rangle .$$
(14)

Bob and Charlie perform unitary transformation \({\sigma }_{z}^{B}\otimes {\sigma }_{z}^{C}\) on photons b 1 and c 1 of state \({|{\phi }_{11}^{\mathrm{(4)}}\rangle }_{{a}_{1}{b}_{1}{c}_{1}}^{1}\) to get \({|{\phi }_{11}^{\mathrm{(1)}}\rangle }_{{a}_{1}{b}_{1}{c}_{1}}^{1}\).

For the three states \({|{\phi }_{2}\rangle }_{{a}_{1}{b}_{1}{c}_{1}{a}_{2}{b}_{2}{c}_{2}}\), \({|{\phi }_{3}\rangle }_{{a}_{1}{b}_{1}{c}_{1}{a}_{2}{b}_{2}{c}_{2}}\) and \({|{\phi }_{4}\rangle }_{{a}_{1}{b}_{1}{c}_{1}{a}_{2}{b}_{2}{c}_{2}}\), we have the similar results

$$\begin{array}{l}{|{\phi }_{11}^{\mathrm{(1)}}\rangle }_{{a}_{1}{b}_{1}{c}_{1}}^{2}=\alpha \beta (|HHV\rangle +|HVH\rangle )+\delta \eta (|VHH\rangle +|VVV\rangle ),\\ {|{\phi }_{11}^{\mathrm{(1)}}\rangle }_{{a}_{1}{b}_{1}{c}_{1}}^{3}=\alpha \delta (|HHV\rangle +|VHH\rangle )+\beta \eta (|HVH\rangle +|VVV\rangle ),\\ {|{\phi }_{11}^{\mathrm{(1)}}\rangle }_{{a}_{1}{b}_{1}{c}_{1}}^{4}=\alpha \eta (|HHV\rangle +|VVV\rangle )+\beta \delta (|HVH\rangle +|VHH\rangle ).\end{array}$$
(15)

The four quantum states \({|{\phi }_{11}^{\mathrm{(1)}}\rangle }_{{a}_{1}{b}_{1}{c}_{1}}^{1}\), \({|{\phi }_{11}^{\mathrm{(1)}}\rangle }_{{a}_{1}{b}_{1}{c}_{1}}^{2}\), \({|{\phi }_{11}^{\mathrm{(1)}}\rangle }_{{a}_{1}{b}_{1}{c}_{1}}^{3}\) and \({|{\phi }_{11}^{\mathrm{(1)}}\rangle }_{{a}_{1}{b}_{1}{c}_{1}}^{4}\) are not destroyed by quantum non-demolition detections. They are used as the initial states in the second step of the first round and rewritten as \({|{\phi }_{12}\rangle }_{{a}_{1}{b}_{1}{c}_{1}}^{1}\), \({|{\phi }_{12}\rangle }_{{a}_{1}{b}_{1}{c}_{1}}^{2}\), \({|{\phi }_{12}\rangle }_{{a}_{1}{b}_{1}{c}_{1}}^{3}\) and \({|{\phi }_{12}\rangle }_{{a}_{1}{b}_{1}{c}_{1}}^{4}\).

In the second step, for quantum state

$${|{\phi }_{12}\rangle }_{{a}_{1}{b}_{1}{c}_{1}}^{1}=\tfrac{1}{\sqrt{{\alpha }^{4}+{\beta }^{4}+{\delta }^{4}+{\eta }^{4}}}({\alpha }^{2}|HHV\rangle +{\beta }^{2}|HVH\rangle +{\delta }^{2}|VHH\rangle +{\eta }^{2}|VVV\rangle ),$$
(16)

photons are all flipped by HWP 90° and relabeled as a 2, b 2 and c 2. We will get

$${|{\phi }_{12}\rangle }_{{a}_{2}{b}_{2}{c}_{2}}^{1}=\tfrac{1}{\sqrt{{\alpha }^{4}+{\beta }^{4}+{\delta }^{4}+{\eta }^{4}}}({\alpha }^{2}|VVH\rangle +{\beta }^{2}|VHV\rangle +{\delta }^{2}|HVV\rangle +{\eta }^{2}|HHH\rangle ).$$
(17)

After parity checks and PBSs measurement, we obtain four quantum states

$$\begin{array}{l}{|{\phi }_{12}^{\mathrm{(1)}}\rangle }_{{a}_{1}{b}_{1}{c}_{1}}^{1}=\tfrac{1}{{\alpha }^{4}+{\beta }^{4}+{\delta }^{4}+{\eta }^{4}}[{\alpha }^{4}|HHV\rangle +{\beta }^{4}|HVH\rangle +{\delta }^{4}|VHH\rangle +{\eta }^{4}|VVV\rangle ],\\ {|{\phi }_{12}^{\mathrm{(2)}}\rangle }_{{a}_{1}{b}_{1}{c}_{1}}^{1}=\tfrac{1}{{\alpha }^{4}+{\beta }^{4}+{\delta }^{4}+{\eta }^{4}}[{\alpha }^{2}{\beta }^{2}(|HHV\rangle +|HVH\rangle )+{\delta }^{2}{\eta }^{2}(|VHH\rangle +|VVV\rangle )],\\ {|{\phi }_{12}^{\mathrm{(3)}}\rangle }_{{a}_{1}{b}_{1}{c}_{1}}^{1}=\tfrac{1}{{\alpha }^{4}+{\beta }^{4}+{\delta }^{4}+{\eta }^{4}}[{\alpha }^{2}{\delta }^{2}(|HHV\rangle +|VHH\rangle )+{\beta }^{2}{\eta }^{2}(|HVH\rangle +|VVV\rangle )],\\ {|{\phi }_{12}^{\mathrm{(4)}}\rangle }_{{a}_{1}{b}_{1}{c}_{1}}^{1}=\tfrac{1}{{\alpha }^{4}+{\beta }^{4}+{\delta }^{4}+{\eta }^{4}}[{\alpha }^{2}{\eta }^{2}(|HHV\rangle +|VVV\rangle )+{\beta }^{2}{\delta }^{2}(|HVH\rangle +|VHH\rangle )].\end{array}$$
(18)

The probabilities of getting quantum states \({|{\phi }_{12}^{\mathrm{(1)}}\rangle }_{{a}_{1}{b}_{1}{c}_{1}}^{1}\), \({|{\phi }_{12}^{\mathrm{(2)}}\rangle }_{{a}_{1}{b}_{1}{c}_{1}}^{1}\), \({|{\phi }_{12}^{\mathrm{(3)}}\rangle }_{{a}_{1}{b}_{1}{c}_{1}}^{1}\) and \({|{\phi }_{12}^{\mathrm{(4)}}\rangle }_{{a}_{1}{b}_{1}{c}_{1}}^{1}\) are

$$\begin{array}{l}{p}_{12}^{1}=\frac{{\alpha }^{8}+{\beta }^{8}+{\delta }^{8}+{\eta }^{8}}{{({\alpha }^{4}+{\beta }^{4}+{\delta }^{4}+{\eta }^{4})}^{2}},\\ {p}_{12}^{2}=\frac{\mathrm{2(}{\alpha }^{4}{\beta }^{4}+{\delta }^{4}{\eta }^{4})}{{({\alpha }^{4}+{\beta }^{4}+{\delta }^{4}+{\eta }^{4})}^{2}},\\ {p}_{12}^{3}=\frac{\mathrm{2(}{\alpha }^{4}{\delta }^{4}+{\beta }^{4}{\eta }^{4})}{{({\alpha }^{4}+{\beta }^{4}+{\delta }^{4}+{\eta }^{4})}^{2}},\\ {p}_{12}^{4}=\frac{\mathrm{2(}{\alpha }^{4}{\eta }^{4}+{\beta }^{4}{\delta }^{4})}{{({\alpha }^{4}+{\beta }^{4}+{\delta }^{4}+{\eta }^{4})}^{2}}.\end{array}$$
(19)

These are all failed cases, but they can be used as the initial states in the second round.

For quantum state

$${|{\phi }_{12}\rangle }_{{a}_{1}{b}_{1}{c}_{1}}^{2}=\tfrac{\alpha \beta }{\sqrt{\mathrm{2(}{\alpha }^{2}{\beta }^{2}+{\delta }^{2}{\eta }^{2})}}(|HHV\rangle +|HVH\rangle )+\tfrac{\delta \eta }{\sqrt{\mathrm{2(}{\alpha }^{2}{\beta }^{2}+{\delta }^{2}{\eta }^{2})}}(|VHH\rangle +|VVV\rangle ),$$
(20)

its process of concentration is the same as \({|{\phi }_{12}\rangle }_{{a}_{1}{b}_{1}{c}_{1}}^{1}\) and we can get

$${|{\phi }_{12}^{\mathrm{(1)}}\rangle }_{{a}_{1}{b}_{1}{c}_{1}{a}_{2}{b}_{2}{c}_{2}}^{2}=\tfrac{\alpha \beta \delta \eta }{\mathrm{2(}{\alpha }^{2}{\beta }^{2}+{\delta }^{2}{\eta }^{2})}(|HHV\rangle +|HVH\rangle +|VHH\rangle +|VVV\rangle ).$$
(21)

This is the maximally GHZ entangled state. The success and failure probabilities of \({|{\phi }_{12}\rangle }_{{a}_{1}{b}_{1}{c}_{1}}^{2}\) are

$${p}_{\mathrm{12,}s}^{2}=\frac{\mathrm{2(}\alpha \beta \delta \eta {)}^{2}}{{({\alpha }^{2}{\beta }^{2}+{\delta }^{2}{\eta }^{2})}^{2}},\quad {p}_{\mathrm{12,}f}^{2}=\frac{{\alpha }^{4}{\beta }^{4}+{\delta }^{4}{\eta }^{4}}{{({\alpha }^{2}{\beta }^{2}+{\delta }^{2}{\eta }^{2})}^{2}},$$
(22)

where the subscripts s and f represent the success and failure probabilities respectively.

For quantum states

$$\begin{array}{l}{|{\phi }_{12}\rangle }_{{a}_{1}{b}_{1}{c}_{1}}^{3}=\tfrac{\alpha \delta }{\sqrt{\mathrm{2(}{\alpha }^{2}{\delta }^{2}+{\beta }^{2}{\eta }^{2})}}(|HHV\rangle +|VHH\rangle )+\tfrac{\beta \eta }{\sqrt{\mathrm{2(}{\alpha }^{2}{\delta }^{2}+{\beta }^{2}{\eta }^{2})}}(|HVH\rangle +|VVV\rangle ),\\ {|{\phi }_{12}\rangle }_{{a}_{1}{b}_{1}{c}_{1}}^{4}=\tfrac{\alpha \eta }{\sqrt{\mathrm{2(}{\alpha }^{2}{\eta }^{2}+{\beta }^{2}{\delta }^{2})}}(|HHV\rangle +|VVV\rangle )+\tfrac{\beta \delta }{\sqrt{\mathrm{2(}{\alpha }^{2}{\eta }^{2}+{\beta }^{2}{\delta }^{2})}}(|HVH\rangle +|VHH\rangle ),\end{array}$$
(23)

the success and failure probabilities of \({|{\phi }_{12}\rangle }_{{a}_{1}{b}_{1}{c}_{1}}^{3}\) and \({|{\phi }_{12}\rangle }_{{a}_{1}{b}_{1}{c}_{1}}^{4}\) are respectively

$$\begin{array}{l}{p}_{\mathrm{12,}s}^{3}=\frac{\mathrm{2(}\alpha \beta \delta \eta {)}^{2}}{{({\alpha }^{2}{\delta }^{2}+{\beta }^{2}{\eta }^{2})}^{2}},\quad {p}_{\mathrm{12,}f}^{3}=\frac{{\alpha }^{4}{\delta }^{4}+{\beta }^{4}{\eta }^{4}}{{({\alpha }^{2}{\delta }^{2}+{\beta }^{2}{\eta }^{2})}^{2}},\\ {p}_{\mathrm{12,}s}^{4}=\frac{\mathrm{2(}\alpha \beta \delta \eta {)}^{2}}{{({\alpha }^{2}{\eta }^{2}+{\beta }^{2}{\delta }^{2})}^{2}},\quad {p}_{\mathrm{12,}f}^{4}=\frac{{\alpha }^{4}{\eta }^{4}+{\beta }^{4}{\delta }^{4}}{{({\alpha }^{2}{\eta }^{2}+{\beta }^{2}{\delta }^{2})}^{2}}.\end{array}$$
(24)

The total success probability of the first round is

$$\begin{array}{l}{P}_{1}={p}_{11}^{2}{p}_{\mathrm{12,}s}^{2}+{p}_{11}^{3}{p}_{\mathrm{12,}s}^{3}+{p}_{11}^{4}{p}_{\mathrm{12,}s}^{4}\\ \quad =\frac{\mathrm{4(}\alpha \beta \delta \eta {)}^{2}}{{\alpha }^{2}{\beta }^{2}+{\delta }^{2}{\eta }^{2}}+\frac{\mathrm{4(}\alpha \beta \delta \eta {)}^{2}}{{\alpha }^{2}{\delta }^{2}+{\beta }^{2}{\eta }^{2}}+\frac{\mathrm{4(}\alpha \beta \delta \eta {)}^{2}}{{\alpha }^{2}{\eta }^{2}+{\beta }^{2}{\delta }^{2}}.\end{array}$$
(25)

Discussion

Blindness and correctness analysis of the proposed BQC protocol

In the following, we will show that the proposed BQC protocol is secure by analyzing the blindness and correctness.

First, we show the blindness of the proposed BQC protocol.

  1. (1)

    Bob performs one of four Pauli operations randomly chosen by Alice on his photons and the initial states \({|GHZ\rangle }_{{A}_{{t}_{2}}^{\prime }{B}_{j}{C}_{{t}_{1}}^{\prime }}=\frac{1}{2}(|001\rangle +|010\rangle +|100\rangle +|111\rangle )\) are correspondingly changed into one of \(\{{|GH{Z}_{1}\rangle }_{{A}_{{t}_{2}}^{\prime }{B}_{j}{C}_{{t}_{1}}^{\prime }}\), \({|GH{Z}_{2}\rangle }_{{A}_{{t}_{2}}^{\prime }{B}_{j}{C}_{{t}_{1}}^{\prime }}\), \({|GH{Z}_{3}\rangle }_{{A}_{{t}_{2}}^{\prime }{B}_{j}{C}_{{t}_{1}}^{\prime }}\), \({|GH{Z}_{4}\rangle }_{{A}_{{t}_{2}}^{\prime }{B}_{j}{C}_{{t}_{1}}^{\prime }}\}\). Whether Bob colludes with Charlie or not, they guess the correct Bell state with the probability of \(\tfrac{1}{4}\). When this BQC protocol is repeated n times, the probability of obtaining correct quantum states is \(\mathop{\mathrm{lim}}\limits_{n\to \infty }\,{(\tfrac{1}{4})}^{n}=0\).

  2. (2)

    Alice randomly chooses the phase θ i \((\in \,\{0,\frac{\pi }{4},\frac{2\pi }{4},\frac{3\pi }{4},\ldots ,\frac{7\pi }{4}\})\) and disturbs the order of photons A j , B j , C j . Bob and Charlie know nothing about the states \(|{\pm }_{{\theta }_{i}}\rangle \) because of the no-signaling principle. After repeating n times, the probability of guessing correct θ i is \(\mathop{\mathrm{lim}}\limits_{n\to \infty }\,{(\tfrac{1}{8})}^{n}=0\). In the process of entanglement concentration, Bob and Charlie cannot eavesdropping any useful information by exchanging their results because of difference of orders of three photons.

  3. (3)

    The structures of blind brickwork states and blind topological states are private for servers. Therefore, Bob and Charlie can’t obtain anything about Alice’s private information whether they communicate with each other or not. The blindness of BFK single-server protocol and blind topological single-server protocol are showed in refs 1 and 2 in detail respectively.

Second, the correctness of quantum computation in BFK single-server protocol and blind topological single-server protocol are presented in refs 1 and 2 in detail.

So this BQC protocol is blind and correct.

Analysis of the success probabilities in iteration

In the above discussion, we have already elaborated the first round of the entanglement concentration with cross-Kerr nonlinearity in detail. QND provides a strong tool for us to perform a quantum nondemolition measurement that does not destroy entanglement of photons, which ensures that each step can be operated independently. Here, we analyse the second round and the k-th round of entanglement concentration.

For the three cases \({|{\phi }_{21}\rangle }_{{a}_{1}{b}_{1}{c}_{1}}^{2}\), \({|{\phi }_{21}\rangle }_{{a}_{1}{b}_{1}{c}_{1}}^{3}\) and \({|{\phi }_{21}\rangle }_{{a}_{1}{b}_{1}{c}_{1}}^{4}\), only the first step is needed to concentrate the ideal maximally entangled states \({|GHZ\rangle }_{{A}_{{t}_{2}}^{\prime }{B}_{j}{C}_{{t}_{1}}^{\prime }}\). However, we need to implement two steps for the state \({|{\phi }_{21}\rangle }_{{a}_{1}{b}_{1}{c}_{1}}^{1}\). We consider the three states \({|{\phi }_{21}\rangle }_{{a}_{1}{b}_{1}{c}_{1}}^{2}\), \({|{\phi }_{21}\rangle }_{{a}_{1}{b}_{1}{c}_{1}}^{3}\) and \({|{\phi }_{21}\rangle }_{{a}_{1}{b}_{1}{c}_{1}}^{4}\) first.

In the second round, for the quantum states

$${|{\phi }_{21}\rangle }_{{a}_{1}{b}_{1}{c}_{1}}^{2}=\tfrac{{\alpha }^{2}{\beta }^{2}}{\sqrt{\mathrm{2(}{\alpha }^{4}{\beta }^{4}+{\delta }^{4}{\eta }^{4})}}(|HHV\rangle +|HVH\rangle )+\tfrac{{\delta }^{2}{\eta }^{2}}{\sqrt{\mathrm{2(}{\alpha }^{2}{\beta }^{4}+{\delta }^{4}{\eta }^{4})}}(|VHH\rangle +|VVV\rangle ),$$
(26)

its analysis is the same as the Eq. (20). The success and failure probabilities are

$${p}_{\mathrm{21,}s}^{2}=\frac{\mathrm{2(}\alpha \beta \delta \eta {)}^{4}}{{({\alpha }^{4}{\beta }^{4}+{\delta }^{4}{\eta }^{4})}^{2}},\quad {p}_{\mathrm{21,}f}^{2}=\frac{{\alpha }^{8}{\beta }^{8}+{\delta }^{8}{\eta }^{8}}{{({\alpha }^{4}{\beta }^{4}+{\delta }^{4}{\eta }^{4})}^{2}}.$$
(27)

In the k-th (k > 1) round, the success and failure probabilities are

$${p}_{k\mathrm{1,}s}^{2}=\frac{\mathrm{2(}\alpha \beta \delta \eta {)}^{{2}^{k}}}{{({\alpha }^{{2}^{k}}{\beta }^{{2}^{k}}+{\delta }^{{2}^{k}}{\eta }^{{2}^{k}})}^{2}},\quad {p}_{k\mathrm{1,}f}^{2}=\frac{{\alpha }^{{2}^{k+1}}{\beta }^{{2}^{k+1}}+{\delta }^{{2}^{k+1}}{\eta }^{{2}^{k+1}}}{{({\alpha }^{{2}^{k}}{\beta }^{{2}^{k}}+{\delta }^{{2}^{k}}{\eta }^{{2}^{k}})}^{2}}.$$
(28)

For the quantum states

$$\begin{array}{l}{|{\phi }_{21}\rangle }_{{a}_{1}{b}_{1}{c}_{1}}^{3}=\tfrac{{\alpha }^{2}{\delta }^{2}}{\sqrt{\mathrm{2(}{\alpha }^{4}{\delta }^{4}+{\beta }^{4}{\eta }^{4})}}(|HHV\rangle +|VHH\rangle )+\tfrac{{\beta }^{2}{\eta }^{2}}{\sqrt{\mathrm{2(}{\alpha }^{4}{\delta }^{4}+{\beta }^{4}{\eta }^{4})}}(|HVH\rangle +|VVV\rangle ),\\ {|{\phi }_{21}\rangle }_{{a}_{1}{b}_{1}{c}_{1}}^{4}=\tfrac{{\alpha }^{2}{\eta }^{2}}{\sqrt{\mathrm{2(}{\alpha }^{4}{\eta }^{4}+{\beta }^{4}{\delta }^{4})}}(|HHV\rangle +|VVV\rangle )+\tfrac{{\beta }^{2}{\delta }^{2}}{\sqrt{\mathrm{2(}{\alpha }^{4}{\eta }^{4}+{\beta }^{4}{\delta }^{4})}}(|HVH\rangle +|VHH\rangle ),\end{array}$$

the analyses of entanglement concentration are the same as the Eq. (23), the success and failure probabilities in the second round and the k-th round are

$$\begin{array}{ll}{p}_{\mathrm{21,}s}^{3}=\frac{\mathrm{2(}\alpha \beta \delta \eta {)}^{4}}{{({\alpha }^{4}{\delta }^{4}+{\beta }^{4}{\eta }^{4})}^{2}}, & {p}_{k\mathrm{1,}s}^{3}=\frac{\mathrm{2(}\alpha \beta \delta \eta {)}^{{2}^{k}}}{{({\alpha }^{{2}^{k}}{\delta }^{{2}^{k}}+{\beta }^{{2}^{k}}{\eta }^{{2}^{k}})}^{2}},\\ {p}_{\mathrm{21,}f}^{3}=\frac{{\alpha }^{8}{\delta }^{8}+{\beta }^{8}{\eta }^{8}}{{({\alpha }^{4}{\delta }^{4}+{\beta }^{4}{\eta }^{4})}^{2}}, & {p}_{k\mathrm{1,}f}^{3}=\frac{{\alpha }^{{2}^{k+1}}{\delta }^{{2}^{k+1}}+{\beta }^{{2}^{k+1}}{\eta }^{{2}^{k+1}}}{{({\alpha }^{{2}^{k}}{\delta }^{{2}^{k}}+{\beta }^{{2}^{k}}{\eta }^{{2}^{k}})}^{2}},\\ {p}_{\mathrm{21,}s}^{4}=\frac{\mathrm{2(}\alpha \beta \delta \eta {)}^{4}}{{({\alpha }^{4}{\eta }^{4}+{\beta }^{4}{\delta }^{4})}^{2}}, & {p}_{k\mathrm{1,}s}^{4}=\frac{\mathrm{2(}\alpha \beta \delta \eta {)}^{{2}^{k}}}{{({\alpha }^{{2}^{k}}{\eta }^{{2}^{k}}+{\beta }^{{2}^{k}}{\delta }^{{2}^{k}})}^{2}},\\ {p}_{\mathrm{21,}f}^{4}=\frac{{\alpha }^{8}{\eta }^{8}+{\beta }^{8}{\delta }^{8}}{{({\alpha }^{4}{\eta }^{4}+{\beta }^{4}{\delta }^{4})}^{2}}, & {p}_{k\mathrm{1,}f}^{4}=\frac{{\alpha }^{{2}^{k+1}}{\eta }^{{2}^{k+1}}+{\beta }^{{2}^{k+1}}{\delta }^{{2}^{k+1}}}{{({\alpha }^{{2}^{k}}{\eta }^{{2}^{k}}+{\beta }^{{2}^{k}}{\delta }^{{2}^{k}})}^{2}}.\end{array}$$
(29)

For the quantum states

$${|{\phi }_{kj}\rangle }_{{a}_{1}{b}_{1}{c}_{1}}^{1}={\alpha }_{kj}|HHV\rangle +{\beta }_{kj}|HVH\rangle +{\delta }_{kj}|VHH\rangle +{\eta }_{kj}|VVV\rangle ,$$
(30)

(where j = 1, 2) we give the relevant normalized coefficients and the probabilities of relevant quantum states. The iterative process is the same as the Eq. (3).

In the first step of the k-th round, for the quantum states

$${|{\phi }_{k1}\rangle }_{{a}_{1}{b}_{1}{c}_{1}}^{1}={\alpha }_{k1}|HHV\rangle +{\beta }_{k1}|HVH\rangle +{\delta }_{k1}|VHH\rangle +{\eta }_{k1}|VVV\rangle ,$$
(31)

where k > 1 and the coefficients are

$$\begin{array}{l}{\alpha }_{k1}=\frac{{\alpha }^{{2}^{2k-2}}}{\sqrt{{\alpha }^{{2}^{2k-1}}+{\beta }^{{2}^{2k-1}}+{\delta }^{{2}^{2k-1}}+{\eta }^{{2}^{2k-1}}}},\\ {\beta }_{k1}=\frac{{\beta }^{{2}^{2k-2}}}{\sqrt{{\alpha }^{{2}^{2k-1}}+{\beta }^{{2}^{2k-1}}+{\delta }^{{2}^{2k-1}}+{\eta }^{{2}^{2k-1}}}},\\ {\delta }_{k1}=\frac{{\delta }^{{2}^{2k-2}}}{\sqrt{{\alpha }^{{2}^{2k-1}}+{\beta }^{{2}^{2k-1}}+{\delta }^{{2}^{2k-1}}+{\eta }^{{2}^{2k-1}}}},\\ {\eta }_{k1}=\frac{{\eta }^{{2}^{2k-2}}}{\sqrt{{\alpha }^{{2}^{2k-1}}+{\beta }^{{2}^{2k-1}}+{\delta }^{{2}^{2k-1}}+{\eta }^{{2}^{2k-1}}}}.\end{array}$$
(32)

In the second step of the k-th round, for the quantum states

$${|{\phi }_{k2}\rangle }_{{a}_{1}{b}_{1}{c}_{1}}^{1}={\alpha }_{k2}|HHV\rangle +{\beta }_{k2}|HVH\rangle +{\delta }_{k2}|VHH\rangle +{\eta }_{k2}|VVV\rangle ,$$
(33)

where the coefficients are

$$\begin{array}{l}{\alpha }_{k2}=\frac{{\alpha }^{{2}^{2k-1}}}{\sqrt{{\alpha }^{{2}^{2k}}+{\beta }^{{2}^{2k}}+{\delta }^{{2}^{2k}}+{\eta }^{{2}^{2k}}}},\\ {\beta }_{k2}=\frac{{\beta }^{{2}^{2k-1}}}{\sqrt{{\alpha }^{{2}^{2k}}+{\beta }^{{2}^{2k}}+{\delta }^{2k}+{\eta }^{{2}^{2k}}}},\\ {\delta }_{k2}=\frac{{\delta }^{{2}^{2k-1}}}{\sqrt{{\alpha }^{{2}^{2k}}+{\beta }^{{2}^{2k}}+{\delta }^{{2}^{2k}}+{\eta }^{{2}^{2k}}}},\\ {\eta }_{k2}=\frac{{\eta }^{{2}^{2k-1}}}{\sqrt{{\alpha }^{{2}^{2k}}+{\beta }^{{2}^{2k}}+{\delta }^{{2}^{2k}}+{\eta }^{{2}^{2k}}}}.\end{array}$$
(34)

The probabilities of obtaining four quantum states in the first step or the second step of the k-th round are

$$\begin{array}{c}{p}_{kj}^{1}={\alpha }_{kj}^{4}+{\beta }_{kj}^{4}+{\delta }_{kj}^{4}+{\eta }_{kj}^{4},\\ {p}_{kj}^{2}=2({\alpha }_{kj}^{2}{\beta }_{kj}^{2}+{\delta }_{kj}^{2}{\eta }_{kj}^{2}),\\ {p}_{kj}^{3}=2({\alpha }_{kj}^{2}{\delta }_{kj}^{2}+{\beta }_{kj}^{2}{\eta }_{kj}^{2}),\\ {p}_{kj}^{4}=2({\alpha }_{kj}^{2}{\eta }_{kj}^{2}+{\beta }_{kj}^{2}{\delta }_{kj}^{2}),\end{array}$$
(35)

where j = 1, 2. The success probability of the kth round is

$$\begin{array}{rcl}{P}_{k} & = & {p}_{11}^{2}{p}_{\mathrm{12,}f}^{2}{p}_{\mathrm{21,}f}^{2}{p}_{\mathrm{31,}f}^{2}\cdots {p}_{(k-\mathrm{1)1,}f}^{2}{p}_{k\mathrm{1,}s}^{2}\\ & & +{p}_{11}^{3}{p}_{\mathrm{12,}f}^{3}{p}_{\mathrm{21,}f}^{3}\cdots {p}_{(k-\mathrm{1)1,}f}^{3}{p}_{k\mathrm{1,}s}^{3}\\ & & +{p}_{11}^{4}{p}_{\mathrm{12,}f}^{4}{p}_{\mathrm{21,}f}^{4}+\cdots {p}_{(k-\mathrm{1)1,}f}^{4}{p}_{k\mathrm{1,}s}^{4}\\ & & +{p}_{11}^{1}({p}_{12}^{2}{p}_{\mathrm{21,}f}^{2}{p}_{\mathrm{31,}f}^{2}\cdots {p}_{(k-\mathrm{1)1,}f}^{2}{p}_{k\mathrm{1,}s}^{2}\\ & & +{p}_{12}^{3}{p}_{\mathrm{21,}f}^{3}{p}_{\mathrm{31,}f}^{3}\cdots {p}_{(k-\mathrm{1)1,}f}^{3}{p}_{k\mathrm{1,}f}^{3}\\ & & +{p}_{12}^{4}{p}_{\mathrm{21,}f}^{4}{p}_{\mathrm{31,}f}^{4}\cdots {p}_{(k-\mathrm{1)1,}f}^{4}{p}_{k\mathrm{1,}f}^{4})\\ & & +\cdots +{p}_{11}^{1}{p}_{12}^{1}{p}_{21}^{1}{p}_{22}^{1}{p}_{31}^{1}{p}_{32}^{1}\cdots {p}_{(k-\mathrm{1)1}}^{1}{p}_{(k-\mathrm{1)2}}^{1}({p}_{k1}^{2}{p}_{k\mathrm{2,}s}^{2}+{p}_{k1}^{3}{p}_{k\mathrm{2,}s}^{3}+{p}_{k1}^{4}{p}_{k\mathrm{2,}s}^{4}\mathrm{)}.\end{array}$$
(36)

The total probability is \({P}_{total}={\sum }_{k=1}^{n}{P}_{k}\), which depends on the number of iterations and parameters of the initial states. The relationship of the total success probability, parameters and the number of iterations is shown in Fig. 4. It can be seen that the total success probability has kept increasing with the parameters β and δ in the range of \([\mathrm{0,}\tfrac{\sqrt{3}}{2}]\). When n = 4, the success probability has already reached 0.9196. When n = 9, the success probability has already reached 0.9975. Therefore, the entanglement concentration is successful in theory.

Figure 4
figure 4

The success probability P of getting maximally entangled GHZ state relies on the initial coefficients β and δ. Here, we let \(\alpha =\tfrac{1}{2}\), \(\beta \in \{0,\tfrac{\sqrt{3}}{2}\}\), \(\delta \in \{0,\sqrt{\tfrac{3}{4}-{\beta }^{2}}\}\), \(\eta =\sqrt{\tfrac{3}{4}-{\beta }^{2}-{\delta }^{2}}\). n (n = 1, 2, 3, 4) represents the number of iterations.

Full size image

In this paper, we only consider the ideal CNOT gate19,20,21,22,23. In experiment, there exist many nonideal factors such as the double effect of parameter conversion, the imperfect matching of the crystal lattice and phases, and so on. The probabilities of intrinsic error of experimental methods are unavoidable, such as QND measurements and CNOT operations. Thus optimizing the experimental system is a very meaningful research direction. In the BQC protocol, we only give the concrete quantum channel noise model but not universal. So, we will further study entanglement purification of GHZ states.

Methods

The optical devices are used to complete the entanglement concentration, where the parity check devices are based on cross-Kerr nonlinearity that can construct QND38, 39, 41 to improve the successful probability. The cross-Kerr nonlinearity medium is described by the Hamiltonian,

$$H=\hslash \chi {a}_{s}^{\dagger }{a}_{s}{a}_{p}^{\dagger }{a}_{p}$$
(37)

where \({a}_{s}^{\dagger }\) and \({a}_{p}^{\dagger }\) are the creation operators, a s and a p are the annihilation operators, a Fock state |n〉 and a coherent state |α c 〉 interact. The whole system evolves into

$$U(t)|n\rangle |{\alpha }_{c}\rangle ={c}_{0}|0\rangle |{\alpha }_{c}\rangle +{c}_{1}|1\rangle |{\alpha }_{c}{e}^{i\theta }\rangle $$
(38)

where \(U(t)={e}^{-i\theta {a}_{s}^{+}{a}_{s}{a}_{p}^{+}{a}_{p}}\), θ = χt is the phase shift and t is the interaction time (c = 1, 2, 3). θ is proportional to the number of photons in the signal state |α c 〉. X-quadrature measurement can recognize the phase shift of signal states |α c 〉. The cross-Kerr nonlinearity can measure the number of photons but do not destroy the photons.

For the parity check device in Fig. 3, we give an example. Two polarization photons are initially prepared with the forms of \({|\tau \rangle }_{{k}_{1}}={\mu }_{0}|H\rangle +{\mu }_{1}|V\rangle \) and \({|\tau \rangle }_{{k}_{2}}={\lambda }_{0}|H\rangle +{\lambda }_{1}|V\rangle \) that interact with a coherent beam |α c 〉 (c = 1, 2, 3),where real numbers μ 0, μ 1, λ 0 and λ 1 satisfy the normalization condition |μ 0|2 + |μ 1|2 = 1, |λ 0|2 + |λ 1|2 = 1, respectively. Then the composite quantum system \(|{\Upsilon }_{1}\rangle ={|\tau \rangle }_{{k}_{1}}\otimes {|\tau \rangle }_{{k}_{2}}\otimes |{\alpha }_{c}\rangle \) evolves to

$$|{\Upsilon }_{2}\rangle ={\mu }_{0}{\lambda }_{1}|HV\rangle |{\alpha }_{c}{e}^{-2i\theta }\rangle +{\mu }_{1}{\lambda }_{0}|VH\rangle |{\alpha }_{c}{e}^{2i\theta }\rangle +({\mu }_{0}{\lambda }_{0}|HH\rangle +{\mu }_{1}{\lambda }_{1}|VV\rangle )|{\alpha }_{c}\rangle $$
(39)

From the Eq. (39), we can pick up a phase shift 0 related with |HH〉 and |VV〉, and phase shift 2θ related with |HV〉 and |VH〉. One can distinguish |HH〉 and |VV〉 from |HV〉 and |VH〉 by different phase shifts, however, the states \(|{\alpha }_{1}{e}^{\pm 2i\theta }\rangle \) can not be distinguished by the setup.