Abstract
We have investigated numerically toroidal dipolar excitation at optical frequency in metamaterials whose unit cell consists of three identical Ag nanodisks and a SiO2 spacer on Ag substrate. The near-field plasmon hybridization between individual Ag nanodisks and substrate forms three magnetic dipolar resonances, at normal incidence of plane electromagnetic waves. The strong coupling among three magnetic dipolar resonances leads to the toroidal dipolar excitation, when space-inversion symmetry is broke along the polarization direction of incident light. The influences of some geometrical parameters on the resonance frequency and the excitation strength of toroidal dipolar mode are studied in detail. The radiated power from toroidal dipole is also compared with that from conventional electric and magnetic multipoles.
Similar content being viewed by others
Introduction
In 2010, dominant toroidal dipolar response was firstly experimentally observed at microwave, in metamaterials consisting of a three-dimensional (3D) array of four asymmetric split-ring resonators (SRRs)1. In 2012, toroidal dipolar response was then pushed theoretically to the optical frequency, by scaling down the size of SRRs2. The fabrication of 3D array of four asymmetric SRRs is not easy especially at optical wavelengths. In 2013, a simplified two-dimensional (2D) planar scheme was demonstrated in experiment for toroidal dipolar metamaterials which were also comprised of four asymmetric SRRs3. In the past several years, SRRs-based toroidal metamaterials have been drawing a lot of attentions4,5,6,7,8,9,10,11,12,13,14,15,16, thanks to their novel electromagnetic properties and a variety of potential applications such as low-threshold lasing6, polarization transformers12, electromagnetically induced transparency (EIT)13, and circular dichroism (CD)16.
Recently, toroidal dipolar response was also investigated in metamolecules with magnetic resonance17,18,19,20,21,22,23,24,25, plasmonic cavities26,27,28,29,30,31,32, and high-refractive-index dielectric nanostructures33,34,35,36,37,38,39,40,41. For example, the toroidal dipolar response in the optical regime was demonstrated experimentally in metamolecules that were formed by six pairs of asymmetric double-bars17. The toroidal dipolar response was also showed theoretically in metamolecules consisting of six gold disks on a gold substrate separated by a SiO2 layer, under the excitation of radially polarized light22. The theoretical and experimental evidence of toroidal dipolar response was presented in a plasmonic cavity comprising seven round holes drilled in a thick silver film26. A pronounced spectral feature in far-field scattering related to toroidal dipolar response was observed experimentally in high-refractive-index silicon nanoparticles, when the resonance frequencies of toroidal and electric dipole modes were tuned to be overlapped39.
In this work, we will theoretically study the excitation of toroidal dipolar mode at optical frequency in metamaterials composed of three Ag nanodisks with equal size and a SiO2 spacer on Ag substrate. It is found that under normal incidence of plane electromagnetic waves, the near-field plasmon hybridization between individual Ag nanodisks and substrate forms three magnetic dipolar resonances. The further strong coupling among three magnetic dipolar resonances will result into the excitation of toroidal dipolar mode, when space-inversion symmetry breaking is introduced in the polarization direction of incident light, through placing the Ag nanodisks in different locations. We have investigated in detail the influences of some geometrical parameters on the resonance frequency and the excitation strength of toroidal dipolar mode. The radiated power from toroidal dipole is also compared with that from conventional electric and magnetic multipoles. We hope that the numerical results presented in this work could be helpful to experimentally observe toroidal dipolar response at optical frequency.
Results
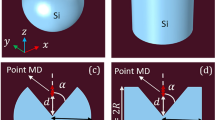
Figure 1 schematically shows the toroidal metamaterials composed of three Ag nanodisks and a SiO2 spacer on Ag substrate. d and h are the diameter and height of Ag nanodisks, and t is the thickness of SiO2 spacer. The relative positions of Ag nanodisks are determined by radius R and rotation angle θ. The periods along the x and y axes are p x and p y . K in , E in , and H in are the wave vector, electric field, and magnetic field of incident light, respectively.
Figure 2(a) shows the reflection (Ref., red circle) and absorption (Abs., green triangle) spectra of toroidal metamaterials under normal incidence of light, in the frequency range from 360 to 400 THz. The spectra are calculated by the commercial software package “EastFDTD”, which is based on finite-difference-time-domain (FDTD) method42. In our calculations, the relative permittivity of Ag is from experimental data43, and SiO2 has a refractive index of 1.45. In Fig. 2(a), there are two resonance modes centered at f 1 = 379.25 THz and f 2 = 384.75 THz, which correspond to wavelengths of λ 1 = 791 nm and λ 2 = 780 nm, respectively. At both f 1 and f 2 resonances, the reflection spectra have a dip, while the absorption spectra have a peak. To find the physical mechanisms of the resonant modes, Fig. 2(b–c) plot the magnetic field distributions at the resonance frequencies of f 1 and f 2 . For resonant mode at f 1 , one can clearly see three field “hotspots” under Ag nanodisks. Moreover, the directions of magnetic fields have a head-to-tail distribution, which implies the excitation of a toroidal dipolar mode1. However, resonant mode at f 2 does not have such a head-to-tail distribution, though there are also three field “hotspots”. It is well known that, the near-field plasmon hybridization between individual metal nanoparticle and a metal substrate can form a magnetic dipolar resonance44, 45, which has been widely explored for perfect absorption46,47,48. In our case, such plasmon hybridization forms three magnetic dipolar resonances under Ag nanodisks, resulting into the appearance of three field “hotspots”. In a similar approach reported in ref. 1, the further interactions among the magnetic dipolar resonances lead to the excitation of the toroidal dipolar mode.
(a) Reflection and absorption spectra of toroidal metamaterials at normal incidence. (b,c) Magnetic field distributions on the xy plane across the center of SiO2 spacer, at the resonance frequencies of f 1 and f 2 . Red arrows show the directions of magnetic fields, and colors give the intensity of magnetic fields. Geometrical parameters: d = 150 nm, h = 50 nm, t = 30 nm, R = 120 nm, θ = 120°, p x = p y = 500 nm.
To further demonstrate that resonant mode at f 1 is closely related to the excitation of a toroidal dipolar mode, in Fig. 3 we have calculated the radiated power I p , I m , I EQ , I MQ , and I T from electric dipolar moment p, magnetic dipolar moment m, electric quadrupole moment EQ, magnetic quadrupole moment MQ, and toroidal dipolar mement T, respectively. In our calculations, the used equations2 are expressed as
where r is position vector, J is volume current density, ω is frequency of incident light, c is light speed in vacuum, i is unit imaginary number, dv indicates the volume integration carried out in a unit cell, ∑ represents sigma summation, δ αβ is delta function, and α, β = x, y, z. It is clearly seen in Fig. 3(a) that, the radiated power I T from toroidal dipolar mement T has a peak exactly at f 1 , which clearly indicates that resonant mode at f 1 is closely related with the excitation of a toroidal dipolar mode. Near the frequency of f 1 , the radiated power I T is larger than the radiated power I m from magnetic dipolar moment m and the radiated power I MQ from magnetic quadrupole moment MQ, but it is still smaller than the radiated power I p from electric dipolar moment p and the radiated power I EQ from electric quadrupole moment EQ. By decomposing the x, y and z components of radiated power in Fig. 3(b–d), it is found that the z component I T, z dominates the radiated power I T , and it can be comparable with the z component I p,z and I EQ,z , as shown in Fig. 3(d).
(a) Radiated power from electric dipolar moment (I p , solid black square), magnetic dipolar moment (I m , solid red circle), electric quadrupole dipolar moment (I EQ , hollow black square), magnetic quadrupole dipolar moment (I MQ , hollow red circle), and toroidal dipolar mement (I T , green triangle). (b,c) The same as (a) but for x, y and z components of radiated power, respectively. Two vertical gray lines label the resonance frequencies of f 1 and f 2 in Fig. 2(a).
Discussion
To study the influence of rotation angle θ on the toroidal dipolar mode, we present in Fig. 4(a) the contour plot of absorption spectra of toroidal metamaterials as a function of light frequency and rotation angle θ. The toroidal dipolar mode will blue-shift until θ increases to about 115°, because of the continuously strengthened interactions of magnetic dipolar resonances between the left two nanodisks and the right one. But, it will have a red-shift when θ is further increased, since the left two nanodisks’ interactions are gradually weakened with increasing θ. Figure 4(b–e) show the magnetic field distributions on the xy plane across the center of SiO2 spacer at a, b, c, and d points, respectively. For these points, the directions of magnetic fields under Ag nanodisks also have a vortex distribution (i.e., a head-to-tail distribution), a character of toroidal dipolar mode. As exhibited in Fig. 4(c), three field “hotspots” are simultaneously the most obvious, suggesting a relatively stronger excitation of toroidal dipolar mode for θ to be about 115°. The right field “hotspot” in Fig. 4(a) and the left two field “hotspots” in Fig. 4(d) become much weaker, which indicates a weak excitation of toroidal dipolar mode. When θ is smaller than 110° or larger than 140°, in principle, it is not a toroidal resonance and just is a magnetic dipole resonance.
(a) Contour plot of absorption spectra of toroidal metamaterials as a function of light frequency and rotation angle θ at normal incidence. The overlaid black line and solid circles give the resonance position of toroidal dipolar mode. (b–e) Magnetic field distributions on the xy plane across the center of SiO2 spacer, at a, b, c, and d points. Red arrows show the directions of magnetic fields, and colors give the intensity of magnetic fields.
We have also investigated the influence of radius R on the toroidal dipolar mode. Figure 5(a) shows the contour plot of absorption spectra of toroidal metamaterials as a function of light frequency and radius R. The toroidal dipolar mode is obviously red-shifted as R is varied from 105 to 150 nm, since the interactions of magnetic dipolar resonances among Ag nanodisks become weak with increasing R. Figure 5(b–e) show the magnetic field distributions on the xy plane across the center of SiO2 spacer at e, f, g, and h points, respectively. At the four points, the directions of the magnetic fields under Ag nanodisks all have a head-to-tail distribution, indicating the excitation of a toroidal dipolar mode. When radius R is increased further, the right field “hotspot” will get stronger, while the left two field “hotspots” will get weaker.
(a) Contour plot of absorption spectra of toroidal metamaterials as a function of light frequency and radius R at normal incidence. The overlaid black line and solid circles give the resonance position of toroidal dipolar mode. (b–e) Magnetic field distributions on the xy plane across the center of SiO2 spacer, at e, f, g, and h points. Red arrows show the directions of magnetic fields, and colors give the intensity of magnetic fields.
In conclusion, we have theoretically studied the excitation of toroidal dipolar mode at optical frequency in metamaterials composed of three Ag nanodisks and a SiO2 spacer on Ag substrate. The Ag nanodisks have identical size, but are placed in different locations to break space-inversion symmetry in the polarization direction of incident light. Under normal incidence of linearly polarized light, the near-field plasmon hybridization between individual Ag nanodisks and substrate forms three magnetic dipolar resonances, and their further interactions lead to the excitation of toroidal dipolar mode. We have investigated in detail the influences of some geometrical parameters on the resonance frequency and the excitation strength of toroidal dipolar mode. The radiated power from toroidal dipole is also compared with that from conventional electric and magnetic multipoles. Our designed metamaterials may be helpful to experimentally observe toroidal dipolar response at optical frequency.
References
Kaelberer, T., Fedotov, V. A., Papasimakis, N., Tsai, D. P. & Zheludev, N. I. Toroidal dipolar response in a metamaterial. Science 330, 1510–1512 (2010).
Huang, Y. W. et al. Design of plasmonic toroidal metamaterials at optical frequencies. Opt. Express 20, 1760–1768 (2012).
Fan, Y., Wei, Z., Li, H., Chen, H. & Soukoulis, C. M. Low-loss and high-Q planar metamaterial with toroidal moment. Phys. Rev. B 87, 115417 (2013).
Dong, Z. G., Ni, P. G., Zhu, J., Yin, X. B. & Zhang, X. Toroidal dipole response in a multifold double-ring metamaterial. Opt. Express 20, 13065–13070 (2012).
Guo, L. Y., Li, M. H., Ye, Q. W., Xiao, B. X. & Yang, H. L. Electric toroidal dipole response in split-ring resonator metamaterials. Eur. Phys. J. B 85, 208 (2012).
Huang, Y. W. et al. Toroidal lasing spaser. Sci. Rep. 3, 1237 (2013).
Wang, S. L., Xiao, J. J., Zhang, Q. & Zhang, X. M. Resonance modes in stereometamaterial of square split ring resonators connected by sharing the gap. Opt. Express 22, 24358–24366 (2014).
Ye, Q. W. et al. The magnetic toroidal dipole in steric metamaterial for permittivity sensor application. Phys. Scr. 88, 055002 (2013).
Savinov, V., Fedotov, V. A. & Zheludev, N. I. Toroidal dipolar excitation and macroscopic electromagnetic properties of metamaterials. Phys. Rev. B 89, 205112 (2014).
Li, M. H., Guo, L. Y., Dong, J. F. & Yang, H. L. Resonant transparency in planar metamaterial with toroidal moment. Appl. Phys. Express 7, 082201 (2014).
Guo, L. Y., Li, M. H., Yang, H. L., Huang, X. J. & Wu, S. Toroidal dipolar responses in a planar metamaterial. J. Phys. D: Appl. Phys. 47, 415501 (2014).
Gao, J., Zhang, K., Yang, G. & Wu, Q. A novel four-face polarization twister based on three-dimensional magnetic toroidal dipoles. IEEE Trans. Magn. 50, 4002104 (2014).
Li, H. M. et al. Low-loss metamaterial electromagnetically induced transparency based on electric toroidal dipolar response. Appl. Phys. Lett. 106, 083511 (2015).
Ding, C. F. et al. Stable terahertz toroidal dipolar resonance in a planar metamaterial. Phys. Status Solidi B 252, 1388–1393 (2015).
Papasimakis, N., Fedotov, V. A., Savinov, V., Raybould, T. A. & Zheludev, N. I. Electromagnetic toroidal excitations in matter and free space. Nat. Mater. 15, 263–271 (2016).
Raybould, T. A. et al. Toroidal circular dichroism. Phys. Rev. B 94, 035119 (2016).
Dong, Z. G. et al. Optical toroidal dipolar response by an asymmetric double-bar metamaterial. Appl. Phys. Lett. 101, 144105 (2012).
Dong, Z. G. et al. All-optical hall effect by the dynamic toroidal moment in a cavity-based metamaterial. Phys. Rev. B 87, 245429 (2013).
Li, J. et al. Optical responses of magnetic-vortex resonance in double-disk metamaterial variations. Phys. Lett. A 378, 1871–1875 (2014).
Zhang, Q., Xiao, J. J. & Wang, S. L. Optical characteristics associated with magnetic resonance in toroidal metamaterials of vertically coupled plasmonic nanodisks. J. Opt. Soc. Am. B 31, 1103–1108 (2014).
Li, J. et al. From non- to super-radiating manipulation of a dipolar emitter coupled to a toroidal metastructure. Opt. Express 23, 29384–29389 (2015).
Bao, Y. J., Zhu, X. & Fang, Z. Y. Plasmonic toroidal dipolar response under radially polarized excitation. Sci. Rep. 5, 11793 (2015).
Zhang, X. L., Wang, S. B., Lin, Z. F., Sun, H. B. & Chan, C. T. Optical force on toroidal nanostructures: Toroidal dipole versus renormalized electric dipole. Phys. Rev. A 92, 043804 (2015).
Watson, D. W., Jenkins, S. D., Ruostekoski, J., Fedotov, V. A. & Zheludev, N. I. Toroidal dipole excitations in metamolecules formed by interacting plasmonic nanorods. Phys. Rev. B 93, 125420 (2016).
Tang, C. J. et al. Toroidal dipolar response in metamaterials composed of metal-dielectric-metal sandwich magnetic resonators. IEEE Photonics J. 8, 4600209 (2016).
Ögüt, B., Talebi, N., Vogelgesang, R., Sigle, W. & van Aken, P. A. Toroidal plasmonic eigenmodes in oligomer nanocavities for the visible. Nano Lett. 12, 5239–5244 (2012).
Talebi, N., Ögüt, B., Sigle, W., Vogelgesang, R. & van Aken, P. A. On the symmetry and topology of plasmonic eigenmodes in heptamer and hexamer nanocavities. Appl. Phys. A 116, 947–954 (2014).
Fedotov, V. A., Rogacheva, A. V., Savinov, V., Tsai, D. P. & Zheludev, N. I. Resonant transparency and non-trivial non-radiating excitations in toroidal metamaterials. Sci. Rep. 3, 2967 (2013).
Guo, L. Y., Li, M. H., Huang, X. J. & Yang, H. L. Electric toroidal metamaterial for resonant transparency and circular cross-polarization conversion. Appl. Phys. Lett. 105, 033507 (2014).
Li, J. Q. et al. Excitation of plasmon toroidal mode at optical frequencies by angle-resolved reflection. Opt. Lett. 39, 6683–6686 (2014).
Zhang, Q., Xiao, J. J., Zhang, X. M., Han, D. Z. & Gao, L. Core-shell-structured dielectric-metal circular nanodisk antenna: gap plasmon assisted magnetic toroid-like cavity modes. ACS Photonics 2, 60–65 (2015).
Kim, S. H. et al. Subwavelength localization and toroidal dipole moment of spoof surface plasmon polaritons. Phys. Rev. B 91, 035116 (2015).
Kafesaki, M., Basharin, A. A., Economou, E. N. & Soukoulis, C. M. THz metamaterials made of phonon-polariton materials. Photonics Nanostruct. 12, 376–386 (2014).
Basharin, A. A. et al. Dielectric metamaterials with toroidal dipolar response. Phys. Rev. X 5, 011036 (2015).
Li, J. et al. Toroidal dipolar response by a dielectric microtube metamaterial in the terahertz regime. Opt. Express 23, 29138–29144 (2015).
Liu, W., Zhang, J. F., Lei, B., Hu, H. J. & Miroshnichenko, A. E. Invisible nanowires with interfering electric and toroidal dipoles. Opt. Lett. 40, 2293–2296 (2015).
Liu, W., Shi, J. H., Lei, B., Hu, H. J. & Miroshnichenko, A. E. Efficient excitation and tuning of toroidal dipoles within individual homogenous nanoparticles. Opt. Express 23, 24738–24747 (2015).
Liu, W., Zhang, J. F. & Miroshnichenko, A. E. Toroidal dipole-induced transparency in core-shell nanoparticles. Laser Photonics Rev. 9, A564–A570 (2015).
Miroshnichenko, A. E. et al. Nonradiating anapole modes in dielectric nanoparticles. Nat. Commun. 6, 8069 (2015).
Liu, W., Lei, B., Shi, J. H., Hu, H. J. & Miroshnichenko, A. E. Elusive pure anapole excitation in homogenous spherical nanoparticles with radial anisotropy. J. Nanomater. 2015, 672957 (2015).
Wang, R. & Negro, L. D. Engineering non-radiative anapole modes for broadband absorption enhancement of light. Opt. Express 24, 19048–19062 (2016).
Website: www.eastfdtd.com.
Johnson, P. B. & Christy, R. W. Optical constants of the noble metals. Phys. Rev. B 6, 4370–4379 (1972).
Hao, J. et al. High performance optical absorber based on a plasmonic metamaterial. Appl. Phys. Lett. 96, 251104 (2010).
Tang, C. J. et al. Ultrathin amorphous silicon thin-film solar cells by magnetic plasmonic metamaterial absorbers. RSC Adv. 5, 81866–81874 (2015).
Watts, C. M., Liu, X. L. & Padilla, W. J. Metamaterial electromagnetic wave absorbers. Adv. Mater. 24, OP98–OP120 (2012).
Cui, Y. X. et al. Plasmonic and metamaterial structures as electromagnetic absorbers. Laser Photonics Rev. 8, 495–520 (2014).
Ra’di, Y., Simovski, C. R. & Tretyakov, S. A. Thin perfect absorbers for electromagnetic waves: theory, design, and realizations. Phys. Rev. Appl. 3, 037001 (2015).
Acknowledgements
This work is financially supported by the State Key Program for Basic Research of China (SKPBRC) under Grant Nos 2013CB632703 and 2012CB921501, the National Natural Science Foundation of China (NSFC) under Grant Nos 11574270, 11304159, 11104136, 91221206, and 51271092, the Natural Science Foundation of Zhejiang Province under Grant Nos LY14A040004 and LY15A040005, the Natural Science Foundation of Jiangsu Province (No. BK20161512), the Qing Lan Project of Jiangsu Province, and the Specialized Research Fund for the Doctoral Program of Higher Education of China under Grant No. 20133223120006.
Author information
Authors and Affiliations
Contributions
Chaojun Tang, Qiugu Wang and Jing Chen did the calculations. Chaojun Tang, Qiugu Wang and Jing Chen wrote the manuscript. Chaojun Tang, Jing Chen and Fanxin Liu supervised the project. Chaojun Tang, Bo Yan, Qiugu Wang, Jing Chen, Zhendong Yan, Fanxin Liu, Naibo Chen, and Chenghua Sui discussed the results and reviewed the manuscript.
Corresponding authors
Ethics declarations
Competing Interests
The authors declare that they have no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Tang, C., Yan, B., Wang, Q. et al. Toroidal Dipolar Excitation in Metamaterials Consisting of Metal nanodisks and a Dielectrc Spacer on Metal Substrate. Sci Rep 7, 582 (2017). https://doi.org/10.1038/s41598-017-00708-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-017-00708-5
This article is cited by
-
Terahertz binary computing in a coupled toroidal metasurface
Scientific Reports (2024)
-
Polarization-Sensitive High-Q Four-Arm Structured Toroidal Terahertz Metamaterial
Journal of Electronic Materials (2021)
-
Multiband and Broadband Absorption Enhancement of Monolayer Graphene at Optical Frequencies from Multiple Magnetic Dipole Resonances in Metamaterials
Nanoscale Research Letters (2018)
-
“Optical and Surface Enhanced Raman Scattering properties of Ag modified silicon double nanocone array”
Scientific Reports (2017)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.