Abstract
The search for new control methods over light-matter interactions is one of the engines that advances fundamental physics and applied science alike. A specific class of light-matter interaction interfaces are setups coupling photons of distinct frequencies via matter. Such devices, nontrivial in design, could be endowed with multifunctional tasking. Here we envisage for the first time an optomechanical system that bridges optical and robust, high-frequency x-ray photons, which are otherwise notoriously difficult to control. The x-ray-optical system comprises of an optomechanical cavity and a movable microlever interacting with an optical laser and with x-rays via resonant nuclear scattering. We show that optomechanically induced transparency of a broad range of photons (10 eV–100 keV) is achievable in this setup, allowing to tune nuclear x-ray absorption spectra via optomechanical control. This paves ways for metrology applications, e.g., the detection of the 229Thorium clock transition, and an unprecedentedly precise control of x-rays using optical photons.
Similar content being viewed by others
Introduction
In cavity optomechanics1, the coupling of electromagnetic radiation to mechanical motion degrees of freedom2 can be used to connect quantum system with different resonant frequencies. For instance, via a common movable microlever, an optical cavity can be coupled to a microwave resonator to bridge the two frequency regimes3,4,5,6. Going towards shorter photon wavelengths is highly desirable and timely: in addition to improved detection, x-rays are better focusable and carry much larger momenta, potentially facilitating the entanglement of light and matter at a single-photon level. Unfortunately, a direct application of the so-far employed interface concept for a device that mediates an optical and an x-ray photon is bound to fail. First, the required high-performance cavities are not available for x-rays. Second, exactly the potentially advantageous high momentum carried by an x-ray photon renders necessary a different paradigm. We note here that x-rays are resonant to transitions in atomic nuclei which can be regarded as x-ray cavities with good quality. The rapidly developing field of x-ray quantum optics7,8,9,10,11,12 has recently reported so far key achievements and promising predictions for the mutual control of x-rays and nuclei13,14,15,16,17,18,19,20,21,22.
Here we present an innovative solution for coupling x-ray quanta to an optomechanical, solid-state device which can serve as a node bridging optical and x-ray photons in a quantum network. We demonstrate theoretically that using resonant interactions of x-rays with nuclear transitions, in conjunction with an optomechanical setup interacting with optical photons, an optical-x-ray interface can be achieved. Such a device would allow to tune x-ray absorption spectra and eventually to shape x-ray wavepackets or spectra for single photons19, 23,24,25,26,27,28 by optomechanical control. The role of the x-ray cavity is here adopted by a nuclear transition with long coherence time that eventually stores the high-frequency photon. Our calculations show that optomechanically induced transparency of x-rays can be achieved in the optical-x-ray interface paving the way for both metrology29 and an unprecedently precise control of x-rays using optical photons. In particular, a metrology-relevant application for the nuclear clock transition of 229Th, which lies in the vacuum ultraviolet (VUV) region, is presented.
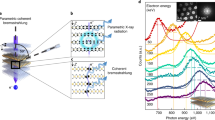
The optomechanical-nuclear system under investigation is illustrated in Fig. 1a. An optomechanical cavity of length L driven by an optical laser has an embedded layer in the tip of the microlever containing Mössbauer nuclei that interact with certain sharply defined x-ray frequencies. The nuclei in the layer have a stable or very long-lived ground state, and a first excited state that can be reached by a resonant x-ray Mössbauer, i.e., recoilless, transition. Typically, this type of nuclear excitation or decay occurs without individual recoil, leading to a coherent scattering in the forward direction30. Another type of excitation including the nuclear transition together with the motion of the microlever, i.e., phonons, can also be driven by red or blue-detuned x-rays. The nuclear two-level system can be therefore coupled to the mechanical motion of the microlever of mass M. The term “phonon” is used here to describe the vibration of the center of mass of the cantilever, visible in the tip displacement y. According to the specifications1 of various mechanical microlever designs, the phonons in this setup are expected to be in the MHz regime. We choose to label the space coordinate with y since the notation x will be used in the following for the x-ray field. An effective model of nuclear harmonic oscillator interacting with x-rays can be constructed to describe the hybridization31, 32 of the x-ray-nuclei-optomechanical systems. To this end the well-known optomechanical Hamiltonian1, 33,34,35,36,37 is extended to include also the x-ray interaction with the nuclear layer embedded in the tip of the microlever. Since the nuclear transition widths are very narrow (10−9–10−15 eV), we assume that the nuclei interact with a single mode of the x-ray field.
Sketch of the optomechanical interface between optical and x-ray photons. (a) The optical cavity is composed of a fixed mirror and a movable microlever whose oscillating frequency ω m can be controlled. A layer containing Mössbauer nuclei that can resonantly interact with x-rays is embedded in the tip of the microlever. (b) Level scheme of the effective nuclear harmonic oscillator. Lower (upper) three states correspond to the ground (excited) state g (e) while v (n) denotes the number of fluctuated cavity photons (number of phonons). Vertical green arrows depict the x-ray absorption by nuclei (with x-ray detuning Δ), and red diagonal arrows illustrate the beam splitter interaction between cavity photons and the microlever’s mechanical motion. The full yellow ellipse indicates the initial state of the system.
The full Hamiltonian of the system sketched in Fig. 1a is a combination of the optomechanical Hamiltonian1, 33, 36 and nuclear interaction with x-ray photons, which can be written in the interaction picture and linearized version as (see Methods and Supplementary Information for detailed derivation) as
Here, ω m is the optomechanically modified oscillation angular frequency of the microlever, Δ c is the effective optical laser detuning to the cavity frequency obtained after the linearization procedure, and G the coupling constant of the system. The operators \({\widehat{a}}^{ {\dagger } }\) \((\widehat{a})\) and \({\widehat{b}}^{ {\dagger } }\) \((\widehat{b})\) act as cavity photon and phonon creation (annihilation) operators, respectively. As further notations in Eq. 1, Δ = ω x − ω n is the x-ray detuning with ω n the nuclear transition angular frequency and ω x (k x ) is the x-ray angular frequency (wave vector), respectively. Ω is the Rabi frequency describing the coupling between the nuclear transition currents38 and the x-ray field, Y ZPF is the zero-point fluctuation, ħ the reduced Planck constant, and e and g denote the nuclear excited and ground state, respectively. The linearization procedure leading to the Hamiltonian in Eq. (1) was performed in the red-detuned regime, namely, cavity detuning Δ c = −ω m , which results in the so-called “beam-splitter” interaction1 with the optomechanical coupling strength G. We use the master equation involving the linearized interaction Hamiltonian to determine the dynamics of the interface system and the nuclear x-ray absorption spectra as detailed in Methods.
Figure 2 demonstrates the x-ray/VUV absorption spectra for several nuclear targets, together with an illustration of the corresponding Lamb-Dicke parameter η = k x Y ZPF. We consider nuclear transitions from the ground state to the first excited state in 229Th, 73Ge and 67Zn, with the relevant nuclear and optomechanical parameters presented in Table 1. The chosen optomechanics setup parameters39 are M = 0.14 μg, the inherent phonon frequency ω 0 = 2π × 0.95 MHz, the optomechanical damping rate γ 0 = 2π × 0.14 kHz, the optical cavity decay rate κ = 2π × 0.2 MHz, cavity frequency ω c ~ 1015 Hz and the optomechanical coupling constant \({G}_{0}=\frac{{\omega }_{c}}{L}{Y}_{{\rm{ZPF}}}\sqrt{{\bar{n}}_{{\rm{cav}}}}=2\pi \times 3.9\) Hz. These parameters have been experimentally demonstrated39. The required optomechanical system is a 25-mm-long Fabry-Pérot cavity made of a high-reflectivity mirror pad (reflectivity >0.99991) that forms the end-face39. A realistic estimate of the optical thickness values for the nuclear x-ray absorption is presented in the Supplementary Information.
Optomechanically tunable x-ray/VUV absorption spectra and the corresponding ratio of the x-ray wavelength and the zero-point fluctuation Y ZPF. The microlever has an embedded layer with (a) 229Th, (b) 73Ge, (c) 67Zn nuclei. Further parameters are taken from refs 1, 39 and the phonon number is chosen to be n = 5 × 106. Green solid line illustrates the spectra in the absence of the optomechanical coupling. Red dashed (blue dashed-dotted) lines show the optomechanically modified spectra under the action of an optical laser with about P = 2 nW (P = 5 nW). Red arrows indicate the first phonon lines. (d–f) Illustrations of the corresponding ratio of the x-ray wavelength and the zero-point fluctuation Y ZPF which determine the value of the Lamb-Dicke parameter.
For a comprehensive explanation, we begin with the case in the absence of optomechanical coupling, i.e., G = 0. Green lines in Fig. 2 illustrate a central nuclear absorption line with detuning Δ = 0 corresponding to m = n, and sidebands that occur with excitation or decay of phonons in the system m = n ± 1, n ± 2, …. The width of the peaks is determined by the value of \(s={\rm{\Gamma }}\mathrm{/2}+\kappa +{\gamma }_{m}\) (see Methods) of the order of MHz, similar in scale with the inhomogeneous broadening of the nuclear transition, which we neglect in the following. In order to resolve the sidebands, a constraint has to be imposed on the oscillation frequency of the microlever, i.e., the microlever frequency ω m > s, and the Franck-Condon coefficients \(|{F}_{n}^{m}|\mathop{ > }\limits_{ \tilde {}}0.1\) for at least the first phonon lines m = n ± 1 (see Methods). As a consequence, nuclear species with large Lamb-Dicke parameters η allow the observation of x-ray absorption sidebands. For example, compared to 229Th (η = 9.92 × 10−9) in Fig. 2a which presents only the zero phonon line, the spectra of 73Ge (η = 1.69 × 10−5) in Fig. 2b show an observable sideband as indicated by the red arrow. Moreover, there are several sidebands appearing in the spectrum of 67Zn (η = 11.87 × 10−5) depicted in Fig. 2c. Further Mössbauer nuclei with suitable first excited states whose decay rates are lower than the phonon angular frequency of around 6 MHz are for instance30 45Sc, 157Gd and 181Ta.
We are now ready to discuss the results including the optomechanical coupling, G > 0, illustrated by the blue and red dashed lines in Fig. 2. Remarkably, the optomechanical coupling introduces a dip at the center of each line. As illustrated also in Fig. 1b, the line splittings are caused by the optomechanical coupling G, which links different phonon Fock states via the beam splitter interaction1. We stress here that the nuclear x-ray absorption is only modified by the optomechanical coupling and does not have to do with x-ray recoil which is not occuring in our scheme. The depth and the spacing of the dips are proportional to the input optical laser power which modifies the strength G. Figure 2 shows that the absorption gradually goes to zero with increasing laser power P. The diagonalization of the Hamiltonian shows that the two split peaks around the zero phonon line are approximately positioned at \({\rm{\Delta }}=\pm \sqrt{{(G\sqrt{m+v+2mv}+s)}^{2}-2{s}^{2}}\). These two eigenvalues correspond to transitions between the ground state |g, v, n〉 and the two eigenstates \(\sqrt{\frac{(1+m)v}{(1+v)m}}|e,v-1,m+1\rangle \mp \sqrt{\frac{m+v+2\,mv}{(1+v)m}}|e,v,m\rangle +|e,v+1,m-1\rangle \) (see Methods). These eigenstates result in an analog of the so-called optomechanically induced transparency34,35,36 in the x-ray domain and offer means of controlling x-ray spectra. This is a new mechanism compared to typical target vibration experiments of Mössbauer samples23,24,25,26, in the classical phonon regime. The width of the splitting indicates that, with sufficient phonon numbers, the compelling optomechanical coupling can be accomplished by an optical laser. This feature may render control of x-ray quanta by means of weak optical lasers possible. In order to demonstrate this possibility, laser power parameters of few nW are used in the calculation to implement full transparency of x-rays around the nuclear resonance (see blue dashed-dotted and red dashed lines in Fig. 2).
Since the natural nuclear linewidths are far more narrow than present x-ray sources, the suitable solution for resolving the phonon sidebands of the keV x-ray or VUV resonance energies is to employ a Mössbauer drive setup. 67Zn Mössbauer spectroscopy for instance is a well-established technique with exceptionally high sensitivity for the gamma-ray energy. This has been exploited40 for precision measurements of hyperfine interactions 67Ga decay schemes, which populate excited states in 67Zn. The decay cascade will eventually populate the first excited level, which then releases single photons close to the resonance energy of the nuclear layer on the microlever. Assuming 50 mCi source activity and a solid angle corresponding to a 20 × 20 μm2 67Zn layer placed 10 cm away, the rate of x-ray photons close to the resonance is approx. 40 Hz. The fine-tuning for matching the exact resonance energy is achieved by means of the Doppler shift using a piezoelectric drive with μm/s velocities40.
While the 7.8 eV transition of 229Th is not traditionally regarded as a Mössbauer case, studies have shown that when embedded in VUV-transparent crystals, thorium nuclei are expected to be confined to the Lamb-Dicke regime41,42,43. In this regime one expects clear parallels to nuclear forward scattering techniques as known from traditional Mössbauer transitions. The uniquely low lying state and the very narrow transition width of approx. 10−19 eV makes 229Th a candidate for a stable and accurate nuclear frequency standard29. The most important step in this direction would be a precise measurement of the nuclear transition frequency, at present considered to be 7.8 ± 0.5 eV44. However, two major difficulties have been encountered in such measurements. First, the extremely narrow linewidth of 10−5 Hz makes very difficult both the excitation and the detection of fluorescence for this transition. Second, the isomeric transition has a disadvantageous signal to background ratio and strong fake signals from the environment have been so far impairing experiments45,46,47.
The VUV spectra of 229Th illustrated in Fig. 2a reveal that our chip-scale system could be used to determine the nuclear clock transition energy43, 44, 48. For this exceptional case with VUV nuclear transition energy, the excitation could be achieved with VUV lasers at present in development49. Two important advantages arise in the VUV-optomechanical interface: (i) the width \(s\gg {\rm{\Gamma }}\) broadens the VUV absorption linewidth by 10 orders of magnitude, namely, \(s\sim {10}^{10}\,{\rm{\Gamma }}\), facilitating the excitation and speeding up the nuclear target’s decoherence. (ii) The VUV spectra are optomechanically tunable. This can offer a clear signature of nuclear excitation circumventing false signals which unavoidably appear from either crystal sample45 or surrounding atmosphere46, 47.
We have put forward the theoretical formalism for optomechanically induced transparency of x-rays via optical control. In particular, our results show that the induced transparency may be achieved for nuclear transitions, with possible relevance for metrological studies, e.g., detection of nuclear clock transition. The opposite situation, of x-ray photons controlling the optomechanical setup, may open new possibilities for connecting quantum network devices50 on atomic and mesoscopic scales.
Methods
The full Hamiltonian of the system sketched in Fig. 1a is a combination of the optomechanical Hamiltonian and nuclear interaction with x-ray photons1, 33, 36 (see also Supplementary Information),
Here, ω 0 denotes the inherent phonon, ω c the resonant cavity, and ω n the nuclear transition angular frequency, respectively, and Ω is the Rabi frequency describing the coupling between the nuclear transition currents38 and the x-ray field. The operators \({\widehat{x}}^{ {\dagger } }\) \((\widehat{x})\) act as x-ray photon creation (annihilation) operators, respectively. The optomechanical coupling constant is given by G 0 = ω c Y ZPF/L, where Y ZPF denotes the zero-point fluctuation. Typically, the Hamiltonian expression above is transformed in the interaction picture and linearized with respect to the cavity photon number at equilibrium1, 36, i.e., the balance between external pumping and cavity loss. It is therefore convenient to neglect external cavity driving terms by classical optical fields in the Hamiltonian of the system1, 35, 36. We will see below that one can effectively attribute the modified properties of the system to the new optomechanical coupling constant G. By an unitary transformation to the rotating frame1 (see Supplementary Information), we obtain the Hamiltonian in the interaction picture
where Δ c = ω l − ω c is the optical laser detuning to the cavity frequency, ω l the optical laser angular frequency and Δ = ω x − ω n the x-ray detuning. The final step is to linearize the Hamiltonian by performing the transformation \(\widehat{a}\to \sqrt{{\overline{n}}_{cav}}+\widehat{a}\), where \({\overline{n}}_{cav}\) is the averaged cavity photon number, and \(\widehat{a}\) becomes the photon number fluctuation1, 36. The expression \({\overline{n}}_{cav}+\langle v|{\widehat{a}}^{ {\dagger } }\widehat{a}|v\rangle \) gives the photon number of the full cavity field. We neglect the first order terms of \({\widehat{a}}^{ {\dagger } }{\widehat{b}}^{ {\dagger } }\) and \(\widehat{a}\widehat{b}\) in the rotating wave approximation, and the second order terms proportional to \({\widehat{a}}^{ {\dagger } }\widehat{a}\). The zero order terms \({\overline{n}}_{{\rm{cav}}}({\widehat{b}}^{ {\dagger } }+\widehat{b})\) may be omitted1 after implementing an averaged cavity length shift \(\delta L=\hslash {\omega }_{c}{\overline{n}}_{cav}/(Lm{\omega }_{0}^{2})\) and the averaged cavity angular frequency shift \(\delta {\omega }_{c}=\hslash {\omega }_{c}^{2}{\overline{n}}_{cav}/({L}^{2}m{\omega }_{0}^{2})\), leading to the effective detuning1 Δ c → Δ c + δω c . We focus on the red-detuned regime, namely, cavity detuning Δ c = −ω m , which results in the so-called “beam-splitter” interaction1. We obtain the linearized Hamiltonian given in Eq. (1) with the new coupling constant \(G={G}_{0}\sqrt{{\overline{n}}_{{\rm{cav}}}}\). The effective phonon angular frequency ω m = ω 0 + δω 0 is introduced where \(\delta {\omega }_{0}=4{G}^{2}(\frac{{\omega }_{0}}{{\kappa }^{2}+16{\omega }_{0}^{2}})\) is the optomechanically modified oscillation angular frequency of the microlever1. The zero-point fluctuation of the microlever’s mechanical motion can then be written as \({Y}_{{\rm{ZPF}}}=\sqrt{\hslash /(2M{\omega }_{m})}\).
We use the master equation \({\partial }_{t}\widehat{\rho }=\frac{1}{i\hslash }[\widehat{H},\widehat{\rho }]+{\widehat{\rho }}_{dec}\) involving the linearized interaction Hamiltonian to determine the dynamics of the interface system (see Supplementary Information for the explicit form of each matrix). Decoherence processes are described by \({\widehat{\rho }}_{dec}\) including the spontaneous nuclear decay characterized by the rate Γ, the inherent mechanical damping rate of the microlever γ 0 and the optical cavity decay rate κ. The density matrix elements \({\rho }_{\beta d\nu }^{\alpha c\mu }={A}_{\alpha c\mu }^{\ast }{A}_{\beta d\nu }\) correspond to the state vector \(|\psi \rangle={A}_{gv-1n+1}|g,v-1,n+1\rangle+{A}_{gvn}|g,v,n\rangle+\) \({A}_{gv+1n-1}|g,v+1,n-1\rangle\) \(+{A}_{ev-1m+1}|e,v-1,m+1\rangle +{A}_{evm}|e,v,m\rangle +{A}_{ev+1m-1}|e,v+1,m-1\rangle \) where the system is initially prepared39, 51 in the nuclear ground state with \({\overline{n}}_{{\rm{cav}}}\) fluctuated cavity photons at the level of v and n phonons |g, v, n〉, and the nuclear excited state with m phonons |e, v, m〉 is reached by x-ray absorption, as illustrated in Fig. 1b. Four additional states with n ± 1 and m ± 1 phonons are coupled by the beam splitter interaction. In the red-detuned regime1 the mechanics of the optically tunable microlever can be described as \({\partial }_{t}^{2}y+{\gamma }_{m}{\partial }_{t}y+{\omega }_{m}^{2}y=0\), where y(t) denotes the displacement of the microlever as illustrated in Fig. 1(a), and the optomechanical damping rate shift is given by \(\delta {\gamma }_{0}=4{G}^{2}(\frac{1}{\kappa }-\frac{\kappa }{{\kappa }^{2}+16{\omega }_{0}^{2}})\). The effective optomechanical damping rate γ m = γ 0 + δγ 0. A relevant quantity is the average number of photons inside the cavity, which depends on the optical laser power \(P\) and is given by ref. 1 \({\overline{n}}_{{\rm{cav}}}=\frac{\kappa P}{\hslash {\omega }_{l}[{({\omega }_{l}-{\omega }_{c})}^{2}+{(\kappa \mathrm{/2})}^{2}]}\).
The x-ray absorption spectrum of the interface system is determined by the off-diagonal terms of the Hamiltonian \(\widehat{H}\), i.e., \(\langle e,v,m|\widehat{H}|g,v,n\rangle =\frac{\hslash {\rm{\Omega }}}{2}\langle m|{e}^{i{k}_{x}{Y}_{{\rm{ZPF}}}({\widehat{b}}^{ {\dagger } }+\widehat{b})}|n\rangle \). The phase term η = k x Y ZPF is the so-called Lamb-Dicke parameter, and for \(\eta \sqrt{n} < 1\), \({F}_{n}^{m}=\langle m|{e}^{i\eta ({\widehat{b}}^{ {\dagger } }+\widehat{b})}|n\rangle \) denotes the Franck-Condon coefficient33
Typically, only low nuclear excitation is achieved in nuclear scattering with x-rays, such that the master equation in the perturbation region \({\rm{\Gamma }}\mathrm{/2}+\kappa +{\gamma }_{m} > G\gg {\rm{\Omega }}\) can be used, corresponding to the stable regime. We note here that nuclear scattering experiments and simulations have confirmed in this low excitation regime the validity of the semi-classical limit for x-ray-nucleus interaction52. The steady state solution reads
where the total decoherence rate notation \(s={\rm{\Gamma }}\mathrm{/2}+\kappa +{\gamma }_{m}\) was introduced. By replacing \({F}_{n}^{m}\) with \(|{F}_{n}^{m}|\), the sum of the imaginary part of Eq. (6) for corresponding transitions, namely, \({\sum }_{m=n-6}^{n+6}{\rm{Im}}[{\rho }_{gvn}^{evm}({\rm{\Delta }})]\), provides the x-ray absorption spectrum. Eq. (6) shows that the x-ray absorption is directly dependent on the numbers of photons \({\overline{n}}_{{\rm{cav}}}\) and averaged number of phonons m and n and their statistics.
References
Aspelmeyer, M., Kippenberg, T. J. & Marquardt, F. Cavity optomechanics. Rev. Mod. Phys. 86, 1391–1452 (2014).
Brawley, G. et al. Non-linear optomechanical measurement of mechanical motion. Nature Commun. 7, 10988, doi:10.1038/ncomms10988 (2015).
Barzanjeh, S., Abdi, M., Milburn, G. J., Tombesi, P. & Vitali, D. Reversible optical-to-microwave quantum interface. Phys. Rev. Lett. 109, 130503, doi:10.1103/PhysRevLett.109.130503 (2012).
Bochmann, J., Vainsencher, A., Awschalom, D. D. & Cleland, A. N. Nanomechanical coupling between microwave and optical photons. Nature Phys. 9, 712–716 (2013).
Andrews, R. W. et al. Bidirectional and efficient conversion between microwave and optical light. Nature Phys. 10, 321–326 (2014).
Barzanjeh, S. et al. Microwave quantum illumination. Phys. Rev. Lett. 114, 080503, doi:10.1103/PhysRevLett.114.080503 (2015).
Suckewer, S., Skinner, C. H., Milchberg, H., Keane, C. & Voorhees, D. Amplification of stimulated soft x-ray emission in a confined plasma column. Phys. Rev. Lett. 55, 1753–1756 (1985).
Rocca, J. J. et al. Demonstration of a discharge pumped table-top soft-x-ray laser. Phys. Rev. Lett. 73, 2192–2195 (1994).
Lemoff, B. E., Yin, G. Y., Gordon, C. L. III, Barty, C. P. J. & Harris, S. E. Demonstration of a 10-hz femtosecond-pulse-driven XUV laser at 41.8 nm in Xe IX. Phys. Rev. Lett. 74, 1574–1577 (1995).
Glover, T. E. et al. Controlling x-rays with light. Nature Phys. 6, 69–74 (2010).
Rohringer, N. et al. Atomic inner-shell x-ray laser at 1.46 nanometres pumped by an x-ray free-electron laser. Nature 481, 488–491 (2012).
Adams, B. W. et al. X-ray quantum optics. J. Mod. Opt. 60, 2–21 (2013).
Röhlsberger, R., Schlage, K., Sahoo, B., Couet, S. & Rüffer, R. Collective Lamb shift in single-photon superradiance. Science 328, 1248–1251 (2010).
Röhlsberger, R., Wille, H. C., Schlage, K. & Sahoo, B. Electromagnetically induced transparency with resonant nuclei in a cavity. Nature 482, 199–203 (2012).
Liao, W.-T., Pálffy, A. & Keitel, C. H. Coherent storage and phase modulation of single hard-x-ray photons using nuclear excitons. Phys. Rev. Lett. 109, 197403, doi:10.1103/PhysRevLett.109.197403 (2012).
Heeg, K. P. et al. Vacuum-assisted generation and control of atomic coherences at x-ray energies. Phys. Rev. Lett. 111, 073601, doi:10.1103/PhysRevLett.111.073601 (2013).
Liao, W.-T. & Pálffy, A. Proposed entanglement of x-ray nuclear polaritons as a potential method for probing matter at the subatomic scale. Phys. Rev. Lett. 112, 057401, doi:10.1103/PhysRevLett.112.057401 (2014).
Liao, W.-T. Coherent Control of Nuclei and X-Rays (Springer, 2014).
Vagizov, F., Antonov, V., Radeonychev, Y., Shakhmuratov, R. & Kocharovskaya, O. Coherent control of the waveforms of recoilless γ-ray photons. Nature 508, 80–83 (2014).
Liao, W.-T. & Ahrens, S. Gravitational and relativistic deflection of x-ray superradiance. Nature Photon. 9, 169–173 (2015).
Heeg, K. P. et al. Interferometric phase detection at x-ray energies via fano resonance control. Phys. Rev. Lett. 114, 207401, doi:10.1103/PhysRevLett.114.207401 (2015).
Heeg, K. P. et al. Tunable subluminal propagation of narrow-band x-ray pulses. Phys. Rev. Lett. 114, 203601, doi:10.1103/PhysRevLett.114.203601 (2015).
Perlow, G. J. Quantum beats of recoil-free γ radiation. Phys. Rev. Lett. 40, 896–899 (1978).
Mketchyan, A., Arutyunyan, G., Arakelyan, A. & Gabrielyan, R. Modulation of Mössbauer radiation by coherent ultrasonic excitation in crystals. Phys. Stat. Sol. B 92, 23–29 (1979).
Helistö, P., Ikonen, E. & Katila, T. Enhanced transient effects due to saturated absorption of recoilless γ radiation. Phys. Rev. B 34, 3458–3461 (1986).
Popov, S. L., Smirnov, G. V. & Shvyd’ko, Y. V. Observed strengthening of radiative mechanism for a nuclear reaction in the interaction of radiation with nuclei in a vibrating absorber. JETP Lett. 49, 747–750 (1989).
Kocharovskaya, O., Kolesov, R. & Rostovtsev, Y. Coherent optical control of Mössbauer spectra. Phys. Rev. Lett. 82, 3593–3596 (1999).
Vagizov, F., Kolesov, R., Olariu, S., Rostovtsev, Y. & Kocharovskaya, O. Experimental observation of vibrations produced by pulsed laser beam in MgO: 57Fe. Hyperfine Interact. 167, 917–921 (2006).
Peik, E. & Tamm, C. Nuclear laser spectroscopy of the 3.5 eV transition in Th-229. Europhys. Lett. 61, 181–186 (2003).
Röhlsberger, R. Nuclear Condensed Matter Physics With Synchrotron Radiation: Basic Principles, Methodology and Applications (Springer-Verlag, 2004).
Shkarin, A. B. et al. Optically mediated hybridization between two mechanical modes. Phys. Rev. Lett. 112, 013602, doi:10.1103/PhysRevLett.112.013602 (2014).
Sete, E. A. & Eleuch, H. Controllable nonlinear effects in an optomechanical resonator containing a quantum well. Phys. Rev. A 85, 043824, doi:10.1103/PhysRevA.85.043824 (2012).
Eschner, J., Morigi, G., Schmidt-Kaler, F. & Blatt, R. Laser cooling of trapped ions. J. Opt. Soc. Am. B 20, 1003–1015 (2003).
Weis, S. et al. Optomechanically induced transparency. Science 330, 1520–1523 (2010).
Agarwal, G. S. & Huang, S. Electromagnetically induced transparency in mechanical effects of light. Phys. Rev. A 81, 041803, doi:10.1103/PhysRevA.81.041803 (2010).
Agarwal, G. S. Quantum Optics (Cambridge University Press, 2012).
Faust, T., Rieger, J., Seitner, M. J., Kotthaus, J. P. & Weig, E. M. Coherent control of a classical nanomechanical two-level system. Nature Phys. 9, 485–488 (2013).
Shvyd’ko, Y. V. et al. Storage of nuclear excitation energy through magnetic switching. Phys. Rev. Lett. 77, 3232–3235 (1996).
Gröblacher, S., Hammerer, K., Vanner, M. R. & Aspelmeyer, M. Observation of strong coupling between a micromechanical resonator and an optical cavity field. Nature 460, 724–727 (2009).
Long, G. J. & Grandjean, F. (eds) Mössbauer Spectroscopy Applied to Magnetism and Materials Science (Springer Science + Business Media, New York, 1993).
Rellergert, W. G. et al. Constraining the evolution of the fundamental constants with a solid-state optical frequency reference based on the 229Th nucleus. Phys. Rev. Lett. 104, 200802, doi:10.1103/PhysRevLett.104.200802 (2010).
Kazakov, G. A. et al. Performance of a 229-Thorium solid-state nuclear clock. New J. Phys. 14, 083019, doi:10.1088/1367-2630/14/8/083019 (2012).
Liao, W.-T., Das, S., Keitel, C. H. & Pálffy, A. Coherence-enhanced optical determination of the th229 isomeric transition. Phys. Rev. Lett. 109, 262502, doi:10.1103/PhysRevLett.109.262502 (2012).
Beck, B. R. et al. Energy splitting of the ground-state doublet in the nucleus Th229. Phys. Rev. Lett. 98, 142501, doi:10.1103/PhysRevLett.98.142501 (2007).
Stellmer, S., Schreitl, M. & Schumm, T. Radioluminescence and photoluminescence of Th:CaF2 crystals. Sci. Rep. 5, 15580, doi:10.1038/srep15580 (2015).
Shaw, R. W., Young, J. P., Cooper, S. P. & Webb, O. F. Spontaneous ultraviolet emission from 233Uranium/229Thorium samples. Phys. Rev. Lett. 82, 1109–1111 (1999).
Utter, S. B. et al. Reexamination of the optical gamma ray decay in 229Th. Phys. Rev. Lett. 82, 505–508 (1999).
Jeet, J. et al. Results of a direct search using synchrotron radiation for the low-energy 229Th nuclear isomeric transition. Phys. Rev. Lett. 114, 253001, doi:10.1103/PhysRevLett.114.253001 (2015).
Nomura, Y. et al. Coherent quasi-cw 153 nm light source at 33 MHz repetition rate. Optics Lett. 36, 1758–1760 (2011).
Azuma, K., Tamaki, K. & Lo, H.-K. All-photonic quantum repeaters. Nature Commun. 6, 6787, doi:10.1038/ncomms7787 (2015).
Chan, J. et al. Laser cooling of a nanomechanical oscillator into its quantum ground state. Nature 478, 89–92 (2011).
Kong, X., Liao, W.-T. & Pálffy, A. Field control of single x-ray photons in nuclear forward scattering. New J. Phys. 16, 013049, doi:10.1088/1367-2630/16/1/013049 (2014).
Acknowledgements
The authors would like to thank Markus Aspelmeyer for fruitful discussions. WTL is supported by the Ministry of Science and Technology, Taiwan (Grant No. MOST 105-2112-M-008-001-MY3). WTL is also supported by the National Center for Theoretical Sciences, Taiwan. AP gratefully acknowledges funding by the EU FET-Open project 664732.
Author information
Authors and Affiliations
Contributions
W.T.L. and A.P. contributed equally to this work. W.T.L. performed the numerical calculations. W.T.L. and A.P. discussed the results and wrote the manuscript text.
Corresponding authors
Ethics declarations
Competing Interests
The authors declare that they have no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Liao, WT., Pálffy, A. Optomechanically induced transparency of x-rays via optical control. Sci Rep 7, 321 (2017). https://doi.org/10.1038/s41598-017-00428-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-017-00428-w
This article is cited by
-
Slowing down x-ray photons in a vibrating recoilless resonant absorber
Scientific Reports (2022)
-
Acoustically induced transparency for synchrotron hard x-ray photons
Scientific Reports (2021)
-
Towards a 229Th-Based Nuclear Clock
Measurement Techniques (2018)
-
Tailored plasmon-induced transparency in attenuated total reflection response in a metal–insulator–metal structure
Scientific Reports (2017)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.