Abstract
Understanding the fine scale and subnational spatial distribution of reproductive, maternal, newborn, child, and adolescent health and development indicators is crucial for targeting and increasing the efficiency of resources for public health and development planning. National governments are committed to improve the lives of their people, lift the population out of poverty and to achieve the Sustainable Development Goals. We created an open access collection of high resolution gridded and district level health and development datasets of India using mainly the 2015–16 National Family Health Survey (NFHS-4) data, and provide estimates at higher granularity than what is available in NFHS-4, to support policies with spatially detailed data. Bayesian methods for the construction of 5 km × 5 km high resolution maps were applied for a set of indicators where the data allowed (36 datasets), while for some other indicators, only district level data were produced. All data were summarised using the India district administrative boundaries. In total, 138 high resolution and district level datasets for 28 indicators were produced and made openly available.
Similar content being viewed by others
Background & Summary
Reproductive, maternal, newborn, child health and development, adolescent’s health, climate change, ending poverty and hunger and promoting gender equality and literacy among boys and girls are all central to the Sustainable Development Goals (SDG) agenda for 2030. With the commitment of World leaders who pledged common action and endeavour across such a broad and universal policy agenda, SDGs have the ambition of building a better future for all people, achieving improved health and quality of life of current and future generations, implement sustainable development and equal access to health for all, and leaving no one behind1.
In India, women and children comprise approximately 70% of the population2. As part of its interventions at national and sub-national levels, the Ministry of Women and Child Development promotes social and economic empowerment of women and the care, development, and protection of children3. However, despite the gains over the last three decades, uplifting the condition of women and children remains a challenge4,5.
Over recent decades, the Government of India has shown a commitment to addressing several development concerns, especially those affecting children, adolescents, and women4. Through a series of initiatives in the context of its national development agenda, the Government has successfully lifted more than 250 million people out of multidimensional poverty through economic growth and empowerment6,7, improved health and sanitation conditions, electricity and housing as well as nutrition and education among vulnerable populations and enhanced social inclusion and social protection in the country8. Moreover, it is widely recognised that there is an association between air pollution and adverse health outcomes9,10, and increasingly studies have investigated the impact of the burden of air pollution on the economy11. Climate action strategies for clean and efficient energy systems have been put in place8,12, and progress observed towards the achievement of the climate-related SDGs (SDG 13)1. However India presents wide variations between and within states in terms of the effects of air pollution on health and the economy11.
Despite progress in all areas and while the reforms implemented to achieve the SDGs have reduced the disparities across many socio-economic, health and environmental indicators, within country inequalities are still widespread13,14,15. The country is ranked 120 out of 193 UN Member States, with a score of 60.07, where the score measures a country’s total progress towards achieving all 17 SDGs and a score of 100 signifies that all goals have been achieved16,17.
Regional level studies have shown heterogeneities in maternal, newborn and child health indicators, and inequalities in child undernutrition and in access to health care affect the most vulnerable groups in the country15,18,19,20,21. Some areas of India still lag behind on women’s education, economic empowerment, access to maternal and child health services, child mortality and malnutrition22. When looking at individual health and development indicators, data from the NFHS-4 survey show how inequalities persist. For example, there is a difference of 48 percentage points between women in the richest quintile (73%) and those in the poorest quintile (25%) in the percentage of women attended four or more times during pregnancy by any provider23.
Reproductive, maternal, newborn, child, and adolescent health and development indicators are essential to track progress towards the SDGs and to inform development policies, ensuring that no one is left behind. Monitoring progress towards the SDGs for 2030 is typically done at national level24,25, while concerns about health and wealth inequity indicate that there is a need for analysis of health indicators at the microgeographic level or for population subgroups15. With geospatial approaches being used to produce fine scale estimates of SDG-related indicators, sub-national maps are now widely produced to support planning and implementation of health and development interventions in different settings, and geographically disaggregated information are increasingly serving the targeting of resources and more precise policy applications26,27,28.
Here, using the most recent sources of data at the time of writing, including household surveys and other openly available data sources, we assembled a collection of subnational reproductive, maternal, newborn, child, and adolescent health and development indicators for India, to support policy and planning activities and to improve geographic targeting towards the achievement of the SDGs. A health and development atlas consisting of a collection of 138 datasets for 28 indicators at subnational scales, including estimated 5 km × 5 km high-resolution maps of India with relative prediction uncertainties mapped, as well as district level maps of India, was assembled to support the review of development and health strategies and inform future actions.
Methods
Gridded estimates of selected reproductive, maternal, newborn, child, and adolescent health and development indicators were produced for India at a spatial resolution of 5 km. Where the construction of gridded estimates was not feasible, district level estimates were produced.
The indicators mapped in this work were collected from a range of sources, including geolocated and nationally and sub-nationally representative household surveys and pre-existing subnational datasets. These covered indicators on child, adolescent and women’s health, nutrition, and wellbeing, as well as selected climatic indicators. For each indicator, the most appropriate data source was selected, according to criteria such as date, administrative level unit, sample size and policy priority. Where possible, for selected indicators and using the latest available household survey for India at the time of writing, geospatial modelling techniques were applied to estimate 5 km spatial resolution maps. Conversely, district level maps only were produced in the following cases: i) where indicators or rates were derived through application of a model to the household survey data; ii) for indicators classified as rare events; iii) where input data sources were already at district level and no finer scale resolutions were available. For cases i) and ii) we define the data produced as maps of rare events or model-based indicators at district level, and the main source of data was the NFHS-4. All datasets were finally harmonised and aggregated at district level. Figure 1 shows a flowchart of the data preparation and processing methods adopted to generate gridded and district level reproductive, maternal, newborn, child, and adolescent health and development indicators datasets in India. Details of each indicator including definition, geographical level of aggregation of the output dataset, data source and year are outlined in Tables1,2.
Data collection, preparation, and processing
Estimating 5 km × 5 km high resolution datasets using cluster level proportions from household surveys
India NFHS-4: Geolocated and sub-nationally representative household survey
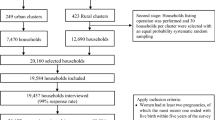
The 2015–16 India National Family Health Survey (NFHS-4) was conducted by the Ministry of Health and Family Welfare, Government of India and International Institute for Population Sciences, Mumbai, with the technical assistance of ICF through the Demographic and Health Surveys (DHS) Program (funded by USAID). NFHS-4 provides estimates of fertility, mortality, family planning, reproductive, maternal and child health, wealth and nutrition indicators at the national and state levels. Most of the indicators are also provided for the 640 districts of India (as per the Census, 2011)22.
NFHS-4 is based on a two-stage stratified sample of households, where 28,586 primary sampling units (PSUs), also called enumeration areas (EAs) or clusters, were first selected with probability proportional to the EA size and by urban and rural areas, with a total of 28,522 PSUs completed. The 2011 census served as the sampling frame for the selection of PSUs, where PSUs were villages in rural areas and Census Enumeration Blocks in urban areas. PSUs with fewer than 40 households were linked to the nearest PSU22. This first stage of selection provided a listing of households for the second stage, where segments of PSUs of approximately 100–150 households were randomly selected for the survey using systematic sampling with probability proportional to segment size. Survey clusters can therefore be either PSUs or segments of PSUs. Subsequently, in every selected rural and urban cluster, 22 households were randomly selected with systematic sampling, to create statistically reliable estimates of key demographic and health variables29,30. PSUs or EAs are usually pre-existing geographical areas which are derived from census. The boundaries of the EAs are defined by the country’s census bureau, as are the urban and rural status of each cluster. In recent DHS surveys geolocations (latitude and longitude) for each survey cluster are available. The survey cluster coordinates represent an estimated centre of the cluster and are collected in the field through GPS receivers. The georeferenced datasets can be linked to individual and household records in DHS household surveys through unique cluster identifiers. To protect the confidentiality of respondents, cluster locations are displaced up to 5 km in rural areas and up to 2 km in urban areas at the processing stage. A further 1% of the rural clusters can be displaced up to 10 km. Because displacement affects the physical location of the data, it is necessary to account for displacement when undertaking spatial modelling with DHS surveys31,32.
Construction of the indicators for high resolution mapping using NFHS-4
Cluster-level proportions of reproductive, maternal, newborn, child, and adolescent health and development indicators were calculated and used as input data to construct 5 km × 5 km gridded high resolution maps using geospatial modelling techniques, where the GPS from the surveys and spatial covariates were exploited to predict surfaces33,34,35,36.
The construction of cluster level indicators from the India NFHS-4 survey followed the definitions and instructions of the DHS programme22,37,38. Details of each indicator are outlined in Tables 1 and 2.
Geospatial covariates for high resolution mapping
We considered variables that are known to influence or are proxies for other variables that are known to influence the health and development indicators in this study. We categorized them as geographical, socioeconomic, and environmental variables; see Table SI.1. We also called these variables “geospatial covariates”. Geospatial covariates are important for model construction, parameter estimation and prediction. They provide information on the observed spatial distribution of the response variables and are utilized as predictors to improve the predictions of the response variables28,35,39. Since the geospatial covariates were collated from different sources, we adjusted them such that they are all gridded datasets at the 1 km × 1 km resolution. For modelling purposes, we aggregated the geospatial covariate gridded datasets further to a 5 km × 5 km resolution. The geospatial covariates at each health and development surveyed cluster location were extracted using ESRI ArcGIS v10.6.
Constructing high resolution maps for indicators with geospatial modelling techniques
To construct prediction and uncertainty surfaces for the health and development indicators, we used the following: the health and development indicator datasets, the geospatial covariate gridded datasets, and the boundary information. The methodology involved constructing models, fitting the models, prediction with the models and validating the models; see Fig. 2 for an illustration of the workflow.
Flow chart outlining the model constructing, fitting, and validating process of the health and development indicators. (a) The DHS geolocated household survey dataset of iron tablets or syrup received during antenatal care visits. (b) Geospatial covariates stack at the 1 × 1 km resolution. (c) Prediction (mean) surface for antenatal iron or syrup coverage at the 5 km × 5 km resolution. (d) Uncertainty (standard deviation) for antenatal iron or syrup coverage at the 5 km × 5 km resolution.
The model construction was two-staged. In the first stage, we checked for multicollinearity amongst the geospatial covariates. In the second stage, we employed the backward stepwise model selection algorithm to select the optimal set of geospatial covariates for the target indicator.
To check for multicollinearity, we first created a Pearson correlation matrix for the geospatial covariates and any pairs with a Pearson correlation coefficient r > 0.8 were flagged. The flagged covariates were then individually fitted in non-Bayesian binomial generalised linear models (GLMs). We then calculated the Bayesian information criteria (BIC) of the models. The covariate in the model with a lower BIC was retained while the covariate in the model with the greater BIC was omitted. To further ensure that multicollinearity between the remaining geospatial covariates was not present, we calculated the variance inflation factors (VIFs) and any covariate that had a VIF > 4 was omitted.
After checking for multicollinearity, a backward model selection algorithm was used to select the best subset of geospatial covariates for the target indicator. To obtain the optimal set of geospatial covariates, the following steps were followed:
-
1.
The remaining geospatial covariates were fitted in a non-Bayesian binomial GLM and the BIC was calculated.
-
2.
A covariate was removed from the fitted model and the BIC recalculated.
-
3.
If the recalculated BIC was less than the previously calculated BIC, this subset of covariates was preferred.
-
4.
These steps were performed iteratively until the recalculated BIC is not less than the BIC calculated from the previous iteration.
Using the optimal set of geospatial covariates obtained and each health and development indicator as input data, a Bayesian point-referenced spatial binomial GLM fitted in INLA was fitted.
For i = 1,…,n, let Y(si) denote the number of events of the target indicator at the survey cluster location si. For example, Y(si) may be the number of women who use modern contraception or may be the number of women who received iron tablets or syrup during antenatal care visits; see Tables 1,2 for the full list of health development indicators considered in this study. Furthermore, let m(si) denote the total number of surveys conducted within the survey cluster location. The Bayesian point-referenced spatial binomial GLM is given as follows:
Y(si) follows a Binomial distribution with the parameter p(si) which denotes the proportion of events happening at the survey cluster si. Following the examples above, this may be the proportion of women who use modern contraception or the proportion of women who received iron tablets or syrup during antenatal care visits. The model then assumes a logit link on p(si) with the linear predictors which consist of the fixed effects xʹ(si)β, spatial random effects ω(si) and independent identical (iid) random effects ϵ(si) as shown in Eq. (1).
The fixed effects are given by the geospatial covariates xʹ(si) selected from the backward model selection algorithm mentioned above and β is a vector of regression coefficients to be estimated. The spatial random effects follow a multivariate normal distribution with zero-mean and some covariance matrix Σω as shown in Eq. (2). In this study, elements of the covariance matrix are calculated with the exponential covariance function as shown in Eq. (3). The exponential covariance function is calculated with the spatial variance \({\sigma }_{\omega }^{2}\), the spatial decay parameter ϕ and the n × n Euclidean distance matrix D between the survey cluster locations. The parameters \({\sigma }_{\omega }^{2}\) and ϕ are unknown and are to be estimated in INLA. The iid random effects follow a normal distribution with a mean of zero and an unknown variance \({\sigma }_{\epsilon }^{2}\) which will be estimated along with the other parameters mentioned above.
We estimated the parameters of Eq. (1) in the Bayesian framework with the integrated nested Laplace approximation (INLA) method in conjunction with the stochastic partial differential equation (SPDE) approach40,41. More specifically, the parameters are the regression coefficients β, the spatial range (3/ϕ), the variance of the spatial random effect \({\sigma }_{\omega }^{2}\), and the variance of the iid random effect \({\sigma }_{\epsilon }^{2}\). The INLA method was developed by Rue et al.41 as an alternative to the traditional Markov Chain Monte Carlo methods used for modelling and parameter estimation in the Bayesian framework. It reduces computation time through analytic approximations with the Laplace method; see41,42 for a more comprehensive commentary on INLA. The SPDE approach projects continuous Gaussian fields, such as Eq. (2), as discrete Gaussian Markov random fields to further reduce computation cost43. This projected surface is called a “mesh” since the projection involves triangulating the spatial domain under consideration. The decision lies in the number of triangles to create within the spatial domain as more triangles will improve the approximation but increases computation time44. The SPDE approach implemented with the INLA method is useful for high dimensional problems such as parameter estimation for spatial models. The INLA method can be implemented in the statistical programming software R45 with the INLA package40,41.
To fit Eq. (1) with the INLA-SPDE approach, we specify non-informative priors N(0,1000) on β, LogGamma(2,1) on the variance of the iid random effect, and penalized complexity46 priors \(p\left({r}_{sp} < {r}_{0}\right)=0.01\) and \(p\left({\sigma }_{\omega } < 3\right)=0.01\) for (3/ϕ) and \({\sigma }_{\omega }^{2}\) respectively. Here, rsp denotes the spatial range to avoid confusion with the Pearson correlation coefficient and r0 is calculated as 5% of the extent of India in the east-west direction. The parameter σω is called the partial sill and is the square-root of \({\sigma }_{\omega }^{2}\). The mesh was constructed by supplying the coordinates of the surveyed clusters and additional arguments to determine the number of triangles to construct within our study domain.
After fitting the model with INLA, we predict using the geospatial covariate gridded datasets at the 5 km × 5 km resolution. We extract the mean and the standard deviation from the distribution of the prediction at each grid to create the prediction and uncertainty surfaces.
An application of the modelling framework just described showing how to construct 5 km × 5 km high resolution map and uncertainty for the percentage of women who received iron tablets or syrup during antenatal care visits is presented in SI.2 to SI.6.
Tables SI.7 show the summary statistics of the fitted models for each health and development indicator calculated at 5 km × 5 km high-resolution using INLA.
Estimating district level proportions and rates from household surveys for other indicators based on NFHS-4
Construction of indicators at district level using NFHS-4
The India NFHS-4 survey was constructed to be representative at national, province and district level for most of the indicators. In the case of rare events indicators such as stillbirth rates, or where more sophisticated estimation methods were needed such as mortality rates, indicators were constructed and mapped at district level (denoted in this work as “NFHS-4 rare events indicators or model-based district level indicators”). Mortality rates and the fertility rates were modelled using a generalised linear model and consider the number of occurrences (birth or deaths) as a random variable47. The distribution of the random variable of occurrences is assumed to be Poisson in the case of fertility rates and binomial for mortality rates. The child mortality rate was calculated using a synthetic cohort life table approach which combines mortality probabilities for specific age segments (12–23, 24–35, 36–47, and 48–59) into the standard age segment (1 to 4 years). Given the scarcity of occurrences measuring the events of interest across small-scale geographical areas (i.e., clusters) district level estimates were created. For example, for stillbirth rates the amount of cluster with no data was around 90% while for teenage pregnancies it was about 75%.
The confidence intervals for modelled rates, mortality, and fertility rates were calculated using the delta method to estimate the standard error using the variance-covariance matrix of the modelled rates47. The confidence intervals for proportions (e.g., teenage pregnancies) were calculated using the Wilson Score method48,49,50,51. The confidence intervals for the stillbirth rate were calculated using Byar’s approximation for counts above 552,53,54 while tables of the exact probabilities were used for counts below 555.
The construction of district level indicators from the India NFHS-4 survey followed the definitions and instructions of the DHS programme22,37,38. Details of each indicator are outlined below in Tables 1,2.
District or State level data not available through household surveys or already estimated
For indicators where data was not available in the NFHS-4, we used data from other openly available data sources, these included: the Socioeconomic Data and Applications Centre (SEDAC) https://sedac.ciesin.columbia.edu/56,57, from which we derived Global Annual PM2.5 Grids for years 2000–2015, satellite-derived night-time lights processed by WorldPop (2016)58,59 which was used as a proxy for energy consumption and, Institute for Health Metrics and Evaluation (IHME) http://www.healthdata.org/, used to obtain the data on women aged 15 to 49 who have completed secondary education for 2010, 2015 and 201760.
Summarization at the district level and joining to boundaries
The data for 28 health and development indicators including high-resolution estimates and district level estimates were matched and summarised using an adapted vector geographical boundary (shapefile), based on the 2011 census, obtained from DataMeet Community Maps Project61.
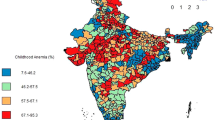
Figure 3 below shows an example of an indicator at 5 km × 5 km high resolution (left panel) and summarised at the district level (right panel) for the percentage of women receiving iron Tablets or syrup during ANC visits. Indicator at high resolution allow users to summarise the data to a custom based area, while district area allows the comparability of the data at a known administrative level.
Data Records
The different types of data available described in this article referring to India are listed in Table 3. The high-resolution maps of the modelled indicators with their associated uncertainty have been compiled62. All the indicators estimated in this article have been summarised at the district level and have been compiled in a shapefile and CSV63 for those rare events/ model-based indicators confidence intervals were calculated and compiled at the district level in a shapefile and a CSV64.
The input data used to produce this work are freely available after approval of registration and with a signed data access agreement on the websites of the data providers (i.e., NFHS-4). All other data sources were openly available and are referenced in Table SI.1.
Technical Validation
Model validation for the bayesian point-referenced spatial binomial GLM model used to construct high resolution maps
To access the performance of the model constructed for the target indicator, we used the k-fold cross validation and computed several evaluation metrics. The k-fold cross validation partitions the dataset into k parts then trains the model with k-1 parts of the dataset and tests the trained model with the kth part of the dataset. We calculated the following evaluation metrics:
the Pearson’s correlation coefficient, the root mean squared error, the mean absolute error, and the percentage bias. In the evaluate metrics above, pi is used to denote the observed values – i.e., the proportions of the target indicators partitioned for testing – and \({\widehat{p}}_{i}\) is used to denote the predicted mean values from the Bayesian point-referenced spatial binomial GLM.
The notation ρ(⋅) is used to the denote the Pearson’s correlation coefficient in Eq. (4). Explicitly this is calculated with the covariance of the observed and predicted values and the standard deviation of the observed and predicted values
Here, note that the vectors \(\widehat{{\boldsymbol{p}}}=\left({\widehat{p}}_{1},\ldots ,{\widehat{p}}_{{n}_{test}}\right)\) and \({\boldsymbol{p}}=\left({p}_{1},\ldots ,{p}_{{n}_{test}}\right)\) where ntest is the number of observations partitioned for testing. Better predictive performance is reflected from a greater Pearson’s correlation coefficient. The root mean squared error (RMSE), mean absolute error (MAE) and percentage bias is given in Eqs. (5–7) respectively. Better predictive performance is reflected from smaller RMSE, MAE and percentage bias values.
Table SI.8 show the summary of model validation metrics for each health and development indicator calculated at 5 km × 5 km high-resolution using INLA.
Confidence intervals for estimates of district level indicators calculated using NFHS-4
For those indicators where NFHS-4 district level estimates were produced (rare events and model-based district level indicators), we provided raster data of uncertainty associated with the indicators by mapping the difference between upper and lower limit of the 95% confidence interval relative to the point estimator of the indicator. The narrower the confidence interval, i.e., the smaller the value, lesser the uncertainty around the estimated indicator and thus higher the precision. More information on how confidence intervals were constructed can be found in the section “Construction of indicators at district level using NFHS-4”.
Accuracy of data
The accuracy and quality of estimates from survey data such as those provided by the DHS (NFHS) have been assessed in several reports outside this work65,66. Input data (e.g. survey clusters and covariates) carry some degree of uncertainty which may affect the actual values in small areas. In particular, the low birth weight indicator has a low degree of correlation (see SI.8) and the quality of the birthweight data from the DHS surveys has been widely investigated. The authors recommend using the birthweight indicator with caution67,68,69. Authors recommend to use the birthweight indicator with caution. The introduction of cluster location random displacement can introduce uncertainty although in general studies have shown that the impact of displacement is considered to be limited70,71. Other sources of uncertainty may also be due to temporal miss-match of some of the covariates, as discussed in previous works72,73.
Most of the data used in this work, and in particular NFHS-4 round, refer to years 2015–16. At the time of writing, NFHS-4 round was the latest available survey for India. Upcoming work will focus on constructing a similar atlas using the new NFHS-5 data just released and assessing changes between the round 4 and 5.
Usage Notes
The datasets presented here can be used both to (i) support applications measuring sub-national metrics of reproductive, maternal, newborn, child, and adolescent health and development for India and (ii) to inform planning decisions, target interventions and development programs. However, considering that the gridded high-resolution datasets represent modelling outputs generated using ancillary covariates, to avoid circularity, they should not be used to make predictions or explore relationships about any of those ancillary datasets74. Thus, before using the gridded high-resolution datasets in correlation analyses against factors which are included in their construction (e.g., correlating children stunting with temperature), ideally the modelling process should be re-run using the code provided with this work75, with the applicable covariates removed.
Moreover, when using estimates produced as a result of a modelled output, a degree of uncertainty always needs to be taken into account. Please, refer to the uncertainty data which were produced in the context of this work.
Code availability
The code for modelling, prediction and validation is publicly available via the project GitHub repository75. The code was written and ran in R version 4.0.4, and it is dependent on the R package INLA. Further documentation regarding the scripts can be found in the README file within the GitHub repository.
Instructions and code for constructing reproductive, maternal, newborn, child, and adolescent health and development indicators using NFHS surveys and DHS data which were used as input data can be found on the DHS Programme GitHub repository (www.github.com/DHSProgram).
References
General Assembly of the United Nations. Transforming our world: the 2030 Agenda for Sustainable Development. Resolution adopted by the General Assembly on 25 September 2015. A/RES/70/1 (2015).
Government Of India. Censusindia.Gov.In. https://censusindia.gov.in/census.website/ (2011).
Ministry Of Women & Child Development (WCD). Wcd.Nic.In. Accessed May 4. https://wcd.nic.in/about-us/about-ministry.
Unicef India. Gender Equality. Accessed May 4. https://www.unicef.org/india/what-we-do/gender-equality (2022).
UN Women India. UN Women – Asia-Pacific. Accessed May 4. https://asiapacific.unwomen.org/en/countries/india.
OPHI & UNDP. Global Multidimensional Poverty Index 2019. Illuminating inequalities. (United Nations Development Programme and Oxford Poverty and Human Development Initiative, 2019).
McCarthy, N. Report: India Lifted 271 Million People Out Of Poverty In A Decade. Forbes (2019).
UNDP & Government of India. India Voluntary National Review on SDGs. https://sustainabledevelopment.un.org/memberstates/india [Accessed on 25/04/2022]. (2020).
Ahmed, M., Shuai, C., Abbas, K., Rehman, F. U. & Khoso, W. M. Investigating health impacts of household air pollution on woman’s pregnancy and sterilization: Empirical evidence from Pakistan, India, and Bangladesh. Energy 247, 123562, https://doi.org/10.1016/j.energy.2022.123562 (2022).
Sagar, A., Balakrishnan, K., Guttikunda, S., Roychowdhury, A. & Smith, K. R. India Leads the Way: A Health-Centered Strategy for Air Pollution. Environmental Health Perspectives 124, A116–A117, https://doi.org/10.1289/EHP90 (2016).
Pandey, A. et al. Health and economic impact of air pollution in the states of India: the Global Burden of Disease Study 2019. The Lancet Planetary Health 5, e25–e38, https://doi.org/10.1016/S2542-5196(20)30298-9 (2021).
Ganguly, T., Selvaraj, K. L. & Guttikunda, S. K. National Clean Air Programme (NCAP) for Indian cities: Review and outlook of clean air action plans. Atmospheric Environment: X 8, 100096, https://doi.org/10.1016/j.aeaoa.2020.100096 (2020).
You, F. et al. Maternal Mortality in Henan Province, China: Changes between 1996 and 2009. PLOS ONE 7, e47153, https://doi.org/10.1371/journal.pone.0047153 (2012).
Wang, H. et al. Global, regional, and national under-5 mortality, adult mortality, age-specific mortality, and life expectancy, 1970–2016: a systematic analysis for the Global Burden of Disease Study 2016. The Lancet 390, 1084–1150, https://doi.org/10.1016/S0140-6736(17)31833-0 (2017).
Panda, B. K., Kumar, G. & Awasthi, A. District level inequality in reproductive, maternal, neonatal and child health coverage in India. BMC Public Health 20, 58, https://doi.org/10.1186/s12889-020-8151-9 (2020).
Sachs, J., Schmidt-Traub, G., Kroll, C. & Lafortune, G. The Decade of Action for the Sustainable Development Goals. Sustainable Development Report 2021. (Cambridge: Cambridge University Press. https://doi.org/10.1017/9781009106559, 2021).
UNDP. Sustainable Development Report. Rankings. https://dashboards.sdgindex.org/rankings [Accessed on 23/04/2022].
Lim, S. S. et al. Measuring the health-related Sustainable Development Goals in 188 countries: a baseline analysis from the Global Burden of Disease Study 2015. The Lancet 388, 1813–1850, https://doi.org/10.1016/S0140-6736(16)31467-2 (2016).
Panda, B. K. & Mohanty, S. K. Progress and prospects of health-related sustainable development goals in india. Journal of Biosocial Science 51, 335–352, https://doi.org/10.1017/S0021932018000202 (2019).
Pradhan, J. & Arokiasamy, P. Socio-economic inequalities in child survival in India: A decomposition analysis. Health Policy 98, 114–120, https://doi.org/10.1016/j.healthpol.2010.05.010 (2010).
Subramanyam, M. A., Kawachi, I., Berkman, L. F. & Subramanian, S. V. Socioeconomic Inequalities in Childhood Undernutrition in India: Analyzing Trends between 1992 and 2005. PLOS ONE 5, e11392, https://doi.org/10.1371/journal.pone.0011392 (2010).
International Institute for Population Sciences (IIPS), I. & ICF. India National Family Health Survey NFHS-4 2015-16. Mumbai, India: IIPS and ICF. Available at http://dhsprogram.com/pubs/pdf/FR339/FR339.pdf (2017).
UNICEF. https://data.unicef.org/countdown-2030/country/India/1/.
Barros, A. J. D. et al. Equity in maternal, newborn, and child health interventions in Countdown to 2015: a retrospective review of survey data from 54 countries. The Lancet 379, 1225–1233, https://doi.org/10.1016/S0140-6736(12)60113-5 (2012).
Victora, C. et al. Countdown to 2030 for reproductive, maternal, newborn, child, and adolescent health and nutrition. The Lancet Global Health 4, e775–e776, https://doi.org/10.1016/S2214-109X(16)30204-2 (2016).
Ferreira, L. Z. et al. Geospatial estimation of reproductive, maternal, newborn and child health indicators: a systematic review of methodological aspects of studies based on household surveys. International Journal of Health Geographics 19, 41, https://doi.org/10.1186/s12942-020-00239-9 (2020).
Nilsen, K. et al. A review of geospatial methods for population estimation and their use in constructing reproductive, maternal, newborn, child and adolescent health service indicators. BMC Health Services Research 21, 370, https://doi.org/10.1186/s12913-021-06370-y (2021).
Utazi, C. E. et al. Mapping vaccination coverage to explore the effects of delivery mechanisms and inform vaccination strategies. Nature Communications 10, 1633, https://doi.org/10.1038/s41467-019-09611-1 (2019).
ICF International. Demographic and Health Survey Sampling Household Listing Manual. (ICF International, 2012) (2012).
Burgert-Brucker, C. R., Dontamsetti, T., Mashall, A. & Gething, P. W. Guidance for use of the DHS program modeled map surfaces. DHS Spatial Analysis Reports, no. 14., (Rockville, MD: ICF International., 2016).
Burgert, C. R., Colston, J., Roy, T. & Zachary, B. Geographic displacement procedure and georeferenced data release policy for the demographic and health surveys. DHS Spatial Analysis Reports, no. 7., (Calverton, MD: ICF International, 2013).
Perez-Heydrick, C., Warren, J., Burgert, C. & Emch, M. Guidelines on the Use of DHS GPS Data. (ICF International, 2013). (2013).
Alegana, V. A. et al. Fine resolution mapping of population age-structures for health and development applications. Journal of The Royal Society Interface 12, 20150073, https://doi.org/10.1098/rsif.2015.0073 (2015).
Bosco, C. et al. Exploring the high-resolution mapping of gender-disaggregated development indicators. Journal of The Royal Society Interface 14, 20160825, https://doi.org/10.1098/rsif.2016.0825 (2017).
Steele, J. E. et al. Mapping poverty using mobile phone and satellite data. Journal of The Royal Society Interface 14, 20160690, https://doi.org/10.1098/rsif.2016.0690 (2017).
DHS Spatial Interpolation Working Group. Spatial Interpolation with Demographic and Health Survey Data: Key Considerations. (ICF International, 2014). (2014).
Rutstein, S. & Rojas, G. Guide to DHS Statistics: Demographic and Health Surveys. (ORC Macro, Calverton, Maryland., 2003).
The DHS Program Code Share Project. In DHS Program Github site. (2022).
Alegana, V. A., Pezzulo, C., Tatem, A. J., Omar, B. & Christensen, A. Mapping out-of-school adolescents and youths in low- and middle-income countries. Humanities and Social Sciences Communications 8, 213, https://doi.org/10.1057/s41599-021-00892-w (2021).
Lindgren, F. & Rue, H. Bayesian Spatial Modelling with R-INLA. Journal of Statistical Software 63, 1–25, https://doi.org/10.18637/jss.v063.i19 (2015).
Rue, H., Martino, S. & Chopin, N. Approximate Bayesian inference for latent Gaussian models by using integrated nested Laplace approximations. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 71, 319–392, https://doi.org/10.1111/j.1467-9868.2008.00700.x (2009).
Gómez-Rubio, V. Bayesian inference with INLA. (CRC Press., 2020).
Lindgren, F., Rue, H. & Lindström, J. An explicit link between Gaussian fields and Gaussian Markov random fields: the stochastic partial differential equation approach. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 73, 423–498, https://doi.org/10.1111/j.1467-9868.2011.00777.x (2011).
Moraga, P. Geospatial health data: Modeling and visualization with R-INLA and shiny., (CRC Press., 2019).
Team., R. C. R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. https://www.R-project.org/ 2021).
Simpson, D., Rue, H., Riebler, A., Martins, T. G. & Sørbye, S. H. Penalising model component complexity: A principled, practical approach to constructing priors. Statistical science 32(1), 1–28 (2017).
Pullum, T. W. in IUSSP Int. Popul. Conf. 22 (2017).
Wilson, E. B. Probable Inference, the Law of Succession, and Statistical Inference. Journal of the American Statistical Association 22, 209–212, https://doi.org/10.2307/2276774 (1927).
Newcombe, R. G. Two-sided confidence intervals for the single proportion: comparison of seven methods. Stat Med 17, 857–872, https://doi.org/10.1002/(sici)1097-0258(19980430)17:8<857::aid-sim777>3.0.co;2-e (1998).
Agresti, A. & Coull, B. A. Approximate Is Better than “Exact” for Interval Estimation of Binomial Proportions. The American Statistician 52, 119–126, https://doi.org/10.2307/2685469 (1998).
Newcombe, R. G. & DG., A. in Statistics with confidence (2nd edn). London: BMJ Books; 2000: 46-8. (ed Altman, D. G. et al. (eds)) (2000).
Breslow, N. E. & Day, N. E. Statistical methods in cancer research. Volume II–The design and analysis of cohort studies. IARC Sci Publ, 1–406 (1987).
Bégaud, B. et al. An easy to use method to approximate Poisson confidence limits. Eur J Epidemiol 20, 213–216, https://doi.org/10.1007/s10654-004-6517-4 (2005).
Armitage, P. & Berry, G. Statistical methods in medical research. (Oxford: Blackwell, 2002).
Crow, E. L. & Gardener, R. S. Confidence intervals for the expectation of a poisson variable. Biometrika 46, 441–453, https://doi.org/10.1093/biomet/46.3-4.441 (1959).
van Donkelaar, A. et al. Global Estimates of Fine Particulate Matter Using a Combined Geophysical-Statistical Method with Information from Satellites. Environmental Science & Technology 50(7), 3762–3772, https://doi.org/10.1021/acs.est.5b05833 (2016).
van Donkelaar, A. et al. Global Annual PM2.5 Grids from MODIS, MISR and SeaWiFS Aerosol Optical Depth (AOD) with GWR, 1998–2016. Palisades, NY: NASA Socioeconomic Data and Applications Center (SEDAC). https://doi.org/10.7927/H4ZK5DQS. Accessed 07/06/21. (2018).
US NOAA (National Oceanic and Atmospheric Administration) National Centers for Environmental Information. VIIRS DNB cloud free composites. 2012-2016. Version 1 nighttimeday/night band composites [Data set]. Retrieved March 2017. Available from: https://www.ngdc.noaa.gov/eog/viirs/download_dnb_composites.html (2017).
Lloyd, C. T. et al. Global spatio-temporally harmonised datasets for producing high-resolution gridded population distribution datasets. Big Earth Data 3, 108–139, https://doi.org/10.1080/20964471.2019.1625151 (2019).
Graetz, N. et al. Mapping disparities in education across low- and middle-income countries. Nature 577, 235–238, https://doi.org/10.1038/s41586-019-1872-1 (2020).
Assembly Constituencies Maps are provided by Data{Meet} Community Maps Project & made available under the Creative Commons Attribution 2.5 India. (Accessed in May 2021).
Chan, H. M. T. et al. High-resolution prediction and uncertainty gridded dataset of reproductive, maternal, newborn, child and adolescent health and development indicators for 2015-16 India, version 1.1. WorldPop, University of Southampton. https://doi.org/10.5258/SOTON/WP00738, (2022).
Tejedor-Garavito, N. et al. Reproductive, maternal, newborn, child, and adolescent health and development indicators at district level for 2015-16 India, version 1.0. WorldPop, University of Southampton. https://doi.org/10.5258/SOTON/WP00739 (2022).
Dreoni, I. et al. Confidence intervals for selected reproductive, maternal, newborn, child, and adolescent health and development indicators at district level for 2015-16 India, version 1.0. WorldPop, University of Southampton. https://doi.org/10.5258/SOTON/WP00740 (2022).
Pullum, T. W. & Staveteig, S. An assessment of the quality and consistency of age and date reporting in DHS Surveys, 2000–2015. (ICF, Rockville, Maryland, USA, 2017).
Harkare, H. V., Corsi, D. J., Kim, R., Vollmer, S. & Subramanian, S. V. The impact of improved data quality on the prevalence estimates of anthropometric measures using DHS datasets in India. Scientific Reports 11, 10671, https://doi.org/10.1038/s41598-021-89319-9 (2021).
Blanc, A. K. & Wardlaw, T. Monitoring low birth weight: an evaluation of international estimates and an updated estimation procedure. Bull World Health Organ 83, 178–185 (2005).
Blencowe, H. et al. National, regional, and worldwide estimates of low birthweight in 2015, with trends from 2000: a systematic analysis. Lancet Glob Health 7, e849–e860, https://doi.org/10.1016/s2214-109x(18)30565-5 (2019).
Biks, G. A. et al. Birthweight data completeness and quality in population-based surveys: EN-INDEPTH study. Population Health Metrics 19, 17, https://doi.org/10.1186/s12963-020-00229-w (2021).
Burgert, C. R., Colston, J., Roy, T. & Zachary, B. Geographic displacement procedure and georeferenced data release policy for the Demographic and Health Surveys. (ICF International, Calverton, Maryland, USA, 2013).
Gething, P., Tatem, A., Bird, T. & Burgert-Brucker, C. R. Creating spatial interpolation surfaces with DHS data. (ICF International, Rockville, Maryland, USA, 2015).
Leyk, S. et al. The spatial allocation of population: a review of large-scale gridded population data products and their fitness for use. Earth Syst. Sci. Data 11, 1385–1409, https://doi.org/10.5194/essd-11-1385-2019 (2019).
Thomson, D. R., Leasure, D. R., Bird, T., Tzavidis, N. & Tatem, A. J. How accurate are WorldPop-Global-Unconstrained gridded population data at the cell-level?: A simulation analysis in urban Namibia. PLOS ONE 17, e0271504, https://doi.org/10.1371/journal.pone.0271504 (2022).
Balk, D. L. et al. Determining global population distribution: methods, applications and data. Adv Parasitol 62, 119–156, https://doi.org/10.1016/s0065-308x(05)62004-0 (2006).
health_dev: Subnational reproductive, maternal, newborn, child and adolescent health and development atlas for India, version 1.1. Zenodo https://doi.org/10.5281/zenodo.6975135 (2022).
Acknowledgements
The work is funded by the Children’s Investment Foundation Fund (CIFF) (R-2009-05106). The authors acknowledge the support of the PMO Team at WorldPop and would like to thank Evidence Measurement Evaluation (EME) team and India Programme Team at CIFF for their inputs and continuous support, and all staff at CIFF who provided feedback at each stage of this work, and in particular Stuti Tripathi, Awdhesh Yadav and Kerri Wazny. Moreover, the authors would like to thank the DHS Program staff for their input on the construction of some of the indicators. This work was approved by the ethics and research governance committee at the University of Southampton (ERGO 64920). Moreover, the authors would like to thank Chigozie Edson Utazi and Oliver Pannell for their support in the initial stages of the project. This study was carried out with support from a grant provided by the Children’s Investment Fund Foundation (CIFF) (Grant number: R-2009-05106). The views expressed are those of the authors and do not necessarily reflect the views of CIFF. Maps used on this website are for general illustration only, and are not intended to be used for reference purposes. The representation of political boundaries does not necessarily reflect the position of the author(s) or their organisation’s view on the legal status of a country or territory.
Author information
Authors and Affiliations
Contributions
C.P., N.T.G., H.M.T.C. and I.D. drafted the manuscript, acquired and assembled the raw data. H.M.T.C. produced the modelled high resolution surfaces and datasets. C.P. and I.D. calculated the indicators from raw data. I.D. produced district level datasets. H.M.T.C. and I.D. performed the technical validation of the raw data and final datasets. N.T.G., D.K. and M.B. led all GIS related aspects of the work. C.P. led aspects related to the indicators construction. N.T.G., H.M.T.C., A.B., M.B. and D.K. produced the final datasets and prepared figures. A.J.T., S.G. and M.S. aided drafting the manuscript and contributed to the funding acquisition. C.P., N.T.G., S.G., M.S. and A.J.T. conceived the study and led the research activity planning and execution. All authors read and approved the final version of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Pezzulo, C., Tejedor-Garavito, N., Chan, H.M.T. et al. A subnational reproductive, maternal, newborn, child, and adolescent health and development atlas of India. Sci Data 10, 86 (2023). https://doi.org/10.1038/s41597-023-01961-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41597-023-01961-2