Abstract
The variability of climate has profoundly impacted a wide range of macroecological processes in the Late Quaternary. Our understanding of these has greatly benefited from palaeoclimate simulations, however, high-quality reconstructions of ecologically relevant climatic variables have thus far been limited to a few selected time periods. Here, we present a 0.5° resolution bias-corrected dataset of global monthly temperature, precipitation, cloud cover, relative humidity and wind speed, 17 bioclimatic variables, annual net primary productivity, leaf area index and biomes, covering the last 120,000 years at a temporal resolution of 1,000–2,000 years. We combined medium-resolution HadCM3 climate simulations of the last 120,000 years with high-resolution HadAM3H simulations of the last 21,000 years, and modern-era instrumental data. This allows for the temporal variability of small-scale features whilst ensuring consistency with observed climate. Our data make it possible to perform continuous-time analyses at a high spatial resolution for a wide range of climatic and ecological applications - such as habitat and species distribution modelling, dispersal and extinction processes, biogeography and bioanthropology.
Measurement(s) | temperature • precipitation process • vegetation layer • atmospheric wind speed • cloud • humidity |
Technology Type(s) | computational modeling technique |
Factor Type(s) | geographic location • temporal interval |
Sample Characteristic - Environment | climate system |
Sample Characteristic - Location | Earth (planet) |
Machine-accessible metadata file describing the reported data: https://doi.org/10.6084/m9.figshare.12436484
Similar content being viewed by others
Background & Summary
Global climate in the Late Quaternary has played a major role in the formation of a wide range of macroecological patterns. Reconstructing climatic conditions has been crucial in advancing our understanding of the spatial and temporal dynamics of these processes, ranging from the distribution of species ranges1,2 and extinctions3, to early human expansions4 and population genetics5.
Climate models can provide the spatial coverage that localised empirical reconstructions are lacking, yet, currently available simulation data for the Late Pleistocene and the Holocene suffer from one of two drawbacks that limit their use for ecological applications. On the one hand, a number of equilibrium and transient simulations, from general circulation models (e.g. HadCM36) or earth system models of intermediate complexity (e.g. LOVECLIM4), provide reconstructions at a high temporal resolution, however, the relatively low spatial resolution of the simulated data, and significant biases when compared to empirical observations7, make additional curating of model outputs necessary in order to generate ecologically meaningful data. On the other hand, several high-resolution and bias-corrected palaeoclimate datasets provide climatic variables in great spatial detail, but their temporal coverage of the Late Pleistocene and the Holocene is usually limited to a few snapshots of key time periods. A number of these datasets have been made available in readily accessible formats since the mid-2000s, and have since been used extensively in ecological applications: the ecoClimate database8 provides data for the Mid-Holocene (~6,000 BP) and the Last Glacial Maximum (~21,000 BP); WorldClim9 contains an additional reconstruction of the Last Interglacial Period (~130,000 BP); paleoClim10 covers the last 21,000 years.
Here, we fill the gap between these two types of available data, by deriving a high-resolution (0.5°) bias-corrected time series of global terrestrial climate and vegetation data covering the last 120,000 years. Gridded reconstructions (Table 1) are available at 2,000 year time steps between 120,000 and 22,000 BP, and 1,000 year time steps between 21,000 BP and the pre-industrial modern era. Our data include monthly temperature and precipitation, and 17 bioclimatic variables, which have been used extensively in species distribution models (e.g.11). We also provide monthly cloudiness, relative humidity and wind speed (which can be used to derive various measures of apparent temperature), as well as reconstructions of global biomes, leaf area index and net primary productivity. Our data show a good agreement with empirical reconstructions of temperature, precipitation and vegetation for the mid-Holocene, the Last Glacial Maximum and the Last Interglacial, performing equally well as existing high-resolution snapshots of these time periods.
Methods
Monthly climatic variables
Our dataset is based on simulations of monthly mean temperature (°C), precipitation (mm month−1), cloudiness (%), relative humidity (%) and wind speed (m s−1) of the HadCM3 general circulation model6,12,13. At a spatial grid resolution of 3.75° × 2.5°, these data cover the last 120,000 years in 72 snapshots (2,000 year time steps between 120,000 BP and 22,000 BP; 1,000 year time steps between 22,000 BP and the pre-industrial modern era), each representing climatic conditions averaged across a 30-year post-spin-up period. We denote these data by
where \(m=1,\ldots ,12\) represents a given month, and \(t\in {T}_{{\rm{120}}{\rm{k}}}\) represents a given one of the 72 points in time for which simulations are available, denoted \({T}_{{\rm{120}}{\rm{k}}}\).
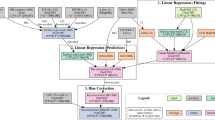
We downscaled and bias-corrected these data in two stages (Fig. 1). Both are based on variations of the Delta Method14, under which a high-resolution, bias-corrected reconstruction of climate at some time t in the past is obtained by applying the difference between modern-era low-resolution simulated and high-resolution observed climate – the correction term – to the simulated climate at time t. The Delta Method has previously been used to downscale and bias-correct palaeoclimate simulations, e.g. for the widely used WorldClim database9. A recent evaluation of three methods commonly used for bias-correction and downscaling15 showed that the Delta Method reduces the difference between climate simulation data and empirical palaeoclimatic reconstructions overall more effectively than two alternative methods (statistical downscaling using Generalised Additive Models, and Quantile Mapping). We therefore used this approach for generating our dataset.
Downscaling to ~1° resolution
A key limitation of the Delta Method is that it assumes the modern-era correction term to be representative of past correction terms15. This assumption is substantially relaxed in the Dynamic Delta Method used in the first stage of our approach to downscale the data in Eq. (1) to a ~1° resolution. This involves the use of a set of high-resolution climate simulations that were run for a smaller but climatically diverse subset of \({T}_{120k}\). Simulations at this resolution are very computationally expensive, and therefore running substantially larger sets of simulations is not feasible; however, these selected data can be very effectively used to generate a suitable time-dependent correction term for each \(t\in {T}_{120k}\). In this way, we are able to increase the resolution of the original climate simulations by a factor of ~9, while simultaneously allowing for temporal variability in the correction term. In the following, we detail the approach.
We used high-resolution simulations of the same variables as in Eq. (1) from the HadAM3H model13,16,17, available at a 1.25° × 0.83° resolution for the last 21,000 years in 9 snapshots (2,000 year time steps between 12,000 BP and 6,000 BP; 3,000 year time steps otherwise). We denote these by
respectively, where \(t\in {T}_{21k}\), represents a given one of the 9 points in time for which simulations are available, denoted \({T}_{{\rm{21}}{\rm{k}}}\).
For each variable \(X\in \{T,P,C,H,W\}\), we considered the differences between the medium- and the high-resolution data at times \(t\in {T}_{21k}\) for which both are available,
where the \( \boxplus \)-notation indicates that the coarser-resolution data was interpolated to the grid of the higher-resolution data. For this, we used an Akima cubic Hermite interpolant18, which (unlike a bilinear interpolant) is smooth but (unlike a bicubic interpolant) avoids potential overshoots. For each \(t\in {T}_{120k}\) and each \(\tau \in {T}_{21k}\),
provides a 1.25° × 0.83° resolution downscaled version of the data \({X}_{{\rm{HadCM3}}}(m,t)\) in Eq. (1). The same is true, more generally, for any weighted linear combination of the Δ\({X}_{{\rm{HadAM3H}}}^{{\rm{HadCM3}}}(m,\tau )\), which is the approach taken here, yielding
where \({\sum }_{\tau \in {T}_{21k}}\mathop{\overbrace{w(t,\tau )}}\limits^{\ge 0}=1\) for any given \(t\in {T}_{125k}\). We discuss the choice of an additive approach for all climatic variables later on. Crucially, in contrast to the classical Delta Method – which, for all \(t\in {T}_{125k}\), would correspond to \(w(t,{\rm{present}}\,{\rm{day}})=1\) and \(w(t,\tau )=0\) otherwise (cf. Eq. (5)) –, the resolution correction term that is added to \({X}_{{\rm{HadCM3}}}^{ \boxplus }(m,t)\) in Eq. (3) need not be constant over time. Instead, the high-resolution heterogeneities that are applied to the medium-resolution HadCM3 data are chosen from the broad range of patterns simulated for \({T}_{21k}\). The strength of this approach lies in the fact that the last 21,000 years account for a substantial portion of the range of climatic conditions present during the whole Late Quaternary. Thus, by choosing the weights \(w(t,\tau )\) for a given time \(t\in {T}_{125k}\) appropriately, we can construct a \({T}_{21k}\)-data-based correction term corresponding to a climatic state that is, in a sense yet to be specified, close to the climatic state at time t. Here, we used atmospheric CO2 concentration, a key determinant of the global climatic state19, as the metric according to which the \(w(t,\tau )\) are chosen; i.e. we assigned a higher weight to Δ\({X}_{{\rm{HadAM3H}}}^{{\rm{HadCM3}}}(m,\tau )\) the closer the CO2 level at time \(\tau \) was to that at time t. Specifically, we used
and rescaled these to \(w(t,\tau )=\frac{w{\prime} (t,\tau )}{{\sum }_{\tau \in {T}_{21k}}w{\prime} (t,\tau )}\) (Supplementary Fig. 1). In the special case of \(t\in {T}_{21k}\), we have \(w(t,t)=1\) and \(w(t,\tau )=0\) for \(\tau \ne t\), for which Eq. (3) simplifies to
Formally, the correction term in Eq. (3) corresponds to an inverse square distance interpolation of the Δ\({X}_{{\rm{HadAM3H}}}^{{\rm{HadCM3}}}\) with respect to CO220. We also note that, for our choice of \(w(t,\tau )\), the correction term is a smooth function of t, as would be desired. In particular, this would not the case for the approach in Eq. (2) (unless \(\tau \) is the same for all \(t\in {T}_{125k}\)).
The additive approach in Eq. (3) does not by itself ensure that the derived precipitation, relative humidity, cloudiness and wind speed are non-negative and that relative humidity and cloudiness do not exceed 100% across all points in time and space. We therefore capped values at the appropriate bounds, and obtain
Supplementary Fig. 2 shows that this step only affects a very small number of data points, whose values are otherwise very close to the relevant bound.
Bias-correction and downscaling to 0.5° resolution
In the second stage of our approach, we applied the classical Delta Method to the previously downscaled simulation data. Similar to the approach in Eq. (3), this is achieved by applying a correction term, which is now given by the difference between present-era high-resolution observational climate and coarser-resolution simulated climate, to past simulated climate. This further increases the resolution and removes remaining biases in the data in Eq. (4).
Since our present-era simulation data correspond to pre-industrial conditions (280 ppm atmospheric CO2 concentration)6,12,13, it would be desirable for the observational dataset used in this step to be approximately representative of these conditions as well, so that the correction term can be computed based on the simulated and observed climate of a similar underlying scenario. There is generally a trade-off between the quality of observation-based global climate datasets of recent decades, and the extent to which they reflect anthropogenic climate change (which, by design, is not captured in our simulated data) – both of which increase towards the present. Fortunately, however, significant advances in interpolation methods21,22,23 have produced high-quality gridded datasets of global climatic conditions reaching as far back as the early 20th century23. Thus, here we used 0.5° resolution observational data representing 1901–1930 averages (~300 ppm atmospheric CO2) of terrestrial monthly temperature, precipitation and cloudiness23. For relative humidity and wind speed, we used a global data representing 1961–1990 average (~330 ppm atmospheric CO2) monthly values24 due to a lack of earlier datasets. We denote the data by
We extrapolated these maps to current non-land grid cells using an inverse distance weighting approach so as to be able to use the Delta Method at times of lower sea level. The resulting data were used to bias-correct and further downscale the ~1° data in Eq. (3) to a 0.5° grid resolution via
where \(X\in \{T,P,C,H,W\}\). In particular, the data for the present are identical to the empirically observed climate,
Finally, we again capped values at the appropriate bounds, and obtained
Similar as in the analogous step in the first stage of our approach (Eq. (4)), only a relatively small number of data points is affected by the capping; their values are reasonably close to the relevant bounds, and their frequency decreases sharply with increasing distance to the bounds (Supplementary Fig. 2).
In principle, capping values, where necessary, can be circumvented by suitably transforming the relevant variable first, then applying the additive Delta Method, and back-transforming the result. In the case of precipitation, for example, a log-transformation is sometimes used, which is mathematically equivalent to a multiplicative Delta Method, in which low-resolution past simulated data is multiplied by the relative difference between high- and low-resolution modern-era data14; thus, instead of Eq. (5), we would have \({P}_{0.{5}^{\circ }}(m,t)\,:={P}_{ \sim {1}^{\circ }}^{ \boxplus }(m,t)\cdot \frac{{P}_{{\rm{obs}}}(m,0)}{{P}_{ \sim {1}^{\circ }}^{ \boxplus }(m,0)}\). However, whilst this approach ensures non-negative values, it has three important drawbacks. First, if present-era observed precipitation in a certain month and grid cell is zero, i.e. \({P}_{{\rm{obs}}}(m,0)=0\), then \({P}_{0.{5}^{\circ }}(m,t)=0\) at all points in time, t, irrespectively of the simulated climate change signal. Specifically, this makes it impossible for current extreme desert areas to be wetter at any point in the past. Second, if present-era simulated precipitation in a grid cell is very low (or indeed identical to zero), i.e. \({P}_{ \sim {1}^{\circ }}^{ \boxplus }(m,0)\approx 0\), then \({P}_{0.{5}^{\circ }}(m,t)\) can increase beyond all bounds. Very arid locations are particularly prone to this effect, which can generate highly improbable precipitation patterns for the past. In our scenario of generating global maps for a total of 864 individual months, this lack of robustness of the multiplicative Delta Method would be difficult to handle. Third, the multiplicative Delta Method is not self-consistent: applying it to the sum of simulated monthly precipitation does not produce the same result as applying it to simulated monthly precipitation first and then taking the sum of these values. The natural equivalent of the log-transformation for precipitation is the logit-transformation for cloudiness and relative humidity, however, this approach suffers from the same drawbacks.
Minimum and maximum annual temperature
Diurnal temperature data are not included in the available HadCM3 and HadAM3H simulation outputs. We therefore used the following approach to estimate minimum and maximum annual temperatures. Based on the monthly HadCM3 and HadAM3H temperature data, we created maps of the mean temperature of the coldest and the warmest month. In the same way as described above, we used these data to reconstruct the mean temperature of the coldest and warmest month at a 1.25° × 0.83° resolution by means of the Dynamic Delta Method, yielding
for \(t\in {T}_{120k}\). We then used observation-based 0.5° resolution global datasets of modern-era (1901–1930 average) minimum and maximum annual temperature23, denoted
to estimate past minimum and maximum annual temperature as
respectively. This approach assumes that the difference between past and present mean temperature of the coldest (warmest) month is similar to the difference between the past and present temperature of the coldest (warmest) day. Instrumental data of the recent past suggest that this assumption is well justified across space (Supplementary Fig. 3).
Land configuration
We used a reconstruction of mean global sea level25 and a global elevation and bathymetry map26, interpolated to a 0.5° resolution grid, to create land configuration maps for the last 120,000 years. Maps of terrestrial climate through time were obtained by cropping the global data in Eq. (6a and b) to the appropriate land masks. Values in non-land grid cells were set to missing values, except in the case of below-sea-level inland grid cells, such as the Aral, Caspian and Dead sea.
Bioclimatic data, net primary productivity, leaf area index, biome
Based on our reconstructions of minimum and maximum annual temperature, and monthly temperature and precipitation, we derived 17 bioclimatic variables27 listed in Table 1. In addition, we used the Biome4 global vegetation model28 to compute net primary productivity, leaf area index and biome type at a 0.5° resolution for all \(t\in {T}_{120k}\), using reconstructed minimum annual temperature, and monthly temperature, precipitation and cloudiness. Similar to a previous approach21, we converted cloudiness to the percent of possible sunshine (required by Biome4) by using a standard conversion table and applying an additional latitude- and month-specific correction. Since Biome4 estimates ice biomes only based on climatic conditions and not ice sheet data, it can underestimate the spatial extent of ice. We therefore changed simulated non-ice biomes to ice, and set net primary production and leaf area index to 0, in grid cells covered by ice sheets according to the ICE-6g dataset29 at the relevant points in time. Whilst our data represent potential natural biomes, and as such do not account for local anthropogenic land use, maps of actual land cover can readily be generated by superimposing our data with available reconstructions of global land use during the Holocene30.
Data Records
Our dataset, containing the variables listed in Table 1, is available as a single NetCDF file on the Figshare data repository31. All maps are provided at 2,000 year time steps between 120,000 BP and 22,000 BP, and 1,000 year time steps between 22,000 BP and the (pre-industrial) modern era. We used a 0.5° equirectangular grid, with longitudes ranging between 179.75°E and 179.75°W, and latitudes ranging between 59.75°S and 89.75°N.
Technical Validation
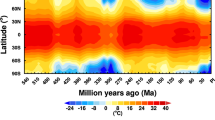
Proxy data-based reconstructions of past climatologies allow us to evaluate our dataset by means of empirical records, and compare its performance against that of existing model-based snapshots of specific time periods. Here, we used empirical reconstructions of mean annual temperature, temperature of the coldest and warmest month, and annual precipitation for the Mid-Holocene and the Last Glacial Maximum32, and reconstructions of mean annual temperature for the Last Interglacial Period33. Overall, our data are in good agreement with the available empirical reconstructions (Fig. 2, Supplementary Fig. 4). For each variable and time period, residual biases across the value spectrum are approximately normally distributed around zero, with the possible exception of precipitation, where, at the lower end of the value spectrum, a few empirical reconstructions suggest slightly higher values than our dataset (Supplementary Fig. 4). By construction of the Delta Method, our modern-era data is identical to the observed climate. Simulated vegetation, a product of temperature, precipitation and cloud cover data, also corresponds well to empirical biome reconstructions available for the Mid-Holocene and Last Glacial Maximum34 (Fig. 2). The performance of our data under the available empirical palaeoclimatic reconstructions is well within the range of that of downscaled and bias-corrected outputs from other climate models available for specific points in the past (Fig. 3).
Comparison between modelled mid-Holocene and Last Glacial Maximum temperature, precipitation and vegetation (maps), and pollen-based empirical reconstructions (markers; uncertainties not shown)32,34. For visualisation purposes, empirical biomes were aggregated to a 2° grid, and the set of 27 simulated biomes was grouped into 9 megabiomes.
Quantitative comparison between our data and empirical reconstructions of available climatic variables32,33, and data from other climate models. Blue bars and black error bars represent the median and the upper and lower quartiles of the set of absolute differences between our data and the available empirical reconstructions (cf.15 for details). Supplementary Fig. 4 shows all individual data points that these summary statistics are based on. Grey error bars show the equivalent measures for palaeoclimate data available on WorldClim v1.49, i.e. from the IPSL-CM5A-LR, MRI-CGCM3, BCC-CSM1-1, CNRM-CM5 and CCSM4 models (Mid-Holocene), the MPI-ESM-P and MIROC-ESM models (Mid-Holocene and Last Glacial Maximum) and the CCSM4 model (Last Glacial Maximum and Last Interglacial Period).
Usage Notes
The dataset comes with fully commented R, Python and Matlab scripts that demonstrate how annual and monthly variables can be read from the NetCDF file, and how climatic data for specific points in time and space can be extracted and analysed.
Code availability
Code used to generate our dataset is available on the Open Science Framework35.
References
Nogués-Bravo, D. Predicting the past distribution of species climatic niches. Global Ecology and Biogeography 18 (2009).
Svenning, J.-C., Fløjgaard, C., Marske, K. A., Nógues-Bravo, D. & Normand, S. Applications of species distribution modeling to paleobiology. Quaternary Science Reviews 30 (2011).
Lorenzen, E. D. et al. Species-specific responses of Late Quaternary megafauna to climate and humans. Nature 479 (2011).
Timmermann, A. & Friedrich, T. Late Pleistocene climate drivers of early human migration. Nature 538 (2016).
Eriksson, A. et al. Late Pleistocene climate change and the global expansion of anatomically modern humans. Proceedings of the National Academy of Sciences 109 (2012).
Singarayer, J. S. & Valdes, P. J. High-latitude climate sensitivity to ice-sheet forcing over the last 120 kyr. Quaternary Science Reviews 29 (2010).
Flato, G. et al. Evaluation of Climate Models. In Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assess-ment Report of the Intergovernmental Panel on Climate Change (eds. Stocker, T. F. et al.) 741–866 (Cambridge University Press, 2013).
Lima-Ribeiro, M. S. et al. Ecoclimate: a database of climate data from multiple models for past, present, and future for macroecologists and biogeographers. Biodiversity Informatics 10 (2015).
Hijmans, R. J., Cameron, S. E., Parra, J. L., Jones, P. G. & Jarvis, A. Very high resolution interpolated climate surfaces for global land areas. International Journal of Climatology 25 (2005).
Brown, J. L., Hill, D. J., Dolan, A. M., Carnaval, A. C. & Haywood, A. M. PaleoClim, high spatial resolution paleoclimate surfaces for global land areas. Scientific Data 5 (2018).
Pearson, R. G. & Dawson, T. P. Predicting the impacts of climate change on the distribution of species: are bioclimate envelope models useful? Global Ecology and Biogeography 12 (2003).
Singarayer, J. S. & Burrough, S. L. Interhemispheric dynamics of the African rainbelt during the late Quaternary. Quaternary Science Reviews 124 (2015).
Valdes, P. J. et al. The BRIDGE HadCM3 family of climate models: HadCM3@ Bristol v1. 0. Geoscientific Model Development 10, 3715–3743 (2017).
Maraun, D. & Widmann, M. Statistical downscaling and bias correction for climate research (Cambridge University Press, 2018).
Beyer, R., Krapp, M. & Manica, A. An empirical evaluation of bias correction methods for paleoclimate simulations. Climate of the Past. In press (2020).
Hudson, D. & Jones, R. Regional climate model simulations of present-day and future climates of southern Africa (Hadley Centre for Climate Prediction and Research, 2002).
Arnell, N. W., Hudson, D. & Jones, R. Climate change scenarios from a regional climate model: Estimating change in runoff in southern Africa. Journal of Geophysical Research: Atmospheres 108 (2003).
Akima, H. A new method of interpolation and smooth curve fitting based on local procedures. Journal of the ACM 17, 589–602 (1970).
Lacis, A. A., Schmidt, G. A., Rind, D. & Ruedy, R. A. Atmospheric CO2: Principal control knob governing Earth’s temperature. Science 330 (2010).
Shepard, D. A two-dimensional interpolation function for irregularly-spaced data. In Proceedings of the 1968 23rd ACM national conference, 517–524 (1968).
New, M., Hulme, M. & Jones, P. Representing twentieth-century space–time climate variability. Part I: Development of a 1961–90 mean monthly terrestrial climatology. Journal of Climate 12 (1999).
Harris, I., Jones, P. D., Osborn, T. J. & Lister, D. H. Updated high-resolution grids of monthly climatic observations–the CRU TS3. 10 Dataset. International Journal of Climatology 34 (2014).
Harris, I., Osborn, T. J., Jones, P., & Lister, D. Version 4 of the CRU TS monthly high-resolution gridded multivariate climate dataset. Scientific Data 7, 109 (2020).
New, M., Lister, D., Hulme, M. & Makin, I. A high-resolution data set of surface climate over global land areas. Climate Research 21 (2002).
Spratt, R. M. & Lisiecki, L. E. A Late Pleistocene sea level stack. Climate of the Past 12 (2016).
Amante, C. & Eakins, B. W. ETOPO1 arc-minute global relief model: procedures, data sources and analysis (2009).
O’Donnell, M. S. & Ignizio, D. A. Bioclimatic predictors for supporting ecological applications in the conterminous United States. US Geological Survey Data Series 691 (2012).
Kaplan, J. O. et al. Climate change and Arctic ecosystems: 2. Modeling, paleodata-model comparisons, and future projections. Journal of Geophysical Research: Atmospheres 108 (2003).
Peltier, W., Argus, D. & Drummond, R. Space geodesy constrains ice age terminal deglaciation: The global ICE-6G_C (VM5a) model. Journal of Geophysical Research: Solid Earth 120 (2015).
Klein Goldewijk, K., Beusen, A., Doelman, J. & Stehfest, E. New anthropogenic land use estimates for the Holocene: HYDE 3.2. Earth System Science Data 9 (2017).
Beyer, R., Krapp, M. & Manica, A. Late Quaternary climate, bioclimate and vegetation. figshare https://doi.org/10.6084/m9.figshare.12293345.v3 (2020).
Bartlein, P. et al. Pollen-based continental climate reconstructions at 6 and 21 ka: a global synthesis. Climate Dynamics 37 (2011).
Turney, C. S. & Jones, R. T. Does the Agulhas Current amplify global temperatures during super-interglacials? Journal of Quaternary Science 25 (2010).
Harrison, S. BIOME 6000 DB classified plotfile version 1. University of Reading, https://doi.org/10.17864/1947.99 (2017).
Beyer, R. Late Quaternary Environment. Open Science Framework https://doi.org/10.17605/osf.io/p86rt (2020).
Acknowledgements
R.M.B., M.K. and A.M. were supported by ERC Consolidator Grant 647797 LocalAdaptation. The authors are grateful to Paul Valdes for support with the HadCM3 and HadAM3H climate data.
Author information
Authors and Affiliations
Contributions
R.M.B. developed and implemented the methods, generated the dataset, and wrote the manuscript. M.K. developed the methods, prepared the climate model outputs, and revised the manuscript. A.M. developed the methods and revised the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
The Creative Commons Public Domain Dedication waiver http://creativecommons.org/publicdomain/zero/1.0/ applies to the metadata files associated with this article.
About this article
Cite this article
Beyer, R.M., Krapp, M. & Manica, A. High-resolution terrestrial climate, bioclimate and vegetation for the last 120,000 years. Sci Data 7, 236 (2020). https://doi.org/10.1038/s41597-020-0552-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41597-020-0552-1
This article is cited by
-
The Persian plateau served as hub for Homo sapiens after the main out of Africa dispersal
Nature Communications (2024)
-
Bone collagen from subtropical Australia is preserved for more than 50,000 years
Communications Earth & Environment (2023)
-
Reassessing the origin of lentil cultivation in the Pre-Pottery Neolithic of Southwest Asia: new evidence from carbon isotope analysis at Gusir Höyük
Vegetation History and Archaeobotany (2023)
-
Following the niche: the differential impact of the last glacial maximum on four European ungulates
Communications Biology (2022)
-
Ecosystem productivity affected the spatiotemporal disappearance of Neanderthals in Iberia
Nature Ecology & Evolution (2022)