Abstract
The ratio of plant transpiration to total terrestrial evapotranspiration (T/ET) captures the role of vegetation in surface-atmosphere interactions. However, several studies have documented a large variability in T/ET. In this paper, we present a new T/ET dataset (also including transpiration, evapotranspiration data) for China from 1981 to 2015 with spatial and temporal resolutions of 0.05° and 8 days, respectively. The T/ET dataset is based on a model-data fusion method that integrates the Priestley-Taylor Jet Propulsion Laboratory (PT-JPL) model with multivariate observational datasets (transpiration and evapotranspiration). The dataset is driven by satellite-based leaf area index (LAI) data from GLASS and GLOBMAP, and climate data from the Chinese Ecosystem Research Network (CERN). Observational annual T/ET were used to validate the model, with R2 and RMSE values were 0.73 and 0.07 (12.41%), respectively. The dataset provides significant insight into T/ET and its changes over the Chinese terrestrial ecosystem and will be beneficial for understanding the hydrological cycle and energy budgets between the land and the atmosphere.
Measurement(s) | ratio of transpiration to total terrestrial evapotranspiration • evapotranspiration • transpiration |
Technology Type(s) | model-data fusion • computational modeling technique • digital curation |
Factor Type(s) | year of data collection |
Sample Characteristic - Environment | terrestrial biome |
Sample Characteristic - Location | China |
Machine-accessible metadata file describing the reported data: https://doi.org/10.6084/m9.figshare.12917642
Similar content being viewed by others
Background & Summary
Evapotranspiration (ET) is a keystone climate variable that uniquely links the hydrological cycle, energy budget, and carbon cycle1,2. This process consists of physical evaporation (soil evaporation and canopy interception evaporation) and biological transpiration (T)3. Quantifying the ratio of transpiration to total evapotranspiration (T/ET) is an important topic of research4, it is crucial for estimating the land water flux and providing insight into the interactions between the terrestrial ecosystem and atmosphere5,6. Furthermore, long-term time series of spatially and temporally continuous T/ET products can be used to generate relatively more accurate carbon cycle projections because the biological process impacts of transpiration also control carbon dioxide exchange between the land and atmosphere7. This can help improve our understanding of feedback mechanisms between environmental factors and hydrological components, especially within the context of climate change8,9.
Multiple approaches have been developed to estimate T/ET at global or regional scales in recent decades. However, their values are still subject to debate1,10,11,12,13,14,15,16. For example, one isotope-based method indicated that T/ET was approximately 0.80–0.90 at the global scale1, which may be an overestimation17,18. Another study reported global T/ET values of approximately 0.64 ± 0.13 using the same method11. Moreover, the isotope-based method is restricted by the observation period; therefore, it is difficult to obtain long-term data series. Models provide an effective way of estimating T/ET on both temporal and spatial scales. However, due to the inaccurate representation of canopy light use, interception loss and root water uptake process in earth system models, the Coupled Model Intercomparison Project phase 5 (CMIP5) models underestimate T/ET, with a mean value of 0.41 ± 0.117. Additionally, these models cannot capture the opposing trends of transpiration and soil evaporation under terrestrial ecosystem greening19, which has been widely monitored around the world, especially in China9. The large T/ET variability reported by previous studies suggests that accuracy continues to be a challenge20. Moreover, to the best of our knowledge, no spatial-temporal continuous and open access T/ET product exists for the entire Chinese terrestrial ecosystem.
Site measurements can provide accurate local information related to T/ET; however, their relative scarcity and inconsistent measurement periods hinder large-scale upscaling7. Fortunately, model-data fusion (MDF) methods are available to assist with data analysis and generate links to models21. By combining multisite observations with a model, MDF can be used to optimize the generic nature of model parameters within plant functional types. If a model with optimized parameters is proved to perform well in T/ET simulations according to the site measurements within a plant functional type, one can assume that the model will accurately capture the T/ET spatial variations of the plant function type under present or future climate conditions7,22. MDF methods are routinely used to optimize model parameters based on evapotranspiration observations alone23,24,25. These studies significantly improved the accuracy of evapotranspiration simulations but still involved large uncertainties in evapotranspiration partitioning26,27. To improve the accuracy of evapotranspiration partitioning, Niu et al. (2019) applied a model-fusion approach that integrates PT-JPL model with multivariate observation datasets to the estimated T/ET value of the Chinese terrestrial ecosystem.
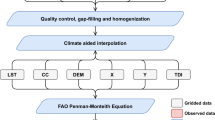
The objective of this study is to provide a long-term spatially and temporally consistent T/ET data source with spatiotemporal resolution (0.05°, 8-days and annual) and describe the accuracies of the dataset and method used. The procedure for producing and validating this dataset is shown schematically in Fig. 1 and described in detail in the Methods section. The proposed dataset will be valuable for addressing scientific questions associated with land-atmosphere interactions, global change, and ecological evolution, among others.
Procedure for producing a spatial-temporal continuous T/ET dataset based on the model-data fusion method. First, model forcing data and constraining data were prepared, respectively. Second, the sensitivity parameters of the PT-JPL model were optimized using the model-data fusion method. Third, the T/ET dataset is calculated using the PT-JPL model with optimization parameters. DEMC stands for Differential Evolution Markov Chain.
Methods
Three main steps are followed to create the T/ET dataset of Chinese terrestrial ecosystems from 1981–2015:
-
1.
Data preparation. An ensemble dataset with 0.05° spatial resolution and 8-day temporal resolution (including leaf area index, net radiation, air temperature, relative humidity) and land cover data were prepared to facilitate the PT-JPL model. Meanwhile, 127 records of annual evapotranspiration for 39 sites, and 48 records of annual transpiration for 26 sites which were obtained from published literature and ChinaFLUX were used to calibrate the PT-JPL model. Annual T/ET for 18 sites collected from published literature and daily evapotranspiration acquired from 6 ChinaFLUX sites were used to validate the PT-JPL model with optimized parameters.
-
2.
Implementation of MDF method. We optimized the sensitivity PT-JPL parameters using a model-data fusion method. Firstly, the Sobol’ method was used to identify the sensitivity parameters of the PT-JPL model. Then, the Differential Evolution Markov Chain (DEMC) that integrated the PT-JPL model with multiple observational data (i.e., annual evapotranspiration and transpiration data) was used to optimize the sensitivity parameters.
-
3.
T/ET simulation. The PT-JPL model with optimized parameters was used to simulate evapotranspiration and transpiration at the annual and daily scale, respectively. T/ET values were calculated as the quotient of simulated transpiration and evapotranspiration.
Each step is explained in more detail below.
Data Sets
Forcing datasets
We used multiple datasets as the input of the PT-JPL model. All datasets used are summarized in Table 1, and detailed processing methods are described below.
Leaf area index. LAI is a major input data for the PT-JPL model. Specifically, the arithmetic mean value of Long-term Global Mapping (GLOBMAP) LAI28 and Global Land Surface Satellite (GLASS) LAI29,30 were used to drive the model. To derive long-term LAI records back to 1981, the GLOBMAP LAI was generated by the quantitative fusion of MODIS and AVHRR data, with a spatial resolution of 0.08°, a half-monthly temporal resolution for the period ranging from 1981 to 2000, and an 8-day temporal resolution for the period ranging from 2001 to 2015. Compared with field measurement data, the GLOBALMAOP LAI has an error of 0.81 LAI on average, with R2 value being 0.7128. The GLASS LAI was also constructed using AVHRR and MODIS data with a general regression neural network, the spatial and temporal resolution was 0.05° and 8 days, respectively. The GLASS LAI values were closer to the mean values of the high-resolution LAI maps, with the R2 and RMSE values being 0.81 and 0.78, respectively30. We first resampled the LAI datasets to 8-day temporal resolution and 0.05° spatial resolution, respectively. Then, the arithmetic mean values of the LAI datasets were calculated as the input of the PT-JPL model.
Meteorological inputs. Meteorological forcing data such as net radiation, mean air temperature, and relative humidity were prepared using the meteorological raster dataset from the Chinese Ecosystem Research Network (CERN). The mean air temperature and relative humidity were generated from 1098 ground meteorological stations using the ANUSPLIN interpolation computer software31. The interpolated air temperature data was satisfactory with the R2 value being 0.94, compared to seven flux monitoring towers in the Asian region31. In this study, we compared the interpolated relative humidity with sites measurement data from 6 ChinaFLUX sites (Supplementary Table S1), whereby R2 and RMSE values were 0.85 and 0.86 (12.72% compared to the average relative humidity), respectively (Supplementary Fig. S1). The net radiation data were calculated from the FAO Penman model based on site measurement data from the China Meteorological Data Service Center, including 53 radiation sites, which were used to optimize parameters, and 699 weather sites, which were used to calculate the net radiation according to the optimized FAO Penman model and measurement data of these stations. Finally, the grid net radiation data were interpolated using ANUSPLIN software32,33. Compared with the data from observed sites, the simulated net radiation had a relatively high simulation accuracy with the R2 value being 0.72, and the mean relative error being 13%32. The original data had a temporal and spatial resolution of 8 days and 1 km, and they were resampled to a spatial resolution of 0.05° to match that of the LAI data.
Land cover. Land cover data of China obtained from the National Earth System Science Data Center, National Science & Technology Infrastructure of China, was constructed based on Landsat and GF-2. The classification and overall accuracies were ultimately evaluated through the confusion matrix. The comprehensive evaluation accuracy of the first level of land use was >93% and that of the second level was >90%34,35. The vegetation was divided into four types: forest, shrubland, grassland, and cropland. The original spatial resolution was 1 km, which was resampled to 0.05° to match that of LAI data.
Calibration and validation datasets
Site measured annual evapotranspiration and transpiration were used to determine the PT-JPL model, and literature collection annual T/ET data and daily evapotranspiration from ChinaFLUX were used to validate the model across different ecosystems (Table 2). The measured sites have a broad spatial distribution and cover all major ecosystem types in China (Supplementary Fig. S2).
Annual evapotranspiration observations. By synthesizing eddy-covariance water flux data in China from both ChinaFLUX observations and published literature, we constructed the dataset of the actual annual evapotranspiration of typical terrestrial ecosystems across China. The dataset contained 127 records of actual annual evapotranspiration for 39 ecosystems, covering 18 forests, 3 shrublands, 8 grasslands, and 10 croplands (Supplementary Table S2)32,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59. The following methods were adopted in the screening of these data: (1) evapotranspiration data were uniformly measured by the eddy-covariance method, (2) only sites with at least one year of continuous flux measurements were included, (3) only one site was selected when there are multiple sites with in a remote-sensing pixels.
Daily evapotranspiration observations. We obtained the complete time series of 30 min evapotranspiration data from 6 sites, covering 3 forests, 1 shrubland, 1 grassland, and 1 cropland. Supplementary Table S1 shows information on these sites. The routine processing procedures recommend by ChinaFLUX were applied to process the evapotranspiration data, including coordinate rotation, Webb-Pearman-Leuning (WPL) correction, storage term calculation, outlier filter, and gap filling60. Finally, the 30 min evapotranspiration data were collected to obtain 8-day evapotranspiration data for a given ecosystem.
Annual transpiration observations. Transpiration data were collected from published literature, representing 20 forest, 2 shrub, 3 cropland, and 1 grassland sites (Supplementary Table S3)61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86. The following steps were used to screen these data. First, only transpiration data measured by the sap flow method were selected. However, the sap flow method was not applicable for the grassland site; therefore, the transpiration data obtained from the Hydrus-1D model and site measurement data was used in this study. Second, only sites with at least one year of continuous flux measurements were included.
Annual T/ET observations. Field observations of T/ET across 18 sites, including 7 forest, 6 grassland, 2 shrubland, and 3 cropland sites (Supplementary Table S4)51,85,87,88,89,90,91,92,93,94 were collected from previous research studies. These studies experimentally measured at least three out of the four relevant variables, that is, evapotranspiration, transpiration, soil evaporation, and interception loss. We only retained site observations that were complete for at least a year or growing season.
PT-JPL model description
The Priestley-Taylor (PT) equation95 is a simplified but successful model for estimating the potential evapotranspiration from a wet surface95. In the PT-JPL model, the total evapotranspiration is partitioned into canopy transpiration (T), interception evaporation (EI), and soil evaporation (ES), which are expressed as follows:
where α is the PT coefficient of 1.26 for a water body (unitless); Δ is the slope of the saturation-to-vapor pressure curve (kPa °C−1); γ is the psychrometric constant (0.066 kPa °C−1); G is the ground heat flux (W m−2); Rnc is the net radiation to the canopy (W m−2), defined as Rnc = Rn − Rns, where Rn is the net radiation (W m−2); and Rns is the net radiation to the soil (W m−2). Rns can be calculated as \({R}_{ns}={R}_{n}{e}^{-{k}_{Rn}LAI}\), where kRn is the extinction coefficient (unitless).
PT-JPL effectively accomplishes its partitioning using a canopy extinction equation to estimate the radiation penetrating through the canopy96. This canopy extinction equation partition net radiation between the canopy and soil through utilizing the LAI in conjunction with the Beer-Lambert Law of light attenuation. Canopy transpiration are determined by the radiation intercepted according to the Beer-Lambert equation, and transpiration is constrained using four physiological parameters (i.e., fwet, fg,fT, and fM). Soil evaporation is determined using the residual radiation penetrating the canopy, and that are constrained by surface wetness parameter (fwet) and the available soil moisture (fsm). The restricted parameters are described in Table 3.
Model-data fusion method
Global sensitivity analysis
The Sobol’ method98,99, a globally popular sensitivity analysis technique based on variance decomposition, was integrated with multiple observational data (transpiration and evapotranspiration) to determine the sensitivity of parameters in the PT-JPL model. The Sobol’ method can quantify the sensitivity indices of each parameter based on the partial variance and total variances:
where Vm is the partial variance with a first-order index of ϑm on the model output, Vmn is the partial variance with a second-order index of the mth and nth parameter interactions, and V is the total model variance. Sm is a measure ratio from the main effect of the individual parameter ϑm to the total model variance V, Smn defines the sensitivity that results from the interactions between ϑm and ϑn, and STm represents the main effects of ϑm and its interactions with the other parameters and can be calculated using the variance V~m, which is the variation of all parameters except ϑm25. Niu et al. (2019) offer a detailed description of the implemented computational process.
Parameter optimization
To acquire more accurate model simulation results and reduce uncertainties, the DEMC based on Bayes theorem was used to optimize the selected sensitive parameters based on multi-source observed data. This method has been successful at reducing the prior uncertainties of sensitive parameters and improving the accuracy of the model across different biomes25. The likelihood function for multivariate data sets p(O|ϑ) used for parameter estimation is expressed as the product of the individual p(Oi(∙)|ϑ):
where I is the number of datasets, Ti is the total length of observations of the ith data set, \({\Delta }_{i}(t)\) is the model-data mismatch, and \({\sigma }_{i}\) (i = 1,2) is the standard deviation of the model error of the ith dataset100. The detailed disequilibrium method is found in the study by Niu et al. (2019). Table 4 shows the optimized parameters for each biome.
Simulation of T/ET dataset
The PT-JPL model with optimized parameters was used to directly simulate daily transpiration and evapotranspiration at each grid. For an 8-day temporal scale, T/ET values were calculated as the quotient of simulated transpiration and evapotranspiration. Annual T/ET values were calculated from the annual cumulative transpiration and evapotranspiration. All data within the span of a year were used to calculate the annual cumulative transpiration and evapotranspiration, and data gaps (i.e., the pixels without data) were set as zero.
Data Records
The dataset includes not only the T/ET, but also the transpiration and evapotranspiration data, which are directly used to calculate T/ET. Two temporal resolutions (daily and annual) are available, with a spatial resolution of 0.05° × 0.05° (Online-only Table 1). T/ET values are unitless for both annual and daily scales, whereas transpiration and evapotranspiration feature units of mm m−2 day−1 and mm−2 m−2 a−1 for daily and annual scales, respectively. For the annual and daily scale, T/ET values ranged from 0 to 1, and transpiration and evapotranspiration values were greater than zero. Considerable changes among the evapotranspiration components occur during the year, vegetation transpiration was nearly zero due to the cold temperature and low leaf area in northern China in winter. Therefore, T/ET values were also nearly zero or had no value within the same temporal and spatial range. Those pixels were expressed as −9999. Similarly, pixels of desert and construction land were also expressed as −9999.
All data were stored in the Network Common Data Form (NetCDF) files. Data files with different temporal resolution were stored in separate directories, i.e., Annual and Daily (Online-only Table 1). The naming convention for each type of data file was similar. For the annual scale, the naming convention is in accordance with the template Annual_VVVV.nc (e.g. Annual T_ET.nc), where VVVV represents the variable name. Each file contains 35 layers, which represent the annual variable for the period ranging from 1981 to 2015. For the daily scale, the naming convention follows the template Daily_VVVV_TTTT.nc (e.g. Daily_T_ET_1981.nc), where VVVV and TTTT represent the variable name and four-digit year. Each file contains 46 layers, and each layer represents the 8-day average evapotranspiration, transpiration, or T/ET. We stated the starting and ending time of each averaging period in the daily NetCDF files. All datasets101 are accessible on Open Science Framework (https://doi.org/10.17605/OSF.IO/MERZN).
This study provides a continuous spatial-temporal T/ET dataset. T/ET values for the Chinese terrestrial ecosystem for 1981–2015 range from 0.52–0.59 with a mean value of 0.56. The highest annual T/ET value typically occurs in the east monsoon area, whereas values in the temperate-continental and high-cold Tibetan Plateau areas are relatively low (Fig. 2a). The maximum daily T/ET show similar spatial patterns, but the magnitude is higher than that of the annual mean T/ET values (Fig. 2b). Both the annual T/ET and maximum daily T/ET show spatial patterns that are similar to the leaf area index (Fig. 2c).
Technical Validation
Validation using in-site measurements
The accuracy of the simulated T/ET dataset depends on the accuracy of the estimated transpiration and evapotranspiration data8. Therefore, the transpiration and evapotranspiration data were first calculated using annual in-situ measurements of the Chinese terrestrial ecosystem (Online-only Table 1 and supplementary Fig. S3). With respect to evapotranspiration, upon comparing all sites, forest sites, and non-forest sites with observed data, the R2 values were 0.71, 0.68, and 0.64, respectively, and the RMSE values were 153.57 (26.21% compared to the multiyear average value, and similarly hereinafter), 147.27 (25.14%), and 116.12 (19.83%), respectively. Meanwhile, the R2 and RMSE values of regressions between simulated transpiration and observed transpiration were 0.63 and 68.12 (36.80%), respectively. Additionally, the R2 values were 0.65 and 0.69 for forest sites and non-forest sites, respectively. A complete list of sites used to calibrate evapotranspiration and transpiration are presented in Supplementary Tables S2 and S3, respectively. Compared with other studies, Niu et al. (2019) found that the PT-JPL model with optimized parameters was comparable to the performance achieved using models driven by climatic and remote sensing data.
To further validate the model performance, we compared the simulated annual T/ET to the available filed observation T/ET data in China. A complete list of sites used, and T/ET comparison is presented in Supplementary Table S4. The overall accuracy of the T/ET dataset is relatively high with an R2 of 0.73 and a low RMSE of 0.07 (12.41%). The T/ET dataset also showed relatively high R2 and low RMSE for forest and non-forest sites (Online-only Table 1 and Fig. 3a).
We attempted to validate the seasonal dynamic of the simulated database. However, as we were limited by the observational data, only the seasonal fluctuations of evapotranspiration were validated. The R2 and RMSE values for all sites were 0.75 and 0.62 (35.29%), respectively (Online-only Table 1 and Supplementary Fig. S4). Both the simulated and observed evapotranspiration demonstrated distance seasonal cycles and matched well at different ecosystems (Supplementary Fig. S5). The ET values were high during the plant growing season, and almost zero in the winter due to the limitation of low temperature and plant growth. For the individual ecosystem, the R2 were all statistically significant at P < 0.01 and varied from 0.66 at the evergreen broadleaf forest to 0.91 at the mixed forest, and the RMSE values varied from 26.39% at mixed forests to 44.25% at grasslands.
Comparison of T/ET magnitude with previous studies
We compared the simulated T/ET magnitude with that reported by previous studies (Fig. 3). Simulated annual T/ET values (0.56 ± 0.05) were within the approximate range of those calculated by process- and remote sensing-based models (0.51 ± 0.08 and 0.56 ± 0.19, respectively). However, the T/ET value was lower than that obtained using the isotope method and from site measurements. The isotope method is constrained by hydrologic decoupling and may have overestimated T/ET10. The average T/ET derived from site measurements was 0.60, which was slightly higher than that obtained by this study. Canopy interception evaporation was not included in the majority of data; hence, relatively higher T/ET values were obtained when soil evaporation and transpiration were observed separately20.
For Chinese terrestrial ecosystems, the T/ET values simulated by the dataset were close to those derived using measurement data with the S-W model102,103. Specifically, the T/ET values estimated for temperate mixed, evergreen coniferous, and evergreen broadleaf forests (0.65, 0.67, and 0.66, respectively) were similar to those reported by Zhu et al. (2015) for the same forest types (0.66, 0.67, and 0.67, respectively). Hu et al.102 reported a range of the annual ratio of evaporation to evapotranspiration of 0.51–0.67 across four grassland ecosystems. Therefore, T/ET should lie between 0.33 and 0.49; these limits fall within the T/ET range of our data (0.41 ± 0.09).
Comparison of T/ET trends with other products
We also compared our T/ET dataset with other products, namely GLEAM V3.312,104, FLDAS V1105, GLDAS (both V1.0 and V2.1)106, and MsTMIP V1107 (Supplementary Table S5 shows information on these products). The annual trends of T/ET over China for the period ranging from 1981 to 2015 were analyzed using the Mann-Kendall test and Sen’s Method108, as shown in Fig. 4. Out dataset showed a significant increasing trend of annual T/ET over this period at a rate of 0.0022 a−1 (P < 0.01) for the entire study area (Fig. 4a). Greening can directly explain 57.89% of this T/ET trend8. This is consistent with the results at the global scale, i.e., that more than half of the global ET increase since the 1980s can be attributed to greening19,109, which is explained by increased transpiration and reduced soil evaporation9. Compared with other T/ET products, GLEAM and FLDAS also showed a significant upward trend between the 1980s and 2010s, while their slope values, which were 0.0007 a−1 (P < 0.01) and 0.0005 a−1 (P < 0.01), respectively (Fig. 4b and 4c), were lower than those of our simulated results. Meanwhile, the GLDAS 1.0 and MsTMIP products do not reflect the increasing T/ET trend (Fig. 4d, f). The serious discontinuity issues in GLDAS 1.0 forcing data, with large precipitation error in 1996 and temperature errors for the period ranging from 2000 to 2005110, may cause the GLDAS 1.0 product failure to reflect the long-term trend of T/ET. Different models of MsTMIP exhibited large differences in the simulated T/ET trends (Supplementary Fig. S6), T/ET acquired from the ISAM model showed a remarkable decreasing trend, with a value of -0.0003 a−1, while T/ET from other models all showed remarkable increasing trends, with values between 0.0001 of DLEM and 0.0016 Biome-BGC. After 2000, T/ET from GLDEM 2.1 showed a significant increasing trend, with values of 0.0031 a−1 (P < 0.01) (Fig. 4e), which was similar to that for our dataset.
Annual and seasonal T/ET trends acquired from different products. Annual T/ET trends for China according to (a) PT-JPL model with optimization parameters, (b) GLEAM, (c) FLDAS, (d) GLDAS 1.0, (e) GLDAS 2.1, and (f) MsTMIP in mainland China for the period ranging from 1981 to 2015. (g) Seasonal variation of T/ET acquired from different products.
We also compared the spatial patterns of the T/ET trend for different products (Supplementary Fig. S7). Our simulated T/ET exhibited finer spatial heterogeneity, compared to the other products. In the vegetation covered area, our simulated T/ET managed to better reflect regional differences; while in the desert area of northwest China, where vegetation cover was scarce, our simulated results correctly showed the relative lower or nearly zero T/ET, while some other products exhibited abnormally high T/ET values.
Figure 4g shows a comparison of the seasonal variation of simulated T/ET with other products. Overall, most of the products exhibited a similar monthly variation, with maximum values being yielded from June to August, and minimum values in March. We further conducted statistical analysis of the correlations between PT-JPL model simulated T/ET and other products at the seasonal scale, the R2 values exceeded 0.61, and RMSE values were below 38.36% (Supplementary Fig. S8).
Uncertainties
Model-data fusion is a powerful framework for the generation of improved simulation results via the combination of models with various data streams21,111. Observation data, model structure, and model parameters were the three main sources of the uncertainties111.
The challenge of acquiring independent observations that represent the scale of measurement is one of the inherent limitations in satellite-based model evaluation38. Therefore, we have to acknowledge that the spatial and temporal scale of the observation data used in this study is not the ideal dataset for assessing the performance of PT-JPL model. However, there are only a few alternatives for the calculation and validation of the components of ET (or T/ET). Eddy covariance observations are significantly better for the evaluation of remote-sensing-based evapotranspiration outputs, but they do not provide individual components of evapotranspiration. The sap flow method, which directly reflects the transpiration of single plants, was likely to be smaller in spatial scale than the satellite simulated, however, that method still offers insight into how evapotranspiration should by partitioned. Moreover, the observation data also contained errors stemming from the methodology used, but the field data represented the best available means for the calculation and validation of the remote-sensing-based simulation results112.
The PT-JPL model is widely used to simulate evapotranspiration and its individual components based on multiplicative evaporative stress factors97, and the model formulation bore similarities with other remote-sensing based evapotranspiration models (e.g., PM-MOD113 and GLEAM12,104). The simulated evapotranspiration of PT-JPL model was heavily dependent on the accuracy of net radiation97, while net radiation had negligible impact on T/ET8 because of the linear variation of the evapotranspiration components with net radiation. The simulated evapotranspiration components were generally sensitive to relative humidity and vegetation index112. Due to the non-linear relationships between relative humidity and evapotranspiration components (i.e., the model parameter fwet was calculated as a function of relative humidity raised to the fourth power), the simulated transpiration components were more sensitive at high relative humidity values than at lower ones. The evapotranspiration partitioning was particularly sensitive to extreme relative humidity112. Moreover, bias in PT-JPL due to uncertainties in the vegetation index are consistent with errors found when comparing model estimates to field estimates, meaning that the partitioning of PT-JPL was significantly affected by uncertainty in the vegetation index112. Overall, obtaining higher precision forcing data can help improve T/ET simulation results.
Four parameters (k1, k2, β, and Topt) were the most sensitive to the model across different biomes8. Parameter β was more sensitive at low vegetative cover and low precipitation regions, and Topt yielded the highest first-order sensitivity indices in the forest and cropland ecosystems. Niu et al. (2019) provide further details. In this study, observational data from multiple sites and multiple sources were used to calibrate the parameters of a given ecosystem type, that could better reflect ecological and biophysical properties within an ecosystem. Moreover, compared to the traditional Markov chain Monte Carlo approach, the DEMC algorithm, which was used in this study, is more suitable for drawing inference on high-dimensional models25,114.
Overall, despite the uncertainties, the simulated T/ET is consistent with the site observational data. The annual and daily T/ET estimation is close to that of previous studies using a different approach, and the trend of annual T/ET increases are also in line with certain products. Our simulated T/ET showed fine spatial heterogeneity and could accurately reflect the effects of greening on the hydrological cycle.
Usage Notes
Spatial average T/ET should be calculated as the ratio of regional mean transpiration and regional mean evapotranspiration, instead of directly using the regional or national average values of T/ET. The latter method only reflects the arithmetic mean of T/ET for each pixel, that will strengthen the influence of pixels with lower absolute values of evapotranspiration and transpiration, while weakening the effect of pixels with high transpiration and evapotranspiration.
Code availability
The codes for Sobol’ sensitivity analysis, DEMC parameter optimization, PT-JPL model and LAI preparation are available at https://doi.org/10.17605/OSF.IO/MERZN. The codes require MATLAB version 2014a or higher.
References
Jasechko, S. et al. Terrestrial water fluxes dominated by transpiration. Nature 496, 347–350 (2013).
Jung, M. et al. Recent decline in the global land evapotranspiration trend due to limited moisture supply. Nature 467, 951–954 (2010).
Kool, D. et al. A review of approaches for evapotranspiration partitioning. Agric. For. Meteorol. 184, 56–70 (2014).
Fisher, J. B. et al. The future of evapotranspiration: Global requirements for ecosystem functioning, carbon and climate feedbacks, agricultural management, and water resources. Water Resour. Res. 53, 2618–2626 (2017).
Alkama, R. & Cescatti, A. Biophysical climate impacts of recent changes in global forest cover. Science 351, 600–604 (2016).
Zeng, Z. et al. Climate mitigation from vegetation biophysical feedbacks during the past three decades. Nat. Clim. Change 7, 432–436 (2017).
Lian, X. et al. Partitioning global land evapotranspiration using CMIP5 models constrained by observations. Nat. Clim. Change 8, 640–646 (2018).
Niu, Z. et al. An increasing trend in the ratio of transpiration to total terrestrial evapotranspiration in China from 1982 to 2015 caused by greening and warming. Agric. For. Meteorol. 279, 107701 (2019).
Piao, S. et al. Characteristics, drivers and feedbacks of global greening. Nat. Rev. Earth Environ. 1, 14–27 (2020).
Schlesinger, W. H. & Jasechko, S. Transpiration in the global water cycle. Agric. For. Meteorol. 189–190, 115–117 (2014).
Good, S. P., Noone, D. & Bowen, G. Hydrologic connectivity constrains partitioning of global terrestrial water fluxes. Science 349, 175–177 (2015).
Martens, B. et al. GLEAM v3: Satellite-based land evaporation and root-zone soil moisture. Geosci. Model Dev. 10, 1903–1925 (2017).
Coenders-Gerrits, A. M. et al. Uncertainties in transpiration estimates. Nature 506, E1–2 (2014).
Evaristo, J., Jasechko, S. & McDonnell, J. J. Global separation of plant transpiration from groundwater and streamflow. Nature 525, 91–94 (2015).
Ren, X., Lu, Q., He, H., Zhang, L. & Niu, Z. Estimation and analysis of the ratio of transpiration to evapotranspiration in forest ecosystems along the North-South Transect of East China. J. Geogr. Sci. 29, 1807–1822 (2019).
Wei, H. et al. Modeling evapotranspiration and its components in Qianyanzhou Plantation based on remote sensing data. J. Nat. Res. 27, 778–789 (2012).
Schlaepfer, D. R. et al. Terrestrial water fluxes dominated by transpiration: Comment. Ecosphere 5, 9 (2014).
Maxwell, R. M. & Condon, L. E. Connections between groundwater flow and transpiration partitioning. Science 353, 377–380 (2016).
Zhang, Y. et al. Multi-decadal trends in global terrestrial evapotranspiration and its components. Sci. Rep. 6, 19124 (2016).
Gu, C. et al. Partitioning evapotranspiration using an optimized satellite-based ET model across biomes. Agric. For. Meteorol. 259, 355–363 (2018).
Wang-Erlandsson, L., van der Ent, R. J., Gordon, L. J. & Savenije, H. H. G. Contrasting roles of interception and transpiration in the hydrological cycle – Part 1: Temporal characteristics over land. Earth Syst. Dynam. 5, 441–469 (2014).
Kuppel, S. et al. Model-data fusion across ecosystems: from multisite optimizations to global simulations. Geosci. Model Dev. 7, 2581–2597 (2014).
García, M. et al. Actual evapotranspiration in drylands derived from in-situ and satellite data: Assessing biophysical constraints. Remote Sens. Environ. 131, 103–118 (2013).
Zhu, G. F. et al. Simultaneously assimilating multivariate data sets into the two-source evapotranspiration model by Bayesian approach: application to spring maize in an arid region of northwestern China. Geosci. Model Dev. 7, 1467–1482 (2014).
Zhang, K., Ma, J., Zhu, G., Ma, T., Han, T. & Feng, L. Parameter sensitivity analysis and optimization for a satellite-based evapotranspiration model across multiple sites using Moderate Resolution Imaging Spectroradiometer and flux data. J. Geophys. Res. Atmos. 122, 230–245 (2017).
Reinds, G. J., van Oijen, M., Heuvelink, G. B. M. & Kros, H. Bayesian calibration of the VSD soil acidification model using European forest monitoring data. Geoderma 146, 475–488 (2008).
Zhu, G., Su, Y., Li, X., Zhang, K. & Li, C. Estimating actual evapotranspiration from an alpine grassland on Qinghai-Tibetan plateau using a two-source model and parameter uncertainty analysis by Bayesian approach. J. Hydrol. 476, 42–51 (2013).
Liu, Y., Liu, R., Chen, J. M. Retrospective retrieval of long-term consistent global leaf area index (1981–2011) from combined AVHRR and MODIS data. Journal of Geophysical Research: Biogeosci. 117, G04003 (2012).
Xiao, Z. et al. Use of general regression neural networks for generating the GLASS leaf area index product from time-series MODIS surface reflectance. IEEE T. Geosci. Remote 52, 209–223 (2014).
Xiao, Z., Liang, S., Wang, J., Xiang, Y., Zhao, X. & Song, J. Long-time-series global land surface satellite leaf area index product derived from MODIS and AVHRR surface reflectance. IEEE T. Geosci. Remote 54, 5301–5318 (2016).
Wang, J., Wang, J., Ye, H., Liu, Y. & He, H. An interpolated temperature and precipitation dataset at 1-km grid resolution in China (2000–2012). China Scientific Data 2, 88–95 (2017).
Gao, Y., He, H., Zhang, L., Lu, Q., Yu, G. & Zhang, Z. Spatio-temporal variation characteristics of surface net radiation in China over the past 50 years. Int. J Geogr. Inf. Sci. 15, 1–10 (2013). (in Chinese)
Ren, X., He, H., Zhang, L. & Yu, G. Global radiation, photosynthetically active radiation, and the diffuse component dataset of China, 1981–2010. Earth Syst. Sci. Data 10, 1217–1226 (2018).
Liu, J., Liu, M., Deng, X., Zhuang, D., Zhang, Z. & Luo, D. The land use and land cover change database and its relative studies in China. J. Geogr. Sci. 12, 275–282 (2002).
Ning, J. et al. Spatiotemporal patterns and characteristics of land-use change in China during 2010-2015. J. Geogr. Sci. 28, 547–562 (2018).
Zhang, Y. Energy and water budget of a poplar plantation in suburban Beijing (Beijing Forestry University, 2010). (in Chinese)
Cui, S. Study on the CO2 flux of a larch plantation in NE China by the micrometeorological method (Northeast Forestry University, 2007). (in Chinese)
Zhu, G. et al. Energy flux partitioning and evapotranspiration in a sub-alpine spruce forest ecosystem. Hydrol. Process. 28, 5093–5104 (2014).
Lin, E., Jiang, H. & Chen, Y. Water vapor flux variation and net radiation for a Phyllostachys violascens stand in Taihuyuan. Journal of Zhejiang A&F University 30, 313–318 (2013). (in Chinese)
Wang, Z. Energy balance and water vapor flux of snail control and schistosomiasis prevention forests ecosystem in Yangtze River beach land (Chinese Academy of Forestry, 2008). (in Chinese)
Wang, W. et al. Characteristics of latent heat flux over Cunninghamia lanceolata plantations in Huitong county. Journal of Central South University of Forestry & Technology 31, 192–197 (2011). in Chinese.
Guo, L. The Variations of Water Use Efficiency and Evapotranspiration over a Plantation in the Southern Part of Hilly Areas of North-China (Chinese Academy of Forestry, 2010) (in Chinese)
Li, Z., Zhang, Y., Wang, S., Yuan, G., Yang, Y. & Cao, M. Evapotranspiration of a tropical rain forest in Xishuangbanna, southwest China. Hydrol. Process. 24, 2405–2416 (2010).
Tan, Z., Zhang, Y., Schaefer, D., Yu, G., Liang, N. & Song, Q. An old-growth subtropical Asian evergreen forest as a large carbon sink. Atmos. Environ. 45, 1548–1554 (2011).
Wilske, B. et al. Poplar plantation has the potential to alter the water balance in semiarid Inner Mongolia. J. Environ. Manage. 90, 2762–2770 (2009).
Han, S., Huang, L., Wang, Z., Wei, Y., Zhang, X. Ecosystem respiration and its controlling factors in the riparian wetland of Yangtze River. Acta ecologica sinica 29 (2009).
Liu, S., Xu, Z., Zhu, Z., Jia, Z. & Zhu, M. Measurements of evapotranspiration from eddy-covariance systems and large aperture scintillometers in the Hai River Basin, China. J. Hydrol. 487, 24–38 (2013).
Ouyang, Z., Mei, X., Li, Y. & Guo, J. Measurements of water dissipation and water use efficiency at the canopy level in a peach orchard. AgrI. Water Manage. 129, 80–86 (2013).
Zhang, Y., Shen, Y., Xu, X., Sun, H., Li, F. & Wang, Q. Characteristics of the water–energy–carbon fluxes of irrigated pear (Pyrus bretschneideri Rehd) orchards in the North China Plain. Agri. Water Manage. 128, 140–148 (2013).
Tan, Z. et al. Rubber plantations act as water pumps in tropical China. Geophys. Res. Lett. 38, L24406 (2011).
Liu, R., Li, Y. & Wang, Q. Variations in water and CO2 fluxes over a saline desert in western China. Hydrol. Process. 26, 513–522 (2012).
Chen, S. et al. Energy balance and partition in Inner Mongolia steppe ecosystems with different land use types. Agr. Forest Meteorol. 149, 1800–1809 (2009).
Liu, H. & Feng, J. Seasonal and interannual variations of evapotranspiration and energy exchange over different land surfaces in a semiarid area of China. J. Appl. Meteorol. Clim. 51, 1875–1888 (2012).
Shen, Y., Zhang, Y., Scanlon, B. R., Lei, H., Yang, D. & Yang, F. Energy/water budgets and productivity of the typical croplands irrigated with groundwater and surface water in the North China Plain. Agr. Forest Meteorol. 181, 133–142 (2013).
Zhou, G., Wang, Y. Dynamics of carbon budgets in typical corn and rice ecosystems in Liaohe delta. In: Proceedings of Low Carbon Agriculture Symposium. 133–142 (2010). (in Chinese)
Zhou, S. et al. Evapotranspiration of a drip-irrigated, film-mulched cotton field in northern Xinjiang, China. Hydrol. Process. 26, 1169–1178 (2012).
Zheng, H. et al. Spatial variation in annual actual evapotranspiration of terrestrial ecosystems in China: Results from eddy covariance measurements. J. Geogr. Sci. 26, 1391–1411 (2016).
Gu, S. et al. Characterizing evapotranspiration over a meadow ecosystem on the Qinghai-Tibetan Plateau. J. Geophys. Res.: Atmos. 113, D08118 (2008).
Li, J. et al. Characterizing the evapotranspiration of a degraded grassland in the Sanjiangyuan region of Qinghai province. Acta Prataculturae Sinica 21, 223–233 (2012). (in Chinese)
Yu, G., Wen, X., Sun, X., Tanner, B. D., Lee, X. & Chen, J. Overview of ChinaFLUX and evaluation of its eddy covariance measurement. Agr. Forest Meteorol. 137, 125–137 (2006).
Ma, L., Lu, P., Zhao, P., Rao, X., Cai, X. & Zeng, X. Diurnal, daily, seasonal and annual patterns of sap-flux-scaled transpiration from an Acacia mangium plantation in South China. Ann. For. Sci. 65, 9 (2008).
Ouyang, S. et al. Stand Transpiration Estimates from Recalibrated Parameters for the Granier Equation in a Chinese Fir (Cunninghamia lanceolata) Plantation in Southern China. Forests 9, 162 (2018).
Song, L., Zhu, J., Li, M., Zhang, J., Zheng, X. & Wang, K. Canopy transpiration of Pinus sylvestris var. mongolica in a sparse wood grassland in the semiarid sandy region of Northeast China. Agr. Forest Meteorol. 250, 192–201 (2018).
Zhang, H., Wei, W., Chen, L. & Yang, L. Evaluating canopy transpiration and water use of two typical planted tree species in the dryland Loess Plateau of China. Ecohydrology 10, 10 (2017).
Zhang, H., Wei, W., Chen, L. & Wang, L. Effects of terracing on soil water and canopy transpiration of Pinus tabulaeformis in the Loess Plateau of China. Ecol. Eng. 102, 557–564 (2017).
Chang, X., Zhao, W., Liu, H., Wei, X., Liu, B. & He, Z. Qinghai spruce (Picea crassifolia) forest transpiration and canopy conductance in the upper Heihe River Basin of arid northwestern China. Agr. Forest Meteorol. 198–199, 209–220 (2014).
Fang, S., Zhao, C. & Jian, S. Canopy transpiration of Pinus tabulaeformis plantation forest in the Loess Plateau region of China. Environ. Earth Sci. 75, 9 (2016).
Liu, Q., Zeng, H. & Ma, Z. Carbon sequestration of Pinus elliottii plantation in relation with water consumption in subtropical China. Acta Ecologica Sinica 28, 5322–5330 (2008). (in Chinese)
Fu, S., Sun, L. & Luo, Y. Canopy conductance and stand transpiration of Populus simonii Carr in response to soil and atmospheric water deficits in farmland shelterbelt, Northwest China. Agrofor. Syst. 91, 1165–1180 (2017).
Jiao, L., Lu, N., Sun, G., Ward, E. & Fu, B. Biophysical controls on canopy transpiration in a black locust (Robinia pseudoacacia) plantation on the semi-arid Loess Plateau, China. Ecohydrology 9, 1068–1081 (2016).
Zhang, J., Guan, J., Shi, W., Yamanaka, N. & Du, S. Interannual variation in stand transpiration estimated by sap flow measurement in a semi-arid black locust plantation, Loess Plateau, China. Ecohydrology 8, 137–147 (2015).
Yan, M. et al. Sapflow-Based Stand Transpiration in a Semiarid Natural Oak Forest on China’s Loess Plateau. Forests 7, 13 (2016).
Mo, K., Chen, L., Zhou, J., Fang, X., Kang, M. & Zhang, Z. Transpiration responses of a poplar plantation to the environmental conditions on a floodplain in Northern China. Acta Ecologica Sinica 34, 5812–5822 (2014). (in Chinese)
Zhao, W., Chang, X. & Zhang, Z. Transpiration of a Linze jujube orchard in an arid region of China. Hydrol. Process. 23, 1461–1470 (2009).
Gao, J., Meng, P., Zhang, J., Jia, C. & Ren, Y. Analysis on Transpiration and Difference between Evapotranspiration and Precipitation of Apricot Trees in the Rocky Mountain Area of Northern China. J. Agrometeorol. 30, 538–542 (2009).
Ren, Q., Meng, P., Zhang, J., Gao, J. & Li, C. Transpiration Variation of the Poplar Shelterbelts and Its Relation to the Meteorological Factors in the Cropland of North China Plain. Forest Research 21, 797–802 (2008).
Wang, D., Wang, G. & Anagnostou, E. Evaluation of canopy interception schemes in band surface models. J. Hydrol. 347, 308–318 (2007).
Liu, X., Zhang, J., Xie, D., Zhuang, J., Shao, Y. & Zhang, S. Temporal variation for canopy transpiration and its cooling properties in a Quercus acutissima forest of suburban Nanjing. Journal of Zhejiang A&F University 32, 529–536 (2015).
Chen, L. et al. Response of transpiration to rain pulses for two tree species in a semiarid plantation. Int. J. Biometeorol. 58, 1569–1581 (2014).
Chen, L., Zhang, Z., Li, Z., Tang, J., Caldwell, P. & Zhang, W. Biophysical control of whole tree transpiration under an urban environment in Northern China. J. Hydrol. 402, 388–400 (2011).
Ji, X., Zhao, W., Kang, E., Jin, B. & Xu, S. Transpiration from three dominant shrub species in a desert-oasis ecotone of arid regions of Northwestern China. Hydrol. Process. 30, 4841–4854 (2016).
Zhao, P., Kang, S., Li, S., Ding, R., Tong, L. & Du, T. Seasonal variations in vineyard ET partitioning and dual crop coefficients correlate with canopy development and surface soil moisture. Agr. Water Manage. 197, 19–33 (2018).
Chen, Y., Lee, G., Lee, P. & Oikawa, T. Model analysis of grazing effect on above-ground biomass and above-ground net primary production of a Mongolian grassland ecosystem. J. Hydrol. 333, 155–164 (2007).
Jiang, X., Kang, S., Li, F., Du, T., Tong, L. & Comas, L. Evapotranspiration partitioning and variation of sap flow in female and male parents of maize for hybrid seed production in arid region. Agr. Water Manage. 176, 132–141 (2016).
Gao, X., Mei, X., Gu, F., Hao, W., Gong, D. & Li, H. Evapotranspiration partitioning and energy budget in a rainfed spring maize field on the Loess Plateau, China. CATENA 166, 249–259 (2018).
Hou, L., Wenninger, J., Shen, J., Zhou, Y., Bao, H. & Liu, H. Assessing crop coefficients for Zea mays in the semi-arid Hailiutu River catchment, northwest China. Agr. water manage. 140, 37–47 (2014).
Zhou, G. et al. Measured sap flow and estimated evapotranspiration of tropical Eucalyptus urophylla plantations in south China. Acta Botanica Sinica 46, 202–210 (2004).
Liu, X. et al. Partitioning evapotranspiration in an intact forested watershed in southern China. Ecohydrology 8, 1037–1047 (2015).
Tian, F., Zhao, C. & Feng, Z. Simulating evapotranspiration of Qinghai spruce (Picea crassifolia) forest in the Qilian Mountains, northwestern China. J. Arid Environ. 75, 648–655 (2011).
Zhao, W. et al. Evapotranspiration partitioning, stomatal conductance, and components of the water balance: A special case of a desert ecosystem in China. J. Hydrol. 538, 374–386 (2016).
Qiu, G., Li, C. & Yan, C. Characteristics of soil evaporation, plant transpiration and water budget of Nitraria dune in the arid Northwest China. Agr. Forest Meteorol. 203, 107–117 (2015).
Zhang, Y., Kang, S., Ward, E. J., Ding, R., Zhang, X. & Zheng, R. Evapotranspiration components determined by sap flow and microlysimetry techniques of a vineyard in northwest China: Dynamics and influential factors. Agr. Water Manage. 98, 1207–1214 (2011).
Zhou, S., Liu, W. & Lin, W. The ratio of transpiration to evapotranspiration in a rainfed maize field on the Loess Plateau of China. Water Sci. Tech.: W. Sup. 17, 221–228 (2017).
Huang, X., Hao, Y., Wang, Y., Cui, X., Mo, X. & Zhou, X. Partitioning of evapotranspiration and its relation to carbon dioxide fluxes in Inner Mongolia steppe. J. arid environ. 74, 1616–1623 (2010).
Priestley, C. & Taylor, R. On the assessment of surface heat flux and evaporation using large-scale parameters. Month. Weather Rev. 100, 81–92 (1972).
Talsma, C. J. et al. Partitioning of evapotranspiration in remote sensing-based models. Agr. Forest Meteorol. 260, 131–143 (2018).
Fisher, J. B., Tu, K. P. & Baldocchi, D. D. Global estimates of the land–atmosphere water flux based on monthly AVHRR and ISLSCP-II data, validated at 16 FLUXNET sites. Remote Sens. Environ. 112, 901–919 (2008).
Sobol’, I. M. On sensitivity estimation for nonlinear mathematical models. Matematicheskoe modelirovanie 2, 112–118 (1990).
Sobol’, I. M. Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates. Math. Comput. Simul. 55, 271–280 (2001).
Braswell, B. H., Sacks, W. J., Linder, E. & Schimel, D. S. Estimating diurnal to annual ecosystem parameters by synthesis of a carbon flux model with eddy covariance net ecosystem exchange observations. Glob. Change Biol. 11, 335–355 (2005).
Niu, Z. et al. A spatial-temporal continuous dataset of the transpiration to evapotranspiration ratio in China from 1981–2015. Open Science Framework https://doi.org/10.17605/OSF.IO/MERZN (2020).
Hu, Z. M. et al. Partitioning of evapotranspiration and its controls in four grassland ecosystems: Application of a two-source model. Agric. For. Meteorol. 149, 1410–1420 (2009).
Zhu, X. J. et al. Spatiotemporal variations of T /ET (the ratio of transpiration to evapotranspiration) in three forests of Eastern China. Ecolog. Indic. 52, 411–421 (2015).
Miralles, D. G. et al. Global land-surface evaporation estimated from satellite-based observations. Hydrol. Earth Sys. Sc. 15, 453–469 (2011).
McNally, A. et al. A land data assimilation system for sub-Saharan Africa food and water security applications. Sci. Data 4, 1–19 (2017).
Rodel, lM. et al. The global land data assimilation system. B. Am. Meteorol. Soc. 85, 381–394 (2004).
Wei, Y. et al. NACP MsTMIP: Global and North American Driver Data for Multi-Model Intercomparison. ORNL DAAC, Oak Ridge, Tennessee, USA https://doi.org/10.3334/ORNLDAAC/1220 (2014).
Burkey, J. Mann-Kendall Tau-b with Sen’s Method (enhanced). MATLAB Central File Exchange https://www.mathworks.com/matlabcentral/fileexchange/11190-mann-kendall-tau-b-with-sen-s-method-enhanced (2020).
Zeng, Z., Peng, L. & Piao, S. Response of terrestrial evapotranspiration to Earth’s greening. Curr. Opin. Env. Sust. 33, 9–25 (2018).
Wang, W., Cui, W., Wang, X. J. & Chen, X. Evaluation of GLDAS-1 and GLDAS-2 Forcing Data and Noah Model Simulations over China at the Monthly Scale. J. Hydrometeorol. 17, 2815–2833 (2016).
Keenan, T. F., Carbone, M. S., Reichstein, M. & Richardson, A. D. The model-data fusion pitfall: assuming certainty in an uncertain world. Oecologia 167, 587–597 (2011).
Talsma, C. J. et al. Sensitivity of evapotranspiration components in remote sensing-based models. Remote Sens. 10, 1601 (2018).
Mu, Q., Zhao, M. & Running, S. W. Improvements to a MODIS global terrestrial evapotranspiration algorithm. Remote. Sens. Environ. 115, 1781–1800 (2011).
Ter Braak, C. J. A Markov Chain Monte Carlo version of the genetic algorithm Differential Evolution: easy Bayesian computing for real parameter spaces. Sta. Comput. 16, 239–249 (2006).
Wang, L., Good, S. P. & Caylor, K. K. Global synthesis of vegetation control on evapotranspiration partitioning. Geophys. Res. Lett. 41, 6753–6757 (2014).
Wei, Z. et al. Revisiting the contribution of transpiration to global terrestrial evapotranspiration. Geophys. Res. Lett. 44, 2792–2801 (2017).
Miralles, D. G. et al. The WACMOS-ET project – Part 2: Evaluation of global terrestrial evaporation data sets. Hysrol. Earth Syst. Sc. 20, 823–842 (2016).
Lawrence, D. M., et al. Parameterization improvements and functional and structural advances in Version 4 of the Community Land Model. J. Adv. Model. Earth Sy. 3, M03001 (2011).
Lawrence, D. M., Thornton, P. E., Oleson, K. W. & Bonan, G. B. The Partitioning of Evapotranspiration into Transpiration, Soil Evaporation, and Canopy Evaporation in a GCM: Impacts on Land–Atmosphere Interaction. J. Hydrometeorol. 8, 862–880 (2007).
Acknowledgements
This study was supported by the Strategic Priority Research Program of the Chinese Academy of Sciences (XDA19020301) and the National Key Research and Development Program of China (2016YFC0500204). We would like to thank the Chinese Ecosystem Research Network (CERN) (http://www.cnern.org.cn/) for providing the meteorology data, and Han Zheng for providing the annual observational evapotranspiration data.
Author information
Authors and Affiliations
Contributions
H.H. and Z.N. designed the study, Z.N. generated the data, G.Z. and Z.N. contributed to the parameter optimization, K.Z. contributed to the parameter optimization code. Z.N. analyzed the data and wrote the paper. All authors reviewed and edited the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Online-only Table
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
The Creative Commons Public Domain Dedication waiver http://creativecommons.org/publicdomain/zero/1.0/ applies to the metadata files associated with this article.
About this article
Cite this article
Niu, Z., He, H., Zhu, G. et al. A spatial-temporal continuous dataset of the transpiration to evapotranspiration ratio in China from 1981–2015. Sci Data 7, 369 (2020). https://doi.org/10.1038/s41597-020-00693-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41597-020-00693-x