Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Protocol
  • Published:

Machine learning workflows to estimate class probabilities for precision cancer diagnostics on DNA methylation microarray data

Nature Protocols volume 15, pages 479–512 (2020)Cite this article

Subjects

Abstract

DNA methylation data-based precision cancer diagnostics is emerging as the state of the art for molecular tumor classification. Standards for choosing statistical methods with regard to well-calibrated probability estimates for these typically highly multiclass classification tasks are still lacking. To support this choice, we evaluated well-established machine learning (ML) classifiers including random forests (RFs), elastic net (ELNET), support vector machines (SVMs) and boosted trees in combination with post-processing algorithms and developed ML workflows that allow for unbiased class probability (CP) estimation. Calibrators included ridge-penalized multinomial logistic regression (MR) and Platt scaling by fitting logistic regression (LR) and Firth’s penalized LR. We compared these workflows on a recently published brain tumor 450k DNA methylation cohort of 2,801 samples with 91 diagnostic categories using a 5 × 5-fold nested cross-validation scheme and demonstrated their generalizability on external data from The Cancer Genome Atlas. ELNET was the top stand-alone classifier with the best calibration profiles. The best overall two-stage workflow was MR-calibrated SVM with linear kernels closely followed by ridge-calibrated tuned RF. For calibration, MR was the most effective regardless of the primary classifier. The protocols developed as a result of these comparisons provide valuable guidance on choosing ML workflows and their tuning to generate well-calibrated CP estimates for precision diagnostics using DNA methylation data. Computation times vary depending on the ML algorithm from <15 min to 5 d using multi-core desktop PCs. Detailed scripts in the open-source R language are freely available on GitHub, targeting users with intermediate experience in bioinformatics and statistics and using R with Bioconductor extensions.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on Springer Link
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Pipeline of methylation microarray data-based machine learning workflow development and comparison for well-calibrated personalized cancer diagnostics.
Fig. 2: External validation on various tumor types from TCGA.

Similar content being viewed by others

Data and code availability

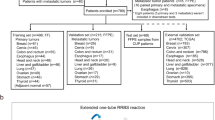
The described collection of R scripts and the associated data files provided in GitHub repositories (https://github.com/mwsill/mnp_training and https://github.com/mematt/ml4calibrated450k) are free software; you can redistribute it and/or modify it under the terms of the GNU General Public License as published by the Free Software Foundation version 2. All analyses were performed within either local (https://www.R-project.org/) or Docker containerized (https://www.docker.com) versions (rocker; https://www.rocker-project.org or https://github.com/rocker-org.) of the R: A language and environment for statistical programming v3.3.3–3.5.2 using the R Studio IDE, a free and open-source integrated development environment for R (v1.0.136 or v1.1.463; https://www.rstudio.com/products/RStudio/). Unprocessed IDAT files containing complete methylation values for the reference set and validation set as published in ref. 1 are available for download from the NCBI GEO under accession number GSE109381 (https://www.ncbi.nlm.nih.gov/geo/query/acc.cgi?acc=GSE109381). The variance-filtered outer- (fold IDs: 1.0, 2.0, …, 5.0) and innerfold (fold IDs: 1.1, 1.2, …, 1.5; 2.1, 2.2, …, 2.5; …; 5.1, 5.2, …, 5.5) training-test set pairs (altogether n = 30; i.e., 1.0–5.5; Fig. 1, part 2, outer and inner CV loops) of .RData files can be generated through scripts on Github (https://github.com/mematt/ml4calibrated450k/blob/master/data/subfunction_load_subset_filter_match_betasKk.R) or are directly downloadable (~5.3 GB) from our Dropbox (http://bit.ly/2vBg8yc). For details on how to prepare the 450k DNA methylation tumor samples from TCGA, please see the GitHub repository (https://github.com/mwsill/mnp_training/blob/master/tsne.R), and to download the source data, visit the NCI GDC Legacy Archive (https://gdc-portal.nci.nih.gov/legacy-archive). The combined TCGA cohort with vRF+MR predictions is available as a .xlsx file (Supplementary Data 1).

References

  1. Capper, D. et al. DNA methylation-based classification of central nervous system tumours. Nature 555, 469–474 (2018).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  2. Capper, D. et al. Practical implementation of DNA methylation and copy-number-based CNS tumor diagnostics: the Heidelberg experience. Acta Neuropathol. 136, 181–210 (2018).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  3. Heyn, H. & Esteller, M. DNA methylation profiling in the clinic: applications and challenges. Nat. Rev. Genet. 13, 679–692 (2012).

    Article  CAS  PubMed  Google Scholar 

  4. Rodríguez-Paredes, M. & Esteller, M. Cancer epigenetics reaches mainstream oncology. Nat. Med. 17, 330–339 (2011).

    Article  PubMed  CAS  Google Scholar 

  5. Sturm, D. et al. New brain tumor entities emerge from molecular classification of CNS-PNETs. Cell 164, 1060–1072 (2016).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  6. Sharma, T. et al. Second-generation molecular subgrouping of medulloblastoma: an international meta-analysis of Group 3 and Group 4 subtypes. Acta Neuropathol. 138, 309–326 (2019).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  7. Baek, S., Tsai, C.-A. & Chen, J. J. Development of biomarker classifiers from high-dimensional data. Brief. Bioinform. 10, 537–546 (2009).

    Article  CAS  PubMed  Google Scholar 

  8. Dupuy, A. & Simon, R. M. Critical review of published microarray studies for cancer outcome and guidelines on statistical analysis and reporting. J. Natl Cancer Inst. 99, 147–157 (2007).

    Article  PubMed  Google Scholar 

  9. Hastie, T., Tibshirani, R. & Friedman, J. The Elements of Statistical Learning: Data Mining, Inference and Prediction 2nd edn (Springer, New York, NY, 2009).

  10. Lee, J. W., Lee, J. B., Park, M. & Song, S. H. An extensive comparison of recent classification tools applied to microarray data. Comput. Stat. Data Anal. 48, 869–885 (2005).

    Article  Google Scholar 

  11. Simon, R. Roadmap for developing and validating therapeutically relevant genomic classifiers. J. Clin. Oncol. 23, 7332–7341 (2005).

    Article  CAS  PubMed  Google Scholar 

  12. Hoadley, K. A. et al. Cell-of-origin patterns dominate the molecular classification of 10,000 tumors from 33 types of cancer. Cell 173, 291–304 (2018).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  13. Fernandez, A. F. et al. A DNA methylation fingerprint of 1628 human samples. Genome Res. 22, 407–419 (2012).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  14. Wiestler, B. et al. Assessing CpG island methylator phenotype, 1p/19q codeletion, and MGMT promoter methylation from epigenome-wide data in the biomarker cohort of the NOA-04 trial. Neuro Oncol. 16, 1630–1638 (2014).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  15. Aryee, M. J. et al. Minfi: a flexible and comprehensive Bioconductor package for the analysis of Infinium DNA methylation microarrays. Bioinformatics 30, 1363–1369 (2014).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  16. Weinhold, L., Wahl, S., Pechlivanis, S., Hoffmann, P. & Schmid, M. A statistical model for the analysis of beta values in DNA methylation studies. BMC Bioinforma. 17, 480 (2016).

    Article  CAS  Google Scholar 

  17. Appel, I. J., Gronwald, W. & Spang, R. Estimating classification probabilities in high-dimensional diagnostic studies. Bioinformatics 27, 2563–2570 (2011).

    CAS  PubMed  Google Scholar 

  18. Kuhn, M. & Johnson, K. Applied Predictive Modeling (Springer Science+Business Media, 2013).

  19. Simon, R. Development and validation of biomarker classifiers for treatment selection. J. Stat. Plan. Inference 138, 308–320 (2008).

    Article  PubMed  PubMed Central  Google Scholar 

  20. Simon, R. Class probability estimation for medical studies. Biom. J. 56, 597–600 (2014).

    Article  PubMed  Google Scholar 

  21. Dankowski, T. & Ziegler, A. Calibrating random forests for probability estimation. Stat. Med. 35, 3949–3960 (2016).

  22. Boström, H. Calibrating random forests. In Seventh International Conference on Machine Learning and Applications (ICMLA’08) 121–126 (2008).

  23. Kruppa, J. et al. Probability estimation with machine learning methods for dichotomous and multicategory outcome: theory. Biom. J. 56, 534–563 (2014).

    Article  PubMed  Google Scholar 

  24. Platt, J. Probabilistic outputs for support vector machines and comparisons to regularized likelihood methods. Adv. Large Margin Classifiers 10, 61–74 (1999).

    Google Scholar 

  25. Hastie, T. & Tibshirani, R. Classification by pairwise coupling. in Advances in Neural Information Processing Systems. Vol. 10, 507–513 (MIT Press, 1997).

  26. Kruppa, J. et al. Probability estimation with machine learning methods for dichotomous and multicategory outcome: applications. Biom. J. 56, 564–583 (2014).

    Article  PubMed  Google Scholar 

  27. Wu, T.-F., Lin, C.-J. & Weng, R. C. Probability estimates for multi-class classification by pairwise coupling. J. Mach. Learn. Res. 5, 975–1005 (2004).

    Google Scholar 

  28. Gurovich, Y. et al. Identifying facial phenotypes of genetic disorders using deep learning. Nat. Med. 25, 60–64 (2019).

    Article  CAS  PubMed  Google Scholar 

  29. Breiman, L. Random forests. Mach. Learn. 45, 5–32 (2001).

    Article  Google Scholar 

  30. Cortes, C. & Vapnik, V. Support-vector networks. Mach. Learn. 20, 273–297 (1995).

    Google Scholar 

  31. Efron, B. & Hastie, T. Computer Age Statistical Inference, Vol. 5 (Cambridge University Press, 2016).

  32. Wang, X., Xing, E. P. & Schaid, D. J. Kernel methods for large-scale genomic data analysis. Brief. Bioinform. 16, 183–192 (2014).

    Article  PubMed  PubMed Central  CAS  Google Scholar 

  33. Zhuang, J., Widschwendter, M. & Teschendorff, A. E. A comparison of feature selection and classification methods in DNA methylation studies using the Illumina Infinium platform. BMC Bioinforma. 13, 59 (2012).

    Article  CAS  Google Scholar 

  34. Zou, H. & Hastie, T. Regularization and variable selection via the elastic net. J. R. Stat. Soc. Ser. B Stat. Methodol. 67, 301–320 (2005).

    Article  Google Scholar 

  35. Freund, Y. & Schapire, R. E. A decision-theoretic generalization of on-line learning and an application to boosting. J. Comput. Syst. Sci. 55, 119–139 (1997).

    Article  Google Scholar 

  36. Schapire, R.E. Using output codes to boost multiclass learning problems. in ICML ’97 Proceedings of the Fourteenth International Conference on Machine Learning 97, 313–321 (1997).

  37. Chen, T. & He, T. Higgs Boson discovery with boosted trees. in Proceedings of the NIPS 2014 Workshop on High-energy Physics and Machine Learning, Vol. 42 (eds Cowan, G. et al.) 69–80 (PMLR, 2015).

  38. He, X. et al. Practical lessons from predicting clicks on ads at Facebook. in Proc. Eighth International Workshop on Data Mining for Online Advertising (ADKDD’14) 1–9 (2014).

  39. Caruana, R. & Niculescu-Mizil, A. An empirical comparison of supervised learning algorithms. in Proceedings of the 23rd International Conference on Machine Learning 161–168 (2006).

  40. Niculescu-Mizil, A. & Caruana, R. Predicting good probabilities with supervised learning. in Proceedings of the 22nd International Conference on Machine Learning 625–632 (2005).

  41. Niculescu-Mizil, A. & Caruana, R. Obtaining calibrated probabilities from boosting. in Proceedings of the Twenty-First Conference on Uncertainty in Artificial Intelligence 413–420 (AUAI Press, 2005).

  42. Van Calster, B. et al. Comparing methods for multi-class probabilities in medical decision making using LS-SVMs and kernel logistic regression. in Artificial Neural Networks—ICANN 2007 (eds Marques de Sa, J. et al.) 139–148 (Springer, 2007).

  43. Zadrozny, B. & Elkan, C. Obtaining calibrated probability estimates from decision trees and naive Bayesian classifiers. in Proceedings of the Eighteenth International Conference on Machine Learning 609–616 (Morgan Kaufmann Publishers, 2001).

  44. Zadrozny, B. & Elkan, C. Transforming classifier scores into accurate multiclass probability estimates. in Proceedings of the Eighth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining 694–699 (ACM, 2002).

  45. Firth, D. Bias reduction of maximum likelihood estimates. Biometrika 80, 27–38 (1993).

    Article  Google Scholar 

  46. Lafzi, A., Moutinho, C., Picelli, S. & Heyn, H. Tutorial: guidelines for the experimental design of single-cell RNA sequencing studies. Nat. Protoc. 13, 2742–2757 (2018).

    Article  CAS  PubMed  Google Scholar 

  47. Rajkomar, A., Dean, J. & Kohane, I. Machine learning in medicine. N. Engl. J. Med. 380, 1347–1358 (2019).

    Article  PubMed  Google Scholar 

  48. Ramaswamy, S. et al. Multiclass cancer diagnosis using tumor gene expression signatures. Proc. Natl Acad. Sci. USA 98, 15149–15154 (2001).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  49. Kickingereder, P. et al. Radiogenomics of glioblastoma: machine learning–based classification of molecular characteristics by using multiparametric and multiregional MR imaging features. Radiology 281, 907–918 (2016).

    Article  PubMed  Google Scholar 

  50. Radovic, A. et al. Machine learning at the energy and intensity frontiers of particle physics. Nature 560, 41–48 (2018).

    Article  CAS  PubMed  Google Scholar 

  51. Butler, K. T., Davies, D. W., Cartwright, H., Isayev, O. & Walsh, A. Machine learning for molecular and materials science. Nature 559, 547–555 (2018).

    Article  CAS  PubMed  Google Scholar 

  52. Wiestler, B. et al. Integrated DNA methylation and copy-number profiling identify three clinically and biologically relevant groups of anaplastic glioma. Acta Neuropathol. 128, 561–571 (2014).

    Article  CAS  PubMed  Google Scholar 

  53. Ritchie, M. E. et al. limma powers differential expression analyses for RNA-sequencing and microarray studies. Nucleic Acids Res. 43, e47 (2015).

    Article  PubMed  PubMed Central  Google Scholar 

  54. Bourgon, R., Gentleman, R. & Huber, W. Independent filtering increases detection power for high-throughput experiments. Proc. Natl Acad. Sci. USA 107, 9546–9551 (2010).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  55. Breiman, L. & Spector, P. Submodel selection and evaluation in regression. The X-random case. Int. Stat. Rev. 60, 291–319 (1992).

    Article  Google Scholar 

  56. Kohavi, R. A study of cross-validation and bootstrap for accuracy estimation and model selection. IJCAI 14, 1137–1145 (1995).

    Google Scholar 

  57. Krijthe, J. H. Rtsne: T-distributed stochastic neighbor embedding using Barnes-Hut implementation. R package version 0.15, https://cran.r-project.org/web/packages/Rtsne/index.html (2015).

  58. Maaten, Lvd & Hinton, G. Visualizing data using t-SNE. J. Mach. Learn. Res. 9, 2579–2605 (2008).

    Google Scholar 

  59. Ester, M., Kriegel, H.-P., Sander, J. & Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. in KDD Proc. 96, 226–231 (AAAI, 1996).

  60. Breiman, L., Friedman, J., Stone, C. & Olshen, R. Classification and Regression Trees (CRC Press, Chapman and Hall, 1984).

    Google Scholar 

  61. Liaw, A. & Wiener, M. Classification and regression by randomForest. R. N. 2, 18–22 (2002).

    Google Scholar 

  62. Kuhn, M. Caret package. J. Stat. Softw. 28, 1–26 (2008).

    Article  Google Scholar 

  63. Kruppa, J., Schwarz, A., Arminger, G. & Ziegler, A. Consumer credit risk: individual probability estimates using machine learning. Expert Syst. Appl. 40, 5125–5131 (2013).

    Article  Google Scholar 

  64. Malley, J. D., Kruppa, J., Dasgupta, A., Malley, K. G. & Ziegler, A. Probability machines: consistent probability estimation using nonparametric learning machines. Methods Inf. Med. 51, 74–81 (2012).

    Article  CAS  PubMed  Google Scholar 

  65. Strobl, C., Boulesteix, A.-L., Zeileis, A. & Hothorn, T. Bias in random forest variable importance measures: illustrations, sources and a solution. BMC Bioinforma. 8, 25 (2007).

    Article  CAS  Google Scholar 

  66. Chen, C., Liaw, A. & Breiman, L. Using Random Forest to Learn Imbalanced Data, Vol. 110 (University of California, Berkeley, 2004).

  67. Friedman, J., Hastie, T. & Tibshirani, R. Regularization paths for generalized linear models via coordinate descent. J. Stat. Softw. 33, 1–22 (2010).

    Article  PubMed  PubMed Central  Google Scholar 

  68. Zou, H. & Hastie, T. Regression shrinkage and selection via the elastic net, with applications to microarrays. J. R. Stat. Soc. Ser. B 67, 301–320 (2003).

    Article  Google Scholar 

  69. Hastie, T. & Qian, J. Glmnet vignette. https://web.stanford.edu/~hastie/glmnet/glmnet_alpha.html (2016).

  70. Tibshirani, R. Regression shrinkage and selection via the lasso. J. R Stat. Soc. Series B Methodol. 58, 267–288 (1996).

    Google Scholar 

  71. Chang, C.-C. & Lin, C.-J. LIBSVM: a library for support vector machines. ACM Trans. Intell. Syst. Technol. 2, 27:21–27:27 (2011).

    Article  Google Scholar 

  72. e1071: Misc Functions of the Department of Statistics, Probability Theory Group (Formerly: E1071), TU Wien v. R package version 1.7-1 (The Comprehensive R Archive Network, Vienna, Austria, 2019).

  73. Fan, R.-E., Chang, K.-W., Hsieh, C.-J., Wang, X.-R. & Lin, C.-J. LIBLINEAR: a library for large linear classification. J. Mach. Learn. Res. 9, 1871–1874 (2008).

    Google Scholar 

  74. Helleputte, T. & Gramme, P. LiblineaR: linear predictive models based on the LIBLINEAR C/C++ Library. R package version 2.10-8 (2017).

  75. Wang, Z., Chu, T., Choate, L. A. & Danko, C. G. Rgtsvm: support vector machines on a GPU in R. arXiv, https://arxiv.org/abs/1706.05544 (2017).

  76. Crammer, K. & Singer, Y. On the algorithmic implementation of multiclass kernel-based vector machines. J. Mach. Learn. Res. 2, 265–292 (2001).

    Google Scholar 

  77. Milgram, J., Cheriet, M. & Sabourin, R. Estimating accurate multi-class probabilities with support vector machines. in Neural Networks, IJCNN’05. Proceedings. 2005 IEEE International Joint Conference. 3, 1906–1911(IEEE, 2005).

  78. Hastie, T., Rosset, S., Tibshirani, R. & Zhu, J. The entire regularization path for the support vector machine. J. Mach. Learn. Res. 5, 1391–1415 (2004).

    Google Scholar 

  79. Hsu, C.-W., Chang, C.-C. & Lin, C.-J. A Practical Guide To Support Vector Machines. (Department of Computer Science & Information Engineering, National Taiwan University, Taipei, Taiwan, 2003).

  80. Chen, T. & He, T. Xgboost: extreme gradient boosting. R package version 0.4-2, https://doi.org/10.1145/2939672.2939785, https://cran.r-project.org/web/packages/xgboost/index.html (2016).

  81. Chen, T., He, T., Benesty, M., Khotilovich, V. & Tang, Y. XGBoost—Introduction to Boosted Trees. XGBoost, https://xgboost.readthedocs.io/en/latest/tutorials/model.html (2017).

  82. Dobson, A. J. & Barnett, A. An Introduction to Generalized Linear Models (CRC Press, 2008).

  83. R Core Team. R: A Language and Environment for Statistical Computing (R Foundation for Statistical Computing, Vienna, Austria, 2017) https://www.R-project.org/

  84. Geroldinger, A. et al. Accurate Prediction of Rare Events with Firth’s Penalized Likelihood Approach (Vienna, Austria, 2015) http://prema.mf.uni-lj.si/files/Angelika_654.pdf

  85. Puhr, R., Heinze, G., Nold, M., Lusa, L. & Geroldinger, A. Firth’s logistic regression with rare events: accurate effect estimates and predictions? Stat. Med. 36, 2302–2317 (2017).

  86. Heinze, G. & Schemper, M. A solution to the problem of separation in logistic regression. Stat. Med. 21, 2409–2419 (2002).

    Article  PubMed  Google Scholar 

  87. Kosmidis, I. brglm: bias reduction in generalized linear models. In The R User Conference, useR! 2011August 16–18 2011, Vol. 111 (University of Warwick, Coventry, UK, 2011).

  88. Shen, J. & Gao, S. A solution to separation and multicollinearity in multiple logistic regression. J. Data Sci. 6, 515–531 (2008).

    Article  PubMed  PubMed Central  Google Scholar 

  89. Zhao, S. D., Parmigiani, G., Huttenhower, C. & Waldron, L. Más-o-menos: a simple sign averaging method for discrimination in genomic data analysis. Bioinformatics 30, 3062–3069 (2014).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  90. Donoho, D. L. & Ghorbani, B. Optimal covariance estimation for condition number loss in the spiked model. Preprint at arXiv, https://arxiv.org/abs/1810.07403v1 (2018).

  91. Agrawal, A., Viktor, H. L. & Paquet, E. SCUT: multi-class imbalanced data classification using SMOTE and cluster-based undersampling. in 2015 7th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K) 1, 226–234 (IEEE, Funchal, Portugal, 2015).

  92. Bischl, B. et al. mlr: machine learning in R. J. Mach. Learn. Res. 17, 1–5 (2016).

    Google Scholar 

  93. Chawla, N. V., Bowyer, K. W., Hall, L. O. & Kegelmeyer, W. P. SMOTE: synthetic minority over-sampling technique. J. Artif. Intell. Res. 16, 321–357 (2002).

    Article  Google Scholar 

  94. Lunardon, N., Menardi, G. & Torelli, N. ROSE: a package for binary imbalanced learning. R J. 6, 79–89 (2014).

  95. Menardi, G. & Torelli, N. Training and assessing classification rules with imbalanced data. Data Min. Knowl. Discov. 28, 92–122 (2014).

    Article  Google Scholar 

  96. Hauskrecht, M., Pelikan, R., Valko, M. & Lyons-Weiler, J. Feature selection and dimensionality reduction in genomics and proteomics. in Fundamentals of Data Mining in Genomics and Proteomics (eds Dubitzky, W. et al.) 149–172 (Springer, 2007).

  97. Guyon, I., Weston, J., Barnhill, S. & Vapnik, V. Gene selection for cancer classification using support vector machines. Mach. Learn. 46, 389–422 (2002).

    Article  Google Scholar 

  98. Hastie, T., Tibshirani, R. & Friedman, J. High-dimensional problems: p N. In The Elements of Statistical Learning: Data Mining, Inference, and Prediction. 649–698 (Springer, New York, NY 2009).

  99. Huber, W. et al. Orchestrating high-throughput genomic analysis with Bioconductor. Nat. Methods 12, 115–121 (2015).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  100. Assenov, Y. et al. Comprehensive analysis of DNA methylation data with RnBeads. Nat. Methods 11, 1138–1140 (2014).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  101. Morris, T. J. et al. ChAMP: 450k chip analysis methylation pipeline. Bioinformatics 30, 428–430 (2013).

    Article  PubMed  PubMed Central  CAS  Google Scholar 

  102. Pidsley, R. et al. A data-driven approach to preprocessing Illumina 450K methylation array data. BMC Genomics 14, 293 (2013).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  103. Horvath, S. DNA methylation age of human tissues and cell types. J. Genome Biol. 14, 3156 (2013).

    Google Scholar 

  104. Johann, P. D., Jäger, N., Pfister, S. M. & Sill, M. RF_Purify: a novel tool for comprehensive analysis of tumor-purity in methylation array data based on random forest regression. BMC Bioinforma. 20, 428 (2019).

    Article  CAS  Google Scholar 

  105. Leek, J., Johnson, W., Parker, H., Jaffe, A. & Storey, J. sva: Surrogate Variable Analysis R package version 3.10. 0 (2014). https://bioconductor.org/packages/release/bioc/html/sva.html

  106. Leek, J. T. & Storey, J. D. Capturing heterogeneity in gene expression studies by surrogate variable analysis. PLoS Genet. 3, e161 (2007).

    Article  PubMed Central  CAS  Google Scholar 

  107. Leek, J. T. & Storey, J. D. A general framework for multiple testing dependence. Proc. Natl Acad. Sci. USA 105, 18718–18723 (2008).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  108. Anders, S. et al. Count-based differential expression analysis of RNA sequencing data using R and Bioconductor. Nat. Protoc. 8, 1765–1786 (2013).

    Article  PubMed  CAS  Google Scholar 

  109. Pedregosa, F. et al. Scikit-learn: machine learning in Python. J. Mach. Learn. Res. 12, 2825–2830 (2011).

    Google Scholar 

  110. Hand, D. J. & Till, R. J. A simple generalisation of the area under the ROC curve for multiple class classification problems. Mach. Learn. 45, 171–186 (2001).

    Article  Google Scholar 

  111. Cullmann, A. D. HandTill2001: multiple class area under ROC curve. R Package (2016). https://cran.r-project.org/web/packages/HandTill2001/index.html

  112. Bickel, J. E. Some comparisons among quadratic, spherical, and logarithmic scoring rules. Decis. Anal. 4, 49–65 (2007).

    Article  Google Scholar 

  113. Brier, G. W. Verification of forecasts expressed in terms of probability. Mon. Weather Rev. 78, 1–3 (1950).

    Article  Google Scholar 

  114. Friedman, D. An effective scoring rule for probability distributions. UCLA Economics Working Papers. Discussion Paper 164, http://www.econ.ucla.edu/workingpapers/wp164.pdf (1979).

  115. Gneiting, T. & Raftery, A. E. Strictly proper scoring rules, prediction, and estimation. J. Am. Stat. Assoc. 102, 359–378 (2007).

    Article  CAS  Google Scholar 

  116. James, G., Witten, D., Hastie, T. & Tibshirani, R. An Introduction to Statistical Learning with Applications in R. 1st edn (Springer-Verlag, New York, NY, 2013).

  117. Mitchell, R. & Frank, E. Accelerating the XGBoost algorithm using GPU computing. PeerJ Comput. Sci. 3, e127 (2017).

    Article  Google Scholar 

  118. Fischer, B., Pau, G. & Smith, M. rhdf5: HDF5 interface to R. R Package Version 2.30.1 (RcoreTeam, Vienna, Austria, 2019).

  119. Qiu, Y., Mei, J., Guennebaud, G. & Niesen, J. RSpectra: solvers for large scale Eigenvalue and SVD problems. R Package Version 0.12-0 (2016). https://cran.r-project.org/web/packages/RSpectra/index.html

  120. Crammer, K. & Singer, Y. On the learnability and design of output codes for multiclass problems. Mach. Learn. 47, 201–233 (2002).

    Article  Google Scholar 

  121. Akulenko, R., Merl, M. & Helms, V. BEclear: batch effect detection and adjustment in DNA methylation data. PLoS ONE 11, e0159921 (2016).

    Article  PubMed  PubMed Central  CAS  Google Scholar 

  122. Price, E. M. & Robinson, W. P. Adjusting for batch effects in DNA methylation microarray data, a lesson learned. Front. Genet. 9, 83 (2018).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  123. Leek, J. T. et al. Tackling the widespread and critical impact of batch effects in high-throughput data. Nat. Rev. Genet. 11, 733–739 (2010).

    Article  CAS  PubMed  Google Scholar 

Download references

Acknowledgements

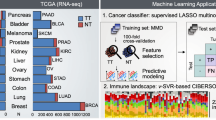
The authors gratefully acknowledge funding from the DKFZ-Heidelberg Center for Personalized Oncology (DKFZ-HIPO) through HIPO-036 and from the German Childhood Cancer Foundation (‘Neuropath 2.0 - Increasing diagnostic accuracy in paediatric neurooncology’ (DKS 2015.01)). M.E.M. gratefully acknowledges funding from the German Federal Ministry for Economic Affairs and Energy within the scope of Zentrales Innovationsprogramm Mittelstand (ZF 4514602TS8). The results shown in the external validation section and Fig. 2 are entirely based on data generated by TCGA Research Network: https://www.cancer.gov/tcga.

Author information

Authors and Affiliations

  1. Institute of Medical Biometry and Informatics (IMBI), University of Heidelberg, Heidelberg, Germany

    Máté E. Maros

  2. Department of Neuroradiology, University Medical Center, Medical Faculty Mannheim of Heidelberg University, Mannheim, Germany

    Máté E. Maros

  3. German Cancer Consortium (DKTK), German Cancer Research Center (DKFZ), partner site Berlin, Berlin, Germany

    David Capper & Andreas von Deimling

  4. Charité–Universitätsmedizin Berlin, corporate member of Freie Universität Berlin, Humboldt-Universität zu Berlin, and Berlin Institute of Health, Department of Neuropathology, Berlin, Germany

    David Capper

  5. Hopp Children’s Cancer Center Heidelberg (KiTZ), Heidelberg, Germany

    David T. W. Jones, Stefan M. Pfister & Martin Sill

  6. Pediatric Glioma Research Group, German Cancer Consortium (DKTK) and German Cancer Research Center (DKFZ), Heidelberg, Germany

    David T. W. Jones

  7. Division of Molecular Genetics, German Cancer Research Center (DKFZ), Heidelberg, Germany

    Volker Hovestadt

  8. Department of Pathology and Center for Cancer Research, Massachusetts General Hospital and Harvard Medical School, Boston, MA, USA

    Volker Hovestadt

  9. Broad Institute of MIT and Harvard, Cambridge, MA, USA

    Volker Hovestadt

  10. Department of Neuropathology, University Hospital Heidelberg, Heidelberg, Germany

    Andreas von Deimling

  11. Division of Pediatric Neurooncology, German Cancer Consortium (DKTK), German Cancer Research Center (DKFZ), Heidelberg, Germany

    Stefan M. Pfister & Martin Sill

  12. Department of Pediatric Oncology, Hematology and Immunology, University Hospital Heidelberg, Heidelberg, Germany

    Stefan M. Pfister

  13. Division of Biostatistics, German Cancer Research Center (DKFZ), Heidelberg, Germany

    Axel Benner & Martin Sill

  14. Oslo Centre for Biostatistics and Epidemiology, Department of Biostatistics, Institute of Basic Medical Sciences, University of Oslo, Oslo, Norway

    Manuela Zucknick

Authors
  1. Máté E. Maros
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. David Capper
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. David T. W. Jones
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Volker Hovestadt
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Andreas von Deimling
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Stefan M. Pfister
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. Axel Benner
    View author publications

    You can also search for this author in PubMed Google Scholar

  8. Manuela Zucknick
    View author publications

    You can also search for this author in PubMed Google Scholar

  9. Martin Sill
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

M.E.M. and M.S. conceptualized and developed machine learning workflows, performed the comparative analyses and wrote the manuscript. M.S. and V.H. performed data preparation. D.C., D.T.W.J., S.M.P. and A.v.D. composed the reference cohort and defined methylation classes. A.B. and M.Z. supervised the statistical aspects and data analysis. M.S. supervised the work and wrote the manuscript. All authors critically reviewed the manuscript and approved the final version.

Corresponding author

Correspondence to Martin Sill.

Ethics declarations

Competing interests

A patent for a ‘DNA-methylation based method for classifying tumor species of the brain’ has been applied for by the Deutsches Krebsforschungszentrum Stiftung des öffentlichen Rechts and Ruprecht-Karls-Universität Heidelberg (EP 3067432 A1) with V.H., D.C., D.T.W.J., S.M.P., A.v.D. and M.S. as inventors. The other authors have no competing interests to declare.

Additional information

Peer review information Nature Protocols thanks Casey Greene, Ludmila Danilova and Levi Waldron for their contribution to the peer review of this work.

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Related links

Key reference using this protocol

Capper, D. et al. Nature 555, 469–474 (2018): https://doi.org/10.1038/nature26000

Publications focused on one particular method

Capper, D. et al. Acta Neuropathol. 136, 181–210 (2018): https://doi.org/10.1007/s00401-018-1879-y

Sharma, T. et al. Acta Neuropathol. 138, 309–326 (2019): https://doi.org/10.1007/s00401-019-02020-0

Supplementary information

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Maros, M.E., Capper, D., Jones, D.T.W. et al. Machine learning workflows to estimate class probabilities for precision cancer diagnostics on DNA methylation microarray data. Nat Protoc 15, 479–512 (2020). https://doi.org/10.1038/s41596-019-0251-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/s41596-019-0251-6

This article is cited by

Comments

By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing