Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Cross-hemispheric gamma synchrony between prefrontal parvalbumin interneurons supports behavioral adaptation during rule shift learning

Nature Neuroscience volume 23, pages 892–902 (2020)Cite this article

Subjects

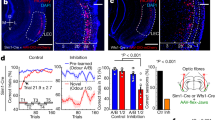
Abstract

Organisms must learn new strategies to adapt to changing environments. Activity in different neurons often exhibits synchronization that can dynamically enhance their communication and might create flexible brain states that facilitate changes in behavior. We studied the role of gamma-frequency (~40 Hz) synchrony between prefrontal parvalbumin (PV) interneurons in mice learning multiple new cue–reward associations. Voltage indicators revealed cell-type-specific increases of cross-hemispheric gamma synchrony between PV interneurons when mice received feedback that previously learned associations were no longer valid. Disrupting this synchronization by delivering out-of-phase optogenetic stimulation caused mice to perseverate on outdated associations, an effect not reproduced by in-phase stimulation or out-of-phase stimulation at other frequencies. Gamma synchrony was specifically required when new associations used familiar cues that were previously irrelevant to behavioral outcomes, not when associations involved new cues or for reversing previously learned associations. Thus, gamma synchrony is indispensable for reappraising the behavioral salience of external cues.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on Springer Link
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Prefrontal PV interneurons are recruited after errors during rule shifts.
Fig. 2: Cross-hemispheric gamma synchrony of PV interneurons increases after errors during rule shifts.
Fig. 3: Cross-hemispheric synchrony does not increase during initial associations and rule reversals.
Fig. 4: Out-of-phase, but not in-phase, gamma-frequency stimulation of PV interneurons disrupts learning during rule shifts but not during initial associations or rule reversals.
Fig. 5: Cross-hemispheric gamma synchrony fails to increase during rule shifts in mutant mice.
Fig. 6: Restoring cross-hemispheric PV interneuron gamma synchrony is required to rescue rule shift performance in Dlx5/6+/− mutant mice.
Fig. 7: Low-dose clonazepam increases cross-hemispheric gamma synchrony during rule shifts in mutant mice.

Similar content being viewed by others

Data availability

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Code availability

Scripts used to analyze dual-site TEMPO data are deposited at https://github.com/sohallab/dual-site-TEMPO.

References

  1. Young, D. A., Davila, R. & Scher, H. Unawareness of illness and neuropsychological performance in chronic schizophrenia. Schizophr. Res. 10, 117–124 (1993).

    CAS  PubMed  Google Scholar 

  2. Shad, M. U., Tamminga, C. A., Cullum, M., Haas, G. L. & Keshavan, M. S. Insight and frontal cortical function in schizophrenia: a review. Schizophr. Res. 86, 54–70 (2006).

    PubMed  Google Scholar 

  3. von der Malsburg, C. The Correlation Theory of Brain Function http://cogprints.org/1380/ (1981).

  4. Abeles, M., Prut, Y., Bergman, H. & Vaadia, E. Synchronization in neuronal transmission and its importance for information processing. Prog. Brain Res. 102, 395–404 (1994).

    CAS  PubMed  Google Scholar 

  5. Singer, W. Neuronal synchrony: a versatile code for the definition of relations? Neuron 49, 111–125 (1999).

    Google Scholar 

  6. Salinas, E. & Sejnowski, T. J. Correlated neuronal activity and the flow of neural information. Nat. Rev. Neurosci. 8, 539–550 (2011).

    Google Scholar 

  7. Fries, P. A mechanism for cognitive dynamics: neuronal communication through coherence. Trends Cogn. Sci. 9, 474–480 (2005).

    PubMed  Google Scholar 

  8. Fries, P. Neuronal gamma-band synchronization as a fundamental process in cortical computation. Annu. Rev. Neurosci. 32, 209–224 (2009).

    CAS  PubMed  Google Scholar 

  9. Sohal, V. S., Zhang, F., Yizhar, O. & Deisseroth, K. Parvalbumin neurons and gamma rhythms enhance cortical circuit performance. Nature 459, 698–702 (2009).

    CAS  PubMed  PubMed Central  Google Scholar 

  10. Fries, P. Rhythms for cognition: communication through coherence. Neuron 88, 220–235 (2015).

    CAS  PubMed  PubMed Central  Google Scholar 

  11. Sohal, V. S. How close are we to understanding what (if anything) gamma oscillations do in cortical circuits? J. Neurosci. 36, 10489–10495 (2016).

    CAS  PubMed  PubMed Central  Google Scholar 

  12. Bastos, A. M., Loonis, R., Kornblith, S., Lundqvist, M. & Miller, E. K. Laminar recordings in frontal cortex suggest distinct layers for maintenance and control of working memory. Proc. Natl Acad. Sci. USA. 115, 1117–1122 (2018).

    CAS  PubMed  PubMed Central  Google Scholar 

  13. Miller, E. K., Lundqvist, M. & Bastos, A. M. Working memory 2.0. Neuron 100, 463–475 (2018).

    CAS  PubMed  PubMed Central  Google Scholar 

  14. Cho, K. K. A. et al. Gamma rhythms link prefrontal interneuron dysfunction with cognitive inflexibility in Dlx5/6 +/− mice. Neuron 85, 1332–1343 (2015).

    CAS  PubMed  PubMed Central  Google Scholar 

  15. Marton, T. F., Seifikar, H., Luongo, F. J., Lee, A. T. & Sohal, V. S. Roles of prefrontal cortex and mediodorsal thalamus in task engagement and behavioral flexibility. J. Neurosci. 38, 2569–2578 (2018).

    CAS  PubMed  PubMed Central  Google Scholar 

  16. Karlsson, M. P., Tervo, D. G. & Karpova, A. Y. Network resets in medial prefrontal cortex mark the onset of behavioral uncertainty. Science 338, 135–139 (2012).

    CAS  PubMed  Google Scholar 

  17. Cardin, J. A. Snapshots of the brain in action: local circuit interactions through the lens of gamma oscillations. J. Neurosci. 36, 10496–10504 (2016).

    CAS  PubMed  PubMed Central  Google Scholar 

  18. Ray, S. & Maunsell, J. H. Do gamma oscillations play a role in cerebral cortex? Trends Cogn. Sci. 19, 78–85 (2015).

    PubMed  Google Scholar 

  19. Bissonette, G. B. et al. Double dissociation of the effects of medial and orbital prefrontal cortical lesions on attentional and affective shifts in mice. J. Neurosci. 28, 11124–11130 (2008).

    CAS  PubMed  PubMed Central  Google Scholar 

  20. Ellwood, I. T. et al. Tonic or phasic stimulation of dopaminergic projections to prefrontal cortex causes mice to maintain or deviate from previously learned behavioral strategies. J. Neurosci. 37, 8315–8329 (2017).

    CAS  PubMed  PubMed Central  Google Scholar 

  21. Canetta, S. et al. Maternal immune activation leads to selective functional deficits in offspring parvalbumin interneurons. Mol. Psychiatry 21, 956–968 (2016).

    CAS  PubMed  PubMed Central  Google Scholar 

  22. Cao, W. et al. Gamma oscillation dysfunction in mPFC leads to social deficits in neuroligin 3 R451C knockin mice. Neuron 97, 1253–1260 (2018).

    CAS  PubMed  Google Scholar 

  23. Siegle, J. H., Pritchett, D. L. & Moore, C. I. Gamma-range synchronization of fast-spiking interneurons can enhance detection of tactile stimuli. Nat. Neurosci. 17, 1371–1379 (2014).

    CAS  PubMed  PubMed Central  Google Scholar 

  24. Kim, H., Ahrlund-Richter, S., Wang, X., Deisseroth, K. & Carlén, M. Prefrontal parvalbumin neurons in control of attention. Cell 164, 208–218 (2016).

    CAS  PubMed  PubMed Central  Google Scholar 

  25. Gunaydin, L. A. et al. Natural neural projection dynamics underlying social behavior. Cell 157, 1535–1551 (2014).

    CAS  PubMed  PubMed Central  Google Scholar 

  26. Lerner, T. N. et al. Intact-brain analyses reveal distinct information carried by SNc dopamine subcircuits. Cell 162, 635–647 (2015).

    CAS  PubMed  PubMed Central  Google Scholar 

  27. Chen, T. W. et al. Ultrasensitive fluorescent proteins for imaging neuronal activity. Nature 499, 295–300 (2013).

    CAS  PubMed  PubMed Central  Google Scholar 

  28. Marshall, J. D. et al. Cell-type-specific optical recording of membrane voltage dynamics in freely moving mice. Cell 167, 1650–1662 (2016).

    CAS  PubMed  PubMed Central  Google Scholar 

  29. Carandini, M. et al. Imaging the awake visual cortex with a genetically encoded voltage indicator. J. Neurosci. 35, 53–63 (2015).

    CAS  PubMed  PubMed Central  Google Scholar 

  30. Pi, H. J. et al. Cortical interneurons that specialize in disinhibitory control. Nature 7477, 521–524 (2013).

    Google Scholar 

  31. Ray, S., Ni, A. M. & Maunsell, J. H. Strength of gamma rhythm depends on normalization. PLoS Biol. 11, e1001477 (2013).

    CAS  PubMed  PubMed Central  Google Scholar 

  32. Shadlen, M. N. & Movshon, J. A. Synchrony unbound: a critical evaluation of the temporal binding hypothesis. Neuron 24, 67–77 (1999).

    CAS  PubMed  Google Scholar 

  33. Palmigiano, A., Geisel, T., Wolf, F. & Battaglia, D. Flexible information routing by transient synchrony. Nat. Neurosci. 7, 1014–1022 (2017).

    Google Scholar 

  34. Tukker, J. J. et al. Distinct dendritic arborization and in vivo firing patterns of parvalbumin-expressing basket cells in the hippocampal area CA3. J. Neurosci. 33, 6809–6825 (2013).

  35. Hu, H., Gan, J. & Jonas, P. Fast-spiking, parvalbumin+ GABAergic interneurons: from cellular design to microcircuit function. Science 345, 1255263 (2014).

    PubMed  Google Scholar 

  36. Otis, J. M. et al. Prefrontal cortex output circuits guide reward seeking through divergent cue encoding. Nature 543, 103–107 (2017).

    CAS  PubMed  PubMed Central  Google Scholar 

  37. Bissonette, G. B. & Roesch, M. R. Neurophysiology of rule switching in the corticostriatal circuit. Neuroscience 345, 64–76 (2017).

    CAS  PubMed  Google Scholar 

  38. Phillips, E. A. K. & Hasenstaub, A. R. Asymmetric effects of activating and inactivating cortical interneurons. eLife 5, e18383 (2016).

    PubMed  PubMed Central  Google Scholar 

  39. Gonzalez-Burgos, G., Cho, R. Y. & Lewis, D. A. Alterations in cortical network oscillations and parvalbumin neurons in schizophrenia. Biol. Psychiatry 77, 1031–1040 (2015).

    CAS  PubMed  PubMed Central  Google Scholar 

  40. Uhlhaas, P. J. & Singer, W. Oscillations and neuronal dynamics in schizophrenia: the search for basic symptoms and translational opportunities. Biol. Psychiatry 77, 1001–1009 (2015).

    PubMed  Google Scholar 

  41. Senkowski, D. & Gallinat, J. Dysfunctional prefrontal gamma-band oscillations reflect working memory and other cognitive deficits in schizophrenia. Biol. Psychiatry 77, 1010–1019 (2015).

    PubMed  Google Scholar 

  42. Green, M. J. Cognitive impairment and functional outcome in schizophrenia and bipolar disorder. J. Clin. Psych. 67, 36–42 (2006).

    Google Scholar 

  43. Minzenberg, M. J. & Carter, C. S. Developing treatments for impaired cognition in schizophrenia. Trends Cogn. Sci. 16, 35–42 (2012).

    PubMed  Google Scholar 

  44. Verret, L. et al. Inhibitory interneuron deficit links altered network activity and cognitive dysfunction in Alzheimer model. Cell 149, 708–721 (2012).

    CAS  PubMed  PubMed Central  Google Scholar 

  45. Iaccarino, H. F. et al. Gamma frequency entrainment attenuates amyloid load and modifies microglia. Nature 540, 230–235 (2016).

    CAS  PubMed  PubMed Central  Google Scholar 

  46. Martorell, A. J. et al. Multi-sensory gamma stimulation ameliorates Alzheimer’s-associated pathology and improves cognition. Cell 177, 256–271 (2019).

    CAS  PubMed  PubMed Central  Google Scholar 

  47. Ohmuro, N. et al. The relationship between cognitive insight and cognitive performance among individuals with at-risk mental state for developing psychosis. Schizophr. Res. 192, 281–286 (2018).

    PubMed  Google Scholar 

  48. Lappin, J. M. et al. Insight in individuals with an at risk mental state. Schizophr. Res. 90, 238–244 (2007).

    PubMed  Google Scholar 

  49. Wang, Y., et al. Dlx5 and Dlx6 regulate the development of parvalbumin-expressing cortical interneurons. J. Neurosci. 30, 5334–5345 (2010).

Download references

Acknowledgements

This work was supported by the National Institute of Mental Health (R01MH106507 to V.S.S. and K99MH108720 to K.K.A.C.), the Brain and Behavior Foundation (NARSAD Young Investigator Award to K.K.A.C.), the McKnight Foundation (Memory and Cognitive Disorders award to V.S.S.) and the Brain Research Foundation (Scientific Innovations Award to V.S.S.). We appreciate helpful feedback on earlier versions of this manuscript from L. Frank and M. Scanziani.

Author information

Authors and Affiliations

  1. Department of Psychiatry, University of California, San Francisco, San Francisco, CA, USA

    Kathleen K. A. Cho & Vikaas S. Sohal

  2. Kavli Institute for Fundamental Neuroscience, University of California, San Francisco, San Francisco, CA, USA

    Kathleen K. A. Cho, Thomas J. Davidson & Vikaas S. Sohal

  3. Weill Institute for Neuroscience, University of California, San Francisco, San Francisco, CA, USA

    Kathleen K. A. Cho & Vikaas S. Sohal

  4. Department of Physiology, University of California, San Francisco, San Francisco, CA, USA

    Thomas J. Davidson & Guy Bouvier

  5. Howard Hughes Medical Institute, San Francisco, CA, USA

    Thomas J. Davidson & Guy Bouvier

  6. Department of Organismic & Evolutionary Biology, Harvard University, Cambridge, MA, USA

    Jesse D. Marshall

  7. Departments of Biology and Applied Physics, Stanford University, Stanford, CA, USA

    Mark J. Schnitzer

  8. Howard Hughes Medical Institute, Stanford, CA, USA

    Mark J. Schnitzer

Authors
  1. Kathleen K. A. Cho
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Thomas J. Davidson
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Guy Bouvier
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Jesse D. Marshall
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Mark J. Schnitzer
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Vikaas S. Sohal
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

K.K.A.C. and V.S.S. designed experiments and wrote the manuscript. K.K.A.C. performed all the experiments, except that G.B. performed and analyzed the opto-tagging experiment. T.J.D. and K.K.A.C. set up the LED photometry rig and the dual-site TEMPO rig. K.K.A.C. generated AAV5-I12b-BG-DIO-eYFP. J.D.M. and M.J.S. provided guidance, advice and feedback on the acquisition and analysis of TEMPO data. K.K.A.C. and V.S.S. analyzed the data.

Corresponding author

Correspondence to Vikaas S. Sohal.

Ethics declarations

Competing interests

The authors declare no competing interests.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Extended data

Extended Data Fig. 1 Photometry signals from PV interneurons and behavior during rule shifts in mice used for photometry experiments.

a, PV-Cre mice had a unilateral FLEX-GCaMP6f injection and fiber-optic implant in mPFC for photometry (scale bar, 100 μm). b, Rule-shift (RS) performance of PV-Cre mice (n = 8) used for photometry experiments. c, Numbers of perseverative (P) or random (R) errors during the rule shift of PV-Cre mice (n = 8). d, Averaged PV interneuron photometry signal (dF/F), aligned to the start of each trial, for correct (white line) vs. incorrect trials (black line; n = 8). e, Averaged PV interneuron photometry signal (dF/F), aligned to the start of the intertrial interval (ITI), for correct (white line) vs. incorrect trials (black line; n = 8) for the first ten seconds of ITIs. f, Peak dF/F during the entire intertrial interval (ITI), usually lasting around two minutes. Signals are significantly higher on incorrect rule shift trials than correct rule shift trials (n = 8 mice; two-way ANOVA; main effect of outcome: F1,14 = 26.53, ***P = 0.0001; task X outcome interaction: F1,14 = 7.47, *P = 0.016; RS correct versus incorrect, post hoc t(14) = 5.58, ***P = 0.0001; IA correct versus incorrect, post hoc t(14) = 1.71, P = 0.22). g, Mouse behavior scored at the time of the peak dF/F signal during rule shift error trials (n = 31 error trials of 8 mice). h, Mouse behavior scored at the time of the peak dF/F signal during initial association error ITI (n = 21 error ITIs of 8 mice). i, Mouse behavior scored at the time of the peak dF/F signal during rule shift error ITI (n = 31 error ITIs of 8 mice). Data are shown as means (b, c); error bars (b, c) and shading (d, e) denote s.e.m. Two-way ANOVA followed by Bonferroni post hoc comparisons were used. Comparisons were not significant unless otherwise noted.

Source data

Extended Data Fig. 2 Cross-hemispheric synchrony of PV interneurons at non-zero phase lag.

a, Schematic: analysis to measure out-of-phase synchrony. In this case, one Ace-mNeon is signal is shifted 90 degrees out-of-phase relative to the other signals, before following the procedure outlined in Fig. 2e. b–d, Out-of-phase 30-50 Hz synchrony (n = 12 mice) did not differ between the baseline period and RS correct trials (two-way ANOVA; frequency X condition interaction: F2,33 = 0.16, P = 0.86; post hoc t(33) = 1.35, P = 0.56), baseline period and RS incorrect trials (two-way ANOVA; frequency X condition interaction: F2,33 = 0.06, P = 0.94; post hoc t(33) = 0.05, P > 0.99), or correct and incorrect trials (two-way ANOVA; frequency X condition interaction: F2,33 = 0.05, P = 0.95; post hoc t(33) = 1.53, P = 0.41). Two-way ANOVA followed by Bonferroni post hoc comparisons were used. Comparisons were not significant.

Source data

Extended Data Fig. 3 Learning during rule shifts in mice used for TEMPO measurements from Sst interneurons, and photometry signals from Sst interneurons during rule shifts.

a, Sst-Cre Ai14 mice had bilateral AAV-DIO-Ace2N-4AA-mNeon ± AAV-Syn-tdTomato injections and fiber-optic implants in mPFC. b, Representative images of tdTomato (red) and Ace-mNeon (green) fluorescence in a coronal section of mPFC (left), alongside a high power image (right). Scale bars: 100 μm and 25 μm, respectively. c, Rule-shift (RS) performance of Sst-Cre Ai14 mice (n = 5) used for dual-site TEMPO imaging. d, Number of perseverative (P) and random (R) errors during the rule shift of Sst-Cre Ai14 mice (n = 5). e, Sst-Cre mice had a unilateral FLEX-GCaMP6f injection and fiber-optic implant in mPFC for photometry (scale bar, 100 μm). f, Rule-shift (RS) performance of Sst-Cre mice (n = 4) used for photometry experiments. g, Numbers of perseverative (P) or random (R) errors during the rule shift Sst-Cre mice (n = 4). h, Averaged Sst interneuron photometry signal (dF/F), aligned to the time of dig, which indicates a decision, for correct (white line) vs. incorrect trials (purple line; n = 4). i, Peak dF/F during the 4-8 sec following the decision (this was the time at which peak Sst activity occurred). Sst interneuron photometry signals are significantly higher on incorrect than correct trials (n = 4 mice; two-tailed, paired t-test; t(3) = 4.65, *P = 0.02). Data are shown as means (c, d, f, g, h); error bars (c, d, f, g) and shading (h) denote s.e.m.

Source data

Extended Data Fig. 4 Cross-hemispheric synchrony between prefrontal PV interneurons for various frequency bands and types of trials.

a, PV-Cre Ai14 mice had bilateral AAV-DIO-Ace2N-4AA-mNeon ± AAV-Syn-tdTomato injections and fiber-optic implants in mPFC. Experimental design: Day 1: Initial association (IA) followed by rule shift (RS) or rule reversal (RR); Day 2: IA followed by the rule change (RS or RR) that was not performed on Day 1. b, During learning of the IA that preceded the RS, synchrony was not different after correct decisions vs. during the baseline period (n = 7 mice; two-way ANOVA; main effect of condition: F1,18 = 0.51, P = 0.48; frequency X condition interaction: F2,18 = 0.20, P = 0.82). c, During learning of this IA, synchrony was not different after incorrect decisions vs. during the baseline period (n = 7 mice; two-way ANOVA; main effect of condition: F1,18 = 0.39, P = 0.54; frequency X condition interaction: F2,18 = 0.07, P = 0.94). d, IA performance was not different across days (n = 7 mice; two-tailed, paired t-test; t(6) = 1.29, P = 0.25). e, There was no difference in synchrony after correct trials during learning of the IA on Day 1 vs. 2 (n = 7 mice; two-way ANOVA; main effect of day: F1,18 = 0.02, P = 0.89; frequency X condition interaction: F2,18 = 1.48, P = 0.26). f, There was no difference in synchrony after incorrect trials during learning of the IA on Day 1 vs. 2 (n = 7 mice; two-way ANOVA; main effect of day: F1,18 = 3.05, P = 0.10; frequency X condition interaction: F2,18 = 0.03, P = 0.97). g, During the RR, synchrony was not different after correct decisions vs. during the baseline period (n = 7 mice; two-way ANOVA; main effect of condition: F1,18 = 0.28, P = 0.60; frequency X condition interaction: F2,18 = 1.24, P = 0.31). h, During the RR, synchrony was not different after incorrect decisions vs. the baseline period (n = 7 mice; two-way ANOVA; main effect of condition: F1,18 = 0.09, P = 0.77; frequency X condition interaction: F2,18 = 0.30, P = 0.74). i, Synchrony after correct decisions did not differ between the IA vs. RS (n = 7 mice; two-way ANOVA; main effect of condition: F1,18 = 0.13, P = 0.73; frequency X condition interaction: F2,18 = 1, P = 0.39). j, Synchrony after correct decisions did not differ between the RR vs. RS (n = 7 mice; two-way ANOVA; main effect of condition: F1,18 = 0.16, P = 0.70; frequency X condition interaction: F2,18 = 2.55, P = 0.11). k, The plot shows the average gamma synchrony on correct vs. incorrect trials, during the first 2 (‘early’) or next 3 (‘late’) trials of a rule shift (RS) or rule reversal (RR). In order to average together values from different mice (n = 7), each synchrony value was computed relative to the average gamma synchrony measured during the first 5 RS and RR trials from the same mouse. We performed ANOVA on the gamma synchrony from each of the first 5 trials during a rule shift (RS) or rule reversal (RR), including the following factors and interaction terms: mouse (F6,59 = 1.72, P = 0.13), type of rule change (RS vs. RR) (F1,59 = 3.74, P = 0.06), correct vs. incorrect trial outcome (F1,59 = 2.64, P = 0.11), an interaction of correct-incorrect X RS-RR (F1,59 = 11.12, **P = 0.0015), and an interaction of correct-incorrect X RS-RR X early vs. late trials (that is first 2 vs. next 3 trials) (F1,59 = 4.28, *P = 0.043). l, Following errors, synchrony during the intertrial interval (ITI) was specifically higher in the 30-50 Hz band during the RS than during the IA (n = 7 mice; two-way ANOVA; condition X frequency interaction: F4,36 = 3.217, *P = 0.023; 30-50 Hz: post hoc t(6) = 3.55, *P = 0.036) or RR (two-way ANOVA; 30-50 Hz: post hoc t(6) = 3.97, *P = 0.022). m, Mouse behavior scored during the initial association error ITI for the first 5 IA dual-site TEMPO trials (n = 10 error ITIs of 8 mice). n, Mouse behavior scored during the rule shift error ITI for the first 5 RS dual-site TEMPO trials (n = 17 error ITIs of 8 mice). There is no difference in seconds of movement between IA and RS (two-tailed, paired t-test; t(6) = 0.52, P = 0.62) nor in seconds of not moving between IA and RS (two-tailed, paired t-test; t(6) = 0.56, P = 0.59). Two-way ANOVA followed by Bonferroni post hoc comparisons were used in panels b–c and e–j, l. Comparisons were not significant unless otherwise noted.

Source data

Extended Data Fig. 5 Types of errors during rule shifts (RS) in the presence of various forms of optogenetic stimulation in PV-Cre mice.

a, d, PV-Cre Ai14 mice had bilateral AAV-DIO-eYFP or AAV-DIO-ChR2 injections and fiber-optic implants in mPFC. Experimental design: Day 1: out-of-phase 40 Hz stimulation during the rule shift (RS); Day 2: no stimulation. b, e, Representative images showing mPFC expression of eYFP (b) or ChR2-eYFP (e) (scale bar, 100 μm). c, f, Optogenetic stimulation increases perseverative errors in ChR2-expressing mice (n = 5) compared to eYFP-expressing (n = 5 mice) controls (two-way ANOVA; main effect of day: F1,8 = 20.8, **P = 0.0018; main effect of virus: F1,8 = 8.96, *P = 0.017; day X virus interaction: F1,8 = 14.89, **P = 0.0048). There is no change in random errors (two-way ANOVA; main effect of day: F1,8 = 0, P > 0.99; main effect of virus: F1,8 = 0, P > 0.99; day X virus interaction: F1,8 = 0.89, P = 0.37). c, Light delivery does not affect the number of perseverative or random errors in eYFP-expressing controls (perseverative: post hoc t(8) = 0.50, P > 0.99; random: post hoc t(8) = 0.67, P > 0.99). f, Optogenetic stimulation of PV interneurons on Day 1 increased the number of perseverative errors compared to no stimulation on Day 2 (post hoc t(8) = 5.95, ***P = 0.0007), but does not affect random errors (post hoc t(8) = 0.67, P > 0.99). g, PV-Cre mice had bilateral AAV-DIO-ChR2-eYFP injections and fiber-optic implants in mPFC. Experimental design: Day 1: out-of-phase 20 Hz stimulation; Day 2: out-of-phase 40 Hz stimulation; Day 3: in-phase 40 Hz stimulation. h, Representative image showing mPFC ChR2 expression (scale bar, 100 μm). i, Out-of-phase 40 Hz stimulation (Day 2) increases perseverative errors but does not affect random errors, relative to out-of-phase 20 Hz stimulation (Day 1) or in-phase 40 Hz stimulation (Day 3) (n = 5 mice; two-way ANOVA; main effect of day: F2,16 = 13.5, ***P = 0.0004; Day 1 vs. Day 2 perseverative: ***P = 0.0002, Day 2 vs. Day 3 perseverative: ****P = 0.00003, Day 1 vs. Day 3 perseverative: P > 0.99; Day 1 vs. Day 2 random: P > 0.99, Day 2 vs. Day 3 random: P > 0.99, Day 1 vs. Day 3 random: P > 0.99). Two-way ANOVA followed by Bonferroni post hoc comparisons were used.

Source data

Extended Data Fig. 6 Behavior and types of errors during rule shifts (RS) in the presence of various forms of optogenetic stimulation in Dlx5/6+/-, Sst-Cre and Sst-Cre mice.

a, e, Sst-Cre mice had bilateral injections of AAV-DIO-eYFP (a, ‘Sst-eYFP’) or AAV-DIO-ChR2-eYFP (e, ‘Sst-ChR2’) along with fiber-optic implants in mPFC. Experimental design: Day 1: no light stimulation; Day 2: out-of-phase 20 Hz stimulation; Day 3: out-of-phase 40 Hz stimulation. b, Representative image showing mPFC ChR2 expression (scale bar, 100 μm). c, g, Light delivery did not affect performance in either Sst-eYFP (c; n = 4 mice) or Sst-ChR2 (g; n = 5) mice (two-way ANOVA; main effect of day: F2,14 = 2.53, P = 0.12; main effect of virus: F1,7 = 0.01, P = 0.92; day X virus interaction: F2,14 = 0.59, P = 0.57). d, Sst-eYFP mice showed no change in perseverative or random errors from Day 1 to Day 2 to Day 3 (n = 4 mice; two-way ANOVA; day X type of error interaction: F2,9 = 1.18, P = 0.35). h, Sst-ChR2 mice showed no change in perseverative or random errors from Day 1 to Day 2 to Day 3 (n = 5 mice; two-way ANOVA; day X type of error interaction: F2,16 = 0.81, P = 0.46). i,m, Dlx5/6+/–, Sst-Cre mice had bilateral control virus (AAV-DIO-eYFP or AAV-i12b-DIO-eYFP) or AAV-DIO-ChR2-eYFP (m) injections and fiber-optic implants in mPFC. Experimental design: Day 1: no stimulation; Day 2: 40 Hz stimulation. j,n, Representative eYFP (j) and ChR2-eYFP (n) expression in the mPFC of Dlx5/6+/–, Sst-Cre mice (scale bar, 100 μm). k,o, Light delivery did not affect performance in Sst-eYFP-expressing (k; n = 4 mice) or Sst-ChR2-expressing (o; n = 8) mutant mice (two-way ANOVA; main effect of day: F1,10 = 0.08, P = 0.79; main effect of virus: F1,10 = 0.002, P = 0.96; day X virus interaction: F1,10 = 2.69, P = 0.13). l, Sst-eYFP expressing mutants showed no change in perseverative or random errors from Day 1 to Day 2 (n = 4 mice; two-way ANOVA; day X type of error interaction: F1,6 = 0.16, P = 0.70). p, Sst-ChR2 expressing mutants showed no change in perseverative or random errors from Day 1 to Day 2 (n = 8 mice; two-way ANOVA; day X type of error interaction: F1,14 = 0.64, P = 0.44). Two-way ANOVA followed by Bonferroni post hoc comparisons were used. Comparisons were not significant unless otherwise noted.

Source data

Extended Data Fig. 7 Single unit recordings from PV interneurons and regular spiking neurons in the mPFC of awake, head-fixed mice.

a, Schematic of opto-silicon probe recording PFC in awake head-fixed mice (top panel). Histology of the recording electrode (bottom panel, scale = 1 mm). b, Example raster plot of a putative PV cell responding to ChR2 activation. Stimulation at 1 Hz (5 ms illumination, 0.25 mW). The blue line represents the duration of ChR2 stimulation (5 ms). c, Average peristimulus time histogram (PSTH) of PV cell responses during 40 Hz ChR2 stimulation (n = 8 PV cells, time bin = 1 ms). The blue line indicates the period of ChR2 stimulation (5 ms flash) at 40 Hz. PV cells fired 0.49 ± 10 spikes per 40 Hz cycle at a latency of 1.82 ± 0.34 ms following the onset of each light flash. d, Baseline subtracted and peak normalized activity of all putative PV cells (green line; n = 8 cells, 3 mice) and all the regular-spiking (RS) cells (black line; n = 237 cells, 4 mice). Mean firing rate of RS cells was 4.9 vs. 2.1 spikes/sec at the peak vs. trough of each cycle, respectively. The blue line indicates the period of ChR2 stimulation (5 ms flash) at 40 Hz. Data are shown as means (c, d) and shading (c, d) denote s.e.m.

Source data

Extended Data Fig. 8 Changes in the power spectra of prefrontal LFPs elicited by in- vs. out-of-phase stimulation of PV interneurons.

a–d, Difference between the power spectra for LFPs recorded during light stimulation vs. at baseline for control mice (PV-Cre mice injected with AAV-DIO-eYFP, n = 6 recordings from 3 mice) receiving (a) in- or (c) out-of-phase stimulation, or for PV-Cre mice (n = 12 recordings from 6 mice) injected with AAV-DIO-ChR2-eYFP receiving (b) in- or (d) out-of-phase stimulation. Positive (negative) values correspond to higher power during periods of stimulation (at baseline). e, Quantification of average change in 40 Hz power in various conditions (relative to baseline). The change was significantly different from 0 for PV-ChR2 in-phase condition (n = 12 recordings from 6 mice; two-tailed, paired t-test; t(11) = 2.24, *P = 0.047) and for PV-ChR2 out-of-phase condition (n = 12 recordings from 6 mice; two-tailed, paired t-test; t(11) = 2.34, *P = 0.039). f, Quantification of average change in 150-200 Hz power in various conditions (relative to baseline). The change was significantly different from 0 for PV-ChR2 in-phase condition (n = 12 recordings from 6 mice; two-tailed, paired t-test; t(11) = 2.40, *P = 0.036) and for PV-ChR2 out-of-phase condition (n = 12 recordings from 6 mice; two-tailed, paired t-test; t(11) = 2.65, *P = 0.023). Two-tailed, paired t-tests were used. Data are shown as means; shading (a–d) and error bars (e,f) denote s.e.m.

Source data

Extended Data Fig. 9 Out-of-phase 40 Hz stimulation does not disrupt the ability of PV-Cre mice to revert to an initial association.

a, Schematic for task: The mouse learns an initial association (IA), then a rule shift (RS). After the mouse learns the RS, the task reverts to the original rule, that is, the rule learned during the IA with out-of-phase 40 Hz stimulation. b, PV-Cre mice had bilateral AAV-DIO-eYFP (‘PV-eYFP’) or AAV-DIO-ChR2-eYFP (‘PV-ChR2’) injections and fiber-optic implants in mPFC. Experimental design: no stimulation during learning of the IA or RS. Then, when the rule reverts to the IA, out-of-phase 40 Hz stimulation is delivered. c, In PV-eYFP mice (n = 5), there was no difference in the number of trials needed to reach the criterion during initial learning of the IA (when no light was delivered) vs. when reverting to the IA after learning the RS (when light stimulation was delivered; two-tailed, paired t-test; t(4) = 1.31, P = 0.261). d, In PV-ChR2 mice (n = 5), there was no difference in the number of trials needed to reach the criterion during initial learning of the IA (when no light was delivered) vs. when reverting to the IA after learning the RS (when light stimulation was delivered; two-tailed, paired t-test; t(4) = 0.466, P = 0.666). Two-tailed, paired t-tests were used. Comparisons were not significant unless otherwise noted.

Source data

Extended Data Fig. 10 Behavior and cross-hemispheric synchrony between prefrontal PV or Sst interneurons during rule shifts, baseline periods, or learning of initial associations in Dlx5/6+/– mice and wild-types.

a, Rule-shift (RS) performance for photometry experiments in Dlx5/6+/–, PV-Cre and Dlx5/6+/+, PV-Cre mice. Compared to wild-type littermates (n = 8), mutant mice (n = 7) make more perseverative errors (two-way ANOVA; main effect of genotype: F1,13 = 43.6, ****P = 0.00002; main effect of error type: F1,13 = 24.7, ***P = 0.0003; error type X genotype interaction: F1,13 = 10.5, **P = 0.006; post hoc t(26) = 6.55, ****P = 0.000001), but similar numbers of random errors (post hoc t(26) = 1.36, P = 0.37). b, Rule-shift performance for mice used in dual-site TEMPO experiments. Compared to wild-type mice (n = 12), mutant mice (n = 8) make more perseverative errors (two-way ANOVA; main effect of genotype: F1,18 = 89.4, ****P = 0.00000002; main effect of error type: F1,13 = 137.3, ****P = 0.0000000007; type of error X genotype interaction: F1,18 = 46.5, ****P = 0.000002; post hoc t(36) = 11.6, ****P = 0.0000000000002), and random errors (post hoc t(36) = 2.43, *P = 0.04). c, Compared to wild-type mice, Dlx5/6+/–, Sst-Cre Ai14 mice make more perseverative errors (n = 5 mice in each cohort; two-way ANOVA; main effect of genotype: F1,8 = 42.3, ***P = 0.0002; main effect of error type: F1,8 = 30.7, ***P = 0.0005; error type X genotype interaction: F1,8 = 17.0, **P = 0.003; post hoc t(16) = 7.12, ****P = 0.000005), but numbers of random errors are comparable (post hoc t(16) = 0.38, P > 0.99). d, Synchrony was not different between Dlx5/6+/+, Sst-Cre Ai14 and Dlx5/6+/–, Sst-Cre Ai14 mice during the baseline period (n = 5 mice in each cohort; two-way ANOVA; main effect of genotype: F1,8 = 0.77, P = 0.41; frequency X genotype interaction: F2,16 = 0.05, P = 0.95). e, Dlx5/6+/–, PV-Cre mice had bilateral AAV-DIO-ChR2-eYFP injections and fiber-optic implants in mPFC. Experimental design: Day 1: no stimulation; Day 2: in-phase 40 Hz stimulation during the first 5 RS trials. f, In-phase 40 Hz stimulation on Day 2 reduces perseverative errors relative to no stimulation on Day 1 (n = 6 mice; two-way ANOVA; main effect of day: F1,10 = 18.32, **P = 0.0016; main effect of error type: F1,10 = 49.9, ****P = 0.000034; post hoc t(10) = 3.98, **P = 0.005); there was no change in random errors (post hoc t(10) = 2.07, P = 0.13). g, Dlx5/6+/–, PV-Cre mice had bilateral AAV-DIO-ChR2-eYFP injections and fiber-optic implants in mPFC. Experimental design: Day 1: out-of-phase 20 Hz stimulation; Day 2: out-of-phase 40 Hz stimulation; Day 3: in-phase 40 Hz stimulation. h, Perseverative errors are reduced by in phase 40 Hz stimulation on Day 3, compared to either out-of-phase 20 Hz stimulation on Day 1 or out-of-phase 40 Hz stimulation on Day 2 (n = 5 mice; two-way ANOVA; main effect of day: F2,16 = 11.6, ***P = 0.0008; main effect of error type: F1,8 = 31.5, ***P = 0.0005; Day 1 vs. Day 2 perseverative: P > 0.99, Day 2 vs. Day 3 perseverative: ***P = 0.0005, Day 1 vs. Day 3 perseverative: **P = 0.0016). There are no changes in random errors across days (post hoc Day 1 vs. Day 2: P > 0.99, Day 2 vs. Day 3: P > 0.99, Day 1 vs. Day 3: P = 0.33). i, Dlx5/6+/–, PV-Cre Ai14 mice had bilateral AAV-DIO-Ace2N-4AA-mNeon ± AAV-Syn-tdTomato injections and fiber-optic implants in mPFC. j, Representative images of tdTomato (red) and Ace-mNeon (green) fluorescence within PV interneurons in a coronal section of mPFC (left), alongside a high power image (right). Scale bars: 100 μm and 25 μm, respectively. k, In mutants, PV interneuron synchrony was not different after correct decisions vs. during the baseline period (n = 8 mice; two-way ANOVA; main effect of condition: F1,21 = 1.89, P = 0.18; frequency X condition interaction: F2,21 = 0.35, P = 0.71). l, PV interneuron synchrony was not different after incorrect decisions vs. during the baseline period (n = 8 mice; two-way ANOVA; main effect of condition: F1,21 = 3.31, P = 0.083; frequency X condition interaction: F2,21 = 0.04, P = 0.96). m, Dlx5/6+/–, Sst-Cre Ai14 mice had bilateral AAV-DIO-Ace2N-4AA-mNeon ± AAV-Syn-tdTomato injections and fiber-optic implants in mPFC. n, Representative images of tdTomato (red) and Ace-mNeon (green) fluorescence in Sst interneurons within a coronal section of mPFC (left) from a Dlx5/6+/–, Sst-Cre Ai14 mouse, alongside a high power image (right). Scale bars: 100 μm and 25 μm, respectively. o, In mutants, Sst interneuron synchrony was not different after correct decisions vs. during the baseline period (n = 5 mice; two-way ANOVA; main effect of frequency: F2,12 = 9.88, **P = 0.003; frequency X condition interaction: F2,12 = 0.58, P = 0.58). p, Sst interneuron synchrony was not different after incorrect decisions vs. during the baseline period (n = 5 mice; two-way ANOVA; main effect of frequency: F2,12 = 4.95, *P = 0.027; frequency X condition interaction: F2,12 = 0.44, P = 0.66). q, Learning of an initial association (IA) was similar in mutants (n = 6) and their wild-type (n = 11) littermates (two-tailed, unpaired t-test; n = 11; t(15) = 0.202, P = 0.842). r, There was no difference in cross-hemispheric PV interneuron synchronization between mutant (n = 6 mice) and wild-type (n = 11 mice) littermates at baseline (two-way ANOVA; main effect of genotype: F1,15 = 0.45, P = 0.51; genotype X frequency interaction F2,30 = 1.11, P = 0.34). s, During learning of an initial association, changes in PV interneuron synchrony following errors (relative to synchrony after correct decisions) are similar in mutants (n = 6 mice) and their wild-type (n = 11 mice) littermates (two-way ANOVA; main effect of genotype: F1,15 = 0.07, P = 0.80; genotype X frequency interaction: F2,30 = 0.16, P = 0.86). Data are shown as means (a–c); error bars (a–c) denote s.e.m. Two-way ANOVA followed by Bonferroni post hoc comparisons were used. Comparisons were not significant unless otherwise noted.

Source data

Supplementary information

Supplementary Information

Supplementary Videos 1–4, Supplementary Fig. 1, Supplementary Table 1.

Reporting Summary

Supplementary Video 1

Representative video showing mouse behavior and task mechanics on a correct trial during the initial association.

Supplementary Video 2

Representative video showing mouse behavior and task mechanics on an incorrect trial during the initial association.

Supplementary Video 3

Representative video showing mouse behavior and task mechanics on a correct trial during the rule shift.

Supplementary Video 4

Representative video showing mouse behavior and task mechanics on an incorrect trial during the rule shift.

Source data

Source Data Fig. 1

Statistical Source Data

Source Data Fig. 2

Statistical Source Data

Source Data Fig. 3

Statistical Source Data

Source Data Fig. 4

Statistical Source Data

Source Data Fig. 5

Statistical Source Data

Source Data Fig. 6

Statistical Source Data

Source Data Fig. 7

Statistical Source Data

Source Data Extended Data Fig. 1

Statistical Source Data

Source Data Extended Data Fig. 2

Statistical Source Data

Source Data Extended Data Fig. 3

Statistical Source Data

Source Data Extended Data Fig. 4

Statistical Source Data

Source Data Extended Data Fig. 5

Statistical Source Data

Source Data Extended Data Fig. 6

Statistical Source Data

Source Data Extended Data Fig. 7

Statistical Source Data

Source Data Extended Data Fig. 8

Statistical Source Data

Source Data Extended Data Fig. 9

Statistical Source Data

Source Data Extended Data Fig. 10

Statistical Source Data

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Cho, K.K.A., Davidson, T.J., Bouvier, G. et al. Cross-hemispheric gamma synchrony between prefrontal parvalbumin interneurons supports behavioral adaptation during rule shift learning. Nat Neurosci 23, 892–902 (2020). https://doi.org/10.1038/s41593-020-0647-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/s41593-020-0647-1

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing