Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Learning by neural reassociation

Nature Neuroscience volume 21, pages 607–616 (2018)Cite this article

Subjects

A Publisher Correction to this article was published on 05 July 2018

This article has been updated

Abstract

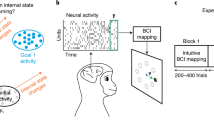
Behavior is driven by coordinated activity across a population of neurons. Learning requires the brain to change the neural population activity produced to achieve a given behavioral goal. How does population activity reorganize during learning? We studied intracortical population activity in the primary motor cortex of rhesus macaques during short-term learning in a brain–computer interface (BCI) task. In a BCI, the mapping between neural activity and behavior is exactly known, enabling us to rigorously define hypotheses about neural reorganization during learning. We found that changes in population activity followed a suboptimal neural strategy of reassociation: animals relied on a fixed repertoire of activity patterns and associated those patterns with different movements after learning. These results indicate that the activity patterns that a neural population can generate are even more constrained than previously thought and might explain why it is often difficult to quickly learn to a high level of proficiency.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on Springer Link
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: BCI learning experiment.
Fig. 2: Conceptual illustrations of three hypothesized neural strategies of learning.
Fig. 3: Visualization of population activity patterns from an example experiment (N20160728).
Fig. 4: Consistent with reassociation, the overall neural repertoire shows minimal changes during short-term learning.
Fig. 5: Consistent with reassociation, population covariability does not change along key dimensions of the intrinsic manifold.
Fig. 6: Consistent with reassociation, population covariability does not track perturbations to the BCI mapping.
Fig. 7: Behavioral learning is consistent with reassociation.
Fig. 8: Partial realignment and subselection are not consistent with the data.

Similar content being viewed by others

Change history

  • 05 July 2018

    In the version of this article initially published, equation (10) contained cos Θ instead of sin Θ as the bottom element of the right-hand vector. The error has been corrected in the HTML and PDF versions of the article.

References

  1. Mitz, A. R., Godschalk, M. & Wise, S. P. Learning-dependent neuronal activity in the premotor cortex: activity during the acquisition of conditional motor associations. J. Neurosci. 11, 1855–1872 (1991).

    Article  PubMed  CAS  Google Scholar 

  2. Asaad, W. F., Rainer, G. & Miller, E. K. Neural activity in the primate prefrontal cortex during associative learning. Neuron 21, 1399–1407 (1998).

    Article  PubMed  CAS  Google Scholar 

  3. Li, C.-S. R., Padoa-Schioppa, C. & Bizzi, E. Neuronal correlates of motor performance and motor learning in the primary motor cortex of monkeys adapting to an external force field. Neuron 30, 593–607 (2001).

    Article  PubMed  CAS  Google Scholar 

  4. Paz, R., Boraud, T., Natan, C., Bergman, H. & Vaadia, E. Preparatory activity in motor cortex reflects learning of local visuomotor skills. Nat. Neurosci. 6, 882–890 (2003).

    Article  PubMed  CAS  Google Scholar 

  5. Rokni, U., Richardson, A. G., Bizzi, E. & Seung, H. S. Motor learning with unstable neural representations. Neuron 54, 653–666 (2007).

    Article  PubMed  CAS  Google Scholar 

  6. Mandelblat-Cerf, Y. et al. The neuronal basis of long-term sensorimotor learning. J. Neurosci. 31, 300–313 (2011).

    Article  PubMed  CAS  Google Scholar 

  7. Ganguly, K. & Carmena, J. M. Emergence of a stable cortical map for neuroprosthetic control. PLoS Biol. 7, e1000153 (2009).

    Article  PubMed  PubMed Central  CAS  Google Scholar 

  8. Chase, S. M., Schwartz, A. B. & Kass, R. E. Latent inputs improve estimates of neural encoding in motor cortex. J. Neurosci. 30, 13873–13882 (2010).

    Article  PubMed  PubMed Central  CAS  Google Scholar 

  9. Ganguly, K., Dimitrov, D. F., Wallis, J. D. & Carmena, J. M. Reversible large-scale modification of cortical networks during neuroprosthetic control. Nat. Neurosci. 14, 662–667 (2011).

    Article  PubMed  PubMed Central  CAS  Google Scholar 

  10. Chase, S. M., Kass, R. E. & Schwartz, A. B. Behavioral and neural correlates of visuomotor adaptation observed through a brain-computer interface in primary motor cortex. J. Neurophysiol. 108, 624–644 (2012).

    Article  PubMed  PubMed Central  Google Scholar 

  11. Gu, Y. et al. Perceptual learning reduces interneuronal correlations in macaque visual cortex. Neuron 71, 750–761 (2011).

    Article  PubMed  PubMed Central  CAS  Google Scholar 

  12. Jeanne, J. M., Sharpee, T. O. & Gentner, T. Q. Associative learning enhances population coding by inverting interneuronal correlation patterns. Neuron 78, 352–363 (2013).

    Article  PubMed  PubMed Central  CAS  Google Scholar 

  13. Mazor, O. & Laurent, G. Transient dynamics versus fixed points in odor representations by locust antennal lobe projection neurons. Neuron 48, 661–673 (2005).

    Article  PubMed  CAS  Google Scholar 

  14. Luczak, A., Barthó, P. & Harris, K. D. Spontaneous events outline the realm of possible sensory responses in neocortical populations. Neuron 62, 413–425 (2009).

    Article  PubMed  PubMed Central  CAS  Google Scholar 

  15. Berkes, P., Orbán, G., Lengyel, M. & Fiser, J. Spontaneous cortical activity reveals hallmarks of an optimal internal model of the environment. Science 331, 83–87 (2011).

    Article  PubMed  PubMed Central  CAS  Google Scholar 

  16. Churchland, M. M. et al. Neural population dynamics during reaching. Nature 487, 51–56 (2012).

    Article  PubMed  PubMed Central  CAS  Google Scholar 

  17. Rigotti, M. et al. The importance of mixed selectivity in complex cognitive tasks. Nature 497, 585–590 (2013).

    Article  PubMed  PubMed Central  CAS  Google Scholar 

  18. Mante, V., Sussillo, D., Shenoy, K. V. & Newsome, W. T. Context-dependent computation by recurrent dynamics in prefrontal cortex. Nature 503, 78–84 (2013).

    Article  PubMed  PubMed Central  CAS  Google Scholar 

  19. Kaufman, M. T., Churchland, M. M., Ryu, S. I. & Shenoy, K. V. Cortical activity in the null space: permitting preparation without movement. Nat. Neurosci. 17, 440–448 (2014).

    Article  PubMed  PubMed Central  CAS  Google Scholar 

  20. Golub, M. D., Yu, B. M. & Chase, S. M. Internal models for interpreting neural population activity during sensorimotor control. Elife 4, e10015 (2015).

    Article  PubMed  PubMed Central  Google Scholar 

  21. Durstewitz, D., Vittoz, N. M., Floresco, S. B. & Seamans, J. K. Abrupt transitions between prefrontal neural ensemble states accompany behavioral transitions during rule learning. Neuron 66, 438–448 (2010).

    Article  PubMed  CAS  Google Scholar 

  22. Sadtler, P. T. et al. Neural constraints on learning. Nature 512, 423–426 (2014).

    Article  PubMed  PubMed Central  CAS  Google Scholar 

  23. Athalye, V. R., Ganguly, K., Costa, R. M. & Carmena, J. M. Emergence of coordinated neural dynamics underlies neuroprosthetic learning and skillful control. Neuron 93, 955–970 (2017).

    Article  PubMed  CAS  Google Scholar 

  24. Vyas, S. et al. Neural population dynamics underlying motor learning transfer. Neuron https://doi.org/10.1016/j.neuron.2018.01.040 (2018).

  25. Golub, M. D., Chase, S. M., Batista, A. P. & Yu, B. M. Brain-computer interfaces for dissecting cognitive processes underlying sensorimotor control. Curr. Opin. Neurobiol. 37, 53–58 (2016).

    Article  PubMed  PubMed Central  CAS  Google Scholar 

  26. Taylor, D. M., Tillery, S. I. H. & Schwartz, A. B. Direct cortical control of 3D neuroprosthetic devices. Science 296, 1829–1832 (2002).

    Article  PubMed  CAS  Google Scholar 

  27. Jarosiewicz, B. et al. Functional network reorganization during learning in a brain-computer interface paradigm. Proc. Natl. Acad. Sci. USA 105, 19486–19491 (2008).

    Article  PubMed  Google Scholar 

  28. Koralek, A. C., Jin, X., Long, J. D. II, Costa, R. M. & Carmena, J. M. Corticostriatal plasticity is necessary for learning intentional neuroprosthetic skills. Nature 483, 331–335 (2012).

    Article  PubMed  PubMed Central  CAS  Google Scholar 

  29. Clancy, K. B., Koralek, A. C., Costa, R. M., Feldman, D. E. & Carmena, J. M. Volitional modulation of optically recorded calcium signals during neuroprosthetic learning. Nat. Neurosci. 17, 807–809 (2014).

    Article  PubMed  PubMed Central  CAS  Google Scholar 

  30. Armenta Salas, M. & Helms Tillery, S. I. Uniform and non-uniform perturbations in brain-machine interface task elicit similar neural strategies. Front. Syst. Neurosci 10, 70 (2016).

    Article  PubMed  PubMed Central  Google Scholar 

  31. Cunningham, J. P. & Yu, B. M. Dimensionality reduction for large-scale neural recordings. Nat. Neurosci. 17, 1500–1509 (2014).

    Article  PubMed  PubMed Central  CAS  Google Scholar 

  32. Krakauer, J. W., Pine, Z. M., Ghilardi, M.-F. & Ghez, C. Learning of visuomotor transformations for vectorial planning of reaching trajectories. J. Neurosci. 20, 8916–8924 (2000).

    Article  PubMed  CAS  Google Scholar 

  33. Paz, R., Nathan, C., Boraud, T., Bergman, H. & Vaadia, E. Acquisition and generalization of visuomotor transformations by nonhuman primates. Exp. Brain Res. 161, 209–219 (2005).

    Article  PubMed  Google Scholar 

  34. Yu, B. M. et al. Gaussian-process factor analysis for low-dimensional single-trial analysis of neural population activity. J. Neurophysiol. 102, 614–635 (2009).

    Article  PubMed  PubMed Central  Google Scholar 

  35. Santhanam, G. et al. Factor-analysis methods for higher-performance neural prostheses. J. Neurophysiol. 102, 1315–1330 (2009).

    Article  PubMed  PubMed Central  Google Scholar 

  36. Churchland, M. M. et al. Stimulus onset quenches neural variability: a widespread cortical phenomenon. Nat. Neurosci. 13, 369–378 (2010).

    Article  PubMed  PubMed Central  CAS  Google Scholar 

  37. Harvey, C. D., Coen, P. & Tank, D. W. Choice-specific sequences in parietal cortex during a virtual-navigation decision task. Nature 484, 62–68 (2012).

    Article  PubMed  PubMed Central  CAS  Google Scholar 

  38. Boyd, S. & Vandenberghe, L. Convex Optimization (Cambridge University Press, Cambridge, 2004).

  39. Charlesworth, J. D., Tumer, E. C., Warren, T. L. & Brainard, M. S. Learning the microstructure of successful behavior. Nat. Neurosci. 14, 373–380 (2011).

    Article  PubMed  PubMed Central  CAS  Google Scholar 

  40. Smith, M. A., Ghazizadeh, A. & Shadmehr, R. Interacting adaptive processes with different timescales underlie short-term motor learning. PLoS Biol. 4, e179 (2006).

    Article  PubMed  PubMed Central  CAS  Google Scholar 

  41. Kording, K. P., Tenenbaum, J. B. & Shadmehr, R. The dynamics of memory as a consequence of optimal adaptation to a changing body. Nat. Neurosci. 10, 779–786 (2007).

    Article  PubMed  PubMed Central  CAS  Google Scholar 

  42. Joiner, W. M. & Smith, M. A. Long-term retention explained by a model of short-term learning in the adaptive control of reaching. J. Neurophysiol. 100, 2948–2955 (2008).

    Article  PubMed  PubMed Central  Google Scholar 

  43. Yang, Y. & Lisberger, S. G. Learning on multiple timescales in smooth pursuit eye movements. J. Neurophysiol. 104, 2850–2862 (2010).

    Article  PubMed  PubMed Central  Google Scholar 

  44. Hwang, E. J., Bailey, P. M. & Andersen, R. A. Volitional control of neural activity relies on the natural motor repertoire. Curr. Biol. 23, 353–361 (2013).

    Article  PubMed  PubMed Central  CAS  Google Scholar 

  45. Cohen, R. G. & Sternad, D. Variability in motor learning: relocating, channeling and reducing noise. Exp. Brain Res. 193, 69–83 (2009).

    Article  PubMed  CAS  Google Scholar 

  46. Shadmehr, R. & Krakauer, J. W. A computational neuroanatomy for motor control. Exp. Brain Res. 185, 359–381 (2008).

    Article  PubMed  PubMed Central  Google Scholar 

  47. Kalman, R. E. A new approach to linear filtering and prediction problems. J. Basic Eng. 82, 35–45 (1960).

    Article  Google Scholar 

  48. Wu, W., Gao, Y., Bienenstock, E., Donoghue, J. P. & Black, M. J. Bayesian population decoding of motor cortical activity using a Kalman filter. Neural Comput. 18, 80–118 (2006).

    Article  PubMed  Google Scholar 

  49. Gilja, V. et al. A high-performance neural prosthesis enabled by control algorithm design. Nat. Neurosci. 15, 1752–1757 (2012).

    Article  PubMed  PubMed Central  CAS  Google Scholar 

  50. Churchland, M. M. & Abbott, L. F. Two layers of neural variability. Nat. Neurosci. 15, 1472–1474 (2012).

    Article  PubMed  CAS  Google Scholar 

Download references

Acknowledgements

This work was supported by NIH R01 HD071686 (A.P.B., B.M.Y. and S.M.C.), NSF NCS BCS1533672 (S.M.C., B.M.Y. and A.P.B.), NSF CAREER award IOS1553252 (S.M.C.), NIH CRCNS R01 NS105318 (B.M.Y. and A.P.B.), Craig H. Neilsen Foundation 280028 (B.M.Y., S.M.C. and A.P.B.), Pennsylvania Department of Health Research Formula Grant SAP 4100077048 under the Commonwealth Universal Research Enhancement program (S.M.C. and B.M.Y.) and Simons Foundation 364994 (B.M.Y.).

Author information

Author notes

  1. These authors contributed equally: Steven M. Chase, Byron M. Yu.

Authors and Affiliations

  1. Department of Electrical and Computer Engineering, Carnegie Mellon University, Pittsburgh, PA, USA

    Matthew D. Golub & Byron M. Yu

  2. Center for the Neural Basis of Cognition, Carnegie Mellon University, Pittsburgh, PA, USA

    Matthew D. Golub, Patrick T. Sadtler, Emily R. Oby, Kristin M. Quick, Aaron P. Batista, Steven M. Chase & Byron M. Yu

  3. Department of Electrical Engineering, Stanford University, Stanford, CA, USA

    Matthew D. Golub & Stephen I. Ryu

  4. Department of Bioengineering, University of Pittsburgh, Pittsburgh, PA, USA

    Patrick T. Sadtler, Emily R. Oby, Kristin M. Quick, Elizabeth C. Tyler-Kabara & Aaron P. Batista

  5. Systems Neuroscience Institute, University of Pittsburgh, Pittsburgh, PA, USA

    Patrick T. Sadtler, Emily R. Oby, Kristin M. Quick & Aaron P. Batista

  6. Department of Neurosurgery, Palo Alto Medical Foundation, Palo Alto, CA, USA

    Stephen I. Ryu

  7. Department of Physical Medicine and Rehabilitation, University of Pittsburgh, Pittsburgh, PA, USA

    Elizabeth C. Tyler-Kabara

  8. Department of Neurological Surgery, University of Pittsburgh, Pittsburgh, PA, USA

    Elizabeth C. Tyler-Kabara

  9. Department of Biomedical Engineering, Carnegie Mellon University, Pittsburgh, PA, USA

    Steven M. Chase & Byron M. Yu

Authors
  1. Matthew D. Golub
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Patrick T. Sadtler
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Emily R. Oby
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Kristin M. Quick
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Stephen I. Ryu
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Elizabeth C. Tyler-Kabara
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. Aaron P. Batista
    View author publications

    You can also search for this author in PubMed Google Scholar

  8. Steven M. Chase
    View author publications

    You can also search for this author in PubMed Google Scholar

  9. Byron M. Yu
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

M.D.G., B.M.Y., S.M.C. and A.P.B. designed the analyses and discussed the results. M.D.G. performed all analyses and wrote the paper. P.T.S., K.M.Q., M.D.G., S.M.C., B.M.Y. and A.P.B. designed the animal experiments. P.T.S. and E.R.O. performed the animal experiments. S.I.R., E.C.T.-K. and E.R.O. performed the animal surgeries. All authors commented on the manuscript. B.M.Y. and S.M.C. contributed equally to this work.

Corresponding authors

Correspondence to Steven M. Chase or Byron M. Yu.

Ethics declarations

Competing interests

The authors declare no competing interests.

Additional information

Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Text and Figures

Supplementary Figures 1–11 and Supplementary Math Note

Life Sciences Reporting Summary

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Golub, M.D., Sadtler, P.T., Oby, E.R. et al. Learning by neural reassociation. Nat Neurosci 21, 607–616 (2018). https://doi.org/10.1038/s41593-018-0095-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/s41593-018-0095-3

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing