ScanNet: an interpretable geometric deep learning model for structure-based protein binding site prediction

Abstract

Predicting the functional sites of a protein from its structure, such as the binding sites of small molecules, other proteins or antibodies, sheds light on its function in vivo. Currently, two classes of methods prevail: machine learning models built on top of handcrafted features and comparative modeling. They are, respectively, limited by the expressivity of the handcrafted features and the availability of similar proteins. Here, we introduce ScanNet, an end-to-end, interpretable geometric deep learning model that learns features directly from 3D structures. ScanNet builds representations of atoms and amino acids based on the spatio-chemical arrangement of their neighbors. We train ScanNet for detecting protein–protein and protein–antibody binding sites, demonstrate its accuracy—including for unseen protein folds—and interpret the filters learned. Finally, we predict epitopes of the SARS-CoV-2 spike protein, validating known antigenic regions and predicting previously uncharacterized ones. Overall, ScanNet is a versatile, powerful and interpretable model suitable for functional site prediction tasks. A webserver for ScanNet is available from http://bioinfo3d.cs.tau.ac.il/ScanNet/.

Main

Despite recent progresses in experimental¹ and AI-based^2,3 protein structure determination, there remains a gap between structure and function⁴. The most accurate functional site prediction method is comparative modeling^{5,6,7,8,9,10,11,12,13}: given a query protein, similar proteins with known functional sites are searched for and their sites are mapped onto the query structure. Comparative modeling has several shortcomings. First and foremost, its coverage is limited, as the pool of experimentally characterized protein folds or structural motifs is small. Second, functional sites are variably preserved throughout evolution. On the one hand, the B cell epitopes (BCEs) of viral proteins frequently undergo antigenic drift, that is, the abolition of recognition by antibodies after only one or few mutations. On the other hand, some protein–protein interactions (PPIs) are mainly driven by few ‘hotspot’ residues: mutations and/or conformational changes of the other interface residues preserve the interaction. Put differently, the invariances in both sequence and conformation spaces of such function-determining structural motifs are in general motif-dependent and therefore unknown. This hampers our ability to both define and recognize such motifs using conventional comparative approaches.

An alternative to comparative modeling is feature-based machine learning^{12,13,14,15,16,17,18}. For each amino acid of a query protein, various features of geometrical (for example, secondary structure, solvent accessibility, molecular surface curvature), physico-chemical (for example, hydrophobicity, polarity, electrostatic potential) and evolutionary (for example, conservation, position–weight matrices, coevolution) nature are calculated. Then, the target property is predicted using a machine learning model for tabular data such as random forest or gradient boosting. Reasoning on mathematically defined features offers three advantages: (1) ability to generalize to proteins with no similarity to any of the train set proteins, (2) high sequence sensitivity, that is, ability to output distinct predictions for highly similar protein sequences and (3) fast inference speed. Machine learning models are, however, limited by the expressiveness of the features used, as these cannot capture the spatio-chemical arrangements of atoms or amino acids characterizing function-bearing motifs. Examples of such function-bearing motifs include Zinc fingers that are signatures of DNA or RNA binding sites¹⁹, or PPI hotspot ‘O-rings’²⁰: namely, exposed hydrophobic/aromatic amino acids surrounded by polar/charged ones. Despite over 50 years of experimental structural determination, new function-determining motifs are still being discovered²¹.

End-to-end differentiable models, that is, deep learning, can potentially overcome the limitations of both approaches. Indeed, deep learning models can learn the data features and their invariances directly by backpropagation, and generalize well despite a large number of parameters. Adapting the deep learning approach to protein structures requires defining an appropriate representation for proteins. Proteins can indeed be represented in multiple, complementary ways, for example as sequences^22,23, residue graphs^24,25,26,27, atomic density maps^{28,29,30,31,32,33,34}, atomic point clouds³⁵ or molecular surfaces^36,37, each capturing different functionally relevant features. Voxelated atomic density maps can be readily processed using classical 3D convolutional neural networks, but the approach is computationally intensive and the predictions are not invariant on rotation of the input structure. Point clouds, graphs and surfaces can be analyzed via geometric deep learning^38,39, that is, end-to-end differentiable models tailored for data with no natural grid-like topology or shared global coordinate system. Graphs can be derived from 3D structures by taking residues as nodes and the distances and angles between them as edges and processed using graph neural networks (GNN) such as message passing neural networks⁴⁰ or graph attention networks⁴¹. By design, GNNs are invariant on Euclidean transformation and expressive, but can be challenging to regularize and interpret. In particular, it is unclear whether—and if yes, which—structural motifs are captured by GNNs. Here, we introduce ScanNet (spatio-chemical arrangement of neighbors neural network), a new geometric deep learning architecture tailored for protein structures. ScanNet builds representations of atoms and amino acids based on the spatio-chemical arrangement of their neighbors and exploits them to predict labels for each amino acid. By construction, ScanNet is end-to-end differentiable with minimal structure preprocessing, yielding fast training and inference. ScanNet predictions are local, invariant on Euclidean transformations and integrate information from multiple scales (atom, amino acid) and modalities (structure, multiple sequence alignment (MSA)) in a synergistic fashion. Its corresponding parametric function is expressive, meaning that it can efficiently approximate known handcrafted features. Through appropriate parameterization and regularization, the filters learned by ScanNet can be readily visualized and interpreted. We showcase the capabilities of ScanNet on two related tasks: prediction of protein–protein binding sites (PPBS) and BCE (that is, antibody binding sites). ScanNet outperforms baseline methods based on machine learning, structural homology and surface-based geometric deep learning. We further visualize and interpret the representations learned by the network. We find that they encompass known handcrafted features and find filters detecting simple, generic structural motifs, such as hydrogen bonds, as well as filters recognizing complex, task-specific motifs, such as O-rings and transmembrane helical domains. Applied to the SARS-CoV-2 spike protein, ScanNet predictions validate known antigenic regions and predict a previously uncharacterized one.

Results

Spatio-chemical arrangement of neighbors network (ScanNet)

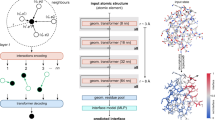
ScanNet takes as input a protein structure file and, optionally, a position–weight matrix derived from a MSA and outputs a residue-wise label probability. Its four main stages, shown in Fig. 1 and detailed in the Methods (Extended Data Figs. 1 and 2), are: atomic neighborhood embedding, atom to amino acid pooling, amino acid neighborhood embedding and neighborhood attention.

Fig. 1: Overview of the ScanNet architecture.

ScanNet inputs are the primary sequence, tertiary structure and, optionally, position–weight matrix computed from a MSA of evolutionarily related proteins. First, for each atom, neighboring atoms are extracted from the structure and positioned in a local coordinate frame (top left). The resulting point cloud is passed through a set of trainable, linear filters detecting specific spatio-chemical arrangements (top middle), yielding an atomic-scale representation (top right). After aggregation of the atomic representation at the amino acid level and concatenation with amino acid attributes, the process is reiterated with amino acids to obtain a representation of an amino acid (bottom). The latter is projected and locally averaged for residue-wise classification.

ScanNet first builds, for each heavy atom, a local coordinate frame centered on its position and oriented according to its covalent bonds. Next, it identifies its closest neighboring atoms. The resulting neighborhood, formally a point cloud with coordinates and attributes (atom group type) is passed through a set of spatio-chemical linear filters to yield an atom-wise representation. Each filter outputs a matching score between its (trainable) spatio-chemical pattern and the neighborhood. The patterns, which are parameterized using Gaussian kernels and sparse bilinear products, are localized in both physical and attribute space. Localization facilitates interpretation and is biologically motivated since motif functionality is often born by a few key atomic groups/amino acids in a specific arrangement, whereas other neighbors are irrelevant and interchangeable. Trainable, localized spatio-chemical patterns generalize to proteins the well-known concept of pharmacophores for small molecules.

Toward calculation of amino acid-wise output, the atom-wise representation is pooled at the amino acid scale and concatenated with embedded amino acid-level information (either amino acid type or position–weight matrix). The constituting atoms of an amino acid have various types and may play different functional roles. In particular, some handcrafted features such as accessible surface area average information over all the atoms, whereas others such as secondary structure consider only subsets (the backbone atoms). Therefore, a trainable, multi-headed attention pooling operation capable of learning which atoms are relevant for each feature is used rather than a conventional symmetric pooling operation such as average or maximum.

The neighborhood embedding procedure is then repeated at the amino acid scale: a local coordinate frame is constructed for each amino acid from its C_α atom, sidechain orientation and local backbone orientation and its nearest neighbors are identified. The resulting neighborhood with learned attributes is passed through a set of trainable filters to yield an amino acid-wise representation.

Finally, spatially consistent output probabilities are obtained by projecting the amino acid representations to scalar values, smoothing them across a local neighborhood and converting to probabilities with a logistic function. The smoothing scheme integrates two specifics of protein binding sites. First, PPIs are frequently driven by key hotspot residues that contribute most of the binding energy, whereas other nearby passenger residues have a small contribution to the binding energy^20,42. Such passenger residues are harder to detect directly as they do not necessarily have the salient features of PPBSs⁴³. Second, some amino acid pairs consistently have opposite binding site labels—in particular, consecutive amino acids along the sequence because their sidechains typically point in opposite directions. Altogether, this motivates the introduction of trainable, attention-based weighted averages, with algebraic weights.

ScanNet for prediction of PPBSs

The PPBS of a protein are defined as the residues directly involved in one or more native, high affinity PPIs. Not every surface residue is a PPBS, as (1) binding propensity competes with structural stability and (2) PPIs are highly partner- and conformation-specific. Knowledge of the PPBS of a protein provides insight about its in vivo behavior, particularly when its partners are unknown and can guide docking algorithms. Prediction of PPBS with conventional approaches is challenging as PPBS structural motifs are more diverse, less conserved and more extended than small molecule binding sites. Additionally, only incomplete and noisy labels can be derived from structural data, as (1) most PPIs of a given protein are not structurally characterized, and (2) a substantial fraction (roughly 15%, ref. ⁴⁴) of the structurally characterized protein–protein interfaces are not physiological but crystal-induced.

We constructed a nonredundant dataset of 20K representative protein chains with annotated binding sites derived from the Dockground database of protein complexes⁴⁵. The PPBS dataset covers a wide range of complex sizes, types, organism taxonomies, protein lengths (Extended Data Fig. 3a–d) and contains around 5M amino acids, of which 22.7% are PPBS. To address the uneven sampling of the protein space, we introduced sample weights for each chain that are inversely proportional to the number of similar chains found in the dataset (Methods and Extended Data Fig. 3h). To investigate the relationship between homology and generalization error, we divided the validation/test sets into four splits based on the degree of homology with respect to their closest train set example (Fig. 2 and Extended Data Fig. 3g).

Fig. 2: Prediction of PPBS with ScanNet.

a–d, Precision-recall curves of PPBS prediction for ScanNet, structural homology and handcrafted features baseline methods (main text). Train and test sets constructed from the redundant Dockground template database⁴⁵. Proteins of the test set are subdivided into four nonoverlapping groups. a, Test 70%, at least 70% sequence identity with at least one train set example. b, Test homology, at most 70% sequence identity with any train set example, at least one train set example belonging to same protein superfamily (H level of CATH classification⁵⁶). c, Test topology, at least one train set example with similar protein topology (T level of CATH classification⁵⁶), none with similar protein superfamily. d, Test none, none of the above. e,f, Illustrations of predicted PPBS for an enzyme (barnase, PDB ID 1BRS, ref. ⁵⁷, Val. Homology dataset) with its inhibitor overlaid (e) and an homodimer (glutamic acid decarboxylase GAD67, PDB ID 2OKJ, ref. ⁵⁸, test topology dataset) (f). The molecular surface of the query protein is shown with coloring based on predicted probability, ranging from low (white) to high (dark blue). The partner protein is shown in cartoon representation (gray transparent). Visualization software, ChimeraX⁵⁹.

We evaluated three models on the PPBS dataset: (1) ScanNet, (2) a machine learning pipeline based on handcrafted features and (3) a structural homology pipeline (see Methods for technical details). For the handcrafted features baseline, we computed for each amino acid various geometric, chemical and evolutionary features, and used xgboost, a state-of-the-art tree-based classification algorithm⁴⁶. For the structural homology pipeline, pairwise local structural alignments between the train set chains and the query chain were first constructed using MultiProt⁴⁷. Then, alignments were weighted and aggregated to produce binding site probabilities for each amino acid. For all three models, the validation set was used for hyperparameters selection and early stopping, and performance is reported on the test set. Training and evaluation of a single model took 1–2 hours for ScanNet (excluding preprocessing time, roughly 10 ms per step using a single Nvidia V100 graphical processing unit (GPU)), a few minutes for the machine learning baseline (excluding feature calculation time, using Intel Xeon Phi processor with 28 cores) and 1 month for the structural homology baseline (Intel Xeon Phi processor with 28 cores). We also evaluated Masif-site³⁶, a surface-based geometric deep learning model. Since Masif-site was not trained on the same dataset, we only report its global test set performance.

We found that for the full test set, ScanNet achieved an area under the precision-recall curve (AUCPR) of 0.694 (Table 1), accuracy of 87.7% (Supplementary Table 1) and 73.5% precision at 50% recall (Extended Data Fig. 4e,f), the best performance by a substantial margin. The next best model was the structural homology baseline, whereas Masif-site and the handcrafted features model performed similarly. The model ranks differed when considering only subsets (Fig. 2a–d). The structural homology baseline performed best in the high homology setting, but its performance degraded rapidly with the degree of relatedness; when the test protein had no similar fold in the train set, it was the worst algorithm. Conversely, the performance of the handcrafted features baseline increased slowly with the degree of homology, meaning that it could not faithfully recognize previously seen folds. In contrast, ScanNet could both recognize previously seen folds and generalize to unseen ones. Visualizations of ScanNet predictions for representative examples (Fig. 2e,f and Supplementary Figs. 1–4) illustrate that predictions are spatially coherent and that in most cases, the binding sites are correctly identified. Overall, the network performed uniformly well across complex types and sizes, protein lengths and organisms (Extended Data Fig. 5). PPBS identification was slightly harder when no or few homologs were found in the MSA (Extended Data Fig. 5b) and slightly easier for enzymes (Extended Data Fig. 5d). We next identified and visualized train and test examples on which ScanNet performed poorly (Supplementary Fig. 5). We found bona fide false negative (undetected interacting patches) and false positives (predicted interacting patches), although for the latter we could not rule out involvement in another PPI for which no structural data was available. Another source of mistake was confusion between types of binding site: we found at least one instance where the incorrectly predicted PPBS were actually RNA binding sites. However, only a minority of RNA binding domain were confused as protein binding (Supplementary Fig. 6). Finally, confusion between crystal and native interfaces was a substantial source of apparent mistakes. We found several train set examples in which the network refused to learn the train label and instead predicted another binding interface with high confidence (Supplementary Fig. 7). The predicted binding sites matched well the interface found in another biological assembly file. We found a posteriori that the biological assembly files used in the train set were annotated as probably incorrect by QSbio⁴⁴. Overall, this demonstrated the robustness of predictions with respect to noise in training labels.

Table 1 Performance evaluation for prediction of PPBs. AUCPR is shown. Proteins of the test set are subdivided into four nonoverlapping groups as described in Fig. 2. For the Masif-site, only the aggregated performance is shown since its training set differs from ours. See Supplementary Tables 1–6 for additional evaluation metrics and variance estimates. Bold entries indicate the best performance

We next performed ablation experiments to investigate the importance of the network components (Table 1 and Extended Data Fig. 4). ScanNet performance decreased but remained above the other methods when discarding the evolutionary information (by replacing the position–weight matrix by the one-hot encoded sequence) or all the atomic-scale information (by removing the first two modules). Removing the sparse regularization on the spatio-chemical patterns and the early stopping yielded an homology-like performance profile, with better performance in the high homology setting but poorer otherwise. Last, training the model on all chains without redundancy reduction nor using sample weights yielded worse performance, highlighting the importance of sample weights.

Finally, we investigated the impact of conformational changes on binding (that is, induced fit) on ScanNet predictions using the Dockground unbound X-ray and simulated datasets⁴⁵. Overall, predictions based on bound and unbound structures were highly consistent, and accuracy decreased only mildly from bound to unbound (Methods, Extended Data Fig. 6 and Supplementary Table 4).

Visualization and interpretation of the representations

What did ScanNet learn? Does the network reason solely by comparison with training instances or does it learn the underlying chemical principles of binding? How will it behave in out-of-sample settings such as disordered regions? To better understand the learned representations, we visualized the spatio-chemical patterns and low-dimensional projections of the representations at the atomic (Fig. 3) and amino acid (Fig. 4) levels. Recall that each pattern is composed by a set of Gaussian kernels characterized by their location in the local coordinate system and specificity in attribute space. At the atomic scale, the origin corresponds to the central atom and the z axis and xz plane are oriented according to its covalent bonds. Figures 3a–f and 4a–f each show one pattern (left), together with a maximally activating neighborhood (right) taken from the validation set and the remaining patterns are provided in Supplementary Data 1, 2. The atomic pattern shown in Fig. 3a has two main components: a NH group located at the center and an oxygen located few Ångstroms away, in the (x < 0, y < 0, z < 0) quadrant, that is, opposite from the two covalent bonds. It is the well-known signature of a N–H–O hydrogen bond, ubiquitous in protein backbones. The corresponding maximally activating atom is indeed a backbone nitrogen within a beta sheet. Patterns may have more than two components, and several possible groups per location. The atomic pattern shown in Fig. 3b features two oxygen atoms and three NH groups in a specific arrangement; the corresponding maximally activating neighborhoods are backbone nitrogens located at contact zones between two helical fragments (right of Fig. 3b and Supplementary Fig. 8). Patterns shown in Fig. 3c,d focus on sidechains. The pattern in Fig. 3c is defined as a carbon in the vicinity of a methyl group and an aromatic ring. The pattern in Fig. 3d consists of SH or NH₂ groups—two sidechain-located hydrogen donors—surrounded by oxygen atoms. Last, patterns may include prescribed absence of atoms in specific regions. The pattern in Fig. 3e is defined by a backbone carbon or oxygen without any NH groups in its vicinity, meaning that it identifies backbones available for hydrogen bonding. The pattern in Fig. 3f identifies a methionine sidechain with one solvent-exposed side, and is associated with high PPBS probability. Together, the filters collectively define a rich representation capturing various properties of a neighborhood, as seen from the 2D t-distributed stochastic neighbor embedding (t-SNE) projections colored by properties (Fig. 3g,h). In the space of filter activities, atoms cluster by coordination number (number of other atoms in the range of van der Waals interactions) and electrostatic potential (calculated with the Adaptive Poisson–Boltzmann Solver⁴⁸).

Fig. 3: Visualization of the learned atomic representation.

a–f, Each panel shows one of the 128 learned spatio-chemical patterns on the left and one corresponding top-activating neighborhood on the right. Each pattern is depicted as follows: only the Gaussian kernels relevant to the pattern are shown; they are represented by their unit ellipsoid. The corresponding location-wise attribute specificity is depicted as a weight logo inside the ellipsoid, similar to a position–weight matrix: attributes with nonzero weights are stacked on top of one another with letter height proportional to their algebraic weight value, sorted from strongest positive (top) to strongest negative (bottom, reversed letters). The unit ellipsoid is colored based on the maximally activating attribute type if it is positive, or gray otherwise. Color code is carbon (beige), oxygen (red), nitrogen (blue) and sulfur (yellow). The frame is overlaid in gray, with axes extending over 3.75 Å. Each filter/neighborhood pair is oriented independently for clarity. Visualizations created with pythreejs. g,h, Two-dimensional projection of the learned atomic-scale representation using t-SNE⁶⁰. Each point corresponds to one atom of a representative set of proteins. Coloring is based on atom coordination index (g) or electrostatic potential at the atom location, computed using APBS⁴⁸ (h).

Fig. 4: Visualization of the learned amino acid representation.

a–f, Each panel shows one of the 128 learned spatio-chemical patterns on the left and one corresponding top-activating neighborhood on the right. Gaussian kernels are depicted similarly to those in Fig. 3. Since the input attributes are learned, each component of a pattern is characterized by a complex specificity in attribute space. We represent it by the distributions of amino acid types and accessible surface areas of its top 1% maximally activating residues. The distributions are shown as a logo (each letter or symbol is proportional to the probability), with a total height proportional to the mean activation of the set. Accessible surface area values are discretized into four quartiles and represented as pie charts (from full gray meaning buried to full blue meaning accessible). Amino acids are colored by chemical properties: negatively charged (red), positively charged (blue), polar (purple), hydrophobic (black), sulfur-containing (green), aromatic (gold) and tiny/proline (gray). The frame is overlaid in gray, with axes extending over 9 Å. Each filter/neighborhood pair is oriented independently for clarity. Visualizations created with pythreejs. g,h, Two-dimensional projection of the learned amino acid scale representation using t-SNE⁶⁰. Each point corresponds to one amino acid of a representative set of proteins. Coloring based on secondary structure (g) or accessible surface area (h) calculated with DSSP⁶¹. Additional t-SNE plots are available in Extended Data Fig. 7.

The amino acid scale patterns can be similarly analyzed: the origin, z axis and xz plane are, respectively, defined by the C_α, sidechain and backbone orientation of the central amino acid. Neighborhoods are shown as backbone segments, with position–weight matrices as attributes; the learned attributes pooled from the atomic scale are not shown. Each Gaussian component of a pattern is characterized by a complex specificity in attribute space. We represent it by the distributions of amino acid types and accessible surface areas of its top 1% maximally activating residues. Patterns in Fig. 4a,b focus only on the central amino acid, that is, they recombine and propagate features from the previous layers. The pattern in Fig. 4a consists of solvent-exposed residues of type frequently encountered in protein–protein interfaces such as leucine or arginine. It is positively correlated with the output probability (r = 0.31). Conversely, the pattern in Fig. 4b, which consists of buried hydrophobic amino acids, is activated by residues within the protein cores and is negatively correlated with the output (r = − 0.32).

Multi-component patterns are also found: the pattern in Fig. 4c consists of an exposed glycine together with an exposed aromatic or leucine amino acid, and is correlated with binding (r = 0.18). The pattern in Fig. 4d is constituted by an exposed hydrophobic amino acid surrounded by exposed, charged amino acids and is strongly correlated with binding (r = 0.29). It is similar to the hotspot O-ring architecture previously described by Bogan and Thorn²⁰. Conversely, the pattern in Fig. 4e, which consists of a central cysteine (possibly involved in a disulfide bond) surrounded by exposed lysines is negatively correlated with binding (r = − 0.13).

Distributed patterns such as that in Fig. 4f are found and hypothetically contribute to prediction by identifying domain-level context. The pattern in Fig. 4f, which consists of multiple aromatic and hydrophobic components, is strongly activated by transmembrane helical domains. Identification of transmembrane domain is indeed required for accurate prediction as the hydrophobic core/hydrophilic rim rule is reversed within membranes. Inversely, we expect that for disordered regions, only the filters with patterns focusing on a single amino acid such as Fig. 4a,b or a linear stretch such as Fig. 4c will contribute to the prediction, whereas the others will be silent. ScanNet will thus effectively behave as a convolutional sequence model with a short kernel width.

Finally, the two-dimensional t-SNE projections of the representation (Fig. 4f,g and Extended Data Fig. 7) show that the filter activities encompass various amino acid-level handcrafted features, including amino acid type, secondary structure, accessible surface area, surface convexity and evolutionary conservation.

Overall, these findings support the hypothesis that ScanNet learns some of the underlying physico-chemical principles of PPIs. To consolidate these findings, we compared ScanNet predictions to experimental alanine scans and residue contributions to the binding energy using Rosetta (Methods and Extended Data Fig. 8). We found that among the binding residues, the ones with higher binding probability and larger attention coefficients tend to contribute more to the binding free energy. Additionally, the amino acid filter activities reflected the type of interaction (van der Waals, electrostatic and so on) involved in binding.

ScanNet for prediction of BCEs

BCE are defined as residues directly involved in a antibody–antigen complex. Although a priori every surface residue is potentially immunogenic, some are preferred in the sense that it is easier to mature antibodies targeting them with high affinity and specificity. Exhaustive, high-throughput experimental determination of BCEs is challenging because they can span across multiple noncontiguous protein fragments. Prediction is challenging owing to their instability throughout evolution and the lack of exhaustive epitope mappings for a given antigen. In silico prediction of BCE can be leveraged for constructing epitope-based vaccines and for designing nonimmunogenic therapeutic proteins.

We derived from the SabDab database⁴⁹ a dataset of 3,756 protein chains (796, 95% sequence identity clusters) with annotated BCE. Here, 8.9% of the residues were labeled as BCE, likely an underestimation of the true fraction. The dataset was split into five subsets for cross-validation training, with no more than 70% sequence identity between pairs of sequences from different subsets. We evaluated ScanNet in three settings: trained from scratch, trained for PPBS prediction without finetuning and trained via transfer learning using the PPBS network as starting point. We compared it with the handcrafted features baseline, structural homology baseline and Discotope, a popular tool based on geometric features and propensity scores⁵⁰. We also report the performance of ScanNet without evolutionary data, of the null predictor and of a predictor based on solvent accessibility only. ScanNet trained via transfer learning outperformed the other models, with an AUCPR of 0.178 and a positive predicted value at L/10 of 27.5% (Fig. 5a and Supplementary Table 5). This represents an enrichment of respectively 143, 153 and 309% over Discotope, solvent accessibility-based and null prediction. ScanNet performed equally well with or without evolutionary information unlike for PPBS. Visualization of representative spatio-chemical patterns associated with high BCE probability sheds light on the similarities and differences between PPBS and BCE (Fig. 5b–e, the remaining filters are provided in Supplementary Data 3). We find asparagine and arginine-containing patterns (Fig. 5b,c) as well as linear epitopes (Fig. 5c, shared with PPBS). The pattern in Fig. 5d consists of exposed residues with alternate charges, and putatively indicates availability for salt-bridge formation. Finally, pattern Fig. 5e is composed of an exposed, charged amino acid in the vicinity of two cysteines forming a disulfide bond. A possible explanation is that disulfide bond-rich regions are more structurally stable, hence it is easier to recognize with high affinity and specificity.

Fig. 5: Prediction of BCEs with ScanNet.

a, Precision-recall curve of BCE prediction for baseline methods, Discotope⁵⁰ and ScanNet. Epitope database constructed from SabDab (timestamp 19 April 2021)⁴⁹; fivefold cross-validation performance is shown. b–e, Each panel shows one learned spatio-chemical pattern whose activity is positively correlated with epitope probability. Same visualization as Fig. 4. f, Application to spike protein of SARS-CoV-2. Predictions performed on a Molecular Dynamics snapshot of the spike trimer with one RBD open⁶². The monomer with open conformation is represented as a molecular surface with colors corresponding to BCE probability, from white (low) to dark blue (high). Representative antibodies binding the main epitopes are superimposed in color, cartoon representation, see the full list in Supplementary Table 6.

We next predicted and visualized BCE of the SARS-CoV-2 spike protein. Predictions are shown with representative antibodies superimposed for the trimer with one open receptor binding domain (RBD) (Fig. 5e) and for the isolated RBD and N-terminal domain (NTD) (Supplementary Fig. 9). For the spike protein, the RBD was correctly identified as a major antigenic site. The six main epitopes previously described⁵¹ all had high probabilities, including the cryptic epitope CR3022 (exposed in the open conformation). The tip of the NTD was also correctly identified as a highly antigenic site. Two linear epitopes located in the S2 fusion machinery are also predicted around Glu 1150 and Arg 1185, respectively. Previously, Shrock et al.⁵² reported that both regions were targeted by antibodies from patients who had recovered from COVID-19. For the first one, a broadly neutralizing mAB targeting this epitope was recently isolated⁵³ and shown to neutralize several beta-coronaviruses but not SARS-CoV-2. Finally, the network predicted with high confidence one previously unreported conformational epitope constituted by three fragments in the vicinity of the glycosylated⁵⁴ Asn 657. Provided that the network is correct, and since the presence of the glycosyl group is unknown at runtime but can be imputed by ScanNet from the Asn-X-Ser/Thr linear motif, two interpretations are possible: either the glycosyl group shields an otherwise highly immunogenic region from antibodies, or it directly induces immune response via glycosyl-binding antibodies. Similarly, we found two additional cryptic epitopes of the NTD that are centered on glycosylated asparagine when performing prediction on the NTD domain alone (Supplementary Fig. 9b).

Overall, ScanNet predictions are in excellent agreement with the known antigenic profile of the spike protein and predict a new epitope that could not be detected via high-throughput linear epitope scanning. We additionally predicted BCE for three other viral protein: HIV envelope protein, influenza HA-1 and influenza HA-3 hemagglutinin (Supplementary Fig. 10). We notably found that the hemagglutinin epitope predictions differed between the HA-1 and HA-3 strand despite the similar fold, suggesting that ScanNet could be suitable for studying antigenic drift.

Discussion

Protein function is borne of a diverse set of structural motifs. These motifs, characterized by their complex spatio-chemical arrangements of atoms and amino acids, cannot be fully encompassed by handcrafted features. Conversely, detection via comparative modeling is challenging because their invariants, that is, the set of function-preserving sequence/conformational perturbations, are unknown. ScanNet is an end-to-end geometric deep learning model capable of learning such motifs together with their invariants directly from raw structural data by backpropagation. We demonstrated, through a detailed comparison of newly compiled datasets of annotated PPBSs and BCEs, that it efficiently leverages these motifs to outperform feature-based methods, comparative modeling and surface-based geometric deep learning. ScanNet reaches an accuracy of 87.7% for PPBS prediction and a positive prediction value at L/10 of 27.5% for BCE prediction. Through appropriate parameterization and regularization, the spatio-chemical patterns learned by the model can be explicitly visualized and interpreted as previously known motifs and as new ones. A breakthrough was recently achieved in protein structure prediction using deep learning², leading to the release of a vast set of accurate protein structure models³. We anticipate that ScanNet will prove insightful for analyzing these proteins, of which little is known regarding their function. A webserver is made available at http://bioinfo3d.cs.tau.ac.il/ScanNet/ and linked to both the Protein Data Bank (PDB) and AlphaFoldDB for ease of use. Very recently, Evans et al.⁵⁵ introduced AlphaFold-multimer, a new approach for prediction of protein complexes from paired MSAs and demonstrated impressive performance. We further compared ScanNet to AlphaFold-mutimer for prediction of partner-specific PPBSs, partner-agnostic PPBSs and BCEs (Methods and Extended Data Fig. 9). We found that AlphaFold outperformed ScanNet for partner-specific PPBS, whereas both performed comparably for partner-agnostic PPBS. For BCEs, ScanNet could identify all the main epitopes of the RBD of the SARS-CoV-2 spike protein, whereas AlphaFold-multimer could only identify one. This showcases the complementarity between MSA-based, partner-specific and structure-based, partner-agnostic approaches. Owing to its generality, it is straightforward to extend ScanNet to other classes of binding sites provided that sufficient training data is available. Extension to partner-specific binding prediction for prediction of interactions and guiding molecular docking is a promising future direction, as the amino acid filter activities are correlated between interacting binding sites (Extended Data Fig. 10). Meanwhile, the learned atom-wise and amino acid-wise representations can be readily used as drop-in replacement for handcrafted features in any structure-based machine learning pipeline. A second class of applications is protein design: ScanNet, which is differentiable with respect to its inputs and does not require evolutionary information, could be used in conjunction with structure prediction tools to guide design of proteins with prescribed binding or nonbinding properties (for example, nonimmunogenic therapeutic proteins).

Finally, interpretable, end-to-end learning, combined with self-supervised learning techniques could pave the way toward a complete dictionary of function-bearing structural motifs found in nature, deepening our understanding of the core principles underlying protein function.

Methods

This section is organized as follows. The first subsection provides all mathematical and implementation details for ScanNet. The next subsection is dedicated to the baseline methods. Then the dataset construction, partition and sample weights are covered. After that, we evaluate the impact of induced fit on changes on ScanNet predictions. We then compare ScanNet to AlphaFold-multimer. The link between ScanNet prediction and binding site predictions is then covered and finally the additional results for the PPBS and BCE prediction tasks are discussed.

ScanNet network

Preprocessing

For PDB parsing, the PDB files are parsed using Biopython⁶³. We gather, for each chain, the amino acid sequence and the point cloud of heavy atoms, formally a list of triplets $\left\{({{{{\rm{coordinates}}}}}_{l},{{{{\rm{residueid}}}}}_{l},{{{{\rm{atomid}}}}}_{l})\,l\in [[1,{N}_{{{{\rm{atoms}}}}}]]\right\}$, for example, ([10.1, 101.3, −12.6], 97, CA). Only atoms belonging to classical residues are considered; exotic residues, additional molecules bound to the chain (for example, heme, ATP, glycosyl groups, ions...) are excluded.

Toward definition of a local reference frame for each atom, we reconstruct the molecular graph (that is, atom as nodes and covalent bonds as edges) using the residue and atom IDs. Each heavy atom has one, two or three neighbors on the molecular graph; if it has only one (for example, for methyl group CH₃), a virtual hydrogen atom is appended to the graph. Two neighbors are selected to define a triplet of points $(l,{i}_{{{{{\mathcal{N}}}}}_{1}(l)},{i}_{{{{{\mathcal{N}}}}}_{2}(l)})$ from which a frame can be derived. The coordinates of atoms l, ${i}_{{{{{\mathcal{N}}}}}_{1}(l)}$ and ${i}_{{{{{\mathcal{N}}}}}_{2}(l)}$ respectively define the center, xz plane and z direction, see later about the frame computation module (FCM) and equation (3). The first (‘previous’) neighbor is chosen as the closest from the N-terminal nitrogen. For the second (‘next’) neighbor, if the atom has three neighbors, the furthest from the C-terminal carbon among the remaining two is used. If both are equally far away, for example, for isoleucine, we choose the first one according to the residue ID. For instance, the two neighbors of the C atom of residue l are the C_α of the residue l and the N of the residue l + 1. The two neighbors of the C_β atom are the C_α atom and the C_γ atom of the sidechain.

Also based on the molecular graph, an attribute is assigned to each heavy atom based on its type and the number of bound hydrogens. Twelve categories are defined: C, CH, CH₂, CH₃, C_π (aromatic carbon), O, OH, N, NH, NH₂, S and SH. Overall, four atomic arrays are constructed:

• The point cloud of atoms and virtual atoms (float, size (N_atoms + N_virtualatoms, 3)).

• The triplets of indices for constructing atomic local frames (integer, size (N_atoms, 3)).

• The atom groups (integer, size (N_atoms,)).

• The residue index of each atom (integer, size (N_atoms,)).

For the amino acid level, four similar arrays are constructed. The point cloud consists of the C_α and the sidechain centers of mass (SCoM) of each amino acid. For glycines—which do not have a sidechain—a virtual SCoM is defined as ${{{{\bf{x}}}_{\mathrm{SCoM}}}}=3{{{{\bf{x}}}}}_{{{\mathrm{C}}}_{\alpha }}-{{{{\bf{x}}}}}_{{\mathrm{C}}}-{{{{\bf{x}}}}}_{{\mathrm{N}}}$, where ${{{{\bf{x}}}}}_{{C}_{\alpha }}$, x_C, x_N denote the vector coordinates of the C_α, N and C atom of the residue, respectively. The reference frame of each amino acid is defined by the C_α (center), previous C_α along the backbone (xz plane) and SCoM (z axis). Previous works^24,30 considered other amino acid frames constructed from the backbone atoms only. Here, our rationale was that neighboring amino acids located in the opposite direction from the sidechain (that is, the interior of the protein) should not matter for functionality. It also facilitates filter interpretation, as for exposed residues the sidechain points toward the exterior of the protein. We also experimented with frames constructed from consecutive C_α and found no difference performance-wise, but have not visualized the corresponding filters.

The per-residue attribute is given by the position–weight matrix (21-dimensional probability distribution, below) or the one-hot-encoded sequence for the models without evolutionary information.

For the derivation of the position–weight matrix, given the sequence, we first construct a MSA by homology search using HHblits 2 (four iterations, default values of other parameters)⁶⁴ on the UniClust30_2018_06 database⁶⁵ (except for the SARS-Cov-2 spike protein for which we used the UniRef30_2020_06). Next, a sequence dependent weight w(S) was computed so as to (1) address sampling redundancy⁶⁶ and (2) focus the alignment around the wild type (WT)⁶⁷:

$$\begin{array}{l}w(S)=\frac{1}{\,{{\mbox{Number of 90\% sequence identity homologs}}}\,}\\\qquad\quad\times \exp \left(-\frac{{D}_{{{{\rm{Hamming}}}}}(S,WT)}{{d}_{0}}\right)\,,\end{array}$$

(1)

where d₀ is adjusted such that the effective number of samples is B_eff ≡ ∑_Sw(S) = 500. If the alignment is initially too small, d₀ = ∞ is used. Focusing the alignments allows to detect local evolutionary conservation patterns as opposed to family-level conservation patterns; this is relevant as protein–protein interfaces are not always conserved at the superfamily level.

ScanNet modules

The following notations are used throughout presentation of the modules: x, global coordinates; f, frames; x^ℓ, local coordinates; a, attributes; a^ℓ, local attributes; L, size of point set; K, number of points in a neighborhood; D, dimension of coordinates; N or M, dimension of attributes and G, number of Gaussian kernels. All upper case letters are integer dimension numbers. The corresponding lower case letter denote running indices, for example, a_ln denotes the nth (n ∈ ((1, N))) attribute of the lth (l ∈ ((1, L))) point of the point cloud and ${x}_{lkd}^{\ell }$ is the dth local coordinate of the kth neighbor of point i. Bold letters denote vectors.

The attribute embedding module (AEM) applies an element-wise nonlinear transformation to the attributes a_ln of each point. Here, we used a element-wise dense layer, that is, a matrix product followed by ReLU nonlinearity for all AEM except for the initial atomic AEM, for which the input is a categorical variable and a one-hot encoding layer is applied. The equation for the AEM is written as:

$${a}_{lm}^{\prime}={{{\rm{ReLU}}}}\left[\mathop{\sum}\limits_{n}{a}_{ln}{w}_{nm}+{\theta }_{m}\right]$$

(2)

The FCM takes as input a point cloud x_ld and a set of triplets of indices (i_l1, i_l2, i_l3) and calculates, for every triplet, a frame ${f}_{ldd}^{\prime}$ of size [L, 4, 3]), constituted by the center and the three unit vectors. The equation is written as:

$$\begin{array}{ll}{{{{\bf{f}}}}}_{{{{\bf{l1}}}}}\,({{{\rm{center}}}})&={{{{\bf{x}}}}}_{{{{{\bf{i}}}}}_{{{{\bf{l1}}}}}}\\ {{{{\bf{f}}}}}_{{{{\bf{l4}}}}}\,(\,{{\mbox{z axis}}}\,)&=\frac{{{{{\bf{x}}}}}_{{{{{\bf{i}}}}}_{{{{\bf{l3}}}}}}-{{{{\bf{x}}}}}_{{{{{\bf{i}}}}}_{{{{\bf{l1}}}}}}}{| | {{{{\bf{x}}}}}_{{{{{\bf{i}}}}}_{{{{\bf{l3}}}}}}-{{{{\bf{x}}}}}_{{{{{\bf{i}}}}}_{{{{\bf{l1}}}}}}| | }\\ {{{{\bf{f}}}}}_{{{{\bf{l3}}}}}\,(\,{{\mbox{y axis}}}\,)&=\frac{{{{{\bf{f}}}}}_{{{{\bf{l4}}}}}\times ({{{{\bf{x}}}}}_{{{{{\bf{i}}}}}_{{{{\bf{l2}}}}}}-{{{{\bf{x}}}}}_{{{{{\bf{i}}}}}_{{{{\bf{l1}}}}}})}{| | {{{{\bf{f}}}}}_{{{{\bf{l4}}}}}\times ({{{{\bf{x}}}}}_{{{{{\bf{i}}}}}_{{{{\bf{l2}}}}}}-{{{{\bf{x}}}}}_{{{{{\bf{i}}}}}_{{{{\bf{l1}}}}}})| | }\\ {{{{\bf{f}}}}}_{{{{\bf{l2}}}}}\,(\,{{\mbox{x axis}}}\,)&=\frac{{{{{\bf{f}}}}}_{{{{\bf{l3}}}}}\times {{{{\bf{f}}}}}_{{{{\bf{l4}}}}}}{| | {{{{\bf{f}}}}}_{{{{\bf{l3}}}}}\times {{{{\bf{f}}}}}_{{{{\bf{l4}}}}}| | }\end{array}$$

(3)

where × denotes the cross-product. Examples of frames overlaid on a protein structure are shown in Extended Data Fig. 1a,b. The FCM has no trainable parameters.

The neighborhood computation module determines, for each point, its K closest neighbors in space (including itself), computes their local coordinates and duplicates their attributes. Its inputs are a set of frames f_lid and attributes a_ln, and outputs are the neighborhoods ${x}_{lkd}^{\ell }$, ${a}_{lkn}^{\ell }$. The nearest neighbor search is implemented naively by computing distances between all pairs of frame centers. For the atomic and amino acid neighborhoods, we use as local coordinates the three Euclidean coordinates of the second frame center in the first frame and take K = 16. For the neighborhood attention module (NAM), we take K = 32 and use five coordinates: the distance between both frame centers $\parallel {{{{\bf{f}}}}}_{l1}-{{{{\bf{f}}}}}_{l1}^{\prime}\parallel$, the dot product between the sidechain directions ${{{{\bf{f}}}}}_{{{{\bf{l4}}}}}.{{{{\bf{f}}}}}_{l4}^{\prime}$, the dot product between the sidechain directions and the center to center vectors ${{{{\bf{f}}}}}_{{{{\bf{l4}}}}}.\frac{{{{{\bf{f}}}}}_{{{{\bf{l1}}}}}^{\prime}-{{{\bf{{f}}}_{l1}}}}{\parallel {{{{\bf{f}}}}}_{{{{\bf{l1}}}}}^{\prime}-{{{{\bf{f}}}}}_{{{{\bf{l1}}}}}\parallel}$ (and symmetric) and the distance between amino acids along the sequence (clipped at ${d}_{\max }=8$). They are shown as d,ω,θ,$\theta ^{\prime}$,d_sequence in Extended Data Fig. 1c. The neighborhood computation module has no trainable parameters.

The neighborhood embedding module (NEM) is the core module of ScanNet. NEM convolves each neighborhood with a set of trainable spatio-chemical filters, akin to convolutional filters in image CNNs (Fig. 1). Its inputs are a set of K points with local coordinates ${x}_{kd}^{\ell }$ and attributes ${a}_{kn}^{\ell }$, where k ∈ [1, K], d ∈ [1, D] and n ∈ [1, N], respectively, denote neighbor, coordinate and attribute indices. NEM outputs a set of M filter activities y_m. It is parameterized using G = 32 Gaussian kernels (as in ref. ⁶⁸) and a bilinear product as follows:

$${y}_{m}={{{\rm{ReLU}}}}\left[\mathop{\sum}\limits_{k,g,n}{W}_{mgn}^{sc}{{{\mathcal{G}}}}({{{{{\mu }}}}}_{{{{\bf{g}}}}},{{{{{\Sigma }}}}}_{{{{{g}}}}},{{{{{x}}}}}_{{{{{k}}}}}){a}_{kn}+\mathop{\sum}\limits_{k,g}{W}_{mg}^{s}{{{\mathcal{G}}}}({{{{{\mu }}}}}_{{{{{g}}}}},{{{{{\Sigma }}}}}_{{{{{g}}}}},{{{{{x}}}}}_{{{{{k}}}}})+{W}_{m}^{b}\right]$$

(4)

where ${{{\mathcal{G}}}}({{{{\mu }}}},{{{{\Sigma }}}},{{{\bf{x}}}})=\exp \left[-\frac{1}{2}{({{{\bf{x}}}}-{{{{\mu }}}})}^{T}{{{{{\Sigma }}}}}^{-1}({{{\bf{x}}}}-{{{{\mu }}}})\right]$ is a Gaussian kernel of center μ and (full) covariance matrix Σ, and W^sc, W^s, W^b are trainable tensors of sizes [M,G,N], [M,G], [M,]. See a graphical sketch in Extended Data Fig. 2d. The Gaussian kernels are trainable and shared between all filters of a given layer, see the implementation in Extended Data Fig. 2e.

The above parameterization offers several advantages over other choices such as multilayer perceptrons^25,69,70 or spherical harmonics^35,71. First, it is straightforward to interpret: a filter m with large entries of the tensor W^sc for some g,n is positively activated by points having attribute n and located near the center of the Gaussian g. Similarly, the matrix W^s encodes attribute-independent spatial sensitivity and W^b is a bias vector. Second, localized filters, that is, filters detecting only one or few combinations of point/attributes can be obtained by simply enforcing sparsity of the weights W^sc and W^s via a regularization penalty. Third, the filters are guaranteed to have an almost compact support, as the Gaussian functions decay rapidly as ∥x∥ → ∞). This ensures that the diameter of the neighborhood is effectively capped irrespective of the local point density—in particular for unpacked or disordered regions. Last but not least, the Gaussian kernels can be initialized using unsupervised learning, thereby improving performance and limiting run-to-run performance variance (initialization protocol detailed below).

For the sparsity regularization, we use the following combination of cost function and norm constraint:

$$\begin{array}{ll}&{{{{\mathcal{R}}}}}_{1}^{2}({{{{{W}}}}}^{{{{\bf{sc}}}}})=\frac{{\lambda }_{1}^{2}}{2GN}\mathop{\sum}\limits_{m}{\left(\mathop{\sum}\limits_{gn}| {W}_{mgn}^{sc}| \right)}^{2}\\ &{{{{\mathcal{R}}}}}_{1}^{2}({{{{{W}}}}}^{{{{\bf{s}}}}})=\frac{{\lambda }_{1}^{2}}{2G}\mathop{\sum}\limits_{m}{\left(\mathop{\sum}\limits_{g}| {W}_{mg}^{s}| \right)}^{2}\\ &\sqrt{\mathop{\sum}\limits_{gn}{({W}_{mgn}^{sc})}^{2}}=\sqrt{\frac{G}{K}},\forall m\end{array}$$

(5)

The so-called ${L}_{1}^{2}$ regularization (as previously described in ref. ⁷²) is a variant of the L₁ regularization (${{{{\mathcal{R}}}}}_{1}({{{{{W}}}^{1}}})={\sum }_{mgn}| {W}_{mgn}^{1}|$) that promotes homogeneity of the filter sparsity values. This can be seen from the expression of the gradients, which is written as:

$$\begin{array}{ll}\frac{\partial {{{{\mathcal{R}}}}}_{1}^{2}}{\partial {W}_{mgn}^{sc}}&=\left(\frac{{\lambda }_{1}^{2}}{GN}\mathop{\sum}\limits_{gn}| {W}_{mgn}^{sc}| \right){{{\rm{sign}}}}({W}_{mgn}^{sc})\\ \frac{\partial {{{{\mathcal{R}}}}}_{1}}{\partial {W}_{mgn}^{sc}}&= {\lambda }_{1} {{{\rm{sign}}}}({W}_{mgn}^{sc})\end{array}$$

(6)

The ${L}_{1}^{2}$ regularization is effectively a L₁ regularization with a filter-dependent regularization strength: filters that are sparse (respectively not sparse) have a small (respectively large) L₁ norm, hence a small (resp. large) effective L₁ regularization strength; which in turn further relaxes or tightens the sparsity constraint. The L₂ filter norm constraint is necessary to ensure a well-defined optimization problem because of the downstream batch norm layers. Indeed, the operation ${W}_{mgn}^{1}\to {\rho }_{m}{W}_{mgn}^{1}$ leaves the final output invariant, as it is exactly compensated by the covariation of the slope of the subsequent batch norm layer through ${\alpha }_{m}\to \frac{{\alpha }_{m}}{{\rho }_{m}}$ (using notations from ref. ⁷³). Therefore, without constraint the optimum would be the asymptote ${W}_{mgn}^{1}\to 0$, α_m → ∞ with ${W}_{mgn}^{1}\times {\alpha }_{m}={W}_{mgn}^{1\star }$, the optimum weight value without any regularization. The norm value is chosen such that the filter output y_m (equation (4)) has roughly variance 1 when the attributes have variance 1.

To determine the value of the regularization penalty ${\lambda }_{1}^{2}$, we searched for a satisfying compromise between interpretability (localized filters) and classification performance. We first determined the order of magnitude of ${\lambda }_{1}^{2}$ as follows: assuming filters weights W¹ with sparse entries (a fraction p of nonzero weight, with typical weight value W), the L₂ norm is written $\parallel W{\parallel }_{2}=\sqrt{pGN}W\equiv \sqrt{G/K}$, that is,$W \sim \frac{1}{\sqrt{KNp}}$ and ${{{{\mathcal{R}}}}}_{1}^{2} \sim \frac{\lambda pGM}{2K}$. Further assuming that the regularization penalties and cross-entropy variations (about 10⁻² per site in our experiments) should approximately balance each other, and with G/K = 2, M = 128 for both atomic and amino acid filters, we find that λ ≅ 10⁻²/pM. With a target p ≅ 10⁻², we conclude that ${\lambda }_{1}^{2} \sim 1{0}^{-2}$. After experimentation, we chose ${\lambda }_{1}^{2}=2.1{0}^{-3}$ for both atomic and amino acid filters, as this value yielded the most satisfactory filter visualizations and prediction performances.

For atomic to amino acid pooling, toward calculation of residue-wise outputs, the learned atomic-scale representation must be aggregated at the amino acid scale. We recall that the constituting atoms of an amino acid may play different functional roles, hence symmetric pooling operations may not be sufficiently expressive. ScanNet instead uses a trainable multi-headed attention pooling. It is written as:

$${y}_{m}^{{{{\rm{amino}}}}\,{{{\rm{acid}}}}}=\mathop{\sum}\limits_{{{{\rm{atom}}}},n}{B}_{mn}{y}_{n}^{{{{\rm{atom}}}}}\frac{\exp \left[{\sum }_{n}{A}_{mn}{y}_{n}^{{{{\rm{atom}}}}}\right]}{{\sum }_{{{{\rm{atom}}}}}\exp \left[{\sum }_{n}{A}_{mn}{y}_{n}^{{{{\rm{atom}}}}}\right]}$$

(7)

where B, A are trainable projection and attention weighting) matrices. Equation (7) generalizes the average pooling (A_m = 0) and maximum pooling (A_m = αB_m with large α) operations. A sparsity regularization is also used for both B, A to simplify correspondence between atomic and amino acid filters.

The NAM computes spatially coherent, residue-wise output probabilities from amino acid frames and spatio-chemical filter activities. The computation is done in four stages (Extended Data Fig. 2a). First, local amino acid scale neighborhoods of size K = 32 are constructed, with graph-type local coordinates: distances, angles and sequence distances (Extended Data Fig. 1c). Second, the five-dimensional edges are projected element-wise into a single algebraic value using trainable Gaussian kernels followed by a dense layer with linear activation function. No bias is used for the dense layer, such that the edge value decays to zero as the distance increases. Third, the filter activities are projected to scalar values and locally averaged using attention-based weights. Our expression of the weighting coefficients slightly differs from the graph attention network formulation of ref. ⁴¹ as follows: each node is characterized by a trainable output feature (unnormalized binding site probability), self-attention (‘passenger’ residues should have weak self-attention), cross-attention (hotspots should have strong cross-attention) and contrast coefficients (residues can follow either the majority or the hotspot residue). The weights may also take negative values depending on the edge values. Finally, a logistic function is applied to obtain normalized probabilities. Intuitively, the purpose of the NAM is to smooth out the probabilities such that if a residue has high binding propensity, its solvent-exposed neighbors should too. To this end, the NAM learns (1) a diffusion kernel on the residue–residue graph (the algebraic edges) and (2) importance coefficients for each node.

Full architecture

A diagram showing the architecture of the network is shown in Extended Data Fig. 2b and a table listing each module with its input(s) and output(s) sizes and comments is provided as Supplementary Table. In total, the network contains 475,000 parameters, of which about 200,000 are nonzero.

Training

For initialization, for the NEMs, the Gaussian kernels were initialized by unsupervised learning; using a subset of the training set, we computed atomic and amino acid neighborhoods and fitted the spatial point density using a Gaussian mixture model (as implemented in Scikit-learn⁷⁴, best of ten runs with Kmeans++ initialization, full covariance matrix and 10⁻¹ covariance matrix regularization). For the trainable graph edges of the NAM computed from distances and angles, we initialized them as a least square parametric fit of the label autocorrelation function (normalized):

$$A({{{\rm{distance}}}},{{{\rm{angles}}}},...)=\frac{\left({\mathbb{E}}\left[{Y}_{i}{Y}_{j}| {d}_{ij}={\rm{distance}},...\right]-{\mathbb{E}}{\left[{Y}_{i}\right]}^{2}\right)}{{\mathbb{E}}\left[{Y}_{i}\right]-{\mathbb{E}}{\left[{Y}_{i}\right]}^{2}}$$

(8)

Intuitively, this initialization choice corresponds to a diffusion kernel over the residue–residue graph. All remaining weights are initialized using symmetric random distributions, see details in the Supplementary Table.

For the padding and protein serialization trick, in our implementation, ScanNet takes as input an entire protein and computes neighborhoods on-the-fly, akin to a fully convolutional segmentation network⁷⁵. Training on GPUs requires fixed size inputs but the lengths of proteins varied by almost two orders of magnitude in our dataset (Extended Data Fig. 3e). To avoid truncating large proteins or wasting most of the computational power, we used the following protein serialization trick. We choose a relatively large maximal protein length (${L}_{\max }=1024,2120$ for the PPBS and BCE datasets), concatenate several proteins into a single example and translate each protein far away from the others, such that no two proteins overlap in space. Since ScanNet exploits only local neighborhoods, the predictions for each protein are fully independent from one another. Before training or prediction, we group proteins in a greedy fashion that minimizes the unused placeholders. Proteins are first sorted by length and the largest ones are first picked; then, we pick among the remaining proteins the largest that fits into the placeholder (if any), concatenate it and continue until the placeholder is full. For the PPBS dataset, we found that about 96% of the amino acids placeholders were used, as opposed to less than 25% with naive padding. This results in a speed-up of about fourfold. Finally, we used masking layers across the network to prevent backpropagating errors for the remaining placeholders that do not contain any residue.

For optimization, the network is trained by minimizing the binary cross-entropy loss function by backpropagation using the ADAM optimizer⁷⁶. We set the maximum number of epochs to 100, the batch size to 1, the learning rate to 10⁻³ (10⁻⁴ for the transfer learning) and perform learning rate annealing and early stopping based on the validation cross-entropy; the optimal model was usually reached before ten epochs. We used batch normalization layers before each ReLU nonlinearity throughout the network to avoid vanishing gradients. Finally, regarding sample weighting, a complication of the protein serialization trick is that residues of a single example may have different sample weight as they come from different proteins. To account for this, we formally replaced the binary cross-entropy loss function and logistic nonlinearity with a categorical cross-entropy and softmax function with two output classes; training labels are multiplied by their weight so as to replicate the weighted loss function.

Regarding software and runtime, the model was implemented in Python using the following scientific computing and machine learning packages: Python v.3.6.12; numpy v.1.19.5 (ref. ⁷⁷); h5py v.2.10.0; keras v.2.2.5 (ref. ⁷⁸); tensorflow v.1.14.0 (ref. ⁷⁹); biopython v.1.78 (ref. ⁶³); numba v.0.52.0 (ref. ⁸⁰); pandas v.1.1.5; scipy v.1.5.4 (ref. ⁸¹); matplotlib v.3.3.3 and scikit-learn v.0.24.2 (ref. ⁷⁴). Training was completed in about 1–2 h using a single Nvidia V100 GPU. The inference time is dominated by the construction of the MSA and the calculation of the position–weight matrix—it is of the order of one to a few minutes depending on sequence length and MSA depth.

Baseline methods

Handcrafted features baseline

For the handcrafted features baseline, we computed for each amino acid geometric, chemical and evolutionary features as described in recent works on prediction of protein–protein/protein–antibody binding sites^{12,13,14,15,16,17,18}. The following features were computed:

• Amino acid type (one-hot encoded, 20 dimensions).

• Secondary structure type (one-hot encoded, eight dimensions); computed with DSSP⁶¹.

• Relative accessible surface area (one dimension); computed with DSSP⁶¹.

• Coordination number (one dimension), defined as the number of C_α atoms in a ball of radius 13 center around the C_α atom of the amino acid.

• Half-sphere exposure index⁸² (one dimension), defined as follows: let N₁ be the coordination number, and N₂ the number of C_α atoms in the intersection of a ball of radius 13 center and above the plane defined by the C_α − C_β vector. The half-sphere exposure index is $\frac{2{N}_{2}-{N}_{1}}{N1}\in [-1,1]$.

• Backbone and sidechain depth⁸³ (two dimensions). The molecular surface was computed using MSMS (probe radius 1.5 Å)⁸⁴, and the distance to the surface was computed and averaged for all backbone (resp. sidechain) atoms.

• Surface convexity index (three dimensions)⁸⁵. For each atom, we construct a ball of radius 5, 8 or 11 Å centered on it, and compute the f fraction of its volume located on the inside of molecular surface; the index is given by 2f − 1 ∈ (−1,−1). The surface convexity index is averaged at the amino acid level.

• Position–weight matrix (21 dimensions)

• Conservation score $C=\log 21+{\sum }_{a}\log PWM(a)$ (one dimension).

In total, 58 features were used. For classification, we used the xgboost algorithm (boosted trees)⁴⁶. The classifier was trained by cross-entropy minimization, using the same training and validation sets. We used 100 boosting rounds (with early stopping on validation loss), and the following four parameters were determined by grid search: tree depth (5,10,20), minimum child weight (5,10,50,100), γ (0.01,0.1,1.0,5.) and η (0.5, 1.0).

Structural homology baseline

Several approaches leveraging sequence and structure homology were previously developed^{5,6,7,8,9,10,10,11}, but were not readily available for large scale benchmarking, which prompted us to develop an in-house structural homology baseline method. It features three key components:

• (1) A nonredundant database of template protein chains with known binding sites. We used here as template the training set of ScanNet for a fair comparison. The template database was further clustered at the 90% (resp. 95%) sequence identity for the PPBS and BCE datasets, for speed gain purposes and to simplify alignment weighting (below).

• (2) A local pairwise structure comparison engine. Compared to sequence homology or global structural homology, local structural homology were shown to outperform other methods in terms of coverage^7,10. Here, we used MultiProt⁴⁷, an algorithm we previously developed that, given two proteins, outputs a set of local structural alignments.

• (3) An alignment weighting scheme. Typically, MultiProt always finds at least few local alignments even when there is no homology between a query and a template protein, albeit with low coverage and low sequence identity. The alignments hence must be weighted so as to give higher importance to the alignments of highest quality¹¹. Formally, for a given query protein with length L, MultiProt produces a set of R local alignments ${{{{\mathcal{A}}}}}_{r},r\in [1,R]$. Each alignment is characterized by:

  • The list of query residues included in the alignment, encoded as a binary vector:

    $$\left\{\begin{array}{ll}{a}_{r,l}=1\quad &\,{{\mbox{if residue}}}\,\,l\in [1,L]\,\,{{\mbox{in local alignment}}}\,{{{{\mathcal{A}}}}}_{r}\\ {a}_{r,l}=0\quad &\,{{\mbox{otherwise}}}\,\\ \quad \end{array}\right.$$

    (9)

  • The coverage of the local alignment: ${{{{\rm{Coverage}}}}}_{r}=\frac{1}{L}{\sum }_{l}{a}_{r,l}$

  • The average root mean square deviation (r.m.s.d.) between matching pairs of C_α atoms

  • The average sequence identity between query and template residues of the local alignment SeqID_r

Combining the alignment and the corresponding binding site labels of the templates, we define the following label alignment matrix:

$$\left\{\begin{array}{ll}{y}_{r,l}=1\quad &\,{{\mbox{if}}}\,\,{a}_{r,l}=1\,\,{{\mbox{and label of aligned template residue}}}\,=1\\ {y}_{r,l}=0\quad &\,{{\mbox{otherwise}}}\,\end{array}\right.$$

(10)

and write the predicted binding site probability as:

$${P}_{l}=\frac{{P}_{0}+\mathop{\sum }\nolimits_{r = 1}^{R}{a}_{r,l}{y}_{r,l}{e}^{{{{\mathcal{W}}}}({{{{\rm{Coverage}}}}}_{r},{{{{\rm{SeqID}}}}}_{r},{{{{\rm{r.m.s.d.}}}}}_{r})}}{1+\mathop{\sum }\nolimits_{r = 1}^{R}{a}_{r,l}{e}^{{{{\mathcal{W}}}}({{{{\rm{Coverage}}}}}_{r},{{{{\rm{SeqID}}}}}_{r},{{{{\rm{r.m.s.d.}}}}}_{r})}}$$

(11)

where ${{{\mathcal{W}}}}({{{\rm{Coverage}}}},{{{\rm{SeqID}}}},{{{\rm{r.m.s.d.}}}})$ is a trainable log-weight function and P₀ is a pseudo-count regularization term, such that P_l = P₀ if no alignment is found for a given residue. The log-weight function ${{{\mathcal{W}}}}$ is parameterized by a two-layer perceptron with 20 hidden nodes and hyperbolic tangent activation function and was trained by cross-entropy minimization on a subset of the validation set; after training, we found that ${{{\mathcal{W}}}}$ is a increasing function of both alignment coverage and sequence identity, in agreement with our intuition that high coverage/sequence identity alignments should be favored. For P₀, we use the fraction of interface residues in the train set (resp. 0.22 and 0.09 for the PPBS and BCE train sets). Note that since the labels were already defined using multiple PDB files and redundancy reduction on templates was used, there was no need to further reweight alignments by ligand diversity as described in ref. ¹¹.

As expected, the baseline performed very well when high quality homologs were available, and underperformed otherwise.

Masif-site

We used the Docker image of Masif-site as made available at https://github.com/LPDI-EPFL/masif. Masif-site predicts binding site propensity at the surface vertex level. To aggregate at the amino acid level, we followed the aggregation scheme provided for the Masif versus Sppider comparison (https://github.com/LPDI-EPFL/masif/blob/master/comparison/masif_site/masif_vs_sppider/masif_sppider_Intpred_comp.ipynb): each surface vertex was first assigned to its closest atom and corresponding amino acid and the binding site probability of an amino acid was taken as the maximum binding site probability over all its corresponding vertices. We stress that the comparison with Masif-site should be interpreted with caution, as: (1) Masif-site predicts at surface vertex level rather than amino acid level. Its residue-wise probabilities are therefore not calibrated, resulting in bad likelihood scores (Supplementary Table 2). (2) We did not retrain Masif-site because of limited computational resources and its training set used was smaller than ours. (3) Our test set overlaps with Masif-site training set, hence Masif-site should overperform on a fraction of our test set.

Discotope

We used the Discotope v.1.1 as made available at https://services.healthtech.dtu.dk/software.php. To emulate the behavior of Discotope v.2.0, which processes entire protein assemblies rather than individual protein chains⁵⁰, we fused each multi-chain antigens into a single chain, and verified on a few examples that the outputs were consistent with the ones from the Discotope v.2.0 webserver.

Data preparation

For the initial database and filtering, we use the Dockground database of protein–protein interfaces⁴⁵ (January 2020, full redundant version) as a starting point for our PPBS database. Each unique PDB chain involved in one interface or more was considered as a single example; we excluded chains with sequence length less than 10, chains involved in a protein–antibody complex (as classified in the SabDab database⁴⁹) or designed proteins (identified as having two or more of the following red flags: no UniProt ID, no known CATH class, no sequence homologs found and engineered, synthetic, designed and/or de novo appearing in chain name). We obtained 70,583 unique chains (grouped in 20,025 clusters at 95% sequence identity) from 41,466 distinct PDB files, involved in 240,506 PPIs.

The dataset covers a wide range of complex sizes, types, organism taxonomies, protein lengths (Extended Data Fig. 3a–d). For the BCEs database, we used the SabDab database (timestamp 19 April 2021, ref. ⁴⁹) and included all antigens with length of ten or more forming an interface with an antibody with both heavy and light chain appearing in the PDB files. We obtained 3,756 chains (grouped in 796 clusters at 95% sequence identity).

Regarding data partition, for the PPBS database, we investigated the impact of homology between train and test set examples on generalization of ScanNet and our baseline models. We enforced a maximum sequence identity (90%) between a val/test example and any train set example, and grouped validation and test examples into four subgroups based on their degrees of homology (Extended Data Fig. 3g):

• (1) Val/Test 70%: at least 70% sequence identity with at least one train set example.

• (2) Val/Test homology: at most 70% sequence identity with any train set example, at least one train set example belonging to same protein superfamily (H level of CATH classification⁵⁶).

• (3) Val/Test topology: at least one train set example with similar protein topology (T level of CATH classification⁵⁶), none with similar protein superfamily.

• (4) Val/Test none: none of the above.

Subgroups are ordered by decreasing degree of homology; generalization is expected to be increasingly difficult. To ensure that the four subsets have approximately equal sizes, the following partitioning algorithm was used. The chains are first iteratively clustered by sequence identity at several levels (100%, 95%, 90% seqID, 70% seqID) using CD-HIT⁸⁶ followed by clustering at homology and topology identifiers. If a 70% (resp. homology) cluster contains several distinct homology (resp. topology) categories, these categories are merged into a single one. Next, we constructed the Val/Test none by randomly drawing topology clusters and assigning all its members to either validation and test; this is repeated until Val/Test none are full. The Val/Test topology sets were constructed by randomly drawing from the remaining topology clusters with more than one homology cluster, and assigning half of the homology clusters to train and half to val/test. Similarly, the Val/Test homology and Val/Test 70% are constructed similarly by drawing homology (resp. 70%) clusters with more than one 70% (resp. 90%) sequence identity cluster, and allocating each 70% (resp. 90%) cluster to either train or val/test. Finally, the remaining 90% clusters are randomly allocated to fill the training, validation and test sets (64/16/20% split).

For the BCE, the dataset was subdivided into fivefold for cross-validation. Antigens were clustered at 70% sequence identity, and each cluster was assigned to one fold at random (except for SARS-CoV-2 antigens, which were all assigned to fold 1).

For label computation, an amino acid of a protein chain is labeled as a binding site if at least one of its heavy atoms is within 4 Å of another heavy atom from another chain within the biological assembly¹². Next, since the same protein may appear in multiple assemblies, we take the union of all its binding sites found across PDB files. This is done by clustering sequences at 95% sequence identity using CD-HIT^86,87, aligning the sequences and labels of each cluster using MAFFT⁸⁸ and propagating the labels along each column. We found that for the PPBS dataset, 91.2% of the binding sites were identified from the original PDB complex file and 8.8% were propagated from other PDB files.

For SabDab, we found that PDB epitopes appeared as accessible in one conformation of the protein and buried in another conformation; labels were propagated from one structure to another only if the residues had similar relative accessible surface area and coordination number (number of amino acids within 13 Å). The propagation criterion is written as:

$$| {{{{\rm{ASA}}}}}_{1}-{{{{\rm{ASA}}}}}_{2}| /\sigma ({{{\rm{ASA}}}})+| {{{{\rm{Coord}}}}}_{1}-{{{{\rm{Coord}}}}}_{2}| /\sigma ({{{\rm{Coord}}}}) < 0.5$$

(12)

For the PPBS, we obtained 22.7% positive labels and 30% when only considering the surface residues, with relative accessible surface ≥25% (distributions shown in Extended Data Fig. 3e,f). For the BCE, we found 8.9% positive labels.

For sample weighting and subsampling, PDB covers unevenly the protein sequence space: many protein families do not have any representative structure, whereas others such as immunoglobulins have tens of thousands. The sampling is also biased within one family, as some genes and/or organisms are more frequently studied than others. To correct for the biases occurring at multiple scales, we apply the following hierarchical reweighting scheme:

$$w=\frac{1}{\mathrm{no. } \, {{{{\mathcal{C}}}}}_{100}}\times \frac{1}{\mathrm{no. } \, \{{{{{\mathcal{C}}}}}_{100}\in {{{{\mathcal{C}}}}}_{95}\}}\times \frac{1}{ \mathrm{no. } \,\{{{{{\mathcal{C}}}}}_{95}\in {{{{\mathcal{C}}}}}_{90}\}}\times \frac{1}{ \mathrm{no. } \,\{{{{{\mathcal{C}}}}}_{90}\in {{{{\mathcal{C}}}}}_{70}\}}$$

(13)

where ${{{{\mathcal{C}}}}}_{T}$ denotes the clusters at sequence identity cutoff, T. This choice is such that each cluster at 70% sequence identity contributes a total weight 1; within each 70% cluster, each of the K 90% clusters contributes a total weight 1/K, and so on. An example of set of weights is illustrated in Extended Data Fig. 3 h.

In addition, this hierarchical choice ensures that the total weight of a cluster is invariant on subsampling at some higher cluster identity level (for example, the total weight of a 90% sequence identity cluster is invariant on subsampling at 100, 95 or 90% sequence identity). For the PPBS dataset, when hierarchical reweighting was used, we found no significant change of performance when training on the full set of chains or on 95% sequence identity representatives and therefore used the 95% sequence identity subset for speed gain purposes. When no reweighting or subsampling was used, performance significantly degraded (Table 1 and Extended Data Fig. 4). For the BCE database, the same approach was followed, without any subsampling—to include as many conformations as possible—and using a 90% sequence identity cutoff for the reweighting scheme, as similar proteins may have different epitopes.

Impact of induced fit on ScanNet predictions

Protein structures undergo induced fit (that is, conformational changes) on binding. The magnitude of conformational changes varies, ranging from minimal rearrangement of sidechain rotamers to extensive allosteric motion. ScanNet is mostly trained on bound chains but applied to unbound ones. Note, however, that for the PPBS dataset, 8.9% of the binding site residues are actually in unbound conformation, as their label was inferred from another PDB file (Data preparation). Owing to its high expressivity, it is a priori capable of picking up signature of bound conformations such as over-stretched sidechains or unpacked helixes (see, for example, 4wwx:B in Supplementary Fig. 7).

We evaluated the predictive performance of ScanNet on unbound chains for two datasets: the Dockground simulated and Dockground X-Ray⁴⁵ (available from http://dockground.compbio.ku.edu/). The Dockground simulated dataset consists of chains extracted from complex PDB files and relaxed using Langevin dynamics simulations⁸⁹. Simulating the bound protein structures separately, without the interacting partner for a short time period (1 ns), relaxes the sidechain conformations of the interface residues and reliably approximates the unbound form of the protein if conformational changes are small (<2 Å r.m.s.d.). We considered only the proteins that appeared in our dataset and excluded four tetramers, obtaining 6,012 chains. We used the binding site labels of the PPBS dataset as ground truth (18.5% positive labels).

The Dockground X-Ray consists of chains that are both crystallized alone and in complex with their partner. It features chains undergoing larger conformational changes than the simulated dataset one. We selected N = 709 (bound, unbound) pairs with at least 95% sequence identity between chains. As some complex components were multi-chains, there was no direct correspondence with our dataset labels (which included inter-domain, intra-protein binding sites); instead, we used as ground truth labels the interface residues of the complex (6.6% positive labels). The reduction in the fraction of positive labels also stems from the longer length of proteins on average (331 and 221 for X-ray and simulated, respectively).

For both datasets, we computed ScanNet predictions separately for the bound and unbound structures, excluded residues that did not match between the bound and unbound structure and compared both predictions residue-wise. Results are reported in Supplementary Table 5 and Extended Data Fig. 6. We find a good agreement between bound and unbound predictions (Pearson correlations of r = 0.86, r = 0.78 for simulated and X-ray datasets, respectively). A slight drop in accuracy between bound and unbound structures was found: from 88.3 to 86.6% for the simulated set and from 91.9 to 91.3% for the X-ray set.

To further quantify the impact of global and local conformational changes on prediction, we calculated for each chain the r.m.s.d. between the bound and unbound atomic coordinates and the r.m.s.d between the bound and unbound solvent accessible surface area. Extended Data Fig. 6e,f shows the per-chain Pearson correlation between bound and unbound predictions against the coordinate (resp. solvent accessibility) r.m.s.d. As expected, structures with larger global/local conformational changes tend to exhibit significant changes in binding site predictions. Overall, we conclude that ScanNet predictions are overall robust to conformational changes, although improvements could be obtained by training on unbound structures.

Comparison between ScanNet and AlphaFold2 binding site predictions

AlphaFold-multimer (AF2) is a recently released model for predicting the structure of protein complexes from paired MSAs⁵⁵. It is difficult to compare fairly AF2 and ScanNet, as the first one assumes knowledge of the partner and predicts partner-specific binding sites, whereas the second one does not assume knowledge of the partner and predicts partner-agnostic binding sites. We nonetheless benchmarked both approaches as follows. We considered Benchmark2, a set of 17 recently released dimers that do not appear in the training sets of AF2 and ScanNet⁹⁰. For each of the 34 chains, we determined the ground truth partner-specific binding sites (that is, involved in the complex) and partner-agnostic binding site (that is, the union of all binding sites involved in any complex found among PDB structures with 95% or more sequence identity to the chain). Next, for both ScanNet and AF2, we predicted a single set of binding sites, which was compared against the two ground truths. For AF2, we predicted the structure of the complex given the pair of sequences, obtaining five models (ColabFold implementation, no relaxation⁹¹). For each residue, the binding site probability was defined as the fraction of models in which it belongs to the interface (taking fractional values ∈ {0, 0.2, 0.4, 0.6, 0.8, 1.0}; we also tested continuous values using the predicted alignment error at contacts, but found no improvement). We assumed that the protein binding sites predicted given one known partner were representative of all the protein binding sites of the protein. Although this is not true in general, an exhaustive prediction of all complexes in which the protein is involved is not possible in practice, because not all its partners are known at inference time. Arguably for most of the UniProt proteins, not even one partner is known; this inference setup is therefore realistic and reasonably fair. For ScanNet, we predicted binding site probabilities for each chain separately (average of 11 models). The AUCPR was computed for each chain separately, and for both the partner-specific and partner-agnostic binding sites. Results are reported in Extended Data Fig. 9a–c. We found that for a partner-specific binding site, AF2 outperformed ScanNet in 27 out of 34 chains (Extended Data Fig. 9 a) whereas for partner-agnostic binding, the performances were comparable (19/34 better for AF2 and 15/34 better for ScanNet, Extended Data Fig. 8b). Generically, ScanNet outperformed AF2 when a protein had multiple binding sites, whereas AF2 outperformed ScanNet when only a single binding site was known. Other examples where ScanNet outperformed AF2 were a mammal cell surface protein (6pnq, Extended Data Fig. 8c) and a rice host-pathogen interaction (5zng) for which no paired MSA can be constructed.

For BCE prediction, we tested AF2 on the RBD of the SARS-CoV-2 spike protein as follows. We first selected six representative antibody–antigen complexes spanning all the known epitopes of the RBD, following ref. ⁵¹ (Supplementary Table 6). We then predicted their structure with AF2, obtaining 6 × 5 = 30 models. The BCE propensity was defined residue-wise as the fraction of all models in which the residue is bound by antibodies. We found that AF2 systematically predicted a single binding mode roughly corresponding to the RBD-C epitope (Extended Data Fig. 8d,e), whereas ScanNet correctly predicted multiple epitopes. We compared AF2 and ScanNet epitope propensity predictions with the empirical antibody hit rate calculated from 290 experimental structures of antibody-spike protein found in the PDB (Extended Data Fig. 8d), and found that the ScanNet profile better correlated (Spearman coefficients of 0.74 and 0.6, respectively). Allegedly, AF2 failure stems from (1) unavailability of a paired MSA, (2) low sensitivity with respect to the antibody sequence and (3) unimodal rather than multimodal prediction.

Link between ScanNet predictions and residue contribution to binding energy

Presumably, residues with high binding probability correspond to hotspots residues, that is, residues with high contribution to the binding free energy of the complexes⁴³. To test this hypothesis, we first compared ScanNet predictions to changes in binding affinity ΔΔG measured after mutation of binding residues to alanine. Positive ΔΔG indicate important residues, and hotspots are typically defined as ΔΔG > 2 kcal mol⁻¹. In the SKEMPI v.2.0 database⁹², we found 2,122 mutations of binding residues to alanine, spread across 130 complexes. We calculated for each residue its binding site probability p and aggregated attention coefficient a (defined as ∑_ia_ij where a is computed as in Extended Data Fig. 2a). The later score quantifies the importance of the residue within the neighborhood; residues with high aggregated attention drive prediction of their neighborhood. Next, we estimated the conditional average ${\mathbb{E}}\left[{{\Delta }}{{\Delta }}G| p,a\right]$ using a one-layer perceptron with 20 hidden units, hyperbolic tangent activation and nonnegative kernel weights to enforce monotonicity (Extended Data Fig. 8a,b). We indeed find that residues with high binding probability and large attention coefficient tend to be more important for binding.

We next performed a similar analysis using the Benchmark 5.5 dataset⁹³ (271 dimers, 10,444 binding sites, available from https://zlab.umassmed.edu/benchmark/) and the Rosetta REF15 all-atom energy function⁹⁴. For each dimer, the binding energy was estimated as the difference between the energy of the complex and the sum of the energies of the unbound structures. The FastRelax protocol of PyRosetta⁹⁵ was used to remove steric clashes before computation of the energies. We similarly find that residues with high binding probability and large attention coefficient tend to contribute a lower energy (Extended Data Fig. 8c,d).

In addition, Rosetta allows to calculate the contribution of individual energy terms to the residue-wise binding energy. This raises the question of whether the types of interaction involved in binding can be predicted from the intermediate layer activities of ScanNet. We grouped the 19 energy terms into eight groups: solvation (fa_sol+lk_ball_wtd+fa_intra_sol_xover4), van der Waals (fa_atr+fa_rep), Coulomb (fa_elec), backbone–sidechain hydrogen bonds (hbond_bb_sc), sidechain–sidechain hydrogen bonds (hbond_sc), sidechain internal energy (fa_intra_rep+fa_dun+yhh_planarity), backbone internal energy (omega+p_aa_pp+rama_prepro+hbond_sr_bb+hbond_lr_bb) and others (pro_close+dslf_fa13+ref).

Next, we computed for each binding residue the vector of activities of the amino acid spatio-chemical filters. We then performed a least absolute shrinkage and selection operator regression to predict residue-wise the value of each energy term from the filter activities (optimal regularization determined by cross-validation with scikit-learn⁷⁴). The regression and correlation coefficients are shown in Extended Data Fig. 8e. We find several hotspot filters associated with negative binding energies, such as filters 81, 17, 57, 41, 2 and 22 (the O-ring filter represented in the main text). As expected, they are also strongly correlated with binding (r = 0.47, 0.19, 0.12, 0.31, 0.09, 0.29, see the filter depiction in Supplementary Data 1).

Each filter displays a distinct energetic profile. For instance, filter 81 is associated with strong van der Waals binding without any cost in solvation energy; consistently, it is activated by hydrophobic residues already fully exposed in the unbound state (see filter depiction in Supplementary Data 1). The O-ring filter 22 is associated with both strong van der Waals and electrostatic energy, but at the expense of a higher solvation cost. Backbone-mediated interactions are also captured; for instance, filter 54, which corresponds to an exposed glycine/lysine tandem, is associated with strong backbone–sidechain hydrogen bonding.

Altogether, the comparative analysis with mutagenesis assays and Rosetta energy supports the claim that ScanNet learns some of the underlying physical principles of binding.

Reporting Summary

Further information on research design is available in the Nature Research Reporting Summary linked to this article.