Abstract
Superspreading events (SSEs) have characterized previous epidemics of severe acute respiratory syndrome coronavirus (SARS-CoV) and Middle East respiratory syndrome coronavirus (MERS-CoV) infections1,2,3,4,5,6. For SARS-CoV-2, the degree to which SSEs are involved in transmission remains unclear, but there is growing evidence that SSEs might be a typical feature of COVID-197,8. Using contact tracing data from 1,038 SARS-CoV-2 cases confirmed between 23 January and 28 April 2020 in Hong Kong, we identified and characterized all local clusters of infection. We identified 4–7 SSEs across 51 clusters (n = 309 cases) and estimated that 19% (95% confidence interval, 15–24%) of cases seeded 80% of all local transmission. Transmission in social settings was associated with more secondary cases than households when controlling for age (P = 0.002). Decreasing the delay between symptom onset and case confirmation did not result in fewer secondary cases (P = 0.98), although the odds that an individual being quarantined as a contact interrupted transmission was 14.4 (95% CI, 1.9–107.2). Public health authorities should focus on rapidly tracing and quarantining contacts, along with implementing restrictions targeting social settings to reduce the risk of SSEs and suppress SARS-CoV-2 transmission.
Similar content being viewed by others
Main
As of 25 August 2020 there were a total of 4,711 laboratory-confirmed cases of SARS-CoV-2 infection in Hong Kong. Since the first case was detected on 23 January, few were confirmed in Hong Kong up to 1 March, after which a substantial increase in international importations of COVID-19 cases (Fig. 1) resulted in a total ban on non-resident entry, mandatory 14-day monitored home quarantine for all resident arrivals and the implementation of various physical distancing measures9. After the number of cases began to subside, distancing measures were progressively relaxed from 8 May onward until a local resurgence of cases from 5 July brought their subsequent reintroduction (and maintenance at the time of writing).
For this study we collected information on 1,038 cases identified in Hong Kong up to 28 April. The majority (51.3%, 533/1,038) of SARS-CoV-2 infections confirmed during the study period (23 January–28 April) were associated with at least 1 of 137 clusters. Cases were linked to clusters (≥2 confirmed cases) based on the reported contact histories between cases (Methods). The median cluster size was 2 and the largest involved 106 cases (Extended Data Fig. 1). Of the cluster cases, 220 (41.3%, 220/533) belonged to 22 (22/137,16.0%) clusters initiated by another local case, compared to 89 (89/533, 16.7%) cases that belonged to 29 local clusters initiated by an imported case (29/137, 21.0%). However, most clusters were characterized as solely overseas-acquired (63.0%, 86/137) clusters and involved 224 cluster cases (42.0%, 224/533) where no onward local transmission could be identified but infection and contact between them (as family, friends or co-workers) was established overseas. Among the 505 sporadic cases not linked to any other case, 90.9% were acquired overseas (459/505), while the remaining 46 (9.1%) were sporadic cases infected locally based on recent travel histories. Overall, 31.4% (326/1,038) of all SARS-CoV-2 infections confirmed in Hong Kong during the study period were acquired within Hong Kong either within clusters or as untraceable sporadic local cases occurring through limited community transmission. Complete cluster composition is detailed in Supplementary Table 1. Of all cases confirmed in Hong Kong, 195 (18.8%, 195/1,038) were asymptomatic at confirmation (Supplementary Table 2) and, of these, most (83.1%, 162/195) were PCR-confirmed from 27 March onward (Extended Data Fig. 2).
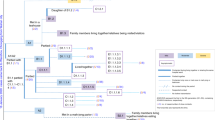
The largest cluster comprised 106 cases and was traced back to a collection of four bars across Hong Kong (Fig. 2a), but the original source could not be determined. The first cases associated with this ‘bar and band’ cluster were reported for two customers who reported exposure to a bar in Lan Kwai Fong on 7 March (onset 11 March) before two staff members from the same bar fell ill on 10 and 11 March (confirmed on 24 and 25 March, Extended Data Fig. 3). Transmission to the other three bars is suspected to have occurred via a number of musicians who performed at the four venues. The earliest onset among the musicians was on 17 March, with most subsequently infected bar cases reporting exposures between 17 and 20 March; this constitutes at least one or more probable SSE (SSE #1). Of the 73 primary bar cases, 39 customers, 20 staff and 14 musicians were infected; the remaining 33 infections were secondary, tertiary or quaternary family, work or social contacts traced to the primary cases. This single outbreak accounted for 10.2% (106/1,038) of all cases in Hong Kong during the study period, regardless of source, and 32.5% of all locally acquired SARS-CoV2 infections (106/326).
a, Transmission network of the ‘bar and band’ cluster of undetermined source (n = 106). b, Transmission network associated with a wedding without clear infector–infectee pairs but linked back to a preceding social gathering and local source (n = 22). c, Transmission network associated with a temple cluster of undetermined source (n = 19). d, All other clusters of SARS-CoV-2 infections where the source and transmission chain could be determined.
The second-largest cluster comprised a total of 22 cases and was linked to two SSEs at a wedding and a preceding social event (Fig. 2b). Ten cases (SSE #2) resulted directly (and two indirectly) from the preceding social exposure (in total 13 cases including the source case); four of these subsequently attended the wedding. Transmission between wedding attendees could not be determined, but at least seven additional infections were confirmed among other guests (SSE #3). Two additional cases were identified among family members of an infected wedding guest. The third-largest cluster totaled 19 cases and was associated with attendance at a local temple, with 12 cases directly linked (SSE #4) to exposure at the temple (Fig. 2c). The seven remaining cases (n = 7/19) were linked via secondary family exposures. The most recent case confirmed in this cluster was a monk who worked at the temple and reported no symptoms before confirmation. It is probable, but not definitive, that given the other 11 primary cases reported attending the temple over multiple days, the monk was the source of some or all of the other 11 temple cases10. All remaining local and imported SARS-CoV-2 clusters in Hong Kong, including three additional SSEs (SSE #5–7), are shown in Fig. 2d. In total we directly observed two to four SSEs (given a superspreading threshold of 6–8 secondary cases; Methods) where the sources were identified, or four to seven SSEs if including SSEs without a determined source.
Among the 533 cluster cases, all 224 solely overseas-acquired cluster cases were excluded from subsequent paired analyses due to uncertainties concerning the chain of transmission while overseas. For the remaining 309 cases within clusters initiated by a local or imported infection, 244 (244/309, 79.0%) were identified into 169 unique infector–infectee transmission pairs, with 91 unique infectors. The median serial interval (time between reported onset dates of all symptomatic infector–infectee pairs, n = 142) was 4 days (interquartile range (IQR), 3–9 days), and the mean of the fitted normal distribution was 5.8 days (Fig. 3a, Supplementary Table 3 and Extended Data Fig. 4a). Seven instances of likely pre-symptomatic transmission were observed where onset of the infectee preceded that of the infector or occurred on the same day. The ages (two-sided t-test, P = 0.18) and sex (χ2 = 0.17 P = 0.68) of the infectors and infectees were not significantly different; however, a significantly higher risk of transmission was observed between cases of similar age (P < 0.001, Extended Data Fig. 5).
a, Serial interval distribution of SARS-CoV-2 infections in Hong Kong among n = 142 symptomatic infector–infectee pairs and the fitted normal distribution. This excludes 27 asymptomatic pairs (either as infector or infectee) due to a lack of symptom onset dates. b, Observed offspring distribution of n = 91 SARS-CoV-2 infectors, n = 153 terminal infectees and n = 46 sporadic local cases in Hong Kong and corresponding fitted negative binomial distribution with parameters R = 0.58 and k = 0.43.
From the observed offspring distribution and negative binomial distribution, we estimated an overall reproductive number, R, of 0.58 (95% confidence interval (CI), 0.45–0.72) and dispersion parameter, k, of 0.43 (95% CI, 0.29–0.67) during the study period (Fig. 3b, Supplementary Table 4 and Extended Data Fig. 4b). Because not all cases could be clearly linked into infector–infectee pairs using epidemiological data alone (35/309, 11.0%), a likelihood model based on the final size of all local clusters (cluster size model) was implemented to account for any potential bias. This increased the estimate of R to 0.74 (95% CI, 0.58–0.97) and decreased k to 0.33 (95% CI, 0.14–0.98). From these estimates we inferred that 17–19% (cluster size model and observed offspring distribution, respectively) of SARS-CoV-2 infections were responsible for 80% of all transmission events in Hong Kong, while 69% of cases did not infect anyone (Supplementary Table 5).
Additional sensitivity analyses slightly increased (R = 0.62, 95% CI, 0.49–0.80) and decreased (k = 0.35, 95% CI, 0.25–0.56) the estimates of R and k, respectively (relative to the observed offspring distribution) following the addition of likely but unconfirmed infector–infectee pairs from the wedding and temple clusters to the observed offspring distribution. Here, we assumed a single wedding guest infected seven other wedding guests and the temple monk infected all 11 other primary cases (Fig. 2b,c). These scenario estimates differed again (R = 0.72, 95% CI, 0.53–0.94; k = 0.19, 95% CI, 0.13–0.26) when assuming a single musician was the source of 67 unresolved bar and band cluster cases, excluding the earlier cases preceding the musician. Given these scenarios, the expected proportion of cases responsible for 80% of all SARS-CoV-2 transmission in Hong Kong was 18% (14–23%) in the first scenario and 13% (10–17%) in the second (Supplementary Table 5).
These results, however, should be interpreted in the context of constrained community transmission given the moderate levels of physical distancing practiced in Hong Kong, including school closures, some adults working at home, cancellation of mass gatherings, as well as improved hygiene and universal mask wearing, which exceeded 98% compliance from February onward11,12. In the absence of such policies it is possible that even greater levels of superspreading could be expected. For example, findings from Shenzhen (China)13 estimated roughly comparable levels of SARS-CoV-2 overdispersion using contact tracing data (k = 0.58, 95% CI, 0.35–1.18), but a study from Singapore14 reported k = 0.11 (95% CI, 0.05–0.25). Other studies utilizing global cluster size datasets have estimated similarly high potential for SARS-CoV-2 superspreading (k = 0.10, 95% CI, 0.05–0.20), which together suggest that as few as 10% of cases could account for 80% of all SARS-CoV-2 transmission15. However, such extreme degrees of overdispersion can be advantageous to disease control efforts if interventions can effectively target the core high-risk groups or settings responsible for the majority of transmission16,17.
We observed transmission within family households most frequently (92/169, 54.4%), followed by social (56/169, 33.1%) and work (20/169, 11.8%) settings. Social settings, however, were associated with both younger cases (P = 0.026, Wilcoxon test) and more secondary cases compared to households with (P < 0.001, negative binomial regression) and without (P = 0.002) controlling for the age of individual infectors, although this was not the case for households versus work settings (Wilcoxon test, P = 0.64; regression, P = 0.92). Social venues such as bars, weddings, religious sites and restaurants, which have also been linked to an increased risk of SSE elsewhere18, therefore appear at increased risk for large outbreaks and likely constitute the core behavioral risk factor for SARS-CoV-2 SSEs. This is certainly due to the greater numbers of contacts expected in such settings; however, owing to a lack of reported numbers on confirmed contacts who tested negative, we were unable to control for this in our study. We also cannot account for any potential selection bias in our results where small family clusters are more readily traceable than smaller social clusters, which might go unrecognized, thus biasing estimates of their frequency and size. Regardless, the potential for increased transmission or SSEs within social settings is apparent, and suppression measures should therefore focus on eliminating the risk of superspreading by reducing the numbers of contacts within such settings. This could be achieved either via venue closures, reduced capacity measures/physical distancing policies and mask usage11.
Previous modeling has suggested that reduced delays between symptom onset and confirmation are important indicators in the control of SARS-CoV-2 outbreaks16. In our analysis, decreasing delays from symptom onset to confirmation did not appear to correlate with smaller local cluster sizes (Fig. 4a) unless excluding the two largest clusters (N < 20) (linear regression, F = 21.09, d.f. = 6, R2 = −0.74, two-sided P = 0.004). However, among recognized transmission pairs, there was no linear relationship between increasing delay to confirmation of infectors and more secondary cases (Fig. 4b). By contrast, for SARS-CoV in 2003, delays in individual case confirmation had an adverse effect on disease control due to increased viral shedding during the late symptomatic period, which was highest approximately seven days after symptom onset19,20,21. For COVID-19, confirmation and isolation of cases will therefore have a limited effect on reducing transmission unless done very quickly, also noting the growing body of evidence of transmission during the pre- and early symptomatic periods22,23,24. In Hong Kong, the median time from symptom onset to confirmation was four days for local cluster cases and six days for infectors and, by this time, any onward transmission may have already occurred, although this does not take into account possible self-isolation prior to confirmation.
a, Distribution and marginal density of delay in days from symptom onset to confirmation of n = 269 local cluster cases by cluster size (excludes 40 asymptomatic cluster cases without reported onset dates). Whiskers identify the minima and maxima of the delays, bounds of boxes the 75th and 25th percentiles, and the center line the median. b, Delay from symptom onset to confirmation of n = 98 symptomatic infectors (excludes two asymptomatic infectors) by the number of secondary infections and setting of contact. There is no linear relationship between an infector’s delay to confirmation and the number of secondary infections (linear regression, F < 0.001, d.f. = 96, R2 = −0.01, two-sided P = 0.98 without adjustment for multiple comparison). The center line of the regression indicates the conditional mean of the model and the shaded area the 95% CI. Note that both the number of secondary cases per infector and days from onset to confirmation are discrete integers (not continuous), but have been plotted here with a slight jitter to aid visualization.
Sequestering confirmed contacts of cases to mandatory government quarantine was very effective at terminating chains of transmission. In total, 51 local cluster cases were placed in quarantine after identification as a close contact of a confirmed case but prior to their own confirmation. This total excludes two imported cases under travel-related home quarantine. Of the 189 cases terminal to the observable chain of transmission, 45 were first placed in government quarantine as contacts (23.8%, n = 45/189). Only one quarantined contact, later confirmed as an asymptomatic case, was found to have passed on infection before sequestration (Fig. 2a,1). The odds, therefore, that a case was placed in government quarantine as a contact and terminated the chain of transmission (terminal case) was 14.4 (95% CI, 1.9–107.2, Supplementary Table 6). The most important public health measures are therefore likely to be early case identification followed by rapid and parallel (before contacts are confirmed as cases) contact tracing and quarantine (though we did not have data on the timing of contract tracing in relation to case confirmation, nor the timing of subsequent testing). Beyond such active suppression measures, intermittent physical distancing in high-risk social environments (together with mask wearing) may also be required to reduce transmission from unidentified infections and pre-symptomatic transmission, but must necessarily be balanced with the social, economic and educational costs associated with such policies. Notably, among infections acquired in Hong Kong, 14.1% (46/326) were sporadic local cases (that is, cases with neither traceable contact with another case/cluster nor a history of recent travel). This untraceable fraction could be interpreted as an upper bound on the proportion of transmission arising from anonymous interactions, fomites and/or aerosols. However, this finding may have to be restricted to the context of places similar to Hong Kong, where there is a widespread adoption of suppression measures12.
Our study has some limitations. Primarily, because this study relies on contact tracing data, any degree of incompleteness in case and/or contact ascertainment could bias our results. Given that the source of 46 sporadic local cases could not be determined, as noted above, nor the source of 22 local index cluster cases, a degree of incompleteness and therefore bias is expected. In fact, the expected difference between R (biased downward) and k (biased upward) from our observed estimates and our cluster size model (Supplementary Table 5) indicates the presence of such bias. However, the inference of R and k in our cluster size model can also be affected by bias, where R may be underestimated due to imperfect case ascertainment or overestimated when larger clusters are more readily observed than smaller clusters25. In either case, however, k is more likely to be overestimated, as imperfect observation, regardless of the cause, tends to bias estimates toward greater transmission homogeneity25. This means that the potential for SARS-CoV-2 superspreading, as already suggested, and shown elsewhere15, could be greater than our results suggest.
It is also possible that some cases may have been incorrectly attributed to clusters where the true source infection was elsewhere, such as an undetected or asymptomatic case, despite evidence of close contact. However, because there appears to be little evidence of widespread community transmission in Hong Kong during the study period (only 31.4% (326/1,038) of all confirmed cases acquired SARS-CoV-2 in Hong Kong), the risk of such an occurrence is low, albeit not zero. Interestingly, our dataset did not contain any instances of nosocomial transmission, which has been observed for SARS-CoV-226,27. It should be noted, however, that hospital infection control in Hong Kong substantially strengthened following the 2002–2003 SARS epidemic. Seroprevalence studies among frontline healthcare workers in Hong Kong will be able to confirm the effectiveness of infection control and whether any unrecognized nosocomial transmission has occurred. Future studies could also incorporate SARS-CoV-2 genetic sequence data to assist in uncovering hidden chains of transmission within the city (including within hospitals) and to discretize clusters more accurately.
Overall, there is substantial heterogeneity in the transmissibility of SARS-CoV-2 infection and therefore potential for superspreading with COVID-19. SSEs pose considerable challenges for local SARS-CoV-2 control as they can quickly overwhelm contact tracing capacity, although most infected persons will generate few or no secondary infections but a small fraction can generate many. Indeed, we observed that 19% (15–24%) of cases were responsible for 80% of all SARS-CoV-2 transmission in Hong Kong (Supplementary Table 5), while 69% (65–71%) of cases did not transmit to anyone. Assuming that local elimination is not possible, disease control efforts should focus on the rapid tracing and quarantine of confirmed contacts, along with the implementation of physical distancing policies including either closures or reduced capacity measures targeting high-risk social settings such as bars, weddings, religious sites and restaurants to prevent the occurrence of SSEs; this would have considerable effect in reducing the overall reproductive number. In lieu of an effective and widely available vaccine, these results have important implications for the control of COVID-19 and the implementation and continuation of public health measures such as physical distancing policies and lockdowns around the world (Table 1).
Methods
Characterization of clusters and chains of SARS-CoV-2 transmission
Using case line lists and contact tracing data collected in Microsoft Excel by the Centre for Health Protection (CHP) of the Department of Health in Hong Kong, we characterized clusters of SARS-CoV-2 infections and chains of transmission within clusters up to 7 May 2020. All cases of SARS-CoV-2 infection were laboratory-confirmed via nasopharyngeal swab and PCR with reverse transcription (RT-PCR). In Hong Kong, all contacts of a confirmed case are traced and sent to mandatory government quarantine facilities for 14 days if negative at identification, or admitted to hospital if testing positive, regardless of symptom presentation. A close contact was defined as someone with prolonged face-to-face interaction with a confirmed case (with or without prior symptoms) in excess of 2 h if both persons were wearing a mask or 15 min without mask usage. However, data on mask usage among cases and contacts was not provided. Quarantined contacts who test positive in quarantine are transferred and isolated in hospital, while those who test negative at the end of the quarantine period are released back into the community. For imported cases, self-isolation at home (home quarantine) was mandatory (for all returning residents) if arriving after 20 March 2020.
We defined clusters as two or more confirmed infections with reported close contact. Local clusters were characterized by the travel history of the index case as either initiated by an imported case (that is, index acquired SARS-CoV-2 infection overseas based on reported onset dates and a recent history of overseas travel given a maximum 14-day incubation period) or initiated by a local case. Clusters of solely imported cases were characterized as overseas-acquired clusters if all cases were determined to have acquired SARS-CoV-2 infection overseas as before. Cases not linked to any cluster were categorized as sporadic local cases or sporadic imported cases if infection was acquired locally or overseas, respectively.
For cases within local and imported clusters (excludes overseas clusters), probable infector–infectee transmission pairs and chains of transmission within clusters were determined from reported contact histories data provided by the CHP. Within clusters, the case with the earliest onset date was considered the source of subsequent cases where contact was confirmed within the primary cluster setting. Subsequent transmission generations and clusters settings (secondary, tertiary, quaternary and so on) were traced back to the primary cluster case based on the reported contact histories only and did not rely on symptom onset dates, meaning that instances of asymptomatic or pre-symptomatic transmission were possible from cases intermediate to the chain of transmission. In such cases, asymptomatic transmission was characterized among infector–infectee pairs where close contact was confirmed and the infector reported no symptoms before confirmation, while pre-symptomatic transmission was characterized when the difference in days between the reported symptom onset of infector–infectee pairs was a non-positive integer. Symptom presentation was screened only at detection/confirmation by a healthcare professional including retrospective self-report of onset dates. Cases within the largest clusters where the source and chain of transmission were highly uncertain were excluded from the paired analysis; however, subsequent generations of transmission where the source case could be linked to the primary setting were not excluded (for example results see Fig. 2a–c). The effect of quarantining contacts on eliminating onward transmission was determined by odds ratios given the terminal or intermediate position of the contact (later confirmed as a case) in the chain of transmission. Each transmission pair was characterized by the reported setting of contact as either family, social, work or local travel (such as on public transport).
Statistical analyses
The age and sex of unique infectors (n = 91) versus infectees (n = 169) were compared using a two-sided t-test and χ2 test, respectively. The age relationship between paired infector and infectee was assessed by linear regression (n = 169). We modeled the relationship between the number of secondary cases per infector by transmission setting using negative binomial regression with and without controlling for infector age. We used ‘family’ as the reference category while excluding ‘travel’ due to the small sample size (n = 99 unique infectors with seven infectors included more than once because they were associated with onward transmission across two or more settings but excluding one pair with transmission related to travel). Differences in the age of infectors (n = 99) by setting and all cases by setting (infectors n = 99 and infectees n = 168, excluding one infectee via travel) were assessed using non-parametric Kruskal–Wallis and Wilcoxon rank-sum tests, without adjustment for multiple comparisons. We modeled the relationship between the delay in days from symptom onset to confirmation and the number of secondary cases per infector by linear regression as a proxy for individual duration of potential infectiousness in the community (n = 98 infectors, including one travel-related infector but excluding two asymptomatic infectors whose delay could not be calculated). The mean delay from symptom onset to confirmation of 269 symptomatic cases within local clusters was also assessed by linear regression by cluster size with (10 discrete cluster sizes) and without (eight discrete cluster sizes) excluding the largest two clusters.
Serial interval and observed offspring distribution
We calculated serial intervals as the difference between the symptom onset dates of each infector–infectee pair, excluding asymptomatic cases, and fitted normal, lognormal, gamma and Weibull distributions using the R package ‘fitdistrplus’ by maximum-likelihood, excluding seven non-positive intervals for the latter three distributions. We generated the observed offspring distribution by calculating the number of secondary cases and similarly fit negative binomial, geometric and Poisson distributions as before. Cases terminal to the inferred chain of transmission and sporadic local cases were considered to have zero secondary cases. We compared each fit distribution using Akaike information criterion (AIC) scores and calculated confidence intervals for parameters from 1,000 bootstrapped replicates.
Superspreading and individual variance of SARS-CoV-2 transmission
Following the approach described by Lloyd Smith et al., estimates of the effective reproductive number (R) were determined from the mean of the negative binomial distribution fit to the observed offspring distribution, and the degree of transmission heterogeneity from the corresponding dispersion parameter k (ref. 28). This was performed for all resolved pairs within clusters, including later generation pairs where prior transmission chains could not be determined from epidemiological data alone, which were excluded from the primary analysis. Owing to potential biases affecting the observed offspring distributions resulting from these exclusions, we performed a sensitivity analysis by generated two additional offspring distributions based on presumed but unconfirmed transmission scenarios (described in the results) where evidence was indicative but insufficient to fully resolve all pairs within clusters in the primary analysis. Furthermore, we implemented a likelihood-based branching process model to jointly infer R and k based on the final size of all local clusters, where sporadic local cases were considered clusters of size one as per Kucharski and Althaus29. For a given range of values for R (0.10–3.00) and k (0.01–55), the probability that an index case generates nj clusters of size j is given by25,30
and the likelihood, assuming that the branching chains are self-limited, is
We repeated the above analyses after sub-setting the data into epochs (epoch one, January–February 2020; epoch two, March–May 2020) by illness onset date of the infector (observed offspring distribution) or the onset date of each cluster’s index case (cluster size model). Following from ref. 15, given parameters R and k, the expected proportion of cases responsible for 80% of transmission in Hong Kong is given by
where X satisfies
and
The proportion of cases responsible for 0% of transmission (that is, did not spread to anyone) was calculated from the negative binomial distributions given all calculated parameters R and k where the number of secondary cases was input as zero (x = 0). Finally, when given R0, the superspreading threshold can be calculated as the 99th percentile of the Poisson(R0) distribution28 where \(\Pr \left( {Z \le Z^{\left( {99} \right)}{\mathrm{|}}Z\sim {\mathrm{Poisson}}\left( {R_0} \right)} \right) = 0.01\). Therefore, with the global consensus of R0 in the range 2–3 (refs. 31,32), we defined the superspreading threshold for SARS-CoV-2 here as 6 to 8 secondary cases. All statistical analyses were performed in R version 3.6.1 (R Foundation for Statistical Computing). Ethics approval for this study was obtained from the Institutional Review Board of the University of Hong Kong. Data collection and analysis were part of a continuing public health outbreak investigation. Accordingly, informed consent to be included in this study was not required.
Reporting Summary
Further information on research design is available in the Nature Research Reporting Summary linked to this article.
Data availability
All anonymized data collected is publicly available at https://github.com/dcadam/covid-19-sse.
Code availability
The code used for analysis is publicly available at https://github.com/dcadam/covid-19-sse.
References
Wang, S. X. et al. The SARS outbreak in a general hospital in Tianjin, China—the case of super-spreader. Epidemiol. Infect. 134, 786–791 (2006).
Shen, Z. et al. Superspreading SARS events, Beijing, 2003. Emerg. Infect. Dis. 10, 256 (2004).
Wallinga, J. & Teunis, P. Different epidemic curves for severe acute respiratory syndrome reveal similar impacts of control measures. Am. J. Epidemiol. 160, 509–516 (2004).
Kim, K., Tandi, T., Choi, J. W., Moon, J. & Kim, M. Middle East respiratory syndrome coronavirus (MERS-CoV) outbreak in South Korea, 2015: epidemiology, characteristics and public health implications. J. Hospital Infect. 95, 207–213 (2017).
Cho, S. Y. et al. MERS-CoV outbreak following a single patient exposure in an emergency room in South Korea: an epidemiological outbreak study. Lancet 388, 994–1001 (2016).
Cowling, B. J. et al. Preliminary epidemiological assessment of MERS-CoV outbreak in South Korea, May to June 2015. Eur. Surveill. 20, 7–13 (2015).
Xu, X.-K. et al. Reconstruction of transmission pairs for novel coronavirus disease 2019 (COVID-19) in mainland China: estimation of super-spreading events, serial interval and hazard of infection. Clin. Infect. Dis. https://doi.org/10.1093/cid/ciaa790 (2020).
Ryu, S., Ali, S., Jang, C., Kim, B. & Cowling, B. Effect of nonpharmaceutical interventions on transmission of severe acute respiratory syndrome coronavirus 2, South Korea, 2020. Emerg. Infect. Dis. https://doi.org/10.3201/eid2610.201886 (2020).
Leung, G. M., Cowling, B. J. & Wu, J. T. From a sprint to a marathon in Hong Kong. N. Engl. J. Med. 382, e45 (2020).
Leung, K. S.-S. et al. A territory-wide study of early COVID-19 outbreak in Hong Kong community: a clinical, epidemiological and phylogenomic investigation. Preprint at medRxiv https://doi.org/10.1101/2020.03.30.20045740 (2020).
Cowling, B. J. et al. Impact assessment of non-pharmaceutical interventions against coronavirus disease 2019 and influenza in Hong Kong: an observational study. Lancet Public Health 5, e279–e288 (2020).
Wu, P. et al. Suppressing COVID-19 transmission in Hong Kong: an observational study of the first four months. Preprint at https://www.researchsquare.com/article/rs-34047/v1 (2020).
Bi, Q. et al. Epidemiology and transmission of COVID-19 in 391 cases and 1,286 of their close contacts in Shenzhen, China: a retrospective cohort study. Lancet Infect. Dis. 20, 911–919 (2020).
Tariq, A. et al. Real-time monitoring the transmission potential of COVID-19 in Singapore, March 2020. BMC Med. 18, 166 (2020).
Endo, A., Centre for the Mathematical Modelling of Infectious Diseases COVID-19 Working Group, Abbott, S., Kucharski, A. & Funk, S. Estimating the overdispersion in COVID-19 transmission using outbreak sizes outside China. Preprint at https://wellcomeopenresearch.org/articles/5-67 (2020).
Hellewell, J. et al. Feasibility of controlling COVID-19 outbreaks by isolation of cases and contacts. Lancet Glob. Health 8, e488–e496 (2020).
Woolhouse, M. E. et al. Heterogeneities in the transmission of infectious agents: implications for the design of control programs. Proc. Natl Acad. Sci. USA 94, 338–342 (1997).
Lu, J. et al. COVID-19 outbreak associated with air conditioning in restaurant, Guangzhou, China, 2020. Emerg. Infect. Dis. 26, 1628–1631 (2020).
Peiris, J. S. et al. Clinical progression and viral load in a community outbreak of coronavirus-associated SARS pneumonia: a prospective study. Lancet 361, 1767–1772 (2003).
Pitzer, V. E., Leung, G. M. & Lipsitch, M. Estimating variability in the transmission of severe acute respiratory syndrome to household contacts in Hong Kong, China. Am. J. Epidemiol. 166, 355–363 (2007).
Li, Y. et al. Predicting super spreading events during the 2003 severe acute respiratory syndrome epidemics in Hong Kong and Singapore. Am. J. Epidemiol. 160, 719–728 (2004).
He, X. et al. Temporal dynamics in viral shedding and transmissibility of COVID-19. Nat. Med. 26, 672–675 (2020).
Ferretti, L. et al. Quantifying SARS-CoV-2 transmission suggests epidemic control with digital contact tracing. Science 368, eabb6936 (2020).
Arons, M. M. et al. Presymptomatic SARS-CoV-2 infections and transmission in a skilled nursing facility. N. Engl. J. Med. 382, 2081–2090 (2020).
Blumberg, S. & Lloyd-Smith, J. O. Inference of R0 and transmission heterogeneity from the size distribution of stuttering chains. PLoS Comput. Biol. 9, e1002993 (2013).
Yuki, F. et al. Clusters of coronavirus disease in communities, Japan, January–April 2020. Emerg. Infect. Dis. (2020); https://doi.org/10.3201/eid2609.202272
Houlihan, C. et al. SARS-CoV-2 virus and antibodies in front-line health care workers in an acute hospital in London: preliminary results from a longitudinal study. Preprint at https://www.medrxiv.org/content/10.1101/2020.06.08.20120584v1 (2020).
Lloyd-Smith, J. O., Schreiber, S. J., Kopp, P. E. & Getz, W. M. Superspreading and the effect of individual variation on disease emergence. Nature 438, 355–439 (2005).
Kucharski, A. & Althaus, C. The role of superspreading in Middle East respiratory syndrome coronavirus (MERS-CoV) transmission. Eur. Surveill. 20, 14–18 (2015).
Nishiura, H., Yan, P., Sleeman, C. K. & Mode, C. J. Estimating the transmission potential of supercritical processes based on the final size distribution of minor outbreaks. J. Theor. Biol. 294, 48–55 (2012).
Zhao, S. et al. Preliminary estimation of the basic reproduction number of novel coronavirus (2019-nCoV) in China, from 2019 to 2020: a data-driven analysis in the early phase of the outbreak. Int. J. Infect. Dis. 92, 214–217 (2020).
Zhang, S. et al. Estimation of the reproductive number of novel coronavirus (COVID-19) and the probable outbreak size on the Diamond Princess cruise ship: a data-driven analysis. Int. J. Infect. Dis. 93, 201–204 (2020).
Acknowledgements
We thank the Department of Health of the Food and Health Bureau of the Government of Hong Kong for conducting the outbreak investigation and providing the data for the analysis. This project was supported by the Health and Medical Research Fund, Food and Health Bureau, Government of the Hong Kong Special Administrative Region (SAR; grant no. COVID190118) and the Theme-based Research Scheme (project no. T11-712/19-N) of the Research Grants Council of the Hong Kong SAR Government.
Author information
Authors and Affiliations
Contributions
The study was conceived by D.C.A. and B.J.C. Data were analyzed by D.C.A., J.Y.W., E.H.Y.L. and T.K.T. and interpreted by D.C.A., P.W., S.C., G.M.L. and B.J.C. D.C.A. wrote the first draft of the manuscript, which was revised by D.C.A., P.W., G.M.L. and B.J.C. All authors approved the final version of the manuscript.
Corresponding author
Ethics declarations
Competing interests
B.J.C. consults for Roche and Sanofi Pasteur. The authors declare no other competing interests.
Additional information
Peer review information Alison Farrell was the primary editor on this article and managed its editorial process and peer review in collaboration with the rest of the editorial team.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 SARS-CoV-2 cluster size in Hong Kong by onset date of the index case.
SARS-CoV-2 cluster size in Hong Kong by onset date of the index case. Arrow indicates the earliest onset position (2020-03-10) of the largest local SARS-CoV-2 cluster (N = 106 cases) which is excluded here for visualization purposes only. The decreasing trend in clusters size was not significant (linear regression, F = 1.25, df = 135, R2 = 0.001, p-value = 0.27). Shaded area indicates the 95% confidence interval of the regression. Final cluster sizes are plotted as integers however a slight vertical jitter is applied here also for visualization purposes.
Extended Data Fig. 2 Epidemic curve of daily SARS-CoV-2 infection in Hong Kong by symptom presentation.
Epidemic curve of daily SARS-CoV-2 infection in Hong Kong by symptom presentation. Asymptomatic cases are indexed here by detection/confirmation date otherwise illness onset date is used. (Total = 1,038; Symptomatic = 843 [81.2%]; Asymptomatic = 195 [18.8%]).
Extended Data Fig. 3 Characteristics of 106 ‘bar and band’ SARS-CoV-2 cluster cases in Hong Kong.
a, Epidemic curve of cases by onset date and transmission generation. Asymptomatic cases are included by date of confirmation. b, Age distribution of cases by generation. c, Period of symptom onset-to-confirmation and isolation of cases Asymptomatic cases are excluded due to a lack of reported onset date. *Two of the first customers described in the results with the earliest exposure dates linked to the cluster. ^Two staff at the first bar with the earliest onset and extended periods from onset to isolation. MThe first musician case who traveled between the other bars and is a potential but unconfirmed source of the remaining primary cases many of which reported exposure to the bar between the infectious period of the musician.
Extended Data Fig. 4 Characteristics of SARS-CoV-2 transmission in Hong Kong with additional fitted distributions.
a, Serial interval distribution among symptomatic SARS-CoV-2 infector-infectee pairs (n = 142) with fitted gamma (solid line), Weibull (dashed line) and lognormal (dotted) distributions. All distributions were fitted excluding observations ≤0. b, Empirical offspring distribution of n = 91 SARS-CoV-2 infectors, n = 153 terminal infectees and n = 46 sporadic local cases in Hong Kong with fitted geometric (solid – triangle) and Poisson distributions (dotted – square). Distribution parameters for a and b are shown in Supplementary Tables 3, 4.
Extended Data Fig. 5 Age comparison among and between 169 SARS-CoV-2 transmission pairs.
a, Age group distribution of infectors and infectees. The mean age difference between infectors (μ = 42.5) and infectees (μ = 46.1) was not significantly different (Two-sided t-test, t = −1.33 [−7.57, 1.49], df = 193.88, p-value = 0.18 without adjustment. Pairs were dependent only on the intermediate position in the transmission chain, so cases could be both an infector and infectee. b, Contact patterns among pairs by age group. The size of each point indicates the relative number of pairs in each combination. A significant positive trend by age group is shown (linear regression, F = 15.24, df = 156, R2 = 0.08, two=sided p-value = 0.000141 without adjustment). Shaded area indicates the 95% confidence interval of the regression. Age was missing for one case confirmed outside of Hong Kong and is excluded here.
Supplementary information
Supplementary Information
Supplementary Tables 1–6.
Rights and permissions
About this article
Cite this article
Adam, D.C., Wu, P., Wong, J.Y. et al. Clustering and superspreading potential of SARS-CoV-2 infections in Hong Kong. Nat Med 26, 1714–1719 (2020). https://doi.org/10.1038/s41591-020-1092-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41591-020-1092-0
This article is cited by
-
Transmission chains of the first local outbreak cause by Delta VariantB.1.617.2 COVID-19 in Guangzhou, Southern China
BMC Infectious Diseases (2024)
-
Evaluating completion rates of COVID-19 contact tracing surveys in New York City
BMC Public Health (2024)
-
Multidrug-resistant tuberculosis
Nature Reviews Disease Primers (2024)
-
Frequency, kinetics and determinants of viable SARS-CoV-2 in bioaerosols from ambulatory COVID-19 patients infected with the Beta, Delta or Omicron variants
Nature Communications (2024)
-
The optimisation of public health emergency governance: a simulation study based on COVID-19 pandemic control policy
Globalization and Health (2023)