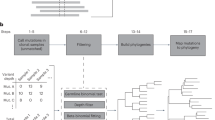
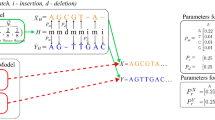
Abstract
Inferring the full genealogical history of a set of DNA sequences is a core problem in evolutionary biology, because this history encodes information about the events and forces that have influenced a species. However, current methods are limited, and the most accurate techniques are able to process no more than a hundred samples. As datasets that consist of millions of genomes are now being collected, there is a need for scalable and efficient inference methods to fully utilize these resources. Here we introduce an algorithm that is able to not only infer whole-genome histories with comparable accuracy to the state-of-the-art but also process four orders of magnitude more sequences. The approach also provides an ‘evolutionary encoding’ of the data, enabling efficient calculation of relevant statistics. We apply the method to human data from the 1000 Genomes Project, Simons Genome Diversity Project and UK Biobank, showing that the inferred genealogies are rich in biological signal and efficient to process.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout





Similar content being viewed by others
Data availability
The TGP30, SGDP31 and UKB32 datasets used here are detailed in the relevant publications. Tree sequences inferred for all TGP (https://doi.org/10.5281/zenodo.3052359) and SGDP (https://doi.org/10.5281/zenodo.3052359) autosomes have been deposited on Zenodo. Tree sequences were compressed using the tszip utility; see the documentation at https://tszip.readthedocs.io/ for further details.
Code availability
tsinfer is freely available under the terms of the GNU GPL; see the documentation at https://tsinfer.readthedocs.io/ for further details. All code used to process data and run evaluations is available at https://github.com/mcveanlab/treeseq-inference.
Change history
07 October 2019
An amendment to this paper has been published and can be accessed via a link at the top of the paper.
References
Darwin, C. Charles Darwin’s Notebooks, 1836–1844: Geology, Transmutation of Species, Metaphysical Enquiries (Cambridge Univ. Press, 1987).
Haeckel, E. Generelle Morphologie der Organismen (G. Reimer, 1866).
Hinchliff, C. E. et al. Synthesis of phylogeny and taxonomy into a comprehensive tree of life. Proc. Natl Acad. Sci. USA 112, 12764–12769 (2015).
Felsenstein, J. Inferring Phylogenies (Sinauer Associates, 2004).
Yang, Z. & Rannala, B. Molecular phylogenetics: principles and practice. Nat. Rev. Genet. 13, 303–314 (2012).
Morrison, D. A. Genealogies: pedigrees and phylogenies are reticulating networks not just divergent trees. Evol. Biol. 43, 456–473 (2016).
Ragan, M. A. Trees and networks before and after Darwin. Biol. Direct 4, 43 (2009).
Griffiths, R. C. The two-locus ancestral graph. Lect. Notes Monogr. Ser. 18, 100–117 (1991).
Griffiths, R. C. & Marjoram, P. Ancestral inference from samples of DNA sequences with recombination. J. Comput. Biol. 3, 479–502 (1996).
Minichiello, M. J. & Durbin, R. Mapping trait loci by use of inferred ancestral recombination graphs. Am. J. Hum. Genet. 79, 910–922 (2006).
Arenas, M. The importance and application of the ancestral recombination graph. Front. Genet. 4, 206 (2013).
Gusfield, D. ReCombinatorics: the Algorithmics of Ancestral Recombination Graphs and Explicit Phylogenetic Networks (MIT Press, 2014).
Rasmussen, M. D., Hubisz, M. J., Gronau, I. & Siepel, A. Genome-wide inference of ancestral recombination graphs. PLoS Genet. 10, e1004342 (2014).
Bordewich, M. & Semple, C. On the computational complexity of the rooted subtree prune and regraft distance. Ann. Comb. 8, 409–423 (2005).
Wang, L., Zhang, K. & Zhang, L. Perfect phylogenetic networks with recombination. J. Comput. Biol. 8, 69–78 (2001).
Hein, J. Reconstructing evolution of sequences subject to recombination using parsimony. Math. Biosci. 98, 185–200 (1990).
Song, Y. S. & Hein, J. Constructing minimal ancestral recombination graphs. J. Comput. Biol. 12, 147–169 (2005).
Gusfield, D., Eddhu, S. & Langley, C. Optimal, efficient reconstruction of phylogenetic networks with constrained recombination. J. Bioinform. Comput. Biol. 02, 173–213 (2004).
Gusfield, D., Bansal, V., Bafna, V. & Song, Y. S. A decomposition theory for phylogenetic networks and incompatible characters. J. Comput. Biol. 14, 1247–1272 (2007).
Kuhner, M. K., Yamato, J. & Felsenstein, J. Maximum likelihood estimation of recombination rates from population data. Genetics 156, 1393–1401 (2000).
Fearnhead, P. & Donnelly, P. Estimating recombination rates from population genetic data. Genetics 159, 1299–1318 (2001).
Song, Y. S., Wu, Y. & Gusfield, D. Efficient computation of close lower and upper bounds on the minimum number of recombinations in biological sequence evolution. Bioinformatics 21, i413–i422 (2005).
Parida, L., Melé, M., Calafell, F., Bertranpetit, J. & The Genographic Consortium Estimating the ancestral recombinations graph (ARG) as compatible networks of SNP patterns. J. Comput. Biol. 15, 1133–1153 (2008).
O’Fallon, B. D. ACG: rapid inference of population history from recombining nucleotide sequences. BMC Bioinformatics 14, 40 (2013).
Mirzaei, S. & Wu, Y. RENT+: an improved method for inferring local genealogical trees from haplotypes with recombination. Bioinformatics 33, 1021–1030 (2016).
Cardona, G., Rosselló, F. & Valiente, G. Extended Newick: it is time for a standard representation of phylogenetic networks. BMC Bioinformatics 9, 532 (2008).
McGill, J. R., Walkup, E. A. & Kuhner, M. K. GraphML specializations to codify ancestral recombinant graphs. Front. Genet. 4, 146 (2013).
Kelleher, J., Etheridge, A. M. & McVean, G. Efficient coalescent simulation and genealogical analysis for large sample sizes. PLoS Comput. Biol. 12, e1004842 (2016).
Kelleher, J., Thornton, K. R., Ashander, J. & Ralph, P. L. Efficient pedigree recording for fast population genetics simulation. PLoS Comput. Biol. 14, e1006581 (2018).
The 1000 Genomes Project Consortium A global reference for human genetic variation. Nature 526, 68–74 (2015).
Mallick, S. et al. The Simons Genome Diversity Project: 300 genomes from 142 diverse populations. Nature 538, 201–206 (2016).
Bycroft, C. et al. The UK Biobank resource with deep phenotyping and genomic data. Nature 562, 203–209 (2018).
Stephens, Z. D. et al. Big data: astronomical or genomical? PLoS Biol. 13, e1002195 (2015).
Ané, C. & Sanderson, M. J. Missing the forest for the trees: phylogenetic compression and its implications for inferring complex evolutionary histories. Syst. Biol. 54, 146–157 (2005).
Danecek, P. et al. The variant call format and vcftools. Bioinformatics 27, 2156–2158 (2011).
Durbin, R. Efficient haplotype matching and storage using the positional Burrows–Wheeler transform (PBWT). Bioinformatics 30, 1266–1272 (2014).
Pedersen, B. S. & Quinlan, A. R. cyvcf2: fast, flexible variant analysis with Python. Bioinformatics 33, 1867–1869 (2017).
Cock, P. J. A. et al. Biopython: freely available Python tools for computational molecular biology and bioinformatics. Bioinformatics 25, 1422–1423 (2009).
Li, N. & Stephens, M. Modeling linkage disequilibrium and identifying recombination hotspots using single-nucleotide polymorphism data. Genetics 165, 2213–2233 (2003).
Kendall, M. & Colijn, C. Mapping phylogenetic trees to reveal distinct patterns of evolution. Mol. Biol. Evol. 33, 2735–2743 (2016).
Shchur, V., Ziganurova, L. & Durbin, R. Fast and scalable genome-wide inference of local tree topologies from large number of haplotypes based on tree consistent PBWT data structure. Preprint at bioRxiv https://doi.org/10.1101/542035 (2019).
Speidel, L., Forest, M., Shi, S. & Myers, S. R. A method for genome-wide genealogy estimation for thousands of samples. Nat. Genet. https://doi.org/10.1038/s41588-019-0484-x (2019).
Kimura, M. & Ota, T. The age of a neutral mutant persisting in a finite population. Genetics 75, 199–212 (1973).
Griffiths, R. C. & Tavaré, S. The age of a mutation in a general coalescent tree. Stoch. Models 14, 273–295 (1998).
Ormond, L., Foll, M., Ewing, G. B., Pfeifer, S. P. & Jensen, J. D. Inferring the age of a fixed beneficial allele. Mol. Ecol. 25, 157–169 (2016).
Nakagome, S. et al. Estimating the ages of selection signals from different epochs in human history. Mol. Biol. Evol. 33, 657–669 (2016).
Smith, J., Coop, G., Stephens, M. & Novembre, J. Estimating time to the common ancestor for a beneficial allele. Mol. Biol. Evol. 35, 1003–1017 (2018).
Albers, P. K. & McVean, G. Dating genomic variants and shared ancestry in population-scale sequencing data. Preprint at bioRxiv https://doi.org/10.1101/416610 (2018).
Keightley, P. D. & Jackson, B. C. Inferring the probability of the derived vs. the ancestral allelic state at a polymorphic site. Genetics 209, 897–906 (2018).
Lunter, G. Haplotype matching in large cohorts using the Li and Stephens model. Bioinformatics 35, 798–806 (2019).
Fisher, R. A. A fuller theory of ‘junctions’ in inbreeding. Heredity 8, 187–197 (1954).
Jombart, T., Kendall, M., Almagro-Garcia, J. & Colijn, C. treespace: statistical exploration of landscapes of phylogenetic trees. Mol. Ecol. Resour. 17, 1385–1392 (2017).
Schliep, K. P. phangorn: phylogenetic analysis in R. Bioinformatics 27, 592–593 (2011).
Gutenkunst, R. N., Hernandez, R. D., Williamson, S. H. & Bustamante, C. D. Inferring the joint demographic history of multiple populations from multidimensional SNP frequency data. PLoS Genet. 5, e1000695 (2009).
Haller, B. C. & Messer, P. W. SLiM 3: forward genetic simulations beyond the Wright–Fisher model. Mol. Biol. Evol. 36, 632–637 (2019).
Haller, B. C., Galloway, J., Kelleher, J., Messer, P. W. & Ralph, P. L. Tree-sequence recording in SLiM opens new horizons for forward-time simulation of whole genomes. Mol. Ecol. Resour. 19, 552–566 (2019).
Oliphant, T. E. A guide to NumPy (Trelgol Publishing, 2006).
McKinney, W. et al. Data structures for statistical computing in Python. Proc. 9th Python in Science Conference 51–56 (2010).
Hunter, J. D. Matplotlib: a 2D graphics environment. Comput. Sci. Eng. 9, 90 (2007).
Regions in the European Union–Nomenclature of Territorial Units for Statistics–NUTS 2013/EU-28 (Eurostat, 2011).
Acknowledgements
This research was conducted by using the UK Biobank Resource under application number 12788. This work was supported by the Wellcome Trust grant 100956/Z/13/Z to G.M. A.W.W. and C.F. thank the Rhodes Trust for their support. We thank J. Novembre and P. Ralph for comments on earlier drafts of this manuscript; P. Ralph and K. Thornton for many useful discussions on tree sequence algorithms. Computation used the Oxford Biomedical Research Computing (BMRC) facility, a joint development between the Wellcome Centre for Human Genetics and the Big Data Institute supported by Health Data Research UK and the NIHR Oxford Biomedical Research Centre. The views expressed are those of the authors and not necessarily those of the NHS, the NIHR or the Department of Health.
Author information
Authors and Affiliations
Contributions
We used the CRediT taxonomy for contributions (https://casrai.org/credit). J.K.: Conceptualization, Data curation, Formal analysis, Investigation, Methodology, Resources, Software, Supervision, Validation, Visualization, Writing—original draft, Writing—review & editing. Y.W.: Conceptualization, Data curation, Formal analysis, Investigation, Methodology, Resources, Software, Supervision, Validation, Visualization, Writing—original draft, Writing—review & editing. A.W.W.: Formal analysis, Investigation, Validation, Visualization, Writing—review & editing. C.F.: Data Curation, Formal analysis, Visualization, Writing—review & editing. P.K.A.: Data curation, Resources, Visualization, Writing—review & editing. G.M.: Conceptualization, Funding acquisition, Methodology, Supervision, Writing—original draft, Writing—review & editing.
Corresponding author
Ethics declarations
Competing interests
G.M. is a shareholder in and non-executive director of Genomics PLC, and is a partner in Peptide Groove LLP. The remaining authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Note and Figs. 1–19
Rights and permissions
About this article
Cite this article
Kelleher, J., Wong, Y., Wohns, A.W. et al. Inferring whole-genome histories in large population datasets. Nat Genet 51, 1330–1338 (2019). https://doi.org/10.1038/s41588-019-0483-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41588-019-0483-y
This article is cited by
-
kalis: a modern implementation of the Li & Stephens model for local ancestry inference in R
BMC Bioinformatics (2024)
-
Strong positive selection biases identity-by-descent-based inferences of recent demography and population structure in Plasmodium falciparum
Nature Communications (2024)
-
Climate change from an ectotherm perspective: evolutionary consequences and demographic change in amphibian and reptilian populations
Biodiversity and Conservation (2024)
-
The history and organization of the Workshop on Population and Speciation Genomics
Evolution: Education and Outreach (2023)
-
Using enormous genealogies to map causal variants in space and time
Nature Genetics (2023)