Main

Cell-free RNA (cfRNA) represents a mixture of transcripts reflecting the health status of multiple tissues1, thereby affording broad clinical utility. Existing applications span oncology and bone marrow transplantation2,3, obstetrics1,4,5, neurodegeneration6 and liver disease7. However, several aspects about the physiologic origins of cfRNA, including the contributing cell types of origin, remain unknown, and current assays focus on tissue-level contributions at best1,3,4,5,6,7. Incorporating knowledge from cellular pathophysiology, which often forms the basis of disease8, into a liquid biopsy would more closely match the resolution afforded by invasive procedures.

We first characterized the landscape of cell-type-specific signal from healthy donor plasma using published exome-enriched cell-free transcriptome data6 (Fig. 1a). After removing low-quality samples (Extended Data Fig. 1 and Methods), we intersected the set of genes detected in healthy individuals (n = 75) with a database of cell-type-specific markers defined in context of the whole body9. Marker genes for blood, brain, and liver cell types were readily detected, as previously observed at tissue level1,3,4,6,7, as well as the kidney, gastrointestinal tract, and pancreas (Fig. 1b).

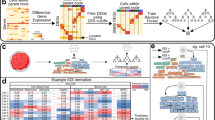
Fig. 1: Cell type decomposition of the plasma cell-free transcriptome using Tabula Sapiens.
figure 1

a, Integration of tissue of origin and single-cell transcriptomics to identify cell types of origin in cfRNA. b, Cell-type-specific markers defined in context of the human body identified in plasma cfRNA. Error bars denote the s.d. of number of cell-type-specific markers (n = 75 patients); the measure of center is the mean. CPM-TMM counts for a given gene across technical replicates were averaged before intersection. c, Cluster heat map of Spearman correlations of the cell type basis matrix column space derived from Tabula Sapiens. Color bar denotes correlation value. d, Mean fractional contributions of cell-type-specific RNA in the plasma cell-free transcriptome (n = 18 patients). e, Top tissues in cfRNA not captured by basis matrix (the set difference of all genes detected in a given cfRNA sample and the row space of the basis matrix intersection with HPA tissue-specific genes). Error bars denote the s.d. of number of HPA tissue-specific genes with NX counts >10 and cell-free CPM expression ≥ 1 (n = 18 patients); the measure of center is the mean.

Full size image

We then sought to deconvolve the fractions of cell-type-specific RNA using support vector regression, a deconvolution method previously applied to decompose bulk tissue transcriptomes into fractional cell type contributions10,11. We used Tabula Sapiens version 1.0 (TSP)12, a multiple-donor whole-body cell atlas spanning 24 tissues and organs, to define a basis matrix whose gene set accurately and simultaneously resolved the distinct cell types in TSP. The basis matrix was defined using the gene space that maximized linear independence of the cell types and does not include the whole transcriptome but rather the minimum discriminatory gene set to distinguish between the cell types in TSP. To reduce multicollinearity, transcriptionally similar cell types were grouped (Extended Data Fig. 2). We observed that the basis matrix defined by this gene set appropriately described cell types as most similar to others from the same organ compartment and corresponded to the highest off-diagonal similarity (Fig. 1c). We also confirmed that the basis matrix accurately deconvolved cell-type-specific RNA fractional contributions from several bulk tissue samples13 (Extended Data Fig. 3 and Supplementary Information).

We used this matrix to deconvolve the cell types of origin in the plasma cell-free transcriptome (Fig. 1d and Extended Data Figs. 4 and 5). Platelets, erythrocyte/erythroid progenitors and leukocytes comprised the majority of observed signal, whose respective proportions were generally consistent with recent estimates from serum cfRNA2 and plasma cfDNA14. Within this set of cell types, we suspect that the observation of platelets as a majority cell type, rather than megakaryocytes2, likely reflects annotation differences in reference data. We observed distinct transcriptional contributions from solid tissue-specific cell types from the intestine, liver, lungs, pancreas, heart, and kidney (Fig. 1d and Extended Data Fig. 4). Altogether, the observation of contributions from many non-hematopoietic cell types underscores the ability to simultaneously non-invasively resolve contributions to cfRNA from disparate cell types across the body.

Some cell types likely present in the plasma cell-free transcriptome were missing in this decomposition because the source tissues were not represented in TSP. Although, ideally, reference gene profiles for all cell types would be simultaneously considered in this decomposition, a complete reference dataset spanning the entire cell type space of the human body does not yet exist. To identify cell type contributions possibly absent from this analysis, we intersected the genes measured in cfRNA missing from the basis matrix with tissue-specific genes from the Human Protein Atlas (HPA) RNA consensus dataset15. This identified both the brain and the testis as tissues whose cell types were not found during systems-level deconvolution and additional genes specific to the blood, skeletal muscle and lymphoid tissues that were not used by the basis matrix (Fig. 1e and Methods).

As an example of how to analyze cell type contributions from tissues that were not present in TSP, we used an independent brain single-cell atlas along with HPA to define cell type gene profiles and examined their expression in cfRNA (Fig. 2a and Extended Data Figs. 6 and 7). There was a strong signature score from excitatory neurons and a reduced signature score from inhibitory neurons. We observed strong signals from astrocytes, oligodendrocytes and oligodendrocyte precursor cells. These glial cells facilitate brain homeostasis, form myelin and provide neuronal structure and support8, consistent with evidence of RNA transport across and the permeability of the blood–brain barrier16,17 and that some brain regions are in direct contact with the blood18. Similarly, we used published cell atlases for the placenta19,20, kidney21 and liver22 to define cell-type-specific gene profiles (Extended Data Figs. 6 and 8) for signature scoring. These observations augment the resolution of previously observed tissue-specific genes reported to date in cfRNA1,2,3,4,5,6,7 and formed a baseline from which to measure aberrations in disease.

Fig. 2: Cellular pathophysiology is non-invasively resolvable in cfRNA.
figure 2

For a given box plot, any cell type signature score is the sum of log-transformed CPM-TMM normalized counts. The horizontal line denotes the median; the lower hinge indicates the 25th percentile; the upper hinge indicates the 75th percentile; whiskers indicate the 1.5 interquartile range; and points outside the whiskers indicate outliers. All P values were determined by a Mann–Whitney U-test; sidedness is specified in the subplot caption. *P < 0.05, **P < 10−2, ***P < 10−4, ****P < 10−5. a, Neuronal and glial cell type signature scores in healthy cfRNA plasma (n = 18) on a logarithmic scale. b, Comparison of the proximal tubule signature score in CKD stages 3+ (n = 51 samples; nine patients) and healthy controls (n = 9 samples; three patients) (P = 9.66 × 10−3, U = 116, one sided). Dot color denotes each patient. c, Hepatocyte signature score between healthy (n = 16) and both NAFLD (n = 46) (P = 3.15 × 10−4, U = 155, one sided) and NASH (n = 163) (P = 4.68 × 10−6, U = 427, one sided); NASH versus NAFLD (P = 0.464, U = 3483, two sided). Color reflects sample collection center. d, Neuronal and glial signature scores in AD (n = 40) and NCI (n = 18) cohorts. Excitatory neuron (P = 4.94 × 10−3, U = 206, one sided), oligodendrocyte (P = 2.28 × 10−3, U = 178, two sided), oligodendrocyte progenitor (P = 2.27 × 10−2, U = 224, two sided) and astrocyte (P = 6.11 × 10−5, U = 121, two sided). Ast, astrocyte; Ex, excitatory neuron; In, inhibitory neuron; Oli, oligodendrocyte; Opc, oligodendrocyte precursor cell.

Source data

Full size image

Cell-type-specific changes drive disease etiology8, and we asked whether cfRNA reflected cellular pathophysiology. We considered trophoblasts in preeclampsia23,24, proximal tubules in chronic kidney disease (CKD)25,26, hepatocytes in non-alcoholic steatohepatitis (NASH)/non-alcoholic fatty liver disease (NAFLD)27 and multiple brain cell types in Alzheimer’s disease (AD)28,29. As an example of why whole-body cell type characterization is relevant, we observed that a previous attempt to infer trophoblast cell types from cfRNA in preeclampsia24 used genes that are not specific or readily measurable within their asserted cell type (Extended Data Fig. 9 and Supplementary Information). However, we found several other cases where cellular pathophysiology can be measured in cfRNA.

The proximal tubule is a highly metabolic, predominant kidney cell type and is a major source for injury and disease progression in CKD25,26. Tubular atrophy is a hallmark of CKD nearly independent of disease etiology30 and is superior to clinical gold standard as a predictor of CKD progression31. Using data from Ibarra et al., we discovered a striking decrease in the proximal tubule cell signature score of patients with CKD (ages 67–91 years, CKD stage 3–5 or peritoneal dialysis) compared to healthy controls (Fig. 2b and Extended Data Fig. 10a,b). These results demonstrate non-invasive resolution of proximal tubule deterioration observed in CKD histology31 and are consistent with findings from invasive biopsy.

Hepatocyte steatosis is a histologic hallmark of NASH and NAFLD phenotypes, whereby the accumulation of cellular stressors results in hepatocyte death27. We found that several genes differentially expressed in NAFLD serum cfRNA7 were specific to the hepatocyte cell type profile derived above (P < 10−10, hypergeometric test). Notable hepatocyte-specific differentially expressed genes (DEGs) include genes encoding cytochrome P450 enzymes (including CYP1A2, CYP2E1 and CYP3A4), lipid secretion (MTTP) and hepatokines (AHSG and LECT2)32. We further observed striking differences in the hepatocyte signature score between healthy and both NAFLD and NASH cohorts and no difference between the NASH and NAFLD cohorts (Fig. 2c and Extended Data Fig. 10).

AD pathogenesis results in neuronal death and synaptic loss29. We used brain single-cell data28 to define brain cell type gene profiles in both the AD and the normal brain. Several DEGs found in cfRNA analysis of AD plasma are brain cell type specific (P < 10−5, hypergeometric test). Astrocyte-specific genes include those that encode filament protein (GFAP33) and ion channels (GRIN2C28). Excitatory neuron-specific genes encode solute carrier proteins (SLC17A728) and SLC8A234), cadherin proteins (CDH835 and CDH2236) and a glutamate receptor (GRM129,37). Oligodendrocyte-specific genes encode proteins for myelin sheath stabilization (MOBP29) and a synaptic/axonal membrane protein (CNTN229). Oligodendrocyte-precursor-cell-specific genes encode transcription factors (OLIG238 and MYT139), neural growth and differentiation factor (CSPG540) and a protein putatively involved in brain extracellular matrix formation (BCAN41).

We then inferred neuronal death in plasma cfRNA between AD and healthy non-cognitive controls (NCIs) and also observed differences in oligodendrocyte, oligodendrocyte progenitor and astrocyte signature scores (Fig. 2d and Extended Data Fig. 10). The oligodendrocyte and oligodendrocyte progenitor cells signature score directionality agrees with reports of their death and inhibited proliferation in AD, respectively42. The observed astrocyte signature score directionality is consistent with the cell type specificity of a subset of reported downregulated DEGs6 and reflects that astrocyte-specific changes, which are known in AD pathology42, are non-invasively measurable.

Taken together, this work demonstrates consistent non-invasive detection of cell-type-specific changes in human health and disease using cfRNA. Our findings uphold and further augment the scope of previous work identifying immune cell types2 and hematopoietic tissues1,2 as primary contributors to the cell-free transcriptome cell type landscape. Our approach is complementary to previous work using cell-free nucleosomes14, which depends on a more limited set of reference chromatin immunoprecipitation sequencing data, which are largely at the tissue level43. Readily measurable cell types include those specific to the brain, lung, intestine, liver, and kidney, whose pathophysiology affords broad prognostic and clinical importance. Consistent detection of cell types responsible for drug metabolism (for example, liver and renal cell types) as well as cell types that are drug targets, such as neurons or oligodendrocytes for Alzheimer’s-protective drugs, could provide strong clinical trial endpoint data when evaluating drug toxicity and efficacy. We anticipate that the ability to non-invasively resolve cell type signatures in plasma cfRNA will both enhance existing clinical knowledge and enable increased resolution in monitoring disease progression and drug response.

Methods

Data processing

Data acquisition

cfRNA: For samples from Ibarra et al. (PRJNA517339), Toden et al. (PRJNA574438) and Chalasani et al. (PRJNA701722), raw sequencing data were obtained from the Sequence Read Archive with the respective accession numbers. For samples from Munchel et al., processed counts tables were directly downloaded.

For all individual tissue single-cell atlases, Seurat objects or AnnData objects were downloaded or directly received from the authors. Data from Mathys et al. were downloaded with permission from Synapse. The liver Seurat object was requested from Aizarani et al. For the placenta cell atlases, a Seurat object was requested from Suryawanshi et al., and AnnData was requested from Vento-Tormo et al. Kidney AnnData were downloaded (https://www.kidneycellatlas.org, Mature Full dataset).

HPA version 19 transcriptomic data, Genotype-Tissue Expression (GTEx) version 8 raw counts and Tabula Sapiens version 1.0 were downloaded directly.

Bioinformatic processing

All analyses were performed using Python (version 3.6.0) and R (version 3.6.1) For each sample for which raw sequencing data were downloaded, we trimmed reads using trimmomatic (version 0.36) and then mapped them to the human reference genome (hg38) with STAR (version 2.7.3a). Duplicate reads were then marked and removed by the MarkDuplicates tool in GATK (version 4.1.1). Finally, mapped reads were quantified using htseq-count (version 0.11.1), and read statistics were estimated using FastQC (version 0.11.8).

The bioinformatic pipeline was managed using snakemake (version 5.8.1). Read and tool performance statistics were aggregated using MultiQC (version 1.7).

Sample quality filtering

For every sample for which raw sequencing data were available, we estimated three quality parameters as previously described44,45: RNA degradation, ribosomal read fraction and DNA contamination.

RNA degradation was estimated by calculating a 3′ bias ratio. Specifically, we first counted the number of reads per exon and then annotated each exon with its corresponding gene ID and exon number using htseq-count. Using these annotations, we measured the frequency of genes for which all reads mapped exclusively to the 3′-most exon as compared to the total number of genes detected. We approximated RNA degradation for a given sample as the fraction of genes where all reads mapped to the 3′-most exon.

To estimate ribosomal read fraction, we compared the number of reads that mapped to the ribosome (region GL00220.1:105,424–118,780, hg38) relative to the total number of reads (SAMtools view).

To estimate DNA contamination, we used an intron-to-exon ratio and quantified the number of reads that mapped to intronic as compared to exonic regions of the genome.

We applied the following thresholds as previously reported44:

  • Ribosomal: >0.2

  • 3′ Bias Fraction: >0.4

  • DNA Contamination: >3

We considered any given sample as low quality if its value for any metric was greater than any of these thresholds, and we excluded the sample from subsequent analysis.

Data normalization

All gene counts were adjusted to counts per million (CPM) reads and per milliliter of plasma used. For a given sample, i denotes gene index, and j denotes sample index:

$$\eta _{ij} = \frac{{\mathrm{Gene}_{ij}}}{{({\mathrm{Library}}\,{\mathrm{size}}_j) \times ({\rm{mL}}\,{\mathrm{plasma}}_j)}}\,{{{\mathrm{where}}}}\,{\mathrm{Library}}\,{\mathrm{size}}_j = \mathop {\sum}\limits_i {G_{ij}}$$
(1)

For individuals who had samples with multiple technical replicates, these plasma volume CPM counts were averaged before nu support vector regression (nu-SVR) deconvolution.

For all analyses except nu-SVR (all work except Fig. 1d,e), we next applied trimmed mean of M values (TMM) normalization as previously described46 using edgeR (version 3.28.1):

$$\frac{{\eta _{ij}}}{{TMM_j}}$$
(2)

CPM-TMM normalized gene counts across technical replicates for a given biological replicate were averaged for the count tables used in all analyses performed.

Sequencing batches and plasma volumes were obtained from the authors in Toden et al. and Chalasani et al. for per-sample normalization. For samples from Ibarra et al., plasma volume was assumed to be constant at 1 ml, as we were unable to obtain this information from the authors; sequencing batches were confirmed with the authors (personal communication). All samples from Munchel et al. were used to compute TMM scaling factors, and 4.5 ml of plasma5 was used to normalize all samples within a given dataset (both PEARL-PEC and iPEC).

Cell type marker identification using PanglaoDB

The PanglaoDB cell type marker database was downloaded on 27 March 2020. Markers were filtered for human (‘Hs’) only and for PanglaoDB’s defined specificity (how often marker was not expressed in a given cell type) and sensitivity (how frequently marker is expressed in cells of this type). Gene synonyms from Panglao were determined using MyGene version 3.1.0 to ensure full gene space.

We then intersected this gene space with a cohort of healthy cfRNA samples (n = 75, NCI individuals from Toden et al.). A given cell type marker was counted in a given healthy cfRNA sample if its gene expression was greater than zero in log +1 transformed CPM-TMM gene count space.

Cell types with markers filtered by sensitivity = 0.9 and specificity = 0.2 and samples with >5 cell type markers on average are shown in Fig. 1b.

Basis matrix formation

Scanpy47 (version 1.6.0) was used. Only cells from droplet sequencing (‘10x’) were used in analysis given that a more comprehensive set of unique cell types across the tissues in Tabula Sapiens was available12. Disassociation genes as reported12 were eliminated from the gene space before subsequent analysis.

Given the non-specificity of the following annotations (for example, other cell type annotations at finer resolution existed), cells with these annotations were excluded from subsequent analysis:

  • ‘epithelial cell’

  • ‘ocular surface cell’

  • ‘radial glial cell’

  • ‘lacrimal gland functional unit cell’

  • ‘connective tissue cell’

  • ‘corneal keratocyte’

  • ‘ciliary body’

  • ‘bronchial smooth muscle cell’

  • ‘fast muscle cell’

  • ‘muscle cell’

  • ‘myometrial cell’

  • ‘skeletal muscle satellite stem cell’

  • ‘slow muscle cell’

  • ‘tongue muscle cell’

  • ‘vascular associated smooth muscle cell’

  • ‘alveolar fibroblast’

  • ‘fibroblast of breast’

  • ‘fibroblast of cardiac tissue’

  • ‘myofibroblast cell’

All additional cells belonging to the ‘Eye’ tissue were excluded from subsequent analysis given discrepancies in compartment and cell type annotations and the unlikelihood of detecting eye-specific cell types. The resulting cell type space still possessed several transcriptionally similar cell types (for example, various intestinal enterocytes, T cells or dendritic cells), which, left unaddressed, would reduce the linear independence of the basis matrix column space and, hence, would affect nu-SVR deconvolution.

Cells were, therefore, assigned broader annotations on a per-compartment basis as follows:

Epithelial, Stromal, Endothelial: Using counts from the ‘decontXcounts’ layer of the adata object, cells were CPM normalized (sc.pp.normalize_total(target_sum = 1 × 106)) and log-transformed (sc.pp.log1p). Hierarchical clustering with complete linkage (sc.tl.dendrogram) was performed per compartment on the feature space comprising the first 50 principal components (sc.pp.pca). Epithelial and stromal compartment dendrograms were then cut (scipy.cluster.hierarchy.cut_tree) at 20% and 10% of the height of the highest node, respectively, such that cell types with high transcriptional similarity were grouped together, but overall granularity of the cell type labels was preserved. This work is available in the script ‘treecutter.ipynb’ on GitHub; the scipy version used is 1.5.1.

The endothelial compartment dendrogram revealed high transcriptional similarity across all cell types (maximum node height = 0.851) compared to epithelial (maximum node height = 3.78) and stromal (maximum node height = 2.34) compartments (Extended Data Fig. 2). To this end, only the ‘endothelial cell’ annotation was used for the ‘endothelial’ compartment.

Immune: Given the high transcriptional similarity and the varying degree of annotation granularity across tissues and cell types, cell types were grouped on the basis of annotation. The following immune annotations were kept:

  • ‘b cell’

  • ‘basophil’

  • ‘erythrocyte’

  • ‘erythroid progenitor’

  • ‘hematopoietic stem cell’

  • ‘innate lymphoid cell’

  • ‘macrophage’

  • ‘mast cell’

  • ‘mature conventional dendritic cell’

  • ‘microglial cell’

  • ‘monocyte’

  • ‘myeloid progenitor’

  • ‘neutrophil’

  • ‘nk cell’

  • ‘plasma cell’

  • ‘plasmablast’

  • ‘platelet’

  • ‘t cell’

  • ‘thymocyte’

All other immune compartment cell type annotations were excluded for being too broad when more detailed annotations existed (that is, ‘granulocyte’, ‘leucocyte’ and ‘immune cell’) or present in only one tissue (that is, ‘erythroid lineage cell’; eye, ‘myeloid cell’; and pancreas/prostate). The ‘erythrocyte’ and ‘erythroid progenitor’ annotations were further grouped to minimize multicollinearity.

Using the entire cell type space spanning all four organ compartments, either 30 observations (for example, measured cells) were randomly sampled or the maximum number of available observations (if less than 30) was subsampled, whichever was greater.

Cell type annotations were then reassigned based on the ‘broader’ categories from hierarchical clustering (‘coarsegrain.py’). Raw count values from the DecontX adjusted layer were used to minimize signal spread contamination that could affect DEG analysis12.

This subsampled counts matrix was then passed to the ‘Create Signature Matrix’ analysis module at https://cibersortx.stanford.edu/, with the following parameters:

  • Disable quantile normalization = True

  • Minimum expression = 0.25

  • Replicates = 5

  • Sampling = 0.5

  • Kappa = 999

  • q value = 0.01

  • No. of barcode genes = 3,000–5,000

  • Filter non-hematopoietic genes = False

The resulting basis matrix was used in our nu-SVR deconvolution code, available on GitHub, under the name ‘tsp_v1_basisMatrix.txt’.

Abbreviations (left) of grouped cell types (right) in Fig. 1d and the Extended Data are as follows:

  • gland cell: ‘acinar cell of salivary gland/myoepithelial cell’

  • respiratory ciliated cell: ‘ciliated cell/lung ciliated cell’

  • prostate epithelia: ‘club cell of prostate epithelium/hillock cell of prostate epithelium/hillock-club cell of prostate epithelium’

  • salivary/bronchial secretory cell: ‘duct epithelial cell/serous cell of epithelium of bronchus’

  • intestinal enterocyte: ‘enterocyte of epithelium of large intestine/enterocyte of epithelium of small intestine/intestinal crypt stem cell of large intestine/large intestine goblet cell/mature enterocyte/paneth cell of epithelium of large intestine/small intestine goblet cell’

  • intestinal crypt stem cell: ‘immature enterocyte/intestinal crypt stem cell/intestinal crypt stem cell of small intestine/transit amplifying cell of large intestine’

  • erythrocyte/erythroid progenitor: ‘erythrocyte/erythroid progenitor’

  • fibroblast/mesenchymal stem cell: ‘fibroblast/mesenchymal stem cell’

  • intestinal secretory cell: ‘intestinal enteroendocrine cell/paneth cell of epithelium of small intestine/transit amplifying cell of small intestine’

  • ionocyte/luminal epithelial cell of mammary gland: ‘ionocyte/luminal epithelial cell of mammary gland’

  • secretory cell: ‘mucus secreting cell/secretory cell/tracheal goblet cell’

  • pancreatic alpha/beta cell: ‘pancreatic alpha cell/pancreatic beta cell’

  • respiratory secretory cell: ‘respiratory goblet cell/respiratory mucous cell/serous cell of epithelium of trachea’

  • basal prostate cell: ‘basal cell of prostate epithelia’

Nu-SVR deconvolution

We formulated the cell-free transcriptome as a linear summation of the cell types from which it originates1,48. With this formulation, we adapted existing deconvolution methods developed with the objective of decomposing a bulk tissue sample into its single-cell constituents10,11, where the deconvolution problem is formulated as:

$$A\theta = b$$
(3)

Here, A is the representative basis matrix (g × c) of g genes for c cell types, which represent the gene expression profiles of the c cell types. θ is a vector (c × 1) of the contributions of each of the cell types, and b is the measured expression of the genes observed in blood plasma (g × 1). The goal here is to learn θ such that the matrix product Aθ predicts the measured signal b. The derivation of the basis matrix A is described in the section ‘Basis matrix formation’.

We performed nu-SVR using a linear kernel to learn θ from a subset of genes from the basis matrix to best recapitulate the observed signal b, where nu corresponds to a lower bound on the fraction of support vectors and an upper bound on the fraction of margin errors49. Here, the support vectors are the genes from the basis matrix used to learn θ; θ reflects the learned weights of the cell types in the basis matrix column space. For each sample, a set of θ was learned by performing a grid search on the two SVR hyperparameters: \(\nu \in \{ 0.05,0.1,0.15,0.25,0.5,0.75\}\) and \(C \in \{ 0.1,0.5,0.75,1,10\}\).

For each sample, we next enforce two constraints: θ can contain only non-negative weights, and the weights in θ must sum to 1. Each θ corresponding to a hyperparameter combination was normalized as previously described in two steps10,11. First, only non-negative weights were kept:

$$\forall \theta _j < 0 \in \left\{ {\theta _1, \ldots ,\theta _c} \right\} \to 0$$
(4)

Second, the remaining non-zero weights were then normalized by their sum to yield the relative proportions of cell-type-specific RNA.

We then determined the basis matrix dot product with the set of normalized weights for each sample. This dot product yields the predicted expression value for each gene in a given cfRNA mixture with imposed non-negativity on the normalized coefficient vector. The root mean square error (RMSE) was then computed using the predicted expression values and the measured values of these genes for each hyperparameter combination in a given cfRNA mixture. The model yielding the smallest RMSE in predicting expression for a given cfRNA sample was then chosen and assigned as the final deconvolution result for a given sample.

Only CPM counts ≥1 were considered in the mixture, b. The values in the basis matrix were also CPM normalized. Before deconvolution, the mixture and basis matrix were centered and scaled to zero mean and unit variance for improved runtime performance. We emphasize that we did not log-transform counts in b or in A, as this would destroy the requisite linearity assumption in equation (3). Specifically, the concavity of the log function would result in the consistent underestimation of θ during deconvolution50.

We used the function nu-SVR from scikitlearn51 version 0.23.2.

The samples used for nu-SVR deconvolution were 75 NCI patients from Toden et al. spanning four sample collection centers. Given center-specific batch effects reported by Toden et al., we report our results on a per-center basis (Fig. 1d and Extended Data Figs. 4 and 5). There was good pairwise similarity of the learned coefficients among biological replicates within and across sample centers (Extended Data Fig. 5a,b). Deconvolution performance yielded RMSE and Pearson r consistent with deconvolved GTEx tissues (Extended Data Fig. 3) whose distinct cell types were in the basis matrix column space (Extended Data Fig. 5c,d). In interpreting the resulting cell type fractions, a limitation of nu-SVR is that it uses highly expressed genes as support vectors and, consequently, assigns a reduced fractional contribution to cell types expressing genes at lower levels or that are smaller in cell volume. Comparison of nu-SVR to quadratic programming1 and non-negative linear least squares52 yielded similar deconvolution RMSE and Pearson correlation. In contrast to the other methods, nu-SVR cell type contributions were the most consistent with the cell type markers detected using PanglaoDB and was, hence, chosen as the deconvolution model for this work.

Evaluating basis matrix on GTEx samples

Bulk RNA sequencing samples from GTEx version 8 were deconvolved with the derived basis matrix from tissues that were present (that is, kidney cortex, whole blood, lung and spleen) or absent (for example, kidney medulla and brain) from the basis matrix derived using Tabula Sapiens version 1.0. For each tissue type, the maximum number of available samples or 30 samples, whichever was smaller, was deconvolved. See Supplementary Note 1 for additional discussion.

Identifying tissue-specific genes in cfRNA absent from basis matrix

To identify cell-type-specific genes in cfRNA that were distinct to a given tissue, we considered the set difference of the non-zero genes measured in a given cfRNA sample with the row space of the basis matrix and intersected this with HPA tissue-specific genes:

$$(G_j - R) \cap HPA$$
(5)

where Gj is the gene set in the jth deconvolved sample, where a given gene in the set’s expression was ≥1 CPM. R is the set of genes in the row space of the basis matrix used for nu-SVR deconvolution. HPA denotes the total set of tissue-specific genes from HPA.

The HPA tissue-specific gene set (HPA) comprised genes across all tissues with Tissue Specificity assignments ‘Group Enriched’, ‘Tissue Enhanced’, ‘Tissue Enriched’ and NX expression ≥10. This approach yielded tissues with several distinct genes present in cfRNA, which could then be subsequently interrogated using single-cell data.

Derivation of cell-type-specific gene profiles in context of the whole body using single-cell data

For this analysis, only cell types unique to a given tissue (that is, hepatocytes unique to the liver or excitatory neurons unique to the brain) were considered so that bulk transcriptomic data could be used to ensure specificity in context of the whole body. A gene was asserted to be cell type specific if it was (1) differentially expressed within a given single-cell tissue atlas, (2) possessed a Gini coefficient ≥0.6 and was listed as specific to the native tissue for the cell type of interest, indicating comprehensive tissue specificity in context of the whole body (Extended Data Figs. 6 and 8).

  1. (1)

    Single-cell differential expression

    For data received as a Seurat object, conversion to AnnData (version 0.7.4) was performed by saving as an intermediate loom object (Seurat version 3.1.5) and converting to AnnData (loompy version 3.0.6). Scanpy (version 1.6.0) was used for all other single-cell analysis. Reads per cell were normalized for library size (scanpy normalize_total, target_sum = 1 × 104) and then logged (scanpy log1p). Differential expression was performed using the Wilcoxon rank-sum test in Scanpy’s filter_rank_genes_groups with the following arguments: min_fold_change = 1.5, min_in_group_fraction = 0.2, max_out_group_fraction = 0.5, corr_method = ‘benjamini-hochberg’. The set of resulting DEGs with Benjamini–Hochberg-adjusted P values <0.01 whose ratio of the highest out-group percent expressed to in-group percent expressed <0.5 was selected to ensure high specific expression in the cell type of interest within a given cell type atlas.

  2. (2)

    Quantifying comprehensive whole-body tissue specificity using the Gini coefficient

    The distribution of all the Gini coefficiets and Tau values across all genes belonging to cell type gene profiles for cell types native to a given tissue were compared using the HPA gene expression Tissue Specificity and Tissue Distribution assignments15 (Extended Data Fig. 7). The Gini coefficient better reflected the underlying distribution of gene expression tissue specificity than Tau (Extended Data Fig. 7) and, hence, were used for subsequent analysis. As the Gini coefficient approaches unity, this indicates extreme gene expression inequality or equivalently high specificity. A single threshold (Gini coefficient ≥ 0.6) was applied across all atlases to facilitate a generalizable framework from which to define tissue-specific cell type gene profiles in context of the whole body in a principled fashion for signature scoring in cfRNA.

    For the following definitions, n denotes the total number of tissues, and xj is the expression of a given gene in the ith tissue.

    The Gini coefficient was computed as defined53:

    $${\mathrm{Gini}} = \frac{{n + 1}}{n} - \frac{{2{\mathop \sum \nolimits_{i = 1}^{n}}\left( {n + 1 - i} \right){x_i}}}{{n{\mathop \sum \nolimits_{i = 1}^{n}}{x_i}}}\, ;\: {x_i}\, {\mathrm{is}}\, {\mathrm{ordered}}\, {\mathrm{from}}\, {\mathrm{least}}\, {\mathrm{to}}\, {\mathrm{greatest}}.$$
    (6)

    Tau, as defined in ref. 53:

    $$\tau = \frac{{\mathop {\sum }\nolimits_{i = 1}^n 1 - \bar x}}{{n - 1}}\ {{{\mathrm{where}}}}\,\bar x = \frac{{x_i}}{{{{{\mathrm{max}}}}\left( {x_i} \right)\forall i \in \{ 1 \ldots n\} }}$$
    (7)

    HPA NX Counts from the HPA object titled ‘rna_tissue_consensus.tsv’ accessed on 1 July 2019 were used for computing Gini coefficients and Tau.

    Note for brain cell type gene profiles: Given that there are multiple sub brain regions in the HPA data, the determined Gini coefficients are lower (for example, not as close to unity compared to other cell type gene profiles) because there are multiple regions of the brain with high expression, which would result in reduced count inequality.

Gene expression in GTEx

We confirmed the specificity of a given gene profile to its corresponding cell type by comparing the aggregate expression of a given cell type signature in its native tissue compared to that of the average across remaining GTEx tissues (Extended Data Figs. 6d and 8f,g). We uniformly observed a median fold change greater than 1 in the signature score of a cell type gene profile in its native tissue relative to the mean expression in other tissues, confirming high specificity.

Raw GTEx data version 8 (accessed 26 August 2019) were converted to log(counts-per-ten-thousand + 1) counts. The signature score was determined by summing the expression of the genes in a given bulk RNA sample for a given cell type gene profile. Because only gene profiles were derived for cell types that correspond to a given tissue, the mean signature score of a cell type profile across the non-native tissues was then computed and used to determine the log fold change.

Cell type specificity of DEGs in AD and NAFLD cfRNA

After observing a significant intersection between the DEGs in AD6 or NAFLD7 in cfRNA with corresponding cell-type-specific genes (Extended Data Fig. 10c,e), we then assessed the cell type specificity of DEGs using a permutation test. To assess whether DEGs that intersected with a cell type gene profile were more specific to a given cell type than DEGs that were generally tissue specific, we performed a permutation test. Specifically, we compared the Gini coefficient for genes in these two groups, computed using the mean expression of a given gene across brain cell types from healthy brain28 or liver22 single-cell data. We considered the cell type gene profiles as defined for signature scoring in Fig. 2.

The starting set of tissue-specific genes was defined using the HPA tissue transcriptional data annotated as ‘Tissue enriched’, ‘Group enriched’ or ‘Tissue enhanced’ (brain, accessed on 13 January 2021; liver, accessed on 28 November 2020). These requirements ensured the specificity of a given brain/liver gene in context of the whole body. For a given tissue, this formed the initial set of tissue-specific genes B.

The union of all brain or liver cell-type-specific genes is the set C. All genes in C (‘cell type specific’) were a subset of the respective initial set of tissue-specific genes:

$$C - B = 0$$
(8)

Genes in B that did not intersect with C and intersected with DEG-up (U) or DEG-down (D) genes in a given disease6,7 were then defined as ‘tissue specific’.

$$T = \left( {B \cap U} \right) \cup (B \cap D) - C$$
(9)

The Gini coefficients reflecting the gene expression inequality across the cell types within corresponding tissue single-cell atlas were computed for the gene sets labeled as ‘cell type specific’ and ‘tissue specific’. Brain reference data to compute Gini coefficients were from the single-cell brain atlas with diagnosis as ‘Normal’28. Liver single cell data were used as-is22. All Gini coefficients were computed using the mean log-transformed CPTT (counts per ten thousand) gene expression per cell type.

A permutation test was then performed on the union of the Gini coefficients for the genes labeled as ‘cell type specific’ and ‘tissue specific’. The purpose of this test was to assess probability that the observed mean difference in Gini coefficient for these two groups yielded no difference in specificity (that is, H0: \(\mu _{{\mathrm{cell}}\,{\mathrm{type}}\,{\mathrm{Gini}}\,{\mathrm{coefficient}}} = \mu _{{\mathrm{tissue}}\,{\mathrm{Gini}}\,{\mathrm{coefficient}}}\)).

Gini coefficients were permuted and reassigned to the list of ‘tissue specific’ or ‘cell type specific’ genes, and then the difference in the means of the two groups was computed. This procedure was repeated 10,000 times. The P value was determined as follows:

$$p = \frac{{\# \,{\mathrm{trials}}\,{\mathrm{with}}\,{\mathrm{permuted}}(\mu _{{\mathrm{cell}}\,{\mathrm{type}}} - \mu _{{\mathrm{tissue}}}) \ge \mu _{{\mathrm{observed}}}}}{{10,000 + 1}}$$
(10)

where \(\mu _{\mathrm{observed}}: = (\mu _{{\mathrm{cell}}\,{\mathrm{type}}\,{\mathrm{Gini}}\,{\mathrm{coefficient}}} - \mu _{{\mathrm{tissue}}\,{\mathrm{Gini}}\,{\mathrm{coefficient}}})\).

The additional 1 in the denominator reflects the original test between the true difference in means (for example, the true comparison yielding μobserved).

NAFLD: We considered the space of reported NAFLD DEGs in serum7. Here, C = hepatocyte gene profile, and B = the liver-specific genes.

AD: First, we intersected a given cell type gene profile in AD with the equivalent Normal profile for comparative analysis. Genes defined as ‘brain cell type specific’ for signature scoring in Fig. 2d were used in this comparison. Of note, no DEG-up genes intersected with any of the brain cell type signatures in Fig. 2d. Microglia, although often implicated in AD pathogenesis, were excluded given their high overlapping transcriptional profile with non-central-nervous-system macrophages54. Inhibitory neurons were also excluded given the low number of cell-type-specific genes intersecting between AD and NCI phenotypes.

Estimating signature scores for each cell type

The signature score is defined as the sum of the log-transformed CPM-TMM normalized counts per gene asserted to be cell type specific, where i denotes the index of the gene in a cell type signature gene profile G in the jth patient sample:

$${\mathrm{Signature}}\,{\mathrm{score}}_j = \mathop {\sum}\limits_i {G_{ij}}$$
(11)

Preeclampsia

For signature scoring of syncytiotrophoblast and extravillous trophoblast gene profiles in PEARL-PEC and iPEC5, a respective cell type gene profile used for signature scoring was derived as described in ‘Derivation of cell-type-specific gene profiles in context of the whole body using single-cell data’ independently using two different placental single-cell datasets19,20. Only the intersection of the cell-type-specific gene profiles for a given trophoblast cell type between the two datasets was included in the respective trophoblast gene profile for signature scoring.

CKD

We compared the signature score of the proximal tubule in CKD (nine patients; 51 samples) and healthy controls (three patients; nine samples). Given that all patient samples were longitudinally sampled over ~30 d (individual samples were taken on different days), we treated the samples as biological replicates and included all time points because the time scale over which renal cell type changes typically occur is longer than the collection period. The sequencing depth was similar between the CKD and healthy cohorts, although it was reduced in comparison to the other cfRNA datasets used in this work. To account for gene measurement dropout, we required that the expression of a given gene in the proximal tubule gene profile was non-zero in at least one sample in both cohorts. Given that all samples were sequenced together, no batch correction was necessary, facilitating a representative comparison between CKD and healthy cohorts.

AD

Microglia, although often implicated in AD pathogenesis, were excluded given their high overlapping transcriptional profile with non-central-nervous-system macrophages54. Inhibitory neurons were also excluded given the low number of cell-type-specific genes intersecting between AD and NCI phenotypes. Brain gene profiles as defined in the AD section of ‘Cell type specificity of DEGs in AD and NAFLD cfRNA’ were used.

Assessing P value calibration for a given signature score

Cell type signature scores were tested between control and diseased samples with a Mann–Whitney U-test. The resulting P values were calibrated with a permutation test. Here, the labels compared in a given test (that is, CKD versus control, AD versus NCI, NAFLD versus control, etc.) were randomly shuffled 10,000 times. We observed a well-calibrated, uniform P-value distribution (Extended Data Fig. 10a), validating the experimentally observed test statistics.

Reporting Summary

Further information on research design is available in the Nature Research Reporting Summary linked to this article