Abstract
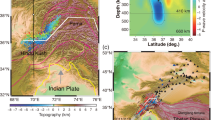
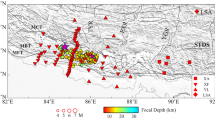
Mantle viscosity plays a key role in the Earth’s internal dynamics and thermal history. Geophysical inferences of the viscosity structure, however, have shown large variability depending on the types of observables used or the assumptions imposed1,2,3. Here, we study the mantle viscosity structure by using the postseismic deformation following a deep (approximately 560 km) earthquake located near the bottom of the upper mantle. We apply independent component analysis4 to geodetic time series to successfully detect and extract the postseismic deformation induced by the moment magnitude 8.2, 2018 Fiji earthquake. To search for the viscosity structure that can explain the detected signal, we perform forward viscoelastic relaxation modelling5,6 with a range of viscosity structures. We find that our observation requires a relatively thin (approximately 100 km), low-viscosity (1017 to 1018 Pa s) layer at the bottom of the mantle transition zone. Such a weak zone could explain the slab flattening7 and orphaning8 observed in numerous subduction zones, which are otherwise challenging to explain in the whole mantle convection regime. The low-viscosity layer may result from superplasticity9 induced by the postspinel transition, weak CaSiO3 perovskite10, high water content11 or dehydration melting12.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
GNSS data were obtained from the Nevada Geodetic Lab (geodesy.unr.edu). We also provide the detected postseismic signal, for example, displacements and time evolution, as source data for Fig. 1. Source data are provided with this paper.
Code availability
The forward modelling code RELAX is available at https://geodynamics.org/cig/software/relax/. The code for the ICA has been made available33 on the Zenodo repository, https://doi.org/10.5281/zenodo.4322548.
References
Karato, S.Rheology of the Earth’s mantle: a historical review. Gondwana Res. 18, 17–45 (2010).
King, S. D. Reconciling laboratory and observational models of mantle rheology in geodynamic modelling. J. Geodyn. 100, 33–50 (2016).
Rudolph, M. L., Lekić, V. & Lithgow-Bertelloni, C. Viscosity jump in Earth’s mid-mantle. Science. 350, 1349–1352 (2015).
Gualandi, A., Serpelloni, E. & Belardinelli, M. E. Blind source separation problem in GPS time series. J. Geod. 90, 323–341 (2016).
Barbot, S. & Fialko, Y. A unified continuum representation of post-seismic relaxation mechanisms: semi-analytic models of afterslip, poroelastic rebound and viscoelastic flow. Geophys. J. Int. 182, 1124–1140 (2010).
Barbot, S. & Fialko, Y. Fourier-domain Green’s function for an elastic semi-infinite solid under gravity, with applications to earthquake and volcano deformation. Geophys. J. Int. 182, 568–582 (2010).
Mao, W. & Zhong, S. Slab stagnation due to a reduced viscosity layer beneath the mantle transition zone. Nat. Geosci. 11, 876–881 (2018).
Grima, A. G., Lithgow-Bertelloni, C. & Crameri, F. Orphaning regimes: the missing link between flattened and penetrating slab morphologies. Front. Earth Sci. 8, 1–19 (2020).
Panasyuk, S. V. & Hager, B. H. A model of transformational superplasticity in the upper mantle. Geophys. J. Int. 133, 741–755 (1998).
Immoor, J. et al. Weak cubic CaSiO3 perovskite in the Earth’s mantle. Nature 603, 276–279 (2022).
Fei, H. et al. A nearly water-saturated mantle transition zone inferred from mineral viscosity. Sci. Adv. 3, e1603024 (2017).
Schmandt, B., Jacobsen, S. D., Becker, T. W., Liu, Z. & Dueker, K. G. Dehydration melting at the top of the lower mantle. Science. 344, 1265–1268 (2014).
Mitrovica, J. X. & Forte, A. M. A new inference of mantle viscosity based upon joint inversion of convection and glacial isostatic adjustment data. Earth Planet. Sci. Lett. 225, 177–189 (2004).
Liu, H., Gurnis, M. & Leng, W. Constraints on mantle viscosity from slab dynamics. J. Geophys. Res. Solid Earth 126, 1–18 (2021).
Pollitz, F. F. Gravitational viscoelastic postseismic relaxation on a layered spherical Earth. J. Geophys. Res. Solid Earth 102, 17921–17941 (1997).
Xu, C., Su, X., Liu, T. & Sun, W. Geodetic observations of the co- and post-seismic deformation of the 2013 Okhotsk Sea deep-focus earthquake. Geophys. J. Int. 209, 1924–1933 (2017).
Avouac, J.-P. From geodetic imaging of seismic and aseismic fault slip to dynamic modeling of the seismic cycle. Annu. Rev. Earth Planet. Sci. 43, 233–271 (2015).
Jia, Z. et al. The 2018 Fiji Mw 8.2 and 7.9 deep earthquakes: one doublet in two slabs. Earth Planet. Sci. Lett. 531, 115997 (2020).
Han, S., Sauber, J. & Pollitz, F. Postseismic gravity change after the 2006–2007 great earthquake doublet and constraints on the asthenosphere structure in the central Kuril Islands. Geophys. Res. Lett. 43, 3169–3177 (2016).
Tian, Z., Freymueller, J.T. & Yang, Z. Postseismic deformation due to the 2012 M w 7.8 Haida Gwaii and 2013 M w 7.5 Craig earthquakes and its implications for regional rheological structure.J. Geophys. Res. Solid Earth 126, (2021).
Forte, A. M., Dziewonski, A. M. & Woodward, R. L. in Dynamics of Earth’s Deep Interior and Earth Rotation (eds. Le Mouël, -L. et al.) 135–166 (1993).
Lau, H. C. P. & Holtzman, B. K. “Measures of dissipation in viscoelastic media” extended: toward continuous characterization across very broad geophysical time scales. Geophys. Res. Lett. 46, 9544–9553 (2019).
van der Hilst, R. Complex morphology of subducted lithosphere in the mantle beneath the Tonga trench. Nature 374, 154–157 (1995).
Huang, X., Xu, Y. & Karato, S. Water content in the transition zone from electrical conductivity of wadsleyite and ringwoodite. Nature 434, 746–749 (2005).
Pearson, D. G. et al. Hydrous mantle transition zone indicated by ringwoodite included within diamond. Nature 507, 221–224 (2014).
NOAA National Geophysical Data Center. 2-minute Gridded Global Relief Data (ETOPO2) v2. NOAA National Centers for Environmental Information. https://doi.org/10.7289/V5J1012Q (2006).
Hayes, G. P., Wald, D. J. & Johnson, R. L. Slab1.0: a three-dimensional model of global subduction zone geometries. J. Geophys. Res. 117, B01302 (2012).
Blewitt, G., Kreemer, C., Hammond, W. C. & Gazeaux, J. MIDAS robust trend estimator for accurate GPS station velocities without step detection. J. Geophys. Res. Solid Earth 121, 2054–2068 (2016).
SONEL. GPS TONGA. https://www.sonel.org/spip.php?page=gps&idStation=894 (2022).
Bevis, M. & Brown, A. Trajectory models and reference frames for crustal motion geodesy. J. Geod. 88, 283–311 (2014).
Jiao, W., Wallace, T. C., Beck, S. L., Silver, P. G. & Zandt, G. Evidence for static displacements from the June 9, 1994 Deep Bolivian Earthquake. Geophys. Res. Lett. 22, 2285–2288 (1995).
Vidale, J. E., Goes, S. & Richards, P. G. Near-field deformation seen on distant broadband seismograms. Geophys. Res. Lett. 22, 1–4 (1995).
Gualandi, A. & Liu, Z. Variational bayesian independent component analysis for InSAR displacement time‐series with application to central California, USA.J. Geophys. Res. Solid Earth 126, (2021).
Dziewonski, A. M. & Anderson, D. L. Preliminary reference Earth model. Phys. Earth Planet. Inter. 25, 297–356 (1981).
Acknowledgements
We thank M. Gurnis, H. Kanamori and R. Bürgmann for useful discussions. This work was partially support by the National Science Foundation grant NSF EAR 2142152.
Author information
Authors and Affiliations
Contributions
S.P. conceived the study, analysed the data, performed the modelling, interpreted the results and wrote the manuscript. J.-P.A. supervised the ICA and modelling and participated in the interpretation. Z.Z. participated in the interpretation. A.G. provided the code for the ICA and guided the time series analysis. All authors discussed the results and commented on the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature thanks Yuri Fialko and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 Observed (black arrows, large circles) and predicted (green arrows, small circles) coseismic deformation.
Same as Fig. 4a, except coseismic displacements are plotted. Error ellipses (grey circles; 95% confidence intervals) are obtained from trajectory modelling.
Extended Data Fig. 2 Predicted postseismic deformation for weak MTZ BH with two different Maxwell times.
a, The same as the right panel of Fig. 2f. b, The same as a, but with weak MTZ BH (Maxwell time of 1.25 years).
Extended Data Fig. 3 Postseismic deformation predicted by different models (MTZ BH with 0.63-year Maxwell time and MTZ B65 with 0.05-year Maxwell time) compared against the data.
a–b, The same as the Fig. 4a,b but with increased viscosity MTZ BH of 0.63-year Maxwell time. c–d, The same as a–b, except with reduced viscosity MTZ B65 of 0.05-year Maxwell time.
Extended Data Fig. 4 Postseismic deformation predicted by our preferred model in presence of a weak asthenosphere.
a–b, The same as the Fig. 4a,b but with a weak asthenosphere of 0.63-year Maxwell time. c–d, The same as a–b, but with a weak asthenosphere of 2.5-year Maxwell time. In each case, the displacements are close to the linear summation of the displacements resulting from modeling the weak asthenosphere and the weak base of MTZ separately. Horizontal displacements are in similar directions, and add constructively, resulting in 10 to 20 % larger displacements at the sites close to the earthquake. On the other hand, due to the uplift in the west of the epicentre and west of the trench produced by the weak asthenosphere, opposite from those produced by weak base of MTZ (Fig. 2), the vertical displacements tend to add destructively in stations in Fiji and Tonga islands (such as LAUT and TONG). This decreases (worsens) the overall fit to the observation by about 14 and 6 %. These results suggest that, in order to explain the observed subsidence around the epicenter and the trench in presence of weak asthenosphere, the weak zone at the base of MTZ is even more strongly required.
Extended Data Fig. 5 Raw and pre-processed GNSS data of station LAUT.
a–c, Raw GNSS data of east, north, and vertical components with uncertainties (blue error bars; one standard deviation). Magenta and green dashed lines denote the timings of steps associated with instrument issues and coseismic displacements, respectively. Solid orange line represents the best-fitting trajectory model. d–f, The same as a–c, except for the timeseries are pre-processed, i.e., linear trend and offsets derived from the trajectory model removed from raw data (a–c).
Extended Data Fig. 6 Independent components other than the postseismic component, and their spatial distributions.
a, The time evolution (top) and the spatial distribution of the most significant seasonal deformation component, shown in the same manner as in Fig. 1, where error ellipses (one standard deviation) are estimated in the same way as those of postseismic displacements. b–d, The same as a, but for the 2nd, 3rd, and 4th most significant seasonal components, respectively.
Extended Data Fig. 7 Postseismic deformation at each pre-processed GNSS timeseries.
a, Pre-processed east (top), north (middle), and up (bottom) components of the GNSS data of station LAUT (the same as Extended Data Fig. 5d–f) are plotted in black, while the contribution from the postseismic deformation in each timeseries is plotted in red. Error bars are for one standard deviation. The time of the earthquake is shown with a solid green line. Note that the scale of up component is larger than those of horizontal components. b–d, Same as a, but for stations NIUM, SAMO, and TONG, respectively. Stations SAMO and TONG have gaps in data close to the end of the analyzed time period.
Extended Data Fig. 8 Ratio of the shear modulus (μ) and viscosity (η) to the reference values (μref, ηref) as a function of depth.
The ratios (solid blue line) with respect to the reference (solid orange line) are calculated based on the Preliminary Reference Earth Model34.
Supplementary information
Source data
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Park, S., Avouac, JP., Zhan, Z. et al. Weak upper-mantle base revealed by postseismic deformation of a deep earthquake. Nature 615, 455–460 (2023). https://doi.org/10.1038/s41586-022-05689-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-022-05689-8
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.