Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Down-conversion of a single photon as a probe of many-body localization

Nature volume 613, pages 650–655 (2023)Cite this article

Subjects

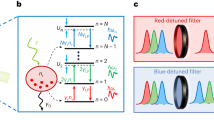
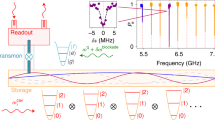
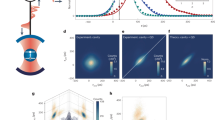
Abstract

Decay of a particle into more particles is a ubiquitous phenomenon to interacting quantum systems, taking place in colliders, nuclear reactors or solids. In a nonlinear medium, even a single photon would decay by down-converting (splitting) into lower-frequency photons with the same total energy1, at a rate given by Fermi’s golden rule. However, the energy-conservation condition cannot be matched precisely if the medium is finite and only supports quantized modes. In this case, the fate of the photon becomes the long-standing question of many-body localization, originally formulated as a gedanken experiment for the lifetime of a single Fermi-liquid quasiparticle confined to a quantum dot2. Here we implement such an experiment using a superconducting multimode cavity, the nonlinearity of which was tailored to strongly violate the photon-number conservation. The resulting interaction attempts to convert a single photon excitation into a shower of low-energy photons but fails owing to the many-body localization mechanism, which manifests as a striking spectral fine structure of multiparticle resonances at the standing-wave-mode frequencies of the cavity. Each resonance was identified as a many-body state of radiation composed of photons from a broad frequency range and not obeying Fermi’s golden rule theory. Our result introduces a new platform to explore the fundamentals of many-body localization without having to control many atoms or qubits3,4,5,6,7,8,9.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on Springer Link
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Experimental setup.
Fig. 2: Spectroscopy data.
Fig. 3: Data interpretation.
Fig. 4: Beyond two-particle states.

Similar content being viewed by others

Data availability

The raw data collected in this study are available from the corresponding author on reasonable request.

Code availability

The code used to analyse the data reported in this study is available from the corresponding author on reasonable request.

References

  1. Klyshko, D. Scattering of light in a medium with nonlinear polarizability. Sov. Phys. JETP 28, 522–526 (1969).

    ADS  Google Scholar 

  2. Altshuler, B. L., Gefen, Y., Kamenev, A. & Levitov, L. S. Quasiparticle lifetime in a finite system: a nonperturbative approach. Phys. Rev. Lett. 78, 2803–2806 (1997).

    Article  ADS  CAS  Google Scholar 

  3. Schreiber, M. et al. Observation of many-body localization of interacting fermions in a quasirandom optical lattice. Science 349, 842–845 (2015).

    Article  ADS  CAS  MATH  Google Scholar 

  4. Smith, J. et al. Many-body localization in a quantum simulator with programmable random disorder. Nat. Phys. 12, 907–911 (2016).

    Article  CAS  Google Scholar 

  5. Roushan, P. et al. Spectroscopic signatures of localization with interacting photons in superconducting qubits. Science 358, 1175–1179 (2017).

    Article  ADS  CAS  Google Scholar 

  6. Lukin, A. et al. Probing entanglement in a many-body–localized system. Science 364, 256–260 (2019).

    Article  ADS  CAS  Google Scholar 

  7. Bluvstein, D. et al. Controlling quantum many-body dynamics in driven Rydberg atom arrays. Science 371, 1355–1359 (2021).

    Article  ADS  CAS  MATH  Google Scholar 

  8. Morong, W. et al. Observation of Stark many-body localization without disorder. Nature 599, 393–398 (2021).

    Article  ADS  CAS  Google Scholar 

  9. Guo, Q. et al. Observation of energy-resolved many-body localization. Nat. Phys. 17, 234–239 (2021).

    Article  ADS  CAS  Google Scholar 

  10. Anderson, P. W. Absence of diffusion in certain random lattices. Phys. Rev. 109, 1492–1505 (1958).

    Article  ADS  CAS  Google Scholar 

  11. Gornyi, I. V., Mirlin, A. D. & Polyakov, D. G. Interacting electrons in disordered wires: Anderson localization and low-t transport. Phys. Rev. Lett. 95, 206603 (2005).

    Article  ADS  CAS  Google Scholar 

  12. Basko, D., Aleiner, I. & Altshuler, B. Metal–insulator transition in a weakly interacting many-electron system with localized single-particle states. Ann. Phys. 321, 1126–1205 (2006).

    Article  ADS  CAS  MATH  Google Scholar 

  13. Basko, D. M., Aleiner, I. L. & Altshuler, B. L. Possible experimental manifestations of the many-body localization. Phys. Rev. B 76, 052203 (2007).

    Article  ADS  Google Scholar 

  14. Oganesyan, V. & Huse, D. A. Localization of interacting fermions at high temperature. Phys. Rev. B 75, 155111 (2007).

    Article  ADS  Google Scholar 

  15. Serbyn, M., Papić, Z. & Abanin, D. A. Local conservation laws and the structure of the many-body localized states. Phys. Rev. Lett. 111, 127201 (2013).

    Article  ADS  Google Scholar 

  16. Huse, D. A., Nandkishore, R. & Oganesyan, V. Phenomenology of fully many-body-localized systems. Phys. Rev. B 90, 174202 (2014).

    Article  ADS  Google Scholar 

  17. Nandkishore, R. & Huse, D. A. Many-body localization and thermalization in quantum statistical mechanics. Annu. Rev. Condens. Matter Phys. 6, 15–38 (2015).

    Article  ADS  Google Scholar 

  18. Abanin, D. A., Altman, E., Bloch, I. & Serbyn, M. Colloquium: Many-body localization, thermalization, and entanglement. Rev. Mod. Phys. 91, 021001 (2019).

    Article  ADS  CAS  Google Scholar 

  19. Choi, J.-Y. et al. Exploring the many-body localization transition in two dimensions. Science 352, 1547–1552 (2016).

    Article  ADS  CAS  MATH  Google Scholar 

  20. Xu, K. et al. Emulating many-body localization with a superconducting quantum processor. Phys. Rev. Lett. 120, 050507 (2018).

    Article  ADS  CAS  Google Scholar 

  21. Mirlin, A. D. Statistics of energy levels and eigenfunctions in disordered systems. Phys. Rep. 326, 259–382 (2000).

    Article  ADS  CAS  Google Scholar 

  22. Serbyn, M. & Moore, J. E. Spectral statistics across the many-body localization transition. Phys. Rev. B 93, 041424 (2016).

    Article  ADS  Google Scholar 

  23. Nandkishore, R., Gopalakrishnan, S. & Huse, D. A. Spectral features of a many-body-localized system weakly coupled to a bath. Phys. Rev. B 90, 064203 (2014).

    Article  ADS  Google Scholar 

  24. Johri, S., Nandkishore, R. & Bhatt, R. N. Many-body localization in imperfectly isolated quantum systems. Phys. Rev. Lett. 114, 117401 (2015).

    Article  ADS  Google Scholar 

  25. Folk, J., Marcus, C. & Harris, J.Jr Decoherence in nearly isolated quantum dots. Phys. Rev. Lett. 87, 206802 (2001).

    Article  ADS  CAS  Google Scholar 

  26. Manucharyan, V. E., Koch, J., Glazman, L. I. & Devoret, M. H. Fluxonium: single Cooper-pair circuit free of charge offsets. Science 326, 113–116 (2009).

    Article  ADS  CAS  Google Scholar 

  27. Meiser, D. & Meystre, P. Superstrong coupling regime of cavity quantum electrodynamics. Phys. Rev. A 74, 065801 (2006).

    Article  ADS  Google Scholar 

  28. Sundaresan, N. M. et al. Beyond strong coupling in a multimode cavity. Phys. Rev. X 5, 021035 (2015).

    Google Scholar 

  29. Martínez, J. P. et al. A tunable Josephson platform to explore many-body quantum optics in circuit-QED. npj Quantum Inf. 5, 19 (2019).

    Article  ADS  Google Scholar 

  30. Kuzmin, R., Mehta, N., Grabon, N., Mencia, R. & Manucharyan, V. Superstrong coupling in circuit quantum electrodynamics. npj Quantum Inf. 5, 20 (2019).

    Article  ADS  Google Scholar 

  31. Mehta, N., Ciuti, C., Kuzmin, R. & Manucharyan, V. E. Theory of strong down-conversion in multi-mode cavity and circuit QED. Preprint at https://arxiv.org/abs/2210.14681 (2022).

  32. Kuzmin, R. et al. Quantum electrodynamics of a superconductor–insulator phase transition. Nat. Phys. 15, 930–934 (2019).

    Article  CAS  Google Scholar 

  33. Nigg, S. E. et al. Black-box superconducting circuit quantization. Phys. Rev. Lett. 108, 240502 (2012).

    Article  ADS  Google Scholar 

  34. Kuzmin, R. et al. Inelastic scattering of a photon by a quantum phase slip. Phys. Rev. Lett. 126, 197701 (2021).

    Article  ADS  CAS  Google Scholar 

  35. Kuzmin, R., Mehta, N., Grabon, N. & Manucharyan, V. E. Tuning the inductance of Josephson junction arrays without SQUIDs. Preprint at https://arxiv.org/abs/2210.12119 (2022).

  36. Naik, R. et al. Random access quantum information processors using multimode circuit quantum electrodynamics. Nat. Commun. 8, 1904 (2017).

    Article  ADS  CAS  Google Scholar 

Download references

Acknowledgements

We acknowledge support from DOE Early Career Award (DE-SC0020160), US ARO MURI programme ‘Exotic states of light in superconducting circuits’ (W911NF-15-1-0397) and Google Faculty Research Award. C.C. acknowledges financial support from FET FLAGSHIP Project PhoQuS (grant agreement no. 820392) and from the French agency ANR through the project NOMOS (ANR-18-CE24-0026) and TRIANGLE (ANR-20-CE47-0011).

Author information

Author notes

  1. Roman Kuzmin

    Present address: Department of Physics, University of Wisconsin-Madison, Madison, WI, USA

Authors and Affiliations

  1. Department of Physics, University of Maryland, College Park, MD, USA

    Nitish Mehta, Roman Kuzmin & Vladimir E. Manucharyan

  2. Université Paris Cité, CNRS, Matériaux et Phénomènes Quantiques, Paris, France

    Cristiano Ciuti

  3. École Polytechnique Fédérale de Lausanne, Lausanne, Switzerland

    Vladimir E. Manucharyan

Authors
  1. Nitish Mehta
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Roman Kuzmin
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Cristiano Ciuti
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Vladimir E. Manucharyan
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

R.K. built the experimental setup and, assisted by N.M., performed the measurements. N.M. fabricated the device and performed data analysis, guided by C.C. and V.E.M. All authors contributed to extensive discussions of the data and writing of the manuscript. V.E.M. managed the project.

Corresponding author

Correspondence to Vladimir E. Manucharyan.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature thanks Rahul Nandkishore and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Extended data figures and tables

Extended Data Fig. 1 Non-interacting spectra.

Left column, excitation frequency versus the applied flux bias for the single-particle eigenstates (solid black lines). The filled black dots are the experimental data used for the fitting procedure described in the text. Middle column, energy of the uncoupled two-particle states added (red lines). Right column, energy of the uncoupled thee-particle states added (green lines). Note that at a frequency of around 8 GHz and above, the three-particle spectrum is almost uniformly spread in energy, as if the system has a natural disorder in the single-particle spectrum.

Extended Data Fig. 2 Dispersion characterization.

Measured standing-wave-mode frequency spacing fk+1 − fk versus frequency fk (k = 1, 2,…) at φext = 0 (black circles) and at φext/2π = 0.5 (red circles). The dispersion varies the mode spacing from 165 to 195 MHz in the frequency range of interest. The non-dispersive mode spacing is extracted to be Δ = v/2ℓ ≈ 197 MHz. The hybridization window width Γ ≈ 1 GHz and the low-frequency cutoff corresponding to j0 = 20 are indicated.

Extended Data Fig. 3 Interaction parameters.

a, Photon–photon interaction frequency scale g as a function of the external flux. b, Colour plot of the matrix elements Ak,k′ versus the mode indices k,k′ when the qubit frequency is tuned to feg = 7.2 GHz (around mode index 39) at φext/2π = 0.36. Note that the width of the local maximum in Ak,k′ is given by Γ/Δ.

Extended Data Fig. 4 Photon loss characterization.

Internal (blue circles) and external (red triangles) quality factors of the bare Fabry–Pérot modes as a function of mode frequency measured at the flux bias φext = 0. For this flux value, the qubit coupling is negligible.

Extended Data Table 1 Summary of device parameters
Full size table

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Mehta, N., Kuzmin, R., Ciuti, C. et al. Down-conversion of a single photon as a probe of many-body localization. Nature 613, 650–655 (2023). https://doi.org/10.1038/s41586-022-05615-y

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/s41586-022-05615-y

This article is cited by

Comments

By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing