Abstract
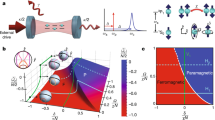
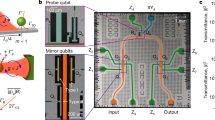
Pumps are transport mechanisms in which direct currents result from a cyclic evolution of the potential1,2. As Thouless showed, the pumping process can have topological origins, when considering the motion of quantum particles in spatially and temporally periodic potentials3. However, the periodic evolution that drives these pumps has always been assumed to be imparted from outside, as has been the case in the experimental systems studied so far4,5,6,7,8,9,10,11,12. Here we report on an emergent mechanism for pumping in a quantum gas coupled to an optical resonator, where we observe a particle current without applying a periodic drive. The pumping potential experienced by the atoms is formed by the self-consistent cavity field interfering with the static laser field driving the atoms. Owing to dissipation, the cavity field evolves between its two quadratures13, each corresponding to a different centrosymmetric crystal configuration14. This self-oscillation results in a time-periodic potential analogous to that describing the transport of electrons in topological tight-binding models, such as the paradigmatic Rice–Mele pump15. In the experiment, we directly follow the evolution by measuring the phase winding of the cavity field with respect to the driving field and observing the atomic motion in situ. The observed mechanism combines the dynamics of topological and open systems, and features characteristics of continuous dissipative time crystals.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The data to reproduce the figures of this study are available in the data repository of ETH Zurich’s Research Collection (http://www.research-collection.ethz.ch) at https://doi.org/10.3929/ethz-b-000547966.
References
Altshuler, B. & Glazman, L. Pumping electrons. Science 283, 1864–1865 (1999).
Cohen, D. Quantum pumping in closed systems, adiabatic transport, and the Kubo formula. Phys. Rev. B 68, 155303 (2003).
Thouless, D. Quantization of particle transport. Phys. Rev. B 27, 6083–6087 (1983).
Switkes, M., Marcus, C., Campman, K. & Gossard, A. An adiabatic quantum electron pump. Science 283, 1905–1908 (1999).
Aleiner, I. & Andreev, A. Adiabatic charge pumping in almost open dots. Phys. Rev. Lett. 81, 1286–1289 (1998).
Blumenthal, M. et al. Gigahertz quantized charge pumping. Nat. Phys. 3, 343–347 (2007).
Giazotto, F. et al. A Josephson quantum electron pump. Nat. Phys. 7, 857–861 (2011).
Lu, H.-I. et al. Geometrical pumping with a Bose–Einstein condensate. Phys. Rev. Lett. 116, 200402 (2016).
Nakajima, S. et al. Topological Thouless pumping of ultracold fermions. Nat. Phys. 12, 296–300 (2016).
Lohse, M., Schweizer, C., Zilberberg, O., Aidelsburger, M. & Bloch, I. A Thouless quantum pump with ultracold bosonic atoms in an optical superlattice. Nat. Phys. 12, 350–354 (2016).
Lohse, M., Schweizer, C., Price, H. M., Zilberberg, O. & Bloch, I. Exploring 4D quantum Hall physics with a 2D topological charge pump. Nature 553, 55–58 (2018).
Nakajima, A. et al. Competition and interplay between topology and quasi-periodic disorder in Thouless pumping of ultracold atoms. Nat. Phys. 17, 844–849 (2021).
Dogra, N. et al. Dissipation-induced structural instability and chiral dynamics in a quantum gas. Science 366, 1496–1499 (2019).
Li, X. et al. First order phase transition between two centro-symmetric superradiant crystals. Phys. Rev. Res. 3, L012024 (2021).
Rice, M. & Mele, E. Elementary excitations of a linearly conjugated diatomic polymer. Phys. Rev. Lett. 49, 1455–1459 (1982).
Xiao, D., Chang, M.-C. & Niu, Q. Berry phase effects on electronic properties. Rev. Mod. Phys. 82, 1959–2007 (2010).
Niu, Q. Quantum adiabatic particle transport. Phys. Rev. B 34, 5093–5100 (1986).
Wang, L., Troyer, M. & Dai, X. Topological charge pumping in a one-dimensional optical lattice. Phys. Rev. Lett. 111, 026802 (2013).
Qian, Y., Gong, M. & Zhang, C. Quantum transport of bosonic cold atoms in double-well optical lattices. Phys. Rev. A 84, 013608 (2011).
Resta, R. Manifestations of Berry’s phase in molecules and condensed matter. J. Phys. Condens. Matter 12, R107 (2000).
Vanderbilt, D. & King-Smith, R. Electric polarization as a bulk quantity and its relation to surface charge. Phys. Rev. B 48, 4442–4455 (1993).
Resta, R. Macroscopic polarization in crystalline dielectrics: the geometric phase approach. Rev. Mod. Phys. 66, 899–915 (1994).
Resta, R. & Vanderbilt, D. in Physics of Ferroelectrics: Topics in Applied Physics Vol. 105 (ed. Lee, Y. P. et al.) 31–68 (Springer, 2007).
Mivehvar, F., Piazza, F., Donner, T. & Ritsch, H. Cavity QED with quantum gases: new paradigms in many-body physics. Adv. Phys. 70, 1–153 (2021).
Jenkins, A. Self-oscillation. Phys. Rep. 525, 167–222 (2013).
El-Ganainy, R. et al. Non-Hermitian physics and PT symmetry. Nat. Phys. 14, 11–19 (2018).
Fruchart, M., Hanai, R., Littlewood, P. B. & Vitelli, V. Non-reciprocal phase transitions. Nature 592, 363–369 (2021).
Baumann, K., Guerlin, C., Brennecke, F. & Esslinger, T. Dicke quantum phase transition with a superfluid gas in an optical cavity. Nature 464, 1301–1306 (2010).
Chiacchio, E. R. & Nunnenkamp, A. Dissipation-induced instabilities of a spinor Bose–Einstein condensate inside an optical cavity. Phys. Rev. Lett. 122, 193605 (2019).
Buča, B. & Jaksch, D. Dissipation induced nonstationarity in a quantum gas. Phys. Rev. Lett. 123, 260401 (2019).
Haroche, S. & Raimond, J.-M. Exploring the Quantum: Atoms, Cavities, and Photons (Oxford Univ. Press, 2006).
Baumann, K., Mottl, R., Brennecke, F. & Esslinger, T. Exploring symmetry breaking at the Dicke quantum phase transition. Phys. Rev. Lett. 107, 140402 (2011).
Fan, J., Chen, G. & Jia, S. Atomic self-organization emerging from tunable quadrature coupling. Phys. Rev. A 101, 063627 (2020).
Zupancic, P. et al. P-band induced self-organization and dynamics with repulsively driven ultracold atoms in an optical cavity. Phys. Rev. Lett. 123, 233601 (2019).
Mekhov, I. B., Maschler, C. & Ritsch, H. Probing quantum phases of ultracold atoms in optical lattices by transmission spectra in cavity quantum electrodynamics. Nat. Phys. 3, 319–323 (2007).
Laflamme, C., Yang, D. & Zoller, P. Continuous measurement of an atomic current. Phys. Rev. A 95, 043843 (2017).
El-Ganainy, R., Khajavikhan, M., Christodoulides, D. N. & Ozdemir, S. K. The dawn of non-Hermitian optics. Commun. Phys. 2, 37 (2019).
Ashida, Y., Gong, Z. & Ueda, M. Non-Hermitian physics. Adv. Phys. 69, 249–435 (2020).
Booker, C., Buča, B. & Jaksch, D. Non-stationarity and dissipative time crystals: spectral properties and finite-size effects. New J. Phys. 22, 085007 (2020).
Kongkhambut, P. et al. Observation of a continuous time crystal. Science https://www.science.org/doi/10.1126/science.abo3382 (2022).
Cosme, J. G., Skulte, J. & Mathey, L. Time crystals in a shaken atom–cavity system. Phys. Rev. A 100, 053615 (2019).
Keßler, H. et al. Observation of a dissipative time crystal. Phys. Rev. Lett. 127, 043602 (2021).
Landig, R. et al. Quantum phases from competing short- and long-range interactions in an optical lattice. Nature 532, 476–479 (2016).
Zhang, X. et al. Observation of a superradiant quantum phase transition in an intracavity degenerate Fermi gas. Science 373, 1359–1362 (2021).
Mivehvar, F., Ritsch, H. & Piazza, F. Superradiant topological Peierls insulator inside an optical cavity. Phys. Rev. Lett. 118, 073602 (2017).
Landini, M. et al. Formation of a spin texture in a quantum gas coupled to a cavity. Phys. Rev. Lett. 120, 223602 (2018).
Kroeze, R. M., Guo, Y., Vaidya, V. D., Keeling, J. & Lev, B. L. Spinor self-ordering of a quantum gas in a cavity. Phys. Rev. Lett. 121, 163601 (2018).
Morales, A. et al. Two-mode Dicke model from nondegenerate polarization modes. Phys. Rev. A 100, 013816 (2019).
Maschler, C., Mekhov, I. B. & Ritsch, H. Ultracold atoms in optical lattices generated by quantized light fields. Eur. Phys. J. D 46, 545–560 (2008).
Resta, R. Quantum-mechanical position operator in extended systems. Phys. Rev. Lett. 80, 1800–1803 (1998).
Acknowledgements
We thank A. Frank for support with the heterodyne electronics; and O. Zilberberg and N. Spaldin for discussion. We acknowledge funding from SNF project numbers IZBRZ2_186312, 182650 and 175329 (NAQUAS QuantERA) and NCCR QSIT, from EU Horizon2020 ERCadvanced grant TransQ (project number 742579) and ITN grant ColOpt (project number 721465).
Author information
Authors and Affiliations
Contributions
D.D., A.B. and X.L. prepared the experiment, D.D., A.B., X.L. and S.H. took and analysed the data. D.D. performed the numerical simulations. T.D. and T.E. supervised the work. All authors contributed to discussions of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature thanks Jonas Larson and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 Non-averaged phase diagram and repeated measurement results.
a, Phase diagram using the phase data ϕ(t) from the heterodyne detector by varying cavity detuning ΔC of cavity 1. The two different self-organized phases can be well observed for values around ϕ = 0 and ϕ = π/2. At low transverse beam fields the system shows no self-organization and ϕ is not well defined. Between the two self-organized phases the dynamical phase with varying ϕ(t) is visible. b, Many repetitions of the same trace with constant ΔC = −1.1 MHz. The extent of the instability region varies slightly at each repetition.c, Same data as in b, but shifted in time such that the onset of pumping coincides for all traces. The dashed line as guide to the eye illustrates that the rate at which the phase evolves is robust.
Extended Data Fig. 2 Schematic representation of the theoretical models.
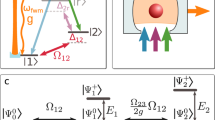
a, Self-consistent loop between cavity field α, optical lattice Vlattice and wavefunction ψ as described by the set of equations Eq. (5) and Eq. (11).b, Minimal model given by the three-level momentum expansion of Eq. (14). The coherent coupling (solid arrows) mixes the condensate mode ψ0 with the spatially modulated ψp,q, which are then mutually coupled by dissipation (dashed arrows).
Extended Data Fig. 3 Comparison of experimental and numerical phase diagrams.
Figures show the amplitude of the intracavity light field dependent on V0 and the cavity detuning Δc for cavity 2. a, Dataset showing in each row a trace of single experimental realization for the given cavity detuning Δc. The transverse beam lattice is linearly ramped to the final transverse lattice strength V0 = 40 Er within 5 ms. b, Corresponding simulation of the experimental results with GPE simulation.
Supplementary information
Rights and permissions
Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Dreon, D., Baumgärtner, A., Li, X. et al. Self-oscillating pump in a topological dissipative atom–cavity system. Nature 608, 494–498 (2022). https://doi.org/10.1038/s41586-022-04970-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-022-04970-0
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.