Abstract
The discovery of the Higgs boson, ten years ago, was a milestone that opened the door to the study of a new sector of fundamental physical interactions. We review the role of the Higgs field in the Standard Model of particle physics and explain its impact on the world around us. We summarize the insights into Higgs physics revealed so far by ten years of work, discuss what remains to be determined and outline potential connections of the Higgs sector with unsolved mysteries of particle physics.
Similar content being viewed by others
Main
Ten years ago, on 4 July 2012, scientists and journalists gathered at CERN, and remotely around the world, for the announcement of the discovery of a new fundamental particle, the Higgs boson. The discovery, by the ATLAS1 and CMS2 collaborations at the Large Hadron Collider (LHC), came almost 50 years after theorists had postulated the existence of such a particle. The significance of the discovery was not only that a new, long-awaited particle had been found, but that the existence of this particle provides first direct evidence that surrounding us there is a new kind of fundamental ‘field’, known as the Higgs field.
Fields in physics are familiar in everyday life, for example in the form of the earth’s magnetic field, and its impact on the needle of a compass. The most important difference between the Higgs field and a magnetic field is that if one removes the magnetic source, the magnetic field disappears. By contrast, the Higgs field is non-zero everywhere, all the time, independently of whether anything else is present in the Universe. In a way, it is reminiscent of the ancient Greek concept of Aether with the crucial difference that it is consistent with Einstein’s theory of special relativity.
Physicists’ current theory of fundamental particles and forces is known as the Standard Model, a theoretical framework that provides a description of elementary particles and the forces that make them interact with one another, with the exception of gravity. Within the Standard Model, the Higgs field is essential to describe the world as we know it.
As we shall see below, the strength of the interaction between any particle and the Higgs field directly affects a fundamental property of that particle: its mass. As such3, it ultimately determines the size of atoms, makes the proton stable and sets the timescale of radioactive (β) decays, which for example impact the lifetime of stars (Table 1). Yet, in everyday life, we do not notice that the Higgs field is all around us. The only way we have of revealing the Higgs field is to perturb it, a little like throwing a stone into water and seeing the ripples. The particle known as the Higgs boson is the manifestation of such a perturbation.
The significance of its discovery in 2012 was such that the Nobel prize was awarded one year later to François Englert and Peter Higgs who, with the late Robert Brout, were the first to discuss the potential importance of such a field for fundamental physics4,5,6. Since then, the Higgs boson has become a powerful tool to study the ways in which the underlying Higgs field affects the fundamental particles of the Standard Model. Furthermore, the ubiquity of the Higgs field means that the Higgs boson is, today, widely used in the search for signatures of particles or effects that are hitherto unknown and lie outside the Standard Model.
The Higgs boson in the Standard Model
In the Standard Model, aside from the Higgs boson, there are two kinds of particles. There are fermions, such as the up and down quarks and the electron, which make up ordinary matter. These specific particles (together with one of the three neutrinos) are called first-generation fermions. Two further sets of fermions (second and third generations) involve heavier particles, not normally present in the world around us. Additionally, there are the force carriers: the photon, the W and Z bosons and the gluon, collectively called vector bosons. When these are exchanged between two fermions, they create an attractive or repulsive force between those fermions: photons carry the electromagnetic force, W and Z bosons the weak force and gluons the strong force.
In the 1960s, as physicists were taking the first steps towards assembling this picture, it remained unclear whether a self-consistent theory that included massive force carriers could be constructed. This question was being posed in the context of nuclear physics and also superconductivity in condensed matter physics. Researchers found that such a theory was ultimately possible if one introduced an interaction of the force carriers with a ‘Higgs’ field, and if one could also engineer a non-zero value for that field4,5,6,7,8,9.
As the electroweak part of the Standard Model was being developed10,11,12, interactions of particles with a Higgs field were to become a central part of its formulation, especially in order to generate masses for the W and Z bosons, as required for consistency with experimental observations, while photons and gluons remain massless.
Remarkably, interactions with the Higgs field also provided a consistent theoretical mechanism for producing fermion masses: each fermion interacts with the Higgs field with a different strength (or ‘coupling’), and the stronger the interaction, the larger the resulting mass for the particle. Within the Standard Model the interaction is known as a ‘Yukawa’ interaction13. Thus any question about the origin of the masses of fermions reduces to a question about the origin of the interactions of fermions with the Higgs field.
Why is the Higgs field non-zero in the first place? According to the Standard Model there is a potential energy density associated with the value of the Higgs field and the lowest potential energy corresponds to a non-zero value of the Higgs field. The Standard Model potential has a form dictated by internal consistency conditions. With some simplifications, labelling the magnitude of the Higgs field as ϕ, the potential has the form
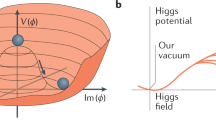
This is illustrated by the red line in Fig. 1. The minimum of the potential, that is, the energetically most favourable choice for ϕ, lies at a value of ϕ that is non-zero, ϕ = 1. An important implication of the non-zero constant value of the Higgs field is the impossibility to carry angular momentum, or more technically having ‘spin 0’. A non-zero value for the spin would break at least one of the well-tested space–time symmetries. Hence, the excitation of the Higgs field, the Higgs boson, must be a spin-0 particle and it is in fact the only known fundamental particle with this property.
The potential energy density \(V(\varphi )\) associated with the Higgs field ϕ, as a function of the value of ϕ. The red curve shows the potential within the Standard Model. The Higgs field has a value corresponding to a minimum of the potential and the region highlighted in black represents our current experimental knowledge of the potential. Alternative potentials that differ substantially from the Standard Model away from that minimum (for example, the blue curve) would be equally consistent with current data.
One of the reasons for the central importance of the discovery of the Higgs boson was that it finally made it possible to start testing the remarkable theoretical picture outlined above. It is not possible to probe the interactions of a given particle with the Higgs field. However, one can instead measure a particle’s interaction with the excitations of the Higgs field, that is, with a Higgs boson. If the Standard Model provides the correct picture for the generation of mass, the strength of any particle’s interaction with the Higgs boson has to be directly related to that particle’s mass.
Aside from providing a powerful way of testing the Higgs mechanism, the interaction of the Higgs boson with other particles is intriguing because it implies the existence of a ‘fifth force’, mediated by the exchange of Higgs bosons. The fact that such a force is stronger for heavier particles makes it qualitatively different from all other interactions in the Standard Model, whose interaction strengths come in multiples of some basic unit of charge, like the electron charge for the electric force. The pattern is, if anything, more reminiscent of gravity, but with important differences. One is that the force mediated by the Higgs boson is active only at very short distances, whereas Einstein’s gravity acts over all distance scales. Another is that the Higgs boson couples directly only to elementary Standard Model particles. By contrast, gravity couples to the total mass. In ordinary matter, that total mass is much larger than the sum of the elementary particle masses, because the strong force contributes substantially to the proton and neutron masses14.
What we know so far and how
The Higgs mechanism provides the simplest model to explain particle masses in a way that is consistent with the electroweak interactions. As physicists we should seek to establish whether it is the model chosen by nature.
Experimental studies of the Higgs boson take place at particle colliders. The likelihood of producing a Higgs boson in a collision becomes larger when the particles that collide interact strongly with the Higgs field, that is, when they are heavy. At the high centre-of-mass energies that are required, particle physicists know how to collide just two things: protons and electrons, as well as their antiparticles. That poses an issue, because electrons and the particles that make up protons are light, that is, they interact only very weakly with the Higgs boson.
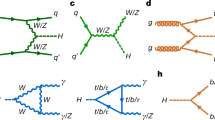
The approach of particle physicists is to exploit the occasional production of heavy particles in the high-energy collision of light particles, and to then have those heavy particles produce a Higgs boson. CERN’s LHC collides protons, which are mostly made of up and down quarks and gluons. The most frequent way of producing a Higgs boson is for a pair of gluons, one from each proton, to collide and create a top quark and a top anti-quark as a very short-lived quantum fluctuation. The top quark is the heaviest known particle (about 184 times the proton mass) and so the top and anti-top quarks interact strongly with the Higgs field, thereby occasionally producing a Higgs boson. A short while later (about 10−22 s), the Higgs boson decays. About 2.6% of decays are to a pair of Z bosons, which themselves also decay almost immediately, for example each to an electron–positron or muon–anti-muon pair (so-called charged leptons), which gives a distinctive experimental signature. This sequence is illustrated in Fig. 2a.
a, Illustration of one process for the production and decay of a Higgs boson at the LHC. b, Total centre-of-mass energy of four leptons (4l; electrons and/or muons and their antiparticles) from the CMS experiment; the peak around 125 GeV corresponds to decays of Higgs bosons, whereas the peak near 91.2 GeV corresponds to decays of single Z bosons (not Higgs-induced), adapted from ref. 95. The decay to Z bosons was one of the channels used for the discovery of the Higgs boson, with the other important discovery channels being the decay to two W bosons and that to two photons (the latter proceeds through a quantum fluctuation with top quarks and W bosons).
The ATLAS and CMS experiments at the LHC select events with four such leptons and record the total of the energy of the leptons (in their centre-of-mass frame). There are a variety of ways in which four leptons can be produced, but for those events in which they come from a Higgs-boson decay, the total energy is expected to cluster around the Higgs mass—the red peak in Fig. 2b. That red peak provides considerable information: (1) the existence of the peak near 125 GeV tells us that there is a new particle, the Higgs boson; (2) the position of the peak indicates the mass of the Higgs boson; (3) other features of the events in the peak, for example the relative angular distributions of the leptons (not shown in the figure), confirm that the Higgs boson carries no intrinsic angular momentum, that is, it is a spin-0 particle; (4) the number of events in the peak is sensitive to the interaction strength of the Higgs boson both with top quarks and with Z bosons. This last point is crucial because the Standard Model Higgs mechanism predicts a very specific interaction strength of each particle with the Higgs boson. Point (4) provides us with a first test of this hypothesis.
There are several potential concerns about the robustness of these kinds of test. For instance, in the process shown in Fig. 2 there is an assumption that there was a quantum fluctuation producing a top–anti-top pair. Even if that assumption is correct, the number of events in the peak tells us about the product of the top and Z interactions, not the top and Z interactions separately. For this reason, the LHC experiments look for the Higgs boson in a multitude of production and decay processes, each one with complementary sensitivity. For example, it is possible to observe Higgs-boson decays in events in which top quarks are not simply an evanescent quantum fluctuation, but are instead produced as short-lived real particles that emerge in their own right from the collision together with the Higgs boson and can be experimentally detected. Doing so15,16, in 2018, was a major milestone in particle physics, as were the highly challenging observations of the Higgs boson decaying to bottom quarks17,18 and τ leptons19,20. Together, these measurements conclusively established that the Higgs mechanism is responsible for the mass of the full third generation of charged fermions.
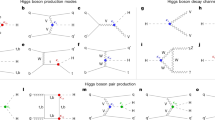
Overall, by assembling information from different production and decay channels, a picture has emerged of Higgs interactions for the heaviest particles—both vector bosons and fermions—that is consistent with the Standard Model hypothesis to within the current measurement accuracies that range from 5% to 20%, as summarized in Fig. 3. On the other hand, interactions with very light particles, such as the electron and up and down quarks of which we are made of, are too rare for current methods to observe.
a, Summary of which Higgs interactions have been conclusively established and future prospects. Photons and gluons are omitted because they are massless and do not interact directly with the Higgs field. Neutrinos are also omitted: their masses are very small relative to those of the other leptons shown, and not individually known. b, Plot of measured strength of interaction of particles with the Higgs boson versus particle mass, as determined by the ATLAS Collaboration (adapted from ref. 96). The straight line shows the expected Standard Model behaviour, in which the interaction strength is proportional to the mass of the fermions (squared mass for W and Z bosons). The CMS Collaboration has similar results97.
Although the discovery of the Standard Model Higgs boson was highly anticipated at the LHC, the ability to explore so many of its features was a surprise. To have established even part of the broad picture of Higgs-boson interactions in just ten years is a major achievement, especially when one considers that, at the time when the LHC was being commissioned, many of the production and decay channels that are central to today’s measurements were believed to be beyond the reach of the LHC21,22.
There are many reasons why this progress has been possible. One of them is that nature happens to have chosen a value for the Higgs mass that is particularly fortunate for experimental studies. Had the Higgs boson been 50 GeV heavier, it would have been almost impossible to detect more than just two basic decay channels (to a pair of W bosons or a pair of Z bosons). Had it been just 10 GeV lighter, the decays to W bosons and Z bosons would probably have been impossible to see so far. It was not just a question of good fortune, however.
The excellent performance of the LHC accelerator and of the ATLAS and CMS detectors, each of them a highly complex system, has been crucial. Furthermore, in the past ten years, there have been major advances in techniques for analysing collider data. One facet has been to learn how to reliably extract information about individual proton–proton collisions when detectors contain not just one proton–proton collision at a time, but dozens filling the detector simultaneously, 40 million times per second23,24. Another reflects the fact that the beautifully clear peak in Fig. 2b is the exception rather than the rule: for most other Higgs-boson studies (for example, Higgs decay to two bottom quarks or two W bosons), experimenters and theorists have had to develop a wide range of technology for differentiating Higgs-boson signals from the many processes with signatures similar to that of a Higgs boson, but that do not involve a Higgs boson. These studies are increasingly benefiting from a combination of new ideas for how to perform the analyses (for example, ref. 25) and the power of machine learning26.
The quantitative interpretation of observed signal rates in terms of Higgs interaction strengths would also not have been possible without several decades of progress in the prediction and modelling of the rich array of effects that occur when protons collide, often associated with the strong interaction. It is crucial, for example, to have excellent theoretical control over the rate of quark and gluon collisions given a certain number of proton collisions27,28. Another facet is that collisions often involve not just one quantum fluctuation, as in Fig. 2, but multiple additional quantum fluctuations, each one of which modifies the probability of Higgs-boson production. The greater the number of quantum fluctuations that one can account for in theoretical predictions (today up to three additional fluctuations29), the more accurately one can relate experimental observations to the Standard Model30,31. Finally, Fig. 2 is a vastly simplified picture and the experiments rely profoundly on accurate simulation32,33 of the full structure of proton–proton collisions, involving the production of hundreds of particles per collision.
What is still to be established?
In many respects, the experimental exploration of the Higgs sector is only in its infancy. There are two broad directions of ongoing investigation: obtaining higher precision in studies of interactions that have already been observed and detecting further kinds of interactions that are, so far, yet to be seen.
We start with the question of precision. Examining Fig. 3b, one sees that the interactions of the Higgs boson with W and Z bosons and the third-generation charged leptons and quarks are currently known to a precision of about 5–20%. We would not consider the theory of electromagnetism established if we had only verified the strength of electromagnetic forces to within 10% accuracy.
One of the reasons for aiming for higher precision is that even though the Standard Model Higgs mechanism outlined above is the simplest model that is consistent with data, it is far from being the only viable one. Indeed, as we shall elaborate on below, it is widely believed that the Standard Model as it stands cannot be a complete description of nature. For example, it is conceivable that the Higgs boson is not an elementary particle, but rather is composed of other, yet-to-be discovered particles. High-precision measurements of Higgs-related processes can be very sensitive to such extensions of the Standard Model. In particular, the rates of Higgs-related processes could be affected by quantum fluctuations involving any new particles. Such effects might be visible even in scenarios where the new particles are too heavy to be directly produced and observed at a given collider. In general, increasing the precision by a factor of four effectively doubles the mass scale that can be indirectly probed for those new particles.
The path for improvement is conceptually straightforward: with 20 times more data to come in the next 15–20 years from the approved high-luminosity upgrade of the LHC, and foreseeable improvements in analysis techniques and theoretical calculations, the ATLAS and CMS experiments expect to determine the currently observed set of interactions to within a couple of percent34. Reaching beyond that requires a different kind of collider. An electron–positron collider with centre-of-mass energies of around 250 GeV (a ‘Higgs factory’)35,36,37,38,39 is widely considered to be a promising option (see the European Strategy for Particle Physics40). Advantages are that electrons and positrons, in contrast to protons, are simple fundamental particles, and that the main Higgs-boson production mechanisms at an electron–positron collider are largely free of complications associated with strong interactions. Such a collider could improve the precision of our knowledge of the Higgs interactions by a further factor of about ten41.
Let us now turn to a discussion of interactions that are yet to be observed. Notwithstanding the good prospects for dramatically improving the precision of Higgs measurements connected with the vector bosons and third-generation (heaviest) quarks and leptons, recall that the relevance of the Higgs sector for our everyday life is that it is believed to generate masses for the first (lightest) generation of fundamental particles, the electron and up and down quarks. Even though experimentally testing our theoretical expectations for the interactions between first-generation fermions and the Higgs boson is highly challenging, there are prospects for the second generation, and in particular the interactions of the Higgs boson with the muon, which can be observed through the \(H\to {\mu }^{+}{\mu }^{-}\) decay. So far the data is suggestive of such decays42,43, and definitive observation of \(H\to {\mu }^{+}{\mu }^{-}\), if it occurs at a rate that is compatible with the Standard Model, is expected to come in the next decade. Measurements involving the rest of the second generation are more difficult.
The LHC can exclude anomalously large interactions of the Higgs boson with charm quarks34 (for example, using ideas such as those in refs. 44,45). It has long been thought that to definitively observe \(H\to c\bar{c}\) decays would require a future \({e}^{+}{e}^{-}\) collider (or alternatively an electron–proton collider46). Significant recent improvements in sensitivity to this decay channel at the LHC47,48 raise the question of whether future developments can bring its observation within reach of the high-luminosity LHC. For other Yukawa interactions, the path is less clear.
Investigations are ongoing to establish the potential sensitivity of a future \({e}^{+}{e}^{-}\) collider to electron and strange-quark Yukawa interactions (see, for example, ref. 49), although currently it seems that it will be challenging to obtain a statistically conclusive signal. For the coupling of up and down quarks to the Higgs boson, there are currently no concrete possibilities in sight unless those couplings are very strongly enhanced relative to the Standard Model expectation. There has been discussion of whether precise atomic physics measurements could be sensitive to the Higgs forces involving light quarks50; however, this seems challenging51.
Central to all of Higgs physics is the Higgs potential. Recall that the Higgs field is non-zero everywhere in the Universe, and so produces non-zero masses for fermions and electroweak bosons, because the minimum of the Higgs potential, equation (1) and Fig. 1, lies at a non-zero value of the Higgs field ϕ. One of the most important open questions in Higgs physics is whether the potential written in that equation is the one chosen by nature. We cannot directly explore the potential across different values of the Higgs field. However, it turns out that the specific shape of the potential in the immediate vicinity of the minimum determines the probability of an important process—the splitting of a Higgs boson into two (or even three) Higgs bosons; this kind of process is referred to as a Higgs-boson self-interaction. Accurate observation of such a process is widely considered to be the best (but not the only52) way of experimentally establishing whether the world we live in is consistent with that simple potential. By the end of the high-luminosity LHC’s operation in 15–20 years, the ATLAS and CMS experiments are expected to see first indications of the simultaneous production of two Higgs bosons. However, gathering conclusive evidence for a contribution to Higgs-pair production from the splitting of a first Higgs boson almost certainly requires a more powerful collider and several options are under discussion36,53,54,55,56.
These are but some of the questions that are being explored. Other important ones that the LHC experiments are starting to be sensitive to include the lifetime of the Higgs boson57,58,59,60 and the nature of Higgs interactions at energies well above the electroweak energy scale61,62.
Higgs and major open questions of particle physics and cosmology
Many of the above measurements are of interest not just owing to the fundamental nature of the Higgs sector within the Standard Model, but because they are also sensitive to scenarios that extend the role of the Higgs sector beyond that in the Standard Model. Even though the Standard Model has successfully passed all the numerous experimental tests so far, it leaves open several major questions. To various degrees, the Higgs boson is tied to potential solutions to these puzzles.
We close our discussion with an overview of some of these possible connections, illustrated in Fig. 4, as they play an important role in guiding ongoing experimental and theoretical research directions in particle physics. There is a lot of ground to cover, so we will begin with and give more emphasis to aspects closely related to the Higgs boson, and only briefly mention later some of the more speculative ideas.
One major puzzle is that the weak and Higgs interactions are much stronger, by a factor of about 1032, than the gravitational interaction. This is especially challenging if one harbours the hope—as do many physicists—that all the known interactions might come from a unifying and simpler framework. Over the past decades, the desire to explain the origin of this large difference, the so-called ‘hierarchy problem’, has motivated a range of theoretical proposals.
One possibility is for the Higgs boson not to be an elementary particle, but rather a composite object made of other, as yet undiscovered particles63. Examples of other well studied proposals are new (approximate) space–time symmetries64,65,66 and new space dimensions67,68,69,70. More recently, some more speculative ideas suggested possible connections between the weak scale and cosmological evolution71,72,73 or the amount of dark energy in the Universe74,75.
Without one of these proposals, or a new mechanism yet to be thought of, the hierarchy between the weak and the gravitational interaction can only arise if distinct parameters in some ultimate fundamental theory cancel to within 1 part in 1032. This is known as the fine-tuning problem of the Higgs sector.
The discovery of the Higgs boson brought such questions unavoidably to the fore. The mere existence of the Higgs boson, and the (still approximate) picture of its properties, already exclude many theoretical ideas. In comparison with the decades before its discovery, we now have a much clearer target and sharper questions to answer with our theoretical models.
Another important question is why there is more matter than antimatter in the Universe. This so-called baryonic asymmetry cannot be explained within the Standard Model. Such an asymmetry can be generated if a suitable set of conditions is met76. One promising avenue that is being explored follows the history of the Universe as it cooled down after the Big Bang.
When the Universe was very hot, the minimum of the Higgs potential at a non-zero value of the Higgs field was largely irrelevant because temperature fluctuations were much larger than the depth of the potential. As the Universe cooled, the situation changed. Within the Standard Model that change is smooth. Other promising scenarios, which involve new particles interacting with the Higgs boson, would generate a sharper transition, which sets the stage for generating the observed baryon asymmetry77, although further ingredients are also needed.
These scenarios involve more complex structures for the Higgs potential, and at least one new particle at the electroweak energy scale, which can be searched for at the LHC either through its direct production or through its indirect impact on the Higgs couplings, in particular the Higgs self-interaction. A measurement of the latter is therefore essential to shed light on this question. Early-Universe phase transitions could also produce gravitational signatures that can be detected by future gravitational wave experiments78,79.
In addition to the questions directly related to the Higgs boson mentioned above, there are also other contexts in which the Higgs boson can play an important role. One example of this is the question of dark matter. Astrophysical and cosmological observations show that the majority of the matter in the Universe is dark and not made of any particle we know of. Such observations rely on the gravitational effects of the dark matter on ordinary, Standard Model matter. At the same time, we know very little about the non-gravitational properties of dark matter. New particles with masses around the electroweak and Higgs mass scales can be promising dark-matter candidates.
As the Higgs mechanism is responsible for generating similar masses of the Standard Model particles, it is possible that it plays some role in generating the dark-matter mass as well80,81,82. There are also scenarios in which the dark-matter sector involves more than one kind of particle. Similar to particles in the Standard Model, they could have their own interactions, and a whole set of other closely related particles. In this case, the Higgs boson would provide a portal to a new ‘dark world’83.
The origin of the pattern of masses and interactions among different generations of the Standard Model particles is an intriguing puzzle. For example, first-generation quarks are much lighter than third-generation quarks, which in the Standard Model needs to be arranged manually by setting correspondingly disparate values of the Yukawa couplings. Understanding the origin of this pattern has also been the focus of decades of efforts. As the Higgs sector is responsible for generating the masses of these particles, it is tempting to think that the actual Higgs sector may be structurally different from the Standard Model, in a way that causes the observed pattern to emerge naturally84,85,86.
The models that explore such ideas often lead to predictions of modified interactions between the Higgs boson and the quarks (and/or leptons). One signature of such models is that the Higgs boson could decay into a pair of quarks or leptons with different flavour. Similarly, one may also ask whether the Higgs mechanism has a role in generating the extremely small masses for neutrinos and various models have been envisaged in this respect87.
The questions above relate the Higgs boson with known or unknown elementary particles. However, there are also mysteries in fundamental physics that go beyond such types of questions and speculative, yet intriguing, links have been proposed with the Higgs sector. For example, it has been noted that the Standard Model self-interaction of the Higgs boson becomes very close to zero if it is measured88,89,90 at energies nine orders of magnitude beyond the Higgs mass91,92. A curious and connected fact is that it seems likely that the Standard Model Higgs sector has a ground state with lower energy than the state we live in. Hence, quantum mechanics would allow a ‘tunnelling’ process through which our whole Universe can decay, even though the probability of such an event happening within the 14-billion year age of the Universe is tiny. The final possibility that we mention for new dynamics of the Higgs field at high energies is a possible link to inflation, which is a period of exponential expansion in the early niverse that is essential to explain the striking long-distance uniformity of the cosmic microwave background. The Higgs boson, having spin 0, may be responsible for driving inflation93.
The Higgs boson is an invaluable tool in the search for answers to several of the above questions. Many of the proposed solutions predict the existence of new particles that generally interact directly with the Higgs boson. These particles are actively searched for at high-energy colliders. Still, even if the direct production of these particles lies outside our reach, for instance because the LHC is not energetic enough, their involvement in quantum fluctuations may affect Higgs-boson production and decay, in the same way that top-quark quantum fluctuations mediate Higgs production in Fig. 2. The expected future advances in precision measurements of the Higgs boson, as mentioned above, will bring considerably improved sensitivity to such scenarios.
Conclusions
The discovery of the Higgs boson at the LHC marked the beginning of a new era of particle physics. In the ten years since, the exploration of the Higgs sector has progressed far beyond original expectations, owing to ingenious advances both experimental and theoretical. Every Higgs-related measurement so far has been consistent with the Standard Model, the simplest of all current models of particle physics: a remarkable win for Occam’s razor. Today, it is clear that the Higgs mechanism, first proposed in the 1960s, is responsible not only for the masses of the W and Z bosons and but also for those of the three heaviest fermions. This directly implies the existence of a fifth force, mediated by the Higgs boson. Still, much remains to be probed. Whatever is found in the coming decades, we will be wiser: either with solid evidence for parts of the Standard Model that remain crucially to be established, such as the nature of the Higgs potential, or by opening a window to new horizons and the major mysteries of the Universe.
References
ATLAS Collaboration et al. Observation of a new particle in the search for the Standard Model Higgs boson with the ATLAS detector at the LHC. Phys. Lett. B 716, 1–29 (2012). This article reports the discovery of the Higgs boson by the ATLAS Collaboration.
CMS Collaboration et al. Observation of a new boson at a mass of 125 GeV with the CMS experiment at the LHC. Phys. Lett. B 716, 30–61 (2012). This article reports the discovery of the Higgs boson by the CMS Collaboration.
Quigg, C. & Shrock, R. Gedanken worlds without Higgs: QCD-induced electroweak symmetry breaking. Phys. Rev. D 79, 096002 (2009).
Englert, F. & Brout, R. Broken symmetry and the mass of gauge vector mesons. Phys. Rev. Lett. 13, 321–323 (1964). Englert and Brout explain how gauge bosons can acquire a mass through their interaction with scalar fields.
Higgs, P. W. Broken symmetries, massless particles and gauge fields. Phys. Lett. 12, 132–133 (1964).
Higgs, P. W. Broken symmetries and the masses of gauge bosons. Phys. Rev. Lett. 13, 508–509 (1964). Higgs explains how gauge bosons can acquire a mass through their interaction with scalar fields.
Anderson, P. W. Plasmons, gauge invariance, and mass. Phys. Rev. 130, 439–442 (1963).
Guralnik, G. S., Hagen, C. R. & Kibble, T. W. B. Global conservation laws and massless particles. Phys. Rev. Lett. 13, 585–587 (1964).
Kibble, T. W. B. Symmetry breaking in nonAbelian gauge theories. Phys. Rev. 155, 1554–1561 (1967).
Glashow, S. L. Partial symmetries of weak interactions. Nucl. Phys. 22, 579–588 (1961).
Salam, A. & Ward, J. C. Electromagnetic and weak interactions. Phys. Lett. 13, 168–171 (1964).
Weinberg, S. A model of leptons. Phys. Rev. Lett. 19, 1264–1266 (1967).
Yukawa, H. On the interaction of elementary particles I. Proc. Phys. Math. Soc. Jap. 17, 48–57 (1935).
Durr, S. et al. Ab-Initio determination of light hadron masses. Science 322, 1224–1227 (2008).
ATLAS Collaboration. Observation of Higgs boson production in association with a top quark pair at the LHC with the ATLAS detector. Phys. Lett. B 784, 173–191 (2018).
CMS Collaboration et al. Observation of \(t\bar{t}\) H production. Phys. Rev. Lett. 120, 231801 (2018).
ATLAS Collaboration et al. Measurements of WH and ZH production in the \(H\to b\bar{b}\) decay channel in pp collisions at 13 TeV with the ATLAS detector. Eur. Phys. J. C 81, 178 (2021).
CMS Collaboration et al. Observation of Higgs boson decay to bottom quarks. Phys. Rev. Lett. 121, 121801 (2018).
ATLAS Collaboration et al. Measurements of Higgs boson production cross-sections in the H→τ+τ− decay channel in pp collisions at s=13TeV with the ATLAS detector. Preprint at https://arxiv.org/abs/2201.08269 (2022).
CMS Collaboration et al. Measurement of the inclusive and differential Higgs boson production cross sections in the decay mode to a pair of τ leptons in pp collisions at s=13 TeV. Phys. Rev. Lett. 128, 081805 (2022).
CMS Collaboration. CMS technical design report, volume II: physics performance. J. Phys. G 34, 995–1579 (2007).
ATLAS Collaboration et al. Expected performance of the ATLAS experiment – detector, trigger and physics. Preprint at https://arxiv.org/abs/0901.0512 (2008).
Cacciari, M. & Salam, G. P. Pileup subtraction using jet areas. Phys. Lett. B 659, 119–126 (2008).
Bertolini, D., Harris, P., Low, M. & Tran, N. Pileup per particle identification. J. High Energ. Phys. 10, 059 (2014).
Marzani, S., Soyez, G. and Spannowsky, M. Looking Inside Jets: An Introduction to Jet Substructure and Boosted-object Phenomenology Vol. 958 (Springer, 2019); https://doi.org/10.1007/978-3-030-15709-8
Guest, D., Cranmer, K. & Whiteson, D. Deep learning and its application to LHC physics. Ann. Rev. Nucl. Part. Sci. 68, 161–181 (2018).
Gao, J., Harland-Lang, L. & Rojo, J. The structure of the proton in the LHC precision era. Phys. Rep. 742, 1–121 (2018).
Ball, R. D. et al. The PDF4LHC21 combination of global PDF fits for the LHC Run III. Preprint at https://arxiv.org/abs/2203.05506 (2022).
Anastasiou, C., Duhr, C., Dulat, F., Herzog, F. & Mistlberger, B. Higgs boson gluon-fusion production in QCD at three loops. Phys. Rev. Lett. 114, 212001 (2015). Calculation of Higgs boson production probability taking into account the highest number of quantum fluctuations possible today.
Heinrich, G. Collider physics at the precision. Frontier, Phys. Rep. 922, 1–69 (2021).
de Florian, D. et al. Handbook of LHC Higgs cross sections: 4. Deciphering the nature of the Higgs sector. Preprint at https://arxiv.org/abs/1610.07922 (2016). This report summarizes the global theoretical knowledge of Higgs boson production and decay.
Buckley, A. et al. General-purpose event generators for LHC physics. Phys. Rep. 504, 145–233 (2011).
Campbell, J. M. et al. Event generators for high-energy physics experiments. Preprint at https://arxiv.org/abs/2203.11110 (2022).
Dainese, A. et al (eds) Report on the Physics at the HL-LHC, and Perspectives for the HE-LHC CERN Yellow Reports: Monographs Vol. 7/2019 (CERN, 2019); https://doi.org/10.23731/CYRM-2019-007
Abada, A. et al. FCC-ee: The Lepton Collider: future circular collider conceptual design report volume 2. Eur. Phys. J. ST 228, 261–623 (2019).
Roloff, P., Franceschini, R., Schnoor, U. & Wulzer, A. The Compact Linear e+e− Collider (CLIC): physics potential. Preprint at https://arxiv.org/abs/1812.07986 (2018).
Baer, H. et al. The International Linear Collider Technical Design Report – Volume 2: Physics. Preprint at https://arxiv.org/abs/1306.6352 (2013).
CEPC Study Group. CEPC Conceptual Design Report: Volume 2 – physics & detector. Preprint at https://arxiv.org/abs/1811.10545 (2018).
Bai, M. et al. C3: A “cool” route to the Higgs boson and beyond. Preprint at https://arxiv.org/abs/2110.15800 (2021).
2020 Update of the European Strategy for Particle Physics (Brochure) Technical Report (CERN, 2020); https://doi.org/10.17181/CERN.JSC6.W89E
de Blas, J. et al. Higgs boson studies at future particle colliders. J. High Energ. Phys. 1, 139 (2020).
ATLAS Collaboration. A search for the dimuon decay of the Standard Model Higgs boson with the ATLAS detector. Phys. Lett. B 812, 135980 (2021).
CMS Collaboration et al. Evidence for Higgs boson decay to a pair of muons. J. High Energ. Phys. 1, 148 (2021).
Bishara, F., Haisch, U., Monni, P. F. & Re, E. Constraining light-quark Yukawa couplings from Higgs distributions. Phys. Rev. Lett. 118, 121801 (2017).
Soreq, Y., Zhu, H. X. & Zupan, J. Light quark Yukawa couplings from Higgs kinematics. J. High Energ. Phys. 12, 045 (2016).
André, K. D. J. et al. An experiment for electron-hadron scattering at the LHC. Eur. Phys. J. C 82, 40 (2022).
ATLAS Collaboration. Direct constraint on the Higgs-charm coupling from a search for Higgs boson decays into charm quarks with the ATLAS detector. Preprint at https://arxiv.org/abs/2201.11428 (2022).
CMS Collaboration. Search for Higgs boson decay to a charm quark-antiquark pair in proton-proton collisions at \(\sqrt{s}\) = 13 TeV. Preprint at https://arxiv.org/abs/2205.05550 (2022).
d’Enterria, D., Poldaru, A. & Wojcik, G. Measuring the electron Yukawa coupling via resonant s-channel Higgs production at FCC-ee. Eur. Phys. J. Plus 137, 201 (2022).
Delaunay, C., Ozeri, R., Perez, G. & Soreq, Y. Probing atomic Higgs-like forces at the precision frontier. Phys. Rev. D 96, 093001 (2017).
Flambaum, V. V., Geddes, A. J. & Viatkina, A. V. Isotope shift, nonlinearity of King plots, and the search for new particles. Phys. Rev. A 97, 032510 (2018).
McCullough, M. An indirect model-dependent probe of the Higgs self-coupling. Phys. Rev. D 90, 015001 (2014).
Abada, A. et al. FCC-hh: the Hadron Collider: future circular collider conceptual design report volume 3. Eur. Phys. J. ST 228, 755–1107 (2019).
CEPC Study Group. CEPC Conceptual Design Report: Volume 1 – accelerator. Preprint at https://arxiv.org/abs/1809.00285 (2018).
Franceschini, R. & Greco, M. Higgs and BSM physics at the future muon collider. Symmetry 13, 851 (2021).
Delahaye, J. P. et al. Muon colliders. Preprint at https://arxiv.org/abs/1901.06150 (2019).
Caola, F. & Melnikov, K. Constraining the Higgs boson width with ZZ production at the LHC. Phys. Rev. D 88, 054024 (2013).
Campbell, J. M., Ellis, R. K. & Williams, C. Bounding the Higgs width at the LHC using full analytic results for gg- > e−e+μ−μ+. J. High Energy Phys. 4, 060 (2014).
ATLAS Collaboration. Constraints on off-shell Higgs boson production and the Higgs boson total width in \(ZZ\to 4\ell \) and \(ZZ\to 4\ell \) final states with the ATLAS detector. Phys. Lett. B 786, 223–244 (2018).
CMS Collaboration. First evidence for off-shell production of the Higgs boson and measurement of its width. Preprint at https://arxiv.org/abs/2202.06923 (2022).
ATLAS Collaboration. Measurement of the associated production of a Higgs boson decaying into b-quarks with a vector boson at high transverse momentum in pp collisions at \(\sqrt{s}=13\) TeV with the ATLAS detector. Phys. Lett. B 816, 136204 (2021).
CMS Collaboration et al. Inclusive search for highly boosted Higgs bosons decaying to bottom quark-antiquark pairs in proton-proton collisions at \(\sqrt{s}=13\) TeV. J. High Energy Phys. 12, 085 (2020).
Kaplan, D. B. & Georgi, H. SU(2) x U(1) breaking by vacuum misalignment. Phys. Lett. B 136, 183–186 (1984).
Fayet, P. Supersymmetry and weak, electromagnetic and strong interactions. Phys. Lett. B 64, 159 (1976).
Fayet, P. Spontaneously broken supersymmetric theories of weak, electromagnetic and strong interactions. Phys. Lett. B 69, 489 (1977).
Dimopoulos, S. & Georgi, H. Softly broken supersymmetry and SU(5). Nucl. Phys. B 193, 150–162 (1981).
Arkani-Hamed, N., Dimopoulos, S. & Dvali, G. R. The Hierarchy problem and new dimensions at a millimeter. Phys. Lett. B 429, 263–272 (1998).
Antoniadis, I., Arkani-Hamed, N., Dimopoulos, S. & Dvali, G. R. New dimensions at a millimeter to a Fermi and superstrings at a TeV. Phys. Lett. B 436, 257–263 (1998).
Randall, L. & Sundrum, R. A Large mass hierarchy from a small extra dimension. Phys. Rev. Lett. 83, 3370–3373 (1999).
Randall, L. & Sundrum, R. An Alternative to compactification. Phys. Rev. Lett. 83, 4690–4693 (1999).
Graham, P. W., Kaplan, D. E. & Rajendran, S. Cosmological relaxation of the electroweak scale. Phys. Rev. Lett. 115, 221801 (2015).
Arkani-Hamed, N. et al. Solving the hierarchy problem at reheating with a large number of degrees of freedom. Phys. Rev. Lett. 117, 251801 (2016).
Giudice, G. F., McCullough, M. & You, T. Self-organised localisation. J. High Energ. Phys. 10, 093 (2021).
Arvanitaki, A., Dimopoulos, S., Gorbenko, V., Huang, J. & Van, K. Tilburg, A small weak scale from a small cosmological constant. J. High. Energy Phys. 05, 071 (2017).
Arkani-Hamed, N., D’Agnolo, R. T. & Kim, H. D. Weak scale as a trigger. Phys. Rev. D 104, 095014 (2021).
Sakharov, A. D. Violation of CP invariance, C asymmetry, and baryon asymmetry of the universe. Pisma Zh. Eksp. Teor. Fiz. 5, 32–35 (1967).
Cohen, A. G., Kaplan, D. B. & Nelson, A. E. Progress in electroweak baryogenesis. Ann. Rev. Nucl. Part. Sci. 43, 27–70 (1993).
Caprini, C. et al. Science with the space-based interferometer eLISA. II: gravitational waves from cosmological phase transitions. J. Cosmol. Astropart. Phys. 04, 001 (2016).
Caprini, C. et al. Detecting gravitational waves from cosmological phase transitions with LISA: an update. J. Cosmol. Astropart. Phys. 03, 024 (2020).
Silveira, V. & Zee, A. Scalar Phantoms. Phys. Lett. B 161, 136–140 (1985).
Burgess, C. P., Pospelov, M. & ter Veldhuis, T. The minimal model of nonbaryonic dark matter: a singlet scalar. Nucl. Phys. B 619, 709–728 (2001).
McDonald, J. Gauge singlet scalars as cold dark matter. Phys. Rev. D 50, 3637–3649 (1994).
Patt, B. & Wilczek, F. Higgs-field portal into hidden sectors. Preprint at https://arxiv.org/abs/hep-ph/0605188 (2006).
Barr, S. M. & Zee, A. A new approach to the electron-muon mass ratio. Phys. Rev. D 15, 2652 (1977).
Bjorken, J. D. & Weinberg, S. A mechanism for nonconservation of muon number. Phys. Rev. Lett. 38, 622 (1977).
Babu, K. S. & Nandi, S. Natural fermion mass hierarchy and new signals for the Higgs boson. Phys. Rev. D 62, 033002 (2000).
de Gouvêa, A. Neutrino mass models. Ann. Rev. Nucl. Part. Sci. 66, 197–217 (2016).
Cabibbo, N., Maiani, L., Parisi, G. & Petronzio, R. Bounds on the fermions and Higgs boson masses in grand unified theories. Nucl. Phys. B 158, 295–305 (1979).
Hung, P. Q. Vacuum instability and new constraints on fermion masses. Phys. Rev. Lett. 42, 873 (1979).
Lindner, M. Implications of triviality for the Standard Model. Z. Phys. C 31, 295 (1986).
Degrassi, G. et al. Higgs mass and vacuum stability in the Standard Model at NNLO. J. High Energy Phys. 8, 098 (2012).
Buttazzo, D. et al. Investigating the near-criticality of the Higgs boson. J. High Energy Phys. 12, 089 (2013).
Bezrukov, F. L. & Shaposhnikov, M. The Standard Model Higgs boson as the inflaton. Phys. Lett. B 659, 703–706 (2008).
Particle Data Group et al. Review of particle physics. Prog. Theor. Exp. Phys. 2020, 083C01 (2020). This review summarizes all current knowledge of particle physics, both theoretical and experimental.
CMS Collaboration et al. Measurements of production cross sections of the Higgs boson in the four-lepton final state in proton–proton collisions at \(\sqrt{s}=13\) TeV. Eur. Phys. J. C 81, 488 (2021).
ATLAS Collaboration. A detailed map of Higgs boson interactions by the ATLAS experiment ten years after the discovery. Nature https://doi.org/10.1038/s41586-022-04893-w (2022). This article describes the current status of our knowledge of Higgs boson interactions, as measured by the ATLAS Collaboration.
CMS Collaboration. A portrait of the Higgs boson by the CMS experiment ten years after the discovery. Nature https://doi.org/10.1038/s41586-022-04892-x (2022). This article describes the current status of our knowledge of Higgs boson interactions, as measured by the CMS Collaboration.
Acknowledgements
Our Perspective on the Higgs sector has been shaped by exchanges with many of our colleagues. In this regard, we especially acknowledge conversations with N. Arkani-Hamed, F. Caola, G. Giudice, C. Grojean, U. Haisch, M. Kado, G. Landsberg, M. Mangano, M. McCullough, P. Nason, M. Reece, G. Servant, R. Sundrum and C. Wagner, and thank a number of them also for valuable comments on this manuscript. G.P.S. is supported by a Royal Society Research Professorship (RP\R1\180112) and by the United Kingdom’s Science and Technology Facilities Council (grant no. ST/T000864/1). L.-T.W. is supported by the US Department of Energy (grant no. DE-SC0009924).
Author information
Authors and Affiliations
Contributions
The authors declare that they contributed equally to the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature thanks Francesco Riva and Shufang Su for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Salam, G.P., Wang, LT. & Zanderighi, G. The Higgs boson turns ten. Nature 607, 41–47 (2022). https://doi.org/10.1038/s41586-022-04899-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-022-04899-4
This article is cited by
-
The precision measurement of the W boson mass and its impact on physics
Nature Reviews Physics (2024)
-
N3LO+N3LL QCD improved Higgs pair cross sections
Journal of High Energy Physics (2023)
-
Particle physics isn’t going to die — even if the LHC finds no new particles
Nature (2022)
-
A portrait of the Higgs boson by the CMS experiment ten years after the discovery
Nature (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.