Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Perpendicular full switching of chiral antiferromagnetic order by current

Nature volume 607, pages 474–479 (2022)Cite this article

Subjects

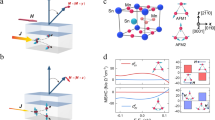
Abstract

Electrical control of a magnetic state of matter lays the foundation for information technologies and for understanding of spintronic phenomena. Spin–orbit torque provides an efficient mechanism for the electrical manipulation of magnetic orders1,2,3,4,5,6,7,8,9,10,11. In particular, spin–orbit torque switching of perpendicular magnetization in nanoscale ferromagnetic bits has enabled the development of stable, reliable and low-power memories and computation12,13,14. Likewise, for antiferromagnetic spintronics, electrical bidirectional switching of an antiferromagnetic order in a perpendicular geometry may have huge impacts, given its potential advantage for high-density integration and ultrafast operation15,16. Here we report the experimental realization of perpendicular and full spin–orbit torque switching of an antiferromagnetic binary state. We use the chiral antiferromagnet Mn3Sn (ref. 17), which exhibits the magnetization-free anomalous Hall effect owing to a ferroic order of a cluster magnetic octupole hosted in its chiral antiferromagnetic state18. We fabricate heavy-metal/Mn3Sn heterostructures by molecular beam epitaxy and introduce perpendicular magnetic anisotropy of the octupole using an epitaxial in-plane tensile strain. By using the anomalous Hall effect as the readout, we demonstrate 100 per cent switching of the perpendicular octupole polarization in a 30-nanometre-thick Mn3Sn film with a small critical current density of less than 15 megaamperes per square centimetre. Our theory reveals that the perpendicular geometry between the polarization directions of current-induced spin accumulation and of the octupole persistently maximizes the spin–orbit torque efficiency during the deterministic bidirectional switching process. Our work provides a significant basis for antiferromagnetic spintronics.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on Springer Link
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Electrical full switching of the perpendicular cluster magnetic octupole under uniaxial tensile strain in the chiral AF order of Mn3Sn.
Fig. 2: Transport properties and magnetic anisotropy of the MBE-grown Mn3Sn layer in the MgO-substrate/W(7 nm)/Mn3Sn(30 nm)/MgO(5 nm) stack.
Fig. 3: Mechanism for the perpendicular switching of the cluster magnetic octupole in the chiral AF order of Mn3Sn.
Fig. 4: Bias-field-direction dependence of the electrical switching assisted by the magnetocrystalline anisotropy and zero-field switching.

Similar content being viewed by others

Data availability

The data that support the findings of this study are available from the corresponding author upon reasonable request.

References

  1. Miron, I. M. et al. Perpendicular switching of a single ferromagnetic layer induced by in-plane current injection. Nature 476, 189–193 (2011).

    Article  ADS  CAS  PubMed  Google Scholar 

  2. Liu, L. et al. Spin-torque switching with the giant spin Hall effect of tantalum. Science 336, 555–558 (2012).

    Article  ADS  CAS  PubMed  Google Scholar 

  3. Fan, Y. et al. Magnetization switching through giant spin–orbit torque in a magnetically doped topological insulator heterostructure. Nat. Mater. 13, 699–704 (2014).

    Article  ADS  CAS  PubMed  Google Scholar 

  4. Wadley, P. et al. Electrical switching of an antiferromagnet. Science 351, 587–590 (2016).

    Article  ADS  CAS  PubMed  Google Scholar 

  5. Fukami, S., Zhang, C., DuttaGupta, S., Kurenkov, A. & Ohno, H. Magnetization switching by spin–orbit torque in an antiferromagnet–ferromagnet bilayer system. Nat. Mater. 15, 535–541 (2016).

    Article  ADS  CAS  PubMed  Google Scholar 

  6. Moriyama, T., Oda, K., Ohkochi, T., Kimata, M. & Ono, T. Spin torque control of antiferromagnetic moments in NiO. Sci. Rep. 8, 14167 (2018).

    Article  ADS  PubMed  PubMed Central  CAS  Google Scholar 

  7. Chen, X. Z. et al. Antidamping-torque-induced switching in biaxial antiferromagnetic insulators. Phys. Rev. Lett. 120, 207204 (2018).

    Article  ADS  CAS  PubMed  Google Scholar 

  8. Manchon, A. et al. Current-induced spin–orbit torques in ferromagnetic and antiferromagnetic systems. Rev. Mod. Phys. 91, 035004 (2019).

    Article  ADS  MathSciNet  CAS  Google Scholar 

  9. Tsai, H. et al. Electrical manipulation of a topological antiferromagnetic state. Nature 580, 608–613 (2020).

    Article  ADS  CAS  PubMed  Google Scholar 

  10. Shi, J. et al. Electrical manipulation of the magnetic order in antiferromagnetic PtMn pillars. Nat. Electron. 3, 92–98 (2020).

    Article  CAS  Google Scholar 

  11. Takeuchi, Y. et al. Chiral-spin rotation of non-collinear antiferromagnet by spin-orbit torque. Nat. Mater. 20, 1364–1370 (2021).

    Article  ADS  CAS  PubMed  Google Scholar 

  12. Dieny, B. & Chshiev, M. Perpendicular magnetic anisotropy at transition metal/oxide interfaces and applications. Rev. Mod. Phys. 89, 025008 (2017).

  13. Garello, K. et al. SOT-MRAM 300MM integration for low power and ultrafast embedded memories. In 2018 IEEE Symposium on VLSI Circuits 81–82 (IEEE, 2018); https://doi.org/10.1109/VLSIC.2018.8502269

  14. Shao, Q. et al. Roadmap of spin–orbit torques. IEEE Trans. Magn. 57, 1–39 (2021).

    Article  Google Scholar 

  15. Jungwirth, T., Marti, X., Wadley, P. & Wunderlich, J. Antiferromagnetic spintronics. Nat. Nanotechnol. 11, 231–241 (2016).

    Article  ADS  CAS  PubMed  Google Scholar 

  16. Baltz, V. et al. Antiferromagnetic spintronics. Rev. Mod. Phys. 90, 015005 (2018).

  17. Nakatsuji, S., Kiyohara, N. & Higo, T. Large anomalous Hall effect in a non-collinear antiferromagnet at room temperature. Nature 527, 212–215 (2015).

    Article  ADS  CAS  PubMed  Google Scholar 

  18. Suzuki, M. T., Koretsune, T., Ochi, M. & Arita, R. Cluster multipole theory for anomalous Hall effect in antiferromagnets. Phys. Rev. B 95, 094406 (2017).

  19. Chen, H., Niu, Q. & MacDonald, A. H. Anomalous Hall effect arising from noncollinear antiferromagnetism. Phys. Rev. Lett. 112, 017205 (2014).

    Article  ADS  PubMed  CAS  Google Scholar 

  20. Kiyohara, N., Tomita, T. & Nakatsuji, S. Giant anomalous Hall effect in the chiral antiferromagnet Mn3Ge. Phys. Rev. Appl. 5, 064009 (2016).

    Article  ADS  CAS  Google Scholar 

  21. Nayak, A. K. et al. Large anomalous Hall effect driven by a nonvanishing Berry curvature in the noncolinear antiferromagnet Mn3Ge. Sci. Adv. 2, e1501870 (2016).

    Article  ADS  PubMed  PubMed Central  CAS  Google Scholar 

  22. Liu, Z. Q. et al. Electrical switching of the topological anomalous Hall effect in a non-collinear antiferromagnet above room temperature. Nat. Electron. 1, 172–177 (2018).

    Article  CAS  Google Scholar 

  23. Hajiri, T., Ishino, S., Matsuura, K. & Asano, H. Electrical current switching of the noncollinear antiferromagnet Mn3GaN. Appl. Phys. Lett. 115, 052403 (2019).

    Article  ADS  CAS  Google Scholar 

  24. You, Y. et al. Room temperature anomalous Hall effect in antiferromagnetic Mn3SnN films. Appl. Phys. Lett. 117, 222404 (2020).

    Article  ADS  CAS  Google Scholar 

  25. Ikhlas, M. et al. Large anomalous Nernst effect at room temperature in a chiral antiferromagnet. Nat. Phys. 13, 1085–1090 (2017).

    Article  CAS  Google Scholar 

  26. Kuroda, K. et al. Evidence for magnetic Weyl fermions in a correlated metal. Nat. Mater. 16, 1090–1095 (2017).

    Article  ADS  CAS  PubMed  Google Scholar 

  27. Li, X. et al. Anomalous Nernst and Righi–Leduc effects in Mn3Sn: Berry curvature and entropy flow. Phys. Rev. Lett. 119, 056601 (2017).

    Article  ADS  PubMed  Google Scholar 

  28. Higo, T. et al. Large magneto-optical Kerr effect and imaging of magnetic octupole domains in an antiferromagnetic metal. Nat. Photon. 12, 73–78 (2018).

    Article  ADS  CAS  Google Scholar 

  29. Taylor, J. M. et al. Anomalous and topological Hall effects in epitaxial thin films of the noncollinear antiferromagnet Mn3Sn. Phys. Rev. B 101, 094404 (2020).

  30. Higo, T. et al. Omnidirectional control of large electrical output in a topological antiferromagnet. Adv. Funct. Mater. 31, 2008971 (2021).

  31. Yoon, J.-Y. et al. Correlation of anomalous Hall effect with structural parameters and magnetic ordering in Mn3+xSn1−x thin films. AIP Adv. 11, 065318 (2021).

    Article  ADS  CAS  Google Scholar 

  32. Sugimoto, S. et al. Electrical nucleation, displacement, and detection of antiferromagnetic domain walls in the chiral antiferromagnet Mn3Sn. Commun. Phys. 3, 111 (2020).

    Article  CAS  Google Scholar 

  33. Cheng, X. M. et al. Antisymmetric magnetoresistance in magnetic multilayers with perpendicular anisotropy. Phys. Rev. Lett. 94, 017203 (2005).

    Article  ADS  CAS  PubMed  Google Scholar 

  34. Roschewsky, N., Lambert, C.-H. & Salahuddin, S. Spin–orbit torque switching of ultralarge-thickness ferrimagnetic GdFeCo. Phys. Rev. B 96, 064406 (2017).

    Article  ADS  Google Scholar 

  35. Gomonay, O. V. & Loktev, V. M. Using generalized Landau–Lifshitz equations to describe the dynamics of multi-sublattice antiferromagnets induced by spin-polarized current. Low Temp. Phys. 41, 698–704 (2015).

    Article  ADS  CAS  Google Scholar 

  36. Fujita, H. Field-free, spin-current control of magnetization in non-collinear chiral antiferromagnets. Phys. Status Solidi Rapid Res. Lett. 11, 1600360 (2017).

  37. Nomoto, T. & Arita, R. Cluster multipole dynamics in noncollinear antiferromagnets. Phys. Rev. Res. 2, 012045(R) (2020).

  38. Liu, J. & Balents, L. Anomalous Hall effect and topological defects in antiferromagnetic Weyl semimetals: Mn3Sn/Ge. Phys. Rev. Lett. 119, 087202 (2017).

    Article  ADS  PubMed  Google Scholar 

  39. Boldrin, D. et al. Giant piezomagnetism in Mn3NiN. ACS Appl. Mater. Interfaces 10, 18863–18868 (2018).

    Article  CAS  PubMed  Google Scholar 

  40. Back, C. H. et al. Magnetization reversal in ultrashort magnetic field pulses. Phys. Rev. Lett. 81, 3251–3254 (1998).

    Article  ADS  CAS  Google Scholar 

  41. Yoon, J. et al. Crystal orientation and anomalous Hall effect of sputter-deposited non-collinear antiferromagnetic Mn3Sn thin films. Appl. Phys. Express 13, 013001 (2019).

    Article  ADS  CAS  Google Scholar 

  42. Featherston, F. H. & Neighbours, J. R. Elastic constants of tantalum, tungsten, and molybdenum. Phys. Rev. 130, 1324–1333 (1963).

    Article  ADS  CAS  Google Scholar 

  43. Tomita, T., Ikhlas, M. & Nakatsuji, S. Large Nernst effect and thermodynamics properties in Weyl antiferromagnet. JPS Conf. Proc. 30, 011009 (2020).

    Google Scholar 

  44. Brown, P. J., Nunez, V., Tasset, F., Forsyth, J. B. & Radhakrishna, P. Determination of the magnetic structure of Mn3Sn using generalized neutron polarization analysis. J. Phys. Condens. Matter 2, 9409–9422 (1990).

    Article  ADS  CAS  Google Scholar 

  45. Seto, Y. & Ohtsuka, M. ReciPro: free and open-source multipurpose crystallographic software integrating a crystal model database and viewer, diffraction and microscopy simulators, and diffraction data analysis tools. J. Appl. Cryst. 55, 397–410 (2022).

  46. Xu, W. J. et al. Scaling law of anomalous Hall effect in Fe/Cu bilayers. Eur. Phys. J. B 65, 233–237 (2008).

    Article  ADS  CAS  Google Scholar 

  47. Kou, X. et al. Magnetic anisotropy and anomalous Hall effect of ultrathin Co/Pd bilayers. J. Appl. Phys. 112, 093915 (2012).

    Article  ADS  CAS  Google Scholar 

  48. Sung, N. H., Ronning, F., Thompson, J. D. & Bauer, E. D. Magnetic phase dependence of the anomalous Hall effect in Mn3Sn single crystals. Appl. Phys. Lett. 112, 132406 (2018).

    Article  ADS  CAS  Google Scholar 

  49. Higo, T. et al. Anomalous Hall effect in thin films of the Weyl antiferromagnet Mn3Sn. Appl. Phys. Lett. 113, 202402 (2018).

    Article  ADS  CAS  Google Scholar 

  50. Abo, G. S. et al. Definition of magnetic exchange length. IEEE Trans. Magn. 49, 4937–4939 (2013).

    Article  ADS  CAS  Google Scholar 

  51. Emori, S., Bauer, U., Ahn, S.-M., Martinez, E. & Beach, G. S. D. Current-driven dynamics of chiral ferromagnetic domain walls. Nat. Mater. 12, 611–616 (2013).

    Article  ADS  CAS  PubMed  Google Scholar 

  52. Ryu, K.-S., Thomas, L., Yang, S.-H. & Parkin, S. Chiral spin torque at magnetic domain walls. Nat. Nanotechnol. 8, 527–533 (2013).

    Article  ADS  CAS  PubMed  Google Scholar 

  53. Avci, C. O. et al. Current-induced switching in a magnetic insulator. Nat. Mater. 16, 309–314 (2017).

    Article  ADS  CAS  PubMed  Google Scholar 

  54. Bodnar, S. Y. et al. Writing and reading antiferromagnetic Mn2Au by Neel spin–orbit torques and large anisotropic magnetoresistance. Nat. Commun. 9, 348 (2018).

    Article  ADS  PubMed  PubMed Central  CAS  Google Scholar 

  55. Jiang, M. et al. Efficient full spin–orbit torque switching in a single layer of a perpendicularly magnetized single-crystalline ferromagnet. Nat. Commun. 10, 2590 (2019).

    Article  ADS  PubMed  PubMed Central  CAS  Google Scholar 

  56. Ikegawa, S., Mancoff, F. B., Janesky, J. & Aggarwal, S. Magnetoresistive random access memory: present and future. IEEE Trans. Electron Devices 67, 1407–1419 (2020).

    Article  ADS  CAS  Google Scholar 

  57. Park, P. et al. Magnetic excitations in non-collinear antiferromagnetic Weyl semimetal Mn3Sn. npj Quantum Mater. 3, 63 (2018).

    Article  ADS  CAS  Google Scholar 

  58. Miwa, S. et al. Giant effective damping of octupole oscillation in an antiferromagnetic Weyl semimetal. Small Sci. 1, 2000062 (2021).

    Article  Google Scholar 

  59. Pai, C.-F. et al. Spin transfer torque devices utilizing the giant spin Hall effect of tungsten. Appl. Phys. Lett. 101, 122404 (2012).

    Article  ADS  CAS  Google Scholar 

  60. Mondal, S. et al. All-optical detection of the spin Hall angle in W/CoFeB/SiO2 heterostructures with varying thickness of the tungsten layer. Phys. Rev. B 96, 054414 (2017).

    Article  ADS  Google Scholar 

Download references

Acknowledgements

We thank R. Uesugi, T. Matsuo, H. Tsai and S. Minami for discussions. This work was partially supported by JST-MIRAI Program (JPMJMI20A1), JST-CREST (JPMJCR18T3), JST-PREST (JPMJPR20L7), MEXT/JSPS-KAKENHI (15H05882, 15H05883, 15K21732, 19H00650, 20K21067, 21H04437, 22H00290), and Spintronics Research Network of Japan (Spin-RNJ). T.H. acknowledges support from the Hattori Hokokai Foundation. S.N. acknowledges support from the CIFAR as a Fellow of the CIFAR Quantum Materials Research Program. Institute for Quantum Matter, an Energy Frontier Research Center was funded by DOE, Office of Science, Basic Energy Sciences under Award (DE-SC0019331). The use of the facilities of the Materials Design and Characterization Laboratory at the Institute for Solid State Physics, and the Laboratory for Magnetic and Electronic Properties at Interface, the University of Tokyo, is acknowledged.

Author information

Author notes

  1. These authors contributed equally: Tomoya Higo, Kouta Kondou

Authors and Affiliations

  1. Department of Physics, University of Tokyo, Bunkyo-ku, Tokyo, Japan

    Tomoya Higo & Satoru Nakatsuji

  2. CREST, Japan Science and Technology Agency, Kawaguchi, Saitama, Japan

    Tomoya Higo, Kouta Kondou, Ryotaro Arita, Yoshichika Otani, Shinji Miwa & Satoru Nakatsuji

  3. Center for Emergent Matter Science (CEMS), RIKEN, Wako, Saitama, Japan

    Kouta Kondou, Ryotaro Arita & Yoshichika Otani

  4. Research Center for Advanced Science and Technology, University of Tokyo, Meguro-ku, Tokyo, Japan

    Takuya Nomoto & Ryotaro Arita

  5. PREST, Japan Science and Technology Agency, Kawaguchi, Saitama, Japan

    Takuya Nomoto

  6. Institute for Solid State Physics, University of Tokyo, Kashiwa, Chiba, Japan

    Masanobu Shiga, Shoya Sakamoto, Xianzhe Chen, Daisuke Nishio-Hamane, Yoshichika Otani, Shinji Miwa & Satoru Nakatsuji

  7. Trans-scale Quantum Science Institute, University of Tokyo, Bunkyo-ku, Tokyo, Japan

    Yoshichika Otani, Shinji Miwa & Satoru Nakatsuji

  8. Institute for Quantum Matter and Department of Physics and Astronomy, Johns Hopkins University, Baltimore, MD, USA

    Satoru Nakatsuji

Authors
  1. Tomoya Higo
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Kouta Kondou
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Takuya Nomoto
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Masanobu Shiga
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Shoya Sakamoto
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Xianzhe Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. Daisuke Nishio-Hamane
    View author publications

    You can also search for this author in PubMed Google Scholar

  8. Ryotaro Arita
    View author publications

    You can also search for this author in PubMed Google Scholar

  9. Yoshichika Otani
    View author publications

    You can also search for this author in PubMed Google Scholar

  10. Shinji Miwa
    View author publications

    You can also search for this author in PubMed Google Scholar

  11. Satoru Nakatsuji
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

T.H. and K.K. contributed equally to this work. S.N. conceived the project. S.N., T.H., K.K., Y.O. and S.M. planned the experiments. T.H., M.S., S.S., X.C. and S.M. developed the magnetic multilayered films. T.H. and D.N.-H. characterized fundamental properties of the films. K.K. and T.H. performed the electrical switching measurements. T.N. and R.A. planned the theoretical studies, performed numerical calculations and provided a theoretical explanation. T.H., K.K., T.N., S.M. and S.N. wrote the manuscript with input from R.A. and Y.O. All authors discussed the results and commented on the manuscript.

Corresponding author

Correspondence to Satoru Nakatsuji.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature thanks Kyung-Jin Lee, Cheng Song and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Extended data figures and tables

Extended Data Fig. 1 Structural analyses for the Mn3Sn stack.

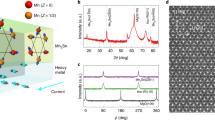
a, Room-temperature spectra obtained by X-ray diffraction (XRD) measurements using the 2θ/ω-scan for the MgO(110)-substrate/W(7 nm)/Mn3Sn(30 nm)/MgO(5 nm) stack (red line) and the substrate (black line). The theoretical spectra for the D019-Mn3Sn and W are presented at the bottom panels. Ta is the post-annealing temperature (Methods). b, XRD patterns of the Φ-scan for the {\(02\bar{2}1\)} planes of the Mn3Sn layer, the {110} planes of the W layer, and the {200} planes of the MgO substrate. c, Surface topography of the MgO(110)-substrate/W(7 nm)/Mn3Sn(30 nm)/MgO(5 nm) stack obtained by atomic force microscopy. The stack has a smooth surface with a root-mean-square (RMS) roughness of 0.6 nm. The scan area is 5 µm × 5 µm. In panels a and b, vertical and horizontal axes are on logarithmic and linear scales, respectively.

Extended Data Fig. 2 RHEED and TEM images for the Mn3Sn stack.

a, In situ RHEED images of (bottom) the MgO (110) substrate after annealing at 800 °C for 10 min, (middle) the W layer annealed at 800 °C for 10 min and (top) the Mn3Sn layer deposited at 260 °C. The incident electron beam is parallel to the MgO [001]-direction. b, Cross-sectional TEM image of the MgO(110)-substrate/W(7 nm)/Mn3Sn(30 nm) stack at room temperature. c, High-resolution electron image for the Mn3Sn layer in the real space. Inset: Simulation image for Mn3Sn. Pink and light blue spheres represent Mn and Sn atoms in the Mn3Sn unit cell (yellow diamond), respectively. d, Electron diffraction patterns of the film (left) and the simulated patterns (right) in the reciprocal space for Mn3Sn (pink), W (orange), and MgO (yellow).

Extended Data Fig. 3 Structural information of the MBE-grown Mn3Sn film on the MgO substrate.

a, Schematics of the interatomic arrangements in the MgO (110) substrate and Mn3Sn (\(01\bar{1}0\)) film plane. b, Crystal structure of the kagome plane in Mn3Sn. Interatomic distances and angles are obtained from the structural information of the bulk Mn3Sn with the lattice constants a = 5.665 Å and c = 4.531 Å43. c, Room-temperature spectra obtained by the X-ray diffraction (XRD) measurements using the 2θ/ω-scan for the (\(02\bar{2}0\)), (\(20\bar{2}0\)) and (\(\bar{2}200\)) planes of Mn3Sn in the MBE-grown MgO(110)-substrate/W(7 nm)/Mn3Sn(30 nm)/MgO(5 nm) stack. d, Schematics for the in-plane atomic arrangement in the Mn3Sn layer of the MBE-grown film. The interatomic distances d1 and d2 and the angle θ12 are experimentally obtained. The distance d3 and the length of the altitude parallel to the x-direction din are calculated from d1, d2, and θ12. The uniaxial tensile strain ε (pink arrows) parallel to the [\(2\bar{1}\bar{1}0\)] direction is schematically illustrated.

Extended Data Fig. 4 Anomalous Hall conductivity of the Mn3Sn layer and estimate of the magnetic anisotropy using angular dependence of the anomalous Hall effect.

a, Magnetic field dependence of the Hall conductivity in the Mn3Sn (30 nm) layer of the MgO(110)-substrate /W(7 nm)/Mn3Sn(30 nm)/MgO(5 nm) stack at 300 K (Method). The Hall conductivity of the Mn3Sn layer in the W/Mn3Sn conducting layer is estimated using the experimentally obtained resistivity of the W(7 nm)/Mn3Sn(30 nm) layer and W(7 nm) layer (Methods). b, Angular (θ) dependence of the Hall voltage normalized by the voltage obtained at θ = 0 for the MBE-grown Mn3Sn stack under 1 T (red circles) at 300 K. The blue solid curve corresponds to the angular dependence expected in the sample with the anisotropy field for the 2-fold magnetic anisotropy field K2/Mr = 1.5 ± 0.1 T, 4-fold magnetic anisotropy field K4/Mr = 0.5 ± 0.1 T, and 6-fold magnetic anisotropy field K2/Mr = 0.4 ± 0.1 T, which are obtained by using the equation (K2/2)sin2θM + (K4/4)sin4θM + (K6/6)sin6θM − μ0MrHsin(θ − θM) = 0. Here K2/4/6, μ0H, Mr, θ and θM denote the 2-/4-/6-fold magnetic anisotropic energy, external magnetic field, remnant (spontaneous) magnetization, magnetic field angle, and angle of the magnetic order parameter (the polarized direction of the cluster magnetic octupole) (see Methods). Inset: Schematic illustration of the measurement set-up for the W/Mn3Sn devices. The purple and green arrows represent the directions of the magnetic field H and current I, respectively. θ and θM are the polar angle of the magnetic field and of the polarized direction of the cluster magnetic octupole (orange arrow) in the z–x plane, respectively.

Extended Data Fig. 5 Magneto-optical Kerr effect (MOKE) and MOKE images of the MBE-grown Mn3Sn film.

a, Field dependence of the polar magneto-optical Kerr rotation angle θK for the MgO(110)-substrate/W(7 nm)/Mn3Sn(30 nm)/MgO(5 nm) stack at room temperature. The field is applied along the perpendicular direction (|| z). b, Evolution of the AF domains as a function of a field perpendicular to the MgO(110)-substrate/W(7 nm)/Mn3Sn(30 nm)/MgO(5 nm) film plane at μ0H = 0 mT(i), 120 mT(ii), and 300 mT(iii). Black and grey regions correspond to the positive and negative values of the polar MOKE signal, respectively.

Extended Data Fig. 6 Electrical and optical observation of the perpendicular full switching in the MBE-grown Mn3Sn film.

a,b, Field (a) and write current (b) dependence of the switching rate of the Hall signal VH/|ΔVHfield| at room temperature in the MgO(110)-substrate/W(7 nm)/Mn3Sn(30 nm)/MgO(5 nm) stack obtained with the post-annealing temperature Ta = 700 °C. The bias magnetic field of 0.1 T and the write/read current are applied along the x direction. c,d, Magneto-optical Kerr effect (MOKE) images of the W/Mn3Sn device obtained in the field (c) and write current (d) sweep measurements. Black and grey regions correspond to the positive and negative values of the polar MOKE signal, respectively. Wch (Wprobe) is the channel (probe) width of the Hall bar.

Extended Data Fig. 7 Magnetic properties of the MBE-grown Mn3Sn film.

a, Field dependence of the magnetization M at 300 K measured in the perpendicular direction of the MgO(110)-substrate/W(7 nm)/Mn3Sn(30 nm)/MgO(5 nm) stack. b, Magnified view of the field dependence of M presented in the panel a. c, Temperature dependence of the remnant M of the MgO(110)-substrate/W(7 nm)/Mn3Sn(30 nm)/MgO(5 nm) film at T = 150-300 K, which is measured from 300 K to 150 K on cooling after the demagnetization process (a field of μ0H = 7 T is applied perpendicular to the film surface and subsequently the field is decreased down to 0 T at 300 K).

Extended Data Fig. 8 Experimental conditions and bias field dependence of the electrical switching of the chiral AF order of Mn3Sn.

a, Sequence used for the electrical switching measurements. A 100-ms-pulse write current Iwrite followed by a d.c. read current of Iread = 0.2 mA is applied, where a wait time of 600 ms is inserted after turning off the write current and before measuring the Hall voltage VH. b, Bias-field dependence of the switching volume fraction ΔVHcurrent/|ΔVHfield| of the W/Mn3Sn devices at room temperature. Here ΔVHcurrent and ΔVHfield are the magnitude of the current- and field-induced switching of the Hall voltage, respectively. The field is applied along the x direction parallel to the electrical current. c, Angular (φ) dependence of the switching volume fraction ΔVHcurrent(φ)/|ΔVHfield| for the W/Mn3Sn devices with γ = +40 degrees. ΔVHcurrent(φ) is estimated under the bias field with the azimuthal angle φ. The vertical broken lines indicate φ = 130 and 310 degrees.

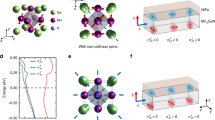
Extended Data Fig. 9 Theoretical consideration for the electrical switching of the chiral AF order in Mn3Sn.

a, configuration-(a): the kagome plane is perpendicular to the current I and parallel to the electrically injected carrier spin polarization p (thick red arrows in the W layer) (kagome ⊥ I || p). b, configuration-(b): the kagome plane is parallel to I and perpendicular to p (kagome || I ⊥ p). c, configuration-(c): the kagome plane is parallel to the current I and parallel to the electrically injected carrier spin polarization p (kagome || I || p). d, Schematics for the current-induced switching of the chiral AF order in the configuration-(b) (kagome || I ⊥ p) with the in-plane compressive strain (δ > 0 and ε < 0). Orange arrows represent the polarization direction of the cluster magnetic octupole. Large (small) green and purple arrows represent the electric current I || x (spin torque (Tcurrent) associated with the spin current with the polarization p, leading to the chiral spin rotation) and bias magnetic field H || z (spin torque (Tfield) associated with H), respectively. Here p is parallel to the spin moments of the spin current (antiparallel to the spin angular momentum). θM is the angle of the polarized direction of the cluster magnetic octupole. e-f, In-plane angle θM of the polarization direction of the cluster magnetic octupole as a function of time t in the W/Mn3Sn bilayer calculated numerically using the LLG equation in the configuration-(b), where the kagome plane is parallel to the current I and the magnetic field H, and perpendicular to the electrically injected carrier spin polarization p (Figs. 3, Methods, Extended Data Figure 9b). I with the current density Jwrite in the W layer is applied for 1 ns < t < 2 ns. A positive Jwrite is applied in (i) and (ii), and negative Jwrite is applied in (iii) and (iv) (See detailed configurations in Fig. 3b). The magnetic field is set to be 0.1 T. e, Perpendicular (chiral spin) switching of the chiral AF order under |Jwrite| = 64 MA cm−2 (corresponding to the region-(B) in Fig. 3c). f, Chiral spin rotation only for one ((ii) for Jwrite > 0 and (iii) for Jwrite < 0) of the initial states under |Jwrite| = 73.5 MA cm−2 (region-(C) in Fig. 3c). g, Chiral spin rotation for both initial states under |Jwrite| = 77.5 MA cm−2 (region-(D) in Fig. 3c). Inset: Magnified view of the in-plane angle θM of the octupole moment as a function of time.

Extended Data Fig. 10 Experimental characterization of the electrical switching of the chiral AF order in Mn3Sn at zero-bias field.

a, Volume fraction of the electrically controllable Hall signal VH/|ΔVHfield| versus write current Iwrite for the W/Mn3Sn devices at zero magnetic field and room temperature. Each panel shows the result of the different switching experiment in the Hall bar with the channel width Wch = 8 μm at room temperature. b, Histogram showing the distribution in the switching rate of the electrically controllable Hall signal ΔVH/|ΔVHfield| in the N = 20 measurements. c, Fluctuation of the switching Hall signal due to SOT, σswitch and σSOT as a function of the Hall cross-area S−1/2 obtained in the zero-field switching experiments using the W/Mn3Sn devices with various channel widths (Wch = 4–32 µm). σSOTzero (red circles) is given by the standard deviation of (ΔVHcurrent − <ΔVHcurrent >)/|ΔVHfield| and σSOT (blue squares) is given by the standard deviation of (VH − <VH>)/|ΔVHfield| (Methods). Thick straight lines are the linear fitting results obtained by the equation σSOTzero and σSOT \(\approx \sqrt{{S}_{{\rm{domain}}}/S}\). d, Domain images obtained by the polar MOKE microscopy for the device with Wch = 32 µm in the zero-field switching experiments. Each panel shows an image obtained after a different switching experiment. Grey and black regions correspond to the positive and negative values of the polar MOKE signal.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Higo, T., Kondou, K., Nomoto, T. et al. Perpendicular full switching of chiral antiferromagnetic order by current. Nature 607, 474–479 (2022). https://doi.org/10.1038/s41586-022-04864-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/s41586-022-04864-1

This article is cited by

Comments

By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing