Abstract
Quantum computers can be protected from noise by encoding the logical quantum information redundantly into multiple qubits using error-correcting codes1,2. When manipulating the logical quantum states, it is imperative that errors caused by imperfect operations do not spread uncontrollably through the quantum register. This requires that all operations on the quantum register obey a fault-tolerant circuit design3,4,5, which, in general, increases the complexity of the implementation. Here we demonstrate a fault-tolerant universal set of gates on two logical qubits in a trapped-ion quantum computer. In particular, we make use of the recently introduced paradigm of flag fault tolerance, where the absence or presence of dangerous errors is heralded by the use of auxiliary flag qubits6,7,8,9,10. We perform a logical two-qubit controlled-NOT gate between two instances of the seven-qubit colour code11,12, and fault-tolerantly prepare a logical magic state8,13. We then realize a fault-tolerant logical T gate by injecting the magic state by teleportation from one logical qubit onto the other14. We observe the hallmark feature of fault tolerance—a superior performance compared with a non-fault-tolerant implementation. In combination with recently demonstrated repeated quantum error-correction cycles15,16, these results provide a route towards error-corrected universal quantum computation.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout





Similar content being viewed by others
Data availability
The data underlying the findings of this work and the quantum circuits are available at https://doi.org/10.5281/zenodo.6244536.
Code availability
All codes used for data analysis are available from the corresponding author upon reasonable request.
References
Nielsen, M. A. & Chuang, I. L. Quantum Computation and Quantum Information: 10th Anniversary Edition (Cambridge Univ. Press, 2010).
Terhal, B. M. Quantum error correction for quantum memories. Rev. Mod. Phys. 87, 307–346 (2015).
Shor, P. W. Fault-tolerant quantum computation. In Proc. 37th Conference on Foundations of Computer Science 56–65 (IEEE, 1996).
Preskill, J. Reliable quantum computers. Proc. R. Soc. Lond. A 454, 385–410 (1998).
Aliferis, P., Gottesman, D. & Preskill, J. Quantum accuracy threshold for concatenated distance-3 codes. Quantum Inf. Comput. 6, 97–165 (2006).
Chao, R. & Reichardt, B. W. Quantum error correction with only two extra qubits. Phys. Rev. Lett. 121, 050502 (2018).
Chamberland, C. & Beverland, M. E. Flag fault-tolerant error correction with arbitrary distance codes. Quantum 2, 53 (2018).
Chamberland, C. & Cross, A. W. Fault-tolerant magic state preparation with flag qubits. Quantum 3, 143 (2019).
Chao, R. & Reichardt, B. W. Flag fault-tolerant error correction for any stabilizer code. PRX Quantum 1, 010302 (2020).
Reichardt, B. W. Fault-tolerant quantum error correction for Steane’s seven-qubit color code with few or no extra qubits. Quantum Sci. Technol. 6, 015007 (2020).
Bombin, H. & Martin-Delgado, M. A. Topological quantum distillation. Phys. Rev. Lett. 97, 180501 (2006).
Steane, A. Multiple-particle interference and quantum error correction. Proc. R. Soc. Lond. A 452, 2551–2577 (1996).
Goto, H. Minimizing resource overheads for fault-tolerant preparation of encoded states of the Steane code. Sci. Rep. 6, 19578 (2016).
Bravyi, S. & Kitaev, A. Universal quantum computation with ideal Clifford gates and noisy ancillas. Phys. Rev. A 71, 022316 (2005).
Ryan-Anderson, C. et al. Realization of real-time fault-tolerant quantum error correction. Phys. Rev. X 11, 041058 (2021).
Abobeih, M. H. et al. Fault-tolerant operation of a logical qubit in a diamond quantum processor. Preprint at https://arxiv.org/abs/2108.01646 (2021).
Shor, P. W. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM J. Comput. 26, 1484–1509 (1997).
Feynman, R. P. Simulating physics with computers. Int. J. Theor. Phys. 21, 467–488 (1982).
Aharonov, D. & Ben-Or, M. Fault-tolerant quantum computation with constant error rate. SIAM J. Comput. 38, 1207–1282 (2008).
Eastin, B. & Knill, E. Restrictions on transversal encoded quantum gate sets. Phys. Rev. Lett. 102, 110502 (2009).
Paetznick, A. & Reichardt, B. W. Universal fault-tolerant quantum computation with only transversal gates and error correction. Phys. Rev. Lett. 111, 090505 (2013).
Beverland, M. E., Kubica, A. & Svore, K. M. Cost of universality: a comparative study of the overhead of state distillation and code switching with color codes. PRX Quantum 2, 020341 (2021).
Nigg, D. et al. Quantum computations on a topologically encoded qubit. Science 345, 302–305 (2014).
Harper, R. & Flammia, S. T. Fault-tolerant logical gates in the IBM quantum experience. Phys. Rev. Lett. 122, 080504 (2019).
Erhard, A. et al. Entangling logical qubits with lattice surgery. Nature 589, 220–224 (2021).
Satzinger, K. J. et al. Realizing topologically ordered states on a quantum processor. Science 374, 1237–1241 (2021).
Andersen, C. K. et al. Repeated quantum error detection in a surface code. Nat. Phys. 16, 875–880 (2020).
Marques, J. F. et al. Logical-qubit operations in an error-detecting surface code. Nat. Phys. 18, 80–86 (2021).
Chen, Z. et al. Exponential suppression of bit or phase errors with cyclic error correction. Nature 595, 383–387 (2021).
Gottesman, D. Quantum fault tolerance in small experiments. Preprint at https://arxiv.org/abs/1610.03507 (2016).
Takita, M., Cross, A. W., Córcoles, A. D., Chow, J. M. & Gambetta, J. M. Experimental demonstration of fault-tolerant state preparation with superconducting qubits. Phys. Rev. Lett. 119, 180501 (2017).
Vuillot, C. Is error detection helpful on IBM 5Q chips? Quantum Inf. Comput. 18, 949–964 (2018).
Linke, N. M. et al. Fault-tolerant quantum error detection. Sci. Adv. 3, e1701074 (2017).
Egan, L. et al. Fault-tolerant control of an error-corrected qubit. Nature 598, 281–286 (2021).
Hilder, J. et al. Fault-tolerant parity readout on a shuttling-based trapped-ion quantum computer. Phys. Rev. X 12, 011032 (2022).
Pogorelov, I. et al. Compact ion-trap quantum computing demonstrator. PRX Quantum 2, 020343 (2021).
Sørensen, A. & Mølmer, K. Entanglement and quantum computation with ions in thermal motion. Phys. Rev. A 62, 022311 (2000).
Nebendahl, V., Häffner, H. & Roos, C. F. Optimal control of entangling operations for trapped-ion quantum computing. Phys. Rev. A 79, 012312 (2009).
Bermudez, A., Xu, X., Gutiérrez, M., Benjamin, S. C. & Müller, M. Fault-tolerant protection of near-term trapped-ion topological qubits under realistic noise sources. Phys. Rev. A 100, 062307 (2019).
Riesebos, L., Fu, X., Varsamopoulos, S., Almudever, C. G. & Bertels, K. Pauli frames for quantum computer architectures. In DAC ’17: Proc. 54th Annual Design Automation Conference 2017 1–6 (Association for Computing Machinery, 2017).
Knill, E. Quantum computing with realistically noisy devices. Nature 434, 39–44 (2005).
Parrado-Rodríguez, P., Ryan-Anderson, C., Bermudez, A. & Müller, M. Crosstalk suppression for fault-tolerant quantum error correction with trapped ions. Quantum 5, 487 (2021).
Maslov, D. Basic circuit compilation techniques for an ion-trap quantum machine. New J. Phys. 19, 023035 (2017).
Ringbauer, M. et al. A universal qudit quantum processor with trapped ions. Preprint at https://arxiv.org/abs/2109.06903 (2021)
Ryan-Anderson, C. Quantum Algorithms, Architecture, and Error Correction. PhD thesis, The Univ. New Mexico (2018).
Hradil, Z., Řeháček, J., Fiurášek, J. & Ježek, M. in Quantum State Estimation 59–112 (Springer, 2004).
Acknowledgements
We acknowledge support from the EU Quantum Technology Flagship grant AQTION under grant agreement number 820495, and by the US Army Research Office through grant number W911NF-21-1-0007; and funding by the Austrian Science Fund (FWF), through the SFB BeyondC (FWF project number F7109), by the Austrian Research Promotion Agency (FFG) contract 872766, and by the IQI GmbH. M. Ringbauer acknowledges funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement number 840450. M. Müller acknowledges support by the ERC Starting Grant QNets grant number 804247. S.H. acknowledges funding by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy ‘Cluster of Excellence Matter and Light for Quantum Computing (ML4Q) EXC 2004/1’ 390534769. The research is also based on work supported by the Office of the Director of National Intelligence (ODNI), Intelligence Advanced Research Projects Activity (IARPA), via the US Army Research Office grant number W911NF-16-1-0070. The views and conclusions contained herein are those of the authors and should not be interpreted as necessarily representing the official policies or endorsements, either expressed or implied, of the ODNI, IARPA or the US Government. The US Government is authorized to reproduce and distribute reprints for governmental purposes notwithstanding any copyright annotation thereon. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the view of the US Army Research Office.
Author information
Authors and Affiliations
Contributions
L.P., I.P. and T.F. carried out the experiments. L.P., I.P., T.F., M. Meth, C.D.M., R.S., M. Ringbauer, P.S. and T.M. contributed to the experimental setup. L.P. analysed the data. S.H. performed the numerical simulations. S.H., M. Rispler and M. Müller performed circuit analysis, characterization and theory modelling. L.P., S.H., I.P., M. Rispler, P.S. and M. Müller wrote the manuscript, with contributions from all authors. R.B., P.S., M. Müller and T.M. supervised the project.
Corresponding author
Ethics declarations
Competing interests
T.M., R.B. and T.F. are connected to Alpine Quantum Technologies, a commercially oriented quantum computing company.
Peer review
Peer review information
Nature thanks the anonymous reviewers for their contribution to the peer review of this work. Peer reviewer reports are available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
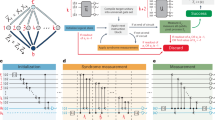
Extended Data Fig. 1 Stabilizer generators of a single logical qubit.
Expectation values of the stabilizer generators and the logical operators of the seven-qubit colour code for the six cardinal states of the Bloch sphere. Results for the non-fault-tolerant and fault-tolerant preparation scheme are depicted in orange and turquoise respectively, whereas results from numerical simulations are shown in lighter coloured bars. 2,500 and 106 runs were performed in the experiment and for simulations for each prepared state, respectively. For the calculation of the expectation values of the logical operators a round of perfect error correction is applied. For the measurements corresponding to the data presented in this figure but also in Fig. 2 the sign of the rotation angle of physical Y-rotations is flipped, effectively implementing an additional deterministic π phase flip on qubit 6 and a π bit flip on qubit 7 at the end of the circuit depicted in Fig. 2a. The effects of this redefinition do not amount to a change of measurement bases and can be readily accounted for in post-processing.
Supplementary information
Rights and permissions
About this article
Cite this article
Postler, L., Heuβen, S., Pogorelov, I. et al. Demonstration of fault-tolerant universal quantum gate operations. Nature 605, 675–680 (2022). https://doi.org/10.1038/s41586-022-04721-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-022-04721-1
This article is cited by
-
An elementary review on basic principles and developments of qubits for quantum computing
Nano Convergence (2024)
-
Protecting expressive circuits with a quantum error detection code
Nature Physics (2024)
-
Logical quantum processor based on reconfigurable atom arrays
Nature (2024)
-
Encoding a magic state with beyond break-even fidelity
Nature (2024)
-
Mobile atoms enable efficient computation with logical qubits
Nature (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.