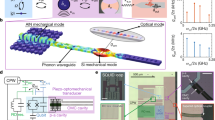
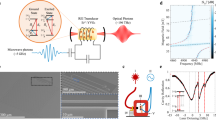
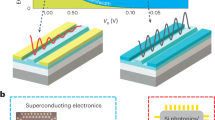
Abstract
Entangling microwave-frequency superconducting quantum processors through optical light at ambient temperature would enable means of secure communication and distributed quantum information processing1. However, transducing quantum signals between these disparate regimes of the electro-magnetic spectrum remains an outstanding goal2,3,4,5,6,7,8,9, and interfacing superconducting qubits, which are constrained to operate at millikelvin temperatures, with electro-optic transducers presents considerable challenges owing to the deleterious effects of optical photons on superconductors9,10. Moreover, many remote entanglement protocols11,12,13,14 require multiple qubit gates both preceding and following the upconversion of the quantum state, and thus an ideal transducer should impart minimal backaction15 on the qubit. Here we demonstrate readout of a superconducting transmon qubit through a low-backaction electro-optomechanical transducer. The modular nature of the transducer and circuit quantum electrodynamics system used in this work enable complete isolation of the qubit from optical photons, and the backaction on the qubit from the transducer is less than that imparted by thermal radiation from the environment. Moderate improvements in the transducer bandwidth and the added noise will enable us to leverage the full suite of tools available in circuit quantum electrodynamics to demonstrate transduction of non-classical signals from a superconducting qubit to the optical domain.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The data and code supporting the figures are available on Zenodo at https://doi.org/10.5281/zenodo.6344913. Source data are provided with this paper.
References
Arute, F. et al. Quantum supremacy using a programmable superconducting processor. Nature 574, 505–510 (2019).
Hisatomi, R. et al. Bidirectional conversion between microwave and light via ferromagnetic magnons. Phys. Rev. B 93, 174427 (2016).
Han, J. et al. Coherent microwave-to-optical conversion via six-wave mixing in Rydberg atoms. Phys. Rev. Lett. 120, 093201 (2018).
Higginbotham, A. P. et al. Harnessing electro-optic correlations in an efficient mechanical converter. Nat. Phys. 14, 1038–1042 (2018).
Bartholomew, J. G. et al. On-chip coherent microwave-to-optical transduction mediated by ytterbium in YVO4. Nat. Commun. 11, 3266 (2020).
Arnold, G. et al. Converting microwave and telecom photons with a silicon photonic nanome- chanical interface. Nat. Commun. 11, 4460 (2020).
Stockill, R. et al. Ultra-low-noise microwave to optics conversion in gallium phosphide. Preprint at https://arxiv.org/abs/2107.04433 (2021).
Sahu, R. et al. Quantum-enabled operation of a microwave-optical interface. Nat. Commun. 13, 1276 (2022).
Mirhosseini, M., Sipahigil, A., Kalaee, M. & Painter, O. Superconducting qubit to optical photon transduction. Nature 588, 599–603 (2020).
Barends, R. et al. Minimizing quasiparticle generation from stray infrared light in supercon-ducting quantum circuits. Appl. Phys. Lett. 99, 113507 (2011).
Campbell, E. T. & Benjamin, S. C. Measurement-based entanglement under conditions of extreme photon loss. Phys. Rev. Lett. 101, 130502 (2008).
Kalb, N. et al. Entanglement distillation between solid-state quantum network nodes. Science 356, 928–932 (2017).
Zhong, C. et al. Proposal for heralded generation and detection of entangled microwave–optical-photon pairs. Phys. Rev. Lett. 124, 010511 (2020).
Kurpiers, P. et al. Quantum communication with time-bin encoded microwave photons. Phys. Rev. Appl. 12, 044067 (2019).
Hatridge, M. et al. Quantum back-action of an individual variable-strength measurement. Science 339, 178–181 (2013).
Inagaki, T. et al. Entanglement distribution over 300 km of fiber. Opt. Express 21, 23241 (2013).
Ursin, R. et al. Entanglement-based quantum communication over 144 km. Nat. Phys. 3, 481–486 (2007).
Yin, J. et al. Satellite-based entanglement distribution over 1200 kilometers. Science 356, 1140–1144 (2017).
Lecocq, F. et al. Control and readout of a superconducting qubit using a photonic link. Nature 591, 575–579 (2021).
Youssefi, A. et al. A cryogenic electro-optic interconnect for superconducting devices. Nat. Electron. 4, 326–332 (2021).
Zeuthen, E., Schliesser, A., Sørensen, A. S. & Taylor, J. M. Figures of merit for quantum transducers. Quantum Sci. Technol. 5, 034009 (2020).
Reagor, M. et al. Quantum memory with millisecond coherence in circuit QED. Phys. Rev. B 94, 014506 (2016).
Campagne-Ibarcq, P. et al. Quantum error correction of a qubit encoded in grid states of an oscillator. Nature 584, 368–372 (2020).
Chakram, S. et al. Seamless high-Q microwave cavities for multimode circuit quantum elec-trodynamics. Phys. Rev. Lett. 127, 107701 (2021).
Bultink, C. C. et al. General method for extracting the quantum efficiency of dispersive qubit readout in circuit QED. Appl. Phys. Lett. 112, 092601 (2018).
Clerk, A. A. et al. Introduction to quantum noise, measurement, and amplification. Rev. Mod. Phys. 82, 1155–1208 (2010).
Brubaker, B. M. et al. Optomechanical ground-state cooling in a continuous and efficient electro-optic transducer. Preprint at https://arxiv.org/abs/2112.13429 (2021).
Blais, A. et al. Cavity quantum electrodynamics for superconducting electrical circuits: An architecture for quantum computation. Phys. Rev. A 69, 062320 (2004).
Gambetta, J. M. et al. Protocols for optimal readout of qubits using a continuous quantum nondemolition measurement. Phys. Rev. A 76, 012325 (2007).
Caves, C. M. Quantum limits on noise in linear amplifiers. Phys. Rev. D 26, 1817–1839 (1982).
Clerk, A. A. & Utami, D. W. Using a qubit to measure photon-number statistics of a driven thermal oscillator. Phys. Rev. A 75, 042302 (2007).
Mallet, F. et al. Quantum state tomography of an itinerant squeezed microwave field. Phys. Rev. Lett. 106, 220502 (2011).
Krantz, P. et al. A quantum engineer’s guide to superconducting qubits. Appl. Phys. Rev. 6, 021318 (2019).
Rosenthal, E. I. et al. Efficient and low-backaction quantum measurement using a chip-scale detector. Phys. Rev. Lett. 126, 090503 (2021).
Touzard, S. et al. Gated conditional displacement readout of superconducting qubits. Phys. Rev. Lett. 122, 080502 (2019).
Gambetta, J. M. et al. Qubit-photon interactions in a cavity: measurement-induced dephasing and number splitting. Phys. Rev. A 74, 042318 (2006).
Place, A. P. M. et al. New material platform for superconducting transmon qubits with co-herence times exceeding 0.3 milliseconds. Nat. Commun. 12, 1779 (2021).
Dolan, G. J. Offset masks for lift-off photoprocessing. Appl. Phys. Lett. 31, 337–339 (1977).
Koch, J. et al. Charge-insensitive qubit design derived from the Cooper pair box. Phys. Rev. A 76, 042319 (2007).
Houck, A. A. et al. Controlling the spontaneous emission of a superconducting transmon qubit. Phys. Rev. Lett. 101, 080502 (2008).
Andrews, R. W. et al. Bidirectional and efficient conversion between microwave and optical light. Nat. Phys. 10, 321–326 (2014).
Aspelmeyer, M., Kippenberg, T. J. & Marquardt, F. Cavity optomechanics. Rev. Mod. Phys. 86, 1391–1452 (2014).
Tamura, Y. et al. The first 0.14-db/km loss optical fiber and its impact on submarine transmission. J. Lightwave Technol. 36, 44–49 (2018).
Acknowledgements
We acknowledge funding from AFOSR MURI grant number FA9550-15-1-0015, from ARO CQTS grant number 67C1098620 and the NSF under grant number PHYS 1734006. We thank J. Beall and K. Cicak for help with our fabrication process. We thank J. Teufel, G. Smith, K. Quinlan, K. Adachi and L. Talamo for feedback on the manuscript.
Author information
Authors and Affiliations
Contributions
R.D.D., C.A.R. and K.W.L. conceived the experiment. B.M.B., M.D.U., J.M.K., S.M. and R.D.D. planned and carried out the measurements. M.D.U. constructed the optical cavity. R.D.D. designed and fabricated the cQED system. S.M. and P.S.B. developed the fabrication process for the chips hosting the electrical circuit and membrane, which were fabricated by S.M. All authors contributed to writing the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature thanks Wolfgang Pfaff, Gary Steele and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 Quantum efficiency measurement.
(a) Protocol for measurement-induced dephasing calibration. A weak measurement pulse is injected into a Ramsey sequence. The Ramsey sequence is then followed by a strong projective measurement of the qubit. (b) The coherence of the qubit ρge decays as a Gaussian function of the weak measurement amplitude \(\sqrt{{\bar{n}}_{{\rm{r}}}}\). The points are data, while the line is a Gaussian fit. (c) Measurement of the SNR slope a of the electro-optic readout, in units of inverse drive voltage, as a function of Γe for four fixed optomechanical damping rates Γo. Each data point is obtained from a fit to a measurement of the sort shown in the inset, where it is seen that the SNR scales linearly as a function of drive voltage (bottom axis) or equivalently readout pulse amplitude (top axis).
Extended Data Fig. 2 Characterisation of the quantum efficiency of the microwave readout apparatus.
The microwave readout efficiency \({\eta }_{{\rm{q}}}^{{\rm{mic}}}\) is measured as a function of the electromechanical damping rate Γe. The points are data, while the line is a model including partial absorption of the readout pulse by the pump power-dependent reflection loss of the LC circuit, power-dependent added noise, fixed transmission losses and the independently measured added noise of the microwave heterodyne measurement chain. The shape of the curve is dominated by power-dependent LC circuit reflection loss, with the quantum efficiency of the microwave readout apparatus approaching zero at high power because the LC circuit is nearly critically coupled. From this model, we estimate 4.7 dB of loss (ηmic = 0.34) between transducer and the cQED system.
Extended Data Fig. 3 Excess backaction from pump photon leakage.
(a) Circulators (total isolation of 63 dB) and interferometric cancellation are used to prevent the strong microwave pump from reaching the cQED system and dephasing the qubit. Cancellation is achieved by sending a microwave cancellation tone with amplitude equal to that of the reflected microwave pump but opposite phase into the second arm of the directional coupler. The phasor sum of this cancellation tone and the reflected microwave pump determines the pump power Pref propagating towards the cQED system. (b) The directional coupler acts as an interferometer, enabling interference between the reflected microwave pump and the cancellation tone. During normal operation of the transducer the cancellation tone is tuned to minimise Pref, but to estimate the effect of pump photons on the qubit the cancellation tone can be tuned to only partially interfere and tune Pref over several decades. The phasor sum shown here is for the case of constructive interference. (c) The number of pump photons in the cQED system \({\bar{n}}_{{\rm{p}}}\) is measured as Pref is varied. During transducer operation the cancellation is typically tuned to achieve Pref < −95 dBm or equivalently \({\bar{n}}_{{\rm{p}}} < 1\times {10}^{-3}\). The cancellation does not stay completely fixed over the course of the experiment due to small thermal drifts slightly changing the amplitude of Pref.
Extended Data Fig. 4 Experimental schematic.
(a) Microwave layout demonstrating the exact configuration of the qubit readout/control pulses and the pumps for the electro-optic transducer. (b) Legend for various different microwave and optical components. (c) Cryogenic portion of the experiment. (d) Demodulation and detection scheme. The two digitisers allow for simultaneous measurement of the microwave and optical signals emitted from the transducer. (e) Simplified schematic of optical beam layout and balanced heterodyne detector.
Extended Data Fig. 5 cQED system.
(a) The cQED system is a superconducting qubit coupled to a 3D quarter-wave post resonator which is in turn evanescently coupled to the waveguide above. A sapphire rod can be translated towards the end of the post resonator via a piezo-electric stepping module (Attocube ANPz101/LT/HV) in order to tune the resonator’s frequency. The sapphire rod is epoxied to a clamp with stycast 2850 and then bolted to the piezo-electric stepping module. A lid with a narrow hole for the sapphire rod to pass through is attached to the top of the waveguide to prevent coupling of modes in the Attocube mount to modes within the waveguide and the quarter-wave resonator. (b) Photo of the cQED system and Attocube mount. A copper braid is attached to the gold-plated copper qubit clamp to help thermalize the superconducting qubit.
Extended Data Fig. 6 Qubit coherence time data.
Qubit coherence times under three different electro-optic transducer operating conditions: transducer off, transducer on with (Γe, Γo)/2π = (1.1, 5.0) kHz and just the laser on with (Γe, Γo)/2π = (0, 5.0) kHz. Turning just the laser on is indistinguishable from the transducer being turned off. Running the electro-optic transducer does reduce the dephasing time of the qubit (see the cyan hexagon). Circles represent T1 times, triangles represent T2 times and hexagons represent Tϕ.
Supplementary information
Supplementary Information
This Supplementary Information file contains the following three sections: Optical readout fidelity, Modelling transducer added noise, and State-space model.
Rights and permissions
Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Delaney, R.D., Urmey, M.D., Mittal, S. et al. Superconducting-qubit readout via low-backaction electro-optic transduction. Nature 606, 489–493 (2022). https://doi.org/10.1038/s41586-022-04720-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-022-04720-2
This article is cited by
-
An integrated microwave-to-optics interface for scalable quantum computing
Nature Nanotechnology (2024)
-
Photonic link from single-flux-quantum circuits to room temperature
Nature Photonics (2024)
-
Continuous wideband microwave-to-optical converter based on room-temperature Rydberg atoms
Nature Photonics (2024)
-
Ultrahigh-quality-factor micro- and nanomechanical resonators using dissipation dilution
Nature Nanotechnology (2024)
-
Single-shot readout of a superconducting qubit using a thermal detector
Nature Electronics (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.