Main

The structure of eukaryotic chromosomes changes markedly as cells traverse the cell division cycle. In interphase, nuclear DNA has a diffuse appearance and individual chromosomes are not discernible. As cells enter mitosis, the replicated chromosomes condense into compact, cylindrical structures comprising two sister-chromatid arms that mature into the iconic chromosome X shape in metaphase, in which the sister chromatids are held together only at the centromere. The sisters are then segregated to the nascent daughter cells in anaphase and telophase using force applied by the mitotic spindle6,7. The prevailing model of chromosome organization posits that consecutive loops of chromatin are organized in a helical staircase conformation8 that is anchored to a central protein scaffold, with condensins I and II and TOP2A being key factors in mitotic chromosome formation3,9,10,11. Although condensins have also been shown to be essential for the maintenance of a compacted chromosome structure2,12, there are conflicting views on the role of TOP2A in this process5,13.

The mechanics and dynamics of many biomolecules have been elucidated by the use of micromechanical measurements, such as atomic force microscopy, and magnetic and optical tweezers14. Nevertheless, few mechanical studies have been performed on chromosomes15. A series of studies quantifying the mechanical stability of amphibian and human chromosomes, analysed by stretching chromosomes with micropipettes16,17,18, revealed that they can be reversibly stretched by up to five times their native length by applying forces in the nanonewton range, and that depletion of condensins results in decreased chromosome stiffness19. Moreover, studies using Hi-C and super-resolution fluorescence microscopy20,21 have provided important information on chromosome structure and organization. To gain direct access to the dynamic structural features of chromosomes, while avoiding fixation and ensemble averaging, we introduce here a workflow to analyse the mechanics and architecture of mitotic chromosomes using a combination of optical tweezers, fluorescence microscopy and microfluidics, which readily allows the manipulation of individual native chromosomes with nanometre precision and piconewton force resolution.

Handling and visualizing chromosomes

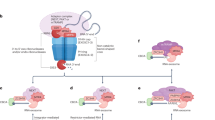
To study native metaphase chromosomes using optical tweezers, we purified chromosomes with biotinylated telomeric ends, which served as molecular ‘handles’ for site-specific attachment to streptavidin-coated microspheres (Fig. 1a). Telomere-specific biotinylation was achieved through fusion of BirA protein to telomere repeat-binding factor 1 (TRF1)22. Biotin treatment of either U2OS-BirA-TRF1 cells or HCT116 cells transduced with a TRF1-BirA lentivirus resulted in biotin incorporation at approximately 98% of telomeres (ntot = 1,434; Extended Data Fig. 1a). We then optimized a chromosome isolation protocol23 that yielded highly concentrated (around 106 chromosomes per ml) native mitotic chromosomes devoid of cell debris and cytoskeletal contaminants (see Methods), which were suitable for telomeric attachment between two microspheres held in optical traps (Fig. 1b, c, Extended Data Fig. 1b–d, Supplementary Video 1, Methods). This permitted us to handle and image chromosomes in a precisely controlled environment and accurately measure forces applied to the chromosome24,25. We visualized the trapped chromosomes using either wide-field fluorescence imaging of eGFP-labelled histone H2B, allowing the individual sister chromatids and the centromeres to be discerned (Fig. 1d), or super-resolution imaging using binding-activated localization microscopy (BALM)26, which permitted the visualization of individual fluorescent intercalators intermittently binding to a chromosome (Fig. 1e, Extended Data Fig. 1e). Our system is also compatible with multi-colour immunofluorescence analysis; for example, staining for histone H3 showed the expected pan-chromosome localization (Extended Data Fig. 1f), and staining for CREST and NCAPH revealed centromeres and chromosome scaffolds, respectively (Fig. 1f, Extended Data Fig. 1g, h, Methods). These different imaging strategies allowed us to confirm known features of chromosome organization.

Fig. 1: Workflow for chromosome attachment and visualization.
figure 1

a, Diagram depicting the experimental workflow. After addition of biotin to U2OS cells expressing BirA–TRF1, proteins located at telomeric ends are covalently biotinylated. Chromosomes were then purified from cells arrested in prometaphase by treatment with nocodazole. b, Schematic depiction of chromosome attachment to microspheres in a microfluidic flow cell with parallel channels (bottom left). After trapping two streptavidin-coated microspheres (1), a chromosome is attached to one microsphere by exploiting the attraction force that the optical trap exerts on the chromosome (2). The chromosome is then flow-stretched (3), bringing it into the imaging plane, and attached to the second microsphere (4). c, Representative bright-field image of a mitotic chromosome showing telomeric attachment of the four chromatid ends. The centromeric region is discernible as a constriction (arrows). Scale bar, 4 μm. d, Representative fluorescence image of H2B–eGFP (bottom) and corresponding bright-field image (top). Note that the chromosome in d was positioned to be in the focal plane for fluorescence imaging and not bright-field imaging. Scale bar, 2 μm. e, Representative BALM super-resolved image of SYTOX orange (SxO) binding events. The centromeric region is indicated with arrowheads. Scale bar, 1 μm. f, An example of immuno-staining of NCAPH and CREST to show the localization of condensin I along the chromatid scaffold and two foci that reveal the position of the centromeres, respectively. Scale bar, 2 μm.

Full size image

Mechanical properties of chromosomes

Optical manipulation enables mechanical features of chromosomes to be characterized with very high resolution. To achieve this, we first recorded force-extension curves by separating the two optical traps at a constant velocity of less than 0.2 µm s−1 (Fig. 2a, b, Supplementary Videos 2, 3). For forces up to typically 10–50 pN, the force-extension behaviour of individual chromosomes was approximately linear,albeit with a large variability in stiffness between different chromosomes. By contrast, at higher forces, the chromosomes exhibited pronounced nonlinear stiffening, such that the force increased markedly with increasing chromosome extension. We determined chromosome length at the onset of this stiffening (stiffening length), which showed a broad distribution that is likely to reflect the known variability in the size of human chromosomes (2.5 ± 1.0 μm and 2.8 ± 1.7 μm for U2OS and HCT116 chromosomes, respectively, mean ± s.e.m.; Extended Data Fig. 2a). Moreover, the force-extension response was reversible at forces up to 300 pN (Fig. 2c, Extended Data Fig. 2b), as reported in micropipette aspiration studies18,19.

Fig. 2: Mechanical characterization of chromosome stretching.
figure 2

a, Representative series of force-extension curves depicting a linear stiffness regime for low forces (F < 10 pN) and a nonlinear stiffness regime at higher forces (F > 20 pN), in which the stiffness of the chromosomes increases with force. Stiffening lengths are indicated with dots. b, Representative bright-field images of stretching a U2OS chromosome. Scale bar, 4 μm. c, Three consecutive cycles of elongation and retraction (direction depicted by arrows). Abrupt declines in the force response (arrowhead) are suggestive of small rupture events and are most abundant during the first stretch cycle (23% of curves; n = 155 compared to 14% of third stretches; n = 79). d, Individual differential stiffness curves (light grey; n = 44) and average curve (dark grey) show a linear stiffness regime up to around 10 pN followed by power-law scaling in the regime between 20 and 200 pN, with a scaling exponent (exp) of γ = 0.82 ± 0.05 (blue). The green line depicts scaling of 3/2 as expected for a WLC. e, Datasets show a universal form of the nonlinear stiffening after rescaling by K0 and Fc, independent of the differences among chromosomes. f, The storage modulus (filled diamonds) and loss modulus (open diamonds) determined at a force of 50 pN with two methods of distance detection for the lower (blue; n = 8) and the higher (green; n = 11) frequencies (Methods). g, Oscillation data measured at 1 Hz (n = 14), overlapped with the differential stiffness derived from force-extension experiments (dark grey line, mean; light-grey shaded region, s.d.). In f, g, data represent mean values ± s.d. The data in a, d, e, g are from the third extension cycle.

Full size image

To quantify the stiffening of chromosomes at high force, we determined the differential stiffness K by evaluating the numerical derivative of the force F with respect to the extension d (Extended Data Fig. 2c, Methods). Beyond a critical force Fc the differential stiffness increased following a power-law dependency; K ~ Fγ (Fig. 2d), in which the stiffening exponent γ characterizes how sensitive the stiffening is to force. Classical models for polymers predict a power-law stiffening, with the freely jointed chain (FJC) being characterized by the stiffening exponent γ = 2 and the worm-like-chain (WLC) by γ = 3/2 (refs. 4,27,28,29). However, we observed a markedly weaker stiffening exponent compared to these classical models (Fig. 2d), with γ = 0.82 ± 0.05 for U2OS chromosomes. Despite a variability in initial stiffness between different chromosomes, all stiffness-force curves could be approximately collapsed onto a single master curve by scaling them to initial stiffness and critical force Fc (Fig. 2e, Methods), which showed that the mechanical behaviour amongst chromosomes is consistent. To investigate whether this anomalous behaviour reflects structural remodelling under load—for example, owing to dynamic cross-linking such as that described for F-actin networks30,31,32—we measured the frequency dependence of the stiffening response. Using microrheology measurements, we quantified this viscoelastic response by applying a fixed pre-tension F to chromosomes, and then a small-amplitude distance oscillation with frequency ω (refs. 28,32). The differential force response is captured by the storage modulus K’(F,ω) and the loss modulus K’’(F,ω), which characterize the elastically stored and the viscously dissipated mechanical energy, respectively (Methods). We determined that the storage modulus was constant over five orders of magnitude in frequency and was 10- to 100-fold larger than the loss modulus (Fig. 2f). When measurements were performed at varying pre-tensions, the storage modulus was consistent with the differential stiffness derived from the force-extension data (Fig. 2g). These results show that chromosomes have a predominantly elastic mechanical response over a wide range of frequencies, which is inconsistent with substantial dynamic remodelling occurring on these time scales. Thus, we attribute the notably weak power-law stiffening response to an intrinsic, nonlinear elastic response of the chromosome.

Chromosome hierarchical mechanics

Models of homogeneous polymers with finite extensibility dc, such as the FJC or WLC, exhibit a nonlinear response at high force, such that F ~ (d − dc)−δ, with δ > 0 (refs. 4,27). This divergent force-extension behaviour implies K ~ Fγ with a stiffening exponent γ =  (δ + 1)/δ, which is strictly larger than 1. Thus, the weak anomalous stiffening exponent (γ < 1) that we determined suggests that the nonlinear mechanical response lies in the inherent heterogenous nature of chromosomes. Heterogeneity of chromosomes is known to arise owing to the presence of specialized proteinaceous structures, such as centromeres, as well as the inherent differences between euchromatic and heterochromatic regions, which is reflected in the appearance of G-banding patterns after Giemsa staining33,34. To capture this heterogeneous nature of chromosomes, we propose a hierarchical worm-like chain (HWLC) model: an assembly with different structural elements represented by a series of WLCs with distinct contour and persistence lengths, which leads to an emergent nonlinear behaviour that is different from the response of the individual elements. Upon mechanical loading, these elements respond in a force-dependent hierarchy that leads to sequential stiffening (Fig. 3a–c, Extended Data Fig. 3). At low force, the response is dominated by the softest element. At higher forces, the stiffness of the next softest element dominates, and so on. The hierarchical nature of this model is characterized by the distribution P(fc) of internal critical forces of the individual elements. We compared our data to two classes of HWLC models: in one, we randomly drew the critical forces of the components from a power-law distribution P(fc) ∝ fc−β (Fig. 3d); and, in the other, we drew them from an exponential distribution \(P\left({f}_{{\rm{c}}}\right)\propto {{\rm{e}}}^{-{f}_{{\rm{c}}}/{f}_{{\rm{c}}}^{* }}\) (Fig. 3e, Supplementary Note 1, Extended Data Fig. 4). Although both models showed anomalous stiffening, the power-law distribution offered a closer agreement to the spread in chromosome stiffness (Fig. 3d, e, Extended Data Fig. 5). The distribution of critical forces of the assembly for both models is in accord with experimental observations (Fig. 3f, Methods). However, only a power-law distribution for critical forces (Fig. 3d) provides a genuine power-law stiffening of the HWLC with an exponent, γ = β + α − 1, in which α is set by the relation between the initial stiffness and the critical force of each element, k0 ∝ fcα (Supplementary Note 1). We conclude that the HWLC model can quantitatively account for the observed nonlinear mechanical response of human chromosomes.

Fig. 3: Sequential stiffening of the HWLC model.
figure 3

a, Stiffness-force curves of a single WLC transition from a constant stiffness directly towards a strain stiffening regime with a power-law scaling of 3/2. b, Stiffness-force curves of an assembly of four WLCs (individual WLC response in grey) in series result in an overall response (black) with an irregular transition zone to nonlinear stiffening that has a weaker stiffening behaviour than an individual WLC. The critical forces of the elements fc,i and of the assembly Fc are indicated on the x axis. c, Stiffness-force curve of an assembly (black) of 100 serial WLCs (individual WLC response in grey) with critical forces drawn from a power-law distribution, P(fc) ∝ fc−β, resulting in a smooth power-law transition regime with an exponent of γ = β + α − 1. d, e, Comparison of the experimental mean and s.d. of U2OS chromosomes (grey) with the mean and s.d. of the HWLC model, with P(fc) ∝  fc−β with β = 0.86 (N = 30 and L = 3 µm) (orange) (d) and \(P({f}_{{\rm{c}}})\propto {\rm{\exp }}(-{f}_{{\rm{c}}}/{f}_{{\rm{c}}}^{* })\) with \({f}_{{\rm{c}}}^{* }\) =160 pN (N = 10 and L = 1 µm) (yellow) (e). f, The theoretical distribution of assembly critical forces Fc for the model parameters from d (orange) and e (yellow), superimposed with experimentally determined assembly critical forces of U2OS chromosomes (n = 29) (Methods).

Full size image

Mechanical role of TOP2A

To investigate the relationship between chromosome structure and mechanics, we depleted TOP2A, which is required for mitotic chromosome formation3,11,35,36, and might also have a specific structural role5,10,11,37. We analysed chromosomes from human HCT116 CDK1as cells, in which TOP2A could be depleted during prometaphase using a ‘degron’ system5 (Extended Data Fig. 6, Methods). We observed two populations of TOP2A-depleted chromosomes—one with a stiffening length equivalent to that of TOP2A-containing chromosomes, and another elongated and hypo-condensed population (Fig. 4a, b, Extended Data Fig. 7a). Hypo-condensed chromosomes were present at a higher frequency in chromosome spreads than in the tweezers (Extended Data Fig. 6f, Supplementary Note 2). Notably, depletion of TOP2A only led to minor quantitative changes in stiffening behaviour, which still followed the HWLC model (Extended Data Fig. 7b, c, Methods). Fluorescence images of hypo-condensed, H2B–eGFP-labelled, TOP2A-depleted chromosomes showed a heterogeneous distribution of histones along the chromosome arms (Fig. 4b). After stretching, the brighter, chromatin-dense regions extended less than the less dense regions (Fig. 4c, Extended Data Fig. 7d), a heterogeneity consistent with our HWLC model.

Fig. 4: Mechanical properties of TOP2A-depleted chromosomes.
figure 4

a, Stretching curves of control chromosomes (blue) and TOP2A-depleted chromosomes (orange). b, Representative bright-field image of a TOP2A-depleted chromosome and corresponding H2B immunofluorescence image. Scale bar, 4 μm. c, The relative extension of darker and brighter H2B–eGFP regions as a function of relative intensity (grey line and shaded region: mean ± s.e.m.). d, Representative bright-field images of a chromosome in its original buffer containing 80 mM KCl and subsequent images after flushing in buffer containing 480 mM KCl followed by buffer containing 80 mM KCl. e, Force-extension curves of a control and a TOP2A-depleted HCT116 chromosome before, during and after exposure to high-salt buffer (480 mM KCl). Changes in length (f) and compliance (g) of chromosomes before and after the exposing control and TOP2A-depleted chromosomes to high-salt buffer. Two-sided Wilcoxon rank-sum test, *P < 0.05; **P < 0.01. Centre, median; box, 25th to 75th percentile; whiskers, minimum and maximum data points (not considered as outliers).

Full size image

To investigate whether TOP2A has a role in preserving the structure of condensed chromosomes, we induced chromosome decompaction (swelling) and re-compaction by alternating the KCl concentration2,38 (Fig. 4d, Supplementary Video 4). During decompaction, we observed a strong elongation and softening of the chromosomes (Fig. 4e). After re-compaction, both control and TOP2A-depleted chromosomes returned to their initial length (Fig. 4f). Nevertheless, there was a significant increase in the compliance (inverse stiffness) of the TOP2A-depleted chromosomes after re-compaction (from 6 ± 1 nm pN−1 to 15 ± 3 nm pN−1 at 200 pN; P = 0.0002), unlike in control chromosomes (Fig. 4g, Methods). Similarly, we observed no change in the stiffening exponent of control chromosomes, whereas that of the hypo-condensed chromosomes (stiffening length greater than 5 µm) decreased significantly from 1.1 ± 0.2 to 0.4 ± 0.1 (P = 0.0017) (Extended Data Fig. 7e). Within the HWLC framework, such a decrease in the stiffening exponent is interpreted as a structural perturbation with a flatter distribution P(fc) of the critical forces of the components. Moreover, the force-extension curves of chromosomes after decompaction did not change after prolonged exposure to high salt, indicating that there was no loss of material on the timescale of the experiment (Extended Data Fig. 7f). We conclude that TOP2A assists in the restoration of the chromosome to its original structure after perturbation. Thus, TOP2A is not only indispensable for chromosome condensation, but it is also important for the preservation of mitotic chromosome structure.

Conclusions

Here, we have introduced a strategy to study mitotic chromosomes using optical tweezers. We have successfully visualized individual human chromosomes at high resolution and analysed their mechanical parameters with a very high control of applied force. The chromosomes exhibited a nonlinear stiffening response with a power-law exponent considerably lower than that predicted by established polymer models. Although the initial stiffness and length of chromosomes was variable, the anomalous nonlinear stiffening was robust, suggesting that this is an inherent characteristic of chromosomes. This stiffening behaviour is distinct from the linear force-extension that has been reported previously using micropipettes18,19, which probably stems from differences in force resolution and chromosome attachment. To explain the observed nonlinear mechanics, we developed a HWLC model based on sequential stiffening of hierarchical elements within a heterogeneous chromosome (Extended Data Fig. 3). Hence, the anomalous stiffening behaviour of a chromosome emerges from its intrinsic heterogeneity. It is tempting to speculate that such a hierarchy of nonlinear mechanical elements could be beneficial for maintaining the structural integrity of chromosomes by limiting the deformation of individual elements.

A future challenge is to identify the molecular basis for this HWLC model, and establish whether it could relate to patterns of heterochromatin and euchromatin39, A-T and G-C content or the distribution of structural proteins along the chromosome33,40,41. A notable feature after depletion of TOP2A—the most abundant non-histone protein in metaphase chromosomes—is a reproducible shift in the stiffening response after perturbing chromosome structure. This is in stark contrast to other examples of elastic stress-stiffening polymer assemblies, in which non-destructive structural perturbations do not alter the stiffening exponent. Of note, the HWLC model can capture such a change in the stiffening exponent in terms of a structural modification. It has been hypothesized that TOP2A has a structural role by stabilizing chromatin loops through simultaneously binding two DNA duplexes in a closed gate5. Indeed, we find that TOP2A is essential to sustain chromosome mechanics after salt-induced chromosome expansion. The ability to manipulate and image chromosomes under controlled conditions makes our method suitable for investigating the structural and mechanical roles of other chromosomal proteins. We foresee that, by selective depletion or exposure to inhibitors, more insight will be obtained into how proteins compact and maintain mitotic chromosomes. In summary, we have transformed an already-powerful single-molecule technique into a quantitative and versatile method for investigating the mitotic chromosome.

Methods

Cell lines and cell culture

All cell lines were cultured in DMEM supplemented with 10% fetal bovine serum (FBS) and penicillin–streptomycin in a humidified incubator at 37 °C and 5% CO2. Unless indicated otherwise, all cell lines were obtained from and authenticated by the ATCC by karyotyping and STR profiling. The U2OS TRF1-BirA cell line22 was a gift from R. J. O’ Sullivan and was authenticated by karyotyping. Endogenous H2B in the U2Os TRF1-BirA cell line was tagged with eGFP, as described previously5. To rapidly deplete TOP2A, we used a HCT116 TOP2A-mAID cell line that also expressed H2B–eGFP, facilitating chromosome identification. The HCT116 TOP2A-mAID H2B-eGFP cell line was a gift from D. F. Hudson and authentic by karyotyping, and was described in a previous report5. All cell lines were routinely tested for mycoplasma and shown to be negative. To achieve tight temporal control over cell synchrony, the HCT116 TOP2A-mAID H2B-eGFP cell line was modified for CDK1as chemical genetics by knock-in of CDK1as and knockout of endogenous CDK1, as described previously42 and based on another previous report43. The constructs for CDK1as were gifts from W. Earnshaw (Addgene 118596 and 118597) and from Z. Izsvak (Addgene 34879). We determined that treatment with 0.25 µM 1NM-PP1 (529581, Sigma-Aldrich) for 16 h efficiently arrests HCT116 TOP2A-mAID H2B-eGFP CDK1as cells at the G2–M boundary (Extended Data Fig. 6a, b). The incubation time and concentration of 1NM-PP1 were optimized by propidium iodide flow cytometry (Extended Data Fig. 5a), performed as described before5. Efficient release from the arrest was achieved with two wash cycles by centrifugation with preheated medium. A Neon transfection system (Thermo Fisher Scientific) was used for transfections of HCT116 and U2OS cell lines according to the manufacturer’s recommendations. 1NM-PP1 and nocodazole were purchased from Sigma-Aldrich. The synthetic auxin indole-3-acetic acid (IAA) sodium salt (sc-215171, Santa Cruz) was used. Six days before chromosome isolation, HCT116 TOP2A-mAID CDK1as cells were transduced with lentiviruses introducing TRF1-BirA into the genome. These cells were treated for 16 h with 0.25 µM 1NM-PP1, before release into 100 ng ml−1 nocodazole (Sigma-Aldrich) with or without 500 µM auxin for 4 h, to arrest cells in prometaphase and deplete TOP2A, respectively. Mitotic cells were detached by shaking and chromosomes were isolated from this population (Extended Data Fig. 6c). Chromosome spreads were performed as described previously5 and showed an altered chromosome morphology following exposure to auxin in accordance with what was reported5. Approximately 75% of TOP2A depleted chromosomes appeared hypocondensed compared to 5% of control chromosomes (Extended Data Fig. 6d). Immunostaining of TOP2A on chromosome spreads was not detectable in auxin-treated samples, confirming efficient depletion of TOP2A (Extended Data Fig. 5e).

Lentiviral production and transduction

Third-generation lentiviral particles were generated for integration of BirA-TRF1. HEK293T cells were grown with 25 µM chloroquine diphosphate (Sigma-Aldrich) for 5 h before being transfected with plasmids pMD2.G, pMDLg/pRRE and pRSV-Rev (Addgene 12259, 12251 and 12253, deposited by D. Trono44) and a transfer plasmid for BirA-TRF1 integration. A Calphos mammalian transfection kit (Clontech) was used for transfections according to the manufacturer’s protocol. Eighteen hours after transfection, the medium was replaced with fresh medium. Forty-eight hours after transfection, the growth medium was collected and centrifuged at 500g for 5 min, and the supernatant containing viral particles was filtered through a 0.45-µm membrane before being concentrated 10× using an Amicon Ultra-15 100 kDa centrifugal unit (Merck-Millipore). The viral concentrate was snap-frozen and stored at −80 °C. For lentiviral transduction, a T-75 flask of 75% confluent HCT116 TOP2A-mAID CDK1as cells was incubated with 7.5 µg ml−1 polybrene in 3 ml 10× lentiviral concentrate and 7 ml growth medium for 1 h with mixing every 15 min. Cells were then seeded in a T-175 flask and the culture was expanded before chromosome isolation.

Chromosome isolation

A previously reported method, with modifications, was used to isolate mitotic chromosomes in large quantities with minimal contamination with cell debris23. In brief, cells were grown with 12.2 mg l−1 biotin (Sigma-Aldrich) for 24 h before isolation. On the day of isolation, 8–10 T175 flasks of cells were treated for 4 h with 200 ng ml−1 nocodazole (Sigma-Aldrich) and then mitotic shake-off was used to enrich for mitotic cells, resulting in 1 × 107–2 × 107 mitotic cells. The mitotic cells were centrifuged at 300g for 5 min, resuspended in 10 ml 75 mM KCl and 5 mM Tris-HCl (pH 8.0) and then incubated for 10 min at room temperature. All subsequent steps were carried out at 4 °C. Cells were centrifuged at 300g for 5 min and then resuspended in 8 ml polyamine (PA) buffer (15 mM Tris-HCl (pH 8.0), 2 mM EDTA, 0.5 mM EGTA, 80 mM KCl, 20 mM NaCl, 0.5 mM spermidine, 0.2 mM spermine and 0.2% Tween-20) for U2OS cells and a PA* buffer (15mM Tris-HCl (pH 7.4), 0.5 mM EDTA-K, 80 mM KCl, 1 mM spermidine, 0.4 mM spermine and 0.1% Tween-20) for HCT116 cells, both supplemented with Complete mini protease and PhosSTOP phosphatase inhibitor cocktails (Roche). This suspension was then lysed in a Dounce homogenizer using 25 strokes with a tight pestle. The suspension was cleared twice of cell debris by centrifugation at 300g for 5 min. Chromosomes were purified using a glycerol step gradient containing two layers (60% and 30% glycerol in PA). After centrifugation at 1,750g for 30 min, the chromosomes were collected from the 60% glycerol fraction and stored at −20 °C in around 60% glycerol in PA buffer at a concentration of 106–107 chromosomes per ml. Chromosomes could be stored for up to two months without undergoing any noticeable change in mechanical properties.

Dual trap optical tweezers with wide-field fluorescence

The dual trap optical set-up was described previously24. In brief, two optical traps were created using a 20 W, 1064 nm CW fibre laser (YLR-20-LP-IPG, IPG Photonics). Two traps were created by splitting the laser beam into two paths using a polarizing beam splitter cube and could be steered independently using one accurate piezo mirror (Nano-MTA2X10, Mad City Labs) and one coarse positioning piezo step mirror (AG-M100N). After the two paths were recombined, they were coupled into a Nikon microscope body using two 300 mm lenses, and focused in the flow cell with a 1.2 NA water immersion objective (Nikon, Plan apo VC NA1.2). Back-focal plane interferometry was used to measure forces, and bead tracking was performed by LED illuminated bright-field imaging on a CMOS camera (DCC1545M, Thorlabs). Wide-field epifluorescence was achieved by illumination with 488, 532, 561 and 639 nm lasers (Cobolt 06-01 Series) and detection by separation of the emission light using an OptoSplit III (Cairn Research) and imaging on an EMCCD camera (iXon 897 Life, Andor Oxford Instruments Technology).

Microfluidics and flow cell preparation

A microfluidic flow-system (u-Flux, LUMICKS B.V.) was used to insert solutions into a five-channel flow cell (LUMICKS B.V.; Fig. 1b). Before each experiment, bleach cleaning was performed to remove residual debris from flow cell, followed by sodium thiosulfate neutralization. Passivation was performed to reduce chromosome attachment to tubing and flow cell walls by incubation for 1 h with 0.05% casein solution, followed by excessive rinsing with PA buffer. Chromosomes diluted in PA buffer (10–20 µl in 500 µl) were inserted into a side channel of the flow cell (Fig. 1b). Streptavidin-coated polystyrene microspheres (diameter: 4.6 µm, Spherotech) in PA buffer (4 µl in 300 µl) were inserted in one of the main channels. Other channels were filled with PA buffer unless stated otherwise.

Chromosome attachment and force-extension

To facilitate attachment of the biotinylated chromosome between two streptavidin-coated microspheres (diameter: 4.6 µm), one trapped microsphere was brought into the proximity of a chromosome in solution, resulting in attachment of the telomeric end of the chromosome to the microsphere (Fig. 1b, Extended Data Fig. 1b). Next, the microspheres were moved to another microfluidic channel and fluid flow was activated (Fig. 1b). The chromosome attached to one of the microspheres was flow-stretched to confirm correct attachment (Extended Data Fig. 1b, c) and then brought into the proximity of the other microsphere to induce attachment of the other chromosome end (Fig. 1c). Note that owing to the relatively small cross-section of chromosomes compared to the microspheres, both telomeric ends from one sister chromatid would attach to the microsphere occasionally. Non-biotinylated chromosomes showed only very limited attachment to the microspheres (Extended Data Fig. 1d).

Immunofluorescence

Chromosomes were incubated overnight at 4 °C with primary antibody in a concentration of 5 µg ml−1 and were subsequently diluted fivefold in PA buffer and stored for 1 h at 4 °C. Next, chromosomes were incubated with secondary antibody in a concentration of 5 µg ml−1 for 1 h at room temperature. After addition of PA buffer to dilute the sample again by fivefold, chromosomes were stored for 30 min at 4 °C. To remove excess antibody, chromosomes were centrifuged at 750g for 5 min on a 20 µl glycerol cushion. The supernatant was then removed, leaving around 100 µl chromosome solution that could be used for imaging. Primary antibodies were anti-NCAPH (1:100, HPA002647, Sigma Aldrich), CREST anti-sera (1:200 HCT-0100, Immunovision), anti-TRF2 (1:100, sc-9143, Santa Cruz), anti-H3S10 (1:400, 06-570, Sigma-Aldrich) and anti-H3-Alexa Fluor 647 (1:200, 15930862, Thermo Fisher Scientific). Secondary antibodies were anti-rabbit IgG-Alexa Fluor 647 (1:500, A-21244, Thermo Fisher Scientific), anti-rabbit IgG-Alexa Fluor 568 (1:500, A-11011, Thermo Fisher Scientific) and anti-human IgG-Alexa Fluor 488 (1:500, A-11013, Thermo Fisher Scientific). Biotinylated TRF1 was detected using streptavidin–Alexa Fluor 568 (1:200, S11226, Invitrogen).

Immunoblotting

SDS–PAGE and immunoblotting was performed as described previously5. In brief, cell pellets were lysed in RIPA buffer containing cOmplete Mini EDTA free (Roche) on ice for 20 min. Samples were then sonicated in a water-cooled Bioruptor Pico (Diagenode) and centrifuged at 21,000g for 15 min at 4 °C. Protein concentration was determined using a Pierce BCA protein assay kit (Thermo Fisher Scientific). Forty micrograms of protein was loaded per well. The primary antibodies were anti-CDK1 (1:1,000, ab133327, Abcam), anti-Myc (1:1,000, sc-40, Santa Cruz) and anti-histone H3.3 (1:5,000, ab176840, Abcam). The secondary antibodies were anti-mouse IgG peroxidase conjugate (1:10,000, A4416, Sigma-Aldrich) and anti-rabbit IgG peroxidase conjugate (1:10,000, A6154, Sigma-Aldrich).

Determination of differential stiffness, stiffening length and compliance

To calculate the differential stiffness from force-distance curves, the force distance curve was first smoothed using a moving average with a window size of 1/15 of the total data points in the force curve, followed by numerical differentiation of force with respect to distance. To determine the onset of stiffening, the plateau stiffness was determined as the most likely stiffness at forces below 50 pN, as estimated from the maximum of a kernel density estimate of the stiffness values. The onset of stiffening was then determined as the point at which the stiffness exceeds the plateau stiffness by one standard deviation of all stiffnesses below 50 pN. To determine the compliance at 200 pN, the inverse of the stiffness of the chromosome at a force of 200 pN was used.

Collapse of stiffness-force curves

To achieve a collapse of the stiffness-force curves they were normalized on a log-log-scale. Therefore, curves were interpolated to a logarithmic force scale to get evenly spaced data after taking the logarithm. In addition, negative values for force and stiffness were discarded. Then the logarithms of force ln(F) and stiffness ln(K) were calculated and fitted with a piecewise function y = ln(K0) for x ≤ ln(Fc) and y = c − ln(Fc) + ln(K0) for x > ln(Fc) to determine the initial stiffness K0 and the critical force Fc. If the determined parameters for K0 and Fc were in the range of the stiffness-force curve, the curves normalized by K0 and Fc were plotted in a double-logarithmic plot to achieve the collapse. The criteria that K0 and Fc had to be positive and within the range of the stiffness-force curve were met by 29 out of 44 curves.

Microrheology

Oscillations of the optical trap were generated by applying a sinusoidal voltage to the analogue input of the piezo mirror controller (Nano-Drive, MCL) to apply the oscillation on top of the digitally controlled mirror position. The signal was first generated digitally using Labview (National Instruments). The analogue voltage was then produced with a digital analogue converter (DAQ, National Instruments). Oscillations were produced with an amplitude of 25 mV corresponding to a trap displacement of roughly 200 nm. The frequency of the oscillation was varied between 2 mHz and 100 Hz. When the frequency was varied in the experiment, the pre-tension was kept constant at 50 pN (Fig. 2f). Experiments for different pre-tension were performed with a frequency of 0.1 Hz (Fig. 2g). To avoid limitations by the frame rate of the bead tracking camera at higher frequencies (>1 Hz), the bead position at high frequencies was calculated from the force and the trap position (Fig. 2f, green line). Data analysis of the oscillations was performed in MATLAB (Mathworks). First, the bead–bead distance and the force were synchronized on the basis of the position of the stationary bead where the force was measured, based on the cross-correlation between the bead position from bead tracking and the measured force. Then the oscillatory data were analysed following a previously described procedure45. In brief, both the force and the bead–bead separation were detrended and fitted with a sine function with a fixed frequency set to the experimental frequency and an additional offset. Then the complex stiffness was calculated as \(k=\frac{{A}_{{\rm{F}}}}{{A}_{{\rm{d}}}}{{\rm{e}}}^{i\left({\phi }_{{\rm{F}}}-{\phi }_{{\rm{d}}}\right)}\) with the amplitude and the phase of the force oscillation AF and φF, and the amplitude and the phase of the distance oscillation Ad and φd, respectively.

Calculating HWLC force responses

Model curves in Fig. 3d, e were constructed by first defining a distribution for each system parameter. For simplicity, the number of sub-chains, N, and the length of each sub-chain, L/N, were kept constant. A power-law or exponential distribution with cut-offs was chosen for the sub-chain critical force, fc. Given these distributions, we analysed the responses of 500 HWLC configurations, each constructed by sampling N values of fc. The force-response of each configuration was computed by summing the extensions of each sub-chain at a given force, found by numerically solving the flexible WLC equation (Supplementary Note 1). The force-response curve was then numerically differentiated, and the mean and standard deviation of the stiffness-force curve were compared to experimental data.

Distribution of F c

The distribution of the critical force of a HWLC assembly, Fc,corresponds to the force at which its softest element starts stiffening. Hence, for a given distribution, P(fc), Fc is distributed as the minimum of N independent samples. Its cumulative distribution function (CDF) satisfies \(P\left({F}_{{\rm{c}}}\le x\right)=1-{\left(1-P\left({f}_{{\rm{c}}}\le x\right)\right)}^{N}.\) This expression can be differentiated to yield the probability density function (PDF),\({P}\left({F}_{{\rm{c}}}=x\right)={N\; P}\left({f}_{{\rm{c}}}=x\right)\,{\left(1-P\left({f}_{{\rm{c}}}\le x\right)\right)}^{N-1}\). Figure 3f shows P(Fc = x) for the power-law distribution with cut-offs and for an exponential distribution with cut-offs. The experimental critical forces were determined as described above.

Statistics and reproducibility

Average values and errors were represented as mean ± s.e.m. unless indicated otherwise. Differences in populations are tested using a two-sided Wilcoxon rank-sum test, where P < 0.05 is regarded as significant (*) and P  < 0.01 as highly significant (**). The sample sizes for representative microscopy images are as follows: Fig. 1cn = 91, Fig. 1d–fn = 3, Fig. 2bn = 91, Fig. 4bn = 5, Fig. 4dn = 20, Extended Data Fig. 1an = 24, Extended Data Fig. 1b, cn = 3, Extended Data Fig. 1en = 10, Extended Data Fig. 1f–hn = 3, Extended Data Fig. 6an = 2, Extended Data Fig. 6e (amount of cells) n = 117 (15 min), n = 120 (20 min), n = 98 (25 min), n = 121 (30 min), n = 110 (40 min), n = 115 (50 min), Extended Data Fig. 6gn = 16 (control), n = 19 (+auxin), Extended Data Fig. 7dn = 5.

Reporting summary

Further information on research design is available in the Nature Research Reporting Summary linked to this paper.