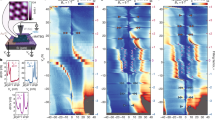
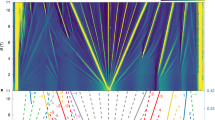
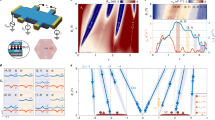
Abstract
Interaction-driven spontaneous symmetry breaking lies at the heart of many quantum phases of matter. In moiré systems, broken spin/valley ‘flavour’ symmetry in flat bands underlies the parent state from which correlated and topological ground states ultimately emerge1,2,3,4,5,6,7,8,9,10. However, the microscopic mechanism of such flavour symmetry breaking and its connection to the low-temperature phases are not yet understood. Here we investigate the broken-symmetry many-body ground state of magic-angle twisted bilayer graphene (MATBG) and its nontrivial topology using simultaneous thermodynamic and transport measurements. We directly observe flavour symmetry breaking as pinning of the chemical potential at all integer fillings of the moiré superlattice, demonstrating the importance of flavour Hund’s coupling in the many-body ground state. The topological nature of the underlying flat bands is manifested upon breaking time-reversal symmetry, where we measure energy gaps corresponding to Chern insulator states with Chern numbers 3, 2, 1 at filling factors 1, 2, 3, respectively, consistent with flavour symmetry breaking in the Hofstadter butterfly spectrum of MATBG. Moreover, concurrent measurements of resistivity and chemical potential provide the temperature-dependent charge diffusivity of MATBG in the strange-metal regime11—a quantity previously explored only in ultracold atoms12. Our results bring us one step closer to a unified framework for understanding interactions in the topological bands of MATBG, with and without a magnetic field.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The data that support the current study are available from the corresponding authors upon reasonable and well motivated request.
References
Cao, Y. et al. Correlated insulator behaviour at half-filling in magic-angle graphene superlattices. Nature 556, 80–84 (2018).
Cao, Y. et al. Unconventional superconductivity in magic-angle graphene superlattices. Nature 556, 43–50 (2018).
Chen, G. et al. Evidence of a gate-tunable Mott insulator in a trilayer graphene moiré superlattice. Nat. Phys. 15, 237–241 (2019).
Yankowitz, M. et al. Tuning superconductivity in twisted bilayer graphene. Science 363, 1059–1064 (2019).
Lu, X. et al. Superconductors, orbital magnets and correlated states in magic-angle bilayer graphene. Nature 574, 653–657 (2019).
Sharpe, A. L. et al. Emergent ferromagnetism near three-quarters filling in twisted bilayer graphene. Science 365, 605–608 (2019).
Serlin, M. et al. Intrinsic quantized anomalous Hall effect in a moiré heterostructure. Science 367, 900–903 (2020).
Chen, G. et al. Tunable correlated Chern insulator and ferromagnetism in a moiré superlattice. Nature 579, 56–61 (2020); publisher correction 581, E3 (2020).
Wong, D. et al. Cascade of electronic transitions in magic-angle twisted bilayer graphene. Nature 582, 198–202 (2020).
Zondiner, U. et al. Cascade of phase transitions and Dirac revivals in magic-angle graphene. Nature 582, 203–208 (2020).
Cao, Y. et al. Strange metal in magic-angle graphene with near Planckian dissipation. Phys. Rev. Lett. 124, 076801 (2020).
Brown, P. T. et al. Bad metallic transport in a cold atom Fermi–Hubbard system. Science 363, 379–382 (2019).
Lee, P. A., Nagaosa, N. & Wen, X.-G. Doping a Mott insulator: physics of high-temperature superconductivity. Rev. Mod. Phys. 78, 17–85 (2006).
Balents, L. Spin liquids in frustrated magnets. Nature 464, 199–208 (2010).
Tanatar, B. & Ceperley, D. M. Ground state of the two-dimensional electron gas. Phys. Rev. B 39, 5005–5016 (1989).
Su rez Morell, E., Correa, J. D., Vargas, P., Pacheco, M. & Barticevic, Z. Flat bands in slightly twisted bilayer graphene: tight-binding calculations. Phys. Rev. B 82, 121407 (2010).
Bistritzer, R. & MacDonald, A. H. Moiré bands in twisted double-layer graphene. Proc. Natl Acad. Sci. USA 108, 12233–12237 (2011).
Xie, Y. et al. Spectroscopic signatures of many-body correlations in magic-angle twisted bilayer graphene. Nature 572, 101–105 (2019).
Kerelsky, A. et al. Maximized electron interactions at the magic angle in twisted bilayer graphene. Nature 572, 95–100 (2019).
Jiang, Y. et al. Charge order and broken rotational symmetry in magic-angle twisted bilayer graphene. Nature 573, 91–95 (2019).
Choi, Y. et al. Electronic correlations in twisted bilayer graphene near the magic angle. Nat. Phys. 15, 1174–1180 (2019). author correction 15, 1205 (2019).
Kim, S. et al. Direct measurement of the Fermi energy in graphene using a double-layer heterostructure. Phys. Rev. Lett. 108, 116404 (2012).
Eisenstein, J. P., Pfeiffer, L. N. & West, K. W. Compressibility of the two-dimensional electron gas: measurements of the zero-field exchange energy and fractional quantum Hall gap. Phys. Rev. B 50, 1760–1778 (1994).
Setiawan, F. & Das Sarma, S. Temperature-dependent many-body effects in Dirac–Weyl materials: interacting compressibility and quasiparticle velocity. Phys. Rev. B 92, 235103 (2015).
Padhi, B., Setty, C. & Phillips, P. W. Doped twisted bilayer graphene near magic angles: proximity to Wigner crystallization, not Mott insulation. Nano Lett. 18, 6175–6180 (2018).
Wu, S., Zhang, Z., Watanabe, K., Taniguchi, T. & Andrei, E. Y. Chern insulators, van Hove singularities and topological flat bands in magic-angle twisted bilayer graphene. Nat. Mater. https://doi.org/10.1038/s41563-020-00911-2 (2021).
Tomarken, S. L. et al. Electronic compressibility of magic-angle graphene superlattices. Phys. Rev. Lett. 123, 046601 (2019).
Nuckolls, K. P. et al. Strongly correlated Chern insulators in magic-angle twisted bilayer graphene. Nature 588, 610–615 (2020).
Saito, Y. et al. Hofstadter subband ferromagnetism and symmetry-broken Chern insulators in twisted bilayer graphene. Nat. Phys. https://doi.org/10.1038/s41567-020-01129-4 (2021).
Das, I. et al. Symmetry-broken Chern insulators and Rashba-like Landau-level crossings in magic-angle bilayer graphene. Nat. Phys. https://doi.org/10.1038/s41567-021-01186-3 (2021).
Streda, P. & Smrcka, L. Thermodynamic derivation of the Hall current and the thermopower in quantising magnetic field. J. Phys. C 16, L895–L899 (1983).
Hofstadter, D. R. Energy levels and wave functions of Bloch electrons in rational and irrational magnetic fields. Phys. Rev. B 14, 2239–2249 (1976).
Georges, A., de’ Medici, L. & Mravlje, J. Strong correlations from Hund’s coupling. Annu. Rev. Condens. Matter Phys. 4, 137–178 (2013).
Polshyn, H. et al. Large linear-in-temperature resistivity in twisted bilayer graphene. Nat. Phys. 15, 1011–1016 (2019).
Bruin, J. N., Sakai, H., Perry, R. S. & Mackenzie, A. P. Similarity of scattering rates in metals showing t-linear resistivity. Science 339, 804–807 (2013).
Chowdhury, D., Werman, Y., Berg, E. & Senthil, T. Translationally invariant non-fermi-liquid metals with critical Fermi surfaces: solvable models. Phys. Rev. X 8, 031024 (2018).
Patel, A. A. & Sachdev, S. Theory of a Planckian metal. Phys. Rev. Lett. 123, 066601 (2019).
Hartnoll, S. A. Theory of universal incoherent metallic transport. Nat. Phys. 11, 54–61 (2015).
Perepelitsky, E. et al. Transport and optical conductivity in the Hubbard model: a high-temperature expansion perspective. Phys. Rev. B 94, 235115 (2016).
Pakhira, N. & McKenzie, R. H. Absence of a quantum limit to charge diffusion in bad metals. Phys. Rev. B 91, 075124 (2015).
Kokalj, J. Bad-metallic behavior of doped Mott insulators. Phys. Rev. B 95, 041110 (2017).
Efros, A. L. Negative density of states: screening, Einstein relation, and negative diffusion. Phys. Rev. B 78, 155130 (2008).
Ortix, C., Lorenzana, J. & Di Castro, C. Coulomb-frustrated phase separation phase diagram in systems with short-range negative compressibility. Phys. Rev.Lett. 100, 246402 (2008).
Acknowledgements
We thank S. Das Sarma, A. Georges, F. Guinea, S. Ilani, A. Kapitulnik, L. Levitov, L. Taillefer, S. Todadri, A. Vishwanath, A. Yacoby, D. Bandurin, S. de la Barrera, C. Collignon, A. Fahimniya, D. Rodan-Legrain, Y. Xie and K. Yasuda for discussions. This work has been primarily supported by the US Department of Energy (DOE), Office of Basic Energy Sciences (BES), Division of Materials Sciences and Engineering under award DE-SC0001819 (J.M.P.). Help with transport measurements and data analysis were supported by the National Science Foundation (DMR-1809802) and the STC Center for Integrated Quantum Materials (NSF grant number DMR-1231319) (Y.C.). P.J.-H. acknowledges support from the Gordon and Betty Moore Foundation’s EPiQS Initiative through grant GBMF9643. P.J.-H. acknowledges partial support by Fundación Ramon Areces. The development of new nanofabrication and characterization techniques enabling this work has been supported by the US DOE Office of Science, BES, under award DE‐SC0019300. K.W. and T.T. acknowledge support from the Elemental Strategy Initiative conducted by MEXT, Japan, grant number JPMXP0112101001, JSPS KAKENHI grant number JP20H00354 and CREST(JPMJCR15F3), JST. This work made use of the Materials Research Science and Engineering Center Shared Experimental Facilities supported by the National Science Foundation (DMR-0819762) and of Harvard’s Center for Nanoscale Systems, supported by the NSF (ECS-0335765).
Author information
Authors and Affiliations
Contributions
J.M.P. and Y.C. fabricated the samples and performed transport measurements and numerical simulations. K.W. and T.T. provided hBN samples. J.M.P., Y.C. and P.J.-H. performed data analysis, discussed the results and wrote the manuscript with input from all co-authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature thanks Philip Phillips, Ke Wang and Shuigang Xu for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 Superconductivity and Landau fan diagram of MATBG.
a, Superconducting curves for the ν = −2 – δ and +2 + δ domes of MATBG. The maximum Tc ≈ 2.7 K is determined from the 50% normal resistance of the ν = −2 – δ curve. b, Landau fan diagram of MATBG at 1 K. The CNP shows the main sequence νLL = ±4, ±8,... and the broken-symmetry states νLL = −1, ±2, ±3. There are fans from ν = ±2, where the sequence νLL = +2, +4, +6 and νLL = −2 are seen, respectively. We also find transport evidence of a correlated Chern gap with Chern number C = 3 from ν = +1.
Extended Data Fig. 2 In-plane magnetic-field dependence of μ and Rxx.
a–c, The in-plane magnetic-field dependence of μ and Rxx is shown at ν = −2 (a), ν = −1 (b) and ν = +3 (c). a, b, The hole-doped side features are qualitatively similar to those on the electron-doped side, but weaker. We note that the ‘dip’ in μ on the electron-doped side is analogous to the ‘peak’ on the hole-doped side. For ν = −1, the peak in Rxx and the ‘peak’ feature in μ enhance under B‖. For ν = −2, the peak in Rxx weakens upon applying B‖, whereas the feature in μ does not exhibit a noticeable change. c, For ν = +3, the trend in μ is similar to that for ν = +1, that is, the ‘dip’ feature is enhanced under B‖, although the dependence is generally weaker. There is no noticeable peak in Rxx at ν = +3.
Extended Data Fig. 3 Thermal activation gap analysis and g factors of the correlated states.
a, b, Fitting of temperature-dependent resistance using the Arrhenius formula \({R}_{xx}^{* }\propto \exp [-\varDelta /(2{k}_{{\rm{B}}}T)]\) at ν = +1 (a) and +2 (b) for in-plane magnetic fields of B‖ = 0–11 T. \({R}_{xx}^{* }\) is the background-removed resistance of MATBG. c, B‖ dependence of the thermal activation gap Δ. The extracted g factors are ~0.57, ~1.31 for the ν = +1, +2 states, respectively.
Extended Data Fig. 4 Overlay of inverse compressibility and superconducting dome, and full-range chemical potential data.
a, Temperature dependence of inverse compressibility dμ/dn for T = 2–70 K at B = 0 T. Negative compressibility near ν = +1, +2 persists up to T ≈ 20 K. b, Comparison between dμ/dn and superconducting Tc dome (red points; 20% normal-state resistance) near ν = −2 – δ. The Tc dome occurs near maximum dμ/dn, which is unexpected within a weak-coupling BCS-type mechanism for the superconductivity. c, Same data as in Fig. 2d, but showing the chemical potential beyond ν = ±4.
Extended Data Fig. 5 Perpendicular magnetic-field dependence of Landau level and Chern gaps.
a–e, Gap extraction from the chemical potential curves at B⊥ = 0–6 T. f–g, Magnetic-field dependence of Landau level gaps (f) and correlated Chern gaps (g). Whereas the νLL = ±4, 0 Landau level gaps have an increasing trend with B⊥, the νLL = ±2 gaps show a relatively weak dependence. Similarly, the three correlated Chern gaps also exhibit weak dependence on B⊥. The reason why the Chern gap at ν = 2 + 2ϕ/ϕ0 is larger than the other two might be the difference in their magnetic ground states, with contributions from both orbital and spin degrees of freedom.
Extended Data Fig. 6 In-plane magnetization of MATBG.
a, \({\left(\frac{\partial {M}_{\parallel }}{\partial \nu }\right)}_{T,{B}_{\parallel }}=-{\left(\frac{\partial \mu }{\partial {B}_{\parallel }}\right)}_{T,\nu }\) versus ν. Peaks are visible near νLL = ±1. T = 4 K. b, Magnetization M‖, from integration of the curve in a. M‖ persists near all filling factors ν = ±1, ±2, ±3. The error bands correspond to a confidence level of 95%.
Supplementary information
Supplementary Information
This file contains Supplementary Information, including Supplementary Figures 1–13 and additional references.
Rights and permissions
About this article
Cite this article
Park, J.M., Cao, Y., Watanabe, K. et al. Flavour Hund’s coupling, Chern gaps and charge diffusivity in moiré graphene. Nature 592, 43–48 (2021). https://doi.org/10.1038/s41586-021-03366-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-021-03366-w
This article is cited by
-
Crystal net catalog of model flat band materials
npj Computational Materials (2024)
-
Angle-resolved transport non-reciprocity and spontaneous symmetry breaking in twisted trilayer graphene
Nature Materials (2024)
-
Engineering correlated insulators in bilayer graphene with a remote Coulomb superlattice
Nature Materials (2024)
-
Evidence for Dirac flat band superconductivity enabled by quantum geometry
Nature (2023)
-
Electrical switching of a bistable moiré superconductor
Nature Nanotechnology (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.