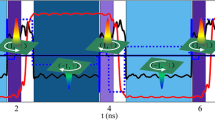
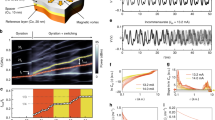
Abstract
The collective dynamics of topological structures1,2,3,4,5,6 are of interest from both fundamental and applied perspectives. For example, studies of dynamical properties of magnetic vortices and skyrmions3,4 have not only deepened our understanding of many-body physics but also offered potential applications in data processing and storage7. Topological structures constructed from electrical polarization, rather than electron spin, have recently been realized in ferroelectric superlattices5,6, and these are promising for ultrafast electric-field control of topological orders. However, little is known about the dynamics underlying the functionality of such complex extended nanostructures. Here, using terahertz-field excitation and femtosecond X-ray diffraction measurements, we observe ultrafast collective polarization dynamics that are unique to polar vortices, with orders-of-magnitude higher frequencies and smaller lateral size than those of experimentally realized magnetic vortices3. A previously unseen tunable mode, hereafter referred to as a vortexon, emerges in the form of transient arrays of nanoscale circular patterns of atomic displacements, which reverse their vorticity on picosecond timescales. Its frequency is considerably reduced (softened) at a critical strain, indicating a condensation (freezing) of structural dynamics. We use first-principles-based atomistic calculations and phase-field modelling to reveal the microscopic atomic arrangements and corroborate the frequencies of the vortex modes. The discovery of subterahertz collective dynamics in polar vortices opens opportunities for electric-field-driven data processing in topological structures with ultrahigh speed and density.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The data that support the findings of this study are available from the corresponding author upon request.
Code availability
The codes that support the findings of this study are available from the corresponding author upon request.
References
Naumov, I. I., Bellaiche, L. & Fu, H. Unusual phase transitions in ferroelectric nanodisks and nanorods. Nature 432, 737–740 (2004).
Huang, F.-T. & Cheong, S.-W. Aperiodic topological order in the domain configurations of functional materials. Nat. Rev. Mater. 2, 17004 (2017).
Choe, S.-B. et al. Vortex core-driven magnetization dynamics. Science 304, 420–422 (2004).
Büttner, F. et al. Dynamics and inertia of skyrmionic spin structures. Nat. Phys. 11, 225–228 (2015).
Yadav, A. K. et al. Observation of polar vortices in oxide superlattices. Nature 530, 198–201 (2016).
Das, S. et al. Observation of room-temperature polar skyrmions. Nature 568, 368–372 (2019).
Nagaosa, N. & Tokura, Y. Topological properties and dynamics of magnetic skyrmions. Nat. Nanotechnol. 8, 899–911 (2013).
Yadav, A. K. et al. Spatially resolved steady-state negative capacitance. Nature 565, 468–471 (2019).
Íñiguez, J., Zubko, P., Luk’yanchuk, I. & Cano, A. Ferroelectric negative capacitance. Nat. Rev. Mater. 4, 243–256 (2019).
Stoica, V. A. et al. Optical creation of a supercrystal with three-dimensional nanoscale periodicity. Nat. Mater. 18, 377–383 (2019).
Büttner, F., Lemesh, I. & Beach, G. S. D. Theory of isolated magnetic skyrmions: from fundamentals to room temperature applications. Sci. Rep. 8, 4464 (2018).
Seidel, J. Domain walls as nanoscale functional elements. J. Phys. Chem. Lett. 3, 2905–2909 (2012).
Gu, Z. et al. Resonant domain-wall-enhanced tunable microwave ferroelectrics. Nature 560, 622–627 (2018).
Cochard, C., Spielmann, T. & Granzow, T. Dielectric tunability of ferroelectric barium titanate at millimeter-wave frequencies. Phys. Rev. B 100, 184104 (2019).
Catalan, G., Seidel, J., Ramesh, R. & Scott, J. F. Domain wall nanoelectronics. Rev. Mod. Phys. 84, 119–156 (2012).
Wu, X. et al. Low-energy structural dynamics of ferroelectric domain walls in hexagonal rare-earth manganites. Sci. Adv. 3, e1602371 (2017).
Luk’yanchuk, I., Sené, A. & Vinokur, V. M. Electrodynamics of ferroelectric films with negative capacitance. Phys. Rev. B 98, 024107 (2018).
Hlinka, J., Paściak, M., Körbel, S. & Marton, P. Terahertz-range polar modes in domain-engineered BiFeO3. Phys. Rev. Lett. 119, 057604 (2017).
Gui, Z. & Bellaiche, L. Terahertz dynamics of ferroelectric vortices from first principles. Phys. Rev. B 89, 064303 (2014).
Zhang, Q., Herchig, R. & Ponomareva, I. Nanodynamics of ferroelectric ultrathin films. Phys. Rev. Lett. 107, 177601 (2011).
Ogawa, N., Seki, S. & Tokura, Y. Ultrafast optical excitation of magnetic skyrmions. Sci. Rep. 5, 9552 (2015).
Hong, Z. et al. Stability of polar vortex lattice in ferroelectric superlattices. Nano Lett. 17, 2246–2252 (2017).
Scott, J. F. Soft-mode spectroscopy: experimental studies of structural phase transitions. Rev. Mod. Phys. 46, 83–128 (1974).
Li, X. et al. Terahertz field-induced ferroelectricity in quantum paraelectric SrTiO3. Science 364, 1079–1082 (2019).
Nova, T. F., Disa, A. S., Fechner, M. & Cavalleri, A. Metastable ferroelectricity in optically strained SrTiO3. Science 364, 1075–1079 (2019).
Bargheer, M. et al. Coherent atomic motions in a nanostructure studied by femtosecond X-ray diffraction. Science 306, 1771–1773 (2004).
Zhu, H. et al. Observation of chiral phonons. Science 359, 579–582 (2018).
Qi, T., Shin, Y.-H., Yeh, K.-L., Nelson, K. & Rappe, A. Collective coherent control: synchronization of polarization in ferroelectric PbTiO3 by shaped THz fields. Phys. Rev. Lett. 102, 247603 (2009).
Chen, F. et al. Ultrafast terahertz-field-driven ionic response in ferroelectric BaTiO3. Phys. Rev. B 94, 180104 (2016).
Kozina, M. et al. Terahertz-driven phonon upconversion in SrTiO3. Nat. Phys. 15, 387–392 (2019).
Kubacka, T. et al. Large-amplitude spin dynamics driven by a THz pulse in resonance with an electromagnon. Science 343, 1333–1336 (2014).
Damodaran, A. R. et al. Phase coexistence and electric-field control of toroidal order in oxide superlattices. Nat. Mater. 16, 1003–1009 (2017).
Li, Q. et al. Quantification of flexoelectricity in PbTiO3/SrTiO3 superlattice polar vortices using machine learning and phase-field modeling. Nat. Commun. 8, 1468 (2017).
Yang, T., Wang, B., Hu, J.-M. & Chen, L.-Q. Domain dynamics under ultrafast electric-field pulses. Phys. Rev. Lett. 124, 107601 (2020).
Trigo, M. et al. Probing unfolded acoustic phonons with X rays. Phys. Rev. Lett. 101, 025505 (2008).
Zhang, L. & Niu, Q. Angular momentum of phonons and the Einstein–de Haas effect. Phys. Rev. Lett. 112, 085503 (2014).
von Hoegen, A., Mankowsky, R., Fechner, M., Först, M. & Cavalleri, A. Probing the interatomic potential of solids with strong-field nonlinear phononics. Nature 555, 79–82 (2018).
Tamura, S., Hurley, D. C. & Wolfe, J. P. Acoustic-phonon propagation in superlattices. Phys. Rev. B 38, 1427–1449 (1988).
Daranciang, D. et al. Ultrafast photovoltaic response in ferroelectric nanolayers. Phys. Rev. Lett. 108, 087601 (2012).
Chollet, M. et al. The X-ray Pump–Probe instrument at the Linac Coherent Light Source. J. Synchrotron Radiat. 22, 503–507 (2015).
Kozina, M. et al. Ultrafast X-ray diffraction probe of terahertz field-driven soft mode dynamics in SrTiO3. Struct. Dyn. 4, 054301 (2017).
Sato, T. et al. A simple instrument to find spatiotemporal overlap of optical/X-ray light at free-electron lasers. J. Synchrotron Radiat. 26, 647–652 (2019).
Glownia, J. M. et al. Pump–probe experimental methodology at the Linac Coherent Light Source. J. Synchrotron Radiat. 26, 685–691 (2019).
Sepliarsky, M., Asthagiri, A., Phillpot, S. R., Stachiotti, M. G. & Migoni, R. L. Atomic-level simulation of ferroelectricity in oxide materials. Curr. Opin. Solid State Mater. Sci. 9, 107–113 (2005).
Sepliarsky, M. & Cohen, R. E. First-principles based atomistic modeling of phase stability in PMN–xPT. J. Phys. Condens. Matter 23, 435902 (2011).
Stachiotti, M. G. & Sepliarsky, M. Toroidal ferroelectricity in PbTiO3 nanoparticles. Phys. Rev. Lett. 106, 137601 (2011).
Gale, J. D. & Rohl, A. L. The General Utility Lattice Program (GULP). Mol. Simul. 29, 291–341 (2003).
Acknowledgements
We acknowledge discussions with M. Trigo, D. Xiao, Z. Hong, I. Luk’yanchuk and V. M. Vinokur. This work was primarily supported by the US Department of Energy, Office of Science, Basic Energy Sciences, Materials Sciences and Engineering Division: experimental design, data collection, data analysis, and part of simulations by Q.L. and H.W. were supported under the DOE Early Career Award; ultrafast measurements and sample synthesis by V.A.S., Y.Y., S.P., L.W.M., C.D., S.Y., A.L., L.-Q.C., V.G., J.W.F. and H.W. were supported under award no. DE-SC-0012375; ancillary ultrafast X-ray measurements by H.L., S.M., Y.A. and P.E. were supported under award no. DE-FG02-04ER46147. M.M., S.D., and R.R. acknowledge support for part of sample synthesis through the Quantum Materials programme (KC 2202) funded by the US Department of Energy, Office of Science, Basic Energy Sciences, Materials Sciences Division under contract no. DE-AC02-05-CH11231. J.H. and M.P. were supported by the Czech Science Foundation (project no. 19-28594X) and acknowledge the access to computing facilities owned by parties and projects contributing to the National Grid Infrastructure MetaCentrum, provided under programme no. Cesnet LM2015042. T.Y. and L.-Q.C. acknowledge partial support from the US Department of Energy, Office of Science, Basic Energy Sciences, under award n0. DE-SC0020145 as part of the Computational Materials Sciences Program and from NSF under award DMR-1744213. Y.Z. and H.W. acknowledge support by ANL-LDRD for preliminary X-ray measurements. Q.L. acknowledges support by the Basic Science Center Project of NSFC under grant no. 51788104 for completing phase-field simulations at Tsinghua University. S.M. acknowledges support from the Office of Science Graduate Student Research (SCGSR) programme (DOE contract no. DE‐SC0014664) and from the UW-Madison Materials Research Science and Engineering Center (NSF DMR-1720415). H.L. acknowledges support by the National Research Foundation of Korea under grant 2017R1A6A3A11030959. Use of the Linac Coherent Light Source is supported by the US Department of Energy, Office of Science, Office of Basic Energy Sciences under contract no. DE-AC02-76SF00515. Use of the Advanced Photon Source is supported by the US Department of Energy, Office of Science, Office of Basic Energy Sciences under contract no. DE-AC02–06CH11357.
Author information
Authors and Affiliations
Contributions
Q.L., V.A.S., Y.Y., M.R.M., S.P., H.J.L., Y.A., S.D.M., T.S., M.C.H., M.C., M.E.K., S.N., D.Z., A.M.L., P.G.E., V.G., J.W.F. and H.W. performed the experiment at the Linac Coherent Light Source. Y.Z., V.A.S., D.A.W. and H.W. performed preliminary experiments at the Advanced Photon Source. M.P. and J.H. performed atomistic modelling. Q.L., C.D., T.Y. and L.-Q.C. performed phase-field simulation. T.Y., L.-Q.C. and. J.H. developed the analytical model. S.D., M.R.M., A.K.Y., L.W.M. and R.R. prepared the samples. S.Y. and C.K. performed THz spectroscopy measurements. Q.L. and H.W. wrote the manuscript with input from all authors. H.W. conceived and supervised the project.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature thanks Igor Luk’yanchuk, Daniel Schick and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 Diffraction patterns of probed Bragg peaks and the corresponding diffraction geometry.
a, Diffraction patterns of 023, 113 and 004 peaks in logarithmic scale as recorded by a two-dimensional X-ray area detector. The projected q-axis labels indicate the approximate directions in reciprocal space. b, Schematics of diffraction geometry for probing the 023, 113 and 004 peaks. The dashed circle represents the horizontal plane. The red and blue stripes represent vortex structure with opposite vorticities. The THz field is polarized vertically.
Extended Data Fig. 2 The response of the FE (a1/a2) structure upon THz field excitation.
a, 3D schematic of diffraction peaks of the film around the 023 or 113 substrate peaks in reciprocal space. The dashed arrows indicate the reciprocal axes through the centres of the FE or vortex SL peaks that are offset along the qy-axis owing to the lattice constant difference along the y-axis. Only two SL and their satellite peaks are shown for simplicity. b, Normalized change of diffraction intensity of the 113 FE satellite peak (red curve) measured at the delay of 4 ps indicated by the red arrow in e, and normalized change of diffraction intensity of the 004 FE SL peak (blue curve) measured at the delay of 35 ps indicated by the blue arrow in g, as a function of the applied THz peak field. Lines are linear and quadratic fits to the measured data, in agreement with the field-driven structure factor modulation and the THz-induced Bragg peak shift (heating), respectively. c, Rocking curve of 023 FE SL peak. d, Normalized change of diffraction intensity as a function of delay measured at various incident angles indicated by the magenta, grey and blue arrows in c. e, Normalized change of diffraction intensity of the 113 FE SL peak and its satellites as a function of delay. The curves are vertically offset for clarity. f, Fourier spectra of e. g, Normalized change of diffraction intensity as a function of delay measured at the lower-angle side of the 004 FE SL peaks, indicated by the green arrow in h. h, Rocking curves of 004 FE SL peak measured at the delay of 35 ps with and without THz excitation. The peak shift shows a strain of 2.5 × 10−5, corresponding to a 2 K temperature rise as calibrated by the temperature-dependent X-ray diffraction measurements shown in Extended Data Fig. 7b.
Extended Data Fig. 3 The dielectric properties of vortex structures as a function of strain and frequency from atomistic calculations.
a, Frequency–strain diagram with the diagonal oscillator strength (Sii) of each mode reflected in the size of the markers (the area is proportional to log(Sii + 1 THz2)), where i represents x, y or z. The dielectric strength of the mth mode (\(\Delta {{\epsilon }}_{ii,m}\)) is directly related to the oscillator strength via \(\Delta {{\epsilon }}_{ii,m}={S}_{ii,m}/{\omega }_{m}^{2}\), where ωm is the mode’s frequency. The 15 lowest-frequency modes are considered; the zz signal is multiplied 5 times for better visibility. The orange area indicates the high-frequency regime. b, Frequency-dependent permittivity for two different strain values, εx = −0.25% and 0.2%. The imaginary part is presented in the main plots, while the left-hand insets show diagonal components \({{\epsilon }}_{xx}^{{\prime\prime} }\), \({{\epsilon }}_{yy}^{{\prime\prime} }\), \({{\epsilon }}_{zz}^{{\prime\prime} }\) and the right-hand insets present off-diagonal spectra \({{\epsilon }}_{xy}^{{\prime\prime} }\), \({{\epsilon }}_{xz}^{{\prime\prime} }\), \({{\epsilon }}_{yz}^{{\prime\prime} }\). The arrows indicate modes that are analysed in the Extended Data Fig. 4. All dielectric properties are calculated for the PTO layer only.
Extended Data Fig. 4 Decomposition of selected modes with strain εx = −0.25% in the atomistic model.
The modes are characterized by the highest oscillator strengths in the x-direction (below the frequency of 0.41 THz, marked by the arrows in Extended Data Fig. 3b), and the first two of them are also described in the main text. a–d, Each column contains microscopic configurations at t = τ/4 of (a) Pb and Ti displacements; (b) O displacements of the mode’s eigenvectors; (c) change in polarization caused by these atomic displacements (overlaid on a \(\nabla \times {\bf{P}}\) map of the equilibrium structure); (d) polarization patterns and the respective \(\nabla \times {\bf{P}}\) map of a structure subjected to the mode’s perturbation. The origin O and vector R in a are related to the calculation of the angular momentum of the vortexon in the boxed region detailed in Supplementary Note 1B. The displacement vectors are scaled arbitrarily, while perturbed (P) configurations are calculated for maximum ionic displacements of 30 pm. We note that there are additional modes with the y-component of the oscillator strength that contribute to the diversity of the collective dynamics in the frequency range 0.3–0.4 THz.
Extended Data Fig. 5 Polarization dependent response and analysis of the vortexon mode.
a, Normalized change of diffraction intensity of 004 vortex Bragg peak as a function of time when the THz field is applied parallel to and perpendicular to the crystalline x-axis. b, Baseline-subtracted normalized change of diffraction intensity of the 004 vortex superlattice peak (red curve) as a function delay. Raw data shown in grey are from Fig. 4b. The green curve shows a sinusoidal wave (see Supplementary Note 5), with its minima (green arrows) deviating from the data (red arrows) at later times. The vertical dashed line indicates the time when the THz field turns on.
Extended Data Fig. 6 Dynamical phase-field simulation results.
a, b, Fourier transform of the simulated polarization dynamics, which is represented by spatially averaged (a) \({P}_{z}^{2}\) and (b) \({P}_{x}^{2}\) in the simulation box on application of the THz-field pulse aligned along the x-, y- or z-axis. c, Calculated frequency spectra of \({P}_{x}^{2}\) with various values of the direct-current (DC) electric field along the x-axis. d, Frequency and amplitude of the vortexon mode as a function of the applied electric field (Ex). Such an in-plane electric field can be applied using a pair of coplanar electrodes, as schematically shown in the inset to d. e, Histograms of the Pb and Sr ionic displacement u away from its equilibrium positions along the x- and z-axes, corresponding to the maximum diffraction intensity change of 4% of 004 SL peak at a delay of 9 ps in the simulation.
Extended Data Fig. 7 Equilibrium characterizations of (PbTiO3)16/(SrTiO3)16 superlattice.
a, Room-temperature RSM of the superlattice grown on DSO substrate, cutting through the substrate specular 004 peak, which shows vortex (V) and FE superlattice diffraction peaks in the qx–qz plane. The satellites (V Sat) due to the in-plane vortex ordering appear along the qx direction around the corresponding superlattice (V) peaks. b, The measured average lattice parameters with linear fits for the vortex and FE structures as a function of temperature. The error bars represent systematic errors of the measurement. c, Room-temperature RSM of the superlattice grown on Sr2Al0.3Ga0.7TaO6 (SAGT) substrate, cutting through the substrate specular 002 peak, which shows the vortex SL diffraction peaks and satellites. d, Room-temperature imaginary dielectric constant extracted from the THz time-domain absorption spectroscopy measurements of superlattices grown on DSO and SAGT substrates. The error bars represent the estimated experimental errors in the frequency ranges of the shaded and unshaded regimes.
Extended Data Fig. 8 X-ray diffraction simulations based on dynamical phase-field modelling.
a, Model geometry of the PTO/STO superlattice film and the DSO substrate. The colour scale denotes the vorticity of the polarization vectors. The boundary conditions (Methods) are marked on the right. b, Schematics for the method used to map the phase-field modelling output to atomistic configurations, based on which kinematic X-ray scattering intensities are calculated (Supplementary Note 2). CoM, center ofmass; V and C denote the vortex and cubic phases of PbTiO3, respectively. c, Measured and simulated H0L-cut (along the qx–qz plane in reciprocal lattice units (r.l.u)) RSMs near the 004 reflection with the intensity shown on a logarithmic colour scale. The fringes in the simulated RSM are due to the finite lateral size of the simulation box.
Extended Data Fig. 9 Structural dynamics excited by 400-nm optical pulses.
a, Normalized changes of 004-vortex peak intensity as a function delay. b, Fourier spectra of a. L and T represent the acoustic waves that travel along the out-of-plane direction with longitudinal and transverse sound speeds, respectively. c, Calculated phonon dispersion curves. The vertical dashed line indicates the boundary of the folded Brillouin zones. The shaded region corresponds to the scattering vectors probed in the experiment. The solid circles show the measured modes upon 400-nm excitation, while the stars show the measured modes upon THz excitation. The error bars show the full-width at half-maximum of the peaks in the Fourier spectra. dSL, superlattice periodicity.
Supplementary information
Supplementary Information
This file contains Supplementary text, Supplementary Notes 1 to 7, Supplementary Tables 1 – 3 and Supplementary References.
Rights and permissions
About this article
Cite this article
Li, Q., Stoica, V.A., Paściak, M. et al. Subterahertz collective dynamics of polar vortices. Nature 592, 376–380 (2021). https://doi.org/10.1038/s41586-021-03342-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-021-03342-4
This article is cited by
-
Giant electric field-induced second harmonic generation in polar skyrmions
Nature Communications (2024)
-
Photoexcitation-induced spin dynamics in 1T-VSe2 investigated by ab initio nonadiabatic molecular dynamics
Science China Materials (2024)
-
Terahertz radiation by quantum interference of excitons in a one-dimensional Mott insulator
Nature Communications (2023)
-
Absence of critical thickness for polar skyrmions with breaking the Kittel’s law
Nature Communications (2023)
-
Polar Solomon rings in ferroelectric nanocrystals
Nature Communications (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.