Abstract
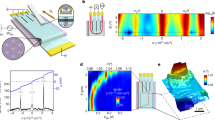
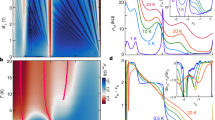
In the 1950s, Pomeranchuk1 predicted that, counterintuitively, liquid 3He may solidify on heating. This effect arises owing to high excess nuclear spin entropy in the solid phase, where the atoms are spatially localized. Here we find that an analogous effect occurs in magic-angle twisted bilayer graphene2,3,4,5,6. Using both local and global electronic entropy measurements, we show that near a filling of one electron per moiré unit cell, there is a marked increase in the electronic entropy to about 1kB per unit cell (kB is the Boltzmann constant). This large excess entropy is quenched by an in-plane magnetic field, pointing to its magnetic origin. A sharp drop in the compressibility as a function of the electron density, associated with a reset of the Fermi level back to the vicinity of the Dirac point, marks a clear boundary between two phases. We map this jump as a function of electron density, temperature and magnetic field. This reveals a phase diagram that is consistent with a Pomeranchuk-like temperature- and field-driven transition from a low-entropy electronic liquid to a high-entropy correlated state with nearly free magnetic moments. The correlated state features an unusual combination of seemingly contradictory properties, some associated with itinerant electrons—such as the absence of a thermodynamic gap, metallicity and a Dirac-like compressibility—and others associated with localized moments, such as a large entropy and its disappearance under a magnetic field. Moreover, the energy scales characterizing these two sets of properties are very different: whereas the compressibility jump has an onset at a temperature of about 30 kelvin, the bandwidth of magnetic excitations is about 3 kelvin or smaller. The hybrid nature of the present correlated state and the large separation of energy scales have implications for the thermodynamic and transport properties of the correlated states in twisted bilayer graphene.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The data in the main text are available at https://github.com/uzondi/MA_Pomeranchuk.
Code availability
The code used in this work is available at https://github.com/erezberg/pomeranchuk_tblg_theory.
References
Pomeranchuk, I. On the theory of He3. Zh. Eksp. Teor. Fiz 20, 919 (1950).
Bistritzer, R. & MacDonald, A. H. Moiré bands in twisted double-layer graphene. Proc. Natl Acad. Sci. USA 108, 12233–12237 (2011).
Cao, Y. et al. Correlated insulator behaviour at half-filling in magic-angle graphene superlattices. Nature 556, 80–84 (2018).
Cao, Y. et al. Unconventional superconductivity in magic-angle graphene superlattices. Nature 556, 43–50 (2018).
Li, G. et al. Observation of Van Hove singularities in twisted graphene layers. Nat. Phys. 6, 109–113 (2010).
Suárez Morell, E., Correa, J. D., Vargas, P., Pacheco, M. & Barticevic, Z. Flat bands in slightly twisted bilayer graphene: tight-binding calculations. Phys. Rev. B 82, 121407 (2010).
Regan, E. C. et al. Mott and generalized Wigner crystal states in WSe2/WS2 moiré superlattices. Nature 579, 359–363 (2020).
Tang, Y. et al. Simulation of Hubbard model physics in WSe2/WS2 moiré superlattices. Nature 579, 353–358 (2020).
Yankowitz, M. et al. Tuning superconductivity in twisted bilayer graphene. Science 363, 1059–1064 (2019).
Lu, X. et al. Superconductors, orbital magnets and correlated states in magic-angle bilayer graphene. Nature 574, 653–657 (2019).
Nuckolls, K. P. et al. Strongly correlated Chern insulators in magic-angle twisted bilayer graphene. Nature 588, 610–615 (2020).
Wu, S., Zhang, Z., Watanabe, K., Taniguchi, T. & Andrei, E. Y. Chern insulators and topological flat-bands in magic-angle twisted bilayer graphene. Preprint at https://arXiv.org/abs/2007.03735 (2020).
Das, I. et al. Symmetry broken Chern insulators and magic series of Rashba-like Landau level crossings in magic angle bilayer graphene. Preprint at https://arXiv.org/abs/2007.13390 (2020).
Sharpe, A. L. et al. Emergent ferromagnetism near three-quarters filling in twisted bilayer graphene. Science 365, 605–608 (2019).
Serlin, M. et al. Intrinsic quantized anomalous Hall effect in a moiré heterostructure. Science 367, 900–903 (2020).
Kerelsky, A. et al. Maximized electron interactions at the magic angle in twisted bilayer graphene. Nature 572, 95–100 (2019).
Xie, Y. et al. Spectroscopic signatures of many-body correlations in magic-angle twisted bilayer graphene. Nature 572, 101–105 (2019).
Jiang, Y. et al. Charge order and broken rotational symmetry in magic-angle twisted bilayer graphene. Nature 573, 91–95 (2019).
Choi, Y. et al. Electronic correlations in twisted bilayer graphene near the magic angle. Nat. Phys. 15, 1174–1180 (2019); correction 15, 1205 (2019).
Tomarken, S. L. et al. Electronic compressibility of magic-angle graphene superlattices. Phys. Rev. Lett. 123, 046601 (2019).
Zondiner, U. et al. Cascade of phase transitions and Dirac revivals in magic-angle graphene. Nature 582, 203–208 (2020).
Po, H. C., Zou, L., Vishwanath, A. & Senthil, T. Origin of Mott insulating behavior and superconductivity in twisted bilayer graphene. Phys. Rev. X 8, 031089 (2018).
Song, Z. et al. All magic angles in twisted bilayer graphene are topological. Phys. Rev. Lett. 123, 036401 (2019).
Ahn, J., Park, S. & Yang, B.-J. Failure of Nielsen-Ninomiya theorem and fragile topology in two-dimensional systems with space-time inversion symmetry: application to twisted bilayer graphene at magic angle. Phys. Rev. X 9, 021013 (2019).
Bultinck, N. et al. Ground state and hidden symmetry of magic-angle graphene at even integer filling. Phys. Rev. X 10, 031034 (2020).
Kumar, A., Xie, M. & MacDonald, A. H. Lattice collective modes from a continuum model of magic-angle twisted bilayer graphene. Preprint at https://arXiv.org/abs/2010.05946 (2020).
Wu, F. & Das Sarma, S. Collective excitations of quantum anomalous Hall ferromagnets in twisted bilayer graphene. Phys. Rev. Lett. 124, 046403 (2020).
Wong, D. et al. Cascade of electronic transitions in magic-angle twisted bilayer graphene. Nature 582, 198–202 (2020).
McWhan, D. B. et al. Electronic specific heat of metallic Ti-doped V2O3. Phys. Rev. Lett. 27, 941–943 (1971).
Spivak, B. & Kivelson, S. A. Phases intermediate between a two-dimensional electron liquid and Wigner crystal. Phys. Rev. B 70, 155114 (2004).
Continentino, M. A., Ferreira, A. S., Pagliuso, P. G., Rettori, C. & Sarrao, J. L. Solid state Pomeranchuk effect. Physica B 359–361, 744–746 (2005).
Pustogow, A. et al. Quantum spin liquids unveil the genuine Mott state. Nat. Mater. 17, 773–777 (2018).
Saito, Y. et al. Isospin Pomeranchuk effect in twisted bilayer graphene. Nature https://www.nature.com/articles/s41586-021-03409-2 (2021).
Kuntsevich, A. Y., Tupikov, Y. V., Pudalov, V. M. & Burmistrov, I. S. Strongly correlated two-dimensional plasma explored from entropy measurements. Nat. Commun. 6, 7298 (2015).
Hartman, N. et al. Direct entropy measurement in a mesoscopic quantum system. Nat. Phys. 14, 1083–1086 (2018).
Park, J. M., Cao, Y., Watanabe, K., Taniguchi, T. & Jarillo-Herrero, P. Flavour Hund’s coupling, correlated Chern gaps, and diffusivity in moiré flat bands. Preprint at https://arXiv.org/abs/2008.12296 (2020).
Chen, S. et al. Electrically tunable correlated and topological states in twisted monolayer-bilayer graphene. Nature Phys. 17, 374–380 (2021).
Spivak, B. & Kivelson, S. A. Transport in two dimensional electronic micro-emulsions. Ann. Phys. 321, 2071–2115 (2006).
Cao, Y. et al. Strange metal in magic-angle graphene with near Planckian dissipation. Phys. Rev. Lett. 124, 076801 (2020).
Polshyn, H. et al. Large linear-in-temperature resistivity in twisted bilayer graphene. Nat. Phys. 15, 1011–1016 (2019).
Uri, A. et al. Mapping the twist-angle disorder and Landau levels in magic-angle graphene. Nature 581, 47–52 (2020).
Acknowledgements
We thank E. Altman, E. Andrei, E. Khalaf, S. Kivelson, S. Das Sarma, G. Shavit, J. Sulpizio, S. Todadri, A. Uri, A. Vishwanath, M. Zaletel and E. Zeldov for suggestions. E.B. is grateful to A. Young for drawing his attention to the unusual physics near ν = ±1, sharing his unpublished data, and for a collaboration on related experimental and theoretical work, proposing that a similar effect to the one discussed here occurs near ν = −1, based on transport measurements. In this work, in contrast, we measured the entropy directly, and mapped the entire phase diagram near ν = ±1 using compressibility measurements. Work at Weizmann was supported by a Leona M. and Harry B. Helmsley Charitable Trust grant, ISF grants (numbers 712539 and 13335/16), a Deloro award, the Sagol Weizmann-MIT Bridge programme, the ERC-Cog (See-1D-Qmatter, grant number 647413), the ISF Research Grants in Quantum Technologies and Science Program (grant numbers 994/19 and 2074/19), the DFG (CRC/Transregio 183), the ERC-Cog (HQMAT, grant number 817799), EU Horizon 2020 (LEGOTOP 788715) and the Binational Science Foundation (NSF/BMR-BSF grant number 2018643). Work at MIT was primarily supported by the US Department of Energy (DOE), Office of Basic Energy Sciences (BES), Division of Materials Sciences and Engineering under award DE-SC0001819 (J.M.P.). Help with transport measurements and with data analysis was supported by the National Science Foundation (grant number DMR-1809802), and the STC Center for Integrated Quantum Materials (NSF grant number DMR-1231319) (Y.C.). P.J.-H. acknowledges support from the Gordon and Betty Moore Foundation’s EPiQS Initiative through grant GBMF9643 and partial support by the Fundación Ramón Areces. The development of new nanofabrication and characterization techniques enabling this work has been supported by the US DOE Office of Science, BES, under award DE-SC0019300. K.W. and T.T. acknowledge support from the Elemental Strategy Initiative conducted by the MEXT, Japan (grant number JPMXP0112101001), JSPS KAKENHI grant number JP20H00354, and the CREST (JPMJCR15F3), JST. This work made use of the Materials Research Science and Engineering Center Shared Experimental Facilities supported by the National Science Foundation (grant number DMR-0819762) and of Harvard’s Center for Nanoscale Systems, supported by the NSF (grant number ECS-0335765).
Author information
Authors and Affiliations
Contributions
A.R., J.M.P, U.Z., Y.C., P.J.-H. and S.I. designed the experiment. A.R. and U.Z. performed the scanning SET experiments, and J.M.P. and Y.C. performed the monolayer graphene sensing experiments. D.R.-L. and Y.C. fabricated the twisted bilayer graphene devices. A.R., J.M.P, U.Z., Y.C., P.J.-H. and S.I. analysed the data. E.B., Y.O. and A.S. developed the theoretical model. K.W. and T.T. supplied the hBN crystals. A.R., J.M.P, U.Z., Y.C., Y.O., A.S., E.B., P.J.-H. and S.I. wrote the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature thanks Emanuel Tutuc and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
This file contains Supplementary Sections 1-11, including Supplementary Figs 1-9 and Supplementary References.
Rights and permissions
About this article
Cite this article
Rozen, A., Park, J.M., Zondiner, U. et al. Entropic evidence for a Pomeranchuk effect in magic-angle graphene. Nature 592, 214–219 (2021). https://doi.org/10.1038/s41586-021-03319-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-021-03319-3
This article is cited by
-
Flat bands, strange metals and the Kondo effect
Nature Reviews Materials (2024)
-
Multiflavor Mott insulators in quantum materials and ultracold atoms
npj Quantum Materials (2024)
-
Spin skyrmion gaps as signatures of strong-coupling insulators in magic-angle twisted bilayer graphene
Nature Communications (2023)
-
Effect of Coulomb impurities on the electronic structure of magic angle twisted bilayer graphene
npj 2D Materials and Applications (2023)
-
Heavy quasiparticles and cascades without symmetry breaking in twisted bilayer graphene
Nature Communications (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.